The Genocchi polynomial has been increasingly used as a convenient tool to solve some fractional calculus problems, due to their nice properties. However, like some other members in the Appell polynomials, the nice properties are always limited to the interval defined in [0, 1]. In this paper, we extend the Genocchi polynomials to the general shifted Genocchi polynomials, , which are defined for interval [a, b]. New properties for this general shifted Genocchi polynomials will be introduced, including the determinant form. This general shifted Genocchi polynomials can overcome the conventional formula of finding the Genocchi coefficients of a function f(x) that involves f^{(n − 1)}(x) which may not be defined at x = 0, 1. Hence, we use the general shifted Genocchi polynomials to derive the operational matrix and hence to solve the Fredholm-type fractional integro-differential equations with arbitrary domain [a, b].

1. Introduction

The Genocchi polynomials, G_n(x), is one of the members of the Appell polynomials, A_n(x), satisfying the differential relation (dA_n (x))/dx = nA_n−1(x), n = 1, 2, 3, ⋯. Besides, many new results are obtained in the field of number theory and combinatory [1–4], the Genocchi polynomials are also applied successfully to solve some kind of fractional calculus problems, and its advantages were described in [5–9] mostly via its operational matrix. However, most of the results are applied over the interval [0, 1]. Furthermore, for function approximation by using the Genocchi polynomials, the conventional formula of finding the Genocchi coefficients of a function f(x) involves f^{(n − 1)}(x) which may not be defined at x = 0, 1. To overcome these drawbacks, we propose the general shifted Genocchi polynomials which are more suitable for larger interval [a, b], where a, b ≥ 0. Hence, in this paper, with the new general shifted Genocchi polynomials, we derive its operational matrix, and then, we solve the fractional integro-differential equation (FIDE) with arbitrary domain, i.e., not limited to interval [0, 1].

FIDE is an equation which contains a fractional derivative term

, where α denotes the fractional order derivative with ⌈α⌉ = n, i.e., (n − 1 < α ≤ n) and an integral kernel operator term

. This paper considers the arbitrary domain FIDE of the 2nd-kind nonhomogeneous Fredholm type of the following special class:

(1)

where f(x) is the unknown function to be solved, K(x, t) is the integral kernel,

is Caputo’s fractional derivative, and h(x) is the nonhomogeneous forced term.

On top of that, solving FIDE is always not an easy task, and reliable numerical methods are needed. Furthermore, for the Fredholm-type problems, the existing numerical methods are mostly applicable for interval [0, 1]. Some of the early published works which for FIDE in [0, 1] are including the collocation method via polynomial spline function [10], the fractional differential transform method [11], and the Taylor expansion method [12]. In this research direction, some researches focus on solving the special class of FIDE, which includes solving fractional partial integro-differential equations by the resolvent kernel method, the Laplace transform [13], and the Laguerre polynomial [14], solving fractional integro-differential equations via the fractional-order Euler polynomials [15] and the Jacobi wavelets [16], solving fourth-order time FIDE with a weakly singular kernel by compact finite difference scheme [17] and nonlinear time-fractional partial integro-differential equation by finite difference scheme [18], and solving nonlinear two-dimensional fractional integro-differential equations via hybrid function [19]. However, the FIDE with the arbitrary domain is relatively less concerned by researchers, and so far, the successful methods applied to this type of problem are limited to the Chebyshev wavelet method [20]. For more methods as well as theories of FIDE/FDE, we refer the readers to some well-known books such as [21, 22].

The rest of the paper is organized as follows: Section 2 is devoted to preliminary results including basic definition, properties and determinant form of the general shifted Genocchi polynomials, , function approximation by , and theorem for the analytical expression of the integral of the product of the two general shifted Genocchi polynomials . Section 3 is the main result of this paper, which includes the derivation of a new operational matrix associated with the general shifted Genocchi polynomials. Besides that, the procedure of approximating the integral kernel in terms of the general shifted Genocchi polynomials and analytical expression of the kernel matrix is also explained in this section. Sections 4 and 5 are devoted to the procedure used in this paper and some numerical examples. Section 6 is the conclusion of this paper.

2. Preliminary Results

Here, first, we recall the function approximation by the original Genocchi polynomials. For this purpose, we may approximate a continuous function f(x) in interval [0, 1] in terms of the Genocchi polynomials, G_n(x), as the basis [23, 24] as follows:

(2)

where G_n(x) are the Genocchi polynomials and the Genocchi coefficients are denoted by c_n. But normally, this process is done by using the truncated Genocchi series as follows:

(3)

where in matrix notation,

(4)

where

is the Genocchi coefficient matrix and

is the Genocchi basis matrix. The Genocchi coefficients, c_n, can be calculated as

(5)

2.1. General Shifted Genocchi Polynomials: Definitions and Basic Properties

Equation (5) fails to work for functions that are not (n − 1)-differentiable at the points x = 0 or x = 1. An example is given as follows where the coefficient, c₃, is undefined:

Let

, we obtain

(6)

To avoid this problem, we define the general shifted Genocchi polynomials by shifting G_n(x) from the interval [0, 1] to the interval [a, b], 0 ≤ a ≤ b, i.e., S_n(x) = G_n((x − a)/(b − a)), which results in the following definition:

Definition 1. The general shifted Genocchi polynomials of order n is defined over the interval [a, b] as

(7)

where

is the general shifted Genocchi number, and let

The generating function for the general shifted Genocchi polynomials can be expressed as

(8)

If we choose a = 2, b = 4, the first few terms of the general shifted Genocchi polynomials are

(9)

Figures 1 and 2 show the first few original Genocchi polynomials and the general shifted Genocchi polynomials.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The first few original Genocchi polynomials (in interval [0, 1]).

Some of the important properties inherited from the classical Genocchi polynomials are

(10)

(11)

(12)

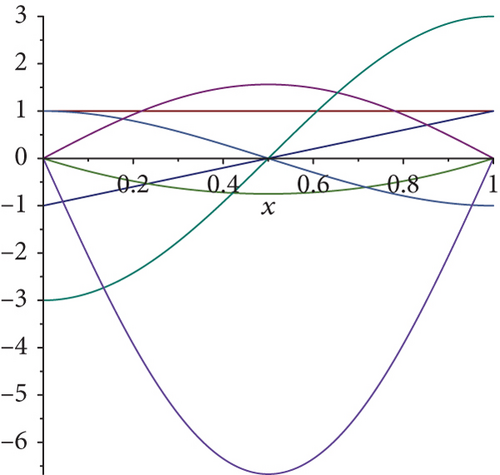
Theorem 2. Given an arbitrary integrable continuous function f(x) ∈ C^N−1(R), it can be approximated in terms of the general shifted Genocchi polynomials up to order N (i.e., polynomial degree = N − 1) by

(13)

Then, the general shifted Genocchi coefficient c_j is given by

(14)

Proof. Let . Using Equations (11) and (12), for 1 ≤ j

(15)

Rearrange the above equation, we obtain c_j = ((b − a)^j−1)/(2(j!))(f^{(j − 1)}(a) + f^{(j − 1)}(b)).

2.2. Determinant Form of the General Shifted Genocchi Polynomial Sequence

In this subsection, we will explain that this new general shifted Genocchi polynomial sequence can be also expressed in determinant form and recurrence relation, via modifying the work in [25, 26] for the shifted Genocchi polynomial sequence. For this process, we shift the order of the general shifted Genocchi polynomial sequence from n to n + 1; that is, we have , where denotes the general shifted Genocchi polynomial sequence.

Lemma 3. The determinant form of the general shifted Genocchi polynomial sequence, , which n > 0, is given by

(16)

and the recurrence relation of the general shifted Genocchi polynomial sequence,

, can be written as

(17)

In order to obtain values for s_i,j, we follow Costabile et al.’s method [25], which we summarize as follows:

Step 1. From , we obtain the general shifted Genocchi number, ; hence, we calculate the lower triangular Toeplitz matrix, T_S, with entries

(18)

Step 2. Calculate the upper triangular matrix S via

(19)

where D₁ = diag{(i + 1)! ∣i = 0, 1, ⋯} and D₂ = diag{1/i!|i = 0, 1, ⋯}. The values for s_i,j can be obtained using the entries of S.

To show the result of the determinant form of the general shifted Genocchi polynomial sequence, we present that

(a = 2, b = 5, n = 3) and

(a = 2, b = 5, n = 4) are given by

(20)

Hence, the determinant form of the above general shifted Genocchi polynomial sequence is as follows:

(21)

2.3. Integral of Product of the General Shifted Genocchi Polynomials

In this subsection, we derive the analytical expression for the integral of the product of the two general shifted Genocchi polynomials which will be used frequently in the later parts of the paper. This results in the following theorem:

Theorem 4. Given any two general shifted Genocchi polynomials , for 0 ≤ x

(22)

where n_(r) is the falling factorial and (m + 1)^{(r + 1)} is the rising factorial. For [a, b], 0 ≤ a ≤ b, we have

(23)

where

Proof. In order to prove this theorem, we need the following expression:

(24)

For

(25)

and hence, using integration by parts, we have

(26)

By using Equation (25), we obtain

(27)

These processes continue recursively for n times, and then, we will obtain

(28)

3. Main Result

3.1. General Shifted Genocchi Polynomial Operational Matrix of Fractional Derivative

In this section, we will derive the analytical expression of the general shifted Genocchi polynomial operational matrix of fractional derivative in the Caputo sense, which is the N × N matrix

, where

(29)

To derive the , we first prove the following Lemma 5.

Lemma 5. Caputo’s fractional derivative of fractional order α of a general shifted Genocchi polynomial, , of order i is given by

(30)

Proof. For n − 1 < α ≤ n, n = ⌈α⌉

(31)

Substitute t = xu,

(32)

where B(x, y) is the beta function which can be found using

for Re(x), Re(y) > 0.

Hence, we obtain the theorem for operational matrix as follows:

Theorem 6. Given a set of the N general shifted Genocchi polynomials, the general shifted Genocchi polynomial operational matrix of fractional derivative in the Caputo sense of order α over the interval [0, 1] is the N × N matrix , given by

(33)

where ρ_i,j is given by

(34)

Proof. Let . Then, using the function approximation as in Theorem 2 and Caputo’s fractional derivative for in Lemma 5, we have

(35)

As the formula given in Theorem 6 may fail to work for a = 0, we use the matrix approach to derive the as given in Theorem 8. To prove Theorem 8, we need the following lemma:

Lemma 7. The matrix Θ_N defined as is given by

(36)

where

(37)

Proof. From Caputo’s fractional derivative of the Genocchi polynomials [5, 23, 24], we have

(38)

Integrate both sides, and we obtain

(39)

Theorem 8. Given a set of the N general shifted Genocchi polynomials, the general shifted Genocchi polynomial operational matrix of Caputo’s fractional derivative of order α over the interval [a, b] is the N × N matrix , given by

(40)

where Θ_N is given in Lemma 7 and

with elements

is given in Theorem 4.

Proof. From Equation (29),

(41)

3.2. Approximation of Integral Kernel by the General Shifted Genocchi Polynomials

Here, we approximate the integral kernel K(x, t) in terms of the truncated series of the general shifted Genocchi polynomials

(42)

We present two approaches for obtaining the kernel matrix K_S.

3.2.1. Method 1: Conventional Genocchi Coefficient Formula

Using the conventional method of finding the Genocchi coefficients for a single variable function f(x), we can extend the formula to a two-variable function K(x, t) which is continuous and (N − 1) differentiable in interval [0, 1]. This results in the following theorem:

Theorem 9. Let K(x, t) be a two-variable continuous function in C^N−1([0, 1]). Then, K(x, t) can be approximated in terms of the general shifted Genocchi polynomials up to order N, i.e., , where S is the general shifted Genocchi polynomial basis matrix and K_S is the N × N integral kernel matrix in the general shifted Genocchi basis given by

(43)

where

(44)

Proof. Assume that the kernel K(x, t) is approximated using N number of the general shifted Genocchi polynomials, i.e.,

(45)

Set . Hence, . Using the formula of the general shifted Genocchi coefficients for (i.e., Theorem 2 with respect to t variable),

(46)

Now using the above expression of ϕ_j(x) together with the formula of the general shifted Genocchi coefficients for (i.e., with respect to x variable) instead, we obtain

(47)

In a similar way, the above approach can be extended to finding the general shifted Genocchi coefficients for the approximation of a multivariable function.

3.2.2. Method 2: Matrix Method

The classical way will not work for the kernel function not differentiable at x, t = 0, 1; then, we can adopt the matrix approach similar to that of finding the general shifted Genocchi coefficients in Theorem 2 to arrive at the following theorem:

Theorem 10. Let K(x, t) be a two-variable continuous function in C^N−1([a, b]). Then, K(x, t) can be approximated in terms of the general shifted Genocchi polynomials up to order N, i.e., , where S is the general shifted Genocchi polynomial basis matrix and K_S is the N × N integral kernel matrix in the general shifted Genocchi basis given by

(48)

where

(49)

Proof. From, K(x, t) ≈ S^T(x)K_SS(t),

(50)

where

. Define

. Thus,

(51)

4. Procedure of Solving Arbitrary Domain Fractional Integro-differential Equation

We will adopt the same approach as the other operational matrix methods for solving FIDE by approximating each term in the equation by the general shifted Genocchi polynomials. From the following class of the 2nd-kind Fredholm FIDE,

(52)

(53)

Now, we approximate each term in Equation (52) with the corresponding approximation using the N order of the general shifted Genocchi polynomials,

(54)

Hence, FIDE in Equation (52) in matrix form becomes:

(55)

where

. Then, we select the N equally spaced points within the interval [a, b], i.e., v_r = a + ((b − a)(r − 1))/(N − 1), r = 1, ⋯, N as the collocation points and substituting these into Equation (55), and we obtain a system of N + 1 algebraic equations in terms of the N general shifted Genocchi coefficients

. Choosing any N − 1 equations from the above system together with the initial conditions, f(x₀) = S^T(x)C = y₀, we can solve for the general shifted Genocchi coefficients

of the unknown function f(x). The approximate solution f^∗(x) = C^TS(x) will be compared to the exact solution f(x) over the interval [a, b].

5. Numerical Examples

Here are two examples of FIDE of Equation (1) which are solved using the proposed method via the general shifted Genocchi polynomials and its operational matrix. The computation was done via Maple software.

Example 1. Consider the following FIDE:

(56)

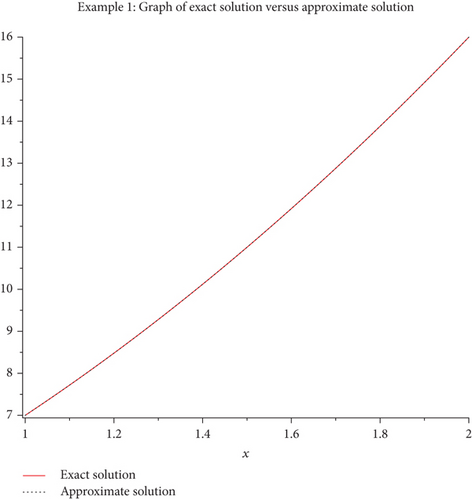
Let f(1) = 7, the exact solution is f(x) = 2x² + 3x + 2. Since [a, b] = [1, 2], we use the general shifted Genocchi polynomials over the interval [1, 2], i.e., to solve the problem. Let us choose N = 4 to approximate .

The proposed method gives the general shifted Genocchi coefficients as c₁ = 23/2, c₂ = 9/2, c₃ = 2/3, c₄ = 0, and therefore, the approximate solution produced is which reproduces the exact solution over the interval [1, 2]. Figure 3 shows both f(x) and f^∗(x) over the interval [1, 2]. The numerical results and absolute errors are shown in Table 1.

Table 1. Comparison of the approximate solution f^∗(x) using N = 4 with exact solution f(x) = 2x² + 3x + 2 and absolute errors for Example 1.

t	Exact sol. f(x)	Approx. sol. f^∗(x)
1.0	7.0000000000	7.0000000000
1.1	7.7200000000	7.7200000000
1.2	8.4800000000	8.4800000000
1.3	9.2800000000	9.2800000000
1.4	10.1200000000	10.1200000000
1.5	11.0000000000	11.0000000000
1.6	11.9200000000	11.9200000000
1.7	12.8800000000	12.8800000000
1.8	13.8800000000	13.8800000000
1.9	14.9200000000	14.9200000000
2.0	16.0000000000	16.0000000000

Example 2. Consider the following FIDE:

(57)

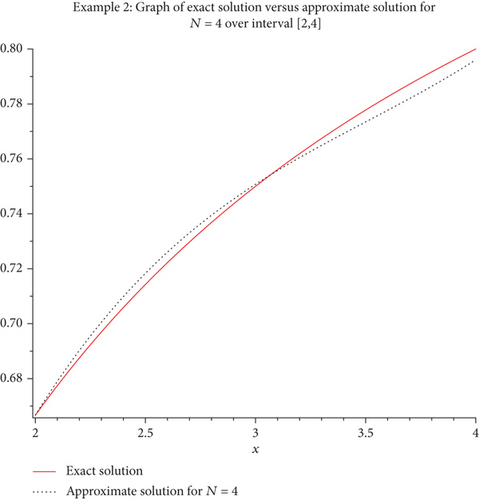
Let f(2) = 2/3, the exact solution is f(x) = x/(x + 1). Let us choose orders of N = 4 of the general shifted Genocchi polynomials over the interval [a, b] = [2, 4] to approximate f(x) and compare the graphs and absolute errors between the exact solution and approximate solutions of orders N = 4. Figure 4 shows both f(x) and f^∗(x) of orders N = 4 over the interval [2, 4]. The numerical results and absolute errors are shown in Table 2, which shows our method of high accuracy.

Table 2. Comparison of the approximate solution f^∗(x) using N = 4 with exact solution f(x) = x/(x + 1) and absolute errors for Example 2.

t	Exact sol. f(x)	Approx. sol. f^∗(x)	Abs. error \|f(x) − f^∗(x)\|
2.0	0.6666666667	0.6666666670	3.00000E − 10
2.1	0.6774193548	0.6790021440	1.58279E − 03
2.2	0.6875000000	0.6902602348	2.76023E − 03
2.3	0.6969696970	0.7005176063	3.54791E − 03
2.4	0.7058823529	0.7098509254	3.96857E − 03
2.5	0.7142857143	0.7183368566	4.05114E − 03
2.6	0.7222222222	0.7260520712	3.82985E − 03
2.7	0.7297297297	0.7330732332	3.34350E − 03
2.8	0.7368421053	0.7394770103	2.63490E − 03
2.9	0.7435897436	0.7453400700	1.75033E − 03
3.0	0.7500000000	0.7507390792	7.39079E − 04
3.1	0.7560975610	0.7557507047	3.46856E − 04
3.2	0.7619047619	0.7604516132	1.45315E − 03
3.3	0.7674418605	0.7649184721	2.52339E − 03
3.4	0.7727272727	0.7692279476	3.49933E − 03
3.5	0.7777777778	0.7734567083	4.32107E − 03
3.6	0.7826086957	0.7776814195	4.92728E − 03
3.7	0.7872340426	0.7819787491	5.25529E − 03
3.8	0.7916666667	0.7864253656	5.24130E − 03
3.9	0.7959183673	0.7910979325	4.82043E − 03
4.0	0.8000000000	0.7960731198	3.92688E − 03

6. Conclusion

In this paper, the 2nd-kind nonhomogeneous Fredholm FIDE is solved using the general shifted Genocchi polynomials . We introduce the general shifted Genocchi polynomials and derive the formula for computing the general shifted Genocchi coefficients. Some new properties for the general shifted Genocchi polynomials were introduced including the determinant form. Also, we derive the analytical expression of the integral of the product of the general shifted Genocchi polynomials, T_{(n, m)}; the integral kernel matrix, K_S; and the general shifted Genocchi polynomial operational matrix of Caputo’s fractional derivatives, . By approximating each term in the FIDE in terms of the general shifted Genocchi polynomials, the equation is transformed into a system of algebraic equations. With the use of the collocation method over the interval [a, b] and the initial condition given, the arbitrary domain Fredholm FIDE can be solved with very high accuracy with only few terms of the general shifted Genocchi polynomials. For future work, we hope we can extend this approach to other types of Appell polynomials, such as the Bernoulli polynomials which had been used widely such as in [27]. Apart from that, we hope we can use this general shifted Genocchi polynomial approach to solve other kinds of fractional calculus problems, such as those in [28, 29], or inverse fractional calculus problems [30, 31].

Conflicts of Interest

The authors declare that they have no conflict of interest.

Acknowledgments

This research was supported by Universiti Tun Hussein Onn Malaysia (UTHM) through Tier 1 (vot Q380).

Open Research

Data Availability

No data were used to support this study.

References

1 Kim T., San Kim D., Kwon J., and Kim H. Y., A note on degenerate Genocchi and poly-Genocchi numbers and polynomials, Journal of Inequalities and Applications. (2020) 2020, no. 1, https://doi.org/10.1186/s13660-020-02378-w.
10.1186/s13660-020-02378-w
Web of Science® Google Scholar
2 Lee D. S. and Kim H. K., On the new type of degenerate poly-Genocchi numbers and polynomials, Advances in Difference Equations. (2020) 2020, no. 1.
10.1186/s13662-020-02886-5
Web of Science® Google Scholar
3 Khan W. A. and Srivastava D., Certain properties of Apostol-type Hermite based Frobenius-Genocchi polynomials, Kragujevac Journal of Mathematics. (2021) 45, no. 6, 859–872, https://doi.org/10.46793/KgJMat2106.859K.
10.46793/KgJMat2106.859K
Web of Science® Google Scholar
4 Duran U., Acikgoz M., and Araci S., Construction of the type 2 poly-Frobenius-Genocchi polynomials with their certain applications, Advances in Difference Equations. (2020) 2020, no. 1.
10.1186/s13662-020-02889-2
Web of Science® Google Scholar
5 Phang C., Isah A., and Toh Y. T., Poly-Genocchi polynomials and its applications, AIMS Mathematics. (2021) 6, no. 8, 8221–8238, https://doi.org/10.3934/math.2021476.
10.3934/math.2021476
Web of Science® Google Scholar
6 Sadeghi Roshan S., Jafari H., and Baleanu D., Solving FDEs with Caputo-Fabrizio derivative by operational matrix based on Genocchi polynomials, Mathematical Methods in the Applied Sciences. (2018) 41, no. 18, 9134–9141, https://doi.org/10.1002/mma.5098, 2-s2.0-85057499448.
10.1002/mma.5098
Web of Science® Google Scholar
7 Dehestani H., Ordokhani Y., and Razzaghi M., The novel operational matrices based on 2D-Genocchi polynomials: solving a general class of variable-order fractional partial integro-differential equations, Computational and Applied Mathematics. (2020) 39, no. 4, 1–32, https://doi.org/10.1007/s40314-020-01314-4.
10.1007/s40314-020-01314-4
Web of Science® Google Scholar
8 Hashemizadeh E., Ebadi M. A., and Noeiaghdam S., Matrix method by Genocchi polynomials for solving nonlinear Volterra integral equations with weakly singular kernels, Symmetry. (2020) 12, no. 12, https://doi.org/10.3390/sym12122105.
10.3390/sym12122105
Web of Science® Google Scholar
9 Isah A. and Phang C., A collocation method based on Genocchi operational matrix for solving Emden-Fowler equations, Journal of Physics: Conference Series. (2020) 1489, article 012022.
Google Scholar
10 Rawashdeh E., Numerical solution of fractional integro-differential equations by collocation method, Applied Mathematics and Computation. (2006) 176, no. 1, 1–6, https://doi.org/10.1016/j.amc.2005.09.059, 2-s2.0-33646161468.
10.1016/j.amc.2005.09.059
Web of Science® Google Scholar
11 Arikoglu A. and Ozkol I., Solution of fractional integro-differential equations by using fractional differential transform method, Chaos, Solitons & Fractals. (2009) 40, no. 2, 521–529, https://doi.org/10.1016/j.chaos.2007.08.001, 2-s2.0-64949197043.
10.1016/j.chaos.2007.08.001
Web of Science® Google Scholar
12 Huang L., Li X.-F., Zhao Y., and Duan X.-Y., Approximate solution of fractional integro-differential equations by Taylor expansion method, Computers & Mathematics with Applications. (2011) 62, no. 3, 1127–1134, https://doi.org/10.1016/j.camwa.2011.03.037, 2-s2.0-79960997911.
10.1016/j.camwa.2011.03.037
Web of Science® Google Scholar
13 Loh J. R., Phang C., and Tay K. G., New method for solving fractional partial integro-differential equations by combination of Laplace transform and resolvent kernel method, Chinese Journal of Physics. (2020) 67, 666–680, https://doi.org/10.1016/j.cjph.2020.08.017.
10.1016/j.cjph.2020.08.017
Web of Science® Google Scholar
14 Daşcıoğlu A. and Varol D., Laguerre polynomial solutions of linear fractional integro-differential equations, Mathematical Sciences. (2021) 15, no. 1, 47–54, https://doi.org/10.1007/s40096-020-00369-y.
10.1007/s40096-020-00369-y
Web of Science® Google Scholar
15 Rezabeyk S., Abbasbandy S., and Shivanian E., Solving fractional-order delay integro-differential equations using operational matrix based on fractional-order Euler polynomials, Mathematical Sciences. (2020) 14, no. 2, 97–107, https://doi.org/10.1007/s40096-020-00320-1.
10.1007/s40096-020-00320-1
Web of Science® Google Scholar
16 Rong L. J. and Chang P., Jacobi wavelet operational matrix of fractional integration for solving fractional integro-differential equation, Journal of Physics: Conference Series. (2016) 693, https://doi.org/10.1088/1742-6596/693/1/012002, 2-s2.0-84964618111.
10.1088/1742-6596/693/1/012002
Google Scholar
17 Xu D., Qiu W., and Guo J., A compact finite difference scheme for the fourth-order time-fractional integro-differential equation with a weakly singular kernel, Numerical Methods for Partial Differential Equations. (2020) 36, no. 2, 439–458, https://doi.org/10.1002/num.22436.
10.1002/num.22436
Web of Science® Google Scholar
18 Guo J., Xu D., and Qiu W., A finite difference scheme for the nonlinear time-fractional partial integro- differential equation, Mathematical Methods in the Applied Sciences. (2020) 43, no. 6, 3392–3412, https://doi.org/10.1002/mma.6128.
10.1002/mma.6128
Web of Science® Google Scholar
19 Maleknejad K., Rashidinia J., and Eftekhari T., Operational matrices based on hybrid functions for solving general nonlinear two-dimensional fractional integro-differential equations, Computational and Applied Mathematics. (2020) 39, no. 2, 1–34, https://doi.org/10.1007/s40314-020-1126-8.
10.1007/s40314-020-1126-8
Web of Science® Google Scholar
20 Heydari M., Hooshmandasl M. R., Maalek Ghaini F. M., and Li M., Chebyshev wavelets method for solution of nonlinear fractional integro-differential equations in a large interval, Advances in Mathematical Physics. (2013) 2013, 12, 482083, https://doi.org/10.1155/2013/482083, 2-s2.0-84888870452.
10.1155/2013/482083
Web of Science® Google Scholar
21 Diethelm K., The Analysis of Fractional Differential Equations, 2010, 2004, Springer, Lecture Notes in Mathematics.
10.1007/978-3-642-14574-2
Web of Science® Google Scholar
22 Podlubny I., Fractional Differential Equations, Mathematics in Science and Engineering, 1999, Academic press New York.
Google Scholar
23 Dehestani H., Ordokhani Y., and Razzaghi M., On the applicability of Genocchi wavelet method for different kinds of fractional-order differential equations with delay, Numerical Linear Algebra with Applications. (2019) 26, no. 5, https://doi.org/10.1002/nla.2259, 2-s2.0-85068769617.
10.1002/nla.2259
Web of Science® Google Scholar
24 Loh J. R. and Phang C., A new numerical scheme for solving system of Volterra integro-differential equation, Alexandria Engineering Journal. (2018) 57, no. 2, 1117–1124, https://doi.org/10.1016/j.aej.2017.01.021, 2-s2.0-85011928537.
10.1016/j.aej.2017.01.021
Web of Science® Google Scholar
25 Costabile F. A., Gualtieri M. I., and Napoli A., Recurrence relations and determinant forms for general polynomial sequences. Application to Genocchi polynomials, Integral Transforms and Special Functions. (2019) 30, no. 2, 112–127, https://doi.org/10.1080/10652469.2018.1537272, 2-s2.0-85055480533.
10.1080/10652469.2018.1537272
Web of Science® Google Scholar
26 Costabile F. A., Polynomial sequences: elementary basic methods and application hints. A survey, Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas. (2019) 113, no. 4, 3829–3862, https://doi.org/10.1007/s13398-019-00682-9, 2-s2.0-85065418492.
10.1007/s13398-019-00682-9
Web of Science® Google Scholar
27 Phang C., Toh Y. T., and Md Nasrudin F. S., An operational matrix method based on poly-Bernoulli polynomials for solving fractional delay differential equations, Computation. (2020) 8, no. 3, https://doi.org/10.3390/computation8030082.
10.3390/computation8030082
PubMed Web of Science® Google Scholar
28 Faghih A. and Mokhtary P., A novel Petrov-Galerkin method for a class of linear systems of fractional differential equations, Applied Numerical Mathematics. (2021) 169, 396–414, https://doi.org/10.1016/j.apnum.2021.07.012.
10.1016/j.apnum.2021.07.012
Web of Science® Google Scholar
29 Faghih A. and Mokhtary P., Non-linear system of multi-order fractional differential equations: theoretical analysis and a robust fractional Galerkin implementation, Journal of Scientific Computing. (2022) 91, no. 2, https://doi.org/10.1007/s10915-022-01814-x, 35340701.
10.1007/s10915-022-01814-x
PubMed Web of Science® Google Scholar
30 Taghavi A., Babaei A., and Mohammadpour A., A stable numerical scheme for a time fractional inverse parabolic equation, Inverse Problems in Science and Engineering. (2017) 25, no. 10, 1474–1491, https://doi.org/10.1080/17415977.2016.1267169, 2-s2.0-85006952345.
10.1080/17415977.2016.1267169
Web of Science® Google Scholar
31 Babaei A. and Banihashemi S., A stable numerical approach to solve a timefractional inverse heat conduction problem, Iranian Journal of Science and Technology, Transactions A: Science. (2018) 42, no. 4, 2225–2236, https://doi.org/10.1007/s40995-017-0360-4, 2-s2.0-85052493249.
10.1007/s40995-017-0360-4
Web of Science® Google Scholar

All articles

Numerical Solution for Arbitrary Domain of Fractional Integro-differential Equation via the General Shifted Genocchi Polynomials

Abstract

1. Introduction

2. Preliminary Results

2.1. General Shifted Genocchi Polynomials: Definitions and Basic Properties

2.2. Determinant Form of the General Shifted Genocchi Polynomial Sequence

2.3. Integral of Product of the General Shifted Genocchi Polynomials

3. Main Result

3.1. General Shifted Genocchi Polynomial Operational Matrix of Fractional Derivative

3.2. Approximation of Integral Kernel by the General Shifted Genocchi Polynomials

3.2.1. Method 1: Conventional Genocchi Coefficient Formula

3.2.2. Method 2: Matrix Method

4. Procedure of Solving Arbitrary Domain Fractional Integro-differential Equation

5. Numerical Examples

6. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Numerical Solution for Arbitrary Domain of Fractional Integro-differential Equation via the General Shifted Genocchi Polynomials

Abstract

1. Introduction

2. Preliminary Results

2.1. General Shifted Genocchi Polynomials: Definitions and Basic Properties

2.2. Determinant Form of the General Shifted Genocchi Polynomial Sequence

2.3. Integral of Product of the General Shifted Genocchi Polynomials

3. Main Result

3.1. General Shifted Genocchi Polynomial Operational Matrix of Fractional Derivative

3.2. Approximation of Integral Kernel by the General Shifted Genocchi Polynomials

3.2.1. Method 1: Conventional Genocchi Coefficient Formula

3.2.2. Method 2: Matrix Method

4. Procedure of Solving Arbitrary Domain Fractional Integro-differential Equation

5. Numerical Examples

6. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information