This paper considers a multiple-input multiple-output (MIMO) multicasting system aided by the intelligent reflecting surface (IRS). We aim to maximize the sum information rate via jointly designing the transmit precoding matrix and the reflecting coefficient (RC) matrix, subject to the transmit power constrains of the Tx and IRS. To tackle the nonconvex problem, we recast the original problem into an equivalent formulation by using some important facts about matrices and proposed a block coordinate descent (BCD) method to optimize the variables. Finally, simulation results validate the effectiveness of active IRS in enhancing the rate performance.

1. Introduction

Recently, intelligent reflecting surface (IRS) has been proposed as an effective approach for wireless communication. An IRS is a metasurface consisting of several programmable elements that can be smartly controlled to manipulate wireless propagation environment [1]. Since passive IRS only reflects incident signals, the power consumption is relatively much smaller than that of traditional active transmitter [2]. For example, IRS-assisted scheme has been investigated in the millimeter-wave (mmWave) networks [3], the antijamming communication networks [4], the simultaneous wireless information and power transfer (SWIPT) networks [5], the unmanned aerial vehicle (UAV) networks [6], the hybrid satellite-terrestrial networks [7], etc. Besides, some novel IRS structures have been proposed, such as the multilayer IRS [8] and the simultaneous transmission and reflection intelligent surface [9]. More and more research suggests the promising application prospect of IRS. However, to overcome the severe double path loss in the reflecting channel, the literature recently introduced a novel active IRS architecture [10], in which each element is integrated with an amplifier [11]. By converting direct current bias power into radio frequency power, the active element can directly amplify the incident signal [12]. Recently, the energy efficiency of active IRS has been studied [13], and the results suggested that active IRS can obtain higher energy efficiency than passive IRS. Then, the literature investigated the active IRS-assisted secure transmission [14] and extends to the spectral and energy efficiency tradeoff of active IRS-assisted network [15]. While the literature indicates that active IRS can obtain higher energy efficiency than passive IRS in multiuser multiple-input single-output (MISO) network [16], recently, the authors studied the beamformer design in active IRS-assisted multiuser multiple-input multiple-output (MIMO) radio networks [17], where a sum mean squared error (MSE) objective was optimized. And the authors investigated the secrecy beamformer in active IRS-assisted wiretap channel with energy harvesting [18], where a max–min fairness problem was addressed by the successive convex approximation algorithm.

However, when considering other objective such as the sum information rate, how to use active IRS in MIMO network deserves more research. Motivated by the above observations, we investigate an active IRS-aided MIMO system, where a multiple-antenna transmitter (Tx) transmits the signal to several multiple-antenna users. Different from the commonly used passive IRS, active IRS is used to assist the signal transmission and to improve the system performance. The main contribution of the work is summarized as follows:

(i)
We consider a multiuser MIMO multicasting network, where both the direct link and the cascaded link are existing. Then, to overcome the main system bottleneck in the passive IRS-aided network incurred by the double fading effect, we propose to use active IRS to amplify and alter the phase of the incident signal, thus improving the spectral efficiency of this network
(ii)
Specifically, we aim to maximize the sum information rate of these users, by jointly designing the precoding matrix at the Tx and the reflecting coefficient (RC) at the IRS. The formulated problem is nonconvex, mainly due to the coupled variables and the complicated logarithmic determinant functions. To handle this obstacle, we reformulate the sum rate maximization problem as an equivalent problem by using some important facts about matrices, where the objective is linearized. Then, a block coordinate descent (BCD) algorithm is developed to handle the reformulated problem, where the subproblems are solved alternatingly until convergence. In fact, several subproblems have closed-form solutions, and the others can be solved by the quadratically constrained quadratic program (QCQP). Thus, the proposed algorithm has polynomial time computational complexity
(iii)
Finally, simulation results verify the effectiveness of the proposed algorithm as well as the superiority of active IRS when compared with other benchmarks. Besides, some meaningful insights can be attained: (1) active IRS can effectively alleviate the double fading attenuation than passive IRS; (2) it is beneficial to design the RC properly, since random RC suffers from certain performance loss; (3) it is better to deploy the active IRS close to the users than Tx to improve the sum rate performance

1.1. Notations

The conjugate, transpose, conjugate transpose, and trace of matrix A are denoted as A^†, A^T, A^H, and Tr(A), respectively. a = vec(A) denotes to stack the columns of matrix A into a vector a. A≽0 indicates that A is a positive semidefinite matrix. ⊙ and ⊗ denote the element-wise product and the Kronecker product, respectively. Diag(a₁, ⋯, a_M) represents a diagonal matrix with a₁, ⋯, a_M on the main diagonal. denotes the real part. denotes a circularly symmetric complex Gaussian random vector with mean 0 and covariance A.

2. System Model and Problem Formulation

2.1. System Model

As shown in Figure 1, the MIMO system consists of one Tx, one IRS, and K users. It is assumed that the Tx and the k-th user have N_t and N_k antennas, while the IRS has M elements, respectively. We denote , , and as the channel coefficient from the Tx to the k-th user, the Tx to the IRS, and the IRS to the k-th user, respectively.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

System model.

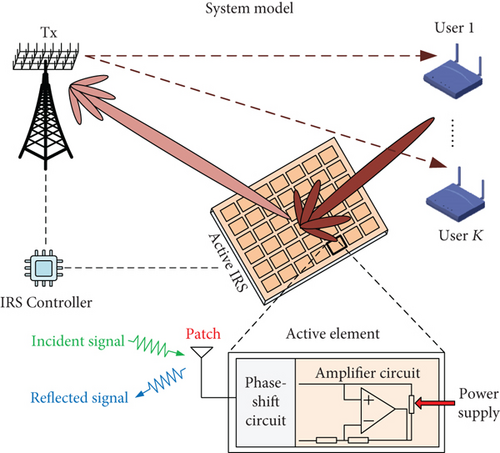
Since active IRS only utilizes power amplifiers and phase-shift circuits that control and reflect the signals, no dedicated digital-to-analog converters (DACs), analog-to-digital converters (ADCs), and mixers are required. In contrast, relays are usually equipped with these mentioned electronic components for transmission and low-noise amplifiers for reception, which leads to higher hardware cost and power consumption than active IRS [19].

In this paper, all CSI is assumed perfectly obtained at the Tx, which is due to the fact that several channel estimation techniques have been investigated for obtaining the CSI such as the progressive refinement method [20] and the parallel factor decomposition method [21], which makes the estimation and acquirement of the CSI become practical. In addition, there exists an IRS controller which coordinates the CSI exchange between the Tx and the IRS [22], thus achieving the joint design.

The intended signal s_k ∈ ℂ^d×1(d ≤ N_t) for the k-th user is precoded by the precoder

. Thus, the transmit signal x ∈ ℂ^d×1 can be expressed as

(1)

Without loss of generality (W.l.o.g), we assume that and s_k, s_i are independent for ∀i ≠ k.

Thus, the received signal at the k-th user is

(2)

where Θ = Diag(θ₁, ⋯, θ_M) ∈ ℂ^M×M denotes the RC matrix of the IRS, with

being the RC of the m-th element. Here, α_m ∈ [0, α_m,max] and ϕ_m ∈ [0, 2π) represent the amplitude and the phase, respectively. For an active IRS, α_m,max is not necessary 1. Here, we assume that α_m and ϕ_m are independent for any m. In fact, α_m and ϕ_m are coupled with each other for practical IRS. Thus, the authors have studied the function relationship between the α_m and ϕ_m for passive IRS [23–25]. However, the coupled relationship between α_m and ϕ_m for active IRS has not been studied yet. We will try to improve this in our future work.

In addition, and denote the additive noise at the IRS and the k-th user, respectively.

Accordingly, the information rate at the k-th user is [26]

(3)

where

is the equivalent channel from the Tx to the k-th user and

denotes the covariance matrix for the k-th user.

2.2. Problem Statement

We aim to maximize the sum rate among these users, via jointly designing the precoder and the RC, subject to the transmit power constraints. The problem is given as follows:

(4a)

(4b)

(4c)

(4d)

where P_s and P_r are the maximum achievable power for the Tx and IRS, respectively.

The main difficulties in solving ((4a)–(4d)) are twofold: firstly, (4a) is nonconvex; secondly, the variables are highly coupled.

3. The Joint Precoder and RC Design

To tackle the difficulty of (4a), we extend the key idea of the popular weighted mean square error minimization (WMMSE) algorithm [27], to reformulate ((4a)–(4d)), and then use the BCD method [28]. We first introduce the following lemmas.

Lemma 1 (see [28].)Define matrix function

(5)

where D is any positive definite matrix. Then, we have the following equations:

Equation 1: for any positive definite matrix P ∈ ℂ^m×m,

(6)

Equation 2: for any positive definite matrix Q, we have

(7)

Equation 3: we have

(8)

For more detailed derivation about these equations, reader can refer to [29, 30].

3.1. Reformulation of the Objective (4a)

By using the above equations, we rewrite R_k(W_k, Θ) as

(9)

where

(10)

Furthermore, the matrix functions Ξ_k(U_k, W_k, Q) are given as

(11)

Combining these relationships, we obtain the following problem:

(12a)

(12b)

(12c)

(12d)

((12a)–(12d)) is still hard to solve due to the coupled variables. However, when several variables are fixed, ((12a)–(12d)) can be turned into convex problem with respect to (w.r.t) the other variables, thus motivating us to propose the BCD algorithm.

3.2. The BCD Algorithm

Specifically, we decouple ((12a)–(12d)) into three subproblems and obtain the solutions alternatingly.

(A)
Subproblem 1: optimizing {U_k, Ψ_k} with given {W_k, Θ}

By the above lemmas, we obtain the following optimal {U_k, Ψ_k}:

(13a)

(13b)

(B)
Subproblem 2: optimizing W_k with given {Θ, U_k, Ψ_k}

Specifically, the subproblem is given as

(14a)

(14b)

(14c)

Then, by utilizing the identity Tr(P^HRST) = vec(P)^H(T^T ⊗ R)vec(S) and defining w_k = vec(W_k), ((14a)–(14c)) can be further recast as

(15a)

(15b)

(15c)

where

and

, respectively.

((15a)–(15c)) is a QCQP problem [31] and can be solved by the toolbox CVX [32].

Specifically, the subproblem is given as

(16a)

(16b)

(16c)

By denoting

, we have

(17)

Thus, ((16a)–(16c)) can be changed into

(18a)

(18b)

(18c)

Then, we turn ((18a)–(18c)) into an equivalent problem w.r.t . Firstly, we introduce the following lemma.

Lemma 2 (see [33].)Let C₁ ∈ ℂ^m×m and C₂ ∈ ℂ^m×m be matrices, and 1 = [1, ⋯,1]^T is a m × 1 vector. Assuming that E ∈ ℂ^m×m is a diagonal matrix E = diag(e₁, ⋯, e₂) and e = E1, then we have

(19)

where

Via Lemma 2, we have the following relationship:

(20)

where

Similarly, we have

(21)

where

and

, respectively.

Furthermore, the power constraint (4c) can be recast as

(22)

where

By combining these above steps, ((18a)–(18c)) can be turned into

(23a)

(23b)

(23c)

((23a)–(23c)) is also a QCQP problem, which can be solved by CVX.

3.3. Summarization and Discussion

The whole BCD algorithm is summarized in Algorithm 1.

Algorithm 1: The BCD algorithm.

1:Initialization: Set a feasible point {W_k, Θ} and i = 0.
2:repeat:
a) Obtain {U_k, Ψ_k} by using equation ((13a) and (13b)).
b) Obtain W_k by solving problem ((15a)–(15c)).
c) Obtain Θ by solving problem ((23a)–(23c)).
d) Update {U_k, Ψ_k, W_k, Θ}.
e) i⟵i + 1.
3:until Converge
4: Output .

Here, we analyze the computational complexity of Algorithm 1. In fact, the main complexities of Algorithm 1 lie in the subproblems ((15a)–(15c)) and ((23b)–(23c)). Besides, the complexity for solving a QCQP problem is given by , where m denotes the number of variables, n denoted the number of constraints, and ϵ is the solution accuracy [34]. Thus, the complexities of ((15a)–(15c)) and ((23b)–(23c)) are given by and , respectively.

Therefore, the total computational complexity of Algorithm 1 is given by

(24)

In addition, the convergence of Algorithm 1 has been analyzed [29]; thus, we omit the details for brevity.

4. Simulation Results

The deployment is given in Figure 2, where there exists one Tx, one IRS, and 3 users. The coordinates of Tx and IRS are (0m, 0m, 10m) and (10m, 50m, 10m), while the users are randomly located in a circle with radius 5m and centered at (0m, 60m, 1.5m), respectively [5].

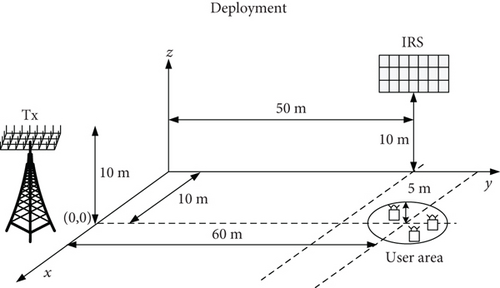
Unless specified, we set P_s = 30 dBm, P_r = 30 dBm, N_t = 8, M = 40 [15], N_k = 2, and [17]. The large-scale path is denoted as , with L₀ denoting the channel gain at d₀ = 1, and β is the path loss exponents. In addition, we assume that the Tx-user link follows the Rician fading with Rician factor 5 with β = −4, the Tx-IRS link follows the Rician fading with Rician factor 3 with β = −2.8 [16], and the IRS-user link follows the Rayleigh fading with β = −2.2 [16, 17]. In addition, all the results are obtained by 200 numbers of channel realizations.

We compare the design with the following methods: (1) the passive IRS scheme 32, (2) the no IRS scheme, and (3) the random IRS scheme, e.g., choosing Θ randomly. These methods are labeled as “proposed design,” “passive IRS,” “no IRS,” and “random IRS,” respectively.

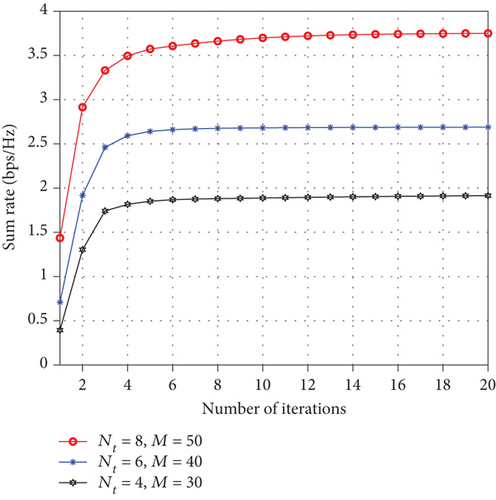
Firstly, we studied the convergence of the BCD method. Figure 3 shows R_s versus the number of iterations with different N_t and M. From this figure, we can see that for different N_t and M, R_s always increase with the iteration numbers and gradually converge within 20 iteration, which confirms the convergence of the BCD method.

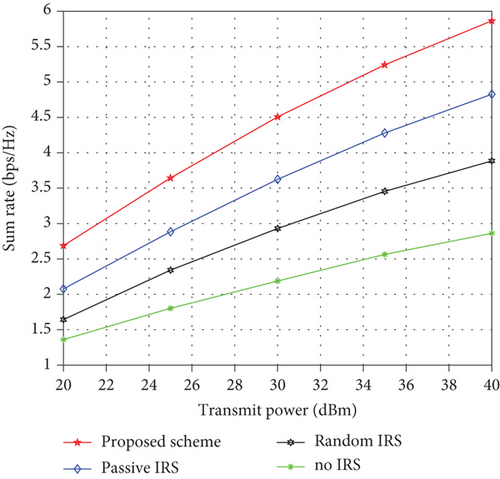
Then, we show the sum rate versus P_s. From Figure 4, we can see that for all these schemes, R_s increase with P_s, and all IRS-aided schemes obtain better performance than the no IRS-aided designs. Besides, the active IRS scheme significantly outperforms the passive IRS design, mainly owing to the power amplification effect which alleviates the impact of double fading attenuation. Thus, the received signal power at the users is enhanced and R_s is improved.

Next, in Figure 5, we show R_s versus M. From this figure, we can see that for all these IRS-aided methods, R_s tends to increase with the increase of M, since more signal can incident the IRS with larger M. In addition, the reflected signal at the IRS will increase with M when the RC is properly designed. However, when using random IRS, only array gain can be obtained, thus suffering from certain performance loss. This result further verifies that more R_s improvement can be achieved by using a larger IRS and optimizing the RC properly.

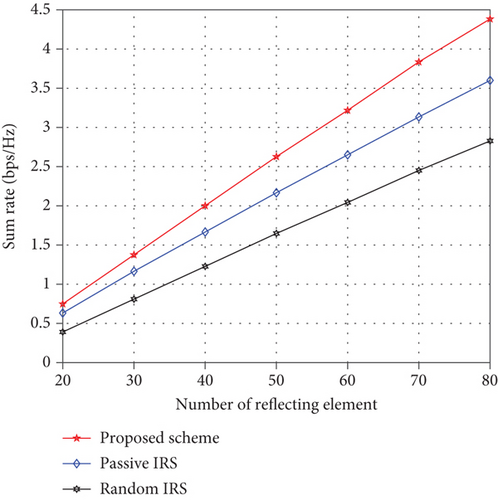
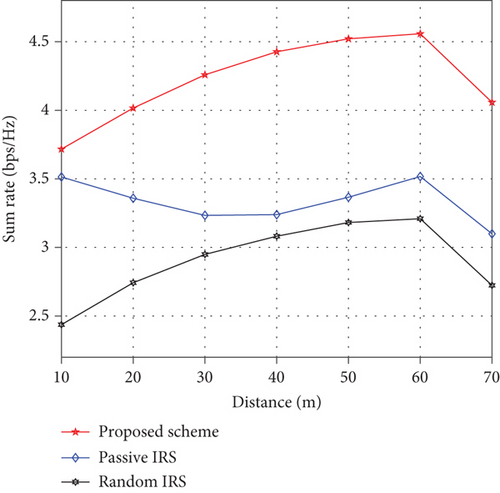
Last, Figure 6 plots R_s versus the Tx-IRS distances, where we assume that the IRS moves along the y-axis from the Tx to the user’s area. From this figure, we can see that the active IRS scheme always outperforms the passive IRS scheme in the considered region. Moreover, for active IRS, the R_s increases when IRS moves from the Tx to the user’s area, while for passive IRS, the R_s first decreases to a low point and then increases. Thus, deploying the active IRS near the users is beneficial to improve the R_s.

5. Conclusion

This work studied the active IRS-aided MIMO multicasting network, where the sum rate was maximized by jointly optimizing the precoder and RC, subject to the transmit power constraint at the Tx and IRS. We decouple the original problem into several subproblems and then proposed a BCD algorithm to optimize the variables. Simulation result verified the performance of the proposed design as well as the superiority of active IRS when compared with other benchmarks.

Conflicts of Interest

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Acknowledgments

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: this work was supported by the industry-university-research cooperation project of Jiangsu province under Grant No. BY2018282.

Open Research

Data Availability

Data are available on request.

References

1 Wu Q., Zhang S., Zheng B., You C., and Zhang R., Intelligent reflecting surface-aided wireless communications: a tutorial, IEEE Transactions on Communications. (2021) 69, no. 5, 3313–3351, https://doi.org/10.1109/TCOMM.2021.3051897.
10.1109/TCOMM.2021.3051897
Web of Science® Google Scholar
2 Liu Y., Liu X., Mu X., Hou T., Xu J., Renzo M. D., and Dhahir N. A., Reconfigurable intelligent surfaces: principles and opportunities, IEEE Communications Surveys & Tutorials. (2021) 23, no. 3, 1546–1577, https://doi.org/10.1109/COMST.2021.3077737.
10.1109/COMST.2021.3077737
Web of Science® Google Scholar
3 Gong S., Xing C., Yue P., Zhao L., and Quek T. Q. S., Hybrid analog and digital beamforming for RIS-assisted mmWave communications, IEEE Transactions on Wireless Communications. (2023) 22, no. 3, 1537–1554, https://doi.org/10.1109/TWC.2022.3205322.
10.1109/TWC.2022.3205322
Web of Science® Google Scholar
4 Sun Y., An K., Luo J., Zhu Y., Zheng G., and Chatzinotas S., Intelligent reflecting surface enhanced secure transmission against both jamming and eavesdropping attacks, IEEE Transactions on Vehicular Technology. (2021) 70, no. 10, 11017–11022, https://doi.org/10.1109/TVT.2021.3104580.
10.1109/TVT.2021.3104580
Web of Science® Google Scholar
5 Niu H., Chu Z., Zhou F., Zhu Z., Zhen L., and Wong K.-K., Robust design for intelligent reflecting surface-assisted secrecy SWIPT network, IEEE Transactions on Wireless Communications. (2022) 21, no. 6, 4133–4149, https://doi.org/10.1109/TWC.2021.3126833.
10.1109/TWC.2021.3126833
Google Scholar
6 Pang X., Zhao N., Tang J., Wu C., Niyato D., and Wong K.-K., IRS-assisted secure UAV transmission via joint trajectory and beamforming design, IEEE Transactions on Communications. (2022) 70, no. 2, 1140–1152, https://doi.org/10.1109/TCOMM.2021.3136563.
10.1109/TCOMM.2021.3136563
Web of Science® Google Scholar
7 Lin Z., Niu H., An K., Wang Y., Zheng G., Chatzinotas S., and Hu Y., Refracting RIS-aided hybrid satellite-terrestrial relay networks: joint beamforming design and optimization, IEEE Transactions on Aerospace and Electronic Systems. (2022) 58, no. 4, 3717–3724, https://doi.org/10.1109/TAES.2022.3155711.
10.1109/TAES.2022.3155711
Web of Science® Google Scholar
8 Sun Y., An K., Zhu Y., Zheng G., Wong K.-K., Chatzinotas S., Ng D. W. K., and Guan D., Energy-efficient hybrid beamforming for multilayer RIS-assisted secure integrated terrestrial-aerial networks, IEEE Transactions on Communications. (2022) 70, no. 6, 4189–4210, https://doi.org/10.1109/TCOMM.2022.3170632.
10.1109/TCOMM.2022.3170632
Web of Science® Google Scholar
9 Niu H., Chu Z., Zhou F., Xiao P., and Dhahir N. A., Weighted sum rate optimization for STAR-RIS-assisted MIMO system, IEEE Transactions on Vehicular Technology. (2022) 71, no. 2, 2122–2127.
10.1109/TVT.2021.3131568
Web of Science® Google Scholar
10 Long R., Liang Y. C., Pei Y., and Larsson E. G., Active reconfigurable intelligent surface-aided wireless communications, IEEE Transactions on Wireless Communications. (2021) 20, no. 8, 4962–4975, https://doi.org/10.1109/TWC.2021.3064024.
10.1109/TWC.2021.3064024
Web of Science® Google Scholar
11 You C. and Zhang R., Wireless communication aided by intelligent reflecting surface: active or passive?, IEEE Wireless Communications Letters. (2021) 10, no. 12, 2659–2663, https://doi.org/10.1109/LWC.2021.3111044.
10.1109/LWC.2021.3111044
Web of Science® Google Scholar
12 Zhi K., Pan C., Ren H., Chai K. K., and Elkashlan M., Active RIS versus passive RIS: which is superior with the same power budget?, IEEE Communications Letters. (2022) 26, no. 5, 1150–1154, https://doi.org/10.1109/LCOMM.2022.3159525.
10.1109/LCOMM.2022.3159525
Web of Science® Google Scholar
13 Liu K., Zhang Z., Dai L., Xu S., and Yang F., Active reconfigurable intelligent surface: fully-connected or sub-connected?, IEEE Communications Letters. (2022) 26, no. 1, 167–171, https://doi.org/10.1109/LCOMM.2021.3119696.
10.1109/LCOMM.2021.3119696
Web of Science® Google Scholar
14 Niu H., Lin Z., An K., Liang X., Hu Y., Li D., and Zheng G., Active RIS-assisted secure transmission for cognitive satellite terrestrial networks, IEEE Transactions on Vehicular Technology. (2023) 72, no. 2, 2609–2614, https://doi.org/10.1109/TVT.2022.3208268.
10.1109/TVT.2022.3208268
Web of Science® Google Scholar
15 Niu H., Lin Z., An K., Wang J., Zheng G., Dhahir N. A., and Wong K. K., Active RIS assisted rate-splitting multiple access network: spectral and energy efficiency tradeoff, IEEE Journal on Selected Areas in Communications. (2023) 41, no. 5, 1452–1467, https://doi.org/10.1109/JSAC.2023.3240718.
10.1109/JSAC.2023.3240718
Web of Science® Google Scholar
16 Ma Y., Li M., Liu Y., Wu Q., and Liu Q., Active reconfigurable intelligent surface for energy efficiency in MU-MISO systems, IEEE Transactions on Vehicular Technology. (2023) 72, no. 3, 4103–4107, https://doi.org/10.1109/TVT.2022.3221720.
10.1109/TVT.2022.3221720
Web of Science® Google Scholar
17 Allu R., Taghizadeh O., Singh S. K., Singh K., and Li C.-P., Robust beamformer design in active RIS-assisted multiuser MIMO cognitive radio networks, IEEE Transactions on Cognitive Communications and Networking. (2023) 9, no. 2, 398–413, https://doi.org/10.1109/TCCN.2023.3235788.
10.1109/TCCN.2023.3235788
Web of Science® Google Scholar
18 Li P. and Bian J., Active RIS-assisted transmission design for wireless secrecy network with energy harvesting, Mathematical Problems in Engineering. (2023) 2023, 9, https://doi.org/10.1155/2023/8897781, 8897781.
10.1155/2023/8897781
Google Scholar
19 Basar E. and Poor H. V., Present and future of reconfigurable intelligent surface-empowered communications [perspectives], IEEE Signal Processing Magazine. (2021) 38, no. 6, 146–152, https://doi.org/10.1109/MSP.2021.3106230.
10.1109/MSP.2021.3106230
Web of Science® Google Scholar
20 You C., Zheng B., and Zhang R., Channel estimation and passive beamforming for intelligent reflecting surface: discrete phase shift and progressive refinement, IEEE Journal on Selected Areas in Communications. (2020) 38, no. 11, 2604–2620, https://doi.org/10.1109/JSAC.2020.3007056.
10.1109/JSAC.2020.3007056
Web of Science® Google Scholar
21 Wei L., Huang C., Alexandropoulos G. C., Yuen C., Zhang Z., and Debbah M., Channel estimation for RIS-empowered multi-user MISO wireless communications, IEEE Transactions on Communications. (2021) 69, no. 6, 4144–4157, https://doi.org/10.1109/TCOMM.2021.3063236.
10.1109/TCOMM.2021.3063236
Web of Science® Google Scholar
22 Wang Z., Liu L., and Cui S., Channel estimation for intelligent reflecting surface assisted multiuser communications: framework, algorithms, and analysis, IEEE Transactions on Wireless Communications. (2020) 19, no. 10, 6607–6620, https://doi.org/10.1109/TWC.2020.3004330.
10.1109/TWC.2020.3004330
Web of Science® Google Scholar
23 Abeywickrama S., Zhang R., Wu Q., and Yuen C., Intelligent reflecting surface: practical phase shift model and beamforming optimization, IEEE Transactions on Communications. (2020) 68, no. 9, 5849–5863, https://doi.org/10.1109/TCOMM.2020.3001125.
10.1109/TCOMM.2020.3001125
Web of Science® Google Scholar
24 Li H., Cai W., Liu Y., Li M., Liu Q., and Wu Q., Intelligent reflecting surface enhanced wideband MIMO-OFDM communications: from practical model to reflection optimization, IEEE Transactions on Communications. (2021) 69, no. 7, 4807–4820, https://doi.org/10.1109/TCOMM.2021.3069860.
10.1109/TCOMM.2021.3069860
Web of Science® Google Scholar
25 Cai W., Liu R., Li M., Liu Y., Wu Q., and Liu Q., IRS-assisted multicell multiband systems: practical reflection model and joint beamforming design, IEEE Transactions on Communications. (2022) 70, no. 6, 3897–3911, https://doi.org/10.1109/TCOMM.2022.3168645.
10.1109/TCOMM.2022.3168645
Web of Science® Google Scholar
26 Niu H. and Ni L., Intelligent reflect surface aided secure transmission in MIMO channel with SWIPT, IEEE Access. (2020) 8, 192132–192140, https://doi.org/10.1109/access.2020.3032759.
10.1109/ACCESS.2020.3032759
Web of Science® Google Scholar
27 Shi Q., Razaviyayn M., Luo Z.-Q., and He C., An iteratively weighted MMSE approach to distributed sum-utility maximization for a MIMO interfering broadcast channel, IEEE Transactions on Signal Processing. (2011) 59, no. 9, 4331–4340, https://doi.org/10.1109/TSP.2011.2147784, 2-s2.0-80051739128.
10.1109/TSP.2011.2147784
Web of Science® Google Scholar
28 Bertsekas D., Nonlinear Programming, 1999, 2nd edition, Athena Scientific, Belmont, MA, USA.
Google Scholar
29 Shi Q., Xu W., Wu J., Song E., and Wang Y., Secure beamforming for MIMO broadcasting with wireless information and power transfer, IEEE Transactions on Wireless Communications. (2015) 14, no. 5, 2841–2853, https://doi.org/10.1109/TWC.2015.2395414, 2-s2.0-84929378752.
10.1109/TWC.2015.2395414
Web of Science® Google Scholar
30 Christensen S., Agarwal R., Carvalho E., and Cioffi J., Weighted sum-rate maximization using weighted MMSE for MIMO-BC beamforming design, IEEE Transactions on Wireless Communications. (2008) 7, no. 12, 4792–4799, https://doi.org/10.1109/T-WC.2008.070851, 2-s2.0-58149123337.
10.1109/T-WC.2008.070851
Web of Science® Google Scholar
31 Boyd S. and Vandenberghe L., Convex Optimization, 2013, Cambridge Univ. Press, Cambridge, U.K..
Google Scholar
32 Grant M. and Boyd S., CVX: Matlab software for disciplined convex programming, version 2.0 beta, September 2012, http://cvxr.com/cvx.
Google Scholar
33 Pan C., Ren H., Wang K., Xu W., Elkashlan M., Nallanathan A., and Hanzo L., Multicell MIMO communications relying on intelligent reflecting surfaces, IEEE Transactions on Wireless Communications. (2020) 19, no. 8, 5218–5233, https://doi.org/10.1109/TWC.2020.2990766.
10.1109/TWC.2020.2990766
Web of Science® Google Scholar
34 Nesterov Y. and Nemirovskii A., Interior-Point Polynomial Algorithms in Convex Programming, 2004, SIAM.
Google Scholar

All articles

Sum Rate Optimization for MIMO Multicasting Network with Active IRS

Abstract