The problem of the distributed cooperative guidance law of multiple missiles attacking a stationary target with impact angle constraint is investigated. A distributed cooperative guidance law, which consists of a nonsingular terminal sliding mode component for ensuring finite time convergence to the desired LOS angle and a coordination component for realizing finite time consensus of time-to-go estimates, is proposed. Analysis shows that the guidance law designed in this study can ensure that missiles’ time-to-go estimates represent real times to go once all the missiles fly along the desired LOS. Therefore, simultaneous arrival can be guaranteed. Furthermore, it is modified to accommodate the communication failure cases. Compared with existing results, this guidance law owns faster convergence rate and can satisfy large impact angles. Numerical simulations are performed to demonstrate the effectiveness of the proposed guidance law.

1. Introduction

Modern battleships are usually mounted with formidable antimissile defensive systems, such as close-in weapon systems that have powerful fire capability. These defensive weapons seriously intimidate the survivability of the conventional antiship missiles. Hence, advanced missile guidance technique is becoming important issue such as the impact angle control guidance (IACG) and cooperative guidance, which aims at, in a specific case, making multiple missiles arrive at a single target simultaneously to saturate the target’s defence [1–5].

Up to now, there are two ways to achieve simultaneous attack of a group of missiles, i.e., the “open loop” and the “closed loop”. The first one usually refers to the impact time control guidance (ITCG), in which a fixed impact time is assigned to each missile, and each member tries to attack the target at the prespecified impact time independently. Some studies based on such method include [1, 6–8]. In [1], a sliding mode control-based guidance law for the impact time control is proposed. Firstly, a switching surface is defined by considering the impact time constraint; then, the guidance law is designed to drive the switching surface to the sliding mode for fulfiling the impact time requirement. In [6], an optimal-theory-based guidance law is presented, in which the acceleration commands are composed of two different commands: the first one serves to reduce the miss-distance, and the second one serves to adjust the impact time. In [7], a novel guidance law is proposed for salvo attack which can satisfy the constraints of both impact time and terminal impact angle. The control of impact time and angle is achieved by making the states of the missile reach a sliding surface within finite time and then stay on it. On the sliding surface, the impact time and angle constraints will be satisfied, which can be verified through analyzing the system dynamic in state space. In [8], an impact time control guidance law is also designed based on sliding mode control. The interception and the desired impact time can be achieved at the same time in the sliding mode. The first approach requires a reasonable common impact time that must be preprogrammed manually before homing. However, choosing a proper common impact time is not an easy task because it is associated with the missiles’ flight conditions in the future, which are usually varying and unknown.

The second one usually refers to consensus-based cooperative guidance, in which the missiles communicate among themselves through online data links to synchronize the arrival times. Despite a number of papers, considering IACG have been published [9–12], papers related to cooperative guidance law for salvo attack are still rare. In [2], a guidance law named cooperative proportional navigation (CPN) is proposed for many-to-one engagements. The structure of the CPN is the same to that of conventional proportional navigation. The difference is that it has a time-varying navigation gain which is adjusted based on the local time-to-go and the time-to-go of all the other missiles. In [13], a modified cooperative guidance law is proposed to address the singularity problems existing in the work of [2]. In [14], optimal and cooperative control methods are used to design the guidance law, in which the missiles need only to communicate with some of the neighboring missiles. In [15], a cooperative guidance law for two pursuers against one evader is derived, which is also based on optimal theory. The approaches in [2, 13–15] can only guarantee the consensus of arrival time but cannot control the impact angles. Besides, the approaches in [2, 13] require that the global information of the time-to-go is available to each missile of the group. In [16], a distributed cooperative guidance law is designed for cooperative simultaneous attack against a stationary target. Similar to [2], a PN structure with time-varying navigation gain is also used to derive the guidance law. However, the design does not take impact angle into consideration. In [17], the derived guidance law consists of two terms: a local term that takes charge of the target capture and the desired impact angle, and a coordinate term to achieve the consensus of impact time. In [18], the distributed optimal tracking control problem for nonlinear multiagent systems is investigated, and the derived method is applied to the cooperative guidance problem. The guidance law design does not take the simultaneous arrival as its control object; instead, it only focuses on the consensus of the impact angle of all the missiles.

Besides, there are some sliding mode control- (SMC-) based cooperative guidance laws [19, 20]. In [19], a distributed cooperative guidance law is presented to make multiple missiles attack the same target simultaneously at the prespecified angles. The guidance process under this guidance law can be divided into two stages: in the first stage, the normal acceleration which is designed based on SMC makes all missiles fly along the desired line of sight (LOS) after a given time; then, the designed tangential acceleration will make the consensus variables reach agreement. In [20], a three-dimensional guidance law is proposed based on the method in [19]. For the approaches in [19, 20], the given time for the first stage needs to be chosen as a large constant to reduce the control input; contradictorily, too large given time will prevent the missiles from arriving at the target simultaneously because the second stage needs enough time to ensure that the consensus variables converge to zero. Besides, the desired impact angles also need to be selected carefully.

In this paper, a distributed cooperative strategy for multiple missiles with impact angle constraint is proposed. The guidance law consists of two components: a nonsingular terminal sliding mode component for ensuring finite time convergence to the desired LOS angles and a coordination component for realizing finite time consensus of the time-to-go estimates of all the missiles. The proposed strategy can ensure that missiles’ time-to-go estimates represent the real time-to-go once all the missiles fly along the desired LOS. Furthermore, the guidance law is modified to accommodate the communication failure cases.

The proposed cooperative guidance scheme can provide several advantages over the published works in the following aspects.

(1)
Compared with the guidance laws in [2, 13], which rely on a centralized communication topology, the method presented in this paper only employs neighbour-to-neighbour communication, and thereby, it is fully distributed. Since the centralized communication topology is difficult to be maintained in realistic situation, the proposed method is more practical
(2)
Unlike the guidance laws presented in [2, 13–15, 21–23], which only investigate the simultaneous arrival problem of multiple missiles, this study provides a strategy that can guarantee that all group members arrive at the target at the same time by imposing the preassigned impact angles. As a result, the mission effectiveness can be greatly increased [24].
(3)
Compared with the guidance laws in [2, 17], which only focus on the convergence of LOS angle errors or the consensus of time-to-go estimates, the method proposed in this paper can achieve finite time convergence of both LOS angle and consensus errors. As we know, the systems with finite-time convergence property usually possess some nice properties, such as better robustness against uncertainties and higher convergence precision

The organization of the paper is as follows. The problem formulation and some preliminaries are provided in Section 2. In Section 3, the distributed guidance law for simultaneous attack of multiple missiles is constructed based on finite control technique. Furthermore, the guidance law is modified to adapt to communication failure cases in Section 4. The simulation results are given in Section 5. Finally, concluding remarks are summarized in Section 6.

2. Problem Formulation and Preliminaries

In this section, we give the problem formulation and some preliminaries.

2.1. Problem Formulation

Consider the scenario where a group of m missiles cooperatively attack a stationary target T as shown in Figure 1. The letter M represents the missile, and the numbers i, i = 1, 2, ⋯, m denote the ith missile. V denotes the velocity of missile. a_m and a_t denote the normal acceleration and the tangential acceleration, respectively. r is the relative range along the LOS, and λ is the angle between the LOS and the horizontal reference line. γ and θ represent the flight path angle and the heading angle of the missile. The kinematics equations for the ith missile attacking a single stationary target can be described by

(1)

(2)

(3)

(4)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Guidance geometry on m to 1 engagement scenario.

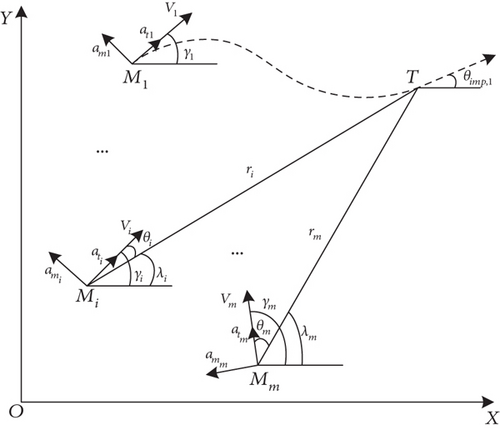
where θ_i = γ_i − λ_i and d_i stands for the lumped disturbance, which satisfies |d_i| ≤ D_i with D_i denoting an unknown positive constant. It should be noted that the condition |θ_i| < π/2 is necessary for the extremization problem to make sense [24]; as implied by (1), the impact can be indefinitely delayed, if this condition does not hold.

Remark 1. Similar to the work in [2], the target is modeled as being stationary, since the maneuverability and the speed of the surface ship are not comparable with those of antiship missiles of high-subsonic or supersonic speed.

As shown in Figure 1, the impact angle, denoted by θ_imp,i, is defined as the flight path angle at the final engagement and is given by

(5)

When the ith missile hits the target with zero miss-distance, from (2) and (5), we can obtain

(6)

which is equal to

(7)

For the ith missile, (7) denotes the relationship between the impact angle θ_imp,i and the final LOS angle λ_F,i.

2.2. Preliminary

2.2.1. Graph Theory

Let be used to describe the communication topology among missiles, where is a set of the node set denoting the index of missiles, is the set of edges, and a weighted adjacency matrix . If there exists information exchange between missiles i and j, i.e., , then a_ij = a_ji = 1, and zero otherwise. We assume that a_ii = 0 for all . The Laplacian matrix is defined as and l_ij = −a_ij for i ≠ j.

The following lemmas are needed in the subsequent technical derivations.

Lemma 2 (see [25].)Zero is an eigenvalue of , with 1 as a right eigenvector, and all nonzero eigenvalues are positive, where 1 represents a column vector whose entries are all equal to one.

Lemma 3 (see [26].)The Laplacian matrix of a connected undirected graph has the following properties: for any satisfying 1^Tx = 0, the inequation holds, where denotes the smallest nonzero eigenvalue of .

Suppose that the communication topology

among the m missiles is undirected and connected, then, the problem considered in this paper can be depicted as follows: to design the missiles’ normal accelerations and tangential accelerations a_m,i, a_t,i, i = 1, ⋯, m, such that for some unspecified final time of engagement t_f,

(8)

3. Main Results

In this section, the special structure of the proposed guidance law which contains two components is presented first; then, the component concerning the impact angle control is derived based on nonsingular terminal sliding mode, and the sufficient condition for stability is given. Lastly, the other component concerning the consensus of time-to-go estimates will be designed based on the finite-time control technique and the consensus protocols.

3.1. The Structure of the Proposed Guidance Law

As mentioned in Section 2, the objective of the guidance law design consists of two parts: the first one is achieving zero impact angle error, and the other one is achieving the consensus of time-to-go estimates. Naturally, we may consider the control form to embrace two components. On the one hand, from (2), (3), and (4), we can see that the normal acceleration has a direct effect on the LOS angle. On the other hand, if we have a look at the coarse time-to-go equation

, with (3), we can say that the tangential acceleration has greatly influence on the time to go. Therefore, we divide normal acceleration a_m,i into two parts:

(9)

where the term a_1,i is used to control the impact angle and the term a_2,i together with the tangential acceleration a_t,i is used to guarantee the consensus of time-to-go estimates.

3.2. Design of the Impact Angle Control Term a_1,i

From (2), the relative degree of two dynamics between the control term a_1,i and the LOS angle λ_i, given by

(10)

is used to design a_1,i to ensure that the λ_i = λ_F,i condition is met at collision. As proved in [27], the |θ_i| = (π/2) is not a stable equilibrium for any r_i ≠ 0 and, as a result, the component of normal acceleration a_1,i can be used to control λ_i.

Inspired by [9], the term a_1,i is designed using the principles on nonsingular terminal sliding mode control (NTSMC). The sliding surface is selected as

(11)

where β_i > 0, α_i = p_i/q_i, and p_i, q_i are all odd integers satisfying p_i > q_i. Then, the term a_1,i that will ensure the existence of sliding mode can be designed as the sum of an equivalent and a discontinuous controller:

(12)

where

(13)

(14)

where M_i is the positive constant, and it is chosen to satisfy M_i > max{|a_2,i|}.

Theorem 4. For the ith missile subjected to the kinematics (1), (2), (3), and (4), if the sliding surface is selected as (11), the control term a_1,i is designed as (12), (13), and (14), and control parameters are chosen to satisfy M_i > max{a_2,i}, β > 0; p_i and q_i are two odd integers guaranteeing p_i > q_i; then, will converge to λ_F,i and 0 in finite time, respectively.

Proof. Consider a Lyapunov function candidate as on differentiating V_L1, and substituting (10), (12), (13), and (14) and simplifying, we obtain

(15)

Recall that the point |θ_i| = (π/2) is not a stable equilibrium, so we assume that for most time during the engagement, cosθ_i has a nonzero value. Let

(16)

Then, (15) becomes

(17)

where ζ > 0 with M_i > max{|a_2,i|} for . Therefore, is the negative definite, and hence, the condition for Lyapunov stability is satisfied for all , and, consequently, the sliding mode occurs within finite time. During the sliding mode s_i = 0, the sliding mode dynamics is given by

(18)

where the state x_i = λ_i − λ_F,i. On integrating (18), it can be shown that the time required for the state x to reach 0 is T_c,i > 0 and is given by

(19)

where T_s,i is the time instant at which the sliding mode occurs. It can be seen from (19) that x_i will converge to zero in finite time. Therefore

can be achieved within finite time.

Here, a problem remains (i.e., is negative-semidefinite), which implies that the sliding mode cannot occur when in the reaching phase. Therefore, it is necessary to show that is not an attractor. To show this, analyze the dynamics of . On substituting (12), (13), and (14) into (10), we get

(20)

Now, for , (20) reduces to

(21)

Since r_i, cosθ_i have nonzero values, and M_i > max{|a_2,i|}, for s_i > 0 and s_i < 0, it can be seen from (21) that , which implies that is not an attractor. Therefore, from any arbitrary initial point, the desired LOS angle λ_F,i can be achieved within finite time with a_1,i.

This completes the proof.

3.3. Design of the Coordination Terms a_2,i and a_t,i

In this subsection, the terms a_2,i and a_t,i which will ensure the consensus of time-to-go estimates are designed based on consensus protocols and finite-time control technique, and a proof for the stability is given by the Lyapunov theory.

The well-known PN structure is given as

(22)

where N₀ ∈ [3, 5] [28] and ρ > 0. Note that the gain ρ can be used to modify the curvature of the flight trajectory while attacking a specified final position. In general, the missiles located far from the target should use a high gain ρ to reduce the flight time, whereas those closer should use a low gain ρ to provide a detour intentionally. Therefore, the time-varying gain plays an important role not only for achieving zero miss distance but also for tuning the time-to-go.

Let

(23)

where the time-varying gain

is defined as

(24)

where N is a navigation constant and Ω_i is a time-varying navigation ratio to be designed. Next, define the relative time-to-go estimate error of the ith missile as

(25)

which is regarded as a performance indicator for a cooperative simultaneous attack of multiple missiles. The

in (25) is defined as

(26)

Based on the time-to-go estimates of each missile and its neighbors, the time-varying navigation ratio of the ith missile is proposed as

(27)

where k_1i and ϱ are positive constants that satisfy k_1i > 0 and 0 < ρ < 1; the tangential acceleration a_t,i is proposed as

(28)

where k_3i and k_4i are positive constants that satisfy k_3i > max{|a_1,i|} and k_4i > D_i. In the following, three lemmas are given first, and then the finite time convergence of ξ_i is validated in Theorem 8.

Lemma 5 (see Appendix A.)If the control parameters α_i and β_i are properly chosen, then the point θ_i = 0 will not be a stable equilibrium before ξ_i converge to zero.

Lemma 6 (see [29].)For positive variables a₁, a₂, ⋯, a_n and 0 < p < 2, the following inequality holds

(29)

Lemma 7 (see [30].)If there exists a continuous positive function V(x) such that

(30)

where a > 0, b > 0, and 0 < μ < 1; then, V(x) will converge to zero in finite time, and the settling time T satisfies

(31)

Theorem 8. For the ith missile subjected to the kinematics (1), (2), (3), and (4) and the communication graph , if the control term a_1,i is designed as (12), (13), and (14), the term a_2,i is designed as (23), (24), and (27), and the tangential acceleration a_t,i is designed as (28); then, the consensus of the time-to-go estimates will be achieved in finite time, and the m missiles will arrive at the target simultaneously with imposing the desired impact angles.

Proof. Expand sinθ_i and cosθ_i in the Taylor series as

(32)

In general cases, the heading angles of each missile are small. Hence, the high-order terms in the above equations can be neglected. Then, the governing equations of the ith missile can be expressed as

(33)

(34)

(35)

On differentiating and substituting (33), (34), and (35) into it, we get

(36)

Let and ξ = [ξ₁, ⋯, ξ_m]. Then, (25) can be written as . Consider the following Lyapunov function candidate:

(37)

Differentiating V_L2 with respect to time and substituting (36) into it yields

(38)

where is used. According to Lemma 5, and without loss of generality, we assume . Define

(39)

Then, by using Lemma 6, we can obtain

(40)

Since , holds. It follows that . According to Lemma 2 and Lemma 3, we have , i.e., . Hence, (38) can be written as

(41)

According to Lemma 7, V_L2 converges to zero within

(42)

which means ξ will converge to zero in finite time. Therefore, the finite time consensus of the time-to-go estimates of all missiles can be guaranteed.

Remark 9. Note that (26) only represents time-to-go estimates, so it is important to show how all the missiles hit the target simultaneously with the proposed guidance law. From (2), it can be seen that θ_i = 0 when . Assume that min_i=1,⋯,m{T_c,i} > T_r1, which can be guarranteed by the properly selected control parameters; then, we have a_m,i = 0, a_t,i = 0, i = 1, ⋯, m for any t > max_i=1,⋯,m{T_c,i}, which means all the missiles will flight toward the target straightly along the desired LOS. Besides, the velocities of the missiles no longer change. For t > max_i=1,⋯,m{T_c,i}, the time-to-go estimate in equation (26) reduces to t_go,i = r_i/V_i, i = 1, ⋯, m, which represents the real time-to-go. As a result, all the missiles will arrive at the target simultaneously, and the impact angle constraint can be satisfied.

4. Modified and Extended to Communication Failure Cases

In the design process of a_2,i and a_t,i mentioned above, we have assumed that the communication graph among the missiles is undirected and connected. In this section, communication failure cases will be investigated, and the guidance law is modified.

Consider the situation that there exists at least one missile undergoes communication failure due to electromagnetic interference or some other things, which means some missiles discontinuously cannot send/receive the information to/from its neighbors. Figure 2 shows one of the possible scenarios, in which M₄ cannot exchange information with its neighbors during a time period. Then, to make the salvo remain robust to such conditions, the control term a_2,i and the tangential acceleration a_t,i is modified as

(43)

(44)

where

denotes the communication topology among the missiles.

Theorem 10. For the ith (i = 1, ⋯, m) missile subjected to the kinematics (1), (2), (3), and (4) and the communication graph . If the control term a_1,i is designed as (12), (13), and (14), the term a_2,i is designed as (43), and the tangential acceleration a_t,i is designed as (44); then, the consensus of time-to-go estimates of all the missiles will be achieved in finite time, and the m missiles will arrive at the target simultaneously with imposing the desired impact angles.

Proof. If there exists a time interval when some group members undergo communication failures, then the control terms a_2,i and a_t,i of all the missiles are switched to

(45)

Then, the governing equations (33), (34), and (35) change into

(46)

(47)

(48)

Differentiating and substituting (46), (47), and (48) into it yields

(49)

Hence, the integral of (49) can be computed as

(50)

As a result, the Lyapunov function V_L2 can be denoted as

(51)

where we assume that the graph always shares the same adjacency matrix with , so as to analyze the dynamics of V_L2 in the communication failure situation. (51) shows that the Lyapunov function candidate V_L2 keeps invariant when some missiles are undergoing communication failures.

Otherwise, if there exists a time interval when the communication among the missiles is normal, which means the communication topology is equal to , we will have

(52)

which are identical to (23), (24), (27), and (28). Following the analysis in Section 3.3, we can have

(53)

Let (t₀, t₁) be the first time interval when such case occurs. Then, ∃η₀, η₁ > 0, such that ι₁(t) > η₀, ι₂ > η₁, t ∈ (t₀, t₁). Likewise, let (t₂, t₃) be the second time interval when such case occurs. Then, ∃η₂, η₃ > 0, such that ι₁(t) > η₂, ι₂ > η₃, t ∈ (t₂, t₃). Continuing this way, from (53), we can obtain

(54)

Then, one can deduce that integrating the inequalities in (54) over each time interval yields (see Appendix B)

(55)

where . From (55), one can imply that ∃0 < t₁ < ⋯<t_n−1, such that

(56)

for all t > 0, where denotes the total communication failure times. Therefore, from (56), we can say that V_L2 converges to zero at a finite time T_r2 bounded as

(57)

Hence, the consensus of time-to-go estimates can be achieved in finite time. By following Remark 9, we can conclude that all the missiles that participated in the cooperative attack will arrive at the target simultaneously, and the desired impact angles can be achieved.

5. Simulation and Results

In this section, simulations are conducted to illustrate the performance of the proposed FTDCG-IAC law. In the simulations, four missiles are expected to attack a stationary target located at the origin with different initial conditions. The initial parameters for the missiles are listed in Table 1. As we see in the last column of Table 1, the maximum disagreement of the time-to-go estimate at the initial time is 13.27 s, which is rather large. For all simulations, the missile’s normal acceleration commands are bounded by 100. Further, the discontinuous functions sign(ξ_i) and sign(θ_i), when |ξ_i| ≤ σ₁, |θ_i| ≤ σ₂, are approximated by the sigmod functions.

(58)

(59)

where b_1,i and b_2,i are both chosen as 40. Parameters employed in the FTDCG-IAC law are chosen as follows: M_i = 120, p_i = 9, q_i = 7, β_i = 9, N = 3, k_1i = k_2i = 1, and k_3i = 124. Under the proposed guidance law, the missiles synchronize their arrival times via exchanging real-time time-to-go estimates with the neighbors through a communication topology. The communication topologies shown in Figure 3 are selected to demonstrate the following simulations.

Table 1. Initial parameters for missiles.

Missile number	Initial position	Initial heading angle	Speed	Designated impact angle	Initial impact time
Missile 1	(-7000, 2000) m	40 deg	260 m/s	-80 deg	29.36 s
Missile 2	(-9000, -4500) m	20 deg	290 m/s	-30 deg	35.12 s
Missile 3	(-6000, -6500) m	-20 deg	210 m/s	70 deg	42.63 s
Missile 4	(-3000, -10100) m	10 deg	320 m/s	120 deg	33.02 s

Besides, the lumped disturbances are assumed as d₁ = 2.2sin(2.4t), d₂ = 1.5sin(4.5t), d₃ = 3.4sin(1.4t), and d₄ = 1.2sin(3.2t).

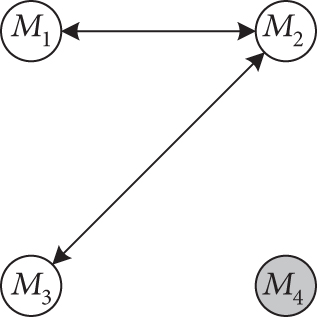
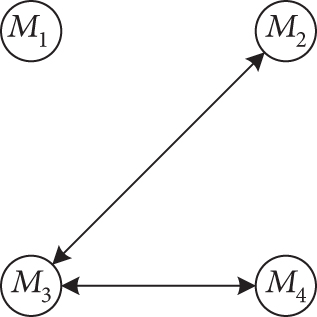
5.1. Case 1: Undirected and Connected Communication Topology

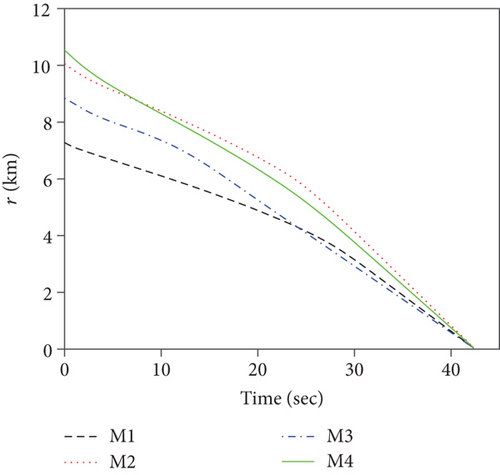
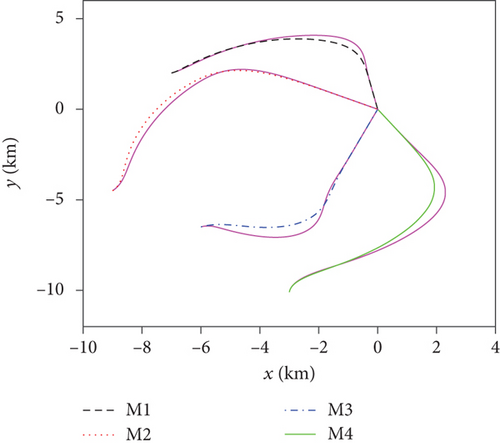
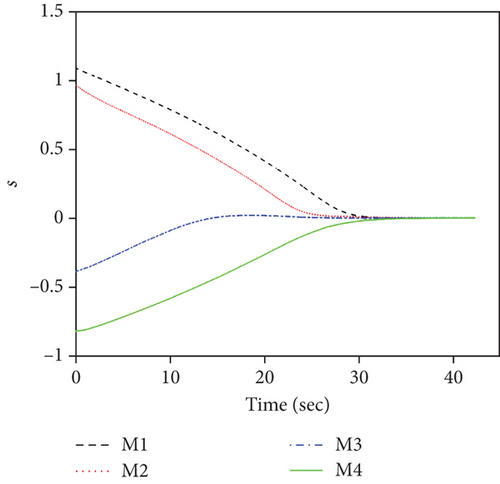
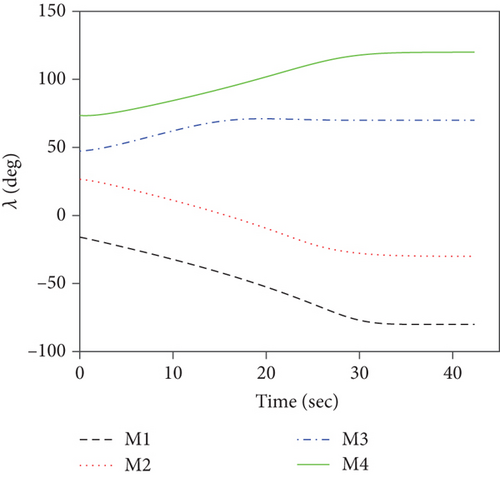
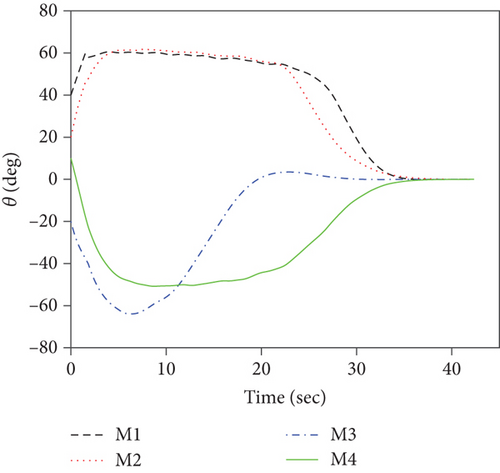
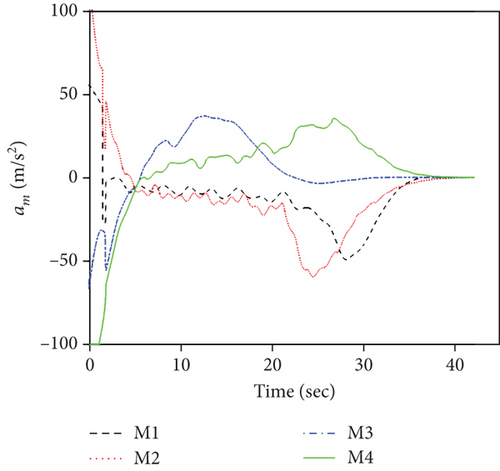
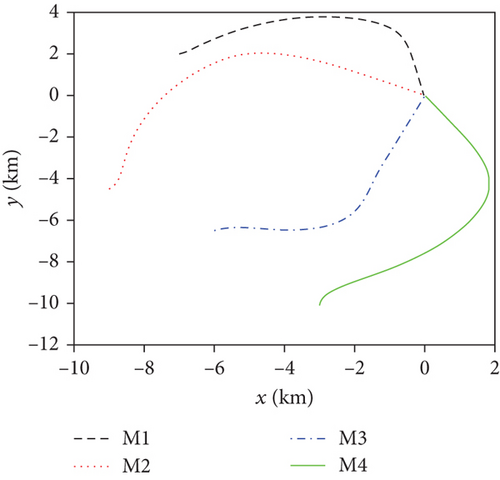
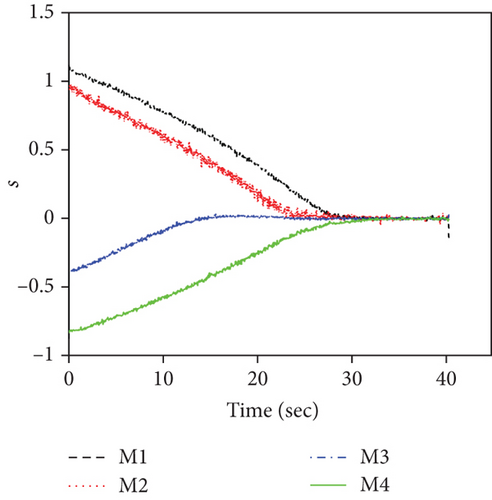
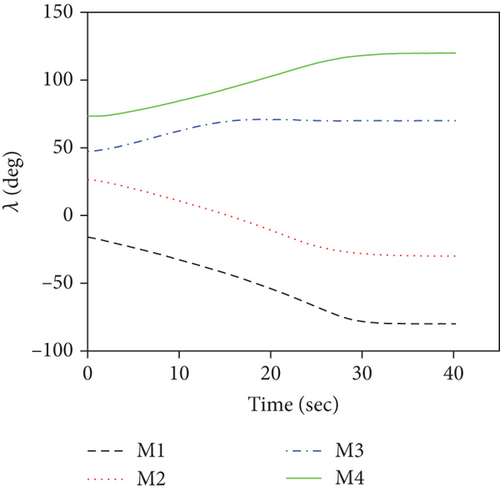
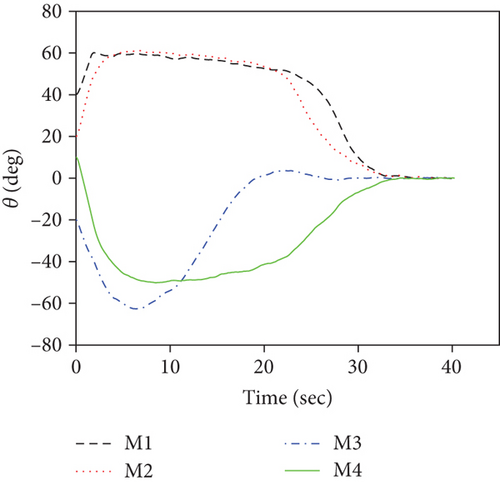
For this case, the communication topology is assumed to be fixed at as shown in Figure 3(a). Simulation results for case 1 are presented in Figure 4. Figure 4(a) depicts the ranges to go r_i, which demonstrates that the FTDCG-IAC law can achieve simultaneous attacks under an undirected connected communication topology, and the arrival time is 42.34 s. The trajectories are shown in Figure 4(b). For comparison, the trajectories under the NTSMCG-IAC law [9], which are represented by lines in pink, are also included. It can be seen from Figures 4(c)–4(e) that the condition λ_i = λ_F,i, θ_i = 0, i = 1, ⋯, 4 is achieved about at 40s. After that, the tangential acceleration a_t,i and the normal acceleration a_m,i keep zero values, which is demonstrated in Figures 4(f) and 4(g). As a result, the FTDCG-IAC law degrades into the NTSMCG-IAC law and then steers the missiles to flight toward the target. This verifies the analysis in Remark 9. Note that the final LOS angles for the four missiles read -80.002°, -29.9959°, 69.9998°, and 119.9830°, respectively. Compared with the designated final LOS angles listed in Table 1, the final LOS angle errors are negligible. Figures 4(h) and 4(i) show the consensus errors of time-to-go estimates ξ_i and time-to-go estimates t_go,i, respectively. As we see from Figures 4(h) and 4(i), the time-to-go estimates achieve a fast consensus in finite time.

5.2. Case 2: Study on Communication Failure Situations with First-Order System Lag and LOS Rate Measurement Noise

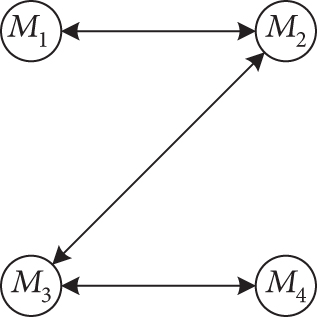
For this case, we assume that communication failure situations occur during the time interval (2 s and 4 s; 12 s and 16 s; and 24 s and 26 s), and the corresponding communication topologies are represented in Figures 3(b)–3(d), respectively. For the rest time of the engagement, the communication topology can still be represented in Figure 3(a). The autopilots are modeled as first-order lag systems with time constants τ₁ = 1/3, τ₂ = 1/3, τ₃ = 1/4, τ₄ = 1/4. Besides, we assume the LOS rate measurents are suffered by white noise. The simulation results for case 2 are presented in Figure 5. As we see from Figures 5(a) and 5(b), the FTDCG-IAC law can still achieve simultaneous attacks for this case, and the arrival time is 40.24 s. From Figures 5(c)–5(e), we can observe that the condition λ_i = λ_F,i, θ_i = 0 can also be achieved, which is important for the simultaneous attacks. Figures 5(f) and 5(g) depict the histories of normal acceleration a_m,i and the tangential acceleration a_t,i, respectively. It can be seen that, once the communication topology among the missiles is back to normal, the control inputs suddenly change. This is due to the switching mode of the controllers and is important to reduce the consensus errors ξ_i as we see in Figures 5(h) and 5(i). From Figure 5(h), we can also observe that during the communication failure time intervals, the consensus errors ξ_i only change slightly, which is due to the sigmoid functions (58) and (59).

5.3. Case 3: Comparative Analysis

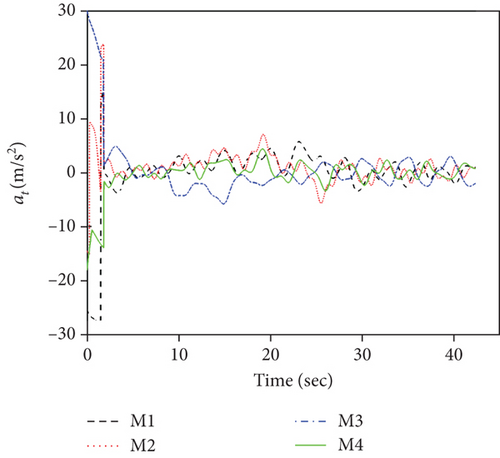
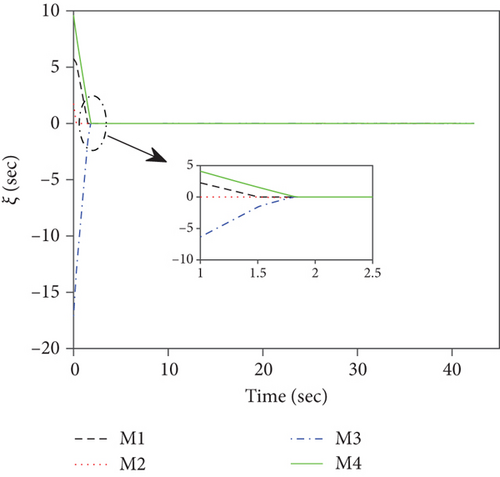
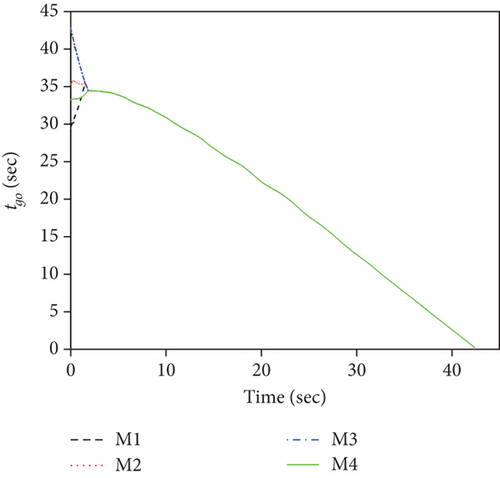
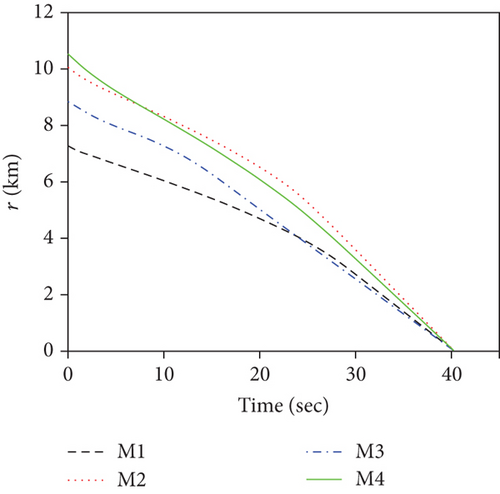
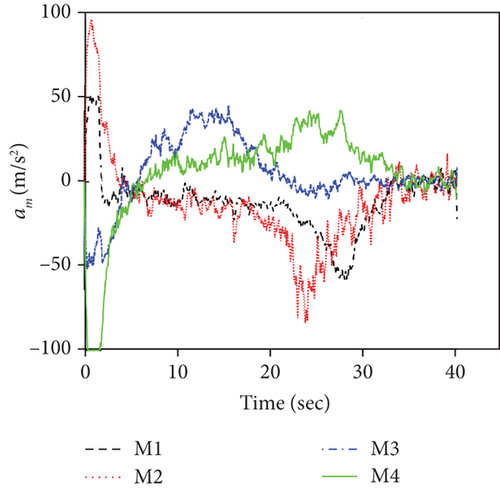
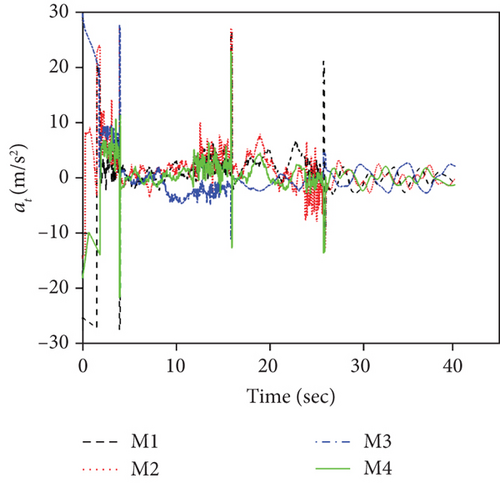
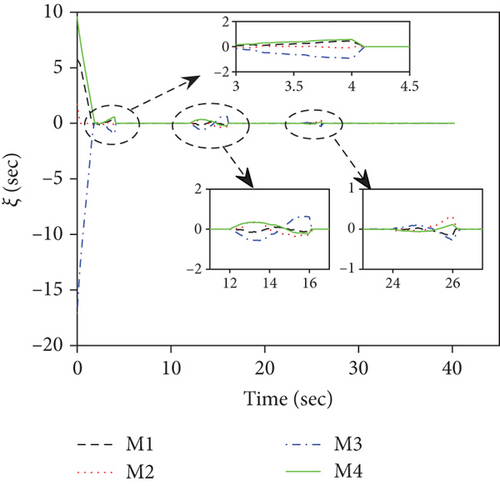
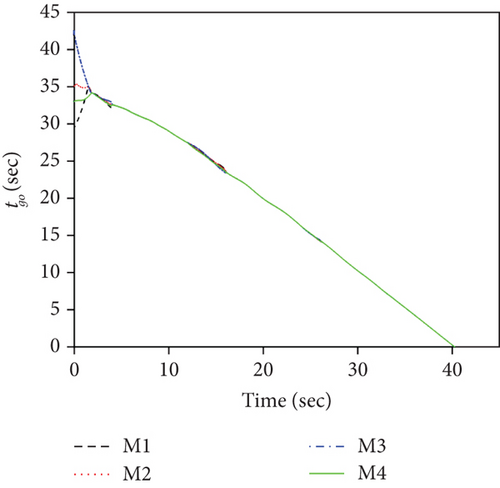
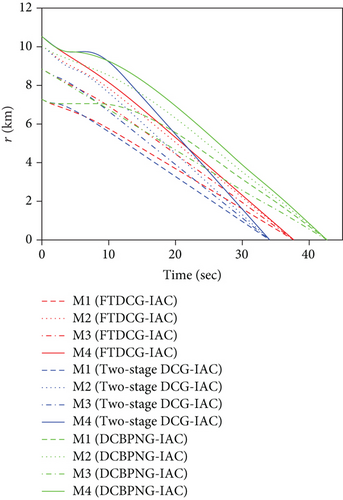
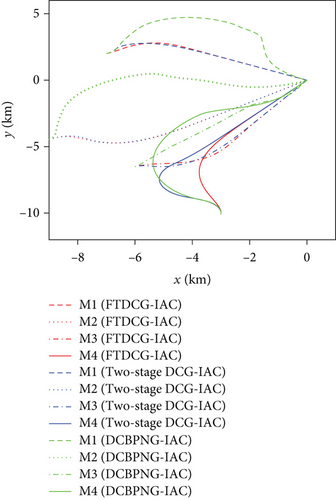
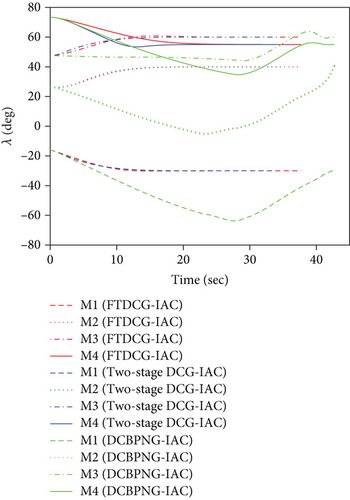
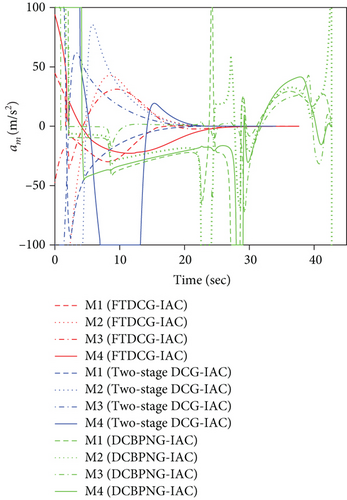
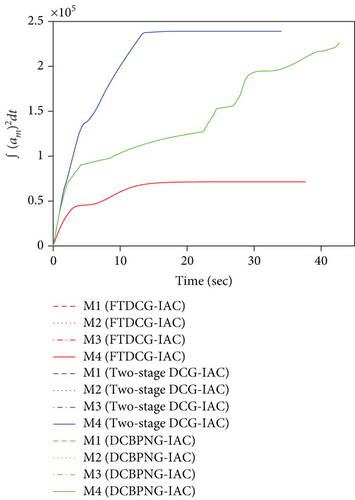
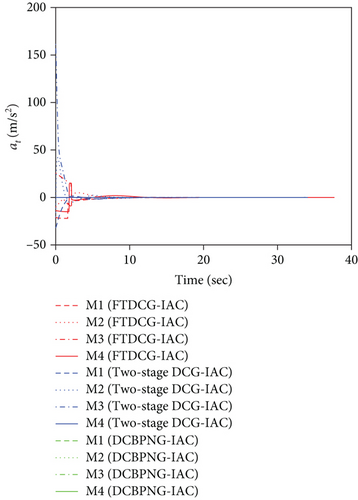
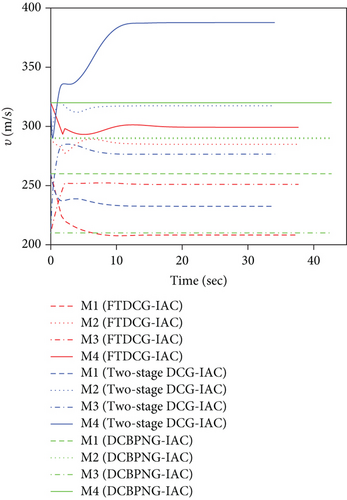
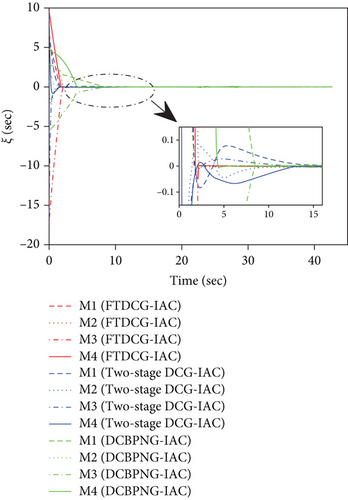
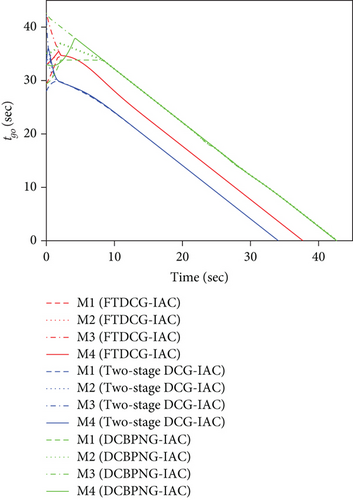
This set of simulations aims at providing comparative studies between the FTDCG-IAC law and the approaches outlined in [19, 20] (two-stage DCG-IAC) and [17] (DCBPNG-IAC). For fair comparison, the initial conditions for the missiles are the same with that in case 1 and case 2, except that the desired impact angles are reset as follows: θ_imp,1 = −30^∘, θ_imp,2 = 40^∘, θ_imp,3 = 60^∘, θ_imp,4 = 55^∘. The control parameters of the comparison methods are listed in Table 2. To achieve a fair comparison, the lumped disturbances d_i are set as zeros. Simulation results for case 3 are presented in Figure 6. In Figure 6(a), we can see that all three methods can achieve simultaneous attack, and the achieved arrival times are 37.692 s,34.08 s, and 42.72 s. Figure 6(b) shows the trajectories of missiles. As we can see from this picture, the missiles under DCBPNG-IAC take larger detours after the control begins; thus, the shaped trajectories are more curved. This is due to the fact that DCBPNG-IAC cannot adjust the magnitude but only the direction of the speed to synchronize the missiles’ arrival times. Although the generated homing trajectories are different, the desired terminal constraints are satisfied as shown in Figure 6(c). In Figure 6(d), which shows the normal acceleration histories, it is observed that the two-stage DCG-IAC generates larger control inputs than the other two methods during the first stage [0, T_c], and DCBPNG-IAC does so to satisfy the impact angle constraints during 20 s and 42.72 s. In general, the two-stage DCG-IAC law and DCBPNG-IAC law demand much more control effort in normal acceleration than the proposed FTDCG-IAC law does as shown in Figure 6(e), which depicts the cost function variations. Note that, in the two-stage method, the time interval [0, T_c] stands for the first stage, during which the desired final LOS angles will be ensured, and the time interval (T_c, t_F) stands for the second-stage, during which the time-to-go estimates will reach an agreement. In order to reduce the control inputs in the first stage, the parameter T_c should be chosen as a large constant. The contradictory thing is that the second stage needs enough time as well to drive the consensus error to its origin. Besides, the initial LOS angle errors should not be allowed to be very large. Figure 6(f) shows the tangential acceleration histories. One can observe that the two-stage DCG-IAC law also generates larger control inputs during the first stage [0, T_c]. As mentioned above, large normal accelerations are generated to achieve the desired LOS during the first stage; therefore, large tangential accelerations are needed to counteract the effects brought by the normal accelerations. Figures 6(g)–6(i) show the speed variations of the missiles, the consensus errors ξ_i, and the time-to-go estimates t_go,i, respectively. As we see from the last two pictures, consensus errors of the time-to-go estimate under the FTDCG-IAC law converge to zero faster than the other two methods, and those under the two-stage DCG-IAC law are only kept bounded during the time interval [0, T_c].

Table 2. Control parameters for comparison methods.

Method	Parameters
DCBPNG-IAC [17]	N_i = 3, k_i = 16.3, K_i = 2, K_ci = 0.3
Two-stage DCG-IAC [19]

6. Conclusion

This paper studies the finite-time distributed guidance law design for cooperative simultaneous attack against a single target of multiple missiles with impact angle constraint. First, the guidance law which consists of two components is proposed. Wherein, a nonsingular terminal sliding mode component is designed for ensuring finite time convergence to the impact angle constraint, and a coordination component is designed for realizing finite time consensus of the time-to-go estimates. The guidance law can ensure that missiles’ time-to-go estimates represent the real time to go once the LOS errors converge to zero. Therefore, all missiles will hit the target simultaneously along the desired LOS. Then, the guidance law is modified and extended to communication failure cases. Compared with existing results, this guidance law owns better performance and is more flexible in assigning impact angles. In the future, we will expand this work to three-dimensional cooperative guidance law by considering more practical factors, such as overload constraints.

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Acknowledgments

This work is supported by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (23KJB120014).

Appendix

A. Proof of Lemma 3

Substituting θ_i = 0 and a_1,i into (34), yields

(A.1)

From (A.1), it is clear that θ_i = 0 is not a stable equilibrium for s_i ≠ 0. From (16) and (17), it can be seen that the convergence rate of V_L1 depends on the control parameters α_i and β_i. Therefore, if the parameters α_i and β_i are properly chosen, then θ_i = 0 will only happen momentarily when ξ_i ≠ 0.

B. Proof of Eq. (55)

Assume that the Lyapunov candidate V_L2 satisfies

(B.1)

for

, where a, b, and μ are positive constants. By separating variables on (B.1), one can obtain

(B.2)

Using the relationship

, integrating both sides of (B.2) yields

(B.3)

which equals to

(B.4)

For simplicity, we define

; then, the inequality (B.4) changes into

(B.5)

Open Research

Data Availability

The underlying data used to support the findings of this study are available from the corresponding author upon request.

References

1 Cho D., Kim H. J., and Tahk M. J., Nonsingular sliding mode guidance for impact time control, Journal of Guidance, Control and Dynamics. (2016) 39, no. 1, 61–68, https://doi.org/10.2514/1.G001167, 2-s2.0-84957652533.
10.2514/1.G001167
Web of Science® Google Scholar
2 Jeon I. S., Lee J. I., and Tahk M. J., Homing guidance law for cooperative attack of multiple missiles, Journal of Guidance, Control and Dynamics. (2010) 33, no. 1, 275–280, https://doi.org/10.2514/1.40136, 2-s2.0-73949138438.
10.2514/1.40136
Web of Science® Google Scholar
3 Chen Z. Y., Chen W. C., Liu X. M., and Cheng J., Three-dimensional fixed-time robust cooperative guidance law for simultaneous attack with impact angle constraint, Aerospace Science and Technology. (2021) 110, article 106523, https://doi.org/10.1016/j.ast.2021.106523.
10.1016/j.ast.2021.106523
Web of Science® Google Scholar
4 Chen Z. Y., Liu X. M., and Chen W. C., Three-dimensional event-triggered fixed-time cooperative guidance law against maneuvering target with the constraint of relative impact angles, Journal of the Franklin Institute. (2023) 360, no. 6, 3914–3966, https://doi.org/10.1016/j.jfranklin.2023.02.027.
10.1016/j.jfranklin.2023.02.027
Web of Science® Google Scholar
5 Liu S. X., Yan B. B., Huang W., Zhang X., and Yan J., Current status and prospects of terminal guidance laws for intercepting hypersonic vehicles in near space: a review, Journal of Zhejiang University-SCIENCE A. (2023) 24, no. 5, 387–403, https://doi.org/10.1631/jzus.A2200423.
10.1631/jzus.A2200423
Web of Science® Google Scholar
6 Jeon I. S., Lee J. I., and Tahk M. J., Impact-time-control guidance law for anti-ship missiles, IEEE Transactions on Control Systems Technology. (2006) 14, no. 2, 260–266, https://doi.org/10.1109/TCST.2005.863655, 2-s2.0-33244497367.
10.1109/TCST.2005.863655
Web of Science® Google Scholar
7 Chen X. T. and Wang J. Z., Sliding-mode guidance for simultaneous control of impact time and angle, Journal of Guidance, Control and Dynamics. (2019) 42, no. 2, 394–401, https://doi.org/10.2514/1.G003893, 2-s2.0-85067411233.
10.2514/1.G003893
Web of Science® Google Scholar
8 Kim H. G., Cho D., and Kim H. J., Sliding mode guidance law for impact time control without explicit time-to-go estimation, IEEE Transactions on Aerospace and Electronic Systems. (2019) 55, no. 1, 236–250, https://doi.org/10.1109/TAES.2018.2850208, 2-s2.0-85049111720.
10.1109/TAES.2018.2850208
Web of Science® Google Scholar
9 Kumar S. R., Rao S., and Ghose D., Nonsingular terminal sliding mode guidance with impact angle constraints, Journal of Guidance, Control and Dynamics. (2014) 37, no. 4, 1114–1130, https://doi.org/10.2514/1.62737, 2-s2.0-84899511647.
10.2514/1.62737
Web of Science® Google Scholar
10 Jeon I. and Lee J., Impact-time-control guidance law with constraints on seeker look angle, IEEE Transactions on Aerospace and Electronic Systems. (2017) 53, no. 5, 2621–2627, https://doi.org/10.1109/TAES.2017.2698837, 2-s2.0-85032330370.
10.1109/TAES.2017.2698837
Web of Science® Google Scholar
11 Kim H., Lee J., and Kim H. J., Look angle constrained impact angle control guidance law for homing missiles with bearings-only measurements, IEEE Transactions on Aerospace and Electronic Systems. (2018) 54, no. 6, 3096–3107, https://doi.org/10.1109/TAES.2018.2843600, 2-s2.0-85048533751.
10.1109/TAES.2018.2843600
Web of Science® Google Scholar
12 Tsalik R. and Shima T., Optimal guidance around circular trajectories for impact-angle interception, Journal of Guidance, Control and Dynamics. (2016) 39, no. 6, 1278–1291, https://doi.org/10.2514/1.G001759, 2-s2.0-84969791377.
10.2514/1.G001759
Web of Science® Google Scholar
13 Chen Y. D., Wang J. N., Wang C. Y., Shan J., and Xin M., A modified cooperative proportional navigation guidance law, Journal of the Franklin Institute. (2019) 356, no. 11, 5692–5705, https://doi.org/10.1016/j.jfranklin.2019.04.013, 2-s2.0-85066437590.
10.1016/j.jfranklin.2019.04.013
Web of Science® Google Scholar
14 Daughtery E., Optimal design of cooperative guidance law for simultaneous strike, 53rd IEEE Conference on Decision and Control, 2014, Los Angeles, CA, USA, 988–993, https://doi.org/10.1109/cdc.2014.7039510, 2-s2.0-84987915454.
10.1109/cdc.2014.7039510
Google Scholar
15 Nikusokhan M. and Nobahari H., Closed-form optimal cooperative guidance law against random step maneuver, IEEE Transactions on Aerospace and Electronic Systems. (2016) 52, no. 1, 319–336, https://doi.org/10.1109/TAES.2015.140623, 2-s2.0-84964370069.
10.1109/TAES.2015.140623
Web of Science® Google Scholar
16 Zhou J. L. and Yang J. Y., Distributed guidance law design for cooperative simultaneous attacks with multiple missiles, Journal of Guidance, Control and Dynamics. (2016) 39, no. 10, 2436–2444.
10.2514/1.G001609
Web of Science® Google Scholar
17 Wang X. L., Zhang Y., and Wu H., Distributed cooperative guidance of multiple anti-ship missiles with arbitrary impact angle constraint, Aerospace Science and Technology. (2015) 46, no. 2015, 299–311, https://doi.org/10.1016/j.ast.2015.08.002, 2-s2.0-84939801117.
10.1016/j.ast.2015.08.002
Web of Science® Google Scholar
18 Sun J. and Liu C., Distributed fuzzy adaptive backstepping optimal control for nonlinear multimissile guidance systems with input saturation, IEEE Transactions on Fuzzy Systems. (2019) 27, no. 3, 447–461.
Web of Science® Google Scholar
19 Wang X. and Yang Q., Cooperative guidance law design for salvo attacks with impact angle constraint, 2017 Chinese Automation Congress (CAC), 2017, Jinan, China, 3241–3246, https://doi.org/10.1109/cac.2017.8243335, 2-s2.0-85050260436.
10.1109/cac.2017.8243335
Google Scholar
20 Wang X. H. and Lu X., Three-dimensional impact angle constrained distributed guidance law design for cooperative attacks, ISA Transactions. (2018) 73, no. 2018, 79–90, https://doi.org/10.1016/j.isatra.2017.12.009, 2-s2.0-85039898633.
10.1016/j.isatra.2017.12.009
PubMed Web of Science® Google Scholar
21 Ma X., Dai K. R., Zou Y., Yu H., Zhang H., and Wang X. F., Fixed-time anti-saturation grouped cooperative guidance law with state estimations of multiple maneuvering targets, Journal of the Franklin Institute. (2023) 360, no. 8, 5524–5547, https://doi.org/10.1016/j.jfranklin.2023.02.031.
10.1016/j.jfranklin.2023.02.031
Web of Science® Google Scholar
22 Liu S. X., Yan B. B., Zhang T., and Yan J., Coverage-based cooperative guidance law for intercepting hypersonic vehicles with overload constraint, Aerospace Science and Technology. (2022) 126, article 107651, https://doi.org/10.1016/j.ast.2022.107651.
10.1016/j.ast.2022.107651
Web of Science® Google Scholar
23 Liu S. X., Yan B. B., Zhang T., and Yan J., Three-dimensional coverage-based cooperative guidance law with overload constraints to intercept a hypersonic vehicle, Aerospace Science and Technology. (2022) 130, article 107908, https://doi.org/10.1016/j.ast.2022.107908.
10.1016/j.ast.2022.107908
Web of Science® Google Scholar
24 Erer K. S. and Tekin R., Impact time and angle control based on constrained optimal solutions, Journal of Guidance, Control and Dynamics. (2016) 39, no. 10, 2445–2451.
10.2514/1.G000414
Web of Science® Google Scholar
25 Ren W., Beard R. W., and Atkins E. M., Information consensus in multivehicle cooperative control, IEEE Control Systems Magazine. (2007) 27, no. 2, 71–82, https://doi.org/10.1109/MCS.2007.338264, 2-s2.0-34147163355.
10.1109/MCS.2007.338264
Web of Science® Google Scholar
26 Olfati-Saber R. and Murray R. M., Consensus problems in networks of agents with switching topology and time-delays, IEEE Transactions on Automatic Control. (2004) 49, no. 9, 1520–1533, https://doi.org/10.1109/TAC.2004.834113, 2-s2.0-4644244041.
10.1109/TAC.2004.834113
Web of Science® Google Scholar
27 Kumar S. R., Rao S., and Ghose D., Sliding-mode guidance and control for all-aspect interceptors with terminal angle constraints, Journal of Guidance, Control, and Dynamics. (2012) 35, no. 4, 1230–1246, https://doi.org/10.2514/1.55242, 2-s2.0-84867034793.
10.2514/1.55242
Web of Science® Google Scholar
28 Zarchan P., Tactical and Strategic Missile Guidance, Vol. 157, 1994, Progress in astronautics and aeronautics, Reston, VA, USA.
Google Scholar
29 Yu H., Shen Y. J., and Xia X. H., Adaptive finite-time consensus in multi-agent networks, Systems and Control Letters. (2013) 62, no. 10, 880–889, https://doi.org/10.1016/j.sysconle.2013.06.011, 2-s2.0-84881279630.
10.1016/j.sysconle.2013.06.011
Web of Science® Google Scholar
30 Yu S., Yu X., Shirinzadeh B., and Man Z., Continuous finite-time control for robotic manipulators with terminal sliding mode, Automatica. (2005) 41, no. 11, 1957–1964, https://doi.org/10.1016/j.automatica.2005.07.001, 2-s2.0-24944498043.
10.1016/j.automatica.2005.07.001
Web of Science® Google Scholar

All articles

Finite-Time Distributed Cooperative Guidance Law with Impact Angle Constraint

Abstract

1. Introduction

2. Problem Formulation and Preliminaries

2.1. Problem Formulation

2.2. Preliminary

2.2.1. Graph Theory

3. Main Results

3.1. The Structure of the Proposed Guidance Law

3.2. Design of the Impact Angle Control Term a_1,i

3.3. Design of the Coordination Terms a_2,i and a_t,i

4. Modified and Extended to Communication Failure Cases

5. Simulation and Results

5.1. Case 1: Undirected and Connected Communication Topology

5.2. Case 2: Study on Communication Failure Situations with First-Order System Lag and LOS Rate Measurement Noise

5.3. Case 3: Comparative Analysis

6. Conclusion

Conflicts of Interest

Acknowledgments

Appendix

A. Proof of Lemma 3

B. Proof of Eq. (55)

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Finite-Time Distributed Cooperative Guidance Law with Impact Angle Constraint

Abstract

1. Introduction

2. Problem Formulation and Preliminaries

2.1. Problem Formulation

2.2. Preliminary

2.2.1. Graph Theory

3. Main Results

3.1. The Structure of the Proposed Guidance Law

3.2. Design of the Impact Angle Control Term a1,i

3.3. Design of the Coordination Terms a2,i and at,i

4. Modified and Extended to Communication Failure Cases

5. Simulation and Results

5.1. Case 1: Undirected and Connected Communication Topology

5.2. Case 2: Study on Communication Failure Situations with First-Order System Lag and LOS Rate Measurement Noise

5.3. Case 3: Comparative Analysis

6. Conclusion

Conflicts of Interest

Acknowledgments

Appendix

A. Proof of Lemma 3

B. Proof of Eq. (55)

Open Research

Data Availability

References

Figures

References

Related

Information

3.2. Design of the Impact Angle Control Term a_1,i

3.3. Design of the Coordination Terms a_2,i and a_t,i