[Retracted] On Fuzzy F∗-Simply Connected Spaces in Fuzzy F∗-Homotopy
Abstract
In this paper, the notions of fuzzy -simply connected spaces and fuzzy -structure homeomorphisms are introduced, and further fuzzy -structure homeomorphism between fuzzy -path-connected spaces are studied. Also, it is shown that every fuzzy -structure subspace of fuzzy -simply connected space is fuzzy -simply connected subspace. Further, the concepts of fuzzy -contractible spaces and fuzzy -retracts are introduced, and it is proved that every fuzzy -contractible space is fuzzy -simply connected.
1. Introduction
Homotopy theory is the main part of algebraic topology which studies topological objects up to homotopy equivalence. Homotopy equivalence is a weaker relation than topological equivalence. The homotopy theory is one among the foremost branches of algebraic topology. The thoughts and techniques of homotopy theory have pervaded many components of topology. Several topologists like Massey [1], Munkres [2], and Hatcher [3], introduced and studied concepts of homotopy theory and fundamental groups. The most appropriate theory for dealing with uncertainties is the theory of fuzzy sets developed by Zadeh [4]. The fuzzy homotopy theory was introduced by Culvacioglu and Citil [5]. Salleh and Tap [6, 7] introduced the concept of the fundamental group to fuzzy topological spaces based on the definition of fuzzy topology introduced by Chang [8]. Based on Chang’s [8] description of fuzzy topology, Salleh and Tap [6, 7, 9] introduced the concept of basic fundamental group of fuzzy topological spaces. Several recent papers contain extensive investigations and applications about fuzzy topological space and fuzzy homotopy theory; see [10–12].
Later on, Guner [13] intensively investigated the concept of fuzzy contractible spaces. Rodabaugh [14, 15] introduced the concept of L-fuzzy retract in 1981. Further fuzzy homotopy theory was intensively developed by Aras [16], Citil and Cuvalcioglu [17], Palmeira and Bedregal [18], etc. and gave many interesting results on fuzzy homotopy theory. In this connection, Madhuri and Amudhambigai [19, 20] introduced the concepts of fuzzy -homotopy and -fundamental group. Also the concept of fuzzy -structure isomorphisms between -fundamental groups are studied in [19, 20]. In this recent work, the concept of fuzzy -structure homeomorphism between fuzzy -path-connected spaces are studied. The notion of fuzzy -simply connected space is introduced, and it is shown that every fuzzy -structure subspace of fuzzy -simply connected space is fuzzy -simply connected. Further, the concepts of fuzzy -contractible spaces and fuzzy -retracts are introduced and it is proved that every fuzzy -contractible space is fuzzy -simply connected. Also in fuzzy -contractible space, each fuzzy -loop based at any fuzzy point is equivalent to the constant fuzzy -loop.
2. Preliminaries
In this section, some basic concepts of fuzzy homotopy have been recalled from the previous literature. Also related results and propositions are studied from various research articles. Some definitions and preliminary results are presented in this section.
Definition 1. Let (X, τ) be a fuzzy topological space. A fuzzy set μ ∈ IX is called fuzzy irreducible if μ ≠ 0X, and for all fuzzy closed sets γ, δ ∈ IX with μ ≤ (γ∨δ), it follows that either μ ≤ γ or μ ≤ δ.
Remark 2. Let (X, τ) be a fuzzy topological space. Any λ ∈ IX is said to be fuzzy irreducible closed if it is both fuzzy irreducible and fuzzy closed.
Definition 3. Suppose that (X, τ) be a fuzzy topological space and assume that α ∈ IX be a fuzzy open set in (X, τ). Then the collection σ and 1 − σ is a fuzzy irreducible closed set in (X, τ)}. Then the collection which is finer than the fuzzy topology τ on X is said to be a -structure on X. A nonempty set X with a -structure denoted by is said to be fuzzy -structure space. Each member of is said to be fuzzy -structure open set, and the complement of each fuzzy -structure open set is said to be fuzzy -structure closed. A -structure on a nonempty set X together with 0X is said to be fuzzy -structure. Then is called a fuzzy -structure space generated by τ.
Definition 4. Suppose that (X, τ) be any topological space and assume that be fuzzy -structure space. Assume also that U ⊂ X and χU denotes the so-called fuzzy characteristic function of the subset U. Then the fuzzy -structure given by τ is , and the pair is called a fuzzy -structure space given by (X, τ).
Note 5. Let I be the unit interval. Let ζ be an Euclidean topology on I, and then is a fuzzy -structure space introduced by the (usual) topological space (I, ζ).
Definition 6. Let and be any two fuzzy -fundamental groups of at xλ and , respectively. A function ⟶ is called a fuzzy -structure homomorphism if f([θ]∘[η]) = f([θ])∘f([η]) for every . Moreover the fuzzy -structure homomorphism is called a fuzzy -structure isomorphism if it is bijective.
Proposition 7. Let be any fuzzy -structure space and let . Let be any fuzzy -loops in . If and , then .
Proposition 8. Let be any fuzzy -structure space. Let , where xλ is a fuzzy point in X. Then ([α]∘[β])∘[γ] = [α]∘([β]∘[γ]).
Proposition 9. Let be any fuzzy -structure space and let be any fuzzy -structure space introduced by (I, ζ). Also, let be the fuzzy -path defined by e(tζ) = xλ for each tζ in , and xλ is fuzzy point in X. Then [α]∘[e] = [e]∘[α] = [α], for each .
Proposition 10. Let be any fuzzy -structure space and xλ be fuzzy point in X. Let . Then there exists a such that .
Remark 11. From Proposition 8, Proposition 9, and Proposition 10, it is seen that forms a group under an operation (namely, multiplication). It is called -fundamental group of based at xλ.
Definition 12. (see [21].)Let f, g : X⟶Y be fuzzy continuous maps and f≅g. If g is a constant, then f is called a fuzzy nulhomotopic map.
Definition 13. Let A ⊂ X. A is an L-fuzzy retract of X in (X, T) (abbreviated F-retract) if there is an F-continuous r : (X, T)⟶(A, T(A)) such that r(x) = x for each x ∈ A.
Definition 14. Let 1X : (X, τ)⟶(X, τ) be an identity mapping. If 1X is fuzzy homotopic to a constant, then (X, τ) is called a fuzzy contractible space.
Proposition 15. Let , , and be any three fuzzy -structure spaces. If and are fuzzy -structure continuous functions, then is a fuzzy -structure continuous function.
Remark 16. Let be any fuzzy -structure space and let . Let β be any fuzzy -path joining xλ with yμ. Also, let be any two fuzzy -loops defined such that
Then
- (i)
on replacing [e] by in the proof of Proposition 9
- (ii)
on replacing [e] by in the proof of Proposition 9
- (iii)
where on replacing [e] by in the proof of Proposition 10
- (iv)
on replacing [e] by in the proof of Proposition 10
- (v)
If , then
Therefore, serves as the left identity and serves as the right identity for any [l].
Proposition 17. Let and be any two fuzzy -structure spaces. Let be any two fuzzy -structure continuous functions, where is fuzzy -structure homotopy between ψ and φ. Let be any fuzzy -structure space introduced by (I, ζ). Also if is a fuzzy -path joining ψ(xλ) with φ(xλ) defined by , where t ∈ I and , then the following Figure 1 of induced fuzzy -structure homomorphisms is commutative.
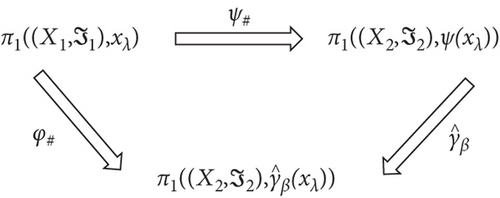
3. Properties of Fuzzy -Simply Connected Spaces
Throughout this paper, the collection of all fuzzy points xt, where 0 < t ≤ 1 over X, is denoted by , and the set of all fuzzy points over I is denoted by . In this section, the concepts of fuzzy -simply connected spaces, fuzzy -null-homotopic functions, fuzzy -contractible spaces, and fuzzy -retractions are introduced, and some interesting properties are studied.
Definition 18. Let and be any two fuzzy -structure spaces. Let be any two fuzzy -structure continuous functions and ϕ≅φ. If φ is a constant function, then ϕ is said to be a fuzzy -null-homotopic function.
Definition 19. Any fuzzy -structure space is said to be a fuzzy -simply connected space if it is fuzzy -path-connected and every fuzzy -loop in is a fuzzy -null-homotopic function.
A fuzzy -structure space which is not fuzzy -simply connected is said to be fuzzy -multiply connected.
Definition 20. Let and be any two fuzzy -structure spaces. If the bijective function and its inverse function are fuzzy -structure continuous functions, then the function φ is said to be a fuzzy -structure homeomorphism.
Proposition 21. Let and be any two fuzzy -structure spaces and let be a fuzzy -structure homeomorphism. If is fuzzy -path-connected, then is also a fuzzy -path-connected space.
Proof. Let be fuzzy -path-connected and be a fuzzy -structure homeomorphism. Let be a fuzzy -structure space introduced by (I, ζ). For t1, t2 ∈ I, let be any two fuzzy points. Since is fuzzy -path connected, there exists a fuzzy -path such that and . Thus, is such that
Also, , as φ is onto.
Therefore, φ∘α is a fuzzy -path in joining from to . Hence, is a fuzzy -path-connected space.
Proposition 22. Let and be any two fuzzy -structure spaces and be a fuzzy -structure space introduced by (I, ζ). Let be any two fuzzy -paths joining from to such that , where . If is a fuzzy -structure continuous function, then are fuzzy -structure continuous functions and .
Proof. Let be any fuzzy -structure space introduced by (I, ζ). Since ϕ, φ, ψ are fuzzy -structure continuous functions and by Proposition 15, ϕ∘φ, ϕ∘ψ are also fuzzy -structure continuous functions. Furthermore, implies that there exists a fuzzy -structure continuous function such that
Proposition 23. Let and be any two fuzzy -structure spaces. Let be any fuzzy -structure homeomorphism. Then is fuzzy -simply connected if and only if is fuzzy -simply connected.
Proof. Let be any fuzzy -structure space introduced by (I, ζ). Since is fuzzy -simply connected, by Definition 19, is fuzzy -path-connected. Let be a fuzzy -structure homeomorphism. Then by Proposition 21, is fuzzy -path-connected. Thus, it is enough to prove that every fuzzy -loop in is fuzzy -null-homotopic. Let be a fuzzy -loop in . Since is fuzzy -simply connected, is a fuzzy -loop in which is fuzzy -path-homotopic to some constant fuzzy -loop , i.e., .
Since ϕ is a fuzzy -structure continuous function and by Proposition 22
Thus, .
Also, l is fuzzy -path-homotopic to some constant fuzzy -loop ϕ∘β. Thus, every fuzzy -loop l in is fuzzy -null-homotopic. Thus, is fuzzy -simply connected.
The converse part is also proved in the reverse direction of ϕ and .
Proposition 24. Let be a fuzzy -structure space. Then, any fuzzy -path-connected space is fuzzy -simply connected if and only if any two fuzzy -paths in having same endpoints are fuzzy -path-homotopic.
Proof. Let be any fuzzy -structure space introduced by (I, ζ). Let be any two fuzzy -paths in such that
Thus, , as in (i) of Remark 16, , as in (iv) of Remark 16, [α] = [β],as in (ii) of Remark 3.
Hence, .
Therefore, any two fuzzy -paths in having same endpoints are fuzzy -path-homotopic.
Conversely, let be any two fuzzy -paths in such that . Thus, , [α] = [β], and , as in (ii) of Remark 16.
Thus,, as in (iv) of Remark 16, and then, as in (i) of Remark 16, which implies that
Thus,
Therefore, for every fuzzy -loop based at in is fuzzy -null-homotopic. Thus, is fuzzy -simply connected.
Definition 25. Let be a fuzzy -structure space and Y⊆X. Let be a fuzzy -structure subspace and be any fuzzy -structure continuous function. Then is said to be fuzzy -retract of if there exists a fuzzy -structure continuous function such that , for all . Also, the function is called as fuzzy -retraction.
Proposition 26. Let be a fuzzy -structure space and Y⊆X. If is fuzzy -simply connected and is the fuzzy -retract of , then is also a fuzzy -simply connected space.
Proof. Let be fuzzy -simply connected and be the fuzzy -retract of . Then is a fuzzy -retraction function. If are any two fuzzy points, then there is a fuzzy -path such that and . Then is a fuzzy -path in such that
Let be the inclusion function. Thus, , that is, where is an identity function on . Also, let is a fuzzy -loop in at . Thus, is a fuzzy -loop in at xt. Since is fuzzy -simply connected, is fuzzy -path homotopic in to the constant fuzzy -loop such that , for all and and hence . Also, by Proposition 22
Thus, and is a constant fuzzy -loop (i.e.,) , for all . Therefore l is fuzzy -null-homotopic in . Hence, is a fuzzy -simply connected space.
Definition 27. Let and be any two fuzzy -structure spaces and . Any fuzzy -structure continuous function ϕ is said to be a fuzzy -homotopy equivalence if there exists a fuzzy -structure continuous function such that φ∘ϕ is fuzzy -homotopic to where is an identity function on and ϕ∘φ is fuzzy -homotopic to where is an identity function on .
Also, any two fuzzy -structure spaces and are said to be of the same fuzzy -homotopy type if there exists a fuzzy -structure continuous function which is fuzzy -homotopy equivalence.
Definition 28. Let be a fuzzy -structure space and be an identity function. If is a fuzzy -null-homotopic function, then is said to be a fuzzy -contractible space.
Proposition 29. Let be a fuzzy -structure space. If is fuzzy -contractible, then each fuzzy -loop α based at any fuzzy point is equivalent to the constant fuzzy -loop at xt.
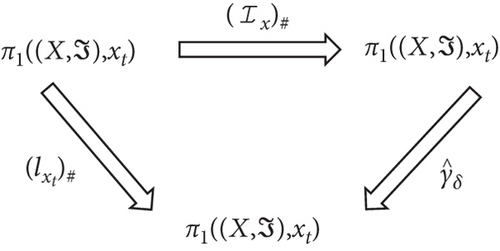
Proof. Let be a fuzzy -contractible space. Then is an identity function and it is fuzzy -homotopic to the constant fuzzy -loop by a fuzzy -homotopy . Thus there is a fuzzy -loop δ at xt which is defined as , where s ∈ I. Let and be any two induced fuzzy -structure homomorphisms. Also, let be defined as , where . Then by Proposition 17, the following Figure 2 shows that .
For each ,and, as in (i) of Remark16;and, as in (iv) of Remark16; and, as in (ii) of Remark16,
Therefore, each fuzzy -loop α is equivalent to the constant fuzzy -loop .
Proposition 30. Every fuzzy -contractible space is fuzzy -simply connected.
Proof. Let be a fuzzy -contractible space and let be the constant fuzzy -loop at . Since is fuzzy -contractible, is a fuzzy -null-homotopic function by a fuzzy -homotopy , so . Thus, the fuzzy -homotopy is defined as:
Let and also let us define a fuzzy -homotopy . Thus, and , where is a constant fuzzy -loop at xt. Thus, . Thus, . Hence, every fuzzy -loop in is fuzzy -null-homotopic. Therefore, is fuzzy -simply connected. Hence, every fuzzy -contractible space is fuzzy -simply connected.
4. Conclusion
In this paper, the notions of fuzzy -simply connected spaces and fuzzy -contractible spaces are introduced, and some important characterizations related to fuzzy -homotopy are discussed. Also it is proved that in fuzzy -contractible space, each fuzzy -loop based at any fuzzy point is equivalent to the constant fuzzy -loop. This is just a beginning of studying fuzzy -simply connected spaces. There is a huge scope of further study in extending the results of fuzzy -homotopy to fuzzy -covering spaces. Further using fuzzy compact and fuzzy Lindelof spaces, types of fuzzy -homotopy can be developed.
Conflicts of Interest
All authors have declared they do not have any competing interests.
Open Research
Data Availability
No data were used to support this study.




