On Topological Indices for Complex Indium Phosphate Network and Their Applications
Abstract
A chemical compound in the form of graph terminology is known as a chemical graph. Molecules are usually represented as vertices, while their bonding or interaction is shown by edges in a molecular graph. In this paper, we computed various connectivity indices based on degrees of vertices of a chemical graph of indium phosphide (InP). Afterward, we found the physical measures like entropy and heat of formation of InP. Then, we fitted curves between different indices and the thermodynamical properties, namely, heat of formation and entropy. Curve fitting was done in MATLAB through different methods based on linearity and nonlinearity. Furthermore, we depicted our results numerically and graphically. These numerical systems may give an approach to concentrate on the thermodynamical properties of the compound design of InP at an exceptional level that will help understand the connection between framework measurement and these actions.
1. Introduction
An application of graph theory in the field of chemistry is to study the molecular structures of chemical compounds. Graph theory tools are implemented to classify fundamental features entailed in structure-property activity interactions of molecules. The term used to illustrate a molecule/chemical compound in the form of a graph is known as a molecular/chemical graph [1, 2]. Molecules are shown as vertices, while their bondings or interactions are shown by edges in a molecular graph. Mostly, molecule graphs are simple graphs, and the measure of the topological index is invariant under graph isomorphisms. Mostly, the degree or distance measure is used to capture the topology of a graphical structure, so the most common indices are based on either degree or distance between the vertices. Indices comprising degree measurements perform a vigorous part in molecular graph theory. Two isomorphic graphs have the same connectivity index, and the cardinalities of vertex and edge sets of a graph are considered as the topological/connectivity indices as well. A connectivity index explains some helpful details about the structure and analysis of the molecular graph.
Many chemical compounds have been analyzed through topological indices in the past few decades. Topological/graphical index is a numeric measure related to chemical compositions asserting the association of chemical structures through numerous physicochemical properties or chemical reactivity [1]. Gao et al. [2] are originators of the field of chemical graph theory. It was acknowledged in 1988 that a lot of researchers had worked in this field and published roughly 500 publications per year. Chemical graph theory, a two-volume comprehensive treatise by Trinajsti, that conveyed the research up to the mid of 1980s, is one of many monographs in the discipline [3].
Chemical compounds are represented by graphs in chemical graph theory, and mathematical tools are employed to address chemistry issues [4]. A topological/connectivity descriptor is a numerical measure that describes the topology of a graph [5]. Connectivity descriptors have gained considerable popularity recently, due to their simple nature. Chemical graph theory relies considerably on these graph descriptors. As a consequence, a topological index may be quantitatively characterized a chemical network that is topologically invariant for labelling as well as distinguishing between isomers [6]. In theoretical chemistry and nanotechnology, there are several graphs associated with numerical descriptors that are significant. Degree-based, distance-based, and counting-related graph descriptors are among the most common types [7]. The degree-based graph descriptors have a prominent place among these descriptors and may be used to characterize chemical substances, either organic or inorganic, and forecast their specific physiochemical characteristics [8].
In [9], the authors suggested a way to analyze the metal-organic chemical compounds from topological perspectives based on mathematical frameworks. Such frameworks were further utilized in [10] to identify the molecular hydrogen stages within few seconds. In [11], authors studied the metal-organic structure by using different topological descriptors including Zagreb indices and Zagreb coindices. A study on the molecular chain in dialkyltin of complex-2, complex-3, and complex-4 of N-salicylidene-L-valine was conducted in [12], and the authors also analyzed these structures by providing different examples and established a comparison among topological indices.
To construct a thermodynamical structure, we need to measure some physical quantities, and entropy and heat of formation are two of them.
Entropy measure tells us how much heat energy we need to produce more in order to perform some valued work. Since this measure is describing the lack of energy due to which performing valuable work is not possible, it is also termed as a measure of the disorder [19]. The entropy of an isolated system has the highest entropy, according to the second law of thermodynamics. Nonisolated systems can lose entropy if they enhance the entropy of their surroundings by at least the same amount. Because entropy is a state function, every process that moves a system from one state to another, whether reversible or irreversible, will change its entropy.
During per unit formation, the heat absorbed or retained is referred to as the heat of formation provided all the elements persist in a normal state. Kilojoule per mole (kJ/mol) is the unit for the measure of the heat of formation. The term enthalpy is also used for the heat of formation. Defining a system in the form of a mathematical framework provides us with an efficient approach to analyze the dynamics of the system. Experimental work is most expensive and very time-consuming so transforming the system into a set of mathematical forms makes this study very coherent. Many software like MATLAB or Python are easily available that provide a very friendly environment to construct mathematical models and study them. As we may fit many mathematical models to the same set of data, it is difficult to decide which one is best suitable for us. There are several statistical tests that might help us decide which mathematical model or framework is the best fit for our data, but we will just consider MSE, RMSE, SSE, or R2.
2. Crystal Structure of Indium Phosphide (InP) [s, t]
Indium phosphide, a semiconductor, belongs to group IIIA-VA. Research of Vasil'Ev and Gachon [20] showed that on decomposing InP in bomb calorimeter, two forms of phosphorous (black and red) were found along with indium. Indium phosphide crystallizes in cubic form with lattice parameter value a : 5.861. Figure 1 demonstrates the crystal structure of InP [21].
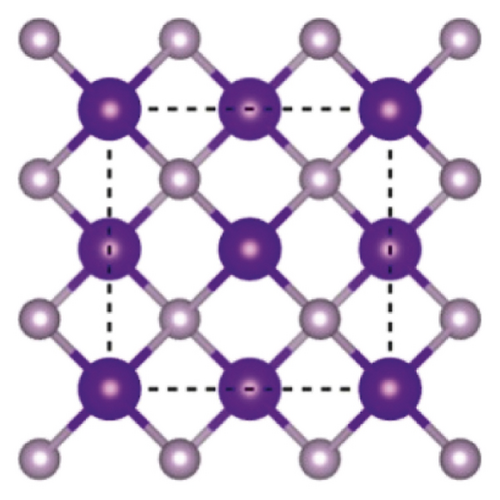
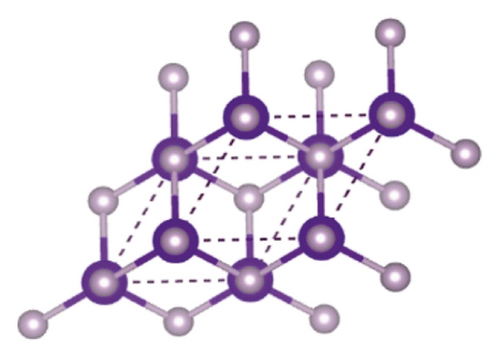
InP with bandgap 1.35 eV value [22] having low toxic nature, perfect composition, shape, and size as well as solution processability, is being used commercially for many years. Quantum dots (QDs) have got extraordinary importance because of having narrow emission line width, highest photoluminescence stability, reproducibility, and yield [23]. Figure 2 represents the synthesis method of InP QDs by adding indium acetate and palmitic acid in 50 ml three-neck flask attached with Schlenk line and having reflux condenser.
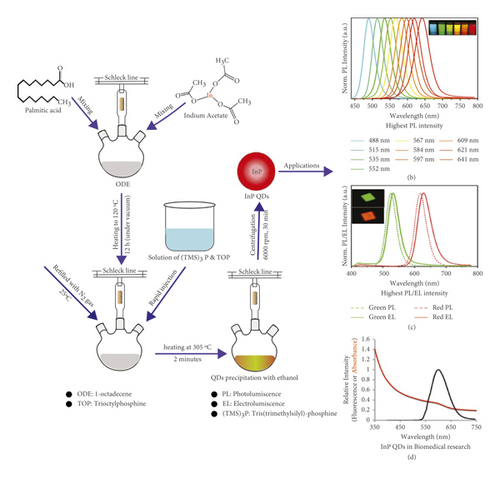
Then this mixture was heated up to 120°C for 12 hours. Then N2 gas was filled in the flask, and the temperature was decreased up to 25°C until the white turbid solution appeared. After this, a solution of (TMS)3P and TOP was quickly injected into the flask. Again heating was done up to 305°C for two minutes and then cool down to room temperature. Precipitated QDs were obtained that undergo centrifugation and washing for obtaining pure InP QDs [26]. InP QDs show highly luminescent power with a far-red absorption peak at 631 nm that makes InP QDs attractive for future applications [24]. Indium phosphide nanocrystal is a cadmium-free and low-toxic nanocrystal with extraordinary properties like the highest thermal conductivity, stokes shift emission [25], elongated electro and photoluminescence (PL) generation, near IR emitter, and highest PL quantum yield [27]. InP has got attention because of its high sensitivity for oxidation forming hydroxides and oxides surfaces. Gallium indium phosphide (GaInP) is a semiconductor that has enormous applications in water splitting by using solar energy. But, as its surface is relatively unstable because of corrosion in acidic media, its surface is modified via MoS2 nanoparticles. MoS2 NPs act as a protective layer and enhance catalysis of GaInP because of their anticorrosion properties and are highly recommended as water splitting photocathodes [28]. Indium phosphide is being used in photoelectrochemistry because of having a thin bandgap (1.35 eV) that can absorb solar radiations by decreasing the reflection of photons, resulting in the solar splitting of water. However, use of InP nanowire arrays on Si provides exceptional behavior in this field because of low cost, highest surface area, and catalytic properties [29]. Indium phosphide a promising candidate has proved its applications in optoelectronic as well as in electronic devices. However, nanostructured InP has demonstrated its future applications in the nanophotonic field and optoelectronic devices because of its extraordinary luminescence efficiency harvesting and energy scavenging properties [30]. A scalable artificial synapse based on InP was demonstrated for future applications with neuromorphic processors [31]. These devices when placed to neural spikes reveal the capability of learning without using any external circuit.
3. Degree-Based Indices for Indium Phosphide
The number of vertices and edges of InP [s, t] are 10st + 3s + 3t + 2 and 16st, respectively. Furthermore, Table 1 gives details about the edge partition, whereas the comparisons of the indices for InP [s, t] are given in Tables 2 and 3.
| (ς(u), ς(v)) | Frequency (total edges) | Set of edges |
|---|---|---|
| (1,4) | 4s + 4t − 4 | |
| (2,4) | 4st + 4s + 4t | |
| (4,4) | 8st − 4s − 4t |
| [s, t] | ||
|---|---|---|
| [1,1] | 16.84 | 14.51 |
| [2,2] | 62.41 | 55.76 |
| [3,3] | 133.23 | 120.56 |
| [4,4] | 229.30 | 208.90 |
| [5,5] | 350.62 | 320.79 |
| [6,6] | 497.20 | 456.21 |
| [7,7] | 669.03 | 615.18 |
| [s, t] | ||||
|---|---|---|---|---|
| [1,1] | 92 | 112 | 452 | 354 |
| [2,2] | 380 | 560 | 6,404 | 7,442 |
| [3,3] | 844 | 1,328 | 30,548 | 39,722 |
| [4,4] | 1,484 | 2,416 | 93,236 | 127,914 |
| [5,5] | 2,300 | 3,824 | 222,500 | 315,026 |
| [6,6] | 3,292 | 5,552 | 454,052 | 656,354 |
| [7,7] | 4,460 | 7,600 | 831,284 | 121,948 |
Theorem 1. Consider the graph of InP [s, t], which has s, t ≥ 1, and an atom bond connectivity index is corresponding to
Theorem 2. Consider the graph of InP [s, t], which has s, t ≥ 1, and geometric arithmetic index is corresponding to the following:
Theorem 3. Consider the graph of that has s, t ≥ 1, and the first and second Zagreb index are corresponding to
The Zagreb coindices for InP [s, t] are computed in Theorem 4.
Theorem 4. The first and second Zagreb coindices for the graph of InP [s, t] with s, t ≥ 1 are corresponding to
Theorem 5. The forgotten index for the graph of InP [s, t] with s, t ≥ 1 is corresponding to
Theorem 6. The forgotten index for the graph of InP [s, t] with s, t ≥ 1 is corresponding to
4. Heat of Formation and Entropy of Indium Phosphide
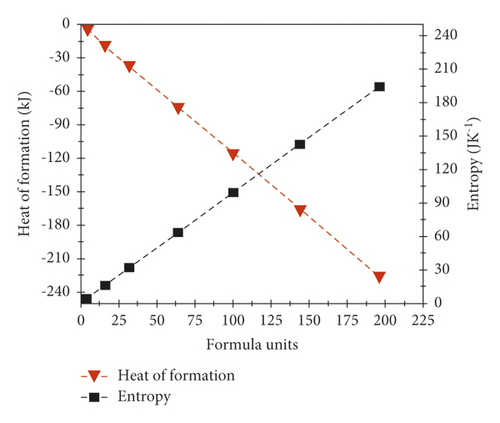
In Section 2, different topological indices , , , , , , , and are calculated for indium phosphide against a different number of unit cells [s, t]. These indices are interrelated with the thermodynamics of InP such as enthalpy/heat of formation and entropy. The values of heat of formation and entropy of InP for 1 ≤ p ≤ 7 and 1 ≤ q ≤ 7 number of unit cells are calculated in Table 4. Standard molar enthalpy of indium phosphide is −69.3 kJmol−14, and standard enthalpy for one formula unit was calculated by dividing standard molar enthalpy to Avogadro’s number. Then by multiplying this obtained value with a number of unit cells, enthalpy for that unit cell can be calculated. Standard molar entropy of indium phosphide is 59.75 Jk−1mol−1, and standard entropy for one formula unit was calculated by dividing standard molar entropy by Avogadro’s number. Then by multiplying this obtained value with a number of unit cells, entropy for that unit cell can be calculated. The result shows that both enthalpy and entropy increase with an increase in a number of unit cells. From the knowledge of equation S = kB lnW, where W represents microstates (locations/energies of molecules or atoms). As a number of microstates increases, it results in an increase of the entropy of system. See [32] for further explanation.
| [s, t] | Formula unites | Heat of formation | Entropy |
|---|---|---|---|
| [1,1] | 4 | −4.6044 | 3.973 |
| [2,2] | 16 | −0.18841 | 0.158 9 |
| [3,3] | 32 | −0.4143 | 0.357 6 |
| [4,4] | 64 | −0.7367 | 0.6357 |
| [5,5] | 100 | −0.0151 | 0.993 3 |
| [6,6] | 144 | −0.0165 | 0.014 3 |
| [7,7] | 196 | −0.0225 | 0.019 4 |
So, according to this equation as a number of moles increases, enthalpy also increases. See [33, 34] for further studies. As chemical graph theory has got a lot of importance in the field of thermochemistry [35], in this study, we demonstrated an explanation of thermodynamic parameters (enthalpy and entropy) of InP using graph theory for easy and better understanding. Tables 2, 3, and 5 are constructed against degree-based indices for InP, and Table 4 is presenting the numerical relation of enthalpy and entropy versus a number of unit cells.
| [s, t] | ||
|---|---|---|
| [1,1] | 308 | 105.48 |
| [2,2] | 1,356 | 587.85 |
| [3,3] | 3,076 | 1,437.62 |
| [4,4] | 5,468 | 2,654.81 |
| [5,5] | 8,532 | 4,239.40 |
| [6,6] | 12, 268 | 6,191.40 |
| [7,7] | 16 ,676 | 8,510.81 |
The graphical appearance of formula units and enthalpy/entropy is shown in Figure 3.
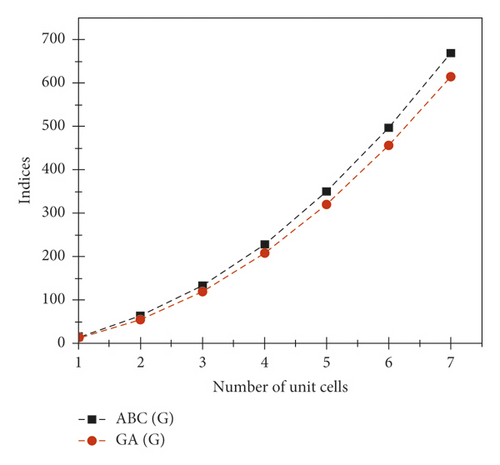
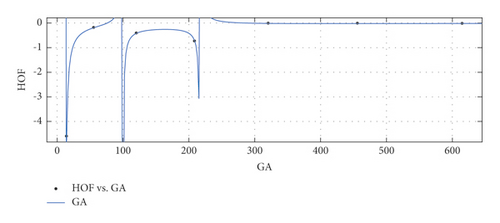
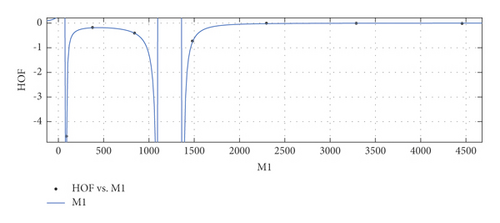
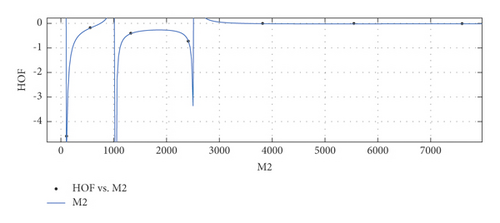
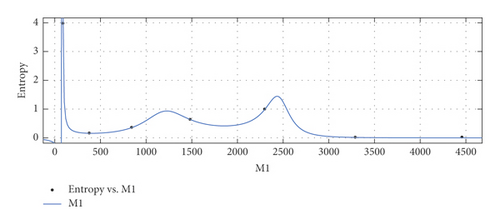
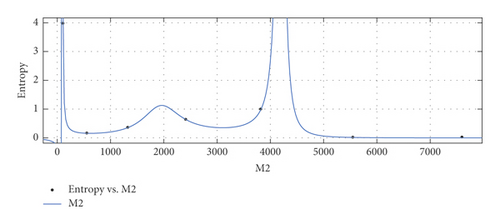
The graphical appearance of and indices is shown in Figure 4.
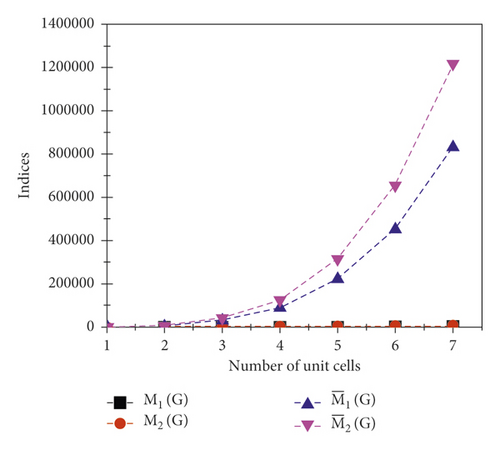
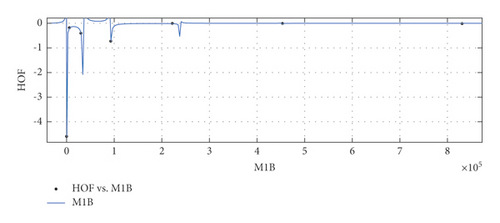
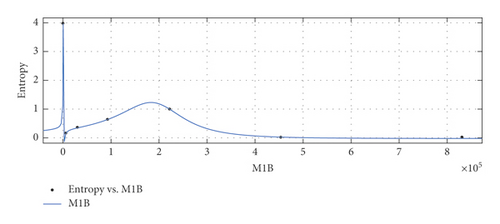
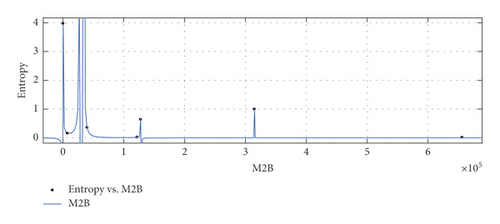
The graphical appearance of , , , and indices is shown in Figure 5.
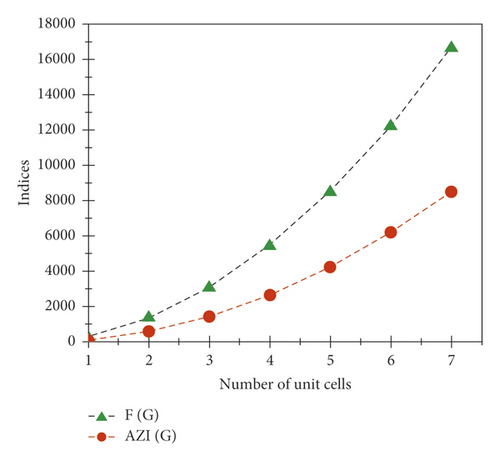
The graphical appearance of and indices is shown in Figure 6.
4.1. Graphical Models
4.1.1. Heat of Formation versus Indices
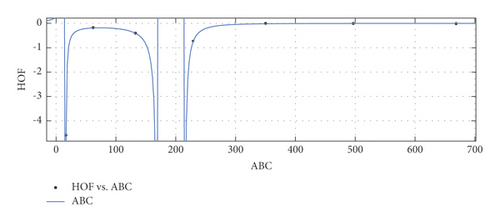
- (i)
General model between ABC and HoF
(25) -
where ABC is normalized by mean 279.8 and standard deviation (std) 239.5.
-
Coefficients: s1 = −0.01039(−0.01401, −0.006777), t1 = 1.837(1.802, 1.871), t2 = 0.936(0.895, 0.977), t3 = 0.1392(0.1352, 0.1431).
-
Goodness of fit: SSE : 0.0006455, R2 : 1, RMSE : 0.01467.
- (ii)
General model between GA and HoF
(26) -
where GA is normalized by mean 256 and std 220.7.
-
Coefficients: s1 = −0.05613(−0.2658, 0.1535), s2 = −0.03786(−0.1777, 0.102), s3 = 0.00644(−0.07428, 0.08716), t1 = 1.992(1.4, 2.584), t2 = 1.105(0.4798, 1.731), t3 = 0.1386(0.09797, 0.1793).
-
Goodness of fit:
-
SSE : 0.0006455, R2 : 1, RMSE : 0.01467.
- (iii)
General model between M1 and HoF
(27) -
where M1 is normalized by mean 1836 and std 1607.
-
Coefficients: s1 = −0.00246(−0.03719, 0.03227), s2 = −0.01174(−0.04567, 0.0222), t1 = 1.839(1.76, 1.917), t2 = 0.9497(0.8772, 1.022), t3 = 0.1455(0.1137, 0.1773).
-
Goodness of fit:
-
SSE:0.0006259, R2 : 1, RMSE : 0.01769.
- (iv)
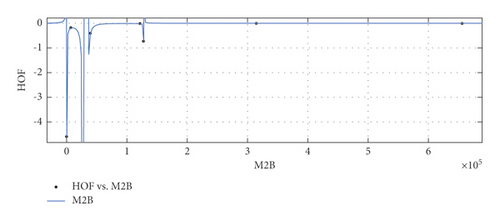
General model between M2 and HoF
(28) -
where M2 is normalized by mean 3056 and std 2762.
-
Coefficients: s1 = −0.0556(−0.2698, 0.1586), s2 = −0.03933(−0.1834, 0.1047), s3 = 0.005922(−0.0726, 0.08445), t1 = 2.005(1.382, 2.627), t2 = 1.141(0.4866, 1.795), t3 = 0.1528(0.116, 0.1897).
-
Goodness of fit:
-
SSE : 4.575e − 05, R2 : 1, RMSE : 0.006764.
- (v)
General model between and HoF
(29) -
where is normalized by mean 2.341e + 05 and std 3.09e + 05.
-
Coefficients: s1 = −0.0001032(−0.0003456, 0.0001393), t1 = 1.141(0.1373, 2.145), t2 = −0.1995(−1.352, 0.9535), t3 = −0.5754(−0.7905, −0.3603), t4 = −0.152(−0.7392, 0.4353), t5 = 0.001936(−0.1587, 0.1626).
-
Goodness of fit:
-
SSE : 0.0005061, R2 : 1, RMSE : 0.0225.
- (vi)
General model between and HoF
(30) -
where is normalized by mean 1.813e + 05 and std 2.356e + 05.
-
Coefficients: .
-
Goodness of fit:
-
SSE : 0.0002722, R2 : 1, RMSE : 0.0165.
- (vii)
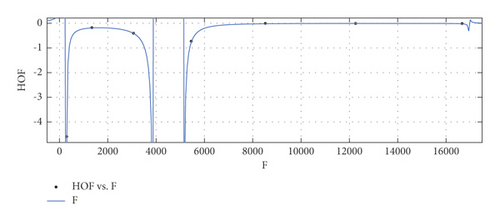
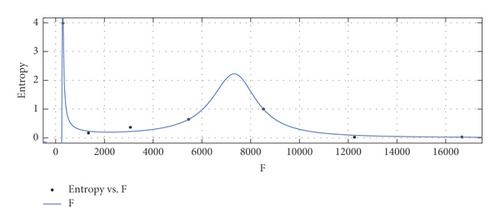
General model between F and HoF
(31) -
where F is normalized by mean 6812 and std 6026.
-
Coefficients: s1 = 0.06101(−1.386, 1.508), t1 = 3.727(−56.79, 64.24), t2 = −1.568(−8.373, 5.238), t3 = −9.128(−144.2, 125.9), t4 = −5.501(−97.13, 86.13), t5 = −0.8817(−16.64, 14.87).
-
Goodness of fit:
-
SSE : 0.0001397, R2 : 1, RMSE : 0.01182.
- (viii)
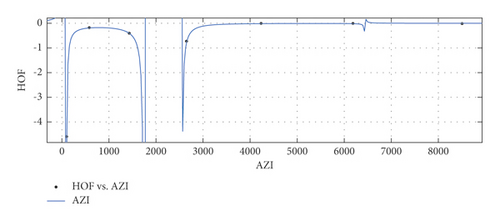
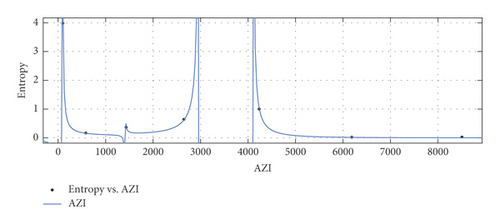
General model between AZI and HoF
(32) -
where AZI is normalized by mean 3390 and std 3103.
-
Coefficients: s1 = 0.01197(−0.4677, 0.4917), t1 = 2.682(−27.74, 33.11), t2 = 0.7507(−19.85, 21.35), t3 = −2.333(−40.24, 35.57), t4 = −1.639(−32.87, 29.59), t5 = −0.2712(−6.037, 5.494).
-
Goodness of fit:
-
SSE : 0.0005286, R2 : 1, RMSE : 0.02299.
4.1.2. Entropy versus Indices
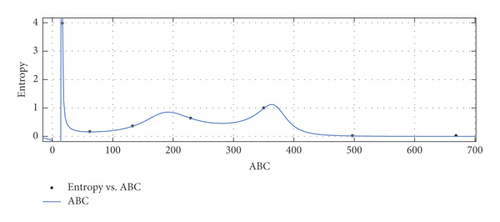
- (i)
General model between ABC and Ent
(33) -
where ABC is normalized by mean 279.8 and std 239.5.
-
Coefficients: s1 = 0.01564(−0.05774, 0.08902), t1 = 1.142(−4.961, 7.245), t2 = −0.1919(−9.587, 9.203), t3 = −0.2868(−2.726, 2.152), t4 = 0.002129(−0.8564, 0.8607), t5 = 0.03417(−0.2806, 0.3489).
-
Goodness of fit:
-
SSE : 0.0003434, R2 : 1, RMSE : 0.01853.
- (ii)
General model between GA and Ent
(34) -
where GA is normalized by mean 256 and std 220.7.
-
Coefficients: s1 = 0.05098(−0.01436,0.1163), t1 = 0.9197(0.7571, 1.082), t2 = −0.198(−0.3045, −0.09157), t3 = 0.004903(−0.09728, 0.1071).
-
Goodness of fit:
-
SSE : 0.03282, R2 : 0.9972, RMSE : 0.1046.
- (iii)
General model between M1 and Ent
(35) -
where M1 is normalized by mean 1836 and std 1607.
-
Coefficients: s1 = 0.01432(−0.04845, 0.07708), t1 = 1.109(−4.663, 6.881), t2 = −0.243(−9.205, 8.719), t3 = −0.311(−2.773, 2.151), t4 = 0.007164(−0.7696, 0.7839), t5 = 0.03441(−0.2578, 0.3267).
-
Goodness of fit:
-
SSE : 0.0003459, R2 : 1, RMSE : 0.0186.
- (iv)
General model between M2 and Ent
(36) -
where M2 is normalized by mean 3056 and std 2762.
-
Coefficients: s1 = 0.01231(−0.03602, 0.06064), t1 = 1.061(−4.145, 6.267), t2 = −0.3195(−8.509, 7.87), t3 = −0.3508(−2.786, 2.084), t4 = 0.01284(−0.6343, 0.66), t5 = 0.03482(−0.2217, 0.2913).
-
Goodness of fit:
-
SSE : 0.0003498, R2 : 1, RMSE : 0.0187.
- (v)
General model between and Ent
(37) -
where is normalized by mean 2.341e + 05 and std 3.09e + 05.
-
Coefficients: .
-
Goodness of fit:
-
SSE : 0.001714, R2 : 0.9999, RMSE : 0.0414.
- (vi)
General model between and Ent
(38) -
where is normalized by mean 1.813e + 05 and std 2.356e + 05.
-
Coefficients: .
-
Goodness of fit:
-
SSE : 0.0002045, R2 : 1, RMSE : 0.0143.
- (vii)
General model between F and Ent
(39) -
where F is normalized by mean 6812 and std 6026.
-
Coefficients: s1 = 0.04603(−0.3185, 0.4105), s2 = 0.08438(−0.2464, 0.4151), t1 = 0.9048(0.5207, 1.289), t2 = −0.1543(−0.4216, 0.113), t3 = 0.04557(−0.3887, 0.4799).
-
Goodness of fit:
-
SSE : 0.0295, R2 : 0.9975, RMSE : 0.1215.
- (viii)
General model between AZI and Ent
(40) -
where AZI is normalized by mean 3390 and std 3103.
-
Coefficients: s1 = 0.02359(−0.2106, 0.2578), s2 = 0.01545(−0.2138, 0.2447), t1 = 1.608(1.255, 1.961), t2 = 0.4886(0.3316, 0.6456), t3 = −0.1166(−0.1464, −0.08689), t4 = −0.02129(−0.2961, 0.2536).
-
Goodness of fit:
-
SSE : 0.0002636, R2 : 1, RMSE : 0.01624.

5. Conclusion
In this paper, we have focused to investigate the relationship between underlying graphical properties and the thermodynamical properties of indium phosphide. Figure 2 clearly depicts the synthesis of indium phosphide in a systematic way as explained before. At first, the topological degree-based indices were calculated that were lately integrated with thermodynamical properties of indium phosphide. Such a link had been established by fitting the curve between each index and each thermodynamical property. Entropy and heat of formation are two types of thermodynamical properties that were indulged in this study. The rational fitting method was applied using MATLAB software as this method was providing the least mean squared error among all built-in methods. Such a multidisciplinary approach would provide a comprehensive insight into the structural properties of indium phosphide in more detail and depth. [36].
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Authors’ Contributions
All authors contributed equally to this study.
Acknowledgments
This research project is supported by the Natural Science Foundation of Anhui Province Higher School (KJ2021A1154).
Open Research
Data Availability
The data used to support the findings of this study are cited at relevant places within the text as references.




