The use of slab tracks in lieu of ballast tracks has introduced new dimensions in track dynamics in high-speed railways. To improve the performance of slab tracks under dynamic frequency responses caused by loads on the Shinkansen railway, the present study aimed to investigate the effect of mechanical properties of track components, including the elasticity modulus and thickness on the resonance frequency of the vertical dynamic responses using the finite element method. Such responses included receptance and decay rate in the asphalt bearing layer (ABL), hydraulically bonded layer (HBL), and concrete bearing layer (CBL). In addition, the study sought to select the optimal layer as an effective layer in the view of reducing the resonance frequency of dynamic responses in comparison with the general model. Based on the data regarding the effects of elasticity modulus and thickness of slab track layers on the resonance of the dynamic frequency responses under the amplitude loads, by changing the load from 20 to 25 tons over the slab track, the receptance under the modulus and thickness change increased up to 34 and 29%. Moreover, the decay rate under the modulus and thickness change increased up to 31 and 37%. Accordingly, by increasing the load amplitude, the CBL and HBL showed lower dynamic responses than other layers. Thus, CBL and HBL were selected as the optimum layers for improving the performance of the slab track of the Shinkansen railway.

1. Introduction

Investigating the effect of dynamic response at low frequency is important. At low-frequency vibration, the environmental problem is the main concern of the track structure for high-speed railways [1, 2]. Furthermore, when a train runs on a track at low frequencies, the interaction force between wheels and rails generates vibration in dynamic frequency responses, including receptance and decay rate on the track structure in high-speed lines. Dynamic frequency responses are transmitted through the infrastructure and the surrounding soil into nearby buildings, and consequently, disturbances for people’s lives and sensitive structures occur [3, 4]. Specifically, other studies showed that under low-frequency vibration, the dynamic responses including receptance and decay rate on the slab track reach their critical regions in which the performance of slab track decreases. In addition, the effect of low-frequency ranges between 1 and 15 Hz on the growth of the resonance frequency of decay rate, and receptance and their amplitudes go up as frequency is decreased, and vice versa [5–7]. Slab tracks in high-speed railways have increased over time [8, 9]. These tracks have been employed as a need in the railway industry considering the reduced maintenance costs, increased bearing capacity, increased speed, and reduced vibration and settlement compared to ballast tracks [10, 11]. The railway tracks are modeled to affect the dynamic behavior, decay, and noise caused by the train’s vibration moving on the rails. The modeling of railway tracks also examines the impact of dynamic track behavior on the slab and ballast tracks, decay, and settlement of the tracks [12]. The decay rate in track components under the thickness and elasticity modulus of layers in railway slab tracks is lower than ballast tracks, leading to significant reductions in repair and maintenance operations. However, repair costs will be higher in the event of the decay in slab tracks compared to ballast tracks. In addition, the vibrations in the slab track increase due to the removal of the ballast and its replacement by the concrete bearing layer (CBL) compared to the ballast track. The lack of accurate knowledge of the track dynamic behavior in train passage conditions is one of the main problems under low frequency in the design of these tracks. Due to the incorrect design, huge costs may be incurred for the repair and maintenance after the implementation. On the other hand, the noise caused by the train movement on the track due to train vibration is an important factor influencing the railway track’s performance [13, 14].

Accordingly, having a thorough understanding of these tracks’ behavior and dynamic performance mechanism is a prerequisite for railway track engineering. Therefore, using track frequency response functions is considered important for achieving this goal. Due to the dynamic nature of the moving trainload on the railway and the varying intensity proportional to time, the track frequency response function is one of the most important parameters that provide good analytical data in the frequency domain. Currently, various slab tracks are implemented in the world. Therefore, the frequency response and noise resulting from the train movement on the rail are significant in identifying the railway track’s dynamic behavior [15]. Thus, the potential decay of rail tracks can be reduced by identifying these two factors. Moreover, these studies can be performed using the finite element method (FEM) under the influence of low, medium, and high frequencies to observe the effect of each layer on the performance of the railway tracks. The Shinkansen model is one of the most widely used railway tracks [16].

Therefore, to improve the slab track’s performance for the Shinkansen railway, it is vital first to investigate the effect of low frequency on the resonance frequency of dynamic responses to find out the critical points under low frequency. Second, the present study is aimed to propose CBL, asphalt bearing layer (ABL), and hydraulically bonded layer (HBL) as the most common stabilizing layers for the resonance frequency generated by the low frequency in terms of changing mechanical properties such as modulus change and thickness change. Accordingly, in this study, with the three-dimensional (3D) modeling of this track using the FEM, the vertical dynamic behavior is examined to investigate the effect of dimensional and mechanical parameters of track components on the resonance frequency of dynamic responses. The above-mentioned track components included the elasticity modulus and thickness of ABL, HBL, and CBL. Finally, the obtained data from all layers are presented based on thickness changes and elasticity modulus changes to compare each layer’s effectiveness in the vertical dynamic behaviors of the track, including receptance and decay rate. Then, prioritizing the effect of the dimensional and mechanical parameters of Shinkansen slab track components (e.g., ABL, HBL, and CBL) on the receptance and track decay rate is examined and compared with the general model. Thus, the present study mainly contributes to helping railway engineers and the railway industry accurately apply the slab track pavement for high-speed railways such as the Shinkansen railway to prevent deterioration in the pavement structure to minimize repairs and costs in the future. Additionally, the proposed method can predict dynamic responses regarding modeling the behavior of the slab for optimum layer designing for high-speed railway infrastructures. The remaining sections of the present study are organized as follows.

Section 2 examines previous studies related to the effect of elasticity modulus and thickness under the vertical dynamic response of the slab track, including receptance and decay rate. In Section 3, the focus is on modeling and slab track components (e.g., ABL, HBL, and CBL) to evaluate the dynamic behavior of track frequency responses (e.g., receptance and decay rate) and hypotheses in the modeling according to the Euler–Bernoulli beam theory in ABAQUS using the FEM. The data relating to changes in elasticity modulus and thickness on Shinkansen slab track layers are discussed in Section 4 and verified according to the previous studies. Finally, Section 5 draws conclusions based on the findings.

2. Literature Review

This section focuses on studies related to examining the effect of the slab track on dynamic frequency responses and the interaction between wheelsets and the rail considering the effects of changes in the modulus and thickness on the track slab.

In this regard, Madshus et al. simulated the vibration caused by the movement of a train on the land around the railway track. They found that increasing track stiffness by creating rigid concrete beams in the subgrade significantly reduces the vibrations created in the land around the track [17]. Likewise, Nguyen et al. analyzed the dynamics of high-speed traffic loads on ballast tracks using a two-axle bogie model for the loading. They concluded that dynamic responses are highly sensitive to rail surface unevenness and decay and the train movement speed [18]. In another study, Sayeed and Shahin modeled the foundation of the ballasted railway to investigate the track dynamics at the critical speed and reported that the amplitude of dynamic track responses suddenly increases when the train speed reaches 75% of the critical speed [19]. One study also evaluated the dynamic modeling of slab tracks. It showed that increasing the track stiffness is highly suitable for reducing the vibrations at high frequencies, while improving the soil subgrade quality is a more appropriate solution at low frequencies [20]. Lei and Zhang presented a new slab track model by studying the structural features of China’s slab track system and its dynamic behavior. Their findings demonstrated that the stiffness of the rail pad and the soil subgrade were effective factors in controlling the dynamic response of the track [21]. Similarly, Zhu et al. studied the effect of track decay on the dynamic response of the concrete structure in a high-speed railway using rail modeling as a beam element by discrete support. They found that among track components, the rail followed by the track slab had the highest receptance [22]. In their study, Shi et al. reported that the resonance frequency of the track on the sand subgrade has the most important effect on the track frequency response under the vertical dynamic response [23]. According to the survey, it was revealed that CBL is appropriate according to lower maintenance requirements and higher availability and the reduction of structure height for high-speed railways such as the Shinkansen in the world [24–26]. Using the static and dynamic behavior of three different types of railway in the track area, Real et al. showed that the slope of stiffness changes in the transition zone between the slab and ballast tracks decreases by decreasing the stiffness of the rubber around the embedded rail [27]. Moreover, Shuber et al. investigated the performance of the railway track system under the harmonic load by the FEM. They represented that the railway track performance depends on the type of the pad, the ballast, the soil, and the interaction of forces between the track and the rail [28]. In another study, Aggestam et al. indicated that the CBL was affected by a frequency response less than the ballast layer based on the receptance [29]. Likewise, Arlaud et al. focused on the numerical modeling of the receptance of high-speed railway tracks at low frequency using the FEM based on elastic materials without considering wheelsets and rail interaction. The findings revealed that under low frequency, receptance significantly increased for minimizing the level of track vibrations to prevent deterioration [5]. According to the Shinkansen railway, Ling et al. conducted research based on modeling a 3D dynamic model of a high-speed train coupled with a flexible ballast track to characterize dynamic performances, including vibration frequency response, ride comfort, and curving performance [30]. They concluded that the 3D dynamic model was appropriate for investigating dynamic performances. Furthermore, Sayeed modeled the dynamic behavior of the ballasted railway track of high-speed railways based on the Shinkansen railway using the FEM and concluded that the amplitude of dynamic track response increases uniformly with the amplitude of train loading and resonance [31]. Moreover, Knothe and Grassie modeled the dynamic analysis of the frequency response in the ballast track in high-speed railways using the multi-rigid-body system dynamics theory. It was found that when the vehicle is treated to be rigid bodies, the vehicle’s components were connected with spring and damping elements under low frequency, and the interaction between wheelsets and the rail is ignored [32]. Zhai et al. also used the multi-rigid-body system to implement the dynamic analysis of frequency response in the rail track to simplify the complexity of the effect of dynamic frequency response in high-speed railways for railway vehicle stability, comfort, and safety assessment [33]. Other studies focused on investigating the dynamic response of track regarding elastic modulus in track materials under the rigid body motion using FEM to prevent any complex problems and simplify the dynamical behavior of train/track in high-speed railways without considering the interaction between wheelsets and the rail [34–40]. Similarly, some studies followed the Carter theory to analyze dynamic frequency response at low frequency and elastic materials. The Carter theory assumes first that the contact surface to a rectangular and uniform strip. Second, the interaction of wheelsets and the rail is not considered since the interaction force is rather small when the train moves in high-speed railways. Additionally, these studies considered a steady-state dynamic analysis in which the rails were well-maintained and perfectly straight in the longitudinal direction based on the multi-body approach while not taking the interaction of the rail and wheelsets into account [16, 41–43].

Fattah et al. [44] also conducted research based on experimental and numerical behavior of railway track over geogrid reinforced ballast underlain by soft clay. They indicated that the ballast over the track reduces the dynamic frequency responses. Majeed et al. [45] evaluated the effect of the low load frequency on the track rail and subgrade layer to improve the dynamic response and settlement. They showed that by an increase of the amplitude load and the load frequency, consequently, the settlement of the subgrade layer settlement is decreased. Other studies also indicated that geogrid reinforcement improves the railway track by reducing the dynamic frequency response and settlement [46, 47]. Fattah et al. [48] also focused on investigating the stress distribution from railway track over geogrid reinforced ballast underlain by clay. They found that the position of the geogrid had no significant effect on the transmitted stresses. This means that the ballast attenuated the induced waves.

Based on the summary of the literature review given in Table 1, it can be seen that no study was available regarding examining the effect of the modulus and thickness of the Shinkansen slab track components under the dynamic frequency responses using the FEM. In addition, until now, there has been no study to select the optimum layer of the Shinkansen slab track under the effect of the modulus and thickness change of the slab track layers considering the various dynamic frequency response and vehicle loading using the FEM. Despite the other studies, the current research seeks to select the most effective layer throughout CBL, HBL, and ABL compared with the general model regarding the two vertical dynamic responses such as receptance and decay rate by elasticity modulus and thickness changes and various vehicle loading using the FEM.

1. Summary of the literature review.

Author	Subject	Method	Track components	Conclusion
Arlaud et al. [5]	Modeling of the receptance of high-speed railway tracks at low frequency	The rigid body motion using FEM	Sleeper track	Low frequency leading to an increase in the receptance

Madshus et al. [17]	Simulating the vibration caused by the movement of a train on the railway track	The rigid body motion using FEM	The sleeper track	Increasing track stiffness leading to reducing the vibrations

Nguyen et al. [18]	Analyzing the dynamic frequency of high-speed traffic loads	A two-axle bogie model	Ballast track	Sensation of the dynamic responses to the rail decay rate

Sayeed and Shahin [19]	Investigating the track dynamics at the critical speed	The rigid body motion using FEM	The ballasted railway	Increasing the amplitude of dynamic track responses in the high-speed railways

Steenbergen et al. [20]	Evaluating the dynamic modeling of slab track	The rigid body motion using FEM	Sleeper track	Increasing the track stiffness for reducing the vibrations

Lei and Zhang [21]	Studying the structural features of China’s slab track system and its dynamic behavior	The rigid body motion using FEM	Sleeper track	Controlling the dynamic response of the track by the stiffness of the rail pad and the soil subgrade

Zhu et al. [22]	Studying the effect of track decay on the slab track in a high-speed railway	The rigid body motion using a beam element	Sleeper track	The track slab with the highest receptance values

Shi et al. [23]	Investigation of the resonance frequency of the track under the vertical dynamic response	Elastic modulus in track materials under the rigid body motion	Subgrade track	The resonance frequency of the track on the sand subgrade with the most important effect on the track frequency response

Other studies [24–27]	Investigating the dynamic response of slab track	Rigid body motion using FEM	Sleeper track	Simplifying the dynamical behavior of train/track in high-speed railways

Real et al. [28]	Evaluating the performance of the railway track system under the harmonic load	The rigid body motion using FEM	Track system, the pad, the ballast, and the soil	The railway track performance depending on the track system and the interaction of forces between the track and the rail

Aggestam et al. [29]	Investigating the dynamic response of the slab track components	The rigid body motion using FEM	CBL	CBL is less affecting than the ballast layer under the receptance

Ling et al. [30]	Modeling a 3D dynamic model of a track high-speed train	The rigid body motion using FEM	The ballasted track	The 3D dynamic model as an appropriate performance for investigating dynamic performances

Sayeed [31]	Modeling the dynamic behavior of the railway track of high-speed railways	The Shinkansen railway using the FEM	The ballasted railway track	Increasing the amplitude of dynamic track response stabilizing the resonance

Knothe and Grassie [32]	Modeling the dynamic analysis of the frequency response in high-speed railways	The multi-rigid-body system	The ballasted track	Elastic materials based on the multi-rigid-body used for damping dynamic frequency response

Zhai et al. [33]	Modeling the dynamic analysis of the frequency response in the slab track	The multi-rigid-body system	The sleeper track	Simplifying the complexity of the effect of dynamic frequency response in high-speed railways

Other studies [34–40]	Investigating the dynamic response of the rail track	Elastic modulus in track materials under the rigid body motion using FEM	The sleeper track	Simplifying the dynamical behavior of train/track in high-speed railways

Fattah et al. [44]	Evaluating the effect of track speed on the behavior of railway track	Ballast system underlain by clay	The ballasted track	Geogrid reinforcement with the improvement of the railway track

Majeed et al. [45]	Evaluation of the effect of the low load frequency on the settlement of railway track	Reinforced ballast overlain by clayey	Subgrade layer settlement	An increase of the amplitude load, and the load frequency, leading to the reduction of the settlement of the subgrade layer

Fattah et al. [46]	Studying settlement of railway track	Reinforced ballast overlain by clayey	The ballasted track	The geogrid leading to a reduction of settlement of railway track

3. Method

To investigate the modulus and thickness effects of Shinkansen slab track components such as CBL, HBL, and ABL on the resonance frequency using FEM, first, model specifications and material characteristics are defined in ABAQUS software, followed by using the two concepts of receptance and track decay rate. The frequency response is used for the validation according to the method of Craig and Kurdila. Then, the modeling of the slab track is considered based on the Euler–Bernoulli beam theory under the harmonic loading of the unit with a length of 30 m [49]. The following sections describe the characteristics of the Shinkansen slab track, dynamic frequency responses, and the modeling procedure.

3.1. Shinkansen Slab Track

The Shinkansen slab track system was first designed and used in Japan in 1972. Figures 1(a) and 1(b) show the Shinkansen slab track geometry and the sleeper cross-section, respectively, along with the details of the layers of track components according to the specifications of the Shinkansen track design in ABAQUS. According to the Shinkansen railway design slab track, the slabs are held longitudinally and laterally by a concrete dowel with 400 mm dia, which is rigidly connected with slab layers. In addition, an elastic layer or a foam plate is applied to avoid the transmission of longitudinal forces and minimize the difference in stiffness between the rigid structure and the track laid on the subsoil. Therefore, in the modeling procedure, the minimum foam plate length is 3.50 m, placed straight on the trough bottom slab. Depending on the subsoil condition and bearing ability, a wedge made of soil and cement can be implemented [24–26]. Table 2 presents the characteristics of the required materials for the modeling of the Shinkansen track in detail. In the modeling, the stiffness and damping of the rail pad are considered as 239 MN/m and 500 kNs/m, respectively. Furthermore, sleepers are placed over CBL, ABL, and HBL, and spacing between them is 0.625 m as shown in Figure 1(b). Moreover, a unit harmonic load in the middle of the slab and between two adjacent sleepers is considered to examine the dynamic frequency responses [24–26].

Details are in the caption following the image — Open in figure viewer PowerPoint

2. Mechanical properties of Shinkansen track components [16].

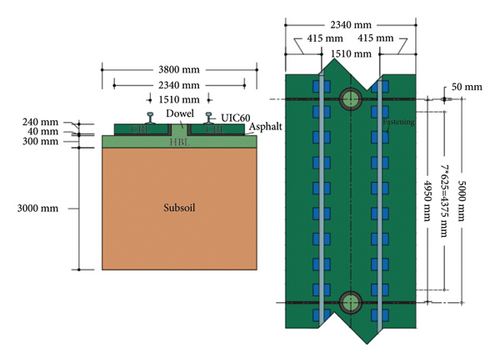
Track components	Unit weight, γ, (kN/m³)	Elasticity modulus, E, (GPa)	Poisson’s ratio, ν	Damping ratio
Rail	76.98	207	0.28	0.015
Sleeper	23.54	70	0.2	0.013
Concrete bearing layer	23.54	35	0.2	0.030
Asphalt bearing layer	22.55	0.2	0.2	0.035
Hydraulically bonded layer	23.54	5	0.2	0.035
Soil subgrade	19.61	0.01	0.4	0.039

3.2. Receptance

Receptance is defined as the ratio of structure deformation to the applied load. Therefore, this parameter indicates the deformation in the unit of meter per newton (m/N) of the applied load. Furthermore, it is the inverse of track stiffness. Additionally, the receptance function is a member of the set of frequency response functions that represents the vibration amplitude of the track structure as a function of the vibration frequency and more accurately displays the deformation of the track structure under unit harmonic excitation [50]. Receptance functions can be obtained by field measurements and structural analysis. A linear system includes F(ρ), H(ρ), and X(ρ) denoting input load as a function of the angular frequency, transfer function, and system deformation response function, respectively. All functions can be complex and represented by the magnitude and phase expressions. The transfer function, which indicates the ratio of deformation to force, is called the “receptance function.” This function can also be represented by magnitude and phase angle expressions. In multi-degree-of-freedom systems (e.g., railway systems), the receptance function can be expressed by equations (1) to (3) [51].

(1)

(2)

(3)

where ω, ω_n, N, and ξ imply the angular frequency of load excitation (rad/sec), the natural angular frequency of mode r (rad/sec), the total number of degrees of freedom, and damping ratio, respectively. In addition, ϕ_ir and H_ij(ρ) demonstrate the element of row i and column r of the modal matrix and the receptance function at point i for harmonic excitation at point j, respectively.

3.3. Track Decay Rate

Decay rate estimation is one of the methods for evaluating the effect of harmonic loads on the response of the frequency level caused by the train movement on the track. The decay rate is defined as the ratio of the vibration caused by the movement of loads to the deformation of the structure. This parameter represents the change in sound or vibration (dB) in meter (dB/m). This method was first presented by Janssens et al. for calculating the vibration resulting from the movement of train wheels on track rails [52]. The track decay rate is calculated according to the following formula, where L₁ is a highly short distance to the center of the rail wheel. In this study, it is considered 1.8 m away from the center of each wheel, and the decay rate is obtained by (4). The track decay rate according to (5) is obtained by substituting equation (4) into equation (1). Therefore, to obtain the track decay caused by the response frequency, equation (5) is presented, where D(f) denotes the track decay rate in the slab track length L₁.

(4)

(5)

where ω_n, N, and ξ imply the natural angular frequency of mode r (rad/sec), the total number of degrees of freedom, and the damping ratio, respectively. In addition, ϕ_ir and H_ij(ρ) demonstrate the element of row i and column r of the modal matrix and the receptance function at point i for harmonic excitation at point j, respectively.

3.4. Modeling Procedure

In this study, the dynamic effects of the components of the Shinkansen slab track were investigated by the FEM in ABAQUS software. The slab track length was 30 m, and the rail modeling was performed based on the UIC60 rail model and the Euler–Bernoulli beam theory. Furthermore, elastic materials placed under the slab have been effective due to the minimum stiffness and minimum slab displacements of the subsoil in relation to train passenger’s comfort and critical speeds under the low-frequency regime [16, 20, 35, 38, 43]. Therefore, track components are assumed to be elastic in the modeling. The beam and the deformable eight-node 3D elements are used in the rail modeling and other components, respectively. The theory of beam on discrete supports controls the modeling. To simulate the viscoelastic behavior of the rail pad, a parallel spring and a damper are used in the modeling.

To simulate infinite boundary conditions in track components, displacements are limited to the normal direction [16, 43, 49, 50]. The slab and rail are fastened at both ends. A finite length of the track is suitable since the model uses finite elements and time-domain analysis. This implies that the reflections of vibrations could occur at the ends. For this reason, structure-borne vibration energy is not fully transmitted away from the excitation in terms of the dynamic response according to the Carter theory under the steady-state dynamic analysis and the multi-body approach at low frequency [34–43]. Thus, the Carter theory at low frequency, infinite boundary conditions in track components, and displacements are limited to normal conditions. However, this effect could be negligible at the center of the track if the length of the model is sufficient. Moreover, the length of the track model is set to 30 m, which results in a small boundary effect on the receptance, decay rate, and consequently slab track displacement. Therefore, the slab model is considered a finite length [53]. However, in the simulations of vehicle-track interaction, these boundary effects are small and considered negligible. Since the rail is modeled by the Euler–Bernoulli beam elements, there is a (nonphysical) discontinuity in slope over the element boundaries due to the applied interpolation polynomials. Thus, insignificant disturbances in the wheel-rail contact force are observed when an element boundary is passed using Euler–Bernoulli beam elements [43, 53, 54].

In addition, the interactions of the rail and wheelsets are not considered according to the Carter theory. Therefore, vertical dynamic responses are examined under the steady-state dynamic analysis, and a unit harmonic load is applied to the middle of the track between the two sleepers, exciting the whole track in the frequency range of 1 to 15 Hz. In addition, in order to investigate the effect of the modulus and thick change of the slab track components, the amplitude loads 20 and 25 tons are applied in the frequency range of 1 to 15 Hz. The amplitude loads are applied regarding the vehicle load of the Shinkansen railway [24–26, 30, 31].

4. Results

In this section, the research findings are examined in terms of the effects of elasticity modulus and thickness on the general model, and the ABL, HBL, and CBL of the Shinkansen slab track regarding the resonance frequency of dynamic frequency responses such as receptance and track decay rate under vehicle loading are taken into account in the following sections.

4.1. Validation of Frequency Response

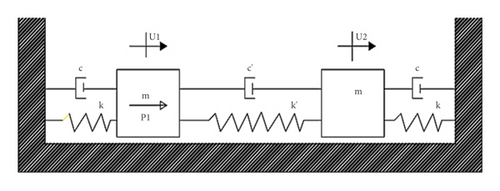
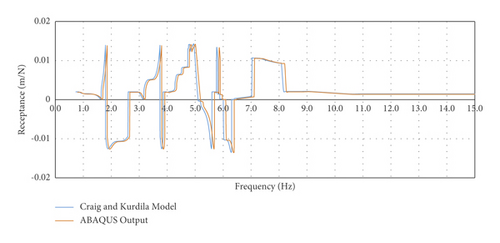
Due to the complexity of dynamic analysis in ABAQUS, the prevention of errors, and ensuring the validity of output findings, a model with two degrees of freedom consisting of mass and spring was modeled in Figure 2(a) based on the study of Craig and Kurdila [44]. In this model, two degrees of freedom are shown in Figure 2(b), where p₁(t) = P₁Cos(ωt), k = 987 kips/in, k^′ = 217 kips/in, m = 1 kip-sec²/in, c = 0.6284 kip-sec/in, and c^′ = 0.0628 kip-sec/in. First, the structure is subjected to frequency analysis, and dynamic frequency responses are evaluated accordingly. The natural frequency of the structure for the general model extracted from ABAQUS output is shown in Figure 2(c) under 1 to 15 Hz to validate the dynamic response based on the study of Craig and Kurdila [49]. As shown in Figure 2(c), the oscillations of the receptance have fluctuating behavior up until by increasing the natural frequency causing stability behavior for both models. Thus, this behavior validates that the natural frequency for oscillation of dynamic response is consistent with the study of Craig and Kurdila [49].

In order to study the all-natural frequency over the slab track, Figure 3 shows the sensitivity of most vibration mode diagrams of track structure with the study of Feng [53] under the load frequency 1 to 3 Hz. Other vibration modes are summarized in Table 3. As shown, it can be inferred that under the unit harmonic excitation, the observed natural frequency over the slab track is in line with the natural frequency tested in the study of Feng [53] due to the low errors observed in vibration modes.

3. Comparison of natural frequency (Hz).

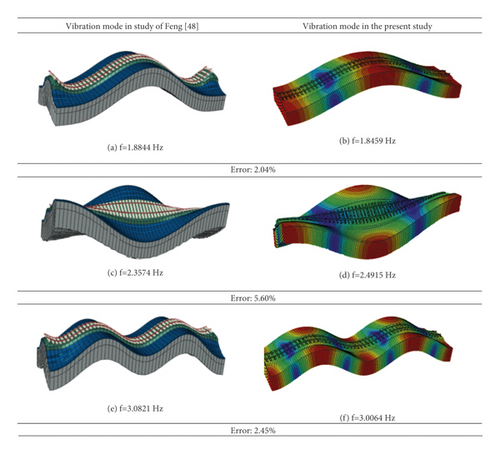
Mode number	Feng [53]	The present study	Error
1	1.8844	1.8459	0.0204
2	2.3574	2.4915	0.0569
3	3.0821	3.0064	0.0246
4	3.8457	3.7713	0.0193
5	4.6165	4.5414	0.0163
6	5.3950	5.3191	0.0141
7	6.1811	6.1045	0.0124
8	6.9751	6.8977	0.0111
9	7.7769	7.6987	0.0100
10	8.5866	8.5077	0.0092
11	9.4044	9.3247	0.0085
12	10.2303	10.1498	0.0079
13	11.0643	10.9830	0.0073
14	11.9066	11.8245	0.0069
15	12.7573	12.6744	0.0065
16	13.6163	13.5326	0.0061
17	14.4839	14.3993	0.0058
18	15.3601	15.2747	0.0056

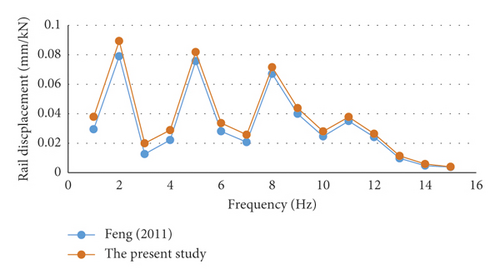
Furthermore, a comparative evaluation of rail displacements was implemented to verify the dynamic response obtained over the slab track. The results of the predicted low frequency were obtained with the study of Feng to estimate the rail displacements for the rail rested on the infinite Euler–Bernoulli cantilever beam under a unit harmonic excitation [53]. As shown in Table 3, it is evident that there is a low and insignificant difference for the applied frequency under two-degree freedom, confirming that the predicted frequency is in line with the refereed study. According to Figure 4, it can be observed that the deflection estimated in the present study has a good correlation and acceptable agreement with the study of Feng [53]. Thus, verification for the frequency and displacements is approved. According to this verification, it can be concluded that dynamic response can be applied for investigating the effects of modulus change and thickness change of the slab track components on dynamic frequency responses.

4.2. Effect of Modulus and Thickness in CBL on the Resonance Frequency

To examine the effect of modulus and thickness in CBL on the resonance frequency of receptance and decay rate, receptance and decay rate were obtained according to equations (1) to (5) under the frequency ranges of 1 to 15 Hz (Figures 5 and 6). As shown in Figures 5(a) and 5(b), the damping oscillations for the dynamic response frequency of receptance and decay rate are increased by increasing frequency for all models. Consequently, the amplitudes are decreased. Additionally, maximum receptance values are reached as the CBL modulus is increased. This implies that increasing CBL modulus causes an increase in receptance. However, a decrease in CBL modulus has no significant effect on damping the oscillation of the resonance frequency of receptance, implying that CBL has similar behavior to the general model in damping oscillations. Furthermore, increasing CBL modulus leads to decreasing decay rate for all models. Similarly, the stiffness of CBL decreases as the elasticity modulus decreases, leading to an increase in the resonance frequency of the decay rate in which damping the oscillations represents a decrease.

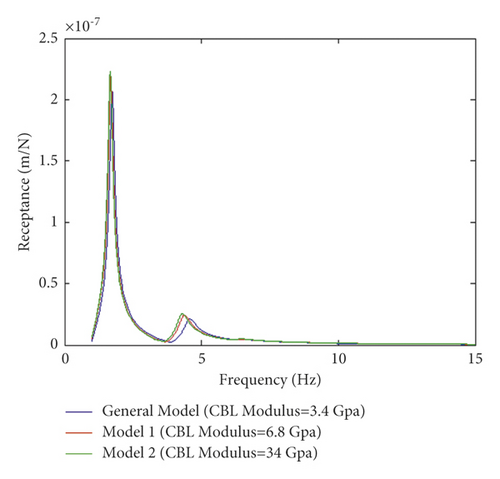
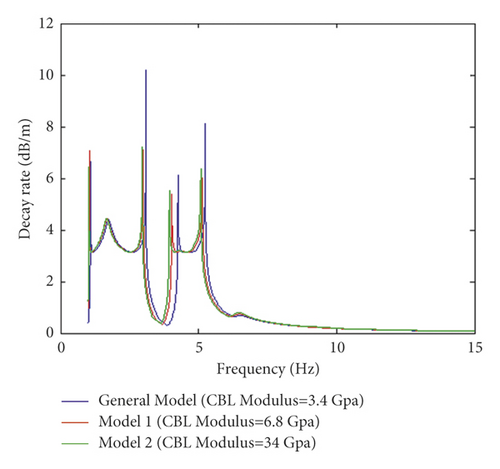
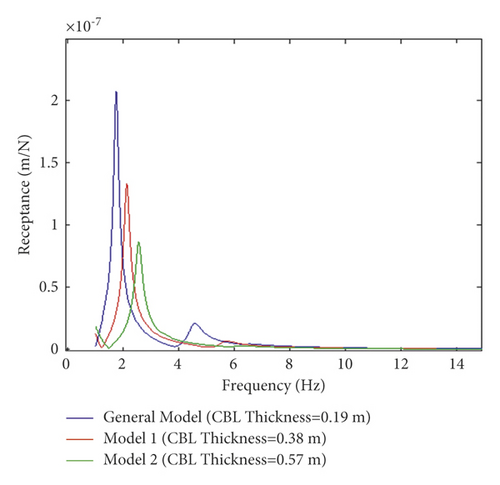
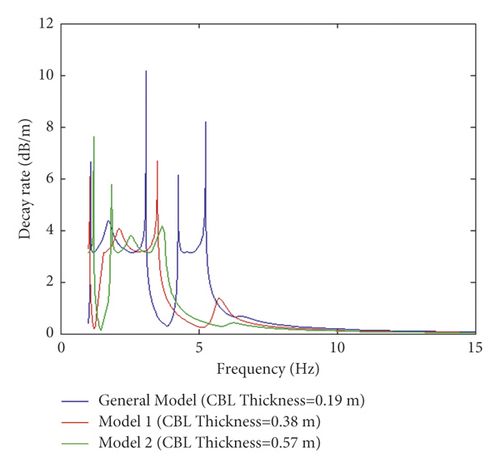
Figures 6(a) and 6(b) show the effect of changing the thickness of CBL from 19 to 57 cm on the resonance frequency of the receptance and track decay rate, respectively. Moreover, maximum receptance and decay rate are observed as the CBL thickness is decreased. An increase in the thickness of the CBL results in an increase in the stiffness of the layer, leading to reductions in the resonance frequency of receptance and the track decay rate on the layer and thus an increase in damping oscillations. Damping the oscillations causes a decline in vertical dynamic responses on the slab track strengthening the slab track. Therefore, by a comparative evaluation of Figures 5 and 6, it can be concluded that decreasing modulus does not significantly affect the damping oscillation of dynamic responses and their resonance in CBL. However, increasing the thickness has a positive impact on damping oscillation of dynamic responses and improving the CBL into the slab track as frequency increases.

4.3. Effect of Modulus and Thickness in HBL on the Resonance Frequency

To evaluate the effect of modulus and thickness in HBL on the resonance frequency of receptance and decay rate, receptance and decay rate were obtained based on equations (1) to (5) under the frequency ranges from 1 to 15 Hz (Figures 7 and 8). As depicted in Figures 7(a) and 7(b), by increasing frequency, the damping oscillation on dynamic responses including receptance and decay rate are increased, whereas their amplitudes decrease. For receptance and decay rate, as the elasticity modulus decreases, the stiffness of the HBL decreases, and thereby, dynamic responses are increased (Figures 7(a) and 7(b)). Increasing amplitudes decrease the effect of damping oscillation on dynamic responses. Furthermore, similar behavior is observed for the resonance frequency in which by reducing the elasticity modulus, the resonance frequency of the dynamic responses increases relatively; damping reduces. Thus, the strength of HBL decreases significantly.

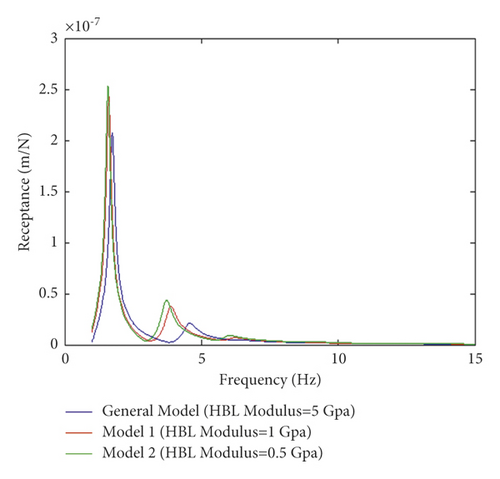
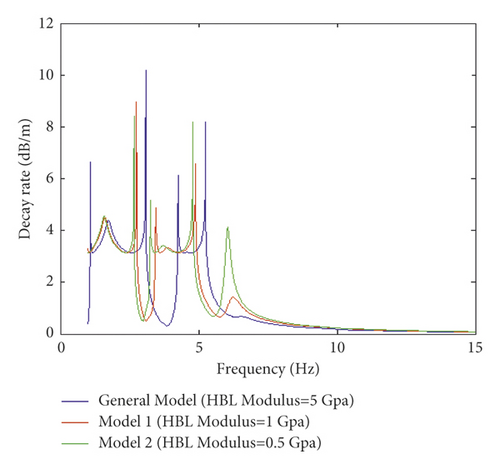
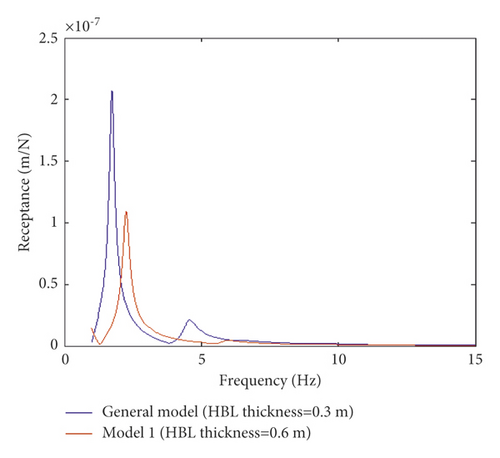
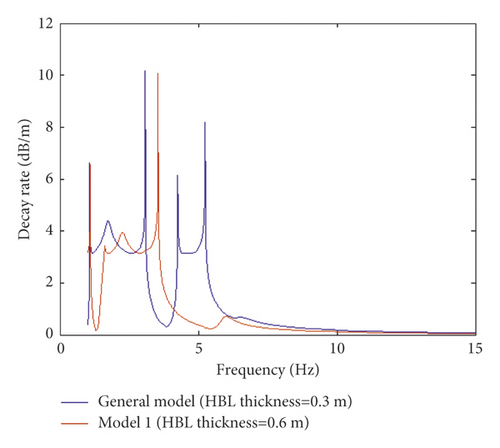
Figures 8(a) and 8(b) illustrate the effect of changing the thickness of HBL on the resonance frequency of receptance and track decay rate from 30 to 60 cm, respectively. Generally, by increasing frequency, dynamic responses including receptance and decay rate are decreased, and the effect of damping oscillation on reducing dynamic response is increased in which the amplitudes are decreased regularly. For the dynamic responses, as the thickness in HBL increases, receptance and decay rate significantly decrease, and damping oscillation intensifies (Figures 8(a) and 8(b)). Furthermore, the effect of the thickness on the resonance frequency of the dynamic responses revealed that an increase in the thickness of the HBL increases the stiffness of the whole track. Accordingly, by increasing the stiffness, the resonance frequency of receptance and track decay rate on the layer represents a decrease, eventually leading to an increase in damping oscillations. Finally, the damped oscillation decreases vertical dynamic responses on the slab track and strengthens the slab track. Thus, through comparing the effect of changing modulus and thickness on the resonance frequency of dynamic response in HBL (Figures 7 and 8), it can be inferred that increasing thickness has a positive effect on the damping oscillation of the dynamic response frequency and their resonance. However, decreasing modulus leads to a negative impact on decreasing damping via increasing frequency and consequently reducing the strength of the layer into the slab track.

4.4. Effect of Modulus and Thickness in ABL on Resonance Frequency

The receptance and decay rate were obtained according to equations (1) to (5) under the frequency ranges of 1 to 15 Hz (Figures 9 and 10). Based on Figures 9(a) and 9(b), by increasing frequency, damping oscillation for all models is increased. And consequently, dynamic frequency responses are decreased in which the amplitudes are decreased although the effect of modulus change is not considered on damping oscillation in ABL. Furthermore, the probe into the effect of damping oscillation on the resonance frequency indicated that no significant effect is observed in changing the resonance frequency for the dynamic response of the track by reducing elasticity modulus in ABL. This represents that the behavior of ABL is similar to that of the general model.

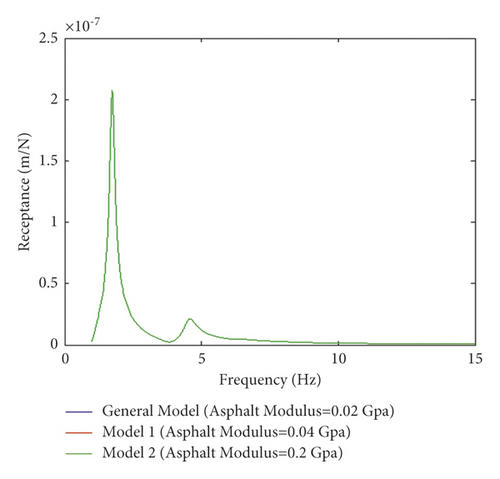
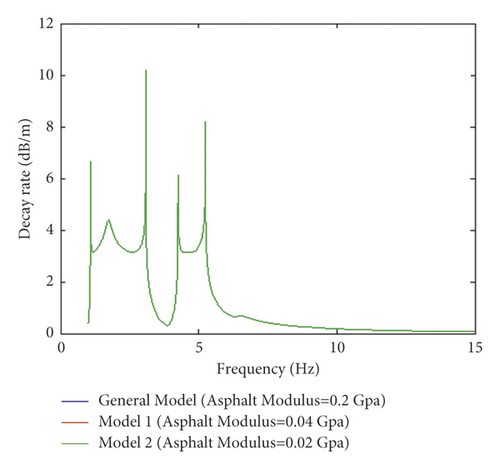
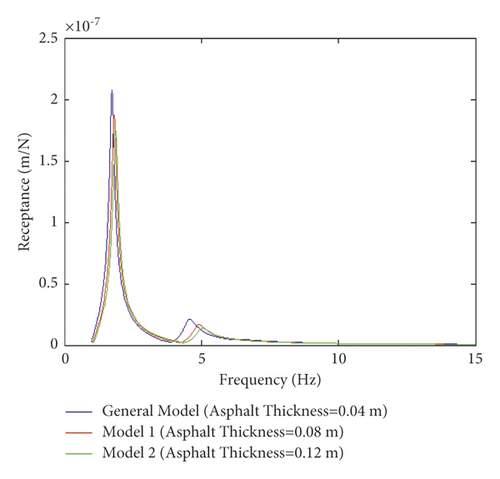
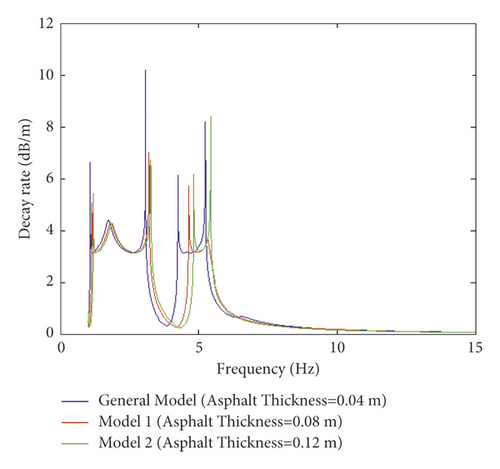
Investigating the effect of thickness over ABL in Figures 10(a) and 10(b) demonstrates that generally increasing frequency positively affects damping oscillation for dynamic frequency responses. Increasing thickness from 4 to 12 cm leads to a reduction in receptance and decay rate in which their resonance frequency responses are declined, thereby decreasing amplitudes. On the other hand, based on the obtained data, no significant effect on the resonance frequency of receptance is observed as the thickness of ABL increases, showing similar behavior to that of the general model. Moreover, an increase in thickness leads to a rise in the stiffness of the slab track. A reduction in decay rate is observed, and consequently, the resonance frequency of decay rate is decreased, and finally, an increase in damping the oscillations. Thus, a comparative evaluation of Figures 9 and 10 indicates that changing the ABL modulus does not affect damping oscillation for dynamic responses and their resonance frequency. However, increasing the thickness contributes to decreasing dynamic responses, and their resonance frequency as frequency is increased, leading to an improvement in the strength of ABL into the slab track.

4.5. Comparison and Validation for the Unit Harmonic Excitation

Table 4 compares the findings of the effect of the slab modulus and thickness of the general model in CBL, HBL, and ABL on the resonance frequency of the dynamic frequency responses including receptance and decay rate. Based on the data, HBL, CBL, and ABL rank as the most influential layers based on the reducing receptance of the slab track by 16% and 12% and no significant reduction in comparison with the general model. Moreover, significant reductions by 68, 62, and 17% are observed for the thickness of HBL, CBL, and ABL compared with the general model, respectively.

4. The effect of modulus and thickness on receptance and decay rate in layers.

Receptance (×10⁻⁷) (m/N)	Modulus			Thickness
Receptance (×10⁻⁷) (m/N)	Maximum	Minimum	Average	Maximum	Minimum	Average
General model	2.50	0.03	1.27	2.10	0.04	1.07
ABL	2.50	0.03	1.27	1.75	0.04	0.89
CBL	2.20	0.04	1.12	0.76	0.04	0.40
HBL	2.10	0.04	1.07	0.65	0.04	0.34
Total average	2.33	0.04	1.18	1.32	0.04	0.68
Decay rate (dB/m)	Maximum	Minimum	Average	Maximum	Minimum	Average
General model	8.30	0.20	4.25	10.1	0.25	5.18
ABL	10.20	0.18	5.19	8.23	0.21	4.22
CBL	6.80	0.17	3.49	7.85	0.19	4.02
HBL	8.30	0.20	4.25	6.75	0.17	3.46
Total average	8.40	0.19	4.58	8.23	0.21	4.43

In addition, CBL, HBL, ABL, and the general model rank as the most effective layers due to the reducing decay rate of the slab track by 18% for CBL and no significant reduction for HBL in comparison with the general model. However, ABL experienced an increasing trend by 22% compared with the general model. Additionally, the decreasing values of the effect of thickness on the decay rate in HBL, CBL, and ABL were 33, 22, and 19% in comparison with the general model, respectively. Thus, considering the effect of the slab modulus and thickness on the resonance frequency of dynamic frequency responses in slab components, it is presented that HBL and CBL have the most significant effects compared to ABL and the general model. Therefore, HBL and CBL are selected as the optimum layers for the slab track of the Shinkansen railway.

Considering the numerical results with those from other studies, the average receptance values on the slab track under the effect of modulus and thickness in the present study were 1.18×10⁻⁷ and 0.68×10⁻⁷, respectively. This is congruent with findings of the study by Gholizadeh and Aghayan and Zougari et al., demonstrating the receptance values of 1.04×10⁻⁷ and 0.78×10⁻⁷, respectively [43, 55]. Furthermore, average decay rates under the effect of modulus and thickness were 4.58 and 4.43, which is consistent with the findings of Li et al. and Jones and Thompson, indicating 4.88 and 4.10 on the slab track, respectively [13, 56]. As shown, the difference between the values of frequency responses is not significant, confirming the credibility of conclusions drawn in the present study with the findings of other studies.

4.6. Simulating the Various Vehicle Loads over the Slab Track Components

In this study, after the comparison and validation of the effect of modulus and thickness on receptance and decay rate in layers, in order to determine the optimum layers for the slab track of the Shinkansen railway under the vehicle loads, the amplitude loads 25 and 20 tons are simulated over the slab track. Then, the results relevant to evaluating the effect of the modulus and thickness change are obtained and shown in Figures 11 and 12. According to Figures 11 and 12, it can be seen that under the effect of the vehicle load 25 tons, the resonance frequency of dynamic frequency responses with the change of modulus and thickness are increased and lead to an increase in the value of the dynamic frequency responses in comparison with the load 11 tons. Moreover, the behavior of the slab track components such as the general model and ABL under both loads is relatively the same. However, CBL and HBL show lower dynamic frequency responses under the vehicle load.

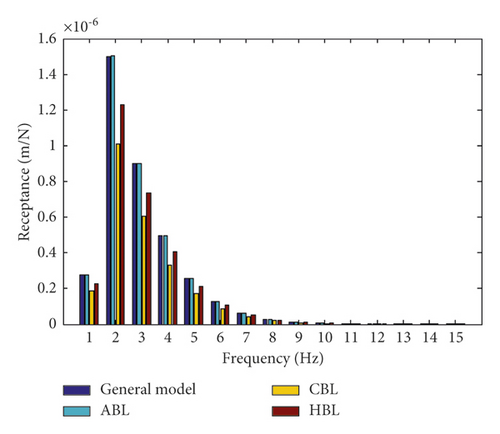
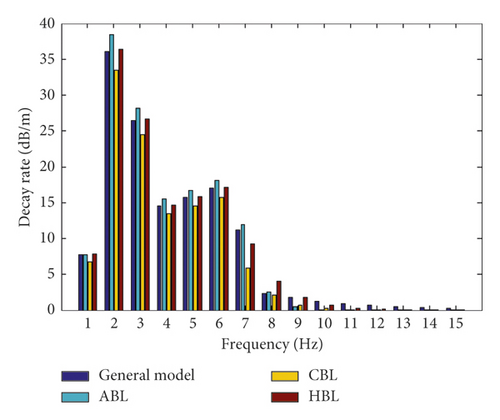
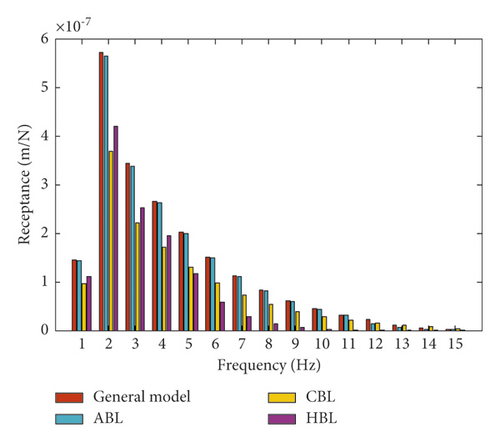
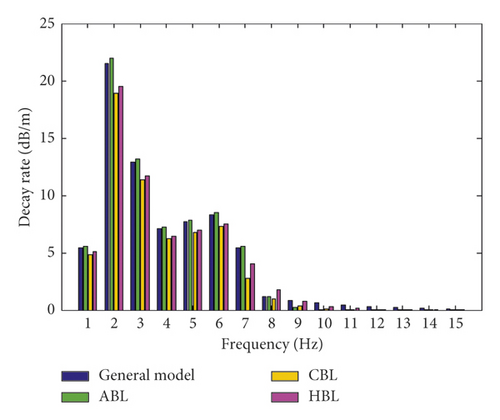
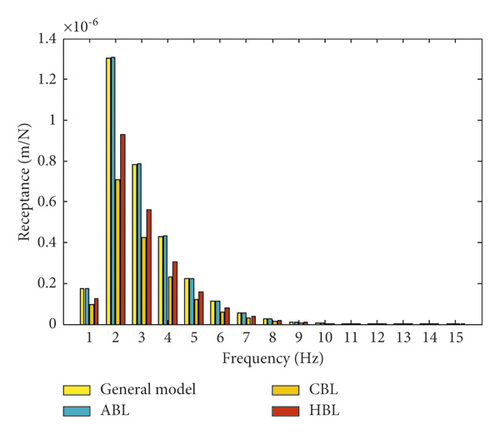
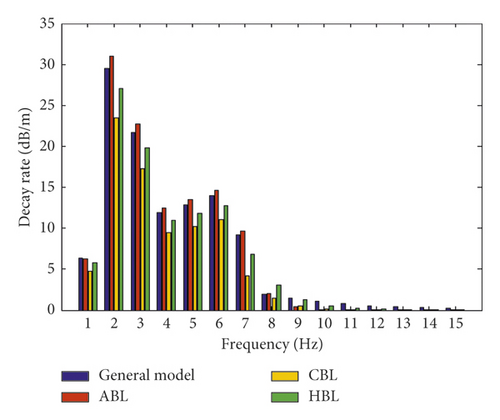
Moreover, in order to characterize the effect of various amplitude loading on the slab track under modulus and thickness change, the dynamic response of receptance and decay rate are compared under 20 and 25 tons. The results are shown in Figure 13. According to Figures 13(a) and 13(b), it can be shown that under the loads, the general model and ABL show the same behavior under the dynamic response. However, CBL and HBL have a lower dynamic response. Furthermore, the dynamic response values are decreased by increasing the loading frequency. This means by changing the load 20 to 25 tons over the slab track, the receptance under the modulus and thickness change increase up to 34 and 29%, respectively. Moreover, the decay rate under the modulus and thickness change increase up to 31 and 37%, respectively. This represents that the loading has significant effects on increasing the dynamic responses. Accordingly, by increasing the load frequency, the CBL and HBL show lower dynamic responses in comparison with other layers (Figures 13(a) and 13(b)). Thus, CBL and HBL are selected as the most optimum layers for the slab track components. Based on Figures 11 to 13, it can be concluded that CBL and HBL are the most influencing layers in damping the resonance and oscillation of dynamic frequency responses. Therefore, CBL and HBL are selected as the most optimum layers for damping the oscillation of the resonance frequency in the slab track of the Shinkansen railway.

5. Conclusion

Recently, the Shinkansen slab track has been known as one of the most widely applied tracks worldwide. Railway engineers and researchers in the field have attempted to optimize the effects of the vertical dynamic response of the railway on the slab track, considering stabilizing the railway pavement by introducing new components. Despite the availability of previous studies, the present study aimed to introduce new layers including HBL, CBL, and ABL to minimize the effect of modulus and thickness on vertical dynamic responses (such as receptance and decay rate) on the Shinkansen railway at low frequency. The simulation procedure based on the FEM was considered regarding the Euler–Bernoulli beam theory and the multi-body approach under a steady-state dynamic. Then, the study further sought to prioritize the suggested layers as the most effective ones based on reducing dynamic vertical dynamic responses considering the modulus and thickness of layers on the resonance frequency. Thus, the main findings are explained as follows:

(1)
The effect of decreasing the elasticity modulus of slab track layers on damping the oscillations of the resonance frequency indicated an increase in CBL, a decrease in HBL, and a similar behavior between ABL and the general model. The results indicated that by increasing the thickness of the slab track layers on damping the oscillation, a decrease was observed in the resonance frequency of receptance and the decay rate and thus an increase of damping oscillations in all layers.
(2)
The results relevant to applying a unit harmonic excitation and investigating the effect of the slab modulus and thickness over the layers under revealed that HBL, CBL, ABL, and the general model were the most influential layers on the resonance frequency of receptance since HBL, CBL, and ABL reduced receptance by 16%, 12%, and no significant reduction in comparison with the general model, respectively. Additionally, 68, 62, and 17% reducing values were found for the thickness of HBL, CBL, and ABL compared with the general model, respectively. Moreover, CBL, HBL, ABL, and the general model ranked the most influential layers due to the reducing decay rate by 18% for CBL and no significant reduction for HBL compared with the general model. However, ABL experienced an increasing trend by 22% in comparison with the general model. By decreasing the values of thickness in HBL, CBL, and ABL were 33, 22, and 19% compared to the general model, respectively.
(3)
The comparison of data of this study with those of other studies proved the credibility of findings in the receptance and decay rate under the vertical frequency responses of the proposed layers in the Shinkansen railway.
(4)
The results of applying vehicle loads over the slab track indicated that by changing the loads 20 to 25 tons over the slab track, the receptance under the modulus and thickness change increased up to 34 and 29%, respectively. Moreover, the decay rate under the modulus and thickness change increased up to 31 and 37%, respectively. This illustrates that the loading has significant effects on increasing the dynamic responses. Accordingly, the CBL and HBL show lower dynamic response than other layers by increasing the load amplitude.
(5)
According to the obtained data of the present study, using CBL and HBL is recommended compared to ABL, and the general model is more efficient in reducing the resonance frequency of receptance and decay rate to strengthen and stabilize the slab track. Therefore, the railway industry and governments that use the Shinkansen railway can benefit from applying CBL and HBL to improve the slab track.

Conflicts of Interest

The authors declare that there are no conflicts of interest.

Open Research

Data Availability

Some or all data, models, or code generated or used during this study are available from the corresponding author upon reasonable request.

References

1 Connolly D. P., Marecki G. P., Kouroussis G., Thalassinakis I., and Woodward P. K., The growth of railway ground vibration problems-a review, The Science of the Total Environment. (2016) 568, 1276–1282, https://doi.org/10.1016/j.scitotenv.2015.09.101, 2-s2.0-84951054909.
10.1016/j.scitotenv.2015.09.101
CAS PubMed Web of Science® Google Scholar
2 Kouroussis G., Connolly D. P., and Verlinden O., Railway-induced ground vibrations-a review of vehicle effects, International Journal of Reality Therapy. (2014) 2, no. 2, 69–110, https://doi.org/10.1080/23248378.2014.897791, 2-s2.0-84977632040.
10.1080/23248378.2014.897791
Google Scholar
3 Auersch L., Realistic axle-load spectra from ground vibrations measured near railway lines, International Journal of Reality Therapy. (2015) 3, no. 4, 180–200, https://doi.org/10.1080/23248378.2015.1076624, 2-s2.0-84973509215.
10.1080/23248378.2015.1076624
Google Scholar
4 Villot M., Augis E., Guigou-Carter C., Jean P., Ropars P., Bailhache S., and Gallais C., Vibration emission from railway lines in tunnel - characterization and prediction, International Journal of Reality Therapy. (2016) 4, no. 4, 208–228, https://doi.org/10.1080/23248378.2016.1220267, 2-s2.0-84982242332.
10.1080/23248378.2016.1220267
Google Scholar
5 Arlaud E., Costa D’Aguiar S., and Balmes E., Receptance of railway tracks at low frequency: numerical and experimental approaches, Transportation Geotechnics. (2016) 9, 1–16, https://doi.org/10.1016/j.trgeo.2016.06.003, 2-s2.0-84978174348.
10.1016/j.trgeo.2016.06.003
Web of Science® Google Scholar
6 Zhu S., Wang J., Cai C., Wang K., Zhai W., Yang J., and Yan H., Development of a vibration attenuation track at low frequencies for urban rail transit, Computer-Aided Civil and Infrastructure Engineering. (2017) 32, no. 9, 713–726, https://doi.org/10.1111/mice.12285, 2-s2.0-85026382068.
10.1111/mice.12285
Web of Science® Google Scholar
7 Zougari A. and MartÍnez J., The experimental validation of a numerical model for the receptance prediction, 286, Proceedings of the MATEC Web of Conferences, 2019, EDP Sciences, 01007.
Google Scholar
8 Esveld C., Recent developments in slab track, Eur Railw Rev. (2003) 9, no. 2, 81–85.
Google Scholar
9 Gautier P.-E., Slab track: review of existing systems and optimization potentials including very high speed, Construction and Building Materials. (2015) 92, 9–15, https://doi.org/10.1016/j.conbuildmat.2015.03.102, 2-s2.0-84930274350.
10.1016/j.conbuildmat.2015.03.102
Web of Science® Google Scholar
10 Atashafrazeh M. and Shirmohammadi H., 2D modeling and analysis of railway track under subjected loads, Jordan Journal of Civil Engineering. (2016) 10, no. 3, https://doi.org/10.14525/jjce.10.3.3602, 2-s2.0-84976448450.
10.14525/JJCE.10.3.3602
Google Scholar
11 Yen S.-T. and Lee Y.-H., Parameter identification and analysis of a slab track system using 3D ABAQUS program, Journal of Transportation Engineering. (2007) 133, no. 5, 288–297, https://doi.org/10.1061/(asce)0733-947x(2007)133:5(288), 2-s2.0-34247192542.
10.1061/(ASCE)0733-947X(2007)133:5(288)
Google Scholar
12 Thompson D. J., Railway Noise and Vibration: Mechanisms, Modeling and Means of Control, 2009, Elsevier, Oxford, England.
Google Scholar
13 Li W., Jiang J., and Dwight R. A., Internal CRC Report R1-105 Report B1: a review of railway noise source identification and mitigation, methods and priorities within the Australian Context, ΧΡΧ Ραιλ Innovations Report. (2011) https://www.epa.nsw.gov.au/~/media/EPA/Corporate%20Site/resources/noise/20130018eparing.ashx.
Google Scholar
14 Li W., Jiang J., Dwight R., and Schulten C., An investigation of a method for track decay rate measurement using train pass-bys, 75, Proceedings of the Australian Acoustical Society Conference 2011: Breaking New Ground, Acoustics, 2011, Gold Coast, Australia, 563–568.
Google Scholar
15 Yue G.-d., Xu Z., Wang L.-d., Liu C., and Zhou W.-j., Vibration analysis for slab track at different train speeds using Bayes wavelet denoising, 231, Proceedings of the Institution of Mechanical Engineers - Part F: Journal of Rail and Rapid Transit, 2017, no. 8, 892–901, https://doi.org/10.1177/0954409716647417, 2-s2.0-85029058544.
10.1177/0954409716647417
Google Scholar
16 Michas G., Slab Track Systems for High-Speed Railways, 2012, Department of Transport Science, Royal Institute of Technology, Stockholm, Sweden, MSc. Thesis.
Google Scholar
17 Madshus C., Kaynia A. M., Harvik L., and Holme J. K., A numerical ground model for railway-induced vibration. Skipp B. O. Ground Dynamics and Man-Made Processes: Prediction, Design and Management, 1998, Thomas Telford, London, 45–55.
Google Scholar
18 Nguyen G. K., Goicolea R. J. M., and Castillo G., Dynamic Analysis of High Speed Railway Traffic Loads on Ballasted Track, 2011, Fifth International Symposium on Environmental Vibration, Chengdu, China.
Google Scholar
19 Sayeed M. A. and Shahin M. A., Three-dimensional numerical modelling of ballasted railway track foundations for high-speed trains with special reference to critical speed, Transportation Geotechnics. (2016) 6, 55–65, https://doi.org/10.1016/j.trgeo.2016.01.003, 2-s2.0-84958259811.
10.1016/j.trgeo.2016.01.003
Web of Science® Google Scholar
20 Steenbergen M. J. M. M., Metrikine A. V., and Esveld C., Assessment of design parameters of a slab track railway system from a dynamic viewpoint, Journal of Sound and Vibration. (2007) 306, no. 1-2, 361–371, https://doi.org/10.1016/j.jsv.2007.05.034, 2-s2.0-34447527273.
10.1016/j.jsv.2007.05.034
Web of Science® Google Scholar
21 Lei X. and Zhang B., Analysis of dynamic behavior for slab track of high-speed railway based on vehicle and track elements, Journal of Transportation Engineering. (2010) 137, no. 4, 227–240.
10.1061/(ASCE)TE.1943-5436.0000207
Google Scholar
22 Zhu S., Yang J., Yan H., Zhang L., and Cai C., Low-frequency vibration control of floating slab tracks using dynamic vibration absorbers, Vehicle System Dynamics. (2015) 53, no. 9, 1296–1314, https://doi.org/10.1080/00423114.2015.1046460, 2-s2.0-84939264772.
10.1080/00423114.2015.1046460
Web of Science® Google Scholar
23 Shi L., Cai Y., Wang P., and Sun H., A theoretical investigation on influences of slab tracks on vertical dynamic responses of railway viaducts, Journal of Sound and Vibration. (2016) 374, 138–154, https://doi.org/10.1016/j.jsv.2016.04.011, 2-s2.0-84981763971.
10.1016/j.jsv.2016.04.011
Web of Science® Google Scholar
24 Miura S., Takai H., Uchida M., and Fukada Y., The mechanism of railway tracks, Japan Railway & Transport Review. (1998) 3, no. 38-45.
Google Scholar
25 Tayabji S., Concrete slab track for freight and high speed service applications, A survey of practice. (2000) https://moam.info/concrete-slab-track-for-freight-and-high-speed-service-_59e98f7d1723dd804fff5147.html.
Google Scholar
26 Orel E. G., Comparison of ballasted and slab track based on LCC analysis, 2020, Sapienza University of Rome, Italy, Thesis of Master Degree.
Google Scholar
27 Real T., Zamorano C., Hernández C., García J. A., and Real J. I., Static and dynamic behavior of transitions between different railway track typologies, KSCE Journal of Civil Engineering. (2016) 20, no. 4, 1356–1364, https://doi.org/10.1007/s12205-015-0635-2, 2-s2.0-84940212579.
10.1007/s12205-015-0635-2
Web of Science® Google Scholar
28 Shuber A., Hamood M., and Jawad W., Performance of railway track system under harmonic loading by finite element method, 162, Proceedings of the MATEC Web of Conferences, 2018, EDP Sciences, Sharm el-Shiekh, Egypt, 01043, https://doi.org/10.1051/matecconf/201816201043, 2-s2.0-85047790078.
10.1051/matecconf/201816201043
Google Scholar
29 Aggestam E., Nielsen J. C. O., and Bolmsvik R., Simulation of vertical dynamic vehicle-track interaction using a two-dimensional slab track model, Vehicle System Dynamics. (2018) 56, no. 11, 1633–1657, https://doi.org/10.1080/00423114.2018.1426867, 2-s2.0-85041174502.
10.1080/00423114.2018.1426867
Web of Science® Google Scholar
30 Ling L., Xiao X.-B., Xiong J.-Y., Zhou L., Wen Z.-F., and Jin X.-S., A 3D model for coupling dynamics analysis of high-speed train/track system, Proceedings of the China's High-Speed Rail Technology, 2018, Singapore, Springer, 309–339, https://doi.org/10.1007/978-981-10-5610-9_18.
10.1007/978-981-10-5610-9_18
Google Scholar
31 Sayeed M. A., Dynamic behaviour of ballasted railway track foundation under various conditions of the train-track-ground system, Journal of Engineering and Applied Science. (2020) 4, no. 1, 86–97.
Google Scholar
32 Knothe K. and Grassie S. L., Modeling of railway track and vehicle/track interaction at high frequencies, Vehicle System Dynamics. (1993) 22, no. 3-4, 209–262, https://doi.org/10.1080/00423119308969027, 2-s2.0-0027601725.
10.1080/00423119308969027
Web of Science® Google Scholar
33 Zhai W., Wang K., and Cai C., Fundamentals of vehicle-track coupled dynamics, Vehicle System Dynamics. (2009) 47, no. 11, 1349–1376, https://doi.org/10.1080/00423110802621561, 2-s2.0-75649085247.
10.1080/00423110802621561
Web of Science® Google Scholar
34 Claus H. and Schiehlen W., Symbolic-numeric analysis of flexible multibody systems^∗, Mechanics of Structures and Machines. (2002) 30, no. 1, 1–30, https://doi.org/10.1081/sme-120001476, 2-s2.0-0036471708.
10.1081/SME-120001476
Google Scholar
35 Lichtberger B., Track Compendium, 2005, Eurailpress Tetzlaff-Hestra GmbH & Co. KG, Hamburg.
Google Scholar
36 Xiao X., Jin X., Deng Y., and Zhou Z., Effect of curved track support failure on vehicle derailment, Vehicle System Dynamics. (2008) 46, no. 11, 1029–1059, https://doi.org/10.1080/00423110701689602, 2-s2.0-50849092529.
10.1080/00423110701689602
Web of Science® Google Scholar
37 Xiao X. B., Study on High-Speed Train Derailment Mechanism in Severe Environment, 2013, Southwest Jiaotong University, Chengdu, China, PhD Thesis.
Google Scholar
38 Xin T. and Gao L., Reducing slab track vibration into bridge using elastic materials in high speed railway, Journal of Sound and Vibration. (2011) 330, no. 10, 2237–2248, https://doi.org/10.1016/j.jsv.2010.11.023, 2-s2.0-79952450422.
10.1016/j.jsv.2010.11.023
Web of Science® Google Scholar
39 Zhong S., Xiao X., Wen Z., and Jin X., The effect of first-order bending resonance of wheelset at high speed on wheel-rail contact behavior, Advances in Mechanical Engineering. (2013) 5, 296106, https://doi.org/10.1155/2013/296106, 2-s2.0-84888603618.
10.1155/2013/296106
Google Scholar
40 Lu X. Z., Kim C. W., and Chang K. C., A numerical framework to solve train-bridge interaction for high speed railway system, Proceedings of the ACEM18, August 2018, Incheon, South Korea, http://www.i-asem.org/publication_conf/acem18/3.ACSM18/T4F.4.CS1210_4736F1.pdf.
Google Scholar
41 Carter F. W., On the action of a locomotive driving wheel, Proceedings of the Royal Society of London - Series A: Containing Papers of a Mathematical and Physical Character. (1926) 112, no. 760, 151–157.
10.1098/rspa.1926.0100
Google Scholar
42 Wang K., Huang C., Zhai W., Liu P., and Wang S., Progress on wheel-rail dynamic performance of railway curve negotiation, Journal of Traffic and Transportation Engineering. (2014) 1, no. 3, 209–220, https://doi.org/10.1016/s2095-7564(15)30104-5, 2-s2.0-84997523821.
10.1016/s2095-7564(15)30104-5
Google Scholar
43 Gholizadeh M. and Aghayan I., 3D modeling of slab track to study track frequency response, Journal of Transportation Infrastructure Engineering. (2017) 3, no. 2, 111–128, In Persian.
Google Scholar
44 Fattah M. Y., Mahmood M. R., and Aswad M. F., Experimental and numerical behavior of railway track over geogrid reinforced ballast underlain by soft clay, Sustainable Civil Infrastructures. (2017) 14, 1–26, https://doi.org/10.1007/978-3-319-61627-8_1.
10.1007/978-3-319-61627-8_1
Google Scholar
45 Majeed Q., Fattah M. Y., and Joni H. H., Effect of load frequency on the track rail and subgrade layer settlement, Journal of Engineering and Applied Sciences. (2019) 14, no. 18, 6723–6730, https://doi.org/10.36478/jeasci.2019.6723.6730.
10.36478/jeasci.2019.6723.6730
Google Scholar
46 Fattah M. Y., Mahmood M. R., and Aswad M. F., Stress distribution from railway track over geogrid reinforced ballast underlain by clay, Earthquake Engineering and Engineering Vibration. (2019) 18, no. No. 1, Springer, 77–93, https://doi.org/10.1007/s11803-019-0491-z, 2-s2.0-85060293934.
10.1007/s11803-019-0491-z
Web of Science® Google Scholar
47 Fattah M. Y., Mahmood M. R., and Aswad M. F., Settlement of railway track on reinforced ballast overlain by clayey, Journal of Transportation and Logistics. (2020) 5, no. 2, Istanbul University Press, https://doi.org/10.26650/JTL.2020.0014.
10.26650/JTL.2020.0014
Google Scholar
48 Fattah M. Y., Al-Haddad S. A., and Hameedi M. K., Load carrying capacity of rectangular foundation on geogrid reinforced sloped sandy soil, 737, Proceedings of the Fourth International Conference on Buildings, Construction and Environmental Engineering – BCEE4, October 2019, Istanbul, Turkey, 012094, https://doi.org/10.1088/1757-899X/737/1/012094.
10.1088/1757-899X/737/1/012094
Google Scholar
49 Craig R. R. and Kurdila A. J., Fundamentals of Structural Dynamics, 2006, John Wiley & Sons, New Jersey, NY, USA.
Google Scholar
50 Dahlberg T., Railway Track Dynamics-A Survey, 2003, Linköping University, Sweden.
Google Scholar
51 Irvine T., Calculating transfer functions from normal modes, Revision E, vibrationdata.(2013) 1.
Google Scholar
52 Janssens M. H. A., Dittrich M. G., de Beer F. G., and Jones C. J. C., Railway noise measurement method for pass-by noise, total effective roughness, transfer functions and track spatial decay, Journal of Sound and Vibration. (2006) 293, no. 3-5, 1007–1028, https://doi.org/10.1016/j.jsv.2005.08.070, 2-s2.0-33645893238.
10.1016/j.jsv.2005.08.070
Web of Science® Google Scholar
53 Feng H., 3D-models of Railway Track for Dynamic Analysis, 2011, Royal Institute of Technology.
Google Scholar
54 Gholampour M., Abadi B. N. R., Farid M., and Cleghorn W. L., Stress-based finite element methods for dynamics analysis of Euler-Bernoulli beams with various boundary conditions, Latin American Journal of Solids and Structures. (2017) 14, no. 9, 1629–1647, https://doi.org/10.1590/1679-78253927, 2-s2.0-85028547088.
10.1590/1679-78253927
Web of Science® Google Scholar
55 Zougari A., Martínez J., and Cardona S., Numerical models of railway tracks for obtaining frequency response Comparison with analytical results and experimental measurements, Journal of Vibroengineering. (2016) 18, no. 2, 1104–1114.
10.21595/jve.2016.16546
Web of Science® Google Scholar
56 Jones C. J. C. and Thompson D. J., Extended validation of a theoretical model for railway rolling noise using novel wheel and track designs, Journal of Sound and Vibration. (2003) 267, no. 3, 509–522, https://doi.org/10.1016/s0022-460x(03)00711-9, 2-s2.0-0141964128.
10.1016/S0022-460X(03)00711-9
Web of Science® Google Scholar

Citing Literature

All articles

Modeling Dynamic Frequency Response on Slab Track of Shinkansen Railway Based on Finite Element Method

Abstract

1. Introduction

2. Literature Review