In civil engineering, arches, such as steel arch roofs and arch bridges, are often subjected to linear temperature gradient field. It is known that the in-plane instability of parabolic arches is caused by the significant axial force. The arch under the linear temperature gradient field produces complex axial force, and so the instability of arches would be affected by temperature gradient field significantly. However, the analytical solutions of in-plane instability of parabolic arches being subjected to the uniformly distributed vertical load and the temperature gradient field are not solved in the opening literature. In this paper, in-plane instability of a fixed steel parabolic arch under linear temperature gradient field and vertical uniform load is analyzed theoretically. Firstly, the cross-sectional effective centroid and effective stiffness of the cross section for arches under the linear temperature gradient field are derived. Secondly, the preinstability internal force analysis of the parabolic arch under the linear temperature gradient field and the vertical uniform load is carried out based on the force methods. Novel theoretical solutions for in-plane instability load for fixed steel parabolic arches under the linear temperature gradient field and the vertical uniform load are obtained. It is found that the gradient temperature, slenderness, and rise-span ratio have important influences on the critical in-plane instability load of the shallow parabolic arch, while there is no significant effect on the deep parabolic arch.

1. Introduction

Long-span steel arch structures are widely applied to engineering, for instance, long-span steel roofs of the terminal, long-span steel arch bridge, etc. For large-span steel roofs, the temperature inside and outside of the roof is different due to sun exposure. In summer, the temperature inside the structure is lower than that outside the structure, while in winter, the temperature inside the structure is higher than that outside the structure. The inconsistence of internal and external temperature will produce linear gradient temperature field and internal force to the structure, and the linear gradient temperature field and internal force affect the bearing capacity of the structure. Except for the linear gradient temperature field caused by solar irradiation, the fire inside the structure will cause the internal temperature of the structure to be higher than the external temperature and then generates the linear gradient temperature field. Hence, the study of the steel arch structure under linear temperature gradient field has a profound significance on the fire resistance design of the steel arch structure.

Many scholars have conducted a series of research studies on the buckling of steel arch structures. Pi and Trahair. [1] studied the inelastic lateral buckling strength and design of steel arches under general loading using an advanced nonlinear inelastic finite element method of analysis. Mallon et al. [2] researched the influence of the initial curvature of thin shallow arches on the dynamic pulse buckling load. Moon et al. [3] investigated the geometrically nonlinear behavior of pin-ended shallow parabolic steel arches subjected to a vertically distributed load for assessing the buckling load. Pi and Bradford. [4] researched the dynamic in-plane buckling of a shallow pin-ended circular arch under a central radial load that is applied suddenly with infinite duration. Bradford et al. [5] researched the prebuckling behavior of a pin-ended circular arch under a uniform radial load. Han et al. [6] researched the in-plane nonlinear behavior and stability of shallow circular arches with elastic horizontal supports under a uniform radial load by the principle of virtual work. Zeng et al. [7] studied the stability analysis of elastic restrained arc steel arch under concentrated load. Kang et al. [8] conducted a dynamic response analysis of an elastically supported arc steel arch structure under blast impact loading. Yan et al. [9] researched a nonuniform shallow arch characterized by three constant stiffness regions under a central concentrated load. Li et al. [10] established an analytical solution to predict the buckling load of the thin-walled arch under a point load at midspan position. Fan et al. [11] carried out an analytical study and a numerical simulation on the nonlinear in-plane buckling behavior of the shallow parabolic steel arches with tension cables and pin joints. Pi and Bradford [12] researched the nonlinear thermoelastic buckling behavior of articulated shallow arc steel arches under the impact of linear temperature gradient field. Bouras and Vrcelj. [13] carried out the nonlinear elastic prebuckling and in-plane buckling analysis of the circular shallow arches under a uniformly distributed load and time-varying uniform temperature field. Song et al. [14] analyzed an in-plane jump buckling and bending behavior for arc steel arches subjected to fire. Asgari et al. [15] theoretically researched the nonlinear thermoelastic behavior of pin-ended functionally graded material (FGM) circular shallow arches. Li and Zheng, [16] investigated the buckling of confined thin-walled functionally graded material (FGM) arch subjected to external pressure. Tang et al. [17] researched the in-plane asymmetric buckling of the heated functionally graded material (FGM) circular arches under uniform pressure fields. Li et al. [18] researched the analytical process of the functionally graded porous (FGP) arch structure in an elevated thermal field. Cai et al. [19] researched the in-plane stability of rotationally restrained parabolic shallow steel arches under a vertical uniform load and temperature changes below 100°C and used the virtual work principle method to establish the nonlinear equilibrium and buckling equations. Pi and Bradford [20] researched nonlinear in-plane buckling of circular arches being subjected to uniform radial and thermal loading. However, only a few scholars have researched the parabolic steel arches under the temperature field, especially the effect of temperature gradient field. Parabolic arches are widely used in practical engineering. The internal force analysis and stability analysis of parabolic arches are important parts of arch design, construction and maintenance, etc. However, the analytical solutions of in-plane instability of parabolic arches being subjected to uniformly distributed vertical load and temperature gradient field are not solved in the opening.

Hence, this paper derives the cross-sectional effective centroid and effective stiffness for parabolic arches under the linear temperature gradient field and obtains the axial and bending actions of parabolic arches under linear temperature gradient field coupled with vertical uniform load. In addition, the analytical solution of the critical load for in-plane instability of the parabolic arches under temperature gradient field coupled with vertical uniform load is also obtained, and it is verified by the numerical simulations software ANSYS.

2. Analysis of Geometrical and Material Properties of Parabolic Arch

2.1. Basic Analysis

2.1.1. Mechanical Model

The fixed parabolic steel arch under linear gradient temperature field coupled with vertical uniformly distributed load is considered as the study object, which is plotted in Figure 1.

Details are in the caption following the image — Open in figure viewer PowerPoint

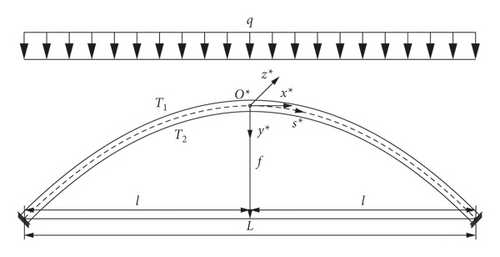
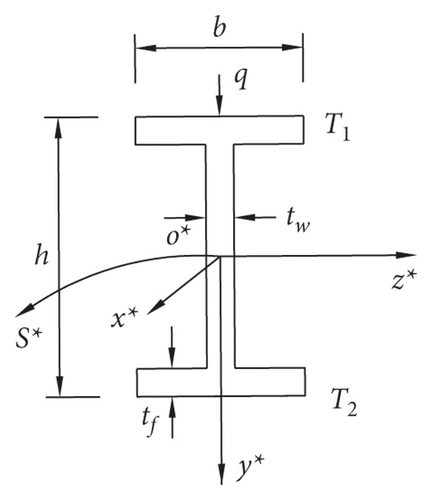
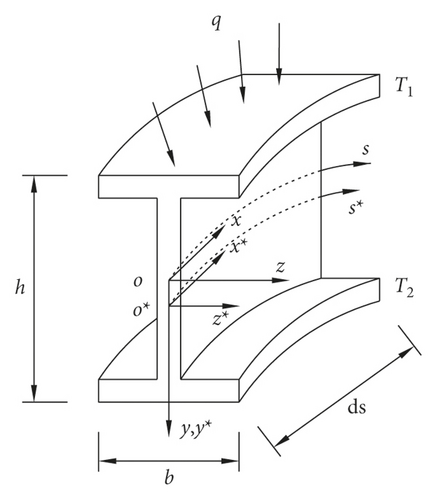
o^∗x^∗y^∗z^∗ denotes the initial coordinates of the parabolic steel arch, o^∗ is situated in the cross-sectional geometric center of vault, and o^∗x^∗, o^∗y^∗, and o^∗z^∗ are the horizontal coordinate axis, the vertical coordinate axis, and the lateral coordinate axis of the initial coordinates, respectively. o^∗s^∗ is the geometric centroid axis of the initial coordinates. Figure 1(a) shows that f, L, l, and S are the rise, span, half-span, and length of the parabolic steel arch, respectively. Figure 1(b) shows that T₁ and T₂ are top and bottom cross-sectional temperatures, respectively. h represents the cross-sectional height.

In addition, the equation of geometric coordinates of the parabolic steel arch can be defined based on Figure 1 as

(1)

where a₁ represents the shape factor of the parabolic steel arch, which can be given by

(2)

x₁ represents nondimensional coordinate of the o^∗x^∗ axis, which is denoted as x₁ = x^∗/l, and so the arc differential ds of the parabolic arch can be calculated by

(3)

2.1.2. Basic Hypothesis

The in-plane instability analysis for parabolic steel arches under the linear temperature gradient field studied in this paper satisfies the following hypothesis.

(1)
The environment temperature is 20^°C.
(2)
Cross-sectional temperature, parabolic arch deformation, temperature dilatation factor a, and Poisson’s ratio v are independent of time.
(3)
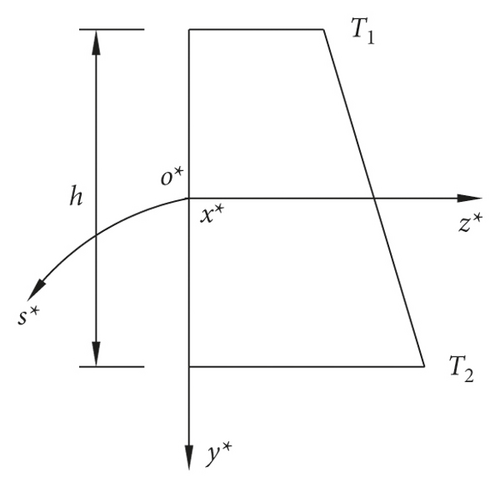
The temperature T of the cross section of the arch varies uniformly along the o^∗s^∗ axis and the o^∗x^∗ axis and linearly along the o^∗y^∗ axis, as shown in Figure 2, where T₁ < T₂.

Hence, the temperature at any point on the cross section of parabolic arch can be calculated by

(4)

where T_a represents the cross-sectional average temperature of the parabolic arch, which can be obtained by

(5)

and ΔT_g represents temperature difference value between top and bottom of the cross section, which can be calculated by

(6)

2.1.3. Modulus of Elasticity

In this paper, steel is chosen as the material for the arch. The modulus of elasticity of steel E_T = ξ_T · E₀, where E₀ is the modulus of elasticity of Q235 steel at temperature 20^°C, and ξ_T is the temperature affection factor, which can be given by

(7)

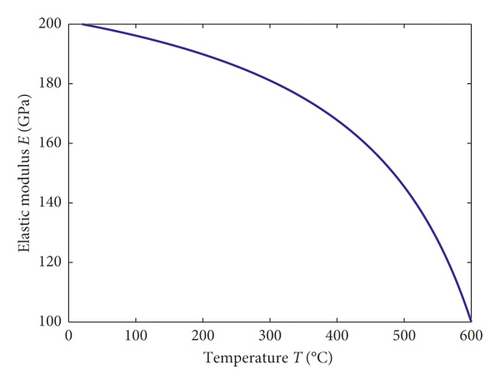
Figure 3 shows the influence of temperature on steel elastic modulus. As shown in the picture, steel elastic modulus decreases with the an increase of material temperature, and the value decreases more remarkably with the augment of temperature.

2.1.4. Effective Stiffness and Effective Centroid

The I section is taken as the cross section of parabolic steel arch studied in this paper, and when the parabolic steel arch is under the linear gradient temperature field, the elastic modulus changes along the o^∗y^∗ axis, and the vertical coordinate of effective centroid also changes. Therefore, the effective coordinate system oxyz can be determined by the location of the effective centroid, which is shown in Figure 4.

ox, oy, and oz denote the effective horizontal axis, effective vertical axis, and effective lateral axis, respectively. os is the effective centroid axis of the effective coordinate system. By substituting (4) into (7), the elastic modulus along the o^∗y^∗ axis is given by

(8)

Accordingly, the vertical coordinate of effective centroid of the o^∗y^∗ axis is given by

(9)

where y_c is the vertical coordinate of effective centroid of the oy axis.

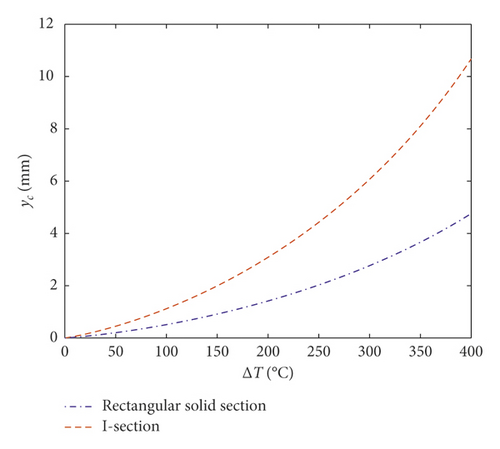
The effect of linear gradient temperature field on the effective center of parabolic arch cross section is shown in Figure 5, and it can be seen that the effective center of shape is shifted to the side with lower temperature under linear gradient temperature field, and the effect of gradient temperature on the I section is greater than that on the rectangular section.

In addition, T_o is the temperature of the effective centroid, which can be given by

(10)

By replacing the vertical coordinate y^∗ with y^∗ = y − y_c, the elastic modulus along the oy axis can be given by

(11)

For ensuring that the analysis of the internal forces of the parabolic arch under gradient temperature is precise, the effective stiffnesses

and

of the arch section are derived, which can be given separately by

(12)

where t_f represents the thickness of the flange plate of the I section, t_w represents the thickness of the web of the I section, and b, h, and A represent the width, height, and area of the I section, separately. Beyond that, the parameters T_s, Ξ₁₂ can be mathematically expressed as

(13)

3. Results and Discussion

3.1. Internal Force Analysis

As the parabolic steel arches are linear elastic, their strain energy in the preinstability state under linear temperature gradient field coupled with vertical uniformly distributed load q can be given by

(14)

with ΔT_o = T_o − 20^°C, where A is the cross-sectional area, E_T, α, and ε_xx0 are the modulus of elasticity, the thermal coefficient of the steel, and the linear normal strain, respectively. ε_xx0 is given by

(15)

where ds₁ is the arc differential after deformation and ρ and ρ₁ are radii of curvature of the parabolic steel arches before and after deformation, respectively. In addition, the axial force N and bending moment M can be expressed as

(16)

(17)

Accordingly, by substituting (16) and (17) into (14), the term of the strain energy can be simplified as

(18)

By substituting equations (3), (16), (17), and (18) into equation (14), the strain energy can be further simplified as

(19)

where

(20)

The accurate solutions of the preinstability axial force N and bending moment M of a parabolic steel arch are essential for the in-plane instability of the arch. However, no accurate solutions of internal forces for arches being subjected to linear temperature gradient filed and vertical uniformly distributed load q can be obtained in the opening literature. The internal force of the arch can be solved by the force method which is based on Castigliano’s theorems, and when an arch is under linear temperature gradient field coupled with vertical uniformly distributed load q, the internal forces for the arch can be herein calculated by the force method in this paper.

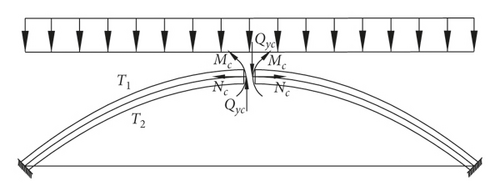
Based on the force method, the parabolic steel arch is cut into two pieces at the top, which is shown in Figure 6. These two parts are the statically determinate structures with unknown additional axial forces (N_c), bending moment (M_c), and shear force (Q_yc). However, according to the principle of structural symmetry, the unknown additional shear force (Q_yc) is equal to zero.

In addition, to make the cut arch equivalent to the original arch, the relative axial displacement Δ_NC and the relative rotation Δ_MC at the cutting location should be equal to zero. Based on Castigliano’s theorems, the relative axial displacement Δ_NC and the relative rotation Δ_MC can be, respectively, given by

(21)

(22)

Substituting (19) into (21) and (22), respectively, the corresponding force method equation can be obtained as

(23)

(24)

Because the segmentations of two part of the parabolic steel arch are the statically determinate structures, based on the principle of force equilibrium, the axial force N and bending moment M can be solved, respectively, as

(25)

(26)

The solutions of the internal force obtained from (25) and (26) have two unknown values (N_c and M_c); to solve them, substituting (25) and (26) into (23) and (24), N_c and M_c can be obtained as

(27)

(28)

where

(29)

Hence, the accurate solutions of axial force N and bending moment M can be obtained by substituting (27) and (28) into (25) and (26).

In order to expound the effect of the linear temperature gradient field on N and M in (23) and (24), the changes of N_c and M_c with rise-span ratio f/L for parabolic arches having temperature difference between the top and base of the cross section ΔT_g (i.e., ΔT_g = 50^°C, 100^°C, 150^°C) are shown in Figures 7(a) and 7(b), respectively, where N_c and M_c are the central axial and bending actions, and T_a = 200^°C, q = 2 × 10⁵ kN/m, and L/γ_x = 30 with γ_x being the radius of gyration of the arch. Beyond that, the changes of N_c and M_c with rise-span ratio f/L for parabolic arches having different average temperatures of the cross section T_a (i.e., T_a = 150^°C, 200^°C, 250^°C) are plotted in Figures 7(c) and 7(d), respectively, where ΔT_g = 100^°C, q = 2 × 10⁵ kN/m, and L/γ_x = 30.

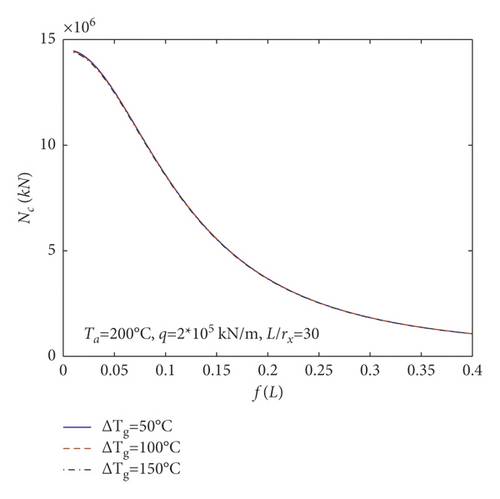
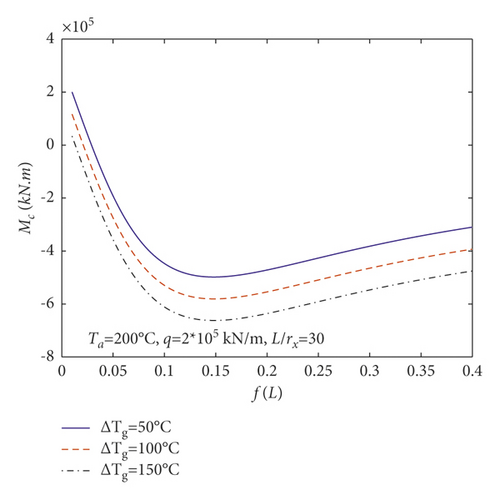
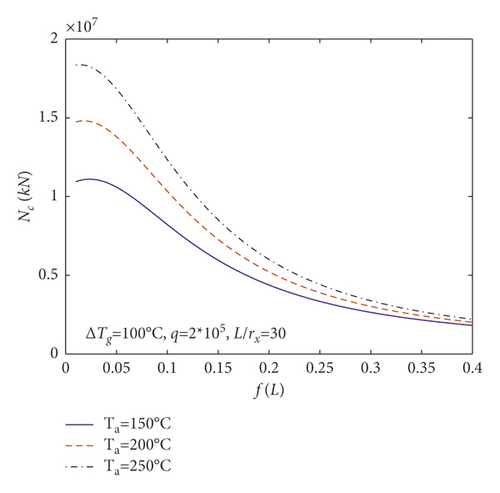
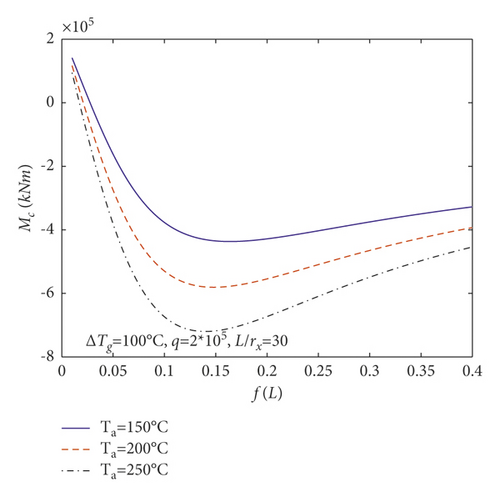
According to Figure 7(a), N_c almost does not change for parabolic arches having different ΔT_g, which is consistent with (27) without ΔT_g. Figure 7(a) also reveals that N_c augments as the rise-span ratio f/L augments at the beginning; after that, it decreases as the rise-span ratio f/L augments in case the rise-span ratio of arches reaches to a certain value. Figure 7(b) shows that M_c decreases as the temperature difference between the top and bottom of the arch section ΔT_g augments. Figure 7(b) also shows that M_c decreases as the rise-span ratio f/L augments initially; after that, it augments as the rise-span ratio f/L augments in case the rise-span ratio of arches reaches to a certain value. Figure 7(c) shows that N_c augments as the average temperature of the arch section T_a augments. Figure 7(d) shows that M_c decreases as the average temperature of the arch section T_a augments.

To demonstrate the influences of the uniformly distributed vertical load on N and M given by (23) and (24), the changes of N_c and M_c with rise-span ratio f/L for parabolic arches having different uniformly distributed vertical loads q (i.e., q = 10⁵ kN/m, 2 × 10⁵ kN/m, 3 × 10⁵ kN/m) are plotted in Figures 8(a) and 8(b), respectively, where ΔT_g = 100^°C, T_a = 200^°C, and L/γ_x = 30.

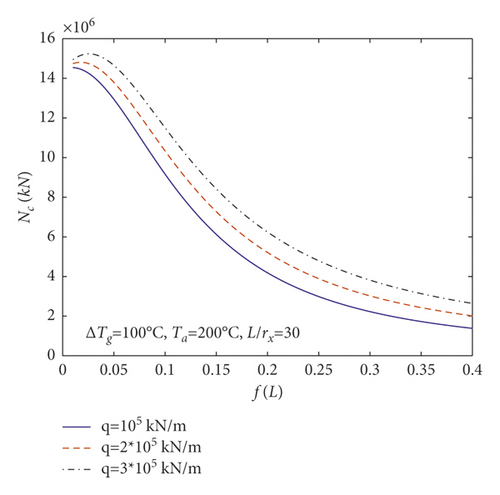
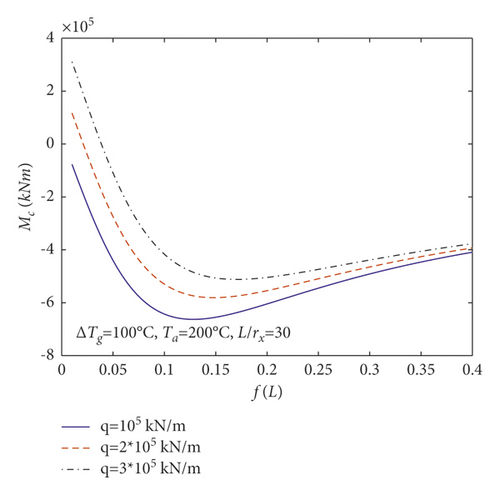
According to Figure 8, the central axial and bending actions N_c and M_c augment as the uniformly distributed vertical load q augments.

Figures 9 and 10 show the variation of the dimensionless internal force with the rise-span ratio for parabolic arch under the linear gradient temperature field and the vertical uniformly distributed load. Figure 9(a) shows that the central axial force N_c augments with the augments of the slenderness ratio L/r_x when temperature difference ΔT_g = 0^°C and the average temperature T_a = 20^°C. The central axial force N_c augments as the rise-span ratio f/L augments when the rise-span ratio f/L is less than 0.1 and then decreases as the rise-span ratio f/L augments when the rise-span ratio f/L is bigger than 0.1. Figure 9(b) shows that the central axial force N_c decreases with the augments of the slenderness ratio L/r_x when temperature difference ΔT_g = 100^°C and the average temperature T_a = 200^°C. The central axial force N_c decreases as the rise-span ratio f/L augments.

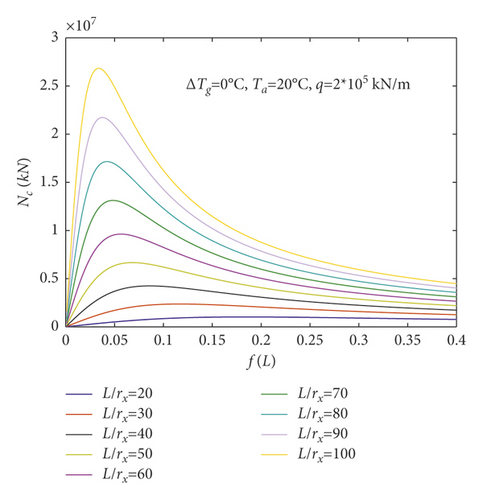
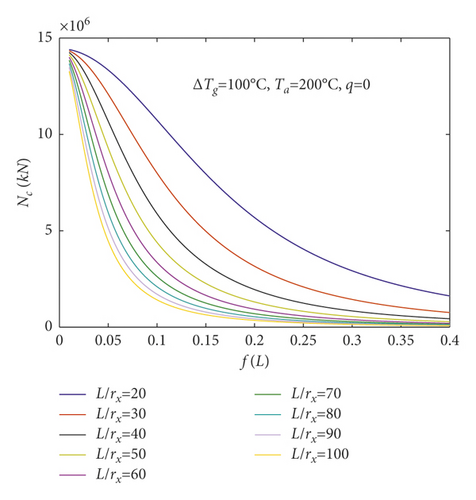
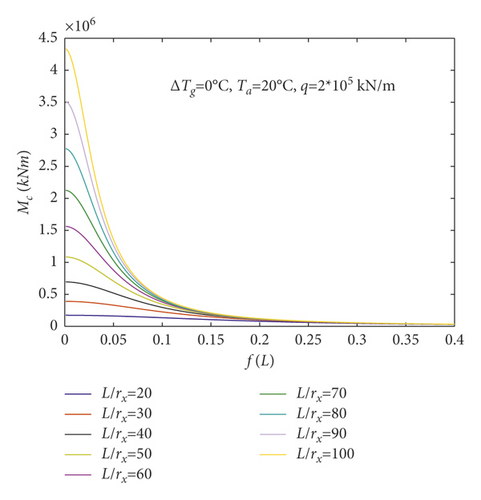
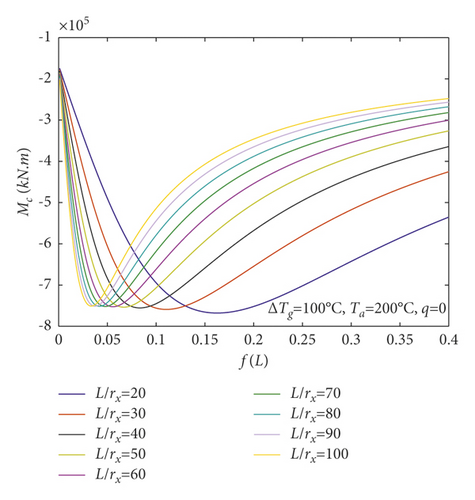
Figure 10(a) shows that the central bending moment M_c augments with the augments of the slenderness ratio L/r_x when temperature difference ΔT_g = 0^°C and the average temperature T_a = 20^°C. The central bending moment M_c decreases as the rise-span ratio f/L augments. Figure 10(b) shows that the central bending moment M_c decreases with the augments of the slenderness ratio L/r_x when temperature difference ΔT_g = 100^°C, the average temperature T_a = 200^°C, and the rise-span ratio f/L is approximately less than 0.1. The central bending moment M_c decreases as the rise-span ratio f/L augments, while the central bending moment M_c augments with the augments of the slenderness ratio L/r_x when the rise-span ratio f/L is approximately bigger than 0.1. The central bending moment M_c augments as the rise-span ratio augments f/L.

3.2. In-Plane Instability Analysis

According to the paper of Pi and Bradford [20], the in-plane instability critical load of parabolic arches boundary load can be compared with the relevant equation of circular arc arch. According to paper of Song et al. [14], the critical axial force of a solidly connected circular arch at both ends can be calculated by the following equation:

(30)

where the parameter ηπ can be expressed as

(31)

For a parabolic arch, the focal collimation distance p can be calculated by the following equation:

(32)

In addition, the radius of curvature of the parabolic arch is given by

(33)

For the sake of solving the critical load of instability of the parabolic arch with fixed ends, the axial force term of (30) can be replaced by the axial force at the top of the arch in the analytical solution of the internal force in the previous section [19].

(34)

Substitute (33) and (34) into (30) and obtain

(35)

Equation (35) is the critical in-plane instability load of a fixed parabolic steel arch under the gradient temperature coupled with vertical uniform load.

The change regular of dimensionless instability critical load with rise-span ratio for parabolic arches having different gradient temperature fields is shown in Figure 11, where N_E2 is the second mode flexural instability load of an axially compressive fixed column having the same length of the fixed parabolic steel arch, which can be expressed as

(36)

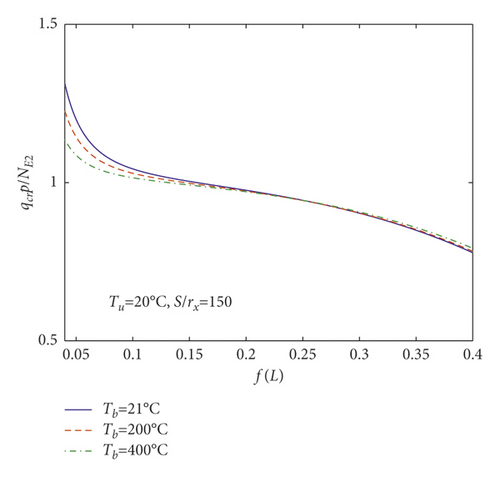
According to Figure 11, when the rise-span ratio is less than 0.15, the dimensionless critical in-plane instability load of parabolic arch is obviously influenced by the temperature gradient field and decreases with the augment of gradient temperature difference. However, when the rise-span ratio is larger than 0.15, the dimensionless critical in-plane instability load of parabolic arch is slightly influenced by the gradient temperature field. In addition, the dimensionless critical in-plane instability load of parabolic arches decreases with the increasing rise-span ratio.

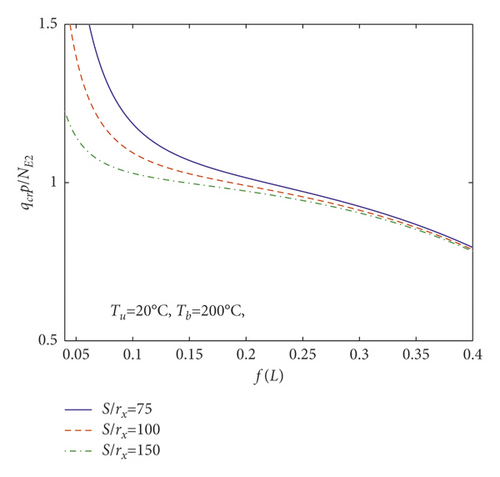
The variation of the dimensionless instability critical load with the rise-span ratio for the parabolic arch under the linear gradient temperature field is shown in Figure 12. As seen from Figure 12, the dimensionless critical in-plane instability load of parabolic arch decreases with the augment of slenderness.

3.3. Finite Element Validation Analysis

Finite element software ANSYS was employed to verify the accuracy of the above theoretical research. A biaxially symmetric I-beam section of the arch has a height h = 250 mm, a width b = 150 mm, a span length L = 5000 mm, a flange thickness t_f = 10 mm, and a web thickness t_w = 6 mm, and the material properties of Q235 steel were selected for modeling, which can be shown in Figure 13.

The beam188 element was chosen to build the parabolic arch mode. According to the help file of the beam188 element of ANSYS, the beam188 element can be used to specify temperature gradients that vary linearly both over the cross section and along the length of the element. The model is built and solved numerically for critical loads and then compared and analyzed with the theoretical solution.

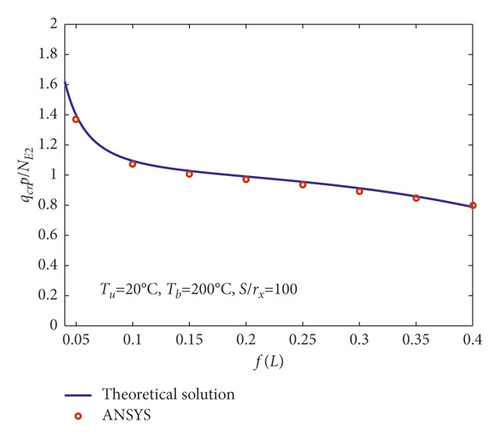
The comparison between the theoretical solution and the finite element results for the dimensionless critical in-plane instability load of the parabolic arch under linear gradient temperature field coupled with vertical uniform load can be seen from Figure 14. According to Figure 14, the theoretical solutions agree well with the finite element consequence data, indicating that (35) can accurately predict the instability critical load of the fixed parabolic steel arch under the gradient temperature field coupled with the vertical uniform load.

4. Conclusion

This paper has presented a theoretical study on the internal forces and critical in-plane instability loads for parabolic arches with I section under the linear gradient temperature field and vertical uniform load. The cross-sectional effective centroid and effective stiffness for parabolic arches under the linear temperature gradient field have been derived. The axial and bending actions of the parabolic arch under linear gradient temperature field coupled with vertical uniform load have also been obtained. In addition, the precise analytical solutions of the critical load for in-plane instability of the parabolic arch under gradient temperature field coupled with vertical uniform load have been obtained, and these solutions have been verified by numerical simulations of ANSYS. The conclusions of this article can be summarized as follows:

(1)
For parabolic arches under the linear gradient temperature field and vertical uniform load, the central axial force and the central bending moment decrease with the augment of slenderness.
(2)
The central axial force of the arch first augments with the augment of the rise-span ratio and then decreases with the augment of the rise-span ratio while the rise-span ratio reaches a certain value. The central bending moment decreases with the augment of the rise-span ratio.
(3)
When the rise-span ratio is less than 0.15, the dimensionless critical in-plane instability load of parabolic arch is obviously influenced by the temperature gradient field and decreases with the augment of gradient temperature difference; however, when the rise-span ratio is larger than 0.15, the dimensionless critical in-plane instability load of parabolic arch is slightly influenced by the gradient temperature field.
(4)
The dimensionless critical in-plane instability load of parabolic arches decreases with the increasing rise-span ratio.
(5)
The dimensionless critical in-plane instability load of parabolic arch decreases with the augment of slenderness.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This study was financially supported by the National Natural Science Foundation of China (grant no. 51 908 146) (Experimental Study on GAMECO Aircraft Maintenance Facility Phase III in Guangzhou Baiyun International Airport). The authors are grateful for the support.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Pi Y.-L. and Trahair N. S., Inelastic lateral buckling strength and design of steel arches, Engineering Structures. (2000) 22, no. 8, 993–1005, https://doi.org/10.1016/s0141-0296(99)00032-2, 2-s2.0-0033884614.
10.1016/S0141-0296(99)00032-2
Web of Science® Google Scholar
2 Mallon N. J., Fey R. H. B., Nijmeijer H., and Zhang G. Q., Dynamic buckling of a shallow arch under shock loading considering the effects of the arch shape, International Journal of Non-linear Mechanics. (2006) 41, no. 9, 1057–1067, https://doi.org/10.1016/j.ijnonlinmec.2006.10.017, 2-s2.0-33846534888.
10.1016/j.ijnonlinmec.2006.10.017
Web of Science® Google Scholar
3 Moon J., Yoon K.-Y., Lee T.-H., and Lee H.-E., In-plane elastic buckling of pin-ended shallow parabolic arches, Engineering Structures. (2007) 29, no. 10, 2611–2617, https://doi.org/10.1016/j.engstruct.2007.01.004, 2-s2.0-34548300022.
10.1016/j.engstruct.2007.01.004
Web of Science® Google Scholar
4 Pi Y.-L. and Bradford M. A., Dynamic buckling of shallow pin-ended arches under a sudden central concentrated load, Journal of Sound and Vibration. (2008) 317, no. 3-5, 898–917, https://doi.org/10.1016/j.jsv.2008.03.037, 2-s2.0-48349083366.
10.1016/j.jsv.2008.03.037
Web of Science® Google Scholar
5 Bradford M. A. and Pi Y.-L., A new analytical solution for lateral-torsional buckling of arches under axial uniform compression, Engineering Structures. (2012) 41, 14–23, https://doi.org/10.1016/j.engstruct.2012.03.022, 2-s2.0-84859763937.
10.1016/j.engstruct.2012.03.022
Web of Science® Google Scholar
6 Han Q., Cheng Y., Lu Y., Li T., and Lu P., Nonlinear buckling analysis of shallow arches with elastic horizontal supports, Thin-Walled Structures. (2016) 109, 88–102, https://doi.org/10.1016/j.tws.2016.09.016, 2-s2.0-84989299969.
10.1016/j.tws.2016.09.016
Web of Science® Google Scholar
7 Zheng Youyi, Zhuangpeng Y., and Donghuang Y., Analysis of buckling for a circular arch with rotational elastic constraints under a central concentrated load, Chinese Journal of Applied Mechanics. (2016) 33, no. 5.
Google Scholar
8 Kang T., Bai Y., Sun H., Yang H., Liu Y., and Ma G., Analysis of dynamic responses of arch structures with elastic supports under explosive impact, Chinese Journal of Applied Mechanics. (2017) 34, no. 04, 679–684+815.
Google Scholar
9 Yan S.-t., Shen X., Chen Z., and Jin Z., On buckling of non-uniform shallow arch under a central concentrated load, International Journal of Mechanical Sciences. (2017) 133, 330–343, https://doi.org/10.1016/j.ijmecsci.2017.08.046, 2-s2.0-85028744822.
10.1016/j.ijmecsci.2017.08.046
Web of Science® Google Scholar
10 Li Z., Zheng J., and Chen Y., Nonlinear buckling of thin-walled fgm arch encased in rigid confinement subjected to external pressure, Engineering Structures. (2019) 186, 86–95, https://doi.org/10.1016/j.engstruct.2019.02.019, 2-s2.0-85061393733.
10.1016/j.engstruct.2019.02.019
Web of Science® Google Scholar
11 Fan L., Zhang Y., Zhuk Y., Goroshko I., and Sareh P., Nonlinear in-plane buckling of shallow parabolic arches with tension cables under step loads, Archive of Applied Mechanics. (2021) 92, no. 1, 335–349, https://doi.org/10.1007/s00419-021-02060-7.
10.1007/s00419-021-02060-7
Web of Science® Google Scholar
12 Pi Y.-L. and Bradford M. A., Nonlinear thermoelastic buckling of pin-ended shallow arches under temperature gradient, Journal of Engineering Mechanics. (2010) 136, no. 8, 960–968, https://doi.org/10.1061/(asce)em.1943-7889.0000134, 2-s2.0-77955628968.
10.1061/(ASCE)EM.1943-7889.0000134
Web of Science® Google Scholar
13 Bouras Y. and Vrcelj Z., Non-linear in-plane buckling of shallow concrete arches subjected to combined mechanical and thermal loading, Engineering Structures. (2017) 152, 413–423, https://doi.org/10.1016/j.engstruct.2017.09.029, 2-s2.0-85032694244.
10.1016/j.engstruct.2017.09.029
Web of Science® Google Scholar
14 Song S., Yea H., and Tan Y., Analysis on the snap-through instability and bending behavior of steel arch under fire, Chinese Journal of Applied Mechanics. (2019) 36, no. 06.
Google Scholar
15 Asgari H., Bateni M., Kiani Y., and Eslami M. R., Non-linear thermo-elastic and buckling analysis of fgm shallow arches, Composite Structures. (2014) 109, 75–85, https://doi.org/10.1016/j.compstruct.2013.10.045, 2-s2.0-84890883317.
10.1016/j.compstruct.2013.10.045
Web of Science® Google Scholar
16 Li Z. and Zheng J., Nonlinear buckling mechanism of an arch subjected to a symmetrically-placed point load, KSCE Journal of Civil Engineering. (2019) 23, no. 11, 4781–4789, https://doi.org/10.1007/s12205-019-5152-2, 2-s2.0-85073507474.
10.1007/s12205-019-5152-2
Web of Science® Google Scholar
17 Tang Y., Tang F., Zheng J., and Li Z., In-plane asymmetric buckling of an fgm circular arch subjected to thermal and pressure fields, Engineering Structures. (2021) 239, https://doi.org/10.1016/j.engstruct.2021.112268.
10.1016/j.engstruct.2021.112268
Web of Science® Google Scholar
18 Li Z., Chen Y., Zheng J., and Sun Q., Thermal-elastic buckling of the arch-shaped structures with fgp aluminum reinforced by composite graphene platelets, Thin-Walled Structures. (2020) 157, https://doi.org/10.1016/j.tws.2020.107142.
10.1016/j.tws.2020.107142
Web of Science® Google Scholar
19 Cai J., Xu Y., Feng J., and Zhang J., In-plane elastic buckling of shallow parabolic arches under an external load and temperature changes, Journal of Structural Engineering. (2012) 138, no. 11, 1300–1309, https://doi.org/10.1061/(asce)st.1943-541x.0000570, 2-s2.0-84869412830.
10.1061/(ASCE)ST.1943-541X.0000570
Web of Science® Google Scholar
20 Pi Y.-L. and Bradford M. A., Nonlinear in-plane elastic buckling of shallow circular arches under uniform radial and thermal loading, International Journal of Mechanical Sciences. (2010) 52, no. 1, 75–88, https://doi.org/10.1016/j.ijmecsci.2009.10.011, 2-s2.0-71649084808.
10.1016/j.ijmecsci.2009.10.011
Web of Science® Google Scholar

All articles

In-Plane Instability of Parabolic Arches under Uniformly Distributed Vertical Load Coupled with Temperature Gradient Field

Abstract

1. Introduction