The traditional target-dependent camera calibration method has been widely used in close-distance and small field of view scenes. However, in view of the field coordinate measurement in the large-scale monitoring area under the complex field environment, the standard target can hardly meet the requirements of covering most of the camera’s field of view. In view of the above problem, a stereo camera calibration method is studied, using the unmanned aerial vehicles (UAV) as feature points, combined with the high-precision position information measured by the real-time kinematic (RTK) positioning system it carries. The measured UAV coordinates are unified in World Geodetic System 1984 (WGS-84). Therefore, through several preset points, the measurement reference coordinate system which is the new world coordinate system we need can be established in any monitoring area, which greatly improves the flexibility of measurement. The experimental results show that the measurement accuracy of the proposed method can reach 0.5% in the monitoring area with a diameter of 100 m. The calibration method has a wide range of application and does not need the traditional standard target, and the measurement reference coordinate system can be established according to the actual needs. It is suitable for field spatial coordinate measurement in long-distance and complex terrain environment.

1. Introduction

Binocular stereo vision simulates human eye vision to realize the mapping from two-dimensional (2D) images to three-dimensional (3D) space and realizes the use of 3D information. At present, this method has been widely used in autonomous driving, robot navigation, virtual reality, and industrial production [1–6]. The process of solving this mapping relationship is called camera calibration, which involves some parameters, including both intrinsic and extrinsic parameters. Intrinsic parameters consist of principal points, focal lengths, and lens distortion. Extrinsic parameters include a rotation matrix and a translation vector between the two cameras.

Various effective calibration methods have been proposed, including traditional calibration methods, self-calibration methods, and camera calibration based on active vision. In the traditional calibration method, the intrinsic and extrinsic parameters of the camera are obtained by mathematical transformation of 3D coordinates and 2D image coordinates by presetting some targets. Faig [7] proposed an imaging model based on the optimization algorithm, which has a complex solution process and high initial value requirements. Abdel-Aziz and Karara [8] proposed the direct linear transformation (DLT) method, which ignored the effects of distortion and obtained unknown parameters of the equation by solving the linear equations. Tsai [9] proposed a two-step method based on radial constraint by combining optimization algorithm and direct linear transformation method on the basis of only considering radial distortion. Zhang [10] is best known for his flexible calibration method, in which he provided a good method for estimating the initial parameters of the camera by using the constraints of the homography between planes. The premise of the application of the above methods is to manufacture specific targets, such as checkerboard or circular targets, which is difficult to achieve in the field with a large field of view due to the size limitation. In response to the above problems, Faugeras et al. [11] and Maybank and Faugeras [12, 13] proposed a camera self-calibration method, which calibrated the camera by taking multiple images with distinct features and relative motion. However, this method had great limitations in sky, desert, sea, and other environments, and its robustness was poor and data reliability was insufficient. Similarly, Ma and Zhang [14–17] proposed a calibration method based on active vision, which required the camera to make specific movement and was not suitable for the occasion when the camera was fixed in the field with a large field of view. Besides, many scholars have proposed camera calibration methods in large field of view environment. For example, Kong et al. [18] proposed a method of camera calibration based on the Global Positioning System (GPS), which directly took the GPS instrument as the feature points, which limited the flexibility of the method in practical use. Xiao et al. [19] proposed a binocular 3D measurement system that uses a cross target with ring coded points. Shang et al. [20] proposed a large field of view calibration method in which the optical center and control point of the camera are close to the coplanar, which has many limitations. Sun et al. [21] proposed a baseline-based camera calibration method in which the calibration target must be randomly placed in the field of view several times. Wang et al. [22–24] proposed a stereo calibration method for out-of-focus cameras when acquiring images for long- and short-distance photogrammetry, which has high robustness and high accuracy. None of these methods enable precise and fast camera calibration at large field of view.

In this paper, a calibration method using the UAV with RTK as a high-precision mobile calibration target is proposed. This method does not need to manufacture large-scale calibration target, which reduces the requirement of calibration conditions, and is suitable for large scene field environment. In addition, by using the WGS-84 earth coordinate system as the intermediary, the measurement reference coordinate system can be flexibly converted to any desired position through several preset coordinate points, even if the position cannot be observed by the binocular cameras simultaneously, which is very suitable for some complex field scenes where the view is partially obscured by trees or hills. Experimental results show that the proposed method performs well in the monitoring area with a diameter of 50-100 m at the distance of 500-1000 m from the cameras.

The subsequent compositions of this article are as follows: Section 2 introduces the basic principles, Section 3 introduces the calibration process and experimental results, and Section 4 summarizes this article.

2. Calibration Theory

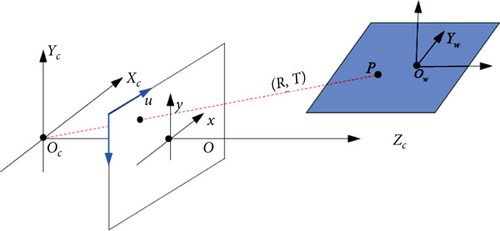
2.1. Camera Imaging Model

This paper focuses on where the camera is 500 m-1000 m away from the center of the monitoring area; therefore, the telephoto lens is used. Considering that the telephoto lens of the camera has very little distortion, the ideal pinhole imaging mode [25] is chosen to describe the mapping relationship between the object space and the image space, as is shown in Figure 1.

According to the pinhole imaging model, the coordinates from the world coordinate system, camera coordinate system, camera physical coordinate system and image pixel coordinate system have undergone three parts of rigid body transformation, projection transformation, and rigid body transformation, respectively. One point in the camera coordinate system is expressed as (X_c, Y_c, Z_c) and in the world coordinate system is expressed as (X_w, Y_w, Z_w), which are named (x, y) and (u, v), respectively, in the camera physical and image pixel coordinate systems. According to the relationship between each coordinate system, the linear transformation relationship between the world coordinate system (X_w, Y_w, Z_w) and the pixel coordinate system (u, v) is established by the following equation.

(1)

where R and T are the rotation matrix and translation vector between the world coordinate system and the camera coordinate system. f is the focal length of the lens. dx and dy are the physical size of the pixel. u₀ and v₀ are the camera principal points. Camera calibration requires the solution of these parameters.

2.2. Coordinate System Conversion

As can be seen from Section 2.1, obtaining the correspondence between the pixel coordinates and the world coordinates of the feature point is the key to estimating the camera parameters. With the help of the UAV working in RTK mode, we can obtain the UAV’s current GPS navigation coordinates P_G(B, L, H), which can be converted into earth rectangular coordinates P_E(X_E, Y_E, Z_E) [18]:

(2)

where N is the radius of curvature of the ellipsoid and E is the first eccentricity of the ellipsoid. Let a, b be the long and short semiaxes of the Earth, respectively, and χ be the ellipsoidal flattening rate of the Earth. Without losing generality [26],

(3)

Also, we know

(4)

By combining equations (2)–(4), the representation of P_G in the WGS-84 earth rectangular coordinate system, P_E, can be obtained. However, the coordinates obtained by the above steps are based on the Earth’s center of mass, which has two disadvantages: first, the scale of the obtained coordinates is too large to estimate the camera parameters; second, the origin and direction of the current coordinate axes have been fixed, which is not conducive to further measurement. Therefore, we need to set the origin and direction of the world coordinate system according to our own needs and complete the camera calibration in this coordinate system which is also called the preset coordinate system. Since coordinates of all measuring points are in the WGS-84 earth rectangular coordinate system, this transformation is not difficult. According to different application scenarios, the preset coordinate systems can be established by the following two ways.

(1)
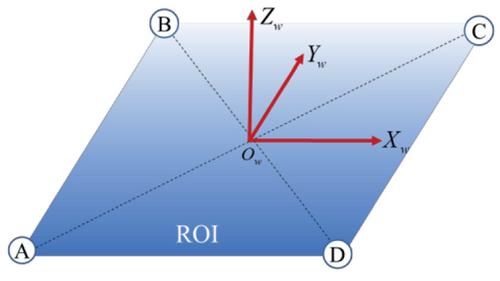
Establishment of the preset coordinate system for a rectangular region of interest

As is shown in Figure 2, the latitude and longitude of A, B, C, and D four points are measured at the four corners of a rectangle and converted to the earth rectangular coordinate system by the above steps. Take the coordinates of the intersection of lines AC and BD as the origin of the preset coordinate system O_w, and the vector between O_w and the midpoint of CD is the direction vector X of the X-axis. Then, the direction vector of the Z-axis can be expressed as

, and the direction vector of the Y-axis can be represented as Z × X.

(2)
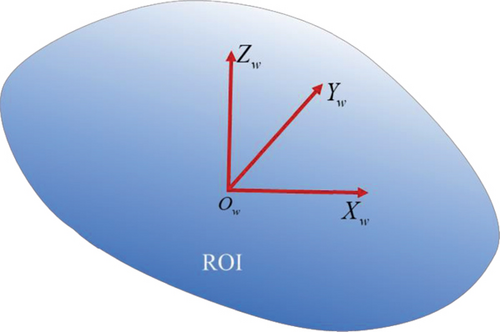
Establishment of the preset coordinate system for a region of interest with a center point

Measure the latitude and longitude of a point as the origin O_w of the preset coordinates and convert the coordinate to the earth rectangular coordinate system under WGS-84. Without loss of generality, in the wild, due north is usually used as the Y-direction vector, due east is the X-direction vector, and the Z direction is perpendicular to them.

The preset coordinate system can be established by the above rules, as is shown in Figure 3. And the transformation vector between the preset coordinate system and the earth rectangular coordinate system is obtained as T_E = O_w.

Normalize the three orthogonal direction vectors:

(5)

where | | represents the modular arithmetic. Then, we can obtain the rotation matrix R_E between the preset coordinate system and the earth rectangular coordinate system:

(6)

Thus, all space coordinates P_EUAV of UAV in the earth rectangular coordinate system can be converted to the preset coordinate system (new world coordinate system):

(7)

2.3. Single-Camera Calibration

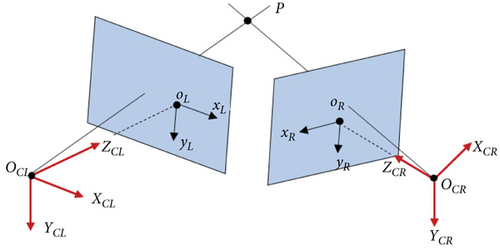
The basic condition of parameter estimation is to find the matching relationship between image coordinates and 3D coordinates. In this paper, the centroid of the UAV is designated as the feature points in the left and right cameras, as shown in Figure 4.

Details are in the caption following the image — Open in figure viewer PowerPoint

First, the initial values of intrinsic parameters are given based on the theoretical values:

(8)

where f is the theoretical focal length and f_x and f_y are the focal lengths (in pixels). dx and dy represent the physical size of pixels in the x and y directions, respectively, and u_max and v_max represent the resolution of the image in the x and y directions, respectively. Subsequently, initial solutions for other parameters (such as extrinsic parameters) can be obtained by DLT [8]. Finally, the constrained adjustment method is used to minimize the reprojection errors:

(9)

where m_n represents the image coordinate of the n-th point, M_n denotes its corresponding spatial coordinate,

is the projection of point M_n in image n according to equation (1), and R and T represent the rotation matrix and translation vector, respectively. It is worth noting that the principal points u₀ and v₀ are set to constant values and do not participate in the iterative process because their values are an order of magnitude smaller than the other parameters. Otherwise, although small reprojection errors can be obtained, these values have no physical significance and cause instability of other parameters. It has been experimentally proven in Reference [27] that the fixation of the principal points has little effect on the final reconstruction accuracy.

2.4. Binocular Calibration

According to Section 2.2, we can convert the GPS navigation coordinates of UAV to the required preset coordinate system. Suppose P is the coordinates of a point in the preset coordinate system and P_L and P_R are its corresponding coordinates in the left and right camera coordinate system, as is shown in Figure 5, their relationship can be described as

(10)

where [R_L, T_L] and [R_R, T_R] describe the extrinsic parameters of the left and right cameras, respectively. Obviously, it is easy to obtain the extrinsic parameters between the left and right cameras as

(11)

In this way, the binocular camera can be calibrated. The advantage of establishing the preset world coordinate system is that we can quickly convert the coordinates P_L (generally in the left camera coordinate system) reconstructed by the binocular camera to the preset coordinate system:

(12)

3. Experiments and Analysis

To verify the effectiveness of the proposed method, we set up a series of experiments. Five groups of camera-lens pairs were calibrated independently. Details of the camera-lens pairs are shown in Table 1.

1. Details of the camera-lens pairs.

Group	Camera resolution	Camera model	Lens model	Pixel size (μm)	Focal length (mm)
1	1920 × 1080	Phantom V341	Nikon 70-200 mm	10	100
2	1024 × 1024	Photron Nova s12	Nikon 70-200 mm	20	130
3	1280 × 800	Phantom VEO 310	Nikon 200-500 mm	20	350
4	1280 × 800	Phantom VEO 310	Nikon 200-500 mm	20	350
5	1920 × 1080	Phantom VEO 440	Nikon 70-200 mm	10	170

In each group, identical camera-lens pairs were used to form a stereo camera, with the two cameras placed vertically, while monitoring an area 500-1000 meters away. The area covered by the cameras varies in diameter from 50 m to 100 m, depending on the focal lengths.

In the experiment, the UAV (DJI M300) with RTK (DJI RTK-2) was used as the high-precision mobile calibration target. The RTK master station was arranged on the ground, and the fuselage was equipped with the RTK slave station. In the range of 10 km, the measuring accuracy of the slave station can reach the order of centimeters [28], which is a satisfactory accuracy compared with the camera monitoring diameter of tens of meters.

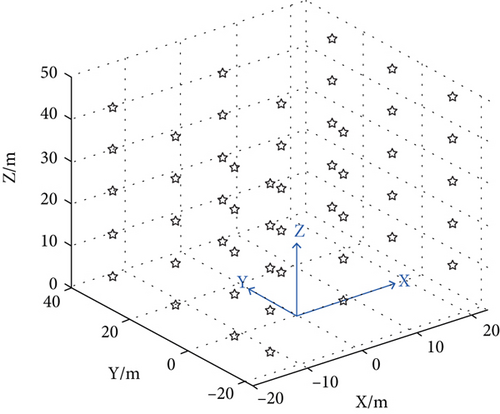
Control the UAV navigate over the monitoring area, and confirm that the UAV is in the field of view of the cameras. At 8 m, 16 m, 24 m, 32 m, and 40 m above the plane X-O-Y in the preset coordinate system, 10 points were suspended to record the GPS navigation coordinates and corresponding image coordinates of the UAV. Figure 6 illustrates the UAV images taken by two cameras. Convert the GPS coordinates to the preset coordinate system, and the position distribution of the UAV is shown in Figure 7.

3.1. Influence of the Feature Point Number on Calibration Results

As we know, the camera parameters can be correctly estimated only if there are at least six sets of 2D and 3D coordinates corresponding to each other. Adding a feature point means that the UAV needs to fly one more time, which will undoubtedly increase our workload. Therefore, it is meaningful to explore the appropriate number of feature points to reduce the work. Five independent experiments were carried out for the five camera-lens pairs described in Table 1.

In each experiment, 6, 10, and 40 UAV images (one image corresponds to a feature point position) were used to calibrate the stereo cameras. Then, the calibration results were used to reconstruct the space positions of another 10 UAVs. It is worth noting that the navigation coordinates measured by the GPS on the fuselage were used as the real space position of the UAV positions. Table 2 reveals the influence of different numbers of feature points on calibration results, in which the mean Euclidean distances of the reconstructed space positions and ideal ones of UAV are used to evaluate the accuracy of the results.

2. Errors between reconstructed positions and ideal positions (unit: m).

Point number	Group 1	Group 2	Group 3	Group 4	Group 5
6	12.69	0.39	8.36	8.68	3.2
10	1.44	0.31	3.32	0.35	0.21
12	0.16	0.32	0.11	0.36	0.19
15	0.13	0.30	0.09	0.28	0.21
20	0.12	0.28	0.09	0.22	0.16
25	0.12	0.28	0.09	0.17	0.17
30	0.11	0.26	0.08	0.15	0.15
35	0.11	0.25	0.08	0.14	0.16
40	0.10	0.22	0.08	0.13	0.15

As is shown in Figure 8, the results of five experiments show that when the number of feature points is less than 12, the reconstruction errors decrease rapidly with the increase in the number of feature points. However, when the number of feature points is greater than 12, the impact of the number of feature points on the accuracy becomes smaller and the reconstruction accuracy only improves slightly. Therefore, 15~30 points are a good choice to balance efficiency and accuracy in practical applications.

3.2. Reconstruction Accuracy

The actual measurement accuracy is an important criterion to evaluate the calibration accuracy. Two markers were placed in the monitoring area of the cameras, and the actual distance between them can be measured by RTK. The same steps were used to calibrate the two cameras, and the coordinates of the two markers were reconstructed according to the calibration results, and then, the distance between them was calculated. Experiments were carried out on the five groups of camera-lens configurations, and the reconstruction errors are shown in Table 3.

3. Distance errors of the two marks (unit: m).

Group number	Measured length	Reconstruction length	Absolute errors	Relative errors
1	24.25	24.36	0.11	0.45%
2	32.83	32.77	0.06	0.18%
3	46.60	46.48	0.12	0.26%
4	46.60	46.50	0.10	0.21%
5	30.00	29.95	0.05	0.17%

It can be seen that the reconstruction results are stable in accuracy, the maximum absolute error is less than 0.12 m, and the relative error is less than 0.5%. This is satisfactory when the monitoring diameter ranges from 50 m to 100 m. The results show that the proposed method is accurate and flexible in calibrating cameras with large field of view in the wild.

4. Conclusion

In this paper, a camera calibration method for long-distance photogrammetry using unmanned aerial vehicles is studied. Instead of traditional targets, the GPS carried by UAV is used to obtain the spatial coordinate information, so as to complete camera calibration. This method overcomes the problem that standard target cannot cover most of the camera’s field of view and enhances the environmental adaptability. In addition, by using the WGS-84 coordinate system as the intermediary, the preset coordinate system can be established in any area of interest, improving the flexibility of measurement. Experimental results show that the absolute measurement error of the proposed method is less than 0.5% in the monitoring area with a diameter of 50-100 m and at the distance of 500-1000 m from the cameras.

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Zhu X. P. and Fu Y., A camera calibration based on traffic video, Electronic Design Engineering. (2012) 20, no. 9, 48–52.
Google Scholar
2 Souto L. A., Castro A., Gonçalves L. M., and Nascimento T. P., Stairs and doors recognition as natural landmarks based on clouds of 3D edge-points from RGB-D sensors for mobile robot localization, Sensors. (2017) 17, no. 1824, 1–16.
10.3390/s17081824
Web of Science® Google Scholar
3 Zhao H. J. and Wu B., Three-dimensional face modeling technology based on 5G virtual reality binocular stereo vision, Communication Systems. (2022) 35, no. 5, https://doi.org/10.1002/dac.4651.
10.1002/dac.4651
PubMed Web of Science® Google Scholar
4 Xia M., Shao H. D., Williams D., Lu S., Shu L., and de Silva C. W., Intelligent fault diagnosis of machinery using digital twin-assisted deep transfer learning, Reliability Engineering & System Safety. (2021) 215, https://doi.org/10.1016/j.ress.2021.107938.
10.1016/j.ress.2021.107938
Web of Science® Google Scholar
5 Shao H. D., Xia M., Wan J. F., and de Silva C. W., Modified stacked autoencoder using adaptive morlet wavelet for intelligent fault diagnosis of rotating machinery, IEEE/ASME Transactions on Mechatronics. (2022) 27, no. 1, 24–33, https://doi.org/10.1109/TMECH.2021.3058061.
10.1109/TMECH.2021.3058061
Web of Science® Google Scholar
6 Xia M., Shao H. D., Ma X. D., and de Silva C. W., A stacked GRU-RNN-based approach for predicting renewable energy and electricity load for smart grid operation, IEEE Transactions on Industrial Informatics. (2021) 17, no. 10, 7050–7059, https://doi.org/10.1109/TII.2021.3056867.
10.1109/TII.2021.3056867
Web of Science® Google Scholar
7 Faig W., Calibration of close-range photogrammetric systems: mathematical formulation, Photogrammetric Engineering and Remote Sensing. (1975) 41, no. 12, 1479–1486.
Web of Science® Google Scholar
8 Abdel-Aziz Y. I. and Karara H. M., Direct linear transformation from comparator coordinates in close-range photogrammetry, Proceedings American society of photogrammetry symposium on close-range photogrammetry. (1971) 1–18.
Google Scholar
9 Tsai R. Y., A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf tv cameras and lenses, IEEE Journal on Robotics and Automation. (1987) 3, no. 4, 323–344, https://doi.org/10.1109/JRA.1987.1087109, 2-s2.0-0023397578.
10.1109/JRA.1987.1087109
Web of Science® Google Scholar
10 Zhang Z. Y., Flexible camera calibration by viewing a plane from unknown orientations, The Seventh IEEE International Conference on Computer Vision, 1999, Kerkyra, Greece.
Google Scholar
11 Faugeras O. D., Luong Q. T., and Maybank S. J., Camera self-calibration: theory and experiments, European Conference on Computer Vision. (1992) 321–334, https://doi.org/10.1007/3-540-55426-2_37, 2-s2.0-85028113208.
10.1007/3-540-55426-2_37
Google Scholar
12 Maybank S. J. and Faugeras O. D., A theory of self-calibration of a moving camera, The International Journal of Computer Vision. (1992) 8, no. 2, 123–151, https://doi.org/10.1007/BF00127171, 2-s2.0-0026900441.
10.1007/BF00127171
Web of Science® Google Scholar
13 Li X. H., Wang G. Y., and Liu J. G., Automatic camera calibration method based on dashed lines MIPPR 2013: remote sensing image processing, geographic information systems, and other applications, 2013, SPIE, 892112-1–892112-8.
Google Scholar
14 Ma S. D. and Zhang Z. Y., Computer Vision, 1998, Beijing Science Press.
Google Scholar
15 Zhao L. G., Wu C. K., and Ning J. F., A camera calibration method based on two orthogonal vanishing points, Concurrency and Computation: Practice and Experiment. (2014) 26, no. 5, 1185–1199.
10.1002/cpe.3055
Web of Science® Google Scholar
16 Sang D. M., A self-calibration technique for active vision systems, IEEE Transactions on Robotics and Automation. (1996) 12, no. 1, 114–120, https://doi.org/10.1109/70.481755, 2-s2.0-0030081439.
10.1109/70.481755
Google Scholar
17 Hu Z. Y. and Wu F. C., A review on some active vision based camera calibration techniques, Chinese Journal of Computers. (2002) 25, no. 11, 1149–1156.
Google Scholar
18 Kong X. F., Chen Q., Gu G. H., Qian W. X., Ren K., and Wang J. J., A GPS-based camera calibration method, China Ordnance Society. (2016) 37, no. 12, 2301–2307.
Google Scholar
19 Xiao Z., Jin L., Yu D., and Tang Z., A cross-target-based accurate calibration method of binocular stereo systems with large-scale field-of-view, Measurement. (2010) 43, no. 6, 747–754, https://doi.org/10.1016/j.measurement.2010.01.017, 2-s2.0-77951139218.
10.1016/j.measurement.2010.01.017
Web of Science® Google Scholar
20 Shang Y., Sun X., Yang X., Wang X., and Yu Q., A camera calibration method for large field optical measurement, Optik. (2013) 124, no. 24, 6553–6558, https://doi.org/10.1016/j.ijleo.2013.05.121, 2-s2.0-84885600965.
10.1016/j.ijleo.2013.05.121
Web of Science® Google Scholar
21 Sun J. H., Wu Z., Liu Q., and Zhang G., Field calibration of stereo vision sensor with large FOV, Optical Precision Engineering. (2009) 17, no. 3, 633–640.
Google Scholar
22 Wang Y. W., Chen X. C., Tao J. Y., Wang K., and Ma M., Accurate feature detection for out-of-focus camera calibration, Applied Optics. (2016) 55, no. 28, 7964–7971, https://doi.org/10.1364/AO.55.007964, 2-s2.0-84989299170, 27828034.
10.1364/AO.55.007964
PubMed Web of Science® Google Scholar
23 Wang Y. W., Wang Y. J., Liu L., and Chen X., Defocused camera calibration with a conventional periodic target based on Fourier transform, Optics Letters. (2019) 44, no. 13, 3254–3257, https://doi.org/10.1364/OL.44.003254, 2-s2.0-85068261189, 31259934.
10.1364/OL.44.003254
PubMed Web of Science® Google Scholar
24 Wang Y. W., Liu L., Cai B. L., Wang K., Chen X., Wang Y., and Tao B., Stereo calibration with absolute phase target, Optics Express. (2019) 27, no. 16, 22254–22267, https://doi.org/10.1364/OE.27.022254, 2-s2.0-85070298743, 31510522.
10.1364/OE.27.022254
PubMed Web of Science® Google Scholar
25 Hartley R. and Zisserman A., Multiple View Geometry in Computer Vision, 2004, Cambridge University Press, https://doi.org/10.1017/CBO9780511811685.010.
10.1017/CBO9780511811685
Google Scholar
26 Kong X. Y. and Guo J. M., Control Surveying, 2015, Wuhan university press.
Google Scholar
27 Zhao H. J., Wang Z., Jiang H. Z., Xu Y., and Dong C., Calibration for stereo vision system based on phase matching and bundle adjustment algorithm, Optics and Lasers in Engineering. (2015) 68, 203–213, https://doi.org/10.1016/j.optlaseng.2014.12.001, 2-s2.0-84921983303.
10.1016/j.optlaseng.2014.12.001
Web of Science® Google Scholar
28 Yan Z. G., Zhang Z. L., and Zhao X. H., The principle of GPS RTK pattern and the practical technology in its application, Surveying and Mapping of Sichuan. (2001) 24, no. 2, 66–69.
Google Scholar

Citing Literature

All articles

Camera Calibration for Long-Distance Photogrammetry Using Unmanned Aerial Vehicles

Abstract

1. Introduction