Estimation of Critical Safety Thickness of the Base against Confined Water Inrush for a Rectangular Foundation Pit
Abstract
Affected by confined aquifer, basal inrush accidents caused by excavation are common in foundation pits, and accurate estimation of the safety thickness of the base is a big concern of engineers. In this paper, a three-dimensional failure mechanism of base inrush was constructed for a rectangular foundation pit. In this mechanism, the strength of the soil mass was assumed to be nonhomogeneous along the depth, and the soil-mass failure satisfied the linear and nonlinear Mohr–Coulomb strength criteria. Then, based on the limit equilibrium theory, the prediction method for the safety thickness of the base against confined water inrush was deduced, and a comparison with existing research works was conducted. Furthermore, the influence laws of soil strength parameters, pit design parameters, and confined water pressure on the critical safety thickness were analyzed. The results show that the critical safety thickness of the base is positively correlated with nonlinear coefficient and confined water pressure but negatively correlated with cohesion, internal friction angle, nonhomogeneity coefficient, and unit weight. The soil strength is a key factor affecting the base safety thickness, which should be paid enough attention to in engineering design and construction. The research findings in this paper can provide a theoretical reference for the prevention and control of basal inrush accidents in confined water strata.
1. Introduction
In recent years, with the continuous advancement of urbanization in the world, the scale of all kinds of infrastructure construction is increasing, and the surface space is gradually becoming crowded. A series of problems such as population surge, traffic congestion, and environmental pollution have also become increasingly prominent. Rational development and utilization of underground space can effectively alleviate the above problems; it is one of the important ways to achieve sustainable and healthy urban development in the future. In the development process of urban underground space, the open-cut method is one of the most commonly used construction methods. In this method, accompanied by a series of complex projects such as urban subways, utility tunnels, and high-rise buildings, a large number of deep foundation pits with complex geological conditions have emerged in recent years, bringing great challenges to project safety construction. According to the existing data, the foundation pit accidents caused by groundwater account for about 45%–70% of all kinds of accidents. Especially in the confined water area, the inrush disaster caused by the action of the bottom confined water is more common, and it is easy to induce the collapse of foundation pits and destruction of supporting structures, which are big concerns of engineering design and construction personnel.
At present, the basal inrush failure mechanism of the foundation pit subjected to confined water has always been the concern of many scholars. The commonly used research methods include theoretical analysis, numerical simulation, and laboratory tests. For instance, Terzaghi [1] concluded that the seepage failure zone of the foundation pit base is mainly near the enclosure structure according to the model test and established the foundation pit inrush discriminant based on the test results. Marsland [2] conducted model tests at a building research station to determine the types of failures that occur due to water seepage in strutted sheeted excavations in noncohesive soils and investigated the influences of the cofferdam width, the penetration depth of the sheeting, and the soil conditions. Liu and Wang [3] analyzed the influence of the pressure water in shallow silty on excavation and proposed a series of measures to ensure safety during the pit excavation. Fontana [4] assessed the safety coefficient by comparing the exit gradient with the critical gradient and concluded that the experimental data and theoretical values were close if the thickness of the sheet pile and the ground surface deformation were properly taken into account. Wudtke [5] investigated the kind and the mechanism of hydraulic heave at excavations in cohesive soils and carried out a series of tests to visualize the failure mechanism in cohesive soil; finally, he proposed a series of factors that the failure type basically depends on. Do et al. [6] investigated basal heave stability of deep excavations in soft clay and employed three methods to estimate factors of safety against basal heave. Do et al. [7] investigated four failure mechanisms of excavations and proposed that reasonable stability of excavations was estimated by the FEM in the case of elastoplastic support system. Ding et al. [8] analyzed the influence laws of induced factors (confined water head, length, and width of the foundation pit) on the plastic deformation failure of foundation pit inrush based on the three-dimensional finite element calculation model. The results show that the uplift deformation and inrush plastic deformation failure of the soil under the foundation pit have a nonlinear relationship with the confined water head and the width of the foundation pit. Goh [9] assessed the basal heave stability of diaphragm wall supported circular excavations in clays using the finite element method and proposed a simplified method for assessing the basal heave factor of safety for axisymmetric supported excavations. Huang et al. [10] proposed a new failure mechanism to evaluate the basal stability of excavations with embedded walls in undrained clay and analyzed two failure field cases in anisotropic clay using this mechanism.
In strata containing confined water, sufficient base safety thickness of the foundation pit is very necessary to prevent inrush disaster. For example, in the current foundation pit codes of China and Japan, the theoretical prediction formula of basal inrush disaster is given on the basis of the pressure balance method. In this method, it is considered that inrush failure occurs if the dead weight of the bottom soil mass is smaller than the confined water pressure; the influence of soil strength is ignored. Specific to this problem, Ma et al. [11] proposed a calculation method for the critical thickness of the foundation pit base based on the relevant theories of structural mechanics. Yang and Zheng [12] took the excavation of a subway station as an example and put forward the calculation formula of base inrush to correct the code method by considering the shearing strength of soil mass. Wang et al. [13] obtained the method for determining the critical thickness of the base plate of the foundation pit based on elastic theory. Liu et al. [14] derived a new checking formula for anti-inrush of the foundation pit by considering shear strength and the dead weight of the foundation pit base and considering seepage factors of the foundation pit base. Sun [15] conducted a series of centrifugal model tests to investigate the failure mechanism of the foundation pit and proposed a theoretical approach to the basal stability analysis of deep excavation against a confined aquifer. Chen et al. [16] established the numerical model of PIP braced excavation in Shanghai soft clay overlying a confined aquifer and investigated the coupling effects of re-excavation and hydraulic uplift on base instability. Hu et al. [17] proposed the basic equation of unsteady seepage and stress coupling and investigated the stability of a deep foundation pit adjacent to water.
It should be noted that the above research works are all conducted on the basis of the linear Mohr–Coulomb failure criterion. A large number of laboratory tests [18–21] have shown that the strength envelope of soil mass is closer to an outer convex curve rather than the traditional linear relationship. Therefore, a nonlinear criterion is more accurate to describe the failure of soil masses. Meanwhile, under the action of long-term overloading within the strata, the soil mass may present obvious nonhomogeneity. By considering these factors and based on the existing research work, the nonlinear failure characteristics and the nonhomogeneity of soil masses are further incorporated in this paper, and a three-dimensional basal inrush failure mechanism for a rectangular foundation pit is constructed. Then the formula for predicting the critical safety thickness of the base is derived on the basis of the limit equilibrium method. The influence laws of different soil parameters, foundation pit design parameters, and confined water pressure on the critical thickness are obtained. The research findings in this paper can provide a theoretical reference for the basal inrush failure of foundation pits in confined water strata.
2. Inrush Failure Mechanism for a Rectangular Foundation Pit
2.1. Calculation Model in Current Technical Codes
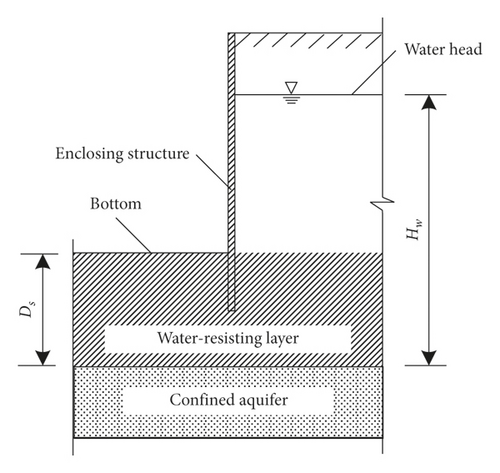
2.2. The Inrush Failure Mechanism Proposed in This Paper
In this paper, a rectangular foundation pit with depth H, width B, and length L is selected for analysis. According to the current codes and the research works by Yang and Zheng [12], Liu et al. [14], and Sun [15], a three-dimensional failure mechanism of base inrush is constructed, as shown in Figure 2. The inrush failure range is considered to be a red cube in Figure 2. Specifically, it is assumed that when the confined water pressure at the bottom exceeds the strength and dead weight of the upper soil mass, the inrush failure will occur. The bottom soil mass will slide upward along the vertical failure surface. The corresponding critical safety thickness is Ds. Meanwhile, the influence of supporting structure is neglected in the proposed mechanism, which can be regarded as the most unfavorable failure case and can ensure the safety of engineering design. Compared with the calculation model in current codes, the presented failure mechanism in Figure 2 considers the influence of soil shear strength, which may be closer to reality. Accordingly, the normal stress at the corresponding soil failure surface is σn, and the shear stress is τn.
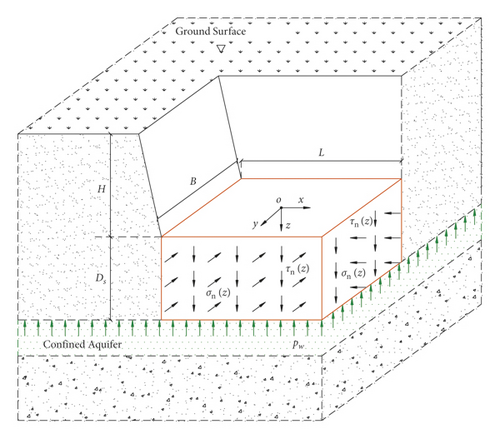
In the mechanism shown in Figure 2, we assume that the failure of the basal soil mass meets the following two criteria.
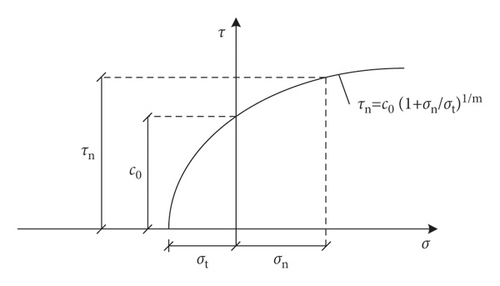
2.2.1. Mohr–Coulomb Failure Criterion
2.2.2. Nonlinear Mohr–Coulomb Failure Criterion
In addition, due to long-term overburden and sedimentation, the soil mass may present a property of nonhomogeneity, which will have a significant impact on its shear strength of itself. According to the research works by Huang et al. [22], Wang et al. [23], and Liu et al. [24], it is assumed that the cohesion of the soil mass increases linearly with depth in Figure 2, as shown in Figure 4.
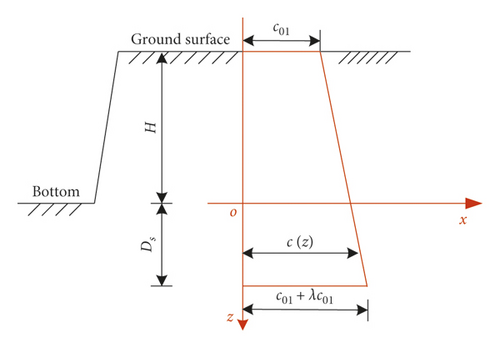
3. Determination of Critical Safety Thickness of the Base
3.1. Critical Safety Thickness Based on Mohr–Coulomb Failure Criterion
When the soil strength parameters and design parameters of the foundation pit are known, the theoretical calculation value of critical safety thickness Ds can be obtained by using equation (12) according to the inrush safety factor.
3.2. Critical Safety Thickness Based on Nonlinear Mohr–Coulomb Failure Criterion
At this time, when the nonlinear strength parameters and the design parameters of the foundation pit are known, the critical safety thickness Ds of the rectangular foundation pit base under the nonlinear Mohr–Coulomb failure criterion can be obtained by using equation (15).
4. Discussion and Analysis
4.1. Comparison with Existing Research Works
In the current codes, the inrush calculation model of the foundation pit base is established on the basis of the pressure balance method without considering the influence of soil strength. To solve this problem, Sun [15] carried out the centrifugal model test of foundation pit inrush and proposed a theoretical prediction method of critical base thickness based on the Mohr–Coulomb criterion. In order to further verify the effectiveness of the calculation method in this paper, when the size B(wi dt h) × L(length) of the foundation pit is 8 m × 16 m, 10 m × 20 m, and 12 m × 24 m, respectively, the method proposed in this paper, the current code method, and the method proposed by Sun [15] are used for a comparative analysis in this section. The specific calculation parameters are as follows: excavation depth H = 3 m, soil cohesion c01 = 30 kPa, internal friction angle φ = 30∘, unit weight γ = 18 kN/m3, and lateral pressure coefficient K0 = 0.8. Meanwhile, this section considers two nonhomogeneity coefficients of λ = 0 and λ = 0.5, respectively, for comparative analysis. Figures 5-7 show the variation curves of the critical safety thickness of the foundation pit base inrush with confined water pressure Pw. It can be seen from Figures 5–7 that the critical safety thickness of the foundation pit base under the three calculation methods increases with the increase of confined water pressure. Meanwhile, the calculation results of this method are slightly smaller than those of the method proposed by Sun [15], but the results of these two methods are close to each other, and both are smaller than the code calculation results. This shows that the code method is relatively conservative under the premise of ensuring the safety of the foundation pit base, while the proposed method in this paper is relatively economical. In addition, by comparing the calculation results in Figures 5–7, it can also be seen that the excavation size of the foundation pit also has a certain influence on base stability. As the excavation size increases, the critical safety thickness of the base also increases accordingly.
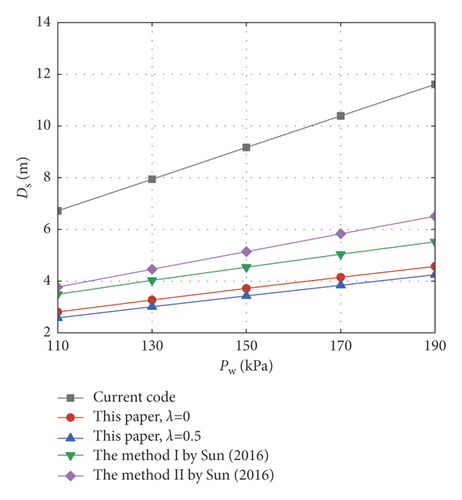
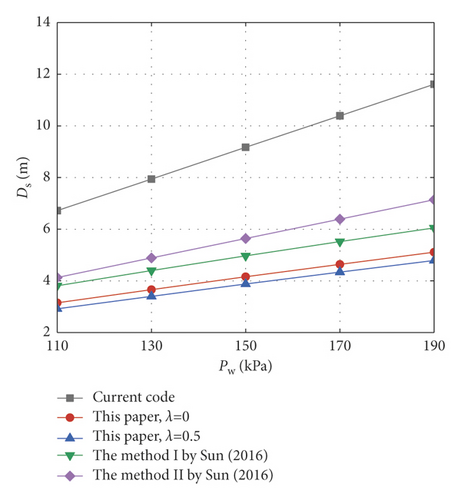
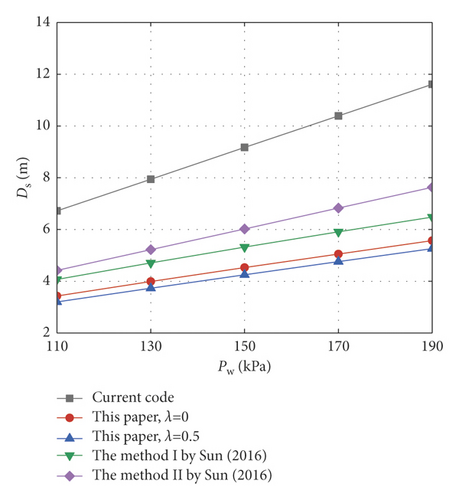
4.2. Effects of Different Linear Mohr–Coulomb Parameters
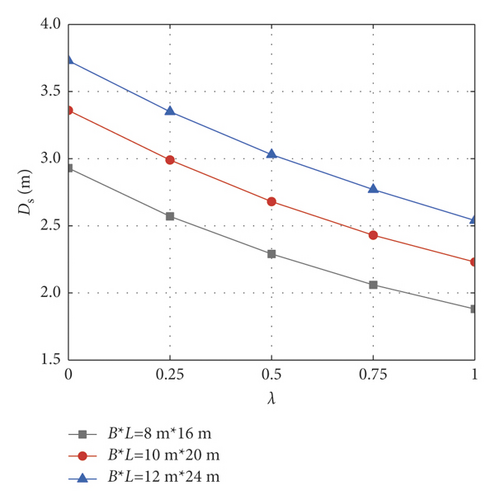
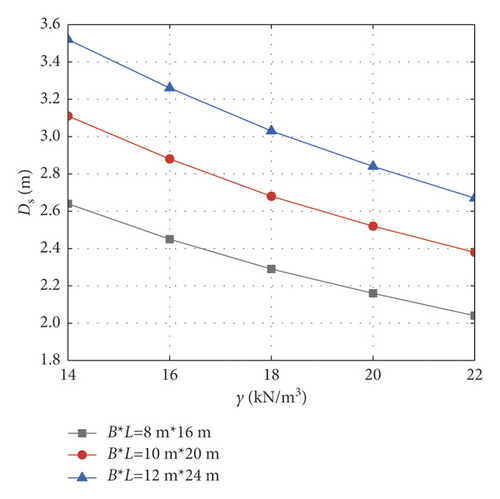
Based on the traditional linear Mohr–Coulomb failure criterion, this section analyzes the influence laws of nonhomogeneity coefficient, cohesion, internal friction angle, and unit weight on the critical safety thickness of the foundation pit base under different excavation sizes. The following parameters are selected as a standard group for calculation: foundation pit size B × L = 10 m × 20 m, excavation depth H = 6 m, cohesion c01 = 30 kPa, internal friction angle φ = 30∘, unit weight γ = 18 kN/m3, lateral pressure coefficient K0 = 0.8, confined water pressure Pw = 150 kPa, and safety factor Kty = 1.1. When analyzing the change of one soil parameter, the other parameters remain unchanged. When cohesion c01 is 10 ~ 50 kPa, internal friction angle φ is 22∘ ~ 38∘, unit weight γ is 14 ~ 22 kN/m3, and nonhomogeneity coefficient λ is 0 ~ 1.0, the corresponding variation curves of the basal critical safety thickness are shown in Figure 8. It can be seen from Figure 8 that under the traditional linear Mohr–Coulomb strength criterion, with the increase of cohesion, internal friction angle, unit weight, and nonhomogeneity coefficient, the whole strength of the soil mass and the capacity of the base against inrush increase accordingly, and the corresponding critical safety thickness of the foundation pit base decreases.
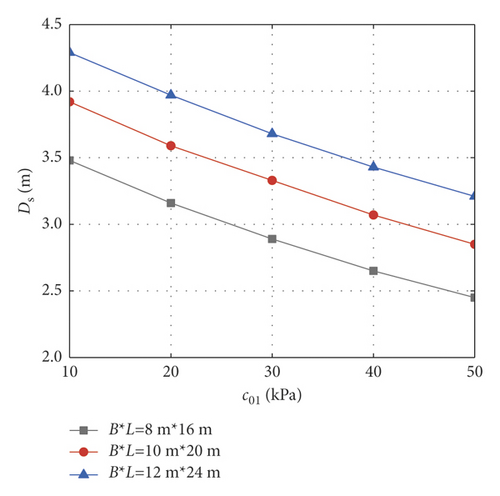
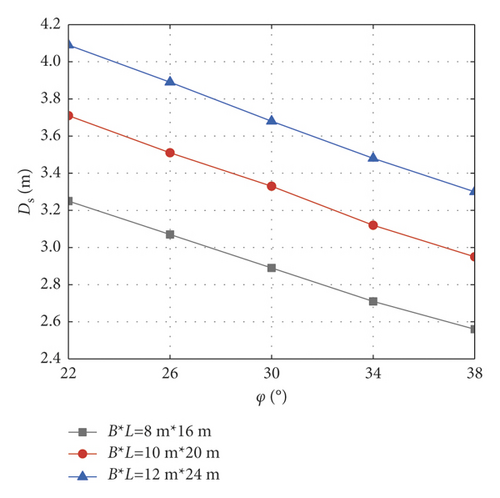
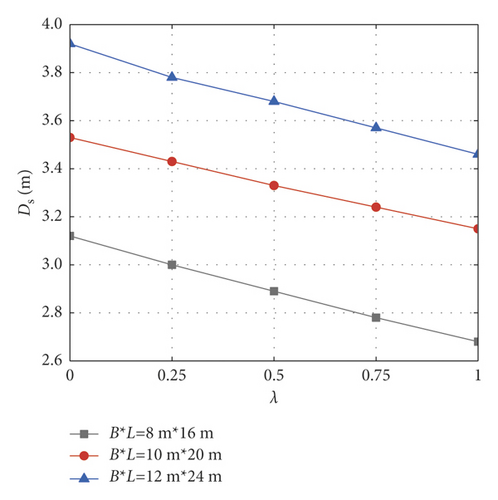
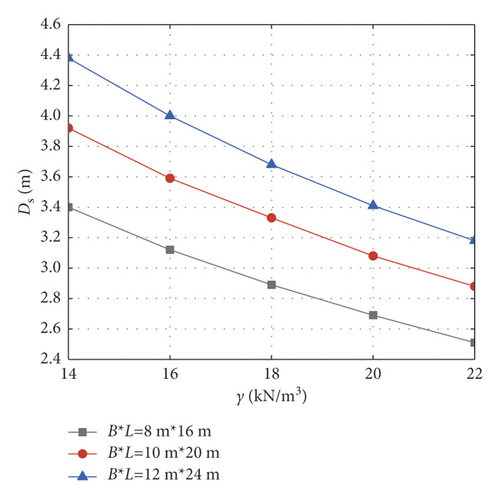
4.3. Effects of Different Nonlinear Mohr–Coulomb Parameters
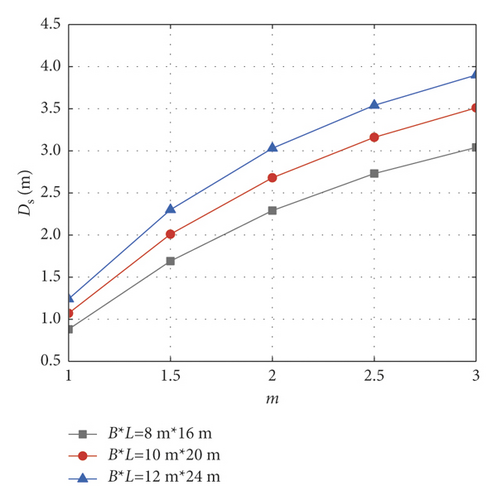
Similarly, based on the nonlinear Mohr–Coulomb strength criterion, this section analyzes the influence laws of initial cohesion at the ground surface, nonhomogeneity coefficient, nonlinear coefficient, and unit weight on the critical safety thickness of the base under different excavation sizes. In the calculation process, the foundation pit size, excavation depth, initial cohesion at the ground surface, lateral pressure coefficient, unit weight, confined water pressure, and safety factor are the same as those of the standard group in Section 4.2. When the initial cohesion at the ground surface c01 is 10 ~ 50 kPa, the unit weight γ is 14 ~ 22 kN/m3, the nonhomogeneity coefficient λ is 0 ~ 1.0, and the nonlinear coefficient m is 1 ~ 3, the variation curves of the basal’s critical safety thickness under different nonlinear strength parameters are shown in Figure 9. It can be seen from Figure 9 that under the nonlinear Mohr–Coulomb strength criterion, the critical safety thickness of the base is negatively correlated with the initial cohesion at the ground surface, nonhomogeneity coefficient, and unit weight, which is consistent with the conclusion in Section 4.2. However, the critical safety thickness is positively correlated with the nonlinear coefficient m. That is, as the nonlinear coefficient of the soil mass increases, the overall strength of the soil mass decreases, and the corresponding critical safety thickness of the base increases.
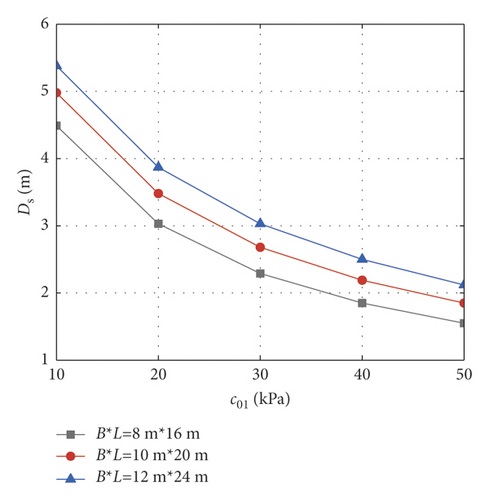
4.4. Recommendations for Engineering Projects
- (1)
Due to the consideration of soil strength parameters in the method proposed in this paper, the corresponding calculation results are smaller than those in the current codes. This shows that the current code method is relatively conservative. Especially in practical engineering, if the soil strength of the foundation pit base is high, it is more economical to adopt the method in this paper; it can reduce the cost of prevention and control of inrush disasters to a certain extent.
- (2)
The influence of soil strength parameters on the inrush failure of the foundation pit base is significant. If the strength of the bottom soil mass is low, the reinforcement of the bottom soil mass can be carried out in advance by a cement-soil mixing pile, high-pressure jet grouting pile, or grouting reinforcement measures, so as to improve the strength parameters of the soil mass and the safety of the base.
- (3)
Increasing the unit weight of basal soil mass is also one of the effective measures to prevent the inrush of the foundation pit. In engineering practice, the basal safety can be improved by means of surcharging load or replacing soil layer with stone to prevent inrush disaster.
5. Conclusions
- (1)
In this paper, focusing on a rectangular foundation pit, a three-dimensional failure mechanism of basal inrush is proposed. By using this mechanism, the theoretical formula for calculating the critical safety thickness against basal inrush is derived on the basis of the limit equilibrium method, and the linear and nonlinear Mohr–Coulomb strength criterion. In addition, the corresponding engineering suggestions are given, which can provide some theoretical reference for the prevention and control of basal inrush disasters of foundation pits in confined water strata.
- (2)
The proposed method is validated by comparing with the current code and the existing research works. The calculation results in this paper are close to those in the existing literature and are smaller than those in the current code. This shows that the results obtained by the current code are conservative, while the method presented in this paper is relatively economical.
- (3)
The influence laws of different excavation sizes, soil strength parameters, and confined water pressure on the basal critical safety thickness are analyzed. The results show that the critical safety thickness decreases with the increase of cohesion, internal friction angle, nonhomogeneity coefficient, and unit weight but increases with the increase of nonlinear coefficient and confined water pressure. The influence of soil strength parameters on the basal inrush failure is significant, and enough attention should be paid to it in engineering design and construction.
Abbreviations
-
- Ds:
-
- The critical safety thickness of the base against confined water inrush
-
- γ:
-
- The unit weight of the soil mass
-
- Hw:
-
- The height of the confined water head
-
- Pw:
-
- Confined water pressure
-
- Kty:
-
- A safety factor to characterizing the inrush stability of the foundation pit base
-
- σn:
-
- The normal stress at the soil failure surface
-
- τn:
-
- The shear stress at the soil failure surface
-
- c:
-
- Cohesion
-
- φ:
-
- Internal friction angle
-
- c0:
-
- Initial cohesion
-
- σt:
-
- Tensile strength
-
- m:
-
- A nonlinear coefficient
-
- λ:
-
- A coefficient reflecting the nonhomogeneity of soil mass
-
- H:
-
- The depth of the rectangular foundation pit
-
- B:
-
- The width of the rectangular foundation pit
-
- σv:
-
- The vertical stress at any position of the soil failure surface
-
- K0:
-
- Lateral pressure coefficient
-
- L:
-
- The length of the rectangular foundation pit
-
- G:
-
- The total weight of the soil mass within the inrush failure area
-
- Fpw:
-
- The total inrush destructive force generated by confined water
-
- F:
-
- The total shear force at the failure surface of soil mass.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Acknowledgments
The authors also would like to acknowledge the financial support from the National Natural Science Foundation of China (No. 51704177), project funded by the China Postdoctoral Science Foundation (2022M711314), the Project of Shandong Province Higher Educational Science and Technology Program (No. J16LG04), the Shandong Co-Innovation Center for Disaster Prevention and Mitigation of Civil Structures (No. XTP201911), and the Doctoral Research Fund of the Shandong Jianzhu University (No. XNBS1501).
Open Research
Data Availability
The data used to support the findings of this study are included within the article.




