In this article, we will determine the source term of the fractional diffusion equation (FDE). Our contribution to this work is the generalization of the common inverse diffusion equation issues and the inverse diffusion equation problems for fractional diffusion equations with energy source and using Caputo fractional derivatives in time and space. The problem is reformulated in a least-squares framework, which leads to a nonconvex minimization problem, which is solved using a Tikhonov regularization. By considering the direct problem with an implicit finite difference scheme (IFDS), the numerical inversions are performed for the source term in several approximate spaces. The inversion algorithm (IA) uniqueness is obtained. Furthermore, the effect of fractional order and regularization parameter on the inversion algorithm is carried out and shows that the inversion algorithm is effective. The order of fractional derivatives expresses the global property of the direct problem and also shows the badly posed nature of the inverted problem in question.

1. Introduction

Describing and simulating the behavior and diffusion process of contaminants in a heterogeneous porous medium are essential for environmental protection. The advection-dispersion equation with whole-order derivatives has played an important role in modeling the diffusion of contaminants over the past forty years, known as the classical diffusion model. However, some research has shown that the classical model is insufficient to present many real problems, where a particle plume propagates faster or slower than expected by the whole-order scattering equation. In the saturated zone of a very heterogeneous aquifer, Adams and Gelhar in [1] showed that the field data are not well simulated by the classical advection-diffusion equation, and the results indicate slower diffusion than normal. Slow diffusion is formulated by the long-tailed spatial density distribution position as time passes, which has been considered and studied in many domains of applied science. Hatano and Hatano in [2] consider dispersive transport of ions in column experiments. Giona et al. in [3] study the relaxation in a complex viscoelastic material. Berkowitz et al. in [4] discuss the anomalous transport heterogeneous porous media. Zhou and Selim in [5] propose an application of the fractional advection-dispersion equation in porous media. Xiong et al. in [6] modeled the transport of the solute in a homogeneous one-dimensional model. Jajarmi et al. in [7] propose a fractional formulation for immunogenic tumor. Baleanu et al. in [8] propose a new comparative study on the general fractional model. Erturk et al. in [9] give a new fractional-order Lagrangian to describe a Beam motion. The slow diffusion called abnormal underdiffusion can be modeled in mathematics by the following fractional temporal diffusion equation:

(1)

There is some theoretical and numerical research on the direct problem for the FDE with initial and boundary conditions. For the theoretical study, Gorenflo et al. in [10] treat the solvability of linear fractional differential equations. Metzler et al. in [11] consider value problems for fractional diffusion equations. Numerical approaches are proposed by Meerschaert and Tadjeran in [12] and Liu et al. in [13]. However, inverse problems governed by the fractional equation get less attention in the literature. According to Podlubnv [14], let us consider an inverse recovery boundary function problem from a data set at an internal point of a semi-infinite one-dimensional temporal fractional equation. A stable algorithm established and analyzed by modification methods. Cheng et al. [15] have investigated the inverse problem of finding the fractional order and the space-dependent diffusion coefficient in equation (1). By additional boundary data, they prove the uniqueness of the inverse problem in the case of null Neumann boundary conditions. Recently, much research has focused on the theory and applications of inverse problems. Li et al. in [16] treat numerical inversions in a fractional equation. Zhang and Xu in [17] consider an inverse problem for a fractional equation. Li et al. in [18] study the stability of the inverse acoustic problem. Jiang et al. in [19] use an inverse source problem with a hyperbolic equation. Maisto et al. in [20] propose resolution limits for strip currents. Can et al. in [21] treat the inverse problem with Mittag-Leffler. Liu et al. in [22] propose a method for solving a nonlinear wave inverse energy problem. Smirnov et al. in [23] consider an inverse problem for the radiative transfer equation. Slodicka et al. in [24] study the uniqueness for an inverse source problem of determining a space dependent source in a time-fractional equation. Le et al. in [25] solve numerically an inverse problem for hyperbolic equations. Bao et al. in [26] study stability for inverse problems in elastic and electromagnetic waves. Sun and Liu in [27] consider an inverse problem for distributed order time-fractional equations. Yang et al. in [28] propose an iterative method for solving the inverse problem of the time-fractional wave equation. Qiu et al. in [29] give a novel homogenization function method for an inverse problem. Cheng and Liu in [30] study a source problem with local measurements. Hrizi et al. in [31] give a new method for a parabolic inverse problem. Tuan et al. in [32] study an identification of inverse source for fractional equation.

Our primary contribution to this work is the generalization of the common inverse diffusion equation issues and the inverse diffusion equation problems for fractional diffusion equations with energy source and using the Caputo fractional derivatives in time and space. In recent years, a great deal of work has been done to examine these mathematical problems, both theoretically and numerically. These mathematical problems have become a significant tool in simulating many real-life difficulties. For recent developments, one can see Hendy, and Bockstal in [33] for reconstruction of a solely time-dependent source in a time-fractional equation. Ansari et al. in [34] study a class of distributed order fractional diffusion equation. Jajarmi et al. in [7] propose a general fractional formulation and tracking control for a tumor. Erturk et al. in [9] use novel fractional-order Lagrangian to describe the motion of beam.

In this paper, we investigated the inverse problem to numerically determine the energy source term for Caputo temporal FDE. In a one-dimensional space, we apply an algorithm based on the least-squares method with Tikhonov regularization. An IFDS is used for the direct problem. Numerical inversions of energy source terms dependent on space are performed in different approximation spaces using numeric inversion. We show the numerical uniqueness of the IA. The inversion results show the effectiveness of the IA for this inverse problem.

In the first part, we consider nonlinear square problem, which are ill-posed and have many solutions and do not give good simulation results. In the second part, we use the Tikhonov regularization, which allows for successful simulations. In Section 2, we provide preliminary results, then study the last square problem, and discuss the existence and uniqueness of the solution to the Tikhonov regularization problem. We examine the solution to the final square problem. Section 3 shows an inversion algorithm that will be tested successfully through three examples of simulations in Section 4.

2. Well-Posedness

Let consider the following system

(2)

(3)

(4)

where l, T > 0, u₀, k ∈ C¹([0, l]), φ, g ∈ C([0, T]), k ≥ 0 in [0, l] and ∂^γu/∂^γt, is the fractional Caputo derivative defined by

(5)

where (3) and the initial condition (4) are the Dirichlet-Neumann boundary conditions, r(x, t) is the energy perturbation term, and k(x) is the spatial diffusion coefficient. The fractional diffusion problem (2)-(4) is a mathematical model to describe the phenomenon of contaminant flux in a medium heterogeneous porous, see Zhou and Selim in [5] and Xiong et al. in [6].

Theorem 1. Let 1/2 < γ < 1, and Ω = (0, l). If r ∈ L²((0, T); Ω), then, for any u₀ ∈ L²(Ω), the problem (2) has a unique solution u ∈ L²((0, T); Ω). Moreover

(6)

Now, we consider r(x, t) = D(x)f(t).In the case where the sourceD(x)is not defined, we look for it by additional observations at the right end ofx = l, we search for it by additional observationsx = l, i.e., it is a limit.

(7)

So, the energy problem is defined by the FDE (3), with the condition defined by (3) - (5) and an additional condition (7).

To find the solution of the energy problem, the function D must be parameterized in the following polynomial form. For x ∈ Ω, we define the family of functions {p_m(x): m = 1, 2, ⋯}, with the following approximate expansion:

(8)

For any D(x), a unique solution of a corresponding direct problem, indicated by u(x, t; D), can be developed using the finite difference scheme in [16], then u(l, t; D) is obtained. Therefore, getting a term source D amounts to finding a vector , which means that one can write u(l, t; D) = u(l, t; P).

2.1. Nonlinear Least Squares Problem

For finding the solution of the energy problem, we solve the following nonlinear least squares problem

(9)

where

(10)

The problem (9) is badly posed so that this problem admits several solutions. For uniqueness, we used Tikhonov’s regularization.

2.2. Tikhonov Regularization

We consider the following regularized problem

(11)

where

(12)

such that α ≥ 0 is the regularization parameter. Now to get D^j = D(x_j), j = 0, 1, 2, ⋯, we assume that

(13)

where j is the number of iterations. δD^j denotes a perturbation of D^j.

From (8), we have

(14)

(15)

with δP^j denotes a perturbation for a given P^j. So, to get P^j+1, from given P^j, it suffices to obtain a disturbance δP^j.

(16)

Therefore, we just have to find a disturbance vector.

(17)

In the following, to make writing easier, P^j and δP^j are abbreviated as P and δP, respectively.

2.3. Linear Problem

We have the direct solution u(l, t; P + δP) is implicitly dependent on P, so with the Taylor expansion to order one, we find

(18)

Using (12), we get

(19)

Hence, in view to (18), we get

(20)

From (12), the objective least squares function becomes

(21)

We approximate the domain [0, T], by t_n(n = 1, 2, ⋯, N), and 0 = t₁ < t₂ < ⋯<t_N = T. Using the finite difference method, we have

(22)

for n = 1, 2, ⋯, N, where τ is a digital differential step. Hence, we define the matrix

(23)

where

(24)

Thus

(25)

Let

(26)

Using (22), (25), and (26), we can write (21) in the following form.

(27)

Lemma 2. The δP^α is a minimum of F_α, if and only if δP^α solves the following normal equation

(28)

Proof.

(29)

For all δP, δP^α ∈ ℝ^m+1. If δP^α satisfies (27), then, F_α(δP) − F_α(δP^α) ≥ 0, thus, δP^α minimizes (28). On the other hand, if δP^α minimizes (27), choose δP = δP^α + tZ, for all t > 0, and Z ∈ ℝ^m+1, we have

(30)

Hence

(31)

Divide by t > 0, and when t⟶0, we get

(32)

If we choose Z = −(H^T(HδP^α − (Ψ − U)) + αδP^α), we get

(33)

this implies that

(34)

which means that δP^α solves the normal equation (28).

2.4. Existence Result

Theorem 3. There exists at least δP^α ∈ ℝ^m+1, minimum point of the function F_α.

Proof. Let (δP_n) ∈ ℝ^m+1 be a minimizing sequence, i.e.,

(35)

when n tends to infinity. We show that (δP_n) is a Cauchy sequence

(36)

However, we have

(37)

(38)

Therefore, we may write

(39)

On the other hand, we have

(40)

By replacing (39) in (40), we get

(41)

By taking the limit as n and m to infinity, we get F_α(δP_n) + F_α(δP_m)⟶2I, thus

(42)

This shows that (δP_n) is a Cauchy sequence and therefore convergent since the Euclidean space is a Hilbert space. Let δPα = lim_n⟶∞δP_n, we have δP^α ∈ ℝ^m+1, by taking into account that F_α is continuous, we conclude that F_α(δP_n)⟶F_α(δP^α), then, δP^α = I. That proves the existence of a minimum of F_α.

2.5. Uniqueness Result

Lemma 4. F_α admits a unique minimum δP^α ∈ ℝ^m+1. This minimum δP^α is the unique solution of the normal equation

(43)

Proof. The question is to prove the uniqueness of the solution for the normal equation, because we have an equivalence between (27) and (28). We observe that the normal will be written as

(44)

In order to show that this equation admits a unique solution, we must prove that the matrix αI + H^TH is positive definite. Indeed, ∀δP ≠ 0,

(45)

Hence

(46)

This proves that the matrix is positive definite, and so invertible, we deduce that equation (28) admits a unique solution, and therefore, F_α admits a unique minimum. Thus, a perturbation can be determined by (28)

(47)

Therefore, the solution can be characterized by (12) with a sufficiently large iteration numbers, or when the perturbation verified the convergence condition

(48)

for a given convergence precision ε.

3. Inversion Algorithm

Step 1. Given the initial iteration P, the digital differential step τ, and the convergence precision ε, it is the additional condition ψ(t).

Step 2. Solve the direct problem using an implicit finite difference scheme featured in [16], get u(l, t_n; P), and u(l, t_n; (p₀, ⋯, p_i + τ, ⋯, p_m)), for n = 1, 2, ⋯, and i = 0, 1, ⋯, m, then obtain the vector U, and the matrix H, by the formula (25).

Step 3. Choose an appropriate regularization parameter α ≥ 0, and obtain a perturbation vector δP^α, using formula (47), then obtain δD^α.

Step 4. If there is , then the IA is finished, and D + δD^α is considered the solution we just want to determine; otherwise, go to Step 2, replacing P with P + δP.

4. Numerical Simulations

In this section, we get T = 1, l = 1, the initial condition u₀(x) = x, the number of spatial grids M = 20, and the number of time grids N = 20, and we propose the following two examples of simulations.

4.1. The First Case

For example, we choose D(x) = 2 + x, 0 ≤ x ≤ 1, as the exact source term. We performed the IA using the formula (47). By taking the initial data P₀ = (0,0.65), the digital differential step τ = 0.4, in the first case, we will do the simulation without the regularization term i.e., α = 0, the computational results are listed in Table 1, where denotes fractional order, D^inv denotes inversion.

1. Effects of fractional order on D.

γ	D^inv	Err
0.55	(1.00000, 1.00000)	1.2972e − 7
0.6	(1.00000, 1.00000)	1.292844e − 7
0.65	(1.00000, 1.00000)	5.54255e − 8
0.7	(1.00000, 1.00000)	6.28358e − 5

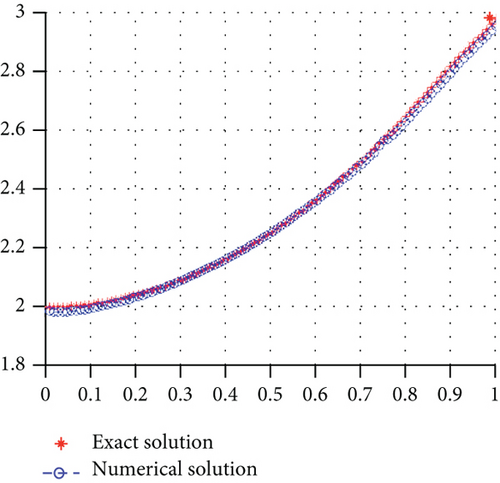
Where Err given by Err=‖D^true − D^inv‖ defines the absolute error in the solutions. The source term and their inversion are shown in Figure 1.

Details are in the caption following the image — Open in figure viewer PowerPoint

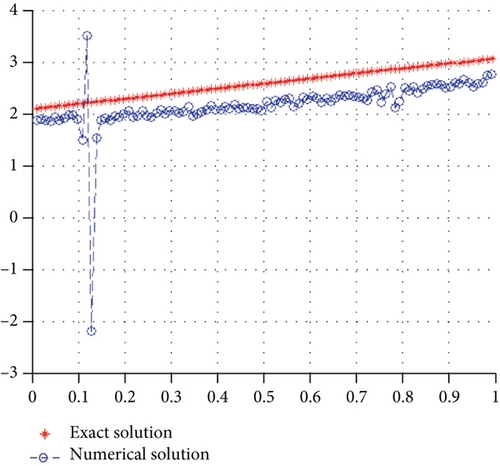
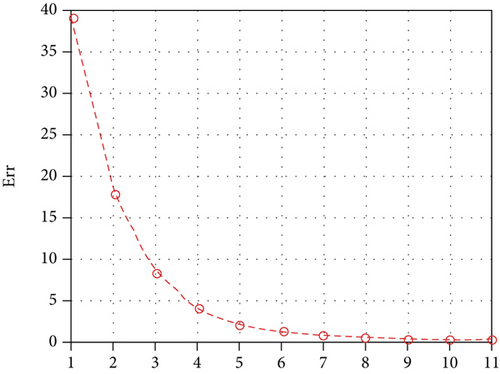
Figure 2 gives the graph of the error during iterations. Now, we put α = 1e⁻⁶, and thus, we get Figure 3.

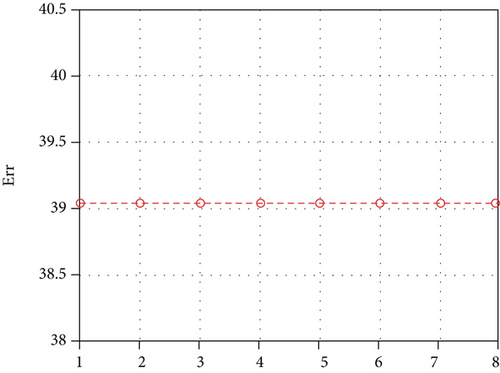
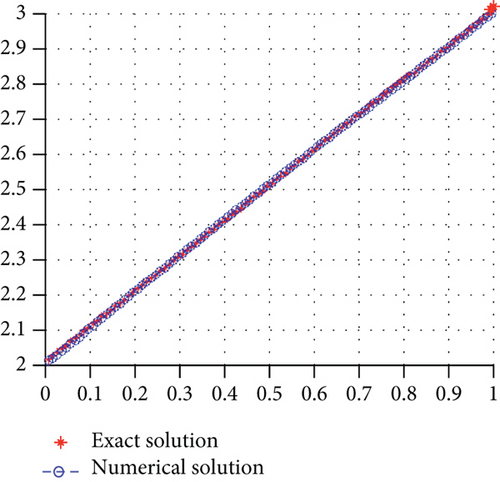
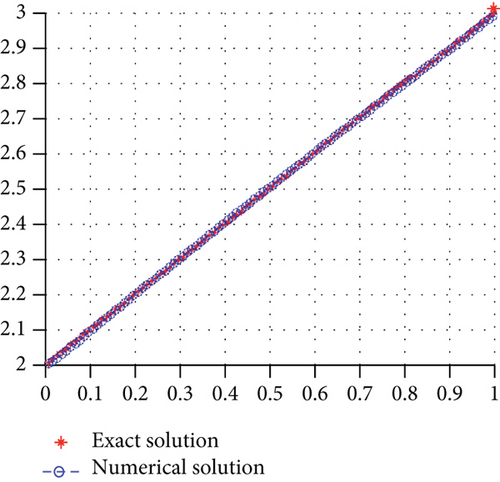
Figure 4 gives the graph of the error during iterations.

4.2. The Second Case

In the following, we use explicit regularization in algorithm execution due to the shortcomings of the problems being considered. Use this in.

(49)

as the exact source term. We performed the IA using the formula (47). Considering the regularization parameter α = 1e⁻⁹, the initial data P₀ = (3.4,0, 1.12), the digital differential step τ = 0.5, and the convergent precision ε = 1e⁻⁹, hence, we get the Table 2.

2. Effects of fractional order on D.

γ	D^inv	Err
0.55	(1.00000, 1.00000, −3.874254e − 9)	5.874788e − 7
0.6	(1.00000, 1.00000, −5.875477e − 9)	1.02157e − 9
0.65	(1.00000, 1.00000, −7.700214e − 8)	5.14785e − 8
0.7	(1.00000, 1.00000, −6.375155e − 6)	1.008547e − 5

Figure 4 gives the graph of the error during iterations.

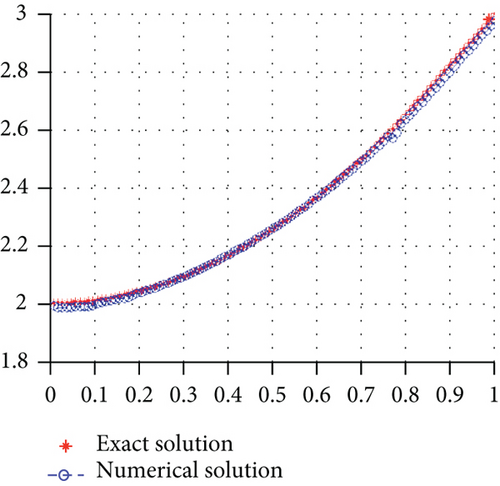
The source term and their inversion are shown in Figures 5(a) and 5(b).

4.3. The Third Case

This part considers the algorithm and we want to reconstruct the trigonometric

(50)

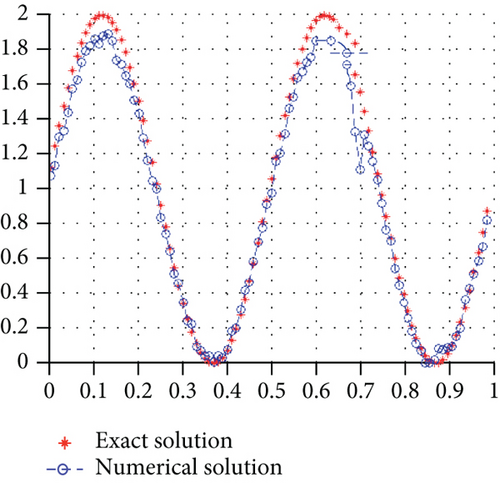
Table 3 shows that the fractional order has a significant effect on the problem and the resulting algorithm. Solution errors reach their minimum in optimal regularization of parameters which correspond to each fractional order while regulating solutions. The regularization parameter is larger when the fractional order is approaching 1. The true source term and the inversion solution are presented by the Figures 6(a) and 6(b).

3. Effects of fractional order on the algorithm.

γ	α	D^inv	Err
0.55	3.212157e − 9	(1.00000, 1.00000, 1.50000)	1.20025e − 7
0.6	6.4757e − 10	(1.00000, 1.00000, 1.50000)	12.30215e − 7
0.65	7.0002e − 8	(1.00000, 1.00000, 1.50000)	1.385470e − 6
0.7	6.15477e − 11	(1.00000, 1.00000, 1.50000)	8.00145e − 9

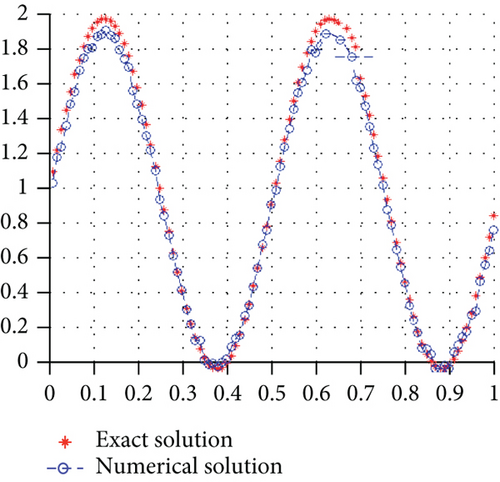
The simulation is concerned by proposing a numerical solution of a one-dimensional fractional system with Caputo derivative. We use an extension of the well-known in literature by inverse problem method. The comparison between the exact solution and the numerical one of the considered system show the effectiveness of our proposed algorithm. The three cases that have been suggested demonstrate the veracity of our findings.

5. Conclusion

Inverse source problem for one dimensional time-space fractional diffusion equations (FDE) are considered. We use numerical approach determine the source term for a Caputo temporal. According to Hadamard sense, these inverse problem is ill-posed. In order to recreate a stable solution for the inverse issue, a new fractional Tikhonov regularization technique is applied. We conclude that the regularization coefficient and digital differential step show major effects on the algorithm, but for the first iteration with convergent precision, the influence on the algorithm is less. It also results from the conclusion that the first iteration with convergent precision has a small effect on the algorithm. Further research in the future can envisaged, and we cite the extension of the proposed method to higher dimensional space, also its application to solve optimal control problems governed by FDE.

Conflicts of Interest

The authors declare that they have no competing interests.

Acknowledgments

This work was funded by the Deanship of Scientific Research at Jouf University under grant no. (DSR-2021-03-0342).

Open Research

Data Availability

Data sharing not applicable to this paper as no data sets were generated or analyzed during the current study.

References

1 Adams E. E. and Gelhar L. W., Field study of dispersion in a heterogeneous aquifer: 2. Spatial moments analysis, Water Resources Research. (1992) 28, no. 12, 3293–3307, https://doi.org/10.1029/92WR01757, 2-s2.0-0027069042.
10.1029/92WR01757
CAS Web of Science® Google Scholar
2 Hatano Y. and Hatano N., Dispersive transport of ions in column experiments: an explanation of long-tailed profiles, Water Resources Research. (1998) 34, no. 5, 1027–1033, https://doi.org/10.1029/98WR00214, 2-s2.0-0031961373.
10.1029/98WR00214
CAS Web of Science® Google Scholar
3 Giona M., Cerbelli S., and Roman H. E., Fractional diffusion equation and relaxation in complex viscoelastic materials, Physica A: Statistical Mechanics and its Applications. (1992) 191, no. 1-4, 449–453, https://doi.org/10.1016/0378-4371(92)90566-9, 2-s2.0-0001780043.
10.1016/0378-4371(92)90566-9
Web of Science® Google Scholar
4 Berkowitz B., Scher H., and Silliman S. E., Anomalous transport in laboratory-scale, heterogeneous porous media, Water Resources Research. (2000) 36, no. 1, 149–158, https://doi.org/10.1029/1999WR900295, 2-s2.0-0033986694.
10.1029/1999WR900295
Web of Science® Google Scholar
5 Zhou L. and Selim H. M., Application of the fractional advection-dispersion equation in porous media, Soil Science Society of America Journal. (2003) 67, no. 4, 1079–1084, https://doi.org/10.2136/sssaj2003.1079.
10.2136/sssaj2003.1079
CAS Web of Science® Google Scholar
6 Xiong Y., Huang G., and Huang Q., Modeling solute transport in one-dimensional homogeneous and heterogeneous soil columns with continuous time random walk, Journal of Contaminant Hydrology. (2006) 86, no. 3-4, 163–175, https://doi.org/10.1016/j.jconhyd.2006.03.001, 2-s2.0-33745970843, 16687188.
10.1016/j.jconhyd.2006.03.001
CAS PubMed Web of Science® Google Scholar
7 Jajarmi A., Baleanu D., Zarghami Vahid K., and Mobayen S., A general fractional formulation and tracking control for immunogenic tumor dynamics, Mathematical Methods in the Applied Sciences. (2022) 45, no. 2, 667–680, https://doi.org/10.1002/mma.7804.
10.1002/mma.7804
Web of Science® Google Scholar
8 Baleanu D., Abadi M. H., Jajarmi A., Vahid K. Z., and Nieto J. J., A new comparative study on the general fractional model of COVID-19 with isolation and quarantine effects, Alexandria Engineering Journal. (2022) 61, no. 6, 4779–4791, https://doi.org/10.1016/j.aej.2021.10.030.
10.1016/j.aej.2021.10.030
Web of Science® Google Scholar
9 Erturk V. S., Godwe E., Baleanu D., Kumar P., Asad J., and Jajarmi A., Novel fractional-order Lagrangian to describe motion of beam on nanowire, Acta Physica Polonica, A. (2021) 140, no. 3, 265–272, https://doi.org/10.12693/APhysPolA.140.265.
10.12693/APhysPolA.140.265
CAS Web of Science® Google Scholar
10 Gorenflo R., Luchko Y., and Zabrejko P. P., On solvability of linear fractional differential equations in Banach spaces, Fractional Calculus and Applied Analysis. (1999) 2, no. 2, 163–176.
Google Scholar
11 Metzler R. and Klafter J., Boundary value problems for fractional diffusion equations, Physica A: Statistical Mechanics and its Applications. (2000) 278, no. 1-2, 107–125, https://doi.org/10.1016/S0378-4371(99)00503-8, 2-s2.0-0033884660.
10.1016/S0378-4371(99)00503-8
CAS Web of Science® Google Scholar
12 Meerschaert M. M. and Tadjeran C., Finite difference approximations for fractional advection-dispersion flow equations, Journal of Computational and Applied Mathematics. (2004) 172, no. 1, 65–77, https://doi.org/10.1016/j.cam.2004.01.033, 2-s2.0-4444368867.
10.1016/j.cam.2004.01.033
Web of Science® Google Scholar
13 Liu F., Zhuang P., Anh V., Turner I., and Burrage K., Stability and convergence of the difference methods for the space-time fractional advection-diffusion equation, Applied Mathematics and Computation. (2007) 191, no. 1, 12–20, https://doi.org/10.1016/j.amc.2006.08.162, 2-s2.0-34547673244.
10.1016/j.amc.2006.08.162
Web of Science® Google Scholar
14 Podlubnv I., Fractional Differential Equations, 1999, Academic Press, San Diego, Boston.
Google Scholar
15 Cheng J., Nakagawa J., Yamamoto M., and Yamazaki T., Uniqueness in an inverse problem for a one-dimensional fractional diffusion equation, Inverse Problems. (2009) 25, no. 11, article 115002, https://doi.org/10.1088/0266-5611/25/11/115002, 2-s2.0-70450198851.
10.1088/0266-5611/25/11/115002
PubMed Web of Science® Google Scholar
16 Li G., Gu W., and Jia X., Numerical inversions for space-dependent diffusion coefficient in the time fractional diffusion equation, Journal of Inverse and Ill-Posed Problems. (2012) 20, no. 3, 339–366, https://doi.org/10.1515/jip-2011-0012, 2-s2.0-84869387476.
10.1515/jip-2011-0012
Web of Science® Google Scholar
17 Zhang Y. and Xu X., Inverse source problem for a fractional diffusion equation, Inverse Problems. (2011) 27, no. 3, article 035010, https://doi.org/10.1088/0266-5611/27/3/035010, 2-s2.0-79951779651.
10.1088/0266-5611/27/3/035010
Web of Science® Google Scholar
18 Li P., Zhai J., and Zhao Y., Stability for the acoustic inverse source problem in inhomogeneous media, SIAM Journal on Applied Mathematics. (2020) 80, no. 6, 2547–2559, https://doi.org/10.1137/20M1334267.
10.1137/20M1334267
Web of Science® Google Scholar
19 Jiang D., Liu Y., and Yamamoto M., Inverse source problem for the hyperbolic equation with a time-dependent principal part, Journal of Differential Equations. (2017) 262, no. 1, 653–681, https://doi.org/10.1016/j.jde.2016.09.036, 2-s2.0-84995470843.
10.1016/j.jde.2016.09.036
Web of Science® Google Scholar
20 Maisto M. A., Solimene R., and Pierri R., Resolution limits in inverse source problem for strip currents not in Fresnel zone, Journal of the Optical Society of America A. (2019) 36, no. 5, 826–833, https://doi.org/10.1364/JOSAA.36.000826, 2-s2.0-85065466896.
10.1364/JOSAA.36.000826
Google Scholar
21 Can N. H., Luc N. H., Baleanu D., Zhou Y., and Long L. D., Inverse source problem for time fractional diffusion equation with Mittag-Leffler kernel, Advances in Difference Equations. (2020) 2020, no. 1, https://doi.org/10.1186/s13662-020-02657-2.
10.1186/s13662-020-02657-2
Web of Science® Google Scholar
22 Liu C. S., Qiu L., and Wang F., Nonlinear wave inverse source problem solved by a method of m-order homogenization functions, Applied Mathematics Letters. (2019) 91, 90–96, https://doi.org/10.1016/j.aml.2018.11.025, 2-s2.0-85058466515.
10.1016/j.aml.2018.11.025
Web of Science® Google Scholar
23 Smirnov A. V., Klibanov M. V., and Nguyen L. H., On an inverse source problem for the full radiative transfer equation with incomplete data, SIAM Journal on Scientific Computing. (2019) 41, no. 5, B929–B952, https://doi.org/10.1137/19M1253605.
10.1137/19M1253605
Web of Science® Google Scholar
24 Slodicka M., Šišková K., and Van Bockstal K., Uniqueness for an inverse source problem of determining a space dependent source in a time-fractional diffusion equation, Applied Mathematics Letters. (2019) 91, 15–21, https://doi.org/10.1016/j.aml.2018.11.012, 2-s2.0-85058155982.
10.1016/j.aml.2018.11.012
Web of Science® Google Scholar
25 Le T. T., Nguyen L. H., Nguyen T. P., and Powell W., The quasi-reversibility method to numerically solve an inverse source problem for hyperbolic equations, Journal of Scientific Computing. (2021) 87, no. 3, 1–23, https://doi.org/10.1007/s10915-021-01501-3.
10.1007/s10915-021-01501-3
Web of Science® Google Scholar
26 Bao G., Li P., and Zhao Y., Stability for the inverse source problems in elastic and electromagnetic waves, Journal de Mathématiques Pures et Appliquées. (2020) 134, 122–178, https://doi.org/10.1016/j.matpur.2019.06.006, 2-s2.0-85068193009.
10.1016/j.matpur.2019.06.006
Web of Science® Google Scholar
27 Sun C. and Liu J., An inverse source problem for distributed order time-fractional diffusion equation, Inverse Problems. (2020) 36, no. 5, article 055008, https://doi.org/10.1088/1361-6420/ab762c.
10.1088/1361-6420/ab762c
Web of Science® Google Scholar
28 Yang F., Wang N., Li X. X., and School of Science, Lan Zhou University of Technology, Langongping, 730050 Lanzhou, China, Landweber iterative method for an inverse source problem of time-fractional diffusion-wave equation on spherically symmetric domain, Journal of Applied Analysis & Computation. (2020) 10, no. 2, 514–529, https://doi.org/10.11948/20180279.
10.11948/20180279
Web of Science® Google Scholar
29 Qiu L., Hu C., and Qin Q. H., A novel homogenization function method for inverse source problem of nonlinear time-fractional wave equation, Applied Mathematics Letters. (2020) 109, article 106554, https://doi.org/10.1016/j.aml.2020.106554.
10.1016/j.aml.2020.106554
Web of Science® Google Scholar
30 Cheng J. and Liu J., An inverse source problem for parabolic equations with local measurements, Applied Mathematics Letters. (2020) 103, article 106213, https://doi.org/10.1016/j.aml.2020.106213.
10.1016/j.aml.2020.106213
Web of Science® Google Scholar
31 Hrizi M., Hassine M., and Malek R., A new reconstruction method for a parabolic inverse source problem, Applicable Analysis. (2019) 98, no. 15, 2723–2750, https://doi.org/10.1080/00036811.2018.1469011, 2-s2.0-85046400679.
10.1080/00036811.2018.1469011
Web of Science® Google Scholar
32 Tuan N. H., Zhou Y., Long L. D., and Can N. H., Identifying inverse source for fractional diffusion equation with Riemann–Liouville derivative, Computational and Applied Mathematics. (2020) 39, no. 2, 1–16, https://doi.org/10.1007/s40314-020-1103-2.
10.1007/s40314-020-1103-2
Web of Science® Google Scholar
33 Hendy A. S. and Van Bockstal K., On a reconstruction of a solely time-dependent source in a time-fractional diffusion equation with non-smooth solutions, Journal of Scientific Computing. (2022) 90, no. 1, 1–33, https://doi.org/10.1007/s10915-021-01704-8.
10.1007/s10915-021-01704-8
Web of Science® Google Scholar
34 Ansari A., Derakhshan M. H., and Askari H., Distributed order fractional diffusion equation with fractional Laplacian in axisymmetric cylindrical configuration, Communications in Nonlinear Science and Numerical Simulation, 2022, 113, https://doi.org/10.1016/j.cnsns.2022.106590.
10.1016/j.cnsns.2022.106590
Google Scholar

Citing Literature

All articles

Determination of an Energy Source Term for Fractional Diffusion Equation

Abstract

1. Introduction