International Journal of Rotating Machinery

Volume 2022, Issue 1 7590924

Research Article

Open Access

Study on Contact Force and Vibration Characteristics of Composite Cylindrical Roller Bearing

Tie Qu,

Corresponding Author

Tie Qu

[email protected]

orcid.org/0000-0003-1227-8643

CITIC Heavy Industries Co., Ltd, Luoyang 471039, China

Search for more papers by this author

Qiang Bian,

Qiang Bian

School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China tyust.edu.cn

Search for more papers by this author

Guang Zeng,

Guang Zeng

School of Aerospace Engineering, Zhengzhou University of Aeronautics, Zhengzhou 450015, China zua.edu.cn

Search for more papers by this author

Chunjiang Zhao,

Chunjiang Zhao

School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China tyust.edu.cn

Search for more papers by this author

Xiangyun Zhang,

Xiangyun Zhang

School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China tyust.edu.cn

Search for more papers by this author

Lifeng Ma,

Lifeng Ma

School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China tyust.edu.cn

Search for more papers by this author

Ming Chen,

Ming Chen

School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China tyust.edu.cn

Search for more papers by this author

Tie Qu,

Corresponding Author

Tie Qu

[email protected]

orcid.org/0000-0003-1227-8643

CITIC Heavy Industries Co., Ltd, Luoyang 471039, China

Search for more papers by this author

Qiang Bian,

Qiang Bian

School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China tyust.edu.cn

Search for more papers by this author

Guang Zeng,

Guang Zeng

School of Aerospace Engineering, Zhengzhou University of Aeronautics, Zhengzhou 450015, China zua.edu.cn

Search for more papers by this author

Chunjiang Zhao,

Chunjiang Zhao

School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China tyust.edu.cn

Search for more papers by this author

Xiangyun Zhang,

Xiangyun Zhang

School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China tyust.edu.cn

Search for more papers by this author

Lifeng Ma,

Lifeng Ma

School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China tyust.edu.cn

Search for more papers by this author

Ming Chen,

Ming Chen

School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China tyust.edu.cn

Search for more papers by this author

First published: 07 October 2022

https://doi.org/10.1155/2022/7590924

Citations: 1

Academic Editor: Cheng Xu

Share a link

Email
Wechat
Bluesky

Abstract

The composite cylindrical roller is composed of a hollow cylindrical roller and a filler body and is a new type of structure roller bearing. In order to explore the influence of different parameters on the contact characteristics and vibration characteristics of bearings, finite element models of static contact, modal analysis, and harmonic response analysis of composite cylindrical roller bearings were established based on ABAQUS software. The effects of filling rate, radial force, and the number of rollers on parameters such as contact force, contact stress, and natural frequency were studied. The results show that when the filling rate of the cylindrical roller increases from 0% to 70%, the natural frequency of bearing and the peak frequency of its harmonic response decrease, the force distribution in the contact area is also more uniform, and the maximum contact stress of the roller is reduced by 29.1%; the radial force has no effect on the peak frequency of the harmonic response of the bearing, but the increase of the radial force will increase the peak value of the response displacement, and the contact force and stress of the rollers will also increase. When the number of rollers increases from 11 to 15, the natural frequency and the peak frequency of harmonic response increase, the peak displacement decreases, the contact force distribution of the rollers in the bearing area is more uniform, and the maximum contact stress of the roller is reduced by 21.1%. The research result can provide a theoretical reference for the structural optimization and engineering application of elastic composite cylindrical roller bearings.

1. Introduction

Cylindrical roller bearings are widely popularized because of their high contact stability and strong bearing capacity [1–3]. In recent years, in order to improve the working characteristics of cylindrical roller bearings, scholars have proposed an elastic composite cylindrical roller bearing (CCRB). CCRB is made by processing solid cylindrical rollers into hollow rollers on the basis of cylindrical roller bearings and adding flexible polytetrafluoroethylene (PTFE) into the hollow rollers [4, 5]. For the study of cylindrical roller bearings with different structures, Jianghong et al. [4] carried out the modal analysis and harmonic response analysis on composite cylindrical roller bearings with different filling degrees. Qishui et al. [6] presented three kinds of composite cylindrical roller structures and analyzed the bending stress of the inner wall of the composite roller under different geometric characteristics. Jing and Yimin [7] established the dynamic model of hollow cylindrical roller bearing and studied the effects of working condition parameters and roller hollowness on the vibration characteristics of the bearing. Zhifeng and Jing [8] proposed an improved planar dynamic model for calculating the vibration characteristics of cylindrical roller bearings and investigated the effect of different operating conditions on the vibration characteristics of the bearings. Mitul Thakorbhai and Dipak [9] built a finite element computational model of a layered hollow cylindrical roller in contact with a plane and determined the optimum hollowness of the roller under specific operating conditions by comparing parameters such as Mises stress and contact deformation. Yunling and Yankui [10] presented a new hollow roller with a revised inner bore and verified the superiority of the proposed scheme by calculating the contact stress and other parameters. Wenjie et al. [11] used Romax software to study the effect of force on the contact characteristics of rollers by modifying the cylindrical roller shape under bias force conditions and obtaining the optimal bias force factor and the corresponding force carrying interval. Wen et al. [12] analyzed the force carrying capacity of composite cylindrical roller bearings for moving trains under specific operating conditions. Jianghong et al. [13] used the contact model of a single composite roller established by ABAQUS software to examine the influence of force on the characteristic parameters of the contact area and verified the correctness of the model by theoretical calculations.

The aforementioned scholars have researched from exploring the contact mechanism of composite rollers to the contact force characteristics of the bearings, respectively, which laid the foundation for the analysis of the contact characteristics of composite cylindrical bearings. Compared with the solid cylindrical roller bearing, the composite cylindrical roller can improve the contact performance between the roller and the raceway, and the running stability and limit speed of the bearing will also be improved. In order to explore the influence of different parameters on the contact characteristics and vibration characteristics of composite cylindrical roller bearings, based on the mechanical contact and modal analysis theory, the contact, modal, and harmonic response analysis model of the composite cylindrical roller bearing is established by ABAQUS software. The influence of bearing structural parameters and working condition parameters on contact force, contact stress, natural frequency, and other parameters is studied. The internal force distribution and vibration characteristics of the composite cylindrical bearing are revealed. The analysis content can provide some theoretical reference for the structural optimization and engineering application of the bearing.

2. Theoretical Analysis

2.1. Bearing Static Contact Force Calculation

For cylindrical roller bearings, the inner ring is subjected to radial force F_r when the center of mass O is displaced δ_r and moved to O^′, and the rollers at different azimuths ψ will interact with the inner ring to produce the force F_ψ, as shown in Figure 1. The force equation is obtained from the interrelationship as [14–16]:

()

where F_max is the maximum contact force, ε is the force distribution coefficient, J_r is the radial force integration factor, and Z is the number of bearing rollers. By the balance of forces theorem, the above equation should satisfy

()

Details are in the caption following the image — Open in figure viewer PowerPoint

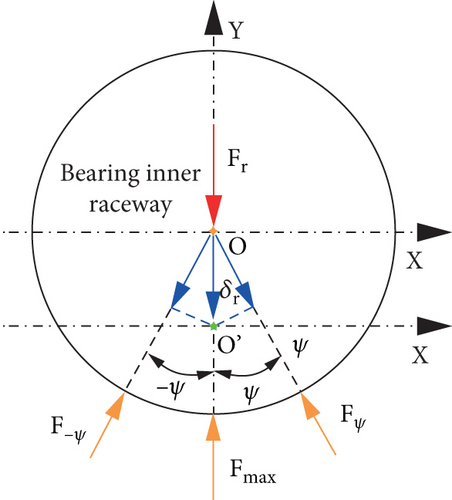
2.2. Roller Line Contact Stress Calculation

According to the Hertzian elastic contact theory, for cylindrical rollers mainly solved by line contact, the basic formula for solving the stress on two mutually contacting surfaces is obtained as [17, 18]

()

where S_max denotes the maximum contact stress, F denotes the action force, E denotes the material modulus of elasticity, υ denotes Poisson’s ratio, subscript 1, 2 represent the contact between two surfaces, ∑ρ represents the curvature of the contact surface, L represents the roller length, b represents the contact half-width, and δ represents the contact deformation.

2.3. Bearing Modal Analysis

The kinetic equation of the bearing during its operation in the general case is [19]

()

In the equation, [M] means the mass matrix, [C] means the damping matrix, [K] means the stiffness matrix, denotes the acceleration vector, denotes the velocity vector, [u] denotes the displacement vector, and [P] denotes the force vector.

The equation when it is in the undamped state is [20]

()

In the absence of external factors, the free vibration of the mechanism is sinusoidal motion, and the function satisfied by the displacement is

()

u_max is the amplitude of the displacement, t is time, and ω is the free frequency of the system. Combining equations (7) and (8) could obtain

()

2.4. Theory of Bearing Harmonic Response Analysis

Harmonic response analysis is to calculate the periodic response of the parts of the mechanism under cyclic harmonic excitation by applying external excitation forces of different frequencies.

In the simple harmonic response analysis, the displacement and force vectors of the object are in the form of simple harmonic waves [21]:

()

In this equation, [u₁] and [u₂] are, respectively, the real and imaginary parts of the displacement and [P₂] are, respectively, the real and imaginary parts of the force. The kinematic equations for the simple harmonic response analysis of the bearing can be obtained by substituting them into equation (1) as

()

3. Finite Element Modeling

The 3D model of the N2208 cylindrical roller bearing is created on the basis of the dimensional parameters shown in Figure 2, and then, the material properties of each component are set in the ABAQUS software [22, 23]. Among them, the density of bearing steel is 7800 kg/m³, the modulus of elasticity is 206000 MPa, and Poisson’s ratio is 0.3; the density of PTFE material is 2200 kg/m³, the modulus of elasticity is 280 MPa, and Poisson’s ratio is 0.4. In addition, according to the parameters shown in the figure, it is known that the bearing filling rate T = d_g/D_g.

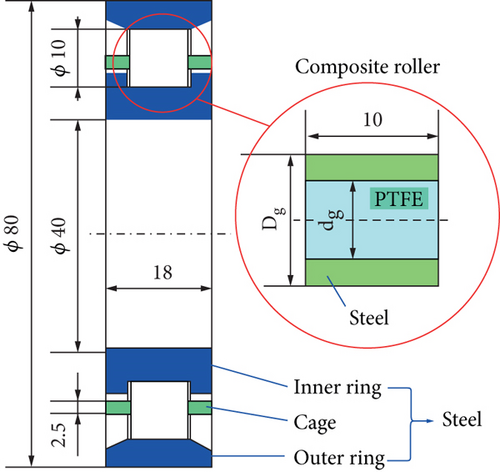
3.1. Establishment of Static Contact Model

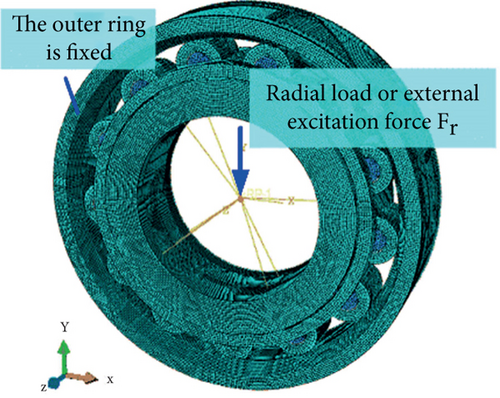
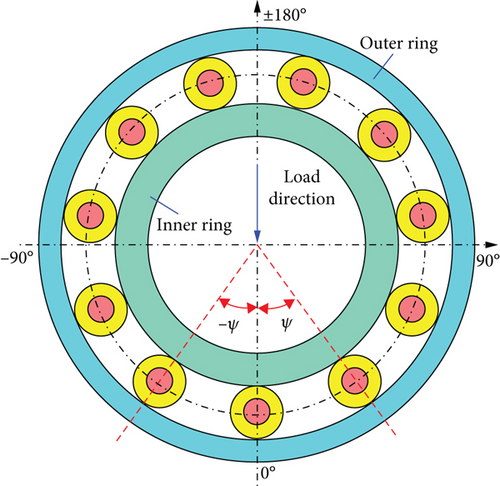
In the first, a dynamic explicit step is created in the step unit with a time of 0.05 s, and the corresponding output variables are specified. Then, the interaction between the parts of the bearing is established in the interaction unit. To simulate the actual loading of the bearing, the inner ring of the bearing is coupled to the geometric center point, and the radial force is applied to this point in the load unit.

3.2. Establishment of Modal Analysis and Harmonic Response Analysis

The modal analysis step of the bearing is established in the step unit, and the Lanczos solver eigenvalue is used for the solution, and the eigenvalue parameter for the solution is taken as 10. Then, based on the modal analysis step, the harmonic response analysis step of the bearing is established, and the sweep frequency range is set from 0 to 30,000 Hz. The boundary conditions and the loading method of the force used in this model are the same as those of the static contact model.

In addition, to enhance the computational accuracy and efficiency of the model, the meshing is carried out in the form of hexahedra, and the element type is C3D8R; the key contact parts are refined accordingly, as shown in Figure 3.

4. Results and Analysis

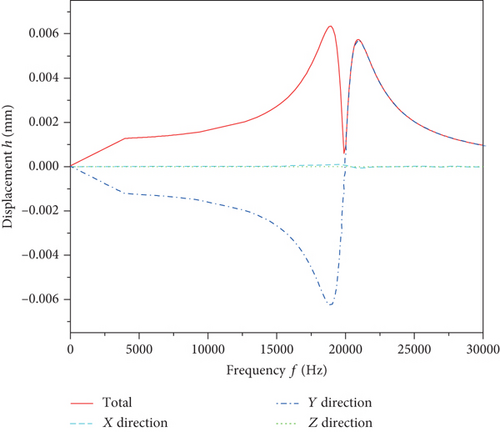
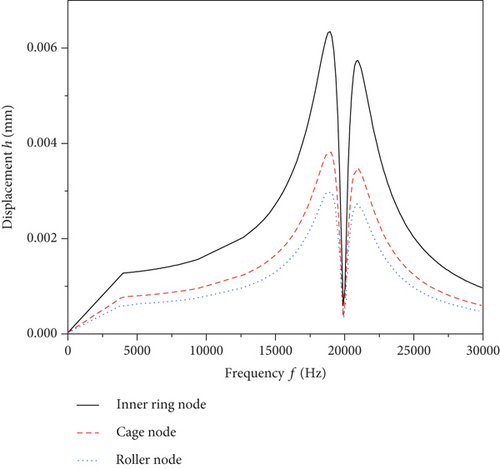
When the filling rate T is 50%, the radial force F_r is 3000 N, and the number of rollers Z is 13, the harmonic response displacement curve of the inner ring node is calculated and shown in Figure 4, and Figure 5 represents the displacement response curve of each component node of the bearing. It can be noticed from the figures that the harmonic response displacement of the inner ring node of the bearing under the action of the external excitation force comes out with two peaks, and the corresponding displacement values are 0.0063 mm and 0.0057 mm, and the frequency values are 19011.8 Hz and 20909.6 Hz. The displacements are mainly concentrated in the Y direction, which is the same as the direction of the force action. As can be observed from Figure 5, the harmonic response frequency of each component of the bearing is consistent, and the inner ring node has the largest harmonic response displacement, followed by the cage node, and the roller node has the smallest displacement.

4.1. Influence of Filling Rate

With the bearing roller number Z = 13 and radial force F_r = 3000 N, the filling rate of the composite material is set at 0, 40%, 50%, 60%, and 70%, respectively, and the inherent frequencies of the bearing are obtained by submitting the calculation model as listed in Table 1. Analyzing the values in Table 1, it can be realized that the inherent frequency of each order of the bearing gradually increases with the increase of the order. Meanwhile, when the filling rate increases from 0 to 70%, the inherent frequency of the bearing is gradually decreasing; that is, the composite cylindrical roller bearing is more prone to resonance.

1. Bearing inherent frequency at different filling rates.

Order	Inherent frequency
Order	T = 0%	T = 40%	T = 50%	T = 60%	T = 70%
1	15420	14741	14149	13219	11871
2	19142	18336	17642	16538	14927
3	19158	18347	17653	16548	14930
4	22117	21212	19994	18017	16451
5	22921	21520	20004	18029	16456
6	25940	25126	21132	20764	19141
7	26725	25081	24217	22265	21241
8	28726	25997	25018	23947	21761
9	29420	28111	26687	25015	24084
10	31152	29190	28156	26045	25186

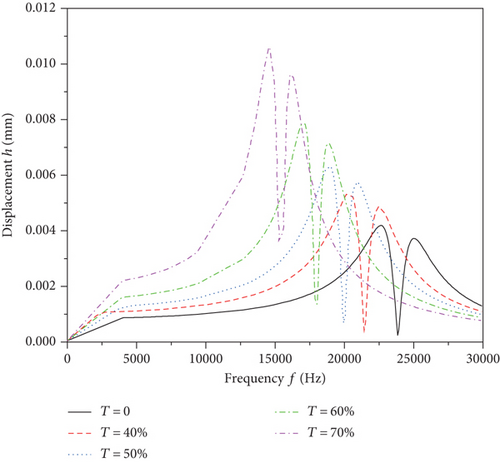
On the basis of the above modal analysis, the harmonic response analysis of the bearing under the same working condition is carried out, and the displacement response curve of the same node of the inner ring of the bearing is obtained as illustrated in Figure 6. Analysis of the data in the figure indicates that the harmonic response frequency and the maximum displacement of the bearing are decreasing with the increase of the filling rate. Among them, the maximum harmonic response frequency of solid roller bearing is 25030.4 Hz, which corresponds to the displacement value of 0.0037 mm only, and the maximum displacement value is 0.0042 mm only, which corresponds to the frequency value of 22694.6 Hz. The harmonic response frequency with a filling rate of 70% is the smallest, and the frequency values corresponding to the double peaks are 14613.6 Hz and 16137.4 Hz, with displacement values of 0.011 mm and 0.0096 mm. Integrating the data in Table 1 and the curves in Figure 6, it can be seen that the harmonic response frequencies of the bearings are all close to the third to sixth order of the inherent frequency, so the shock forces near the above frequencies should be avoided as much as possible in the actual use process.

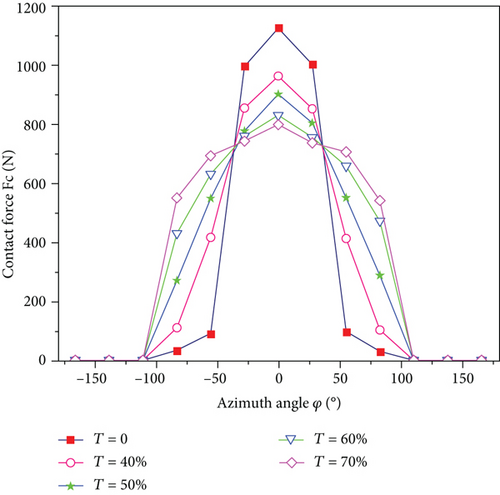
From the established static contact force calculation model for cylindrical rollers, the bearing and inner ring interaction forces at different filling rates are calculated as shown in Figure 7. Figure 8 shows the contact stress variation curve of the bearing rollers under the same working condition. From the change of curve in Figure 7, it can be found that when the filling rate of the bearing increases from 0 to 70%, the maximum action force of the inner raceway and roller decreases from 1125.2 N to 798.262 N, which is relatively reduced by 29.1%, and the force distribution in the bearing area is more uniform; the same trend can also be seen from the change of stress of the roller in Figure 8. This is because when the bearing rollers are filled with composite material, due to the reduction of the elastic modulus of the individual roller, the roller is easier to deform under the same force, which leads to an increase in the contact area between the raceway and the rollers, making the force distribution more uniform. Finally, for the same external force, the force acting on an individual roller will be relatively reduced.

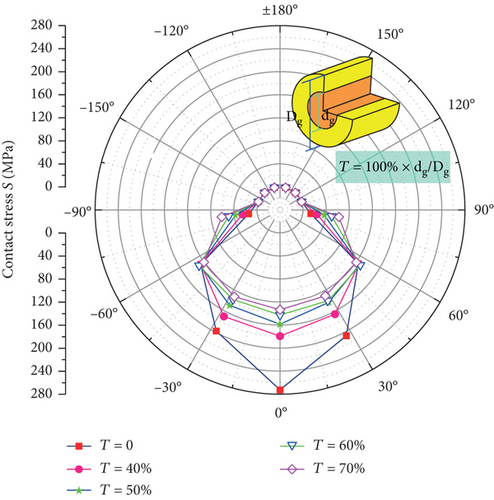
4.2. Influence of Radial Force

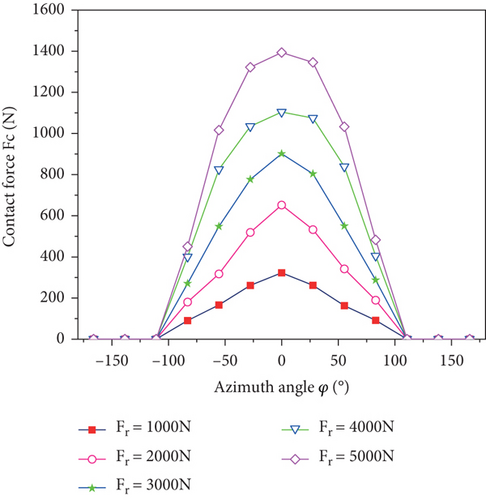
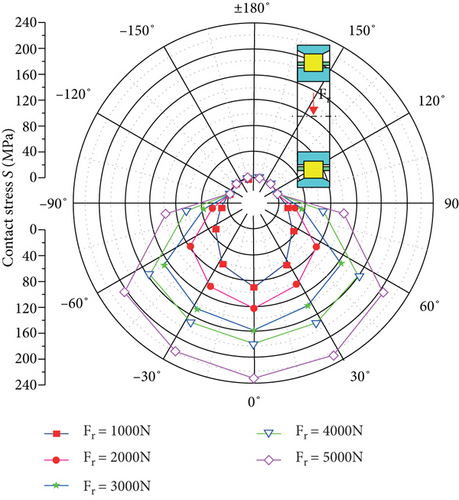
In order to study the effect of radial force on the bearing response, a model of bearing harmonic response and static contact analysis is built with different radial forces when the number of bearing rollers Z = 13 and the filling rate T = 50%, and the harmonic response displacement curve, the contact force between the rollers and the inner raceway, and the variation curve of bearing roller stress are calculated as shown in Figures 9–11.

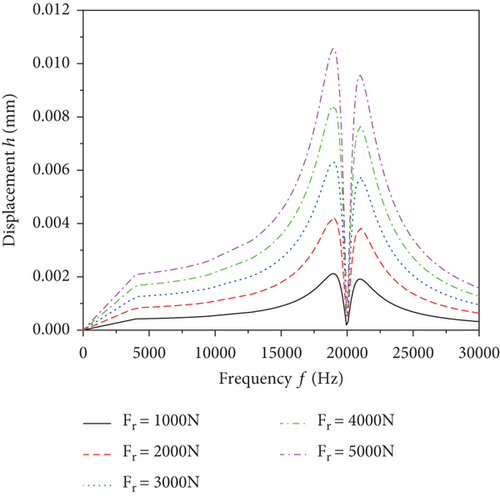
By analyzing the data in Figure 9, it can be observed that the external excitation force of the bearing has no effect on the harmonic response frequency, but the maximum harmonic response displacement of the bearing node is gradually increasing as the force increases. The maximum displacement of the bearing node is 0.0021 mm at a force of 1000 N and 0.011 mm at a force increase to 5000 N, indicating that the external excitation force has a large effect on the harmonic response displacement of the bearing node.

Figure 10 shows the curve of contact force between the bearing raceway and roller when different forces are applied, and Figure 11 shows the change curve of contact stress of the bearing roller. Combining the data in Figures 10 and 11, it can be discovered that as the force increases from 1000 N to 5000 N, the maximum contact force increases from 322.3 N to 1345.8 N and the maximum contact stress increases from 91.3 MPa to 233.8 MPa, and the growth rate gradually decreases, the maximum values are concentrated near the azimuth angle 0°.

4.3. Influence of the Number of Rollers

With the bearing roller filling rate T = 50%, the finite element analysis models of composite cylindrical roller bearings with a different number of rollers are established, respectively, and the inherent frequencies of the bearings are obtained by submitting the calculation models as shown in Table 2. According to the values in the table, with the increase of roller numbers, the inherent frequency of the bearing increases, which is due to the increase in the overall stiffness of the bearing.

2. Bearing inherent frequency at different filling rates.

Order	Inherent frequency
Order	Z = 11	Z = 12	Z = 13	Z = 14	Z = 15
1	13161	13673	14149	14610	15503
2	16373	17026	17642	18229	18802
3	16374	17032	17653	18249	18819
4	16975	18759	19994	21237	21318
5	17484	18768	20004	21244	21319
6	17491	19060	21132	23319	24022
7	21319	22319	24217	25023	26064
8	21364	23023	25018	25964	26259
9	22023	24123	26687	27128	28134
10	22099	24635	28156	28447	29331

Figure 12 shows the harmonic response displacement variation curves of the inner ring nodes with the different numbers of rollers when the radial force F_r = 3000 N is externally excited under the above working conditions. It can be found from the figure that as the roller numbers increase, the peak harmonic response frequency of the bearing decreases and the maximum displacement value increases. In particular, at the number of rollers Z = 11, the harmonic response displacement bimodal peaks correspond to 16599.1 Hz and 18351.9 Hz, and the displacement values are 0.0084 mm and 0.0076 mm. At the roller number Z = 15, the bimodal displacement value only reached 0.0049 mm and 0.0045 mm, and the frequency value reached 21355.9 Hz and 23545.1 Hz. In addition, the analysis data can be pressed to see that the harmonic response peak frequencies are close to the third to sixth order of the bearing inherent frequency, which should be avoided in the engineering application.

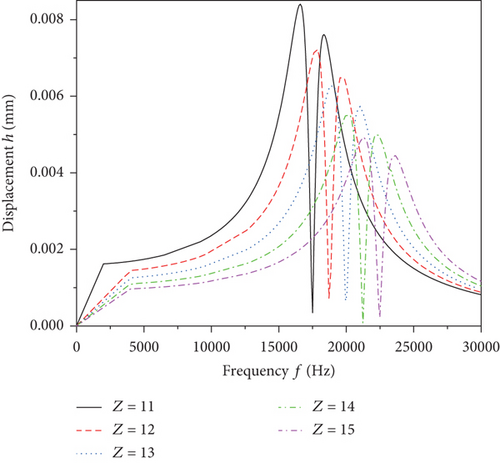
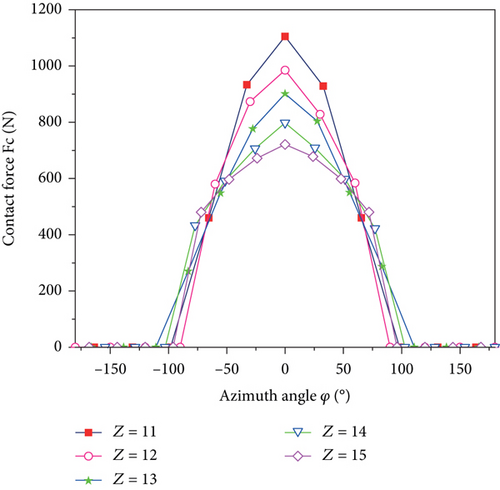
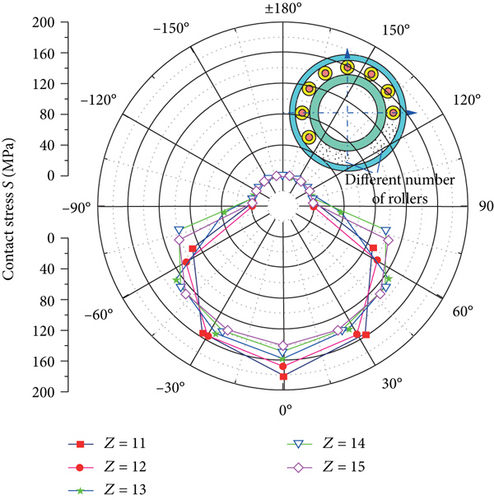
Figures 13 and 14 indicate the roller and inner raceway contact force variation curves and roller contact stress curves of the bearing with the different number of rollers. Comprehensive analysis of Figures 13 and 14 can be obtained that when the number of bearing rollers increases from 11 to 15, the maximum contact force between the rollers and the inner raceway decreases from 1105.2 N to 720.8 N, with a relative reduction of 34.8%; the corresponding contact stress decreases from 180.2 MPa to 142.1 MPa, with a relative reduction of 21.1%. From analyzing the curves in the figure, it can be figured out that the increase in the number of rollers can make the number of rollers in the force-bearing area larger and make the force more uniform.

5. Conclusion

The finite element model of the static contact, modal analysis, and harmonic response analysis of composite cylindrical roller bearing is established by ABAQUS software, and the effects of filling rate, radial force, and the number of rollers on parameters such as contact force, contact stress, and inherent frequency are studied, and the following conclusions are drawn.

(1)
Under the same working condition, a composite cylindrical roller makes the inherent frequency of the bearing lower, which is easier to resonate, but with the increase of the cylindrical roller filling rate, the distribution of force by each roller in the contact area is more uniform, and the contact stress is reduced
(2)
The change of radial force has no effect on the peak frequency of the harmonic response of the bearing, but enlarging the radial force makes the peak response displacement higher, and the contact force and stress of the roller also increase
(3)
With the increase of the roller numbers, the bearing natural frequency and the peak frequency of harmonic response are increased, the peak value of response displacement is decreased, the roller contact force in the bearing area is reduced, and the contact force distribution is more uniform.

Conflicts of Interest

The authors declare no conflict of interest.

Acknowledgments

This research work was supported by the Major Scientific and Technological Projects in Shanxi Province (20201102003), Shanxi Coal Based Low Carbon Joint Fund (No. 1610118), National Natural Science Foundation of China (No. 51375325), and Henan Provincial Science and Technology Research Project (No. 222102240017).

Open Research

Data Availability

The data are in the article.

References

1 Yongcun C., Sier D., Haisheng Y., Wenhu Z., and Rongjun N., Effect of cage dynamic unbalance on the cage's dynamic characteristics in high-speed cylindrical roller bearings, Industrial Lubrication and Tribology. (2019) 71, no. 10, 1125–1135, https://doi.org/10.1108/ilt-12-2018-0462, 2-s2.0-85070308827.
10.1108/ILT-12-2018-0462
Web of Science® Google Scholar
2 Yongcun C., Sier D., Kaiwen D., Hui L., and Wenhu Z., Experimental study on impact of roller imbalance on cage stability, Chinese Journal of Aeronautics. (2021) 34, no. 10, 248–264, https://doi.org/10.1016/j.cja.2020.05.034.
10.1016/j.cja.2020.05.034
Web of Science® Google Scholar
3 Li C., Yin S., Deyu R., and Weize X., Analysis of influencing factors on dynamic performance of high speed cylindrical roller bearing cage, Machine Tools and Hydraulics. (2021) 49, no. 14, 17–23.
Google Scholar
4 Jianghong Y., Lei X., Wen Y., Chao L., Yaoyao D., and Qishui Y., Modal and harmonic response analysis of a rolling bearing coupled by rigid and flexible materials, Materials Express. (2019) 9, no. 9, 1017–1024, https://doi.org/10.1166/mex.2019.1608.
10.1166/mex.2019.1608
Web of Science® Google Scholar
5 Zhu P., Zheng T., Hu T., Hu J., and Zhang J., Contact mechanics response of composite cylindrical roller bearings based on FEM, Journal of Failure Analysis and Prevention. (2021) 21, no. 2, 499–506, https://doi.org/10.1007/s11668-020-01106-2.
10.1007/s11668-020-01106-2
Web of Science® Google Scholar
6 Qishui Y., Wen Y., Dejie Y., and Jianghong Y., Bending stress of rolling element in elastic composite cylindrical roller bearing, Journal of Central South University. (2013) 20, no. 12, 3437–3444, https://doi.org/10.1007/s11771-013-1868-1, 2-s2.0-84891605122.
10.1007/s11771-013-1868-1
Web of Science® Google Scholar
7 Jing L. and Yimin S., An analytical dynamic model of a hollow cylindrical roller bearing, Journal of Tribology-Transactions of the Asme. (2018) 140, no. 6, article 061403, https://doi.org/10.1115/1.4040382, 2-s2.0-85050774625.
10.1115/1.4040382
Web of Science® Google Scholar
8 Zhifeng S. and Jing L., An improved planar dynamic model for vibration analysis of a cylindrical roller bearing, Mechanism Machine Theory. (2020) 153, article 103994, https://doi.org/10.1016/j.mechmachtheory.2020.103994.
10.1016/j.mechmachtheory.2020.103994
Web of Science® Google Scholar
9 Mitul Thakorbhai S. and Dipak V., A finite element analysis of an elastic contact between a layered cylindrical hollow roller and flat contact, Industrial Lubrication and Tribology. (2017) 69, no. 1, 30–41, https://doi.org/10.1108/ILT-11-2015-0189, 2-s2.0-85041950998.
10.1108/ILT-11-2015-0189
Web of Science® Google Scholar
10 Yunling W. and Yankui L., Study on the bearing capacity of a new type of hollow cylindrical roller, Mechanical Design and Manufacture. (2020) 2, 80–82.
Google Scholar
11 Wenjie W., Ming Q., and Yanfang D., Contact stress and load capacity analysis of modified cylindrical roller bearing under eccentric load, Lubrication Engineering. (2021) 46, no. 10, 59–63.
Google Scholar
12 Wen Y., Qishui Y., Jianghong Y., Zhongwen T., and Jianfeng H., Bearing capacity of elastic composite cylindrical roller bearings for middle-low speed multiple units, Electrical and Mechanical Engineering. (2022) 39, no. 4, 507–512.
Google Scholar
13 Jianghong Y., Wen Y., Chao L., and Qishui Y., Contact analysis of elastic composite cylindrical roller bearing, Journal of Mechanical Strength. (2015) 37, no. 6, 1099–1105.
Google Scholar
14 Harris T. A. and Kotzalas M. N., Rolling Bearing Analysis Essential Concepts of Bearing Technology, 2010, Machinery Industry Press, Beijing, China, 144–148.
Google Scholar
15 Liqin W., Design and Numerical Analysis of Rolling Element for Extreme Application, 2013, Harbin Institute of Technology Press, Harbin, China.
Google Scholar
16 Wenbing T., Ya L., Wennian Y., and Yinquan Y., Investigation of the dynamic local skidding behaviour of rollers in cylindrical roller bearings, Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics. (2019) 233, no. 4, 899–909, https://doi.org/10.1177/146441931986.
10.1177/1464419319861616
Web of Science® Google Scholar
17 JiaMing Z., Ming Q., Xiaoxu P., and Jun Y., Structure optimization of cylindrical roller bearing based on orthogonal test, Journal of Mechanical Transmission. (2022) 46, no. 3, 31–38.
Google Scholar
18 Xu H., Xinxin G., Xianwen Z., Xin L., and Qingkai H., Distribution characteristics of stress and displacement of rings of cylindrical roller bearing considering thermal effect, Proceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science. (2018) 233, no. 12, 4348–4358, https://doi.org/10.1177/0954406218820551, 2-s2.0-85061499626.
10.1177/0954406218820551
Web of Science® Google Scholar
19 Fang L., Jiabin C., Wangbiao Q., Kao W., and Zheng P., Harmonic response analysis of spherical roller bearings, Bearing. (2021) 1, 13–16.
Google Scholar
20 Harish Chandra N. and Sekhar A. S., Wavelet transform based estimation of modal parameters of rotors during operation, Measurement. (2018) 130, 264–278.
10.1016/j.measurement.2018.08.008
Web of Science® Google Scholar
21 Storti G. and Machado T., The use of operational modal analysis in the process of modal parameters identification in a rotating machine supported by roller bearings, Journal of Mechanical Science and Technology. (2021) 35, no. 2, 471–480, https://doi.org/10.1007/s12206-021-0105-3.
10.1007/s12206-021-0105-3
Web of Science® Google Scholar
22 Dassault systemes, ABAQUS/CAE User's Manual, 2014, Dassault Systemes Simulia Corp, Providence, RI, USA.
Google Scholar
23 Abaqus V 6 14-1, Abaqus/standard user’s manual and Abaqus CAE manual, 2014, Dassuault Systemes Simulia Corp, Providence, RI, USA.
Google Scholar

Citing Literature

All articles

Study on Contact Force and Vibration Characteristics of Composite Cylindrical Roller Bearing

Abstract

1. Introduction

2. Theoretical Analysis

2.1. Bearing Static Contact Force Calculation