Volume 2022, Issue 1 6227093

Research Article

Open Access

[Retracted] Computing the Energy and Estrada Index of Different Molecular Structures

Retraction(s) for this article

Zeeshan Saleem Mufti,

Zeeshan Saleem Mufti

orcid.org/0000-0002-6765-6595

Department of Mathematics and Statistics, The University of Lahore, Lahore Campus, Lahore, Pakistan uol.edu.pk

Search for more papers by this author

Rukhshanda Anjum,

Rukhshanda Anjum

orcid.org/0000-0001-8736-0006

Department of Mathematics and Statistics, The University of Lahore, Lahore Campus, Lahore, Pakistan uol.edu.pk

Search for more papers by this author

Qin Xin,

Qin Xin

orcid.org/0000-0002-6178-8538

Faculty of Science and Technology, University of the Faroe Islands, Vestarabryggja 15, FO 100 Torshavn, Denmark setur.fo

Search for more papers by this author

Fairouz Tchier,

Fairouz Tchier

orcid.org/0000-0001-7855-508X

Department of Mathematics, King Saud University, P.O.Box 22452, Riyadh 11495, Saudi Arabia ksu.edu.sa

Search for more papers by this author

Iram Anwar-ul-Haq,

Iram Anwar-ul-Haq

Department of Mathematics and Statistics, The University of Lahore, Lahore Campus, Lahore, Pakistan uol.edu.pk

Search for more papers by this author

Yaé Ulrich Gaba,

Corresponding Author

Yaé Ulrich Gaba

[email protected]

orcid.org/0000-0001-8128-9704

Quantum Leap Africa (QLA), AIMS Rwanda Centre, Remera Sector KN 3, Kigali, Rwanda

Search for more papers by this author

Zeeshan Saleem Mufti,

Zeeshan Saleem Mufti

orcid.org/0000-0002-6765-6595

Department of Mathematics and Statistics, The University of Lahore, Lahore Campus, Lahore, Pakistan uol.edu.pk

Search for more papers by this author

Rukhshanda Anjum,

Rukhshanda Anjum

orcid.org/0000-0001-8736-0006

Department of Mathematics and Statistics, The University of Lahore, Lahore Campus, Lahore, Pakistan uol.edu.pk

Search for more papers by this author

Qin Xin,

Qin Xin

orcid.org/0000-0002-6178-8538

Faculty of Science and Technology, University of the Faroe Islands, Vestarabryggja 15, FO 100 Torshavn, Denmark setur.fo

Search for more papers by this author

Fairouz Tchier,

Fairouz Tchier

orcid.org/0000-0001-7855-508X

Department of Mathematics, King Saud University, P.O.Box 22452, Riyadh 11495, Saudi Arabia ksu.edu.sa

Search for more papers by this author

Iram Anwar-ul-Haq,

Iram Anwar-ul-Haq

Department of Mathematics and Statistics, The University of Lahore, Lahore Campus, Lahore, Pakistan uol.edu.pk

Search for more papers by this author

Yaé Ulrich Gaba,

Corresponding Author

Yaé Ulrich Gaba

[email protected]

orcid.org/0000-0001-8128-9704

Quantum Leap Africa (QLA), AIMS Rwanda Centre, Remera Sector KN 3, Kigali, Rwanda

Search for more papers by this author

First published: 28 January 2022

https://doi.org/10.1155/2022/6227093

Citations: 1

Academic Editor: Haidar Ali

Share a link

Email
Wechat
Bluesky

Abstract

Graph energy is an invariant that is derived from the spectrum of the adjacency matrix of a graph. Graph energy is actually the absolute sum of all the eigenvalues of the adjacency matrix of a graph i.e. , and the Estrada index of a graph G is elaborated as , where, λ₁, λ₂, …, λ_n are the eigenvalues of the adjacency matrix of a graph. In this paper, energy E(G) and Estrada index EE(G) of different molecular structures are obtained and also established inequalities among the exact and estimated values of energies and Estrada index of TUC₄C₈ nanosheet and naphthalene.

1. Introduction

Chemical graph theory is a branch of mathematical chemistry and mathematical chemistry gives a natural way to understand the mathematical structures which actually act behind the existing chemical concepts to inaugurate the novel mathematical ideas and mathematical techniques in chemistry. The chemical graph theory is the intersection of graph theory and chemistry. In chemical graph theory, one can pick the molecular structure of different compounds and transform them into a molecular graph and then apply different graph invariants such as the energy of a graph. This graph invariant is much more popular in both mathematicians and chemists and was invented in 1978 by Ivan Gutman [1].

When graph energy was introduced in 1978, no one was attracted to this invariant. Even its chemical roots belong to 1940. Mathematicians were not interested initially but when the 20th century was started, a dramatic change occurred and graph energy got great respect from the whole world when the number of countries such as Pakistan, Australia, Austria, Brazil, Canada, and many more produced numbers of papers in graph energy. The definition of graph energy is motivated by already existing results for the Huckel molecular orbital total π-electron energy [2, 3]. The energy of a graph defined here totally coincides with the total π-electron energy computed using Huckel molecular orbital theory. The energy of a graph will be zero if the graph is totally disconnected.

About 20 years ago Estrada introduced a new index called the Estrada index. The Estrada index is denoted by EE(G) and is defined as [4]. The application of the Estrada index is to measure the folding degree of long-chain proteins [5–8]. To measure the degree of long-chained molecules such as proteins, weighted graphs were used. This index is also used in complex networks to measure the centrality measures of these structures such as social, communication, and metabolic[9–11]. For detailed surveys on the Estrada index, readers can check [4, 12–22].

The motivation of the paper was to find the energy and Estrada index of nanostructures. Matrices are used nowadays for dealing with different types of problems in daily life. We are dealing with square matrices which are very useful in different applications such as in the solving system of equations, by using its determinant to find the area and orthogonal vectors. In this paper, we find the energy of a graph by finding the eigenvalues of its adjacency matrix. Let G be a simple undirected graph in which V denotes the vertex set containing v₁, v₂, …, v_n as atoms and E denotes the edge set e₁, e₂, …, e_n as bonds. The adjacency matrix A(G) of a graph G is a square matrix that can be obtained by the adjacent and nonadjacent vertices in such a way if (i, j)- entry of a matrix is 1 whenever the vertices v_i and v_j are adjacent, otherwise 0. The eigenvalues of the adjacency matrix of order n are λ₁, λ₂, …, λ_n and the set of these eigenvalues is called a spectrum of the graph and since the adjacency matrix is symmetric so all the eigenvalues are real.

2. Methodology

We follow the following steps to compute the energy and Estrada index of the TUC₄C₈ nanosheet and naphthalene:

(1)
We draw a chemical structure in HyperChem [23]. HyperChem is a molecular editor, which offers a wide range of molecular and quantum mechanics calculations.
(2)
The Adjacency matrix is found using TOPOCLUJ [24].
(3)
By using MATLAB, the eigenvalues of the adjacency matrix are found [25].
(4)
A polynomial of your desired order is constructed which best fits the data using the cf toolbox [26].

3. Energy and Estrada Index of TUC₄C₈ Nanosheet

Carbon nanosheets(CNTS) belong to a special class of nanomaterials that consist of a two-dimensional hexagonal lattice of carbon atoms. It plays an important role in basic sciences, engineering, and nanotechnology. Carbon nanosheets are not just used in chemistry it is also used in different field of science it is also used in conducting molecules like in semiconducting or electronic properties of metallic. Carbon nanosheets were discovered in 1991 by S. Iijima. Due to the unique chemical and physical properties of carbon nanosheets(CNTS), there is a hopeful continuous growth of telecommunication. The length range of CNTS is less than 100 nm to 0.5 m. Carbon nanosheets(CNTS) classify into two types: single-walled carbon nanosheets and multiwalled carbon nanosheets.

(1)
Single-walled carbon nanosheets(SWCTs): Single-walled carbon nanosheets consist of single graphene. It does not have any complex structure because of impurity. It bends easily [27].
(2)
Multiwalled carbon nanosheets(MWCTs): Multiwalled carbon nanosheets consist of multigraphene. It has a complex structure due to its high purity. It cannot be bent easily [28, 29].

Now, we construct the quadratic polynomial which best fits the curve. We will also find the difference between E_exact(T), E_estimated(T), and EE_exact(T), EE_estimated(T) of TUC₄C₈ nanosheet 1 as shown in Figure 1.

Details are in the caption following the image — Open in figure viewer PowerPoint

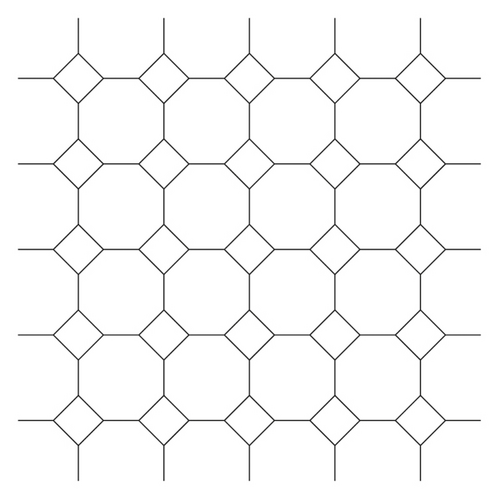
Proposition 1. Let T be the graph of TUC₄C₈ nanosheet, then the energy E(T) and the Estrada index EE(T) of T are given below:

(1)

(2)

The equations (1) and (2) characterize the energy E(N) and Estrada index EE(N), respectively. We have established the inequality E_exact(N) > E_estimated(N), where E_exact and E_estimated show the exact and estimated value of energy. This inequality poses that the exact value E_exact is always greater than E_estimated. So, the error among E_exact and E_estimated is always positive.

But on the other hand, the exact value EE_exact(N) is always smaller than EE_estimated(N) which describes the error between EE_exact and EE_estimated is negative.

In Table 1, m is an integer from 1 to 10 while n is fixed, and in Tables 2 and 3 quadratic equations are constructed.

1. The quadratic equation for the E(N) and EE(G) of TUC₄C₈ nanosheet.

(m, n)	Energy (E(N))	Estrada index (EE(N))
(1, n)	−0.001n² + 7.741n + 1.9175	−0.0001n² + 16.5749n + 3.0418
(2, n)	−0.0011n² + 13.6178n + 3.7202	0.0012n² + 30.0994n + 6.00914
(3, n)	−0.0012n² + 19.5378n + 5.5891	−0.0013n² + 43.6375n + 9.1248
(4, n)	0.0053n² + 25.294n + 7.583	−0.004n² + 57.1646n + 12.172
(5, n)	−0.0182n² + 31.313n + 9.2495	−0.0105n² + 70.6945n + 15.215
(6, n)	−0.1515n² + 38.655n + 9.625	−0.0316n² + 84.2794n + 18.1878
(7, n)	−0.5176n² + 49.0138n + 7.2347	−0.0853n² + 98.0099n + 20.9764
(8, n)	−1.2827n² + 64.7168n + 0.0926	−0.1968n² + 112.015n + 23.4188
(9, n)	−2.6562n² + 88.725n − 14.2985	−0.3985n² + 126.4621n + 25.305
(10, n)	−4.8907n² + 124.633n − 38.947	−0.73n² + 141.557n + 26.377

2. All aforementioned are derived from the coefficient of the curves given in Table 1.

(n)	Energy (E(N))
n²	−18 × 10⁻³m⁴ + 191 × 10⁻²m³ − 696 × 10⁻²m² + 102 × 10⁻¹m − 507 × 10⁻²
n	264 × 10⁻²m⁴ − 2985 × 10⁻¹m³ + 1.1526m²4.1125m + 2.748
1	−213 × 10⁻²m⁴ + 2228 × 10⁻¹m³ − 7712 × 10⁻¹m² + 2.8762m − 389 × 10⁻¹

3. All aforementioned equations are derived from the coefficient of the curves given in Table 1.

(n)	Estrada index EE(N)
n²	−3 × 10⁻⁴m⁴ + 3.6 × 10⁻³m³ − 1.6 × 10⁻²m² + 2.86 × 10⁻²m − 1.6 × 10⁻²
n	1.6 × 10⁻³m⁴ − 2.01 × 10⁻²m³ + 8.74 × 10⁻²m² + 13.379m + 3.127
1	−2 × 10⁻³m⁴ + 2.5 × 10⁻²m³ − 1.081 × 10⁻¹m² + 3.2289m − 1.02 × 10⁻¹

Error among the E_exact and E_estimated are shown in Table 4 and (Table 5).

4. The E_exact(T) and E_estimated(T) of TUC₄C₈ nanosheet.

(m, n)	E_exact(T)	E_estimated(T)	Error
(5, 1)	40.6012	40.5443	0.0569
(5, 2)	71.8027	71.7646	0.0381
(5, 3)	103.5458	103.3415	0.2043
(5, 4)	134.4458	134.2103	0.2355
(5, 5)	165.8416	165.3595	0.4821

5. The EE_exact(T) and EE_estimated(T) of the TUC₄C₈ nanosheet.

(m, n)	EE_exact(T) (N)	EE_estimated(T)	Error
(4, 1)	69.3326	69.3403	−0.0077
(4, 2)	126.4852	126.516	−0.0308
(4, 3)	183.6298	183.689	−0.0592
(4, 4)	240.7664	240.861	−0.0946
(4, 5)	298.895	298.04	−1

4. Energy and Estrada Index of Naphthalene

Naphthalene is a very important polycyclic aromatic hydrocarbon and it is useful in indoor and outdoor environments. It is actually a part of crude oil. The construction of naphthalene is based on two fused benzene rings that are connected with each other. Naphthalene is also used in mothballs which are widely used throughout the world. It is also used as an insect repellent product. Naphthalene is vibrantly volatile and insoluble in water, also the part of coal tar. In this section, we find the energy and Estrada index of naphthalene 2 which is given in Figure 2.

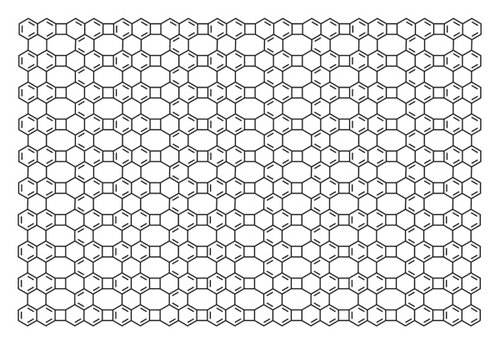
Proposition 2. Let N be the chemical graph of naphthalene. Then, the energy E(N) and Estrada index EE(N) of the chemical graph of naphthalene are given below.

(3)

(4)

Equation (3) represents the energy and (4) represents the Estrada index, respectively. E(N) shows the energy of naphthalene and EE(N) shows the Estrada index of naphthalene. In the case of naphthalene, we observed this inequality E_exact(N) > E_estimated(N), where E_exact(N) and E_estimated shows the exact and estimated value of energy, respectively.

In the case of the Estrada index, we observed this inequality EE_exact(N) < EE_estimated(N) , where EE_exact(N) and EE_estimated reflects the exact and the estimated value of the Estrada index. The detailed analysis has been discussed critically.

In Table 6, m is an integer from 1 to 10 and n is fixed, and in Tables 7 and 8 quadratic equations are constructed.

6. The polynomial of order 2 for the E(G) and EE(N) of naphthalene.

(m, n)	Energy (E(N))	Estrada index (EE(N))
(1, n)	0.0019n² + 14.5781n − 0.9285	−0.0117n² + 28.7981n − 3.5494
(2, n)	0.0023n² + 29.7505n − 1.8301	−0.0413n² + 62.09n − 2.8202
(3, n)	0.0031n² + 44.9205n − 2.7308	0.085n² + 94.4701n − 10.3612
(4, n)	0.0043n² + 60.0881n − 3.6279	0.03015n² + 127.04n − 15.7054
(5, n)	0.0059n² + 75.2533n − 4.5214	0.06667n² + 160.8653n − 19.433
(6, n)	0.0079n² + 90.4161n − 5.4113	1.6043nn² + 196.5316n − 24.9634
(7, n)	0.0103n² + 105.5765n − 6.2976	4.0707n² + 234.1325n − 34.0192
(8, n)	0.0131n² + 120.7345n − 7.1803	9.6511n² + 273.6896n − 45.7622
(9, n)	0.0163n² + 135.8901n − 8.0594	20.5835n² + 316.0045n − 59.6014
(10, n)	0.0199n² + 151.0433n − 8.9349	39.7109n² + 363.9428n − 81.673

7. The polynomial of order 2 derived from the coefficient of the curves given in Table 6.

n	Energy (E(N))
n²	2 × 10⁻⁴m² − 2 × 10⁻⁴m + 1.9 × 10⁻³
n	−1.2 × 10⁻³m² + 15.176m − 5.967 × 10⁻¹
1	1.8 × 10⁻³m² − 9.097 × 10⁻¹m − 1.79 × 10⁻²

8. The polynomial of order 2 derived from the coefficient of the curves given in Table 6.

n	Estrada index EE(N)
n²	−0.0001m⁶ + 0.0041m⁵ − 0.0423m⁴ + 0.1805m³ − 0.2864m² + 0.0798m + 0.0529
n	0.0006m⁶ − 0.0163m⁵ + 0.159m⁴ − 0.5569m³ + 0.1969m² + 34.682m − 5.6672
1	−0.0051m⁶ + 0.1755m⁵ − 2.3788m⁴ + 15.91 m³ − 54.385m² + 83.077m − 45.943

Also, the error between the E_exact(N), E_estimated(N), and EE_exact(N), EE_estimated(N) are shown in Tables 9 and 10.

9. The E_exact(N) and E_estimated(N) values of the naphthalene.

(m, n)	E_exact(N)	E_estimated(N)	Error
(2, 1)	27.9798	27.9227	0.0571
(2, 2)	57.6801	57.6322	0.0479
(2, 3)	87.4421	87.3202	0.1219
(2, 4)	117.2087	117.12	0.0887
(2, 5)	146.9799	146.9514	0.0285
(2, 6)	176.7557	176.739	0.0167
(2, 7)	206.5361	206.248	0.0345
(2, 8)	236.3211	236.248	0.0731
(2, 9)	266.1107	266.0206	0.0901
(2, 10)	295.9049	295.8252	0.0797

10. The EE_exact(N) and EE_estimated(N) values of the Estrada indices of the naphthalene.

(m, n)	EE_exact(N)	EE_estimated(N)	Error
(3, 1)	83.11256	91.6297	–8.51714
(3, 2)	177.7729	186.3548	–8.5819
(3, 3)	272.012	281.2499	–9.2379
(3, 4)	366.2511	376.315	–10.0639
(3, 5)	460.4902	471.5501	–11.0599
(3, 6)	554.7293	566.9552	–12.2259
(3, 7)	648.9684	662.5303	–13.5619
(3, 8)	743.2075	758.2754	–15.0679
(3, 9)	837.4466	854.2309	–16.7843
(3, 10)	932.1173	950.2756	–18.1583

5. Conclusion

In this paper, we compute the energy (E_exact(N)) and Estrada index (EE_estimated(N)) of TUC₄C₈ nanosheet. Similarly, we compute the energy (E_exact(N)) and Estrada index (EE_estimated(N)) of naphthalene. We have observed some inequalities: the exact value of the energy of TUC₄C₈ nanosheet and naphthalene are both greater than the estimated value of TUC₄C₈ nanosheet and naphthalene, respectively.

(1).
E_exact(N) > E_estimated(N)
(2)
E_exact(T) > E_estimated(T)

This concludes that the error among the abovementioned structures is always positive.

Similarly, the exact value of the Estrada index of TUC₄C₈ nanosheet and naphthalene are both smaller than the estimated value of TUC₄C₈ nanosheet and naphthalene, respectively.

(1).
EE_exact(N) < EE_estimated(N)
(2)
EE_exact(T) < EE_estimated(T)

This concludes that the error among the abovementioned structures is always negative.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this article.

Acknowledgments

This work was supported by the Researchers Supporting Project Number (RSP-2021/401), King Saud University, Riyadh, Saudi Arabia. (RSP-2021/401).

Open Research

Data Availability

No data were used to support this study.

References

1 Gutman I., The energy of a graph, Ber. Math. Stat. Sekt.(1978) 1–22.
Google Scholar
2 Coulson C. A., On the calculation of the energy in unsaturated hydrocarbon molecules Mathematical Proceedings of the Cambridge Philosophical Society, 1940, 36, no. 2, Cambridge University Press, 201–203, https://doi.org/10.1017/s0305004100017175, 2-s2.0-0346377577.
10.1017/S0305004100017175
Google Scholar
3 McClelland B. J., Properties of the latent roots of a matrix: the estimation of π-electron energies, The Journal of Chemical Physics. (1971) 54, no. 2, 640–643, https://doi.org/10.1063/1.1674889.
10.1063/1.1674889
CAS Web of Science® Google Scholar
4 de la Peña J. A., Gutman I., and Rada J., Estimating the estrada index, Linear Algebra and Its Applications. (2007) 427, no. 1, 70–76, https://doi.org/10.1016/j.laa.2007.06.020, 2-s2.0-79954497708.
10.1016/j.laa.2007.06.020
Web of Science® Google Scholar
5 Estrada E., Characterization of the folding degree of proteins, Bioinformatics. (2002) 18, no. 5, 697–704, https://doi.org/10.1093/bioinformatics/18.5.697, 2-s2.0-0036083434.
10.1093/bioinformatics/18.5.697
CAS PubMed Web of Science® Google Scholar
6 Estrada E., Characterization of the amino acid contribution to the folding degree of proteins, Proteins: Structure, Function, and Bioinformatics. (2004) 54, no. 4, 727–737, https://doi.org/10.1002/prot.10609, 2-s2.0-1542346456.
10.1002/prot.10609
CAS PubMed Web of Science® Google Scholar
7 Estrada E., Rodríguez-Velázquez J. A., and Randić M., Atomic branching in molecules, International Journal of Quantum Chemistry. (2006) 106, no. 4, 823–832, https://doi.org/10.1002/qua.20850, 2-s2.0-33644954829.
10.1002/qua.20850
CAS Web of Science® Google Scholar
8 Ilić A. and Stevanović D., The Estrada index of chemical trees, Journal of Mathematical Chemistry. (2010) 47, 305–314.
10.1007/s10910-009-9570-0
CAS Web of Science® Google Scholar
9 Estrada E. and Rodríguez-Velázquez J. A., Spectral measures of bipartivity in complex networks, Physical review. E, Statistical, nonlinear, and soft matter physics. (2005) 72, 046105–105, https://doi.org/10.1103/PhysRevE.72.046105, 2-s2.0-33244461772.
10.1103/PhysRevE.72.046105
CAS PubMed Web of Science® Google Scholar
10 Shang Y., Biased edge failure in scale-free networks based on natural connectivity, Indian Journal of Physics. (2012) 86, no. 6, 485–488, https://doi.org/10.1007/s12648-012-0084-4, 2-s2.0-84866291826.
10.1007/s12648-012-0084-4
CAS Web of Science® Google Scholar
11 Shang Y.-L., Local natural connectivity in complex networks, Chinese Physics Letters. (2011) 28, no. 6, 068903, https://doi.org/10.1088/0256-307x/28/6/068903, 2-s2.0-79959390346.
10.1088/0256-307X/28/6/068903
Web of Science® Google Scholar
12 Du Z. and Zhou B., The Estrada index of trees, Linear Algebra and Its Applications. (2011) 435, no. 10, 2462–2467, https://doi.org/10.1016/j.laa.2011.01.041, 2-s2.0-79958836159.
10.1016/j.laa.2011.01.041
Web of Science® Google Scholar
13 Gutman I., Lower bounds for Estrada index, Publications de l’Institut Math?matique (Belgrade). (2008) 83, no. 97, 1–7, https://doi.org/10.2298/pim0897001g, 2-s2.0-58149119497.
10.2298/PIM0897001G
Google Scholar
14 Gutman I. and Graovac A., Estrada index of cycles and paths, Chemical Physics Letters. (2007) 436, no. 1-3, 294–296, https://doi.org/10.1016/j.cplett.2007.01.044, 2-s2.0-33846859092.
10.1016/j.cplett.2007.01.044
CAS Web of Science® Google Scholar
15 Gutman I. and Radenković S., A lower bound for the Estrada index of bipartite molecular graphs, Kragujevac Journal of Science. (2007) 29, 67–72.
Google Scholar
16 Jahanbani A. and Raz H. H., On the harmonic energy and Estrada index of graphs, Mati. (2019) 1, no. 1, 1–20.
Google Scholar
17 Liu J.-p. and Liu B.-l., Bounds of the Estrada index of graphs, Applied Mathematics-A Journal of Chinese Universities. (2010) 25, no. 3, 325–330, https://doi.org/10.1007/s11766-010-2237-6, 2-s2.0-77956035574.
10.1007/s11766-010-2237-6
Google Scholar
18 Rad N. J., Jahanbani A., and Gutman I., Zagreb energy and Zagreb estrada index of graphs, MATCH-Communications in Mathematical and in Computer Chemistry. (2018) 79.
Web of Science® Google Scholar
19 Shang Y., The Estrada index of random graphs, Scientia Magna. (2011) 7, 79–81.
Google Scholar
20 Zhou B., ‘On estrada index’, MATCH commun, MATCH Communications in Mathematical and in Computer Chemistry. (2008) 60, 485–492.
CAS Google Scholar
21 Zhou B. and Du Z., Some lower bounds for Estrada index, Iranian Journal of Mathematical Chemistry. (2010) 1, 67–72.
Google Scholar
22 Zhou B. and Trinajstić N., Estrada index of bipartite graphs, International Journal of Chemical Modeling. (2008) 1, 387–394.
Google Scholar
23 Ivanciuc O., HyperChem release 4.5 for windows, Journal of Chemical Information and Computer Sciences. (1996) 36, no. 3, 612–614, https://doi.org/10.1021/ci950190a.
10.1021/ci950190a
CAS Google Scholar
24 Ursu O. and Diudea M. V., TOPOCLUJ Software Program, 2005, Babes-Bolyai University, Cluj, Romania.
Google Scholar
25 Higham D. J. and Higham N. J., MATLAB Guide, 2016, Society for Industrial and Applied Mathematics, Philadelphia, PA, USA.
10.1137/1.9781611974669
Google Scholar
26 Löfberg J., YALMIP: a toolbox for modeling and optimization in MATLAB, Proceedings of the CACSD Conference. (2004) 3.
Google Scholar
27 Aqel A., Abou El-Nour K. M. M., Ammar R. A. A., and Al-Warthan A., Carbon nanotubes, science and technology part(1) structure,synthesis and characterisation, Arabian Journal of Chemistry. (2012) 5.
10.1016/j.arabjc.2010.08.022
Web of Science® Google Scholar
28 http://en.wikipedia.org/www/Carbonna.
Google Scholar
29 http://www.cientifica.com.
Google Scholar

Citing Literature

All articles

[Retracted] Computing the Energy and Estrada Index of Different Molecular Structures

Retraction(s) for this article

Retracted: Computing the Energy and Estrada Index of Different Molecular Structures

Abstract

1. Introduction

2. Methodology

3. Energy and Estrada Index of TUC₄C₈ Nanosheet

4. Energy and Estrada Index of Naphthalene

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

[Retracted] Computing the Energy and Estrada Index of Different Molecular Structures

Retraction(s) for this article

Retracted: Computing the Energy and Estrada Index of Different Molecular Structures

Abstract

1. Introduction

2. Methodology

3. Energy and Estrada Index of TUC4C8 Nanosheet

4. Energy and Estrada Index of Naphthalene

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

3. Energy and Estrada Index of TUC₄C₈ Nanosheet