A binary liquid system that consists of chlorpheniramine and 1-propanol is prepared at various concentrations by the mole fraction method. The density (ρ), viscosity (η), and ultrasonic velocity (U) of the system are observed at 303 K, 308 K, and 313 K. From the experimental observations, various thermophysical parameters such as adiabatic compressibility (β), free length (L_f), free volume (V_f), viscous relaxation time (τ), and Gibbs free energy (ΔG) are determined. The deviations of the excess parameters (β^E, , , τ^E, and ΔG^E) from their ideal values are calculated. The excess values are fitted with the Redlich–Kister polynomial function, and the corresponding coefficients are derived. Moreover, the standard deviations of the excess parameters are evaluated. The experimental and theoretical data confirmed the existence of hydrogen bonding interactions among the functional groups of the liquid mixture. The strength of intermolecular interactions decreased with increasing the temperature of the mixture. The strength of intermolecular interaction is noticed as 303 K > 308 K > 313 K.

1. Introduction

Intermolecular interactions between binary and ternary liquid mixtures are taking a vital role in the thrust area of theoretical and applied research [1–3]. The intermolecular interactions depend upon various intermolecular forces acting between the molecules present in the liquid system. Moreover, the change in temperature of the solutions leads to a significant change in the bonding and intermolecular forces among the dipoles [4, 5]. The measurement of ultrasonic velocity and related parameters is useful to analyse the strength of the intermolecular interactions between the liquid mixtures [6–8]. Furthermore, the interaction between the solute and solvent at various concentrations can be analysed by the experimental observations of the density (ρ), viscosity (η), and ultrasonic velocity (U) of the system. The adiabatic compressibility (β), free length (L_f), free volume (V_f), viscous relaxation time (τ), and Gibbs free energy (ΔG) can also be theoretically calculated by using the experimental data. The significant changes in those parameters are used to analyse the types of interactions between the functional groups present in the liquid system. The excess parameters that are deviated from their ideal values have also directed to the formation of bonding between the liquid mixtures. Manukonda et al. [9] reported changes in thermophysical changes of the N, N-dimethylaniline and 1-alkanols system. Preeti et al. [10] analysed the changes in the intermolecular interactions between acetonitrile with some alkyl methacrylates at various temperatures. Chlorpheniramine is one of the pharmaceutical valuable compounds. It takes part in the treatment of allergic rhinitis, cough, and the common cold [11]. In general, the interactions of alcohols respond to the temperature of the system. 1-Propanol has self-associative and polar nature. It can be used as a proton donor compound as well as a solvent [12]. The present work is an attempt to study the nature and strength of intermolecular interactions between chlorpheniramine and 1-propanol at 303 K, 308 K, and 313 K. Redlich–Kister polynomial function and standard deviations are also used to validate the experimental and theoretical observations.

2. Materials

The mole fraction method is adopted to prepare the various concentrations of the liquid mixtures. The airtight standard flasks are used to hold the solutions. Digital electronic balance (ACM-78094L, ACMAS Ltd., India) with the accuracy of ±1 mg was used to determine the mass of the liquid components. Specific gravity bottle and Ostwald’s viscometer are used to determine the density and viscosity of the solutions with the accuracy of ±0.01 kg/m³ and ±0.001 Ns/m², respectively. A single frequency 2 MHz ultrasonic interferometer (Mittal Enterprises, India) with the accuracy of ±1 m/s is used to measure the ultrasonic velocity. The double distilled water is used to standardize the density, viscosity, and ultrasonic velocity measurements. AR grade chlorpheniramine and 1-propanol (purity mass fraction >0.99, S. D. Fine Chemicals, India) were used without further purification. The density, viscosity, and ultrasonic velocity of the pure liquids are compared with the available literature [13, 14] and given in Table 1. A constant temperature bath (INSREF model IRI-016C, India) with the accuracy of ±0.01 K is used to sustain the temperature of the solutions.

1. Comparison of density, viscosity, and ultrasonic velocity of pure chlorpheniramine and 1-propanol at 303 K, 308 K, and 313 K in the atmospheric pressure.

S. no.	Liquid	Temperature (K)	(ρ) kg/m³		(η)/10⁻³ N s/m²		(U) m/s		Reference
S. no.	Liquid	Temperature (K)	Expt	Lit	Expt	Lit	Expt	Lit	Reference
1	Chlorpheniramine	303	1260	1264.7	2.791	2.055	1820	1819	[13]
		308	1257	1257.9	2.201	2.1949	1786	1786
		313	1250	1250.1	1.980	2.3750	1766	1765
2	1-Propanol	303	752	752.2	1.095	1.0948	1194	1194	[14]
		308	751	751.3	0.920	0.9187	1192	1192
		313	750	750.1	0.744	0.7426	1190	1191

3. Methods

Various parameters were calculated using the standard relations.

(1)

where d is the distance moved by the reflector and n is the number of oscillations produced by the ultrasonic interferometer [15].

(2)

where f is the frequency of the ultrasonic wave.

(3)

where ρ represents the density of the liquid mixture.

(4)

where K_T is a temperature-dependent constant and is given as

(5)

where M_eff is the effective molecular weight and K is a temperature-independent constant [16].

(6)

where k is the Boltzmann constant, T is the absolute temperature, and h is Planck’s constant.

Excess parameters have been calculated using the following relation [17]:

(7)

where A_i represents any acoustical parameter and x_i is the corresponding mole fraction.

(8)

where x₁, x₂ are the mole fractions, M₁, M₂ are the molar masses, ρ₁, ρ₂ are the densities of the chlorpheniramine and 1-propanol, respectively, and ρ_M is the density of the mixture.

The excess parameters were fitted with the Redlich–Kister [18] equation given as follows:

(9)

The standard deviations were calculated using the following relation:

(10)

where N signifies the number of experimental points, k denotes the number of coefficients, A_i represents any acoustical parameter, and x_i is the corresponding mole fraction. In the mixtures, x₁ and x₂ represent the mole fraction of chlorpheniramine and 1-propanol, respectively.

4. Results and Discussion

The density (ρ), viscosity (η), and ultrasonic velocity (U) of chlorpheniramine and 1-propanol are measured at 303 K, 308 K, and 313 K. Furthermore, adiabatic compressibility (β), free length (L_f), free volume (V_f), viscous relaxation time (τ), and Gibbs free energy (ΔG) are evaluated at various concentrations.

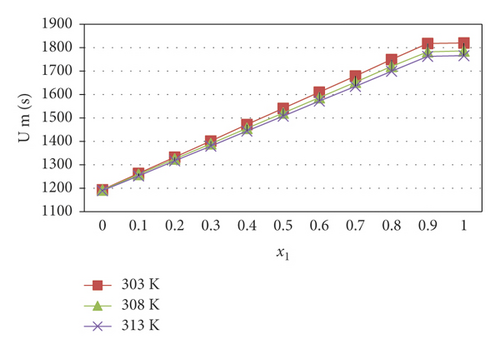
The observed significant changes in these parameters at various temperatures with the mole fraction of chlorpheniramine in the 1-propanol medium are given in Table 2. It is noted that the density of the liquid mixture increased with increasing chlorpheniramine concentration. It leads to the structure maker of the solute to the chosen solvent. This trend may also suggest the increasing solute-solvent interactions with chlorpheniramine concentrations. The shrinkage of chlorpheniramine molecules makes the solution in higher density comparisons than that of 1-propanol. The viscosity reflects the same trend as in the density effect of the solution. While increasing the temperature from 303 K to 313 K, both these parameters decreased. It may suggest the dissociation of the molecular clusters in the mixture. In general, the ultrasonic velocity increases with the active interaction of the solute-solvent system [19]. In the present study, the ultrasonic velocity increases with the chlorpheniramine concentrations, as shown in Figure 1. At the entire concentration, the ultrasonic velocities linearly vary with the mixing of 1-propanol. However, while increasing the temperature, the resonant wavelength of the ultrasonic wave in the solution decreased at the constant ultrasonic frequency. The corresponding changes in ultrasonic velocity with the chlorpheniramine concentrations reveal the existence of intermolecular interactions between the functional groups present in the liquid system. In general, the adiabatic compressibility is inversely proportional to the ultrasonic velocity and density. In this work, both the density and ultrasonic velocity increase with the chlorpheniramine concentration. The adiabatic compressibility decreases with increasing chlorpheniramine concentration. The decreasing trend of adiabatic compressibility signifies an increase in electrostrictive compression. After mixing chlorpheniramine with 1-propanol, the free length (L_f) decreased. In this study, the values of free length are inversely proportional to the ultrasonic velocity data. This result follows the Kincaid model [20].

2. Various data of chlorpheniramine (x₁) and 1-propanol (x₂) at 303 K, 308 K, and 313 K in the atmospheric pressure.

x₁		Ρ (kg/m³)	η/10⁻³ (Ns/m²)	U (m/s)	Β/10⁻¹⁰ (m²/N)	L_f/10⁻¹⁰ (m)	V_f/10⁻¹¹ (m³/mol)	τ/10⁻¹² (s)	ΔG (kJ/mol)
T = 303 K
0.0000		752	1.095	1194	9.327	0.634	0.598	1.358	5.406
0.1203		808	1.283	1264	7.746	0.578	0.877	1.322	5.340
0.2065		865	1.472	1333	6.506	0.529	1.035	1.274	5.249
0.3165		920	1.659	1402	5.529	0.488	1.267	1.220	5.135
0.4077		977	1.847	1472	4.723	0.451	1.436	1.160	5.015
0.5489		1032	2.034	1541	4.080	0.419	1.761	1.104	4.888
0.6382		1088	2.223	1610	3.545	0.391	1.918	1.048	4.756
0.7291		1145	2.398	1679	3.098	0.365	2.101	0.988	4.605
0.8216		1201	2.599	1750	2.718	0.342	2.260	0.940	4.479
0.9326		1256	2.787	1818	2.408	0.322	2.488	0.893	4.352
1.0000		1260	2.791	1820	2.396	0.321	2.697	0.889	4.340
T = 308 K
0.0000	751		0.92	1192	9.371	0.641	0.774	1.147	5.105
0.1203	807		1.062	1259	7.817	0.585	1.157	1.104	5.009
0.2065	863		1.198	1325	6.600	0.538	1.397	1.052	4.882
0.3165	920		1.346	1390	5.625	0.497	1.711	1.007	4.774
0.4077	975		1.501	1456	4.838	0.461	1.928	0.966	4.666
0.5489	1032		1.632	1521	4.188	0.428	2.402	0.909	4.509
0.6382	1087		1.772	1587	3.652	0.400	2.638	0.861	4.371
0.7291	1142		1.915	1653	3.204	0.375	2.876	0.816	4.238
0.8216	1199		2.056	1720	2.819	0.352	3.129	0.771	4.088
0.9326	1254		2.198	1782	2.511	0.332	3.448	0.734	3.967
1.0000	1257		2.201	1786	2.494	0.331	3.744	0.730	3.949
T = 313 K
0.0000	750		0.744	1190	9.415	0.648	1.062	0.932	4.690
0.1203	805		0.882	1253	7.912	0.594	1.518	0.928	4.684
0.2065	861		1.019	1317	6.696	0.547	1.765	0.907	4.623
0.3165	915		1.158	1380	5.738	0.506	2.121	0.884	4.551
0.4077	972		1.297	1444	4.934	0.469	2.371	0.851	4.455
0.5489	1025		1.436	1508	4.290	0.438	2.873	0.819	4.358
0.6382	1081		1.573	1572	3.743	0.409	3.110	0.783	4.238
0.7291	1135		1.712	1635	3.295	0.383	3.347	0.750	4.130
0.8216	1191		1.849	1699	2.908	0.360	3.602	0.715	4.003
0.9326	1246		1.987	1763	2.582	0.339	3.947	0.682	3.883
1.0000	1250		1.980	1766	2.565	0.338	4.315	0.675	3.853

Details are in the caption following the image — Open in figure viewer PowerPoint

It is observed that the free volume (V_f) of the system increased with increasing temperature as well as the concentration of chlorpheniramine. It may be due to the dispersive forces acting on the molecules and signify the dissociation of the bonds in the mixture. Furthermore, increasing the temperature of the solution weakened the intermolecular interactions between the proton donor and acceptor functional groups present in the liquid system. The viscous relaxation time decreased with the increasing mole fraction of chlorpheniramine at the entire range of temperatures. It suggested the rupture in the molecular cluster of the liquid system. The significant changes in the Gibbs free energy with the chlorpheniramine concentration are shown in Figure 2. The plot signifies the decreasing Gibbs free energy with increasing temperature and chlorpheniramine. It confirmed that solute-solvent interaction occurs and reveals the corresponding changes in the equilibrium states and the existence of specific weak hydrogen bonding interaction (N-H…O-H) between the molecules in the liquid system.

The sign and deviation of the excess parameters from their ideal values are useful to analyse the nature and strength of the intermolecular interactions. Fort et al. [21] reported that the negative excess parameters raised due to the existence of hydrogen bonding in the intermolecular interactions and positive values lead to weak interactions between the unlike functional group constituents in the system.

The variations of excess adiabatic compressibility (β^E), excess free length (), excess free volume (), excess viscous relaxation time (τ^E), excess Gibbs free energy (ΔG^E), and excess molar volume are given in Table 3.

3. Excess values of chlorpheniramine with 1-propanol at 303 K, 308 K, and 313 K in the atmospheric pressure.

x₁	β^E/10⁻¹⁰ (m²/N)	/10⁻¹¹ (m)	/10⁻⁸ (m³/mol⁻¹)	τ^E/10⁻¹² (s)	ΔG^E (kJ/mol)	/10⁻⁶ (m³/mol)
T = 303 K
0.0000	0.000	0.000	0.000	0.000	0.000	0.000
0.1203	−0.261	−0.048	−0.081	−0.018	−0.247	0.977
0.2065	−0.538	−0.123	−0.191	−0.063	−0.523	1.223
0.3165	−0.795	−0.196	−0.300	−0.106	−0.781	1.547
0.4077	−1.022	−0.263	−0.406	−0.144	−1.007	1.479
0.5489	−1.199	−0.318	−0.501	−0.176	−1.185	1.660
0.6382	−1.306	−0.357	−0.576	−0.197	−1.292	1.302
0.7291	−1.308	−0.367	−0.611	−0.201	−1.294	0.850
0.8216	−1.151	−0.331	−0.575	−0.178	−1.137	0.345
0.9326	−0.752	−0.216	−0.404	−0.111	−0.738	0.151
1.0000	0.000	0.000	0.000	0.000	0.000	0.000
T = 308 K
0.0000	0.000	0.000	0.000	0.000	0.000	0.000
0.1203	−0.271	−0.051	−0.103	−0.013	−0.257	0.974
0.2065	−0.557	−0.128	−0.236	−0.053	−0.542	1.232
0.3165	−0.824	−0.203	−0.369	−0.092	−0.809	1.524
0.4077	−1.057	−0.271	−0.497	−0.126	−1.043	1.483
0.5489	−1.242	−0.328	−0.612	−0.155	−1.227	1.627
0.6382	−1.353	−0.368	−0.702	−0.174	−1.339	1.282
0.7291	−1.355	−0.378	−0.746	−0.177	−1.340	0.859
0.8216	−1.192	−0.340	−0.703	−0.156	−1.178	0.333
0.9326	−0.779	−0.223	−0.496	−0.097	−0.765	0.167
1.0000	0.000	0.000	0.000	0.000	0.000	0.000
T = 313 K
0.0000	0.000	0.000	0.000	0.000	0.000	0.000
0.1203	−0.281	−0.053	−0.129	−0.009	−0.267	0.976
0.2065	−0.577	−0.133	−0.289	−0.046	−0.563	1.226
0.3165	−0.852	−0.210	−0.448	−0.080	−0.838	1.554
0.4077	−1.094	−0.280	−0.601	−0.112	−1.079	1.473
0.5489	−1.284	−0.340	−0.740	−0.137	−1.269	1.672
0.6382	−1.398	−0.380	−0.848	−0.154	−1.383	1.300
0.7291	−1.398	−0.390	−0.901	−0.157	−1.384	0.884
0.8216	−1.231	−0.351	−0.849	−0.139	−1.216	0.363
0.9326	−0.805	−0.231	−0.601	−0.084	−0.790	0.149
1.0000	0.000	0.000	0.000	0.000	0.000	0.000

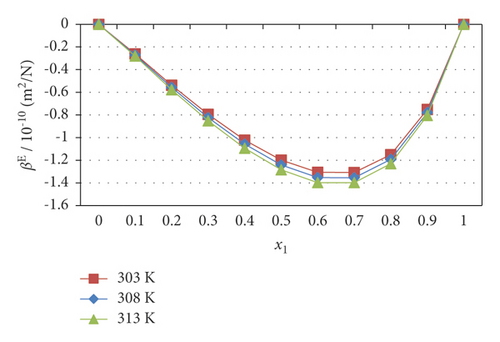
In this study, the above parameters show negative signs. The negative excess adiabatic compressibility (β^E) values are progressively increased and decayed with the increasing concentration of chlorpheniramine, as shown in Figure 3. The negative values slightly decrease with an increase in the entire range of temperature. Moreover, the negative excess compressibility (β^E) increased up to a critical concentration (x₁, 0.5), decreasing in the 1-propanol medium. This trend suggested that the dissociation of dipoles increased in 1-propanol rich concentrations. Furthermore, the nonlinear variations in the excess free volume () also suggested that the strength of intermolecular interaction increased with the increasing mole fraction of chlorpheniramine. The excess viscous relaxation time (τ^E) and excess Gibbs energy (ΔG^E) also supported the experimental observations. The excess free molar volume increase with 1-propanol concentrations and decrease with increasing chlorpheniramine molecules. Furthermore, the positive signifies dispersive force acting on the mixture. It leads to dissociation in order to increase 1-propanol concentrations. The changes in excess parameters reveal the polynomial curve. Therefore, the Redlich–Kister polynomial coefficients and the standard deviation of the theoretical data are also calculated and given in Table 4. The standard deviation values validated the theoretical calculation of these excess parameters.

4. Redlich–Kister coefficients and standard deviations of chlorpheniramine and 1-propanol at 303 K, 308 K, and 313 K in the atmospheric pressure.

Parameters	Temperature (K)	a₀	a₁	a₂	σ
β^E/10⁻¹⁰ (m²/N)	303	−0.454	0.328	−0.214	0.049
	308	−0.324	−0.312	−0.096	0.045
	313	−0.324	0.402	−0.103	0.046
/10⁻¹¹ (m)	303	−1.010	0.481	0.180	0.062
	308	−0.772	0.177	0.202	0.049
	313	−1.170	0.520	0.308	0.063
/10⁻⁸ (m³/mol)	303	−0.255	−0.625	0.542	0.051
	308	−0.309	−1.005	0.973	0.057
	313	−0.341	−1.463	1.397	0.065
τ^E/10⁻¹² (s)	303	−0.093	−0.111	−0.133	0.048
	308	−0.027	−0.089	−0.220	0.052
	313	0.027	−0.034	−0.329	0.047
ΔG^E (kJ/mol)	303	−2.034	1.120	0.570	0.055
	308	0.082	0.438	−0.856	0.048
	313	0.332	−2.146	−2.424	0.062
/10⁻⁶ (m³/mol)	303	0.134	2.825	1.836	0.134
	308	1.974	0.815	1.373	0.683
	313	0.137	0.2068	1.434	0.8545

5. Conclusion

The density (ρ), viscosity (η), and ultrasonic velocity (U) of chlorpheniramine with 1-propanol were measured at 303 K, 308 K, and 313 K in the atmospheric pressure. Using the experimental data, adiabatic compressibility (β), free length (L_f), free volume (V_f), viscous relaxation time (τ), and Gibbs free energy (ΔG) are derived. These parameters significantly vary with the temperature and concentrations of the solute-solvent in the liquid system. The deviations of these parameters from the ideal values are also calculated. The systematic observation reveals that the presence of hydrogen bonding interaction between the amine group and hydroxyl group existed in chlorpheniramine and 1-propanol, respectively. Redlich–Kister coefficients and standard deviations are also supporting the legitimacy of the observations. The experimental and theoretical calculations confirmed the existence of intermolecular interaction between chlorpheniramine and 1-propanol. The strength of the interaction is found greater in the higher chlorpheniramine concentrations. The dissociation is observed in 1-propanol concentrations. Furthermore, while increasing the temperature, the strength of the intermolecular interaction decreased and was found in the order of 303 K > 308 K > 313 K.

Conflicts of Interest

The author declares that there are no conflicts of interest.

Acknowledgments

The author is thankful to the Department of Physics, Research and Technology Transfer Centre, Wollega University, Nekemte, Ethiopia (WU/S1/108), for their support by providing necessary facilities to complete this work.

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 Agarwal H., Kumari L., Sinha L., Prasad O., and Gupta M., Thermoacoustic and DFT analysis of N,N-dimethylacetamide (DMA) with 1-propanol and methanol at 293.15, 303.15, and 313.15 K, Brazilian Journal of Physics. (2021) 51, no. 3, 515–526, https://doi.org/10.1007/s13538-021-00897-5.
10.1007/s13538-021-00897-5
CAS Web of Science® Google Scholar
2 Palaniappan L. and Nithiyanantham S., Molecular interactions from the experimental and validation with estimated theoretical sound velocity, Chemistry Africa. (2020) 3, no. 1, 277–285, https://doi.org/10.1007/s42250-019-00091-w.
10.1007/s42250-019-00091-w
CAS Google Scholar
3 Shakila A., Ravikumar S., Pandiyan V., and Gaba R., Thermodynamic properties of binary liquid mixtures containing aromatic alcohol and aliphatic amines at different temperatures, Journal of Molecular Liquids. (2019) 285, 279–287, https://doi.org/10.1016/j.molliq.2019.04.064, 2-s2.0-85064641556.
10.1016/j.molliq.2019.04.064
CAS Web of Science® Google Scholar
4 Satheesh B., Sreenu D., and Savitha Jyostna T., Thermodynamic studies on non-ideal binary mixtures of isoamyl alcohol and various alkanols at 298.15 to 308.15 K, Journal of Solution Chemistry. (2021) 50, no. 5, 615–629, https://doi.org/10.1007/s10953-020-01048-1.
10.1007/s10953-020-01048-1
CAS Web of Science® Google Scholar
5 Savitha Jyostna T., Sreenu D., Satheesh B., Suresh R., and Sowjanya G., Thermophysical and thermodynamic properties of non-ideal binary mixtures of benzyl acetate with alkyl acetates, Russian Journal of Physical Chemistry. (2021) 95, no. 5, 933–943, https://doi.org/10.1134/s0036024421050228.
10.1134/S0036024421050228
CAS Web of Science® Google Scholar
6 Liu P., Liu Z., Zhao T., Liu F., and Liao Q., Density, viscosity, and spectroscopic nature for the binary system of tetraethylene glycol (1) + water (2) T = (298.15 to 323.15) K, International Journal of Thermophysics. (2021) 42, no. 6, 93–24, https://doi.org/10.1007/s10765-021-02851-8.
10.1007/s10765-021-02851-8
Web of Science® Google Scholar
7 Satheesh B. and Savitha Jyostna T., Volumetric and spectroscopic properties of binary liquid mixtures of isopentyl alcohol with butylamine at T = (288.15-333.15) K, The Journal of Chemical Thermodynamics. (2021) 160, no. 2021, 106508, https://doi.org/10.1016/j.jct.2021.106508.
10.1016/j.jct.2021.106508
CAS Web of Science® Google Scholar
8 Elangovan S. and Mullainathan S., Ultrasonic studies of intermolecular interaction in binary mixture of n-methyl formate with 1-propanol at various temperatures, Indian Journal of Physics. (2013) 87, no. 7, 659–664, https://doi.org/10.1007/s12648-013-0288-2, 2-s2.0-84879204846.
10.1007/s12648-013-0288-2
CAS Web of Science® Google Scholar
9 Manukonda G., Ponneri V., Kasibhatta S., and Sakamuri S., Density, ultrasonic velocity, viscosity and their excess parameters of the binary mixtures of N,N-dimethylaniline+1-alkanols (C3-C5), +2-alkanols (C3-C4), +2-methyl-1-propanol, +2-methyl-2-propanol at 303.15K, Korean Journal of Chemical Engineering. (2013) 30, no. 5, 1131–1141, https://doi.org/10.1007/s11814-013-0014-y, 2-s2.0-84876898055.
10.1007/s11814-013-0014-y
CAS Web of Science® Google Scholar
10 Droliya P. and Nain A. K., Densities, ultrasonic speeds, excess and partial molar properties of binary mixtures of acetonitrile with some alkyl methacrylates at temperatures from 293.15 K to 318.15 K, The Journal of Chemical Thermodynamics. (2018) 123, 146–157, https://doi.org/10.1016/j.jct.2018.03.013, 2-s2.0-85045234111.
10.1016/j.jct.2018.03.013
CAS Web of Science® Google Scholar
11 Sanchez-Gonzalez M., Rizvi S. A., Torres J., and Ferrer G., A randomized controlled pilot trial to test the efficacy of intranasal chlorpheniramine maleate with xylitol for the treatment of allergic rhinitis, Cureus. (2021) 13, e14206, https://doi.org/10.7759/cureus.14206.
10.7759/cureus.14206
PubMed Google Scholar
12 Ortega J., Densities and refractive indices of pure alcohols as a function of temperature, Journal of Chemical & Engineering Data. (1982) 27, no. 3, 312–317, https://doi.org/10.1021/je00029a024, 2-s2.0-0020156674.
10.1021/je00029a024
CAS Web of Science® Google Scholar
13 Elangovan S., Garbi T. D., and Thillaiarasu P., Intermolecular interaction between chlorpheniramine and 1-ethanol at various temperatures, Material Science Research India. (2020) 17, no. 2, 162–169, https://doi.org/10.13005/msri/170208.
10.13005/msri/170208
CAS Google Scholar
14 Sampandam E., Diriba Garbi T., and Alemu Abbo Y., Intermolecular interaction studies of brompheniramine with 1-propanol at 303 K, 308 K and 313 K, Chemistry Africa. (2020) 3, no. 4, 1101–1107, https://doi.org/10.1007/s42250-020-00155-2.
10.1007/s42250-020-00155-2
CAS Google Scholar
15 Elangovan S., Garbi T. D., and Thillaiarasu P., Intermolecular interaction between chlorpheniramine and 1-ethanol at various temperatures, Material Science Research India. (2020) 17, no. 2, 162–169, https://doi.org/10.13005/msri/170208.
10.13005/msri/170208
CAS Google Scholar
16 Chandrasekhar A. C. H. and Krishnaiah A., Ultrasonic behaviour of amine and alcohol mixtures, Physics and Chemistry of Liquids. (1988) 17, no. 4, 315–321, https://doi.org/10.1080/00319108808078567, 2-s2.0-84963255045.
10.1080/00319108808078567
CAS Web of Science® Google Scholar
17 Gurung B. B. and Roy M. N., Study of densities, viscosities and ultrasonic speeds of binary mixtures containing 1,2-dimethoxyethane and an alkan-l-ol at 298.15 K, Journal of Solution Chemistry. (2006) 35, no. 12, 1587–1606, https://doi.org/10.1007/s10953-006-9085-2, 2-s2.0-33845883797.
10.1007/s10953-006-9085-2
CAS Web of Science® Google Scholar
18 Redlich O. and Kister A. T., Algebraic representation of thermodynamic properties and the classification of solutions, Industrial and Engineering Chemistry. (1948) 40, no. 2, 345–348, https://doi.org/10.1021/ie50458a036.
10.1021/ie50458a036
Web of Science® Google Scholar
19 Elangovan S. and Mullainathan S., Intermolecular interactions in methyl formate-ethanol mixtures at 303-313 K according to ultrasonic data, Russian Journal of Physical Chemistry. (2014) 88, no. 4, 601–606, https://doi.org/10.1134/s0036024414040086, 2-s2.0-84898992191.
10.1134/S0036024414040086
CAS Web of Science® Google Scholar
20 Kincaid J. F. and Eyring H., Free volumes and free angle ratios of molecules in liquids, The Journal of Chemical Physics. (1938) 6, no. 10, 620–629, https://doi.org/10.1063/1.1750134, 2-s2.0-0000062003.
10.1063/1.1750134
CAS Web of Science® Google Scholar
21 Fort R. J. and Moore W. R., Viscosities of binary liquid mixtures, Transactions of the Faraday Society. (1966) 62, 1112–1119, https://doi.org/10.1039/tf9666201112, 2-s2.0-11544309057.
10.1039/tf9666201112
CAS Google Scholar

All articles

Thermophysical Studies of Chlorpheniramine with 1-Propanol at 303 K, 308 K, and 313 K in the Atmospheric Pressure

Abstract

1. Introduction

2. Materials

3. Methods

4. Results and Discussion

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Thermophysical Studies of Chlorpheniramine with 1-Propanol at 303 K, 308 K, and 313 K in the Atmospheric Pressure

Abstract

1. Introduction

2. Materials

3. Methods

4. Results and Discussion

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information