Topological indices are numeric parameters which portray the topology of a subatomic structure. In QSAR/QSPR analysis, topological descriptors play a vital role to examine the topology of a network. An interconnection network is a structure whose components are connected physically according to some pattern. In this paper, an interconnection network, ternary hypertree, which is a structural combination of complete ternary tree and hypertree, is introduced. We have evaluated the topological descriptors grounded on the distances for the ternary hypertree. The analytical expressions for Wiener, different types of Szeged, and Mostar indices are determined.

1. Introduction

A connected graph having order n and size n − 1 is termed as a tree that contains no cycle. In computer science, trees are designed as data structures. Trees are helpful to store data information in a hierarchical manner and provide insertion and deletion of data. They are also useful in manipulating hierarchical data, making it easy to search information and aid in multistage decision making. One of the basic tree structures which have many applications in the field of computer science is the rooted tree [1, 2]. Rooted tree is a tree that has a root node from where the children arise. The root node is called the parent node [3, 4]. A binary tree is a rooted tree in which every vertex has at the most two children and each child of a vertex is assigned as its left child or right child [5]. A complete binary tree is a rooted tree in which every node has two children-a right child and a left child. Ternary tree which has at the most three children 3x − 1,3x, 3x + 1, where x ∈ ℤ is a root node, is a rooted tree. Ternary tree is introduced by Barning, a Dutch mathematician in Reference [6]. It is a tool for the ternary search tree which can be used in spell check and as a database when indexing several nonkey fields. In a complete ternary tree, every node has exactly three children.

Hypertree of dimension n is a basic skeleton of complete binary tree, i.e., the vertex x has exactly two children 2x and 2x + 1, where x ∈ 2ⁿ⁻¹ − 1, and the vertices on the same level are connected by a horizontal edge with a label difference of 2ⁱ⁻²; 2 ≤ i ≤ n. The hypertree is an interconnection network which has minimum average distance which results in an efficient multicomputer system [7]. It has an excellent combination of characteristics of the hypercube and the binary tree. Recursive hypertrees are modelled as biological networks such as dendrimers [8–10]. The branching of biological networks is not restricted to two branches. With this motivation, we introduce the concept of ternary hypertree. Ternary hypertrees can be modelled as biological networks for protein interactions and to analyze the spread of diseases.

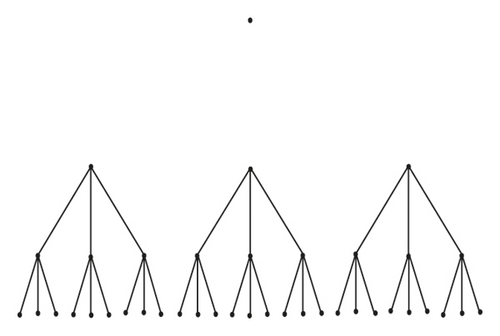
The structure of the ternary hypertree is a combination of a complete ternary tree and hypertree. It is a spanning subgraph of the complete ternary tree. We denote ternary hypertree with dimension n as THT(n).

The level of root node is 1. The root node gives rise to three children, which is at level 2. We label the root node as 1 and their children as 2,3,4. Likewise, if the node is labelled as x; then, the children are labelled as 3x − 1,3x, 3x + 1 where x ∈ [3ⁿ⁻¹ − 1/2]. At each level i; 1 ≤ i ≤ n of the ternary hypertree of dimension n has 3ⁱ⁻¹ nodes. For a ternary hypertree of dimension n, the network has n levels. There are horizontal edges in the level i, 2 ≤ i ≤ n connecting the nodes with a label difference of 3ⁱ⁻² along the complete ternary tree structure. See Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Ternary hypertree of dimension 4.

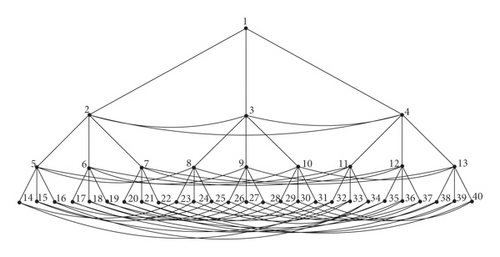
Ternary hypertree consists of (3ⁿ − 1/2) nodes and (3ⁿ − 3) edges. The vertex connectivity is 4 and edge connectivity is 3. Ternary hypertree of dimension n has a diameter of 2n − 3. Also, it is not a regular network. THT(n); n ≥ 3 is nonplanar, i.e., it cannot be embedded in a plane and non-Hamiltonian where every vertex can be visited more than once.

Real-life problems can be converted to graphical representations using mathematical modelling, especially in the field of biology [11–14]. Networks helps in analysing various health problems by modelling the spread of diseases [15–17]. Topological indices are numeric invariants showing a correlation between the subatomic structure and its physical (as well as chemical) properties [18, 19]. Thus, it characterises the topology of a graph [20, 21]. Topological indices analyse the physical, chemical, and biological characteristics of a synthetic framework [22, 23]. Topological indices are essential in the field of chemistry and pharmacology, notably in nanomedicine. It helps in the study of the properties of networks. These descriptors are used in measuring irregularity, connectivity, centrality, and peripherality in networks [24]. Topological indices for various networks have been studied in recent years [25–28].

Computing the topological indices helps in anatomising the properties of the biological network. In the next section, we have discussed some terminologies and two types of topological descriptors (distance-based and degree-based descriptors) of the ternary hypertree are derived and are graphically represented. Section 3 concludes the paper with discussion on the possible applications of ternary hypertree.

2. Topological Indices

The graph Ω considered in the paper is a simple connected graph.

is used to represent the distance between

and

and is the length of the shortest path connecting the vertices,

and

. For 1 ≤ i ≤ n, we represent i = [n]. The cardinality of collection of adjacent vertices of

is termed as the degree of a vertex

, it is denoted by

[29, 30]. Neighbourhood of a vertex,

is represented by

and is defined as follows:

(1)

and

(2)

We denote the cardinality of and as and , respectively.

Let

be the vertex weight and vertex strength and let

be the edge weight and edge strength. The notion of strength-weighted graph Ω_sw = (Ω, V_sw, E_sw), where

, was introduced in Reference [31]. For strength-weighted graph

, the degree of any vertex

. For

, we define

(3)

We refer to References [32–34] for the distance-based topological indices. The formulas of these indices for strength-weighted graph are given in Table 1 and the degree-based formulas of topological indices of graph Ω are illustrated in Table 2.

Table 1. Distance-based topological indices.

Topological indices	Mathematical expressions
Wiener [31]
Szeged [31]
Edge Szeged [31]
Edge vertex Szeged [31]
Mostar [40]
Edge Mostar [40]
Total Mostar [40]
Padmakar Ivan [31]

Table 2. Degree-based topological indices.

Topological indices	Mathematical expressions
First Zagreb [35]
Second Zagreb [35]
Randic [36]
Atom bond connectivity [37]
Sum connectivity [38]
Geometric arithmetic [39]

In this paper, we consider .

If the distance of any two vertices in ℋ, a subgraph of a graph of Ω, lies in the same subgraph, then the subgraph ℋ is called convex. For Ω, Djoković-Winkler’s relation Θ on E(Ω), References [41, 42] can be expressed as follows: if , then is Θ related with . Θ is an equivalence relation in case of partial cubes. Θ partitioned E(Ω) into convex cuts. Θ^∗ (a transitive closure) is an equivalence relation. The edges partition into Θ^∗ classes and let {F_i; 1 ≤ i ≤ k} is the Θ^∗ partition set of E(Ω). Using Θ^∗ relation, we can find the topological indices of any graph [31, 40, 43–45]. For any i ∈ [k], the quotient Ω/F_i graph in which vertex set belongs to the components of Ω − F_i and are adjacent in Ω/F_i if , where , and where C₁, C₂ are components. A partition X = {X₁, X₂, …, X_r} of E(Ω) is coarser than Y = {Y₁, Y₂, …, Y_s} if X_i is the union of one or more sets in Y. To study about the Wiener index, see References [46–48]. We have used Theorem 2.1 and the technique in Reference [48], reduction of original graph Ω into quotient graphs and further into reduced graphs, to compute the Wiener index of ternary hypertree. To compute other distance-based topological indices of ternary hypertree, we use Theorem 1.

Theorem 1. References [49, 50]. “For a connected strength-weighted graph G_sw = (G, (w_v, s_v), s_e), let E = E₁, E₂, …, E_k be a partition of E(G) coarser than F. Let X = W, Sz_v, Sz_e, Sz_ev, Mo, Mo_e, Mo_t, PI. Then,

(4)

where

is defined by ,
is defined by ,
is defined as the number of edges in E_i such that one end in C and the other end in D, for any two connected components C and D of (G/E_i).

Theorem 2. If n ≥ 2 , then

(1)
(2)
Sz(THT(n)) = (3³ⁿ⁻² − 19 × 3²ⁿ + 30 × 3ⁿn − 5 × 3ⁿ + 6 × 3²ⁿn + 39/8)
(3)
Sz_e(THT(n)) = 3³ⁿ/18 − 11 × 3²ⁿ + 18 × 3ⁿn + 9 × 3ⁿ + 3²ⁿ⁺¹n − 33/2
(4)
Sz_ev(THT(n)) = 3³ⁿ/36 − 41 × 3²ⁿ/8 + 33 × 3ⁿn/4 + 7 × 3ⁿ/8 + 3²ⁿ⁺¹n/2 + 15/2
(5)
PI(THT(n)) = 5 × 3²ⁿ/12 − 3 × 3ⁿ + 21/4
(6)
Mo(THT(n)) = 3²ⁿ/4 − 3ⁿ⁺¹n + 11 × 3ⁿ/2 − 63/4
(7)
Mo_e(THT(n)) = 3²ⁿ/2 − 6 × 3ⁿn + 12 × 3ⁿ − 81/2
(8)
Mo_t(THT(n)) = 3 × 3²ⁿ/4 − 9 × 3ⁿn + 35 × 3ⁿ/2 − 225/4

Proof. For a ternary hypertree of dimension n, there are (3ⁿ⁻¹ − 1/2 + 1)Θ^∗ classes. The Θ classes are as follows:

(1)
For 2 ≤ i ≤ n − 1, j = [3⁻¹⁺ⁱ], k = [3], let be the Θ^∗− classes containing the edges (3ⁱ⁻¹ − 1/2 + ⌈j/3⌉ + (k − 1)3ⁱ⁻², 3ⁱ − 1/2 + j + (k − 1)3ⁱ⁻¹).
(2)
Let S = S₁∪S₂ be the Θ^∗− classes, which consist of the horizontal edges and the edges connecting the first and second level. It comprises of S₁ = {(1,2), (1,4), ((3ⁱ⁻¹ − 1/2) + j, (j + 3ⁱ⁻¹ − 1/2) + 3⁻²⁺ⁱ), ((3ⁱ⁻¹/2) + j, (j + 3ⁱ⁻¹ − 1/2) + 2 × 3⁻²⁺ⁱ), ((j + 3ⁱ⁻¹ − 1/2) + 3⁻²⁺ⁱ, j + 3ⁱ⁻¹ − 1/2 + 2 × 3⁻²⁺ⁱ) : i = [n − 1], j = {1,3}} and S₂ = {((3ⁱ⁻¹ − 1/2) + j, (3ⁱ⁻¹ − 1/2) + j + 3ⁱ⁻²), ((3ⁱ⁻¹/2) + j, (j + 3ⁱ⁻¹ − 1/2) + 3ⁱ⁻² × 2), ((3ⁱ⁻¹ − 1/2) + j + 3ⁱ⁻², (j + 3ⁱ⁻¹ − 1/2) + 3⁻²⁺ⁱ × 2) : i = [n − 1], j = 2}.

Let F_i, i = [n − 1] be the partition which is coarser than the Θ^∗ classes. Define F₁ = S and F_i, 2 ≤ i ≤ n − 1 be the edges joining the levels i and i + 1, i.e., .

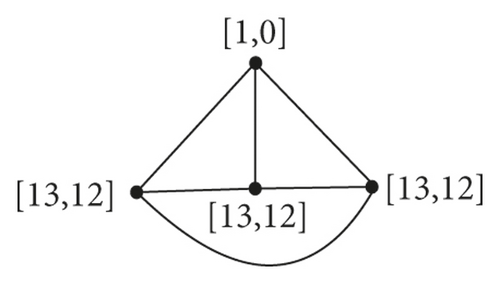
In general, THT(n)/F_i is isomorphic to . In , one vertex is of weight (3ⁿ⁻ⁱ − 1/2) and edge weight 3ⁿ⁻ⁱ − 3 and other 3ⁿ⁻ⁱ⁻¹ vertices with vertex and edge weight (3(3ⁱ − 1)/2) and 3ⁱ⁺¹ − 6, respectively. We can see that GHT(n)/F_n−1 and K₄ are isomorphic, with vertex and edge weights 1 and 0 for one vertex and (3ⁿ⁻¹ − 1/2) and (3ⁿ⁻¹ − 1/2) for the remaining adjacent vertices as shown in Figure 2. Figures 3, 4, and 5 give an example for the quotient graph.

Now, W(THT(n)) is calculated as follows:

(5)

Sz(THT(n)) is calculated as follows:

(6)

The edge-Szeged index of ternary hypertree of dimension n is as follows:

(7)

The edge-vertex Szeged index is as follows:

(8)

The Padmakar Ivan index is as follows:

(9)

The Mostar index of ternary hypertree is as follows:

(10)

(11)

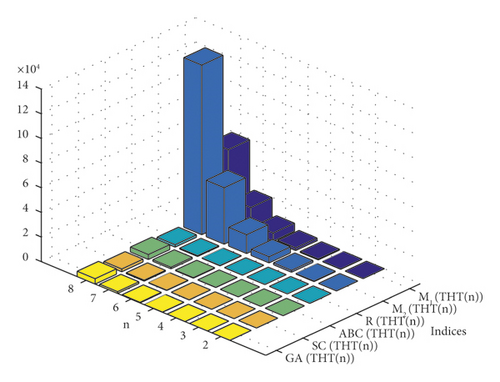
The graphical comparison of numerical values of distance-based indices of THT(n) is given in Figure 6.

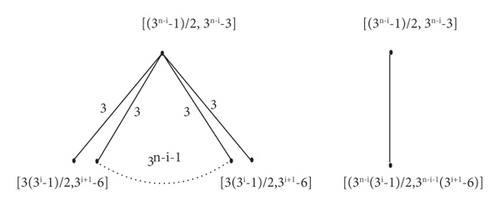
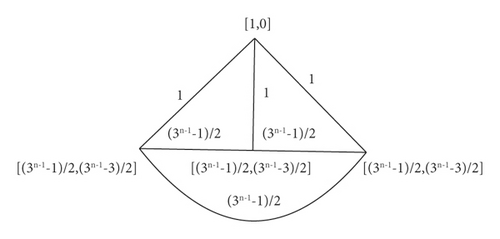
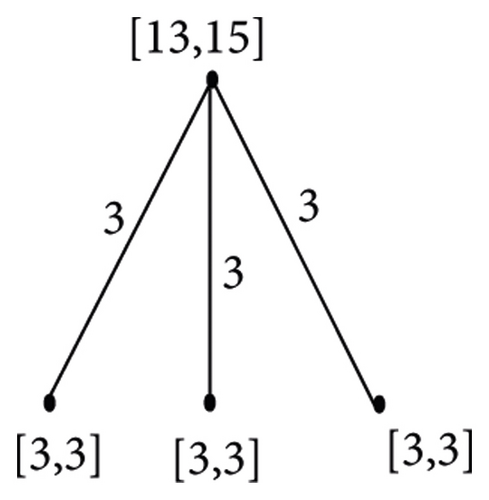
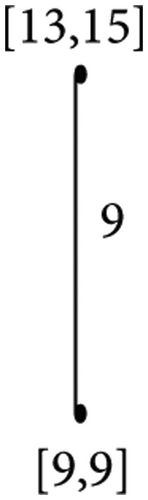
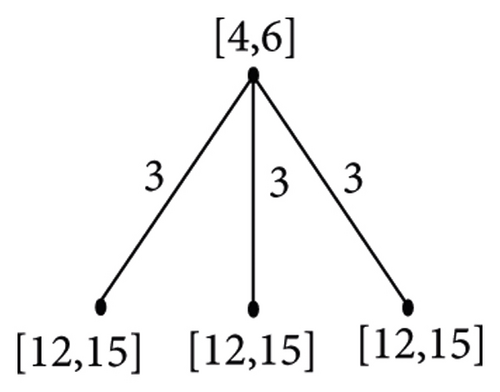
Theorem 3. For n ≥ 2,

(1)
M₁(THT(n)) = 3ⁿ⁺² − 45
(2)
M₂(THT(n)) = 7 × 3ⁿ⁺¹ − 162
(3)
R(THT(n)) = 0.2357(3ⁿ⁻¹ + 3) + 2 × 3ⁿ⁻² − 2
(4)
ABC(THT(n)) = 0.6236(3ⁿ⁻¹ + 3) + 0.6667 × 3ⁿ⁻¹ + 0.5270 × (3ⁿ⁻¹ − 6)
(5)
SC(THT(n)) = 1 + 3ⁿ⁻² + 0.4082 × 3ⁿ⁻¹ + 0.2887(3ⁿ⁻¹ − 6)
(6)
GA(THT(n)) = 2.828 + 2 × 3ⁿ⁻¹ − 6

Proof. Ternary hypertree has (3ⁿ − 3) edges. We divide the edges according to its degrees on either vertex, which is given in Table 1. We denote F_mn as the set of edges such that and .

M₁(THT(n)) is calculated as follows:

(12)

M₂(THT(n)) is calculated as follows:

(13)

Randic index of THT(n) is calculated as follows:

(14)

ABC(THT(n)) is calculated as follows:

(15)

SC(THT(n)) is calculated as follows:

(16)

The geometric arithmetic index of THT(n) is as follows:

(17)

The graphical comparison of numerical comparison of degree-based indices is given in Figure 7.

Table 3. Partition of edges of ternary hypertree of dimension n grounded on the degree vertices.

	No: Of edges
(3,3)	3ⁿ⁻¹
(6,3)	3ⁿ⁻¹ + 3
(6,6)	3ⁿ⁻¹ − 6

3. Conclusion

Hypertree has many chemical applications such as in recursive molecular networks, for example, dendrimers [51]. Also, the topological indices for hypertree are used in the prognosis of physical (as well as chemical) properties of the complex network of molecular and material systems when there are substantial atoms [10, 52–54]. In this article, we have introduced a ternary hypertree, an interconnection network, and evaluated some distance-based and degree-based topological indices of the ternary hypertree. The topological indices of the ternary hypertree may help in determining the chemical properties of complex molecular networks. It can be used to obtain irregularity measures, connectivity measures, centrality measures, and peripherality measures of the ternary hypertree. The degree-based topological indices can help in the study of bioactivity of the ternary hypertree. In future, we can model networks by considering the spread of different viruses and can study their properties. We can also determine the entropy of ternary hypertree in order to analyse data complexity and transmission of information. Also, eccentricity-based topological indices, which help in analysing the toxicological properties, and various topological indices based on different constraints can also be computed. [55].

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Authors’ Contributions

All authors contributed equally to this work.

Acknowledgments

This research work was supported by 1 Anhui Teaching Demonstration Course: Data Structure (NO. 2020SJJXSFK1291). 2 Quality Engineering in Anhui Province: Exploration of Data Structure Curriculum Reform Towards Engineering Education Certification under the Background of New Engineering (NO. 2020jyxm0793). 3 Research Team of Anhui Xinhua University: Machine Learning and Image Processing Research Team (NO. kytd201902).

Open Research

Data Availability

The data used to support the study are cited within the text as references.

References

1 Zhang X., Wu X., Akhter S., Jamil M. K., Liu J. B., and Farahani M. R., Edge-version atom-bond connectivity and geometric arithmetic indices of generalized bridge molecular graphs, Symmetry. (2018) 10, no. 12, 751–786, https://doi.org/10.3390/sym10120751, 2-s2.0-85059034867.
10.3390/sym10120751
CAS Web of Science® Google Scholar
2 Zhang X., Awais H. M., Javaid M., and Siddiqui M. K., Multiplicative Zagreb indices of molecular graphs, Journal of Chemistry. (2019) 2019, 1–19, https://doi.org/10.1155/2019/5294198.
10.1155/2019/6720616
Web of Science® Google Scholar
3 Zhang X., Rauf A., Ishtiaq M., Siddiqui M. K., and Muhammad M. H., On degree based topological properties of two carbon nanotubes, Polycyclic Aromatic Compounds. (2020) 42, no. 3, 866–884, https://doi.org/10.1080/10406638.2020.1753221.
10.1080/10406638.2020.1753221
Web of Science® Google Scholar
4 Zhang X., Jiang H., Liu J. B., and Shao Z., The cartesian product and join graphs on edge-version atom-bond connectivity and geometric arithmetic indices, Molecules. (2018) 23, no. 7, 1731–1817, https://doi.org/10.3390/molecules23071731, 2-s2.0-85055609971.
10.3390/molecules23071731
PubMed Web of Science® Google Scholar
5 West D. B., Introduction to graph theory, 2001, 2, Prenticehall Upper, Saddle River, USA.
Google Scholar
6 Barning F. J. M., On Pythagorean and quasi-Pythagorean triangles and a generation process with the help of unimodular matrices, Math. Centrum Amsterdam Afd. Zuivere Wisk. ZW-001. (1963) .
Google Scholar
7 Goodman J. R. and Sequin C. H., Hypertree: a multiprocessor interconnection topology, IEEE Transactions on Computers. (1981) C-30, no. 12, 923–933, https://doi.org/10.1109/tc.1981.1675731, 2-s2.0-0019654378.
10.1109/TC.1981.1675731
Web of Science® Google Scholar
8 Imran M., Siddiqui M. K., Baig A. Q., and Shaker H., Molecular topological description of bacterial hypertrees, Journal of Intelligent and Fuzzy Systems. (2020) 38, no. 4, 5095–5105, https://doi.org/10.3233/jifs-191714.
10.3233/JIFS-191714
Web of Science® Google Scholar
9 Gao W., Wu H., Siddiqui M. K., and Baig A. Q., Study of biological networks using graph theory, Saudi Journal of Biological Sciences. (2018) 25, no. 6, 1212–1219, https://doi.org/10.1016/j.sjbs.2017.11.022, 2-s2.0-85044632765.
10.1016/j.sjbs.2017.11.022
PubMed Web of Science® Google Scholar
10 Rajan R. S., Kumar K. J., Shantrinal A. A., Rajalaxmi T. M., Rajasingh I., and Balasubramanian K., Biochemical and phylogenetic networks-I: hypertrees and corona products, Journal of Mathematical Chemistry. (2021) 59, no. 3, 676–698, https://doi.org/10.1007/s10910-020-01194-3.
10.1007/s10910-020-01194-3
CAS PubMed Web of Science® Google Scholar
11 Barton P., Jobanputra P., Wilson J., Bryan S., and Burls A., The use of modelling to evaluate new drugs for patients with a chronic condition: the case of antibodies against tumour necrosis factor in rheumatoid arthritis, Health Technology Assessment. (2004) 8, no. 11, 1, https://doi.org/10.3310/hta8110, 2-s2.0-17344389740.
10.3310/hta8110
Web of Science® Google Scholar
12 Harjule P., Tiwari V., and Kumar A., Mathematical models to predict COVID-19 outbreak: an interim review, Journal of Interdisciplinary Mathematics. (2021) 24, no. 2, 259–284, https://doi.org/10.1080/09720502.2020.1848316.
10.1080/09720502.2020.1848316
Web of Science® Google Scholar
13 Ivorra B. and Ramos A. M., Application of the be-codis mathematical model to forecast the international spread of the 2019–20 wuhan coronavirus outbreak, ResearchGate Preprint. (2020) 9, 1–13.
Google Scholar
14 Pavlopoulos G. A., Kontou P. I., Pavlopoulou A., Bouyioukos C., Markou E., and Bagos P. G., Bipartite graphs in systems biology and medicine: a survey of methods and applications, GigaScience. (2018) 7, no. 4, 1–31, https://doi.org/10.1093/gigascience/giy014, 2-s2.0-85053686899.
10.1093/gigascience/giy014
PubMed Web of Science® Google Scholar
15 Kanwal S., Siddiqui M. K., Bonyah E., Sarwar K., Shaikh T. S., and Ahmed N., Analysis of the epidemic biological model of tuberculosis (TB) via numerical schemes, Complexity. (2022) 2022, 1–13, https://doi.org/10.1155/2022/5147951, 5147951.
10.1155/2022/5147951
Web of Science® Google Scholar
16 Mason O. and Verwoerd M., Graph theory and networks in biology, IET Systems Biology. (2007) 1, no. 2, 89–119, https://doi.org/10.1049/iet-syb:20060038, 2-s2.0-33947619951.
10.1049/iet-syb:20060038
CAS PubMed Web of Science® Google Scholar
17 Pavlopoulos G. A., Secrier M., Moschopoulos C. N., Soldatos T. G., Kossida S., Aerts J., Schneider R., and Bagos P. G., Using graph theory to analyze biological networks, BioData Mining. (2011) 4, no. 1, 10–27, https://doi.org/10.1186/1756-0381-4-10, 2-s2.0-79955130092.
10.1186/1756-0381-4-10
PubMed Web of Science® Google Scholar
18 Zhang X., Naeem M., Baig A. Q., and Zahid M. A., Study of hardness of superhard crystals by topological indices, Journal of Chemistry. (2021) 2021, 10, 9604106, https://doi.org/10.1155/2021/9604106.
10.1155/2021/9604106
Web of Science® Google Scholar
19 Zhang X., Siddiqui M. K., Javed S., Sherin L., Kausar F., and Muhammad M. H., Physical analysis of heat for formation and entropy of Ceria Oxide using topological indices, Combinatorial Chemistry & High Throughput Screening. (2022) 25, no. 3, 441–450, https://doi.org/10.2174/1386207323999201001210832.
10.2174/1386207323999201001210832
CAS PubMed Web of Science® Google Scholar
20 Javaid M., Farid F., Liu J. B., and Alanazi A. M., Exact formulae for degree distance indices of sum graphs, Journal of Mathematics. (2022) 2022, 16, 6193727, https://doi.org/10.1155/2022/6193727.
10.1155/2022/6193727
Web of Science® Google Scholar
21 Rajasingh I., Manuel P., Parthiban N., Azubha Jemilet D., and Sundara Rajan R., Transmission in butterfly networks, The Computer Journal. (2016) 59, no. 8, 1174–1179, https://doi.org/10.1093/comjnl/bxv127, 2-s2.0-84992124334.
10.1093/comjnl/bxv127
Web of Science® Google Scholar
22 Hussain A., Numan M., Naz N., Butt S. I., Aslam A., and Fahad A., On topological indices for new classes of benes network, Journal of Mathematics. (2021) 2021, 7, 6690053, https://doi.org/10.1155/2021/6690053.
10.1155/2021/6690053
Web of Science® Google Scholar
23 Imran M., Hayat S., and Mailk M. Y. H., On topological indices of certain interconnection networks, Applied Mathematics and Computation. (2014) 244, 936–951, https://doi.org/10.1016/j.amc.2014.07.064, 2-s2.0-84907317006.
10.1016/j.amc.2014.07.064
Web of Science® Google Scholar
24 Tratnik N., Computing the Mostar index in Networks with Applications to Molecular Graphs, 2019, arXiv preprint arXiv:1904.04131.
Google Scholar
25 Hayat S. and Imran M., Computation of topological indices of certain networks, Applied Mathematics and Computation. (2014) 240, 213–228, https://doi.org/10.1016/j.amc.2014.04.091, 2-s2.0-84901258013.
10.1016/j.amc.2014.04.091
Web of Science® Google Scholar
26 Ma G., Ibrahim M., Abbas G., Siddiqui M. K., and Fufa S. A., On degree-based topological indices of thermodynamic cuboctahedral Bi-metallic structure, Journal of Mathematics. (2022) 2022, 10, 6484704, https://doi.org/10.1155/2022/6484704.
10.1155/2022/6484704
Web of Science® Google Scholar
27 Huang R., Muhammad M. H., Siddiqui M. K., Khalid S., Manzoor S., and Bashier E., Analysis of topological aspects for metal-insulator transition superlattice network, Complexity. (2022) 2022, 11, 8344699, https://doi.org/10.1155/2022/8344699.
10.1155/2022/8344699
Web of Science® Google Scholar
28 Sattar A., Javaid M., and Alam M. N., On the studies of dendrimers via connection-based molecular descriptors, Mathematical Problems in Engineering. (2022) 2022, 1–13, 1053484, https://doi.org/10.1155/2022/1053484.
10.1155/2022/1053484
Web of Science® Google Scholar
29 Gutman I. and Ashrafi A. R., The edge version of the Szeged index, Croatica Chemica Acta. (2008) 81, no. 2, 263–266.
CAS Web of Science® Google Scholar
30 Gutman I., A formula for the Wiener number of trees and its extension to graphs containing cycles, Graph Theory Notes NY. (1994) 27, no. 9, 9–15.
Google Scholar
31 Arockiaraj M., Clement J., and Balasubramanian K., Topological indices and their applications to circumcised donut benzenoid systems, kekulenes and drugs, Polycyclic Aromatic Compounds. (2020) 40, no. 2, 280–303, https://doi.org/10.1080/10406638.2017.1411958, 2-s2.0-85041003934.
10.1080/10406638.2017.1411958
CAS Web of Science® Google Scholar
32 Khadikar P. V., Karmarkar S., and Agrawal V. K., A novel PI index and its applications to QSPR/QSAR studies, Journal of Chemical Information and Computer Sciences. (2001) 41, no. 4, 934–949, https://doi.org/10.1021/ci0003092, 2-s2.0-0035385130.
10.1021/ci0003092
CAS PubMed Web of Science® Google Scholar
33 Mahmiani A., Khormali O., Iranmanesh A., and Yousefidaz M., The new version of Szeged index, Optoelectronics and Advanced Materials-Rapid Communications. (2010) 4, 2182–2184.
CAS Web of Science® Google Scholar
34 Wiener H., Structural determination of paraffin boiling points, Journal of the American Chemical Society. (1947) 69, no. 1, 17–20, https://doi.org/10.1021/ja01193a005, 2-s2.0-8544254107.
10.1021/ja01193a005
CAS PubMed Web of Science® Google Scholar
35 Gutman I. and Trinajstić N., Graph theory and molecular orbitals. Total π-electron energy of alternant hydrocarbons, Chemical Physics Letters. (1972) 17, no. 4, 535–538.
10.1016/0009-2614(72)85099-1
CAS Web of Science® Google Scholar
36 Randic M., Characterization of molecular branching, Journal of the American Chemical Society. (1975) 97, no. 23, 6609–6615, https://doi.org/10.1021/ja00856a001, 2-s2.0-8644280181.
10.1021/ja00856a001
CAS Web of Science® Google Scholar
37 Estrada E., Torres L., Rodriguez L., and Gutman I., An atom-bond connectivity index: modelling the enthalpy of formation of alkanes, Indian journal of chemistry. Sect. A: Inorganic, physical, theoretical & analytical. (1998) 37, 849–855.
Web of Science® Google Scholar
38 Zhou B. and Trinajstić N., On a novel connectivity index, Journal of Mathematical Chemistry. (2009) 46, no. 4, 1252–1270, https://doi.org/10.1007/s10910-008-9515-z, 2-s2.0-70350151674.
10.1007/s10910-008-9515-z
CAS Web of Science® Google Scholar
39 Vukičević D. and Furtula B., Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges, Journal of Mathematical Chemistry. (2009) 46, no. 4, 1369–1376, https://doi.org/10.1007/s10910-009-9520-x, 2-s2.0-70350166990.
10.1007/s10910-009-9520-x
CAS Web of Science® Google Scholar
40 Arockiaraj M., Clement J., and Tratnik N., Mostar indices of carbon nanostructures and circumscribed donut benzenoid systems, International Journal of Quantum Chemistry. (2019) 119, no. 24, 1–15, https://doi.org/10.1002/qua.26043, 2-s2.0-85071865599.
10.1002/qua.26043
Web of Science® Google Scholar
41 Djoković D. Z., Distance-preserving subgraphs of hypercubes, Journal of Combinatorial Theory - Series B. (1973) 14, no. 3, 263–267, https://doi.org/10.1016/0095-8956(73)90010-5, 2-s2.0-33749306854.
10.1016/0095-8956(73)90010-5
Google Scholar
42 Winkler P. M., Isometric embedding in products of complete graphs, Discrete Applied Mathematics. (1984) 7, no. 2, 221–225, https://doi.org/10.1016/0166-218x(84)90069-6, 2-s2.0-0021372972.
10.1016/0166-218X(84)90069-6
Web of Science® Google Scholar
43 Mushtaq S., Arockiaraj M., Klavžar S., Fiona J. C., and Balasubramanian K., Comment on Mostar indices of SiO ₂ nanostructures and melem chain nanostructures, International Journal of Quantum Chemistry. (2022) 122, no. 11, e26894, https://doi.org/10.1002/qua.26894.
10.1002/qua.26894
CAS Web of Science® Google Scholar
44 Xavier D. A., Varghese E. S., and Mathew D., Glued hypertree: comparative analysis and distance-based topological descriptors, Indian Journal of Science and Technology. (2022) 15, no. 15, 658–667, https://doi.org/10.17485/ijst/v15i15.37.
10.17485/IJST/v15i15.37
Google Scholar
45 Xavier D. A., Varghese E. S., Baby A., Mathew D., and Kaabar M. K., Distance based topological descriptors of zinc porphyrin dendrimer, Journal of Molecular Structure. (2022) 1268, 133614, https://doi.org/10.1016/j.molstruc.2022.133614.
10.1016/j.molstruc.2022.133614
CAS Web of Science® Google Scholar
46 Klavžar S. and Gutman I., Wiener number of vertex-weighted graphs and a chemical application, Discrete Applied Mathematics. (1997) 80, no. 1, 73–81, https://doi.org/10.1016/s0166-218x(97)00070-x, 2-s2.0-0002238994.
10.1016/S0166-218X(97)00070-X
Web of Science® Google Scholar
47 Klavžar S. and Nadjafi-Arani M. J., Wiener index in weighted graphs via unification ofΘ∗-classes, European Journal of Combinatorics. (2014) 36, 71–76, https://doi.org/10.1016/j.ejc.2013.04.008, 2-s2.0-84882959719.
10.1016/j.ejc.2013.04.008
Web of Science® Google Scholar
48 Klavžar S., Manuel P., Nadjafi-Arani M. J., Rajan R. S., Grigorious C., and Stephen S., Average distance in interconnection networks via reduction theorems for vertex-weighted graphs, The Computer Journal. (2016) 59, no. 12, 1900–1910, https://doi.org/10.1093/comjnl/bxw046, 2-s2.0-85031321968.
10.1093/comjnl/bxw046
Web of Science® Google Scholar
49 Arockiaraj M., Klavžar S., Clement J., Mushtaq S., and Balasubramanian K., Edge distance-based topological indices of strength-weighted graphs and their application to coronoid systems, carbon nanocones and SiO2 nanostructures, Molecular Informatics. (2019) 38, no. 11-12, 205, 1900039, https://doi.org/10.1002/minf.201900039, 2-s2.0-85073829012.
10.1002/minf.201900039
CAS Web of Science® Google Scholar
50 Liu J. B., Arockiaraj M., Arulperumjothi M., and Prabhu S., Distance based and bond additive topological indices of certain repurposed antiviral drug compounds tested for treating COVID-19, International Journal of Quantum Chemistry. (2021) 121, no. 10, e26617–18, e26617, https://doi.org/10.1002/qua.26617.
10.1002/qua.26617
CAS PubMed Web of Science® Google Scholar
51 Balasubramanian K., Nested wreath groups and their applications to phylogeny in biology and Cayley trees in chemistry and physics, Journal of Mathematical Chemistry. (2017) 55, no. 1, 195–222, https://doi.org/10.1007/s10910-016-0680-1, 2-s2.0-84987673685.
10.1007/s10910-016-0680-1
CAS Web of Science® Google Scholar
52 Balasubramanian K., Ten low-lying electronic states of Pd3, The Journal of Chemical Physics. (1989) 91, no. 1, 307–313, https://doi.org/10.1063/1.457518, 2-s2.0-36549091804.
10.1063/1.457518
CAS Web of Science® Google Scholar
53 Balasubramanian K. and Feng P. Y., Potential energy surfaces for Pt2 + H and Pt + H interactions, The Journal of Chemical Physics. (1990) 92, no. 1, 541–550.
10.1063/1.458457
CAS Web of Science® Google Scholar
54 Ermler W. C., Relativistic Effects in Chemistry Part A: Theory and Techniques by Krishnan Balasubramanian (Arizona State University), 1998, Wiley-Interscience, New York.
Google Scholar
55 Liu J. B., Zhao J., He H., and Shao Z., Valency-based topological descriptors and structural property of the generalized sierpiński networks, Journal of Statistical Physics. (2019) 177, no. 6, 1131–1147, https://doi.org/10.1007/s10955-019-02412-2.
10.1007/s10955-019-02412-2
Web of Science® Google Scholar

All articles

Distance-Based Topological Descriptors on Ternary Hypertree Networks

Abstract

1. Introduction

2. Topological Indices

3. Conclusion

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Distance-Based Topological Descriptors on Ternary Hypertree Networks

Abstract

1. Introduction

2. Topological Indices

3. Conclusion

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information