The problem of position estimation for a noncooperative source has always been widely discussed in the field of wireless communication. Direct position determination (DPD) for a noncooperative source with fast moving receivers is discussed in this paper. The sinc function is used to reconstruct the signals, which is an important step in DPD for wideband signals. A DPD method based on the baseband signal is proposed which is more practical in communication signal with high carrier frequency. And based on the proposed DPD method, a DPD method for multiple noncooperative stationary sources by single-channel receivers is presented. In order to evaluate the performance of the proposed DPD method, the Cramér-Rao lower bound (CRLB) for DPD based on baseband signal is derived. Several numerical investigations are carried out to evaluate the performance of the proposed method.

1. Introduction

Noncooperative source localization based on the emitted signals has been of great interest to academic researchers and industrial practitioners for many years [1–5]. The two-step localization method is the most widely used method for traditional source localization. In the first step, the location-related parameters are extracted from the sampled signals. Then, in the second step, the source location is estimated by the extracted parameters. The two-step localization method is usually suboptimal as it ignores the intrinsic constraint that all the extracted parameters should be consistent with the same source location. In addition, in multiple source localization, the two-step method will usually lead to a parameter-to-source association problem, which may require additional efforts.

Motivated by the shortcomings of the two-step method, DPD methods are proposed [6–8] which estimate the source location directly from the received signals without parameter extraction. There is no intermediate parameters to estimate, and the association of the parameters and location of sources are realized implicitly. For a stationary emitter and moving receivers, a common DPD method is to estimate the source location using the signals containing the information of time difference of arrival (TDOA) and frequency difference of arrival (FDOA).

Weiss and Amar [9, 10] proposed a DPD method for the received signals with delay and Doppler, where a downshift matrix was used to model the time delay. The DPD method Weiss and Amar proposed using time-domain modelling [9] and frequency-domain modelling [10] for the received signals. There is a quantization process in the downshift matrix, which leads to the increase of positioning error.

Li et al. [11] improved the downshift matrix by the fast Fourier transform (FFT) method. Lu et al. [12] adopted a similar modelling approach as that in [11], and an iterative algorithm based on particle filter was designed to solve the DPD problem. When the signal bandwidth is narrow, the cumulative time is short or the receivers are moving slowly, the signal model can be established as a narrowband model. When the narrowband condition is not satisfied, it is usually solved by partitioning the received signals into multiple short-time signal segments. When the signal bandwidth is wide, a scaled formulation was used to solve the wideband source localization problems in passive acoustics and sonar applications [13], since significant biases would be introduced if such signals were approximated with narrowband models. The CRLB for wideband DPD is only for random signal in [13]. However, the DPD CRLB for unknown deterministic signal needs to be solved in practical engineering.

Currently, almost all TDOA- and FDOA-based DPD methods assume a stationary source. Most DPD methods only consider narrowband signal, and only consider wideband signal with low carrier frequency such as sonar. Most DPD methods for multiple sources use the signals received by an antenna array [14–19]. Considering the problem of locating multiple noncooperative stationary sources using multiple fast moving receivers with a single antenna, this paper is dedicated to estimating the sources location directly from the received signals. The contributions of the current study are mainly in three aspects. Firstly, a signal baseband reconstruction-based DPD method is proposed which is suitable for wideband signal. Secondly, a DPD method for multiple noncooperative stationary sources is proposed. And finally, the CRLB for DPD method based on baseband signal is derived. Several numerical investigations are carried out to evaluate the performance of the proposed method.

2. Direct Position Determination for Noncooperative Source

2.1. Problem Formulation

Consider a stationary source located at

and L fast moving receivers, let x = (x, y)^T ∈ Ω, where Ω represents the group containing all possible source locations. The position and velocity of receiver l at time t are assumed to be

and

, l = 1, ⋯, L. Suppose that the source signal is s(t), then the signal received by receiver l can be modelled as

(1)

where c is the speed of wave propagation, η_l(t) = 1/‖r_l(t)‖ is the path attenuation factor and is usually approximately stationary over the signal sampling period and can be assumed to be insensitive to t, and accordingly η_l(t) ≈ η_l, r_l(t) = x − x_l(t) is the position vector from source to receiver, τ_l(t) = (1/c)‖r_l(t)‖ is the propagation time delay from source to receiver, w_l(t) represents zero-mean, white, circular complex Gaussian noise with variance

, and they are assumed to be independent at different receivers.

The received signals can be partitioned into K sections; then, it can be assumed that the time delay varies linearly during each period. Consider that all receivers collect (M + 1) signal samples in kth section with sampling frequency f_s = 1/Δ satisfying the Nyquist rule, and we denote t_k,m = t_k + mΔ, k = 1, ⋯, K, m = −M/2, ⋯, −1, 0, 1, ⋯, M/2, t_k is the middle time in kth section. Then, the discrete form of (1) is

(2)

According to the sampling theorem, we have

(3)

where sinc(x) = sin(πx)/(πx).

Due to the segmentation, it can be assumed that (M + 1)Δ ≪ 1, then the propagation time delay can be represented approximately as

(4)

(5)

where

, d_l,k = ‖r_l(t_k)‖/cΔ.

By (3) and (5), formulation (2) can be rewritten as

(6)

where s_k(n) = s(t_k + nΔ).

Let Λ = [diag(Λ₁, ⋯, Λ_L)] ⊗ I_K, Λ_l = η_lI_M+1, H = diag(H₁, ⋯, H_K), , H_l,k(m + (M/2) + 1, n + (M/2) + 1) = sinc(b_l,km − d_l,k − n), m = −M/2, ⋯, −1, 0, 1, ⋯, M/2, n = −M/2, ⋯, −1, 0, 1, ⋯, M/2, , , , , , , , and .

The received signal vector from all receivers is given as

(7)

where

Note that

is a set of orthogonal bases, so

(8)

When M is big enough, b ≈ 1, |d| ≪ M/2, we have

(9)

where m, n = ±M/2, ⋯, ±1, 0.

Based on (9), we have

(10)

By (7), the maximum likelihood estimator (MLE) of x_T is

(11)

where θ = (s, x, η)^T,

The joint minimization of all variables can be achieved by minimizing each variable gradually

(12)

where

Finally, the source location can be solved by

(13)

where λ_max(x) denotes the maximum eigenvalue of x. Note that

is a (M + 1) × (M + 1) matrix while

is a L × L matrix whose size is usually much smaller than

. By (13), a 2-D search over the region of interest can help determine the MLE of x_T.

2.2. DPD Based on Baseband Signal

In practice, the carrier frequency is always very high, so the received signals are usually sampled after a frequency downconversion treatment. In such scenarios, the sampled signals can be expressed as

(14)

where u(t) = s(t)e^−j2πft is the baseband signal, ε(t) = w(t)e^−j2πft.

According to (5) and (6), we have

(15)

where

Let , , , , , Ψ = diag(Ψ₁, ⋯, Ψ_K), Ψ_k = diag(Ψ_1,k, ⋯, Ψ_L,k), , , , , , and .

We further have

(16)

where

According to (13), the source location based on baseband signal can be solved by

(17)

where

2.3. DPD for Multiple Sources

Consider P stationary sources whose positions are denoted by the vectors of coordinates x_Tp(x_Tp, y_Tp), p = 1, ⋯, P. And the denotation of L fast moving receivers is the same as Section 2.1. Suppose that the signals emitted by these P sources are independent time-frequency overlapped signals. Suppose that the signals are s_p(t), p = 1, ⋯, P, then the signals received by receiver l can be modelled as

(18)

Since the signals are independent of each other, the direct position determination based on baseband signal can be used to locate multiple sources. The sampled baseband signals can be expressed as

(19)

According to (14)–(17) and (19), the following objective function is established to solve the localization problem for P sources

(20)

where

, and

By (20), x_Tp (p = 1, ⋯, P) can be estimated by searching the P local maxima of the objective function V(x) from large to small.

2.4. CRLB for DPD Based on Baseband Signal

When the source signal waveform is unknown, the baseband signal u can be expressed in terms of its real and imaginary parts as . Similarly, can be expressed as . Define the composite unknown vector .

From (12), the measurement vector y is a complex Gaussian random vector with mean

and covariance

. Consequently, y has a multivariate complex Gaussian probability density function (PDF) is given by

(21)

The Fisher information matrix (FIM) is then given by [20]

(22)

where

(23)

(24)

(25)

(26)

where the derivation of D can be referred to Appendix A.

Then, J_θ can be rewritten as

(27)

where

(28)

(29)

Using the partitioned matrix formula [21], the FIM of x is

(30)

Then, the CRLB of x in this case is

(31)

And the CRLB of localization error is

(32)

3. Numerical Results

This section conducts several numerical simulations to investigate the proposed method. Two cases are considered in all. The first case is studied to investigate the performance of the DPD method based on the baseband signal from a single source. The second case is studied to investigate the performance of the DPD method for multiple sources.

3.1. Case 1: DPD for Single Source

In this case, the initial positions of the three fast moving receivers are x₁(t₀) = (30, 5)^T (km), x₂(t₀) = (0, 0)^T (km), and x₃(t₀) = (−30, 5)^T (km). The velocities of the three receivers are v₁(t₀) = (350, 60)^T (m/s), v₂(t₀) = (350, 0)^T (m/s), and v₃(t₀) = (335, 80)^T (m/s). The stationary source is located at x_T = (8.5, 42.6)^T (km). In this case, the source emits signal with BPSK modulation and the bandwidth is 25 kHz. The carrier frequency is set to be f = 303 MHz and the sampling frequency is f_s = 100 kHz. 2500 sampling points are collected for source location.

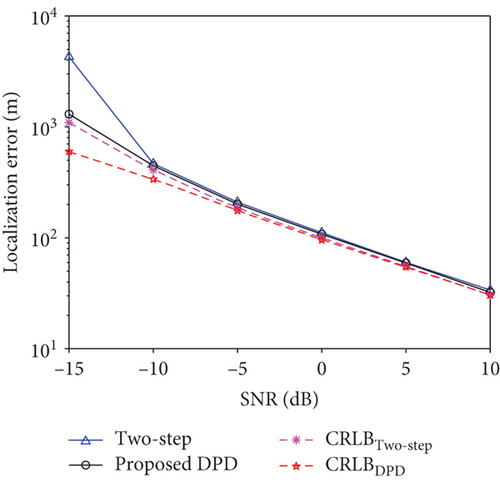
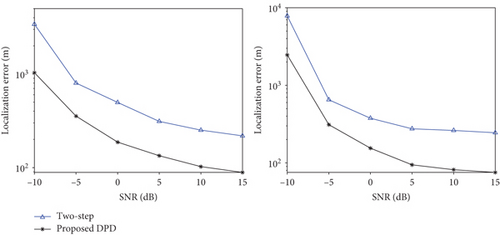
The performance of the proposed DPD method based on baseband signal and the two-step method is evaluated in Figure 1. 100 Monte Carlo simulations are performed at each SNR. In addition, the CRLB of the two-step method CRLB_two-step and the CRLB of the proposed method CRLB_DPD are also presented for comparison. The DPD method outperforms the two-step method especially when SNR is low.

Details are in the caption following the image — Open in figure viewer PowerPoint

3.2. Case 2: DPD for Multiple Sources

In this case, we consider a scenario for two stationary sources localization where one stationary source is located at x_T1 = (8.5, 42.6)^T (km) and the other stationary source is located at x_T2 = (−11.5, 29.6)^T (km). Source 1 and the three moving receivers are present with the same settings as those of case 1 in Section 3.1. Source 2 emits signal with QPSK modulation. The bandwidth and the carrier frequency of the source 2 are the same settings as those of source 1.

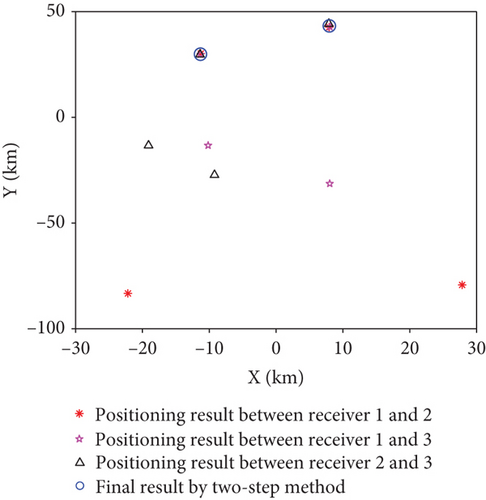
In the two-step method, two pairs of time-frequency difference should be extracted by cross-ambiguity function between two receivers, and the time-frequency differences between different receivers cannot be matched. Therefore, each time-frequency difference is used for positioning, respectively. Then, the ambiguity position is existed by two-step method. Therefore, twelve position is located by six pairs of time-frequency differences, as shown in Figure 2(a). When the two sources are far away from each other, two sources can be located by clustering three nearest positioning points, as shown in Figure 2(b).

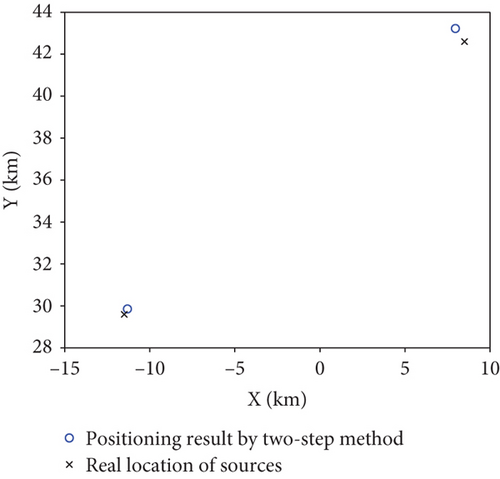
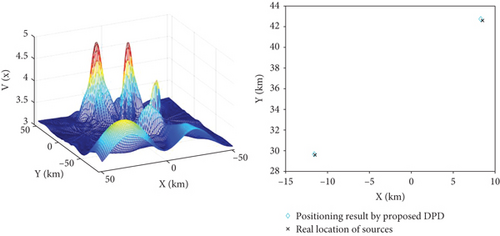
There is no problems of pairing and ambiguity in the DPD method, so the positions of two sources can be located directly. A single positioning result of DPD is shown in Figure 3, which outperforms the two-step method.

The performance of the proposed DPD method based on baseband signal and the two-step method for multiple sources is evaluated in Figure 4. 100 Monte Carlo simulations are performed at each SNR. The DPD method outperforms the two-step method especially for multiple sources.

4. Conclusion

This paper proposes a DPD method for noncooperative source with fast moving receivers. The proposed method uses the sinc function to reconstruct the signal so that the expansion of the baseband signal caused by the fast moving receivers is also considered. When the carrier frequency is high, only the baseband signal can be used for DPD. So a DPD method based on baseband signal by single-channel receivers is presented. And the proposed DPD method can be used not only for a single source but also for multiple sources. In order to evaluate the performance of the proposed DPD method, the CRLB for DPD based on baseband signal is derived. Simulation results show that the proposed DPD method provides more accurate location estimate than the two-step method.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (U20B2038).

Appendix

A. Derivation of D

According to (23), we have

(A.1)

where

According to the definition of Ψ_l,k, we have

(A.2)

(A.3)

where

, M = diag[−M/2, ⋯, M/2],

, and

According to the definition of H_l,k, we have

(A.4)

(A.5)

where ∂d_l,k/∂x = (x − x_l,k)/cΔ‖r_l,k‖, ∂d_l,k/∂y = (y − y_l,k)/cΔ‖r_l,k‖,

, m, n = ±M/2, ⋯, ±1, 0.

Open Research

Data Availability

No data were used to support this study.

References

1 Ho K. C. and Xu W., An accurate algebraic solution for moving source location using TDOA and FDOA measurements, IEEE Transactions on Signal Processing. (2004) 52, no. 9, 2453–2463, https://doi.org/10.1109/TSP.2004.831921, 2-s2.0-4344614137.
10.1109/TSP.2004.831921
Web of Science® Google Scholar
2 Ho K. C. and Yang L., On the use of a calibration emitter for source localization in the presence of sensor position uncertainty, IEEE Transactions on Signal Processing. (2008) 56, no. 12, 5758–5772, https://doi.org/10.1109/TSP.2008.929870, 2-s2.0-70450230668.
10.1109/TSP.2008.929870
Web of Science® Google Scholar
3 Pine K. C., Pine S., and Cheney M., The geometry of far-field passive source localization with TDOA and FDOA, IEEE Transactions on Aerospace and Electronic Systems. (2014) 57, no. 1, 559–572, https://doi.org/10.1109/taes.2021.3087804.
10.1109/taes.2021.3087804
Google Scholar
4 Qu X., Xie L., and Tan W., Iterative constrained weighted least squares source localization using TDOA and FDOA measurements, IEEE Transactions on Signal Processing. (2017) 65, no. 15, 3990–4003, https://doi.org/10.1109/tsp.2017.2703667, 2-s2.0-85020746402.
10.1109/TSP.2017.2703667
Web of Science® Google Scholar
5 Wang D., Yin J., Zhang T., Jia C., and Wei F., Iterative constrained weighted least squares estimator for TDOA and FDOA positioning of multiple disjoint sources in the presence of sensor position and velocity uncertainties, Digital Signal Processing. (2019) 92, 179–205, https://doi.org/10.1016/j.dsp.2019.06.001, 2-s2.0-85067247590.
10.1016/j.dsp.2019.06.001
Web of Science® Google Scholar
6 Weiss A. J., Direct position determination of narrowband radio frequency transmitters, IEEE Signal Processing Letters. (2004) 11, no. 5, 513–516, https://doi.org/10.1109/LSP.2004.826501, 2-s2.0-2442459959.
10.1109/LSP.2004.826501
Web of Science® Google Scholar
7 Amar A. and Weiss A. J., Advances in direct position determination, Processing Workshop Proceedings, 2004 Sensor Array and Multichannel Signal, 2004, Barcelona, Spain, 584–588, https://doi.org/10.1109/SAM.2004.1503016.
10.1109/SAM.2004.1503016
Google Scholar
8 Amar A. and Weiss A. J., Analysis of the direct position determination approach in the presence of model errors, 2004 23rd IEEE Convention of Electrical and Electronics Engineers in Israel, 2004, Tel-Aviv, Israel, 408–411, https://doi.org/10.1109/EEEI.2004.1361178.
10.1109/EEEI.2004.1361178
Google Scholar
9 Weiss A. J. and Amar A., Direct geolocation of stationary wideband radio signal based on time delays and Doppler shifts, 2009, Cardiff, U.K, IEEE Workshop Stat. Signal Process.
10.1109/SSP.2009.5278630
Google Scholar
10 Weiss A. J., Direct geolocation of wideband emitters based on delay and Doppler, IEEE Transactions on Signal Processing. (2011) 59, no. 6, 2513–2521, https://doi.org/10.1109/tsp.2011.2128311, 2-s2.0-79957514647.
10.1109/TSP.2011.2128311
Web of Science® Google Scholar
11 Li J., Yang L., Guo F., and Jiang W., Coherent summation of multiple short-time signals for direct positioning of a wideband source based on delay and Doppler, Digital Signal Processing. (2016) 48, 58–70, https://doi.org/10.1016/j.dsp.2015.09.008, 2-s2.0-84947270364.
10.1016/j.dsp.2015.09.008
CAS Web of Science® Google Scholar
12 Lu Z., Ba B., Wang J., Li W., and Wang D., A direct position determination method with combined TDOA and FDOA based on particle filter, Chinese Journal of Aeronautics. (2018) 31, no. 1, 161–168, https://doi.org/10.1016/j.cja.2017.11.007, 2-s2.0-85039708150.
10.1016/j.cja.2017.11.007
Web of Science® Google Scholar
13 Ma F., Liu Z. M., and Guo F., Direct position determination for wideband sources using fast approximation, IEEE Transactions on Vehicular Technology. (2019) 68, no. 8, 8216–8221, https://doi.org/10.1109/TVT.2019.2921981.
10.1109/TVT.2019.2921981
Web of Science® Google Scholar
14 Yin J. X., Wu Y., and Wang D., Direct position determination of multiple noncircular sources with a moving array, Circuits, Systems, and Signal Processing. (2017) 36, no. 10, 4050–4076, https://doi.org/10.1007/s00034-017-0499-4, 2-s2.0-85025142938.
10.1007/s00034-017-0499-4
Web of Science® Google Scholar
15 Zhou T., Yi W., and Kong L., Direct position determination of multiple coherent sources using an iterative adaptive approach, Signal Processing. (2019) 161, 203–213, https://doi.org/10.1016/j.sigpro.2019.03.023, 2-s2.0-85063694445.
10.1016/j.sigpro.2019.03.023
Web of Science® Google Scholar
16 Hao K. and Wan Q., An efficiency-improved TDOA-based direct position determination method for multiple sources, IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2019, Brighton, UK, 4425–4429, https://doi.org/10.1109/ICASSP.2019.8683421, 2-s2.0-85068970324.
10.1109/ICASSP.2019.8683421
Google Scholar
17 Li J., He Y., Zhang X., and Wu Q., Simultaneous localization of multiple unknown emitters based on UAV monitoring big data, IEEE Transactions on Industrial Informatics. (2021) 17, no. 9, 6303–6313, https://doi.org/10.1109/TII.2020.3048987.
10.1109/TII.2020.3048987
Web of Science® Google Scholar
18 Li J., Li P., Li P., Tang L., Zhang X., and Wu Q., Self-position awareness based on cascade direct localization over multiple source data, IEEE Transactions on Intelligent Transportation Systems. (2022) 1–9, https://doi.org/10.1109/TITS.2022.3170465.
10.1109/TITS.2022.3170465
Web of Science® Google Scholar
19 Wang D., Yin J. X., Chen X., and Jia C. G., Direct position determination of multiple constant modulus sources based on direction of arrival and Doppler frequency shift, Circuits, Systems, and Signal Processing. (2020) 39, no. 1, 268–306, https://doi.org/10.1007/s00034-019-01170-6, 2-s2.0-85068162810.
10.1007/s00034-019-01170-6
Web of Science® Google Scholar
20 Kay S. M., Fundamentals of Statistical Signal Processing: Estimation Theory, 1993, Prentice-Hall, Englewood Cliffs, NJ, USA.
Google Scholar
21 Scharf L. L., Statistical Signal Processing, Detection, Estimation and Time Series Analysis, 1991, Addison-Wesley, Reading, MA, UK.
Google Scholar

All articles

Direct Position Determination for Noncooperative Source with Fast Moving Receivers

Abstract

1. Introduction