In order to improve the performance optimization effect of electronic components, this paper uses the improved GA to construct the performance optimization system of electronic components. Moreover, this paper proposes an optimized reliability allocation process method based on cost function, which further optimizes the reliability design of electronic circuit systems. In addition, this paper conducts a sensitivity analysis of the electronic circuit system and compares and analyzes the evaluation results of component sensitivity and comprehensive importance based on simulation. Finally, this paper compares and demonstrates the different influences of various components in the electronic circuit system on the whole system. The experimental research shows that the performance optimization system of electronic components based on the improved GA proposed in this paper has a certain effect on improving the performance of electronic components.

1. Introduction

With the development of science and technology, the classification and characteristics of basic electronic components are becoming more and more detailed. Moreover, the detection of electronic components also presents the characteristics of many types of tests, complex parameters, and high complexity. At the same time, the detection data of electronic components shows the characteristics of large amount of data and heterogeneous structure. In the face of a large amount of data formed in production inspection, traditional electronic component inspection methods have been unable to adapt to this development trend. Therefore, electronic component manufacturers and product quality inspection institutions need to have more reasonable and applicable methods to deal with this development trend.

Data collection based on the Internet of Things, data mining of big data, and cloud computing remote measurement technology are all reasonable and effective methods and means that can be applied to the detection of electronic components. This paper aims to change the current testing methods in the production and testing of electronic components, so as to effectively improve the information level of traditional industries, significantly improve the production efficiency of enterprises, and create good social and economic benefits for enterprises [1]. Starting from the informatization testing method for the detection of physical parameters of electronic components, research on the key basic common problems in the detection of electronic components, and find an informatization method to analyze and process a large amount of heterogeneous data generated in the detection of components, and address the methods and means of measurement, transmission, storage and analysis of relevant data. Relying on the gradually mature informatization application technologies such as Internet of Things technology, big data mining, and cloud computing, the traditional electronic component detection method is moved towards the direction of informatization processing [2].

With the advancement and development of science and technology, higher and higher requirements are put forward for the quality of products. The quality of the product is measured by the degree of consistency between the performance index of the product and the specified standard value. In practical engineering problems, there are inevitably a lot of uncertain factors, and these factors will cause the technical parameters of the product to deviate from the specified standard values, resulting in quality loss. Many companies try to reduce these uncertainties in the manufacturing and trial stages to improve product quality, but doing so often increases costs with little success [3]. With the in-depth study of uncertainty, high-tech enterprises have clearly realized that the control and assurance of product quality must seek the source; that is, the quality of products is first designed, and then applicated [4]. Current product design methods tend to ignore a wide range of uncertainties, such as lack of knowledge of personnel, design flaws, manufacturing errors, and variability in operating environments, which can have significant impact on product performance. The quality control method has a large impact and even causes critical failure when it lose control [5]. The influence of uncertain factors greatly increases the risk of system failure. Electronic systems (products) are composed of various components. The system structure and functions are increasingly complex and diversified, and they play a very important role in the fields of civil industry, national defense, and military [6]. Electronic components in electronic systems are affected by uncertain factors such as material properties, processing technology, and working environment during manufacturing, assembly, and use. There are often deviations between actual parameter values and nominal values. The cumulative effect of the deviation will improve the performance of the system. The response deviates from the target value and even causes failure [7]. If these uncertain factors are treated as deterministic information, this may lead to problems such as low consistency of batch products and extremely sensitive products to external interference factors, which cannot meet the actual requirements of engineering [8]. In the early design and analysis stage of electronic systems, noise factors and fluctuations in design parameters are ignored, which makes it difficult for the system to achieve stable performance and at the same time ensure reliability requirements. The complex electronic system model of the formula does not fully consider the computational complexity of the system model and the discrete characteristics of design variables, resulting in low efficiency of system optimization and difficulty in obtaining discrete optimal solutions [9]. How to consider the influence of various uncertain factors as comprehensively as possible in the optimization of electronic systems and take corresponding measures to improve the robustness of products is an urgent problem to be solved [10].

With the development of computer optimization technology, designers try to find the optimal solution from the perspective of mathematical optimization equations, which makes the optimization process of robust optimization design more scientific. Scholars take the first derivative of the objective function with respect to the design variables of interest as the optimization objective, in order to make the objective function value insensitive to changes in the design variables. This method is also known as the robust optimization design method based on first-order sensitivity, and its relatively direct and high computational efficiency has been applied by many scholars. Literature [11] takes the first derivative of the performance function as the optimization objective to optimize the structure of the electromagnetic device so that the device performance remains robust to changes in electric and magnetic fields. However, methods based on first-order sensitivity are often considered inaccurate. Literature [12] regards the second-order derivative of the performance function as the optimization objective and combines the worst-case analysis and Taguchi method to simplify the calculation in the optimization process. The goal of robust optimization design based on sensitivity is usually to improve the ability of the system to resist external noise interference, without considering the performance offset introduced by the system’s own structural dimensions and material properties, and the optimization results are usually not practical. Another approach that starts with a mathematical optimization equation perspective is robust optimization design based on random distributions. It represents all uncertain parameters contained in the objective function and constraints as random quantities in a certain distribution form, takes the mean and variance of the output performance of the system as the optimization objective, and searches for a solution that satisfies the constraints and has the smallest objective value [13]. The main disadvantage of this method is that after introducing random variables, a large number of target and constraint values need to be evaluated in the optimization process; in particular, for complex engineering problems with finite element solution or electronic circuit simulation, the optimization speed becomes very slow. In order to improve the optimization speed, the optimization design technology based on approximate model began to develop. Approximate models such as Kriging model, radial basis function, and multilayer neural network model are used to approximate the system output value, which greatly shortens the optimization time [14]. Reliability-based optimal design is also an effective method for optimal design of uncertain systems, and the obtained optimal solution can satisfy the product with low failure rate under this parameter combination [15]. According to the coupling strategy of reliability analysis method and optimization design method, reliability-based optimization design methods can be divided into two categories: double-loop method and single-loop method [16]. The single-cycle method is an improvement to the double-cycle method, so that the reliability analysis process is separated from the sub-cycle of the optimization process and is in the same cycle, thereby improving the optimization efficiency. Literature [17] proposed a single-cycle univariate method. By transforming the parameter distribution and its related objective functions and constraint functions into a standard normal distribution space, the original optimization problem was redefined by using the partial derivative of the constraint equation to make it a single-cycle optimization problem. Literature [18] used the sequential optimization and reliability evaluation method to change the order of the optimization process, verified the constraints in the probability-based optimization loop, and equivalently regarded the probability-based optimization problem as a deterministic optimization problem.

In this paper, BP neural network (GA-BP) learning graph algorithm model based on genetic algorithm is used to predict the non working reliability parameters of electronic components. After testing, the GA-BP prediction model has better accuracy than the linear autoregressive prediction model. At the same time, it also broadens the application scope of neural network, which can be used as a new method for nonoperating reliability life prediction of electronic components.

The main organizational structure of this paper is as follows: Section 1 presents an introduction, which analyzes the research status and background, summarizes the literature views, and leads to the research content of this paper. Section 2 describes the improvement of the nonworking performance analysis algorithm of subcomponents in this paper. The performance optimization and intellectualization of electronic components are very important. Section 3 provides the construction of the algorithm model and the performance verification. Section 4 summarizes the content proposed in this paper and looks forward to the follow-up research.

In this paper, using the improved GA, the performance optimization system of electronic components is constructed to improve the working performance of modern electronic components.

2. Optimal Design of Electronic Circuit System Based on Importance Analysis

2.1. Reliability Model

When establishing a reliability model, the electronic circuit system must meet the requirements that the failure modes of all components are independent of each other and the reliability obeys the exponential distribution. That is, the reliability

is expressed as the failure rate of the i-th component, (i = 1,2 … n. It also needs to meet the reliability of wires, related software, and components related to the power supply system in the electronic circuit system. Therefore, the equivalent failure rate Q and MTBF of the electronic circuit system can be calculated by the following formula:

(1)

According to the analysis in this section, the numerical calculation of the comprehensive importance of the power conversion main circuit is shown in Table 1.

1. Comprehensive importance of each component of the main power conversion circuit.

Component node	Comprehensive importance
C₁	0.23634
Q₁	0.327543
Q₂	0.174326
D₁	0.68781
D₂	0.215433
R_L1	0.000202
R_L2	0.187052
L	0.522776

It can be seen that the order of the cmprehensive importance of the components is D₁ > L > Q₁ > C1 > D₂ > R_L2 > Q₂ > R_L1 without considering the control circuit. The importance of diodes, inductors, and switches is the highest, and the importance of sampling resistors is relatively low.

Based on the evaluation results of comprehensive importance and complexity, the comprehensive importance is normalized, and the sum of the importance is obtained according to the principle of the AGREE distribution method, as shown in Table 2. It is the basis of reliability allocation, as shown in (2).

2. Normalization of the comprehensive importance of each component of the power conversion main circuit.

Component node	Normalization
C₁	0.34360
Q₁	0.69930
Q₂	0.25350
D₁	1.00000
D₂	0.31320
R_L1	0.00030
R_L2	0.27200
L	0.76010

(2)

Thus, the working failure rate of each component is as follows:

(3)

Then, the mean time to failureMTBFs^∗ of the system is as follows:

(4)

It can be seen that the distribution results meet the reliability index requirements of the power conversion main circuit.

Considering the cost optimization of electronic circuit system in reliability allocation, its essence is a nonlinear programming problem with constraints. The cost function used at this stage has good economic practicability. While the allocation meets the system failure rate, it can also come up with the lowest cost solution at the moment, as shown in the following formula:

(5)

In the formula, i is the component serial number, F_cost is the target cost, λ_S is the system failure rate, and λ_G is the expected system target failure rate. λ_imin, λ_imax are the minimum and maximum values of the failure rate of component i, which can be obtained according to the previous reliability distribution based on importance and historical data of similar products.

λ_Q is the work failure rate of switch tubes Q1, Q2Q1, Q2; F_costQ is the cost of switch tubes Q1, Q2Q1, Q2; λ_D is the working failure rate of the freewheeling diodes D1, D2D1, D2; F_costD is the cost of the diodes D₁ and D₂; λ_C is the working failure rate of the input filter capacitor C1C1; and F_costC is the cost of the capacitor C1.

According to the above data, using MATLAB for fitting, we obtain the function form of each component as follows:

(6)

Combined with equation (3), the cost function and constraints of the optimized power conversion main circuit system are constructed, such as (7); the minimum value of nonlinear programming is solved by MATLAB; and the result is shown in (8).

(7)

(8)

According to the optimized allocation of component failure rate and the working environment of the power conversion main circuit system, we can further select the model through the selection of parameters of various influencing factors by referring to the manual and historical data. Here, only the freewheeling diode D₁ is taken as an example for description.

The working failure rate and the basic failure rate of components are affected by various influencing factors. The working failure rate is the result of the comprehensive influence of other stresses on the basis of the basic failure rate. The calculation formula of the general failure model of the component stress prediction method is as follows:

(9)

In the formula, λ is the working failure rate, λ_b is the basic failure rate, E is the environmental coefficient, Q is the quality coefficient, R is the rated value coefficient, A is the application coefficient, K is the type coefficient, and C is the structural coefficient. These parameters can be selected with reference to the electronic product reliability prediction manual.

According to the manual, combined with the freewheeling diode failure model, the values of the relevant factors affecting the freewheeling diode D₁ are selected, and the coefficients of various influencing factors are selected from the table, as shown in the following formula:

(10)

In the formula,

refers to the voltage stress coefficient, and π_r refers to the product performance rating coefficient. It is to obtain the basic failure rate of the freewheeling diode D₁, as shown in the following formula:

(11)

It can be seen that the basic failure rate λ_b obtained based on the work failure rate of comprehensive importance analysis is 0.1144∗10⁻⁶/h, and the basic failure rate calculated based on the optimized work failure rate of cost-optimized allocation is 0.1146∗10⁻⁶/h.

At the operating temperature of 25^°C, the average current of the silicon diode is I_OP = 4.45A. According to the calculated basic failure rate of the freewheeling diode, the corresponding electrical stress S is determined by comparison, as shown in (12) and (13). Under the condition of a certain temperature, when the cost function is not considered, the electrical stress S is taken as 0.75, and the rated average current of the diode is calculated as I_M = 5.9333A. After considering the optimal distribution of the cost function, the electrical stress S is taken as 0.8, and the rated average current of the diode is calculated as

(12)

(13)

2.2. Sensitivity Analysis

Sensitivity analysis is a local analysis, including finite difference method, direct derivation method, and Green’s function method. It should be noted that this method is not suitable for scenarios of nonlinear models and when there are uncertain input factors of different orders of magnitude.

The electronic circuit system belongs to the time-dependent dynamic system, so the direct derivation method can be used, and the differential or differential-algebraic formulas can be used to describe it.

We assume that the component parameter x is incremented by Δx at the nominal value x₀, and the change of the parameter causes the circuit output characteristic function f to increment by Δf at the nominal value f₀f₀; then, the sensitivity of the component parameter x relative to the output characteristic of the circuit is expressed as follows:

(14)

Since (14) shows a differential formula, this expression can also be called the differential sensitivity of the component parameter x. The relative sensitivity of the component parameter x can be expressed as follows:

(15)

The global sensitivity, also known as the importance measure, focuses on the situation when all the input factors change together and each factor comprehensively evaluates the sensitivity in the whole working time and state range. It is a method to analyze the severity and importance of the influence of all uncertain factors and component parameter changes on the output of the system. It comprehensively considers the probability distribution of each input factor, has a wide expansion range, has a large variation range of controllable parameters, and selects the key design variables of the system through accurate evaluation. When using global sensitivity analysis, the model is not limited. At present, the Sobol variance decomposition method is the most widely used global sensitivity analysis method, and a brief introduction is given below.

Sobol’s method can satisfy the sensitivity analysis of most engineering models. The main idea is to decompose a given model f(x₁, x₂, …, x_k) into the sum of 2ⁿ terms of increasing sub-terms, and then the total variance of the model response and the partial variance of each item are calculated to calculate the sensitivity. We assume that the random variable x ∈ Rⁿ(0 ≤ x_i ≤ 1, i = 1,2, …, n) is an independent variable; then, the basic steps of the method and the subitems of the decomposition are shown in the following equation:

(16)

In the formula, f₀ is a constant. However, there are many calculation methods for each subitem of the Sobol method, and the decomposition method based on multiple integrals is commonly used; that is, the value of each item can be calculated by the integral function shown in the following formula:

(17)

In the formula, each subitem has an orthogonal relationship; that is,

(18)

According to (16), the multiple integrals are calculated; namely,

(19)

From this, the total variance of the output mathematical model f(x) and the partial variance of each order can be obtained as shown in the following equations:

(20)

(21)

This is equivalent to the following:

(22)

By squaring and then integrating (16), the expression of the total variance can be obtained:

(23)

Finally, the s-order sensitivity

is obtained as the ratio of the partial variance

of each order to the total variance D as follows:

(24)

2.3. Model Construction of Electronic Circuit System in Simulation Software

The dual-tube buck-boost topology is applied to the power conversion circuit, and the traditional control method of the power conversion circuit adopts the two-mode control method. That is, at any time, only one switch is guaranteed to be controlled. When U_in > U_o, the switch tube Q₁ is in the normal working state of the switch, and the switch tube Q₂ is normally off; the circuit can be equivalent to a buck converter, and it is defined to work in the buck mode at this time. When U_in ≤ U_o, the switch Q₁ is always on, and the switch Q₂ is in the normal working state of the switch. The circuit can be equivalent to a boost converter, and it is defined to work in the boost mode at this time.

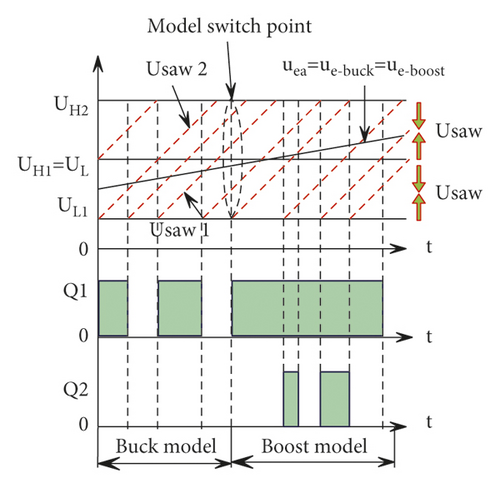
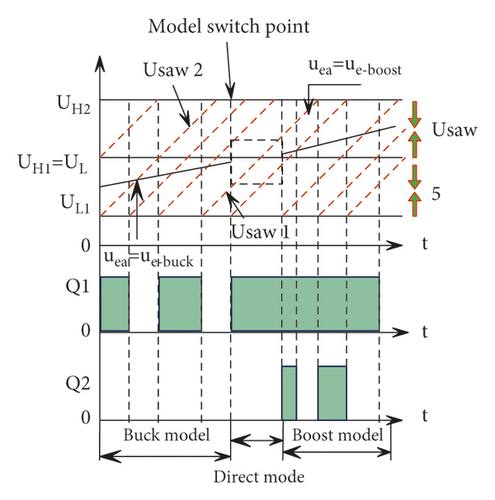
The typical control strategy of the two-mode control mode is single modulation signal-dual carrier two-mode control. As shown in Figure 1(a), in this method, the modulation signals of the switches Q₁ and Q₂ are the same; that is, u_ea = u_{e_buck} = u_{e_boost}u_ea = u_{e_buck} = u_{e_boost}. But the carrier signal u_saw2 of Q₂ is obtained by superimposing a DC component U_bias of the carrier signal u_sawl of Q₁Q₁; that is, u_saw2 = u_saw1 + U_bias. We set U_L1 and U_H1 to be the minimum and maximum values of u_saw1, respectively, and U_L2 and U_H2 to be the minimum and maximum values of u_saw2, respectively. In order to ensure effective switching between the two working modes, U_H1 − U_L1 = U_H2 − U_L2 = U_bias = U_saw, where U_saw is the peak-to-peak value of the carrier signal, and the main working waveform is shown in Figure 1(b).

Details are in the caption following the image — Open in figure viewer PowerPoint

The three-mode control method is based on the single-modulated signal-dual carrier two-mode control method, but additional judgment conditions are required. That is, the values of the input voltage U_in and the output voltage U_o are compared in real time. The specific control method is as follows:

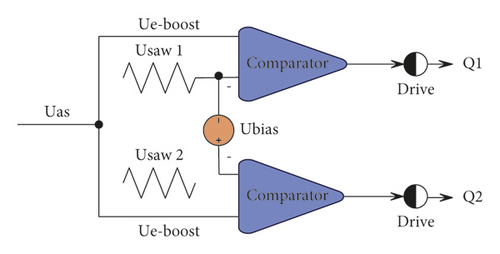
(1)
When it is detected that |U_in − U_o| > ΔU (a constant, which can be set according to the actual situation), that is, when the power conversion circuit works in the non-pass-through mode, the control strategy is shown in Figure 2(a). Among them, the modulation signals of the switches Q₁ and Q₂ are the same; that is, u_ea = u_{e_buck} = ue_{_boost}, u_ea = u_{e_buck} = ue_{_boost}. But the carrier signal u_saw2 of Q₂ is obtained by superimposing a DC component U_bias of the carrier signal u_sawl of Q₁Q₁; that is, u_saw2 = u_sawl + U_bias.
(2)
Once it is detected that |U_in − U_o| = ΔU, that is, when the power conversion circuit enters the direct mode, the control strategy is shown in Figure 2(b); the switch Q₁ is normally on and Q₂ is normally off. At this time, the modulation signal u_ea remains unchanged at the previous moment and does not intersect with the carrier signal u_saw, and the value of the current input voltage U_in needs to be recorded.
(3)
When |U_in − U_o| ≤ ΔU, that is, when the power conversion circuit works in the pass-through mode, the modulation signal u_ea is always kept unchanged and does not intersect with the carrier signal u_saw, and the input voltage U_in is detected in real time.

Once |U′in − U_in| > ΔU is detected, it indicates that the main circuit jumps out of the direct mode; that is, it enters the indirect mode. At this time, the modulation signal u_ea is re-interleaved with the carrier signal u_saw to generate a pulse width modulation signal, and the control strategy changes from Figure 2(b) to Figure 2(a).

The main working waveform of the three-mode control mode is shown in Figure 2(c), where U_saw is the peak-to-peak value of the carrier signal.

To build an electronic circuit system model based on Saber simulation software, it is necessary to design and set the parameters of the power conversion circuit devices, and it mainly includes the parameter design and setting of the following related components.

2.3.1. Power Inductor

The duty ratios D_Buck, D_Boost of the switches Q₁ and Q₂ can be expressed as follows:

(25)

We assume that the inductor current ripple is 20% of the average value of the inductor current; then, the inductance value of the power conversion circuit can be calculated when working in buck mode and boost mode, as follows:

(26)

In the formula, I_L(max), f_s represent the maximum average value of the inductor current and the switching frequency, respectively. In the simulation practice, I_L(max) = 6.95A,f_s = 300 kHz are taken and substituted into (26), and the maximum value of L can be obtained as 71.11uH. Considering the 20% inductance margin, L is actually taken as 90uH.

2.3.2. Input Filter Capacitor

We assume that the input capacitor voltage ripple is 1% of the input voltage; then, the input capacitor value when the main circuit works in buck mode and boost mode can be calculated as follows:

(27)

In the formula, I_0(max), P_o(max), f_s represent the maximum output current, maximum output power, and switching frequency, respectively. In this design, I_o(max) = 6.95A, P_o(max) = 500W, f_s = 300kHz are taken and substituted, and the maximum value of C_in can be obtained as 8.28uF. Considering the conventional 20% capacitance error value, C_in is actually taken as 11 uF (by 5 2.2 uF capacitors in parallel).

2.3.3. Output Filter Capacitor

We assume that the output capacitor voltage ripple is 1% of the output voltage; then, the output capacitor value when the main circuit works in buck mode and boost mode can be calculated as follows:

(28)

In the formula, I_L(max), f_s represent the maximum value of average the inductor current and the switching frequency, respectively. In this design, I_L(max) = 6.95A,f_s = 300kHz are taken and substituted, and the maximum value of C_o can be obtained as 33.1uF. Considering the conventional 20% capacitance error value, C_o is actually taken as 44 uF (20 2.2 uF capacitors are connected in parallel).

2.3.4. Power Switch Tube

The power switches are divided into buck mode switches Q₁ and boost mode switches Q₂.

(1) Switch Tube. Q₁. The voltage and current stress of Q₁ are the maximum value of the input voltage 120V and the maximum value of the input current 6.72A, respectively; then, the maximum value of the drain-source voltage V_DSSQ1 and the maximum value of the drain current I_DQ1 of Q₁ should satisfy the following:

(29)

(2) Switch Tube. Q₂. The voltage and current stress of Q₂ are, respectively, the maximum output voltage 100.8 V and the maximum output current 6.95 A; then, the maximum drain-source voltage V_DSSQ2 and the maximum drain current I_DQ2 of Q₂ should satisfy the following:

(30)

Since a certain type of aerospace electronic product is used, the switching frequency of the switch tube reaches 300 kHz, so that the switching loss accounts for most of the loss of the entire switch tube. Therefore, it is also necessary to choose a switching device with a shorter switching time.

2.3.5. Power Rectifier Tube

The power rectifier is divided into buck mode rectifier D₁ and boost mode rectifier D₂.

(1) Buck Mode Rectifier. D₁. The voltage and current stress of D₁ are the maximum value of input voltage 120 V and the maximum value of inductor current 6.72 A in buck mode, respectively; then, the maximum value of reverse voltage

and the maximum value of forward current

of D₁ should satisfy the following:

(31)

(2) Boost Mode Rectifier. D₂. The voltage and current stress of D₂ are the maximum output voltage 100.8 V and the maximum inductor current 6.95A in boost mode, respectively; then, the maximum reverse voltage

and the maximum forward current

of D₂ should satisfy the following:

(32)

2.3.6. Current Sampling Resistor

In order to simulate the circuit state in the step-down working mode, a square wave input power supply is connected to the MOS transistor Q₁ to keep Q₁ in the state of the switch. By adjusting the duty ratio of the driving square wave signal of Q₁, the output voltage of the power conversion main circuit can be changed. Since the MOS transistor Q₂ is normally off during the buck step-down stage, a power supply with the voltage parameter set to 0 is connected to the MOS transistor Q₂ to keep Q₂ normally off. Here, the MOS transistor Q₁ plays the role of chopping; that is, the DC input of the power conversion main circuit is chopped into a square wave, and the square wave can output a smooth DC voltage after passing through the LC (inductance, resistance) filter. The larger the duty cycle, the higher the average voltage of the square wave and the higher the output voltage.

In Figure 3, the role of the rectifier tube D₁ composed of diodes Pwld1 and Pwld2 is to play a freewheeling role for the inductor L₁. When Q₁ changes from on to off, since the inductor current cannot change abruptly, a very high voltage will be generated, so a new inductor current path needs to be formed during this period to form the role of a freewheeling diode. The rectifier diode D₂ composed of diodes Pwld3 and Pwld4 does not play a necessary role during this period, and the biggest function is to prevent the current output from flowing back.

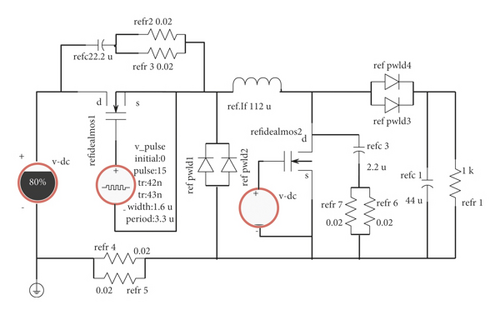
Figure 4 shows the Saber simulation of the power conversion main circuit of the dual-tube buck-boost topology in the boost mode. In the boost working mode, the MOS transistor Q₁ is connected to a constant voltage source V₃ with a voltage of 15 V and is kept normally open, while the MOS transistor Q₂ is connected to a square wave pulse input power supply to maintain the switching state. The charging time of the inductor L can be controlled by controlling the driving duty ratio of the MOS transistor Q₂ through the square wave pulse power supply. The longer the inductor charging time, the higher the output voltage. During simulation, the duty cycle changes when the frequency of the square wave supply changes, and the time it takes for the output voltage to reach steady state is reflected. The lower the frequency, the shorter the steady-state time, and the larger and more stable the output voltage.

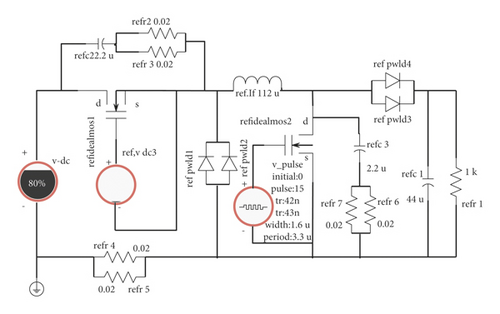
The rectifier diode D₂ of the power conversion main circuit composed of diodes Pwld3 and Pwld4 prevents the output current from flowing back when the MOS transistor Q₂ turns on the inductive energy storage device, and the output capacitor supplies energy to the load during this period. In the boost topology process, R6, R7, and capacitor C3 play the same role as R2, R3, and C2 to buffer and absorb voltage spikes to protect the MOS tube.

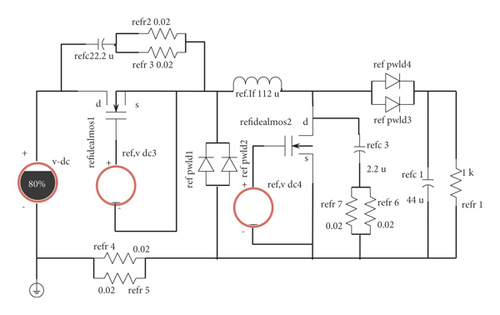
Figure 5 shows the Saber simulation under the straight-through mode of the dual-tube buck-boost power conversion main circuit. Under this mode control, the MOS transistor Q₁ is connected to a 15 V constant voltage power supply to keep Q₁ in the normally on state. The MOS tube Q₂ is connected to a power supply whose voltage parameter is set to 0, which keeps Q₂ normally off, so that the power conversion main circuit works in the direct mode. At this time, the absolute value of the difference between the input and output voltages remains constant.

3. Performance Optimization System of Electronic Components Based on Improved GA

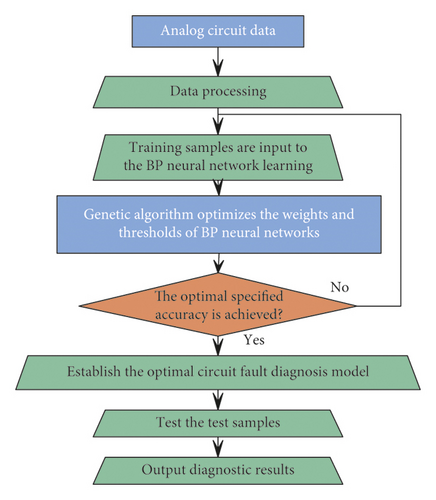
In this paper, the traditional GA is improved and applied to the performance optimization system of electronic components, and the results shown in Figure 6 are obtained.

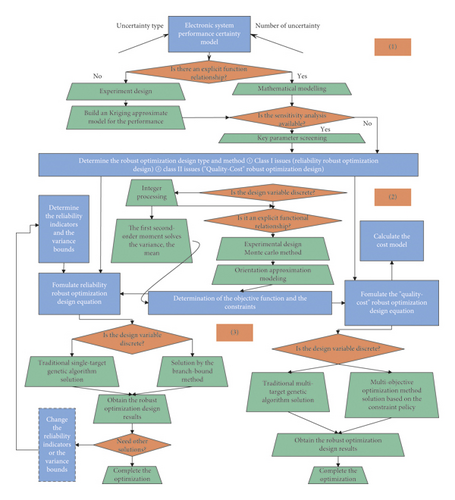
In the process of solving the robust optimization design of electronic systems, special attention should be paid to whether the design variables are in a discrete form and whether there is an explicit functional relationship between the performance response and the design variables. Figure 7 shows the complete robust optimization design implementation scheme.

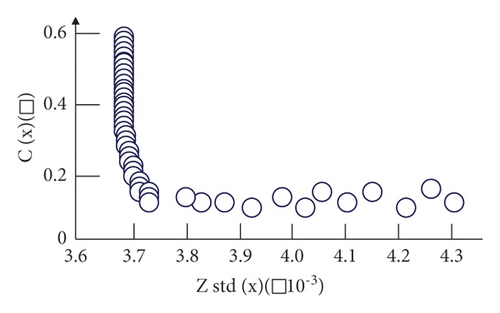
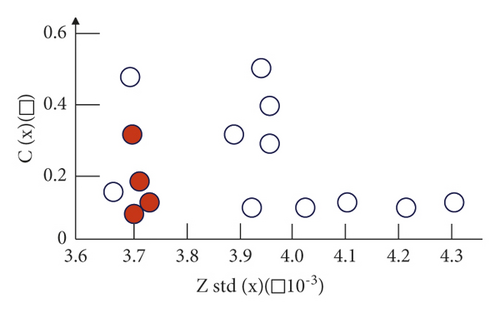
In order to further verify the effectiveness of the method in this paper, an improved multi-objective genetic algorithm is used for optimization, and the Pareto optimal solution set obtained by optimization is shown in Figure 8.

The effect evaluation of the electronic component performance optimization system based on the improved GA is carried out, and the evaluation results in Table 3 are obtained.

3. Evaluation of the effect of the electronic component performance optimization system based on the improved GA.

Num	Performance boost	Num	Performance boost	Num	Performance boost
1	80.803	15	85.684	29	84.846
2	81.874	16	83.026	30	83.425
3	80.881	17	83.403	31	80.943
4	86.546	18	81.920	32	80.130
5	84.401	19	82.094	33	83.319
6	86.605	20	85.243	34	84.585
7	83.048	21	85.309	35	83.571
8	81.539	22	84.287	36	80.419
9	81.764	23	82.921	37	86.963
10	81.506	24	86.663	38	81.309
11	85.016	25	86.093	39	85.705
12	83.398	26	84.843	40	80.073
13	80.277	27	84.905	41	85.088
14	86.180	28	82.828	42	80.311

It can be seen from the above research that the performance optimization system of electronic components based on the improved GA proposed in this paper has a certain effect on improving the performance of electronic components.

4. Conclusion

Complex large-scale equipment systems and electronic component production processes require a large number of multiparameter comprehensive measurements. Therefore, the research and application of distributed network testing technology have become a major trend. In the production and testing of electronic components, it involves the detection of a large number of process parameters and performance parameters. There are nearly 1,000 test parameters for various components used for testing. How to transmit and process such huge test data in real time puts forward extremely high requirements on the concurrency, real time performance, and data processing capability of the test platform. This paper uses the improved GA to construct the performance optimization system of electronic components to improve the performance of modern electronic components. The experimental research shows that the performance optimization system of electronic components based on the improved GA proposed in this paper has a certain effect on improving the performance of electronic components.

This paper studies the performance optimization of electronic components but does not consider the influence of environmental factors, such as temperature and humidity, on the performance of electronic components. Subsequent research can add these interference factors in practice to study the effect of the model.

Conflicts of Interest

The authors declare that there are no conflicts of interest.

Open Research

Data Availability

The labeled dataset used to support the findings of this study is available from the corresponding author upon request.

References

1 Naderi R., Babaei E., Sabahi M., and Daghigh A., Optimization of a new extended cascaded multilevel inverter topology to reduce DC voltage sources and power electronic components, International Journal of Industrial Electronics Control and Optimization. (2021) 4, no. 4, 465–474, https://doi.org/10.22111/IECO.2021.36599.1322.
10.22111/IECO.2021.36599.1322
Google Scholar
2 Barrubeeah M., Rady M., Attar A., Albatati F., and Abuhabaya A., Design, modeling and parametric optimization of thermoelectric cooling systems for high power density electronic devices, International Journal of Low Carbon Technologies. (2021) 16, no. 3, 1060–1076, https://doi.org/10.1093/ijlct/ctab032.
10.1093/ijlct/ctab032
CAS Web of Science® Google Scholar
3 Tran M. K., Akinsanya M., Panchal S., Fraser R., and Fowler M., Design of a hybrid electric vehicle powertrain for performance optimization considering various powertrain components and configurations, Vehicles. (2020) 3, no. 1, 20–32, https://doi.org/10.3390/vehicles3010002.
10.3390/vehicles3010002
Google Scholar
4 Jeong J. and Tae H., Optimization algorithm of gantry route problem for odd-type surface mount device, Journal of Society of Korea Industrial and Systems Engineering. (2020) 43, no. 4, 67–75, https://doi.org/10.11627/jkise.2020.43.4.067.
10.11627/jkise.2020.43.4.067
Google Scholar
5 Long X. J., Shang J. T., and Zhang L., Design optimization of pillar bump structure for minimizing the stress in brittle low K dielectric material layer, Acta Metallurgica Sinica. (2020) 33, no. 4, 583–594, https://doi.org/10.1007/s40195-019-00948-6.
10.1007/s40195-019-00948-6
CAS Web of Science® Google Scholar
6 Ab Majid N. K. and Ismail F. S., Electronics system thermal management optimization using finite element and Nelder-Mead method, TELKOMNIKA (Telecommunication Computing Electronics and Control). (2019) 17, no. 5, 2268–2275, https://doi.org/10.12928/telkomnika.v17i5.12796.
10.12928/telkomnika.v17i5.12796
Google Scholar
7 Chen H., Moser M., Wang S., Jellett C., Thorley K., Harrison G. T., Jiao X., Xiao M., Purushothaman B., Alsufyani M., Bristow H., De Wolf S., Gasparini N., Wadsworth A., McNeill C. R., Sirringhaus H., Fabiano S., and McCulloch I., Acene ring size optimization in fused lactam polymers enabling high n-type organic thermoelectric performance, Journal of the American Chemical Society. (2020) 143, no. 1, 260–268, https://doi.org/10.1021/jacs.0c10365.
10.1021/jacs.0c10365
PubMed Web of Science® Google Scholar
8 Mohamed A. A. S., Zhu L., Meintz A., and Wood E., Planning optimization for inductively charged on-demand automated electric shuttles project at Greenville, South Carolina, IEEE Transactions on Industry Applications. (2020) 56, no. 2, 1010–1020, https://doi.org/10.1109/tia.2019.2958566.
10.1109/TIA.2019.2958566
Web of Science® Google Scholar
9 Ponniran A. and Hashim H., Biomedical image denoising based on hybrid optimization algorithm and sequential filters, Journal of biomedical physics & engineering. (2020) 10, no. 1, 83–92, https://doi.org/10.31661/jbpe.v0i0.1016.
10.31661/jbpe.v0i0.1016
PubMed Google Scholar
10 Ren Z., Alqahtani A., Bagherzadeh N., and Lee J., Thermal TSV optimization and hierarchical floorplanning for 3-D integrated circuits, IEEE Transactions on Components, Packaging, and Manufacturing Technology. (2020) 10, no. 4, 599–610, https://doi.org/10.1109/tcpmt.2020.2970382.
10.1109/TCPMT.2020.2970382
CAS Web of Science® Google Scholar
11 Monteiro R. P., Lima G. A., Oliveira J. P. G., Cunha D. S. C., and Bastos-Filho C. J. A., Improving adaptive filters for active noise control using particle swarm optimization, International Journal of Swarm Intelligence Research. (2018) 9, no. 4, 47–64, https://doi.org/10.4018/ijsir.2018100103, 2-s2.0-85053056777.
10.4018/IJSIR.2018100103
Google Scholar
12 Torun H. M., Swaminathan M., Kavungal Davis A., and Bellaredj M. L. F., A global Bayesian optimization algorithm and its application to integrated system design, IEEE Transactions on Very Large Scale Integration Systems. (2018) 26, no. 4, 792–802, https://doi.org/10.1109/tvlsi.2017.2784783, 2-s2.0-85041168845.
10.1109/TVLSI.2017.2784783
Web of Science® Google Scholar
13 Hui J. H., Gao M., Li M., Li M. R., Zou H. H., and Zhou G., Multi-objectives nonlinear structure optimization for actuator in trajectory correction fuze subject to high impact loadings, Defence Technology. (2021) 17, no. 4, 1338–1351, https://doi.org/10.1016/j.dt.2020.07.004.
10.1016/j.dt.2020.07.004
Web of Science® Google Scholar
14 Gao K., Han F., Dong P., Xiong N., and Du R., Connected vehicle as a mobile sensor for real time queue length at signalized intersections, Sensors. (2019) 19, no. 9, https://doi.org/10.3390/s19092059, 2-s2.0-85065656327.
10.3390/s19092059
Web of Science® Google Scholar
15 Guo W., Xiong N., Chao H. C., Hussain S., and Chen G., Design and analysis of self-adapted task scheduling strategies in wireless sensor networks, Sensors. (2011) 11, no. 7, 6533–6554, https://doi.org/10.3390/s110706533, 2-s2.0-79960787680.
10.3390/s110706533
Web of Science® Google Scholar
16 Wang X., Li Q., Xiong N., and Pan Y., Ant colony optimization-based location-aware routing for wireless sensor networks, Proceedings of the International conference on wireless algorithms, systems, and applications, October 2008, Dallas, TX, USA.
Google Scholar
17 Jiang Y., Tong G., Yin H., and Xiong N., A pedestrian detection method based on genetic algorithm for optimize XGBoost training parameters, IEEE Access. (2019) 7, 118310, https://doi.org/10.1109/access.2019.2936454.
10.1109/ACCESS.2019.2936454
Web of Science® Google Scholar
18 Wan R., Xiong N., and Loc N. T., An energy-efficient sleep scheduling mechanism with similarity measure for wireless sensor networks, Human-centric Computing and Information Sciences. (2018) 8, no. 1, 18–22, https://doi.org/10.1186/s13673-018-0141-x, 2-s2.0-85048859947.
10.1186/s13673-018-0141-x
Web of Science® Google Scholar

All articles

Improved GA and Its Application in Performance Optimization of Electronic Components

Abstract

1. Introduction