This paper introduces a time-varying wastage maximum flow problem (TWMFP) and proposes a time-flow neural network (TFNN) for solving the TWMFPs. The time-varying wastage maximum flow problem is concerned with finding the maximum flow in a network with time-varying arc capacities and additive flow losses on the arcs. This problem has multiple applications in transportation, communication, and financial network. For example, solving the maximum traffic flow of the transportation network and the maximum profit of the financial network. Unlike traditional neural network algorithms, the proposed TFNN does not require any training by means of its time-flow mechanism. The time-flow mechanism is realized by each active neuron sending pulses to its successor neurons. In order to maximize the network flow, the proposed TFNN can be divided into two parts: path-pulse neural networks (PPNNs) and subnet-flow neural networks (SFNN). PPNN is to generate two subnet sets (viz. with wastage arcs and without), and SFNN is to find the maximum flow value of each subnet. The subnet computing strategy of the proposed algorithm greatly improves the solution accuracy of TWMFPs. Theoretical analysis and experiments have proved the effectiveness of TFNN. The experiment results of the transportation network (viz. New York Road) show that the proposed TFNN has better performance (viz. error rate and computational time) compared to classical algorithms.

1. Introduction

The maximum flow problem (MFP) is a classical network optimization problem [1, 2], and it is also a general problem in vehicular networks [3], network optimization [4], social network [5, 6], and other fields. Ford and Fulkerson first solved the maximum flow problem using the labeling algorithm (viz. Ford-Fulkerson (FF) algorithm) [7]. Then, many improved labeling algorithms have been proposed for solving the maximum flow problems [8], such as Edmonds–Karp algorithm [9], and the Cai–Sha algorithm [10]. With the increasing complexity of networks, some intelligent algorithms have been used for solving the MFP, such as the genetic algorithm (GA) [11].

The time-varying wastage maximum flow problem is the maximum flow problem with time-varying arc capacities and additive flow losses on the arcs, which can be applied to intelligent transportation [12, 13], communication network [14], financial analysis [15, 16], and other fields. In financial networks, Eboli [17] has described the balance-sheet as a loss flow on the arc. The time-varying maximum flow problem (TMFP) [18, 19] and wastage maximum flow problem (WMFP) [20] have been investigated extensively. Li and Buzdalov et al. [21, 22] proposed their algorithms for solving the TMFPs. Cai [23] and Song [24] have researched different WMFPs. These existing algorithms were improved labeling algorithms [25]. While to the best of our knowledge, a question with regard to find the maximum flow value of time-varying wastage maximum flow problem remains open.

In this paper, we propose a novel neural network framework for solving the time-varying wastage maximum flow problem (TWMFP). The TWMFP is the maximum flow problem with time-varying arc capacities and additive flow losses on the arcs. The advantages of the proposed time-flow neural network (TFNN) are summarized as follows: first, different with general neural networks, the proposed TFNN does not require any training based on its time-flow mechanism. Second, compared with classical labeling algorithms, the proposed TFNN greatly improves the calculation speed based on its parallel computing feature. Third, unlike existing maximum flow algorithms, the unique group calculation idea of the proposed TFNN improves the accuracy for solving TWMFPs. In addition, the proposed TFNN can find an accurate solution to the general network maximum flow problems, such as MFP and TMFP.

The remainder of this paper is organized as follows: in Section 2, some basic concepts of TWMFP are introduced. In Section 3, the TFNN algorithm is developed and an example of a TWMFP is given. In Section 4, the experimental results are reported. And, Section 5 gives a conclusion to this paper.

2. Mathematical Formulation

The goal of the time-varying wastage maximum flow problem is to find the maximum flow from the departure node to the destination node within a predetermined period, where arc capacities change over time and flow on the arc may be consumed. Such problems introduced in this paper can be applied to fields such as intelligent transportation and financial analysis. For example, in a transportation network, road congestion during peak periods represents time-varying arc capacities and car accident emergency represents consumption/wastage on the arc.

Definition 1. [Wastage Network (WN)]. Let V be a set of network nodes, A = {(v_i, v_j)/v_i, v_j ∈ V} be a set of network arcs, C = {c_ij/(v_i, v_j) ∈ A} be a set of arc capacities, and W = {w_ij/(v_i, v_j) ∈ A} be a set of arc wastage, then the network G = (V, A, C, W) is defined as a wastage network.

Definition 2. [Time-Varying Wastage Network (TWN)]. Assume there is a wastage network G = (V, A, C, W), given a piecewise function C(ξ) = {C_ij(ξ_i)/(v_i, v_j) ∈ A, ξ_i ∈ T_ij} stands for a set of arc capacities, where ξ = (ξ_j/ξ_j = ξ_i + b_ij, (v_i, v_j) ∈ A), ξ_i denotes the depart time of node v_i, b_ij represents the length of arc (v_i, v_j), means a set of time windows, and represent the earliest and latest depart times, z and Z denotes the index and number of time windows. Then, network G = (V, A, C(ξ), W) is a time-varying wastage network.

The arc lengths of time-varying wastage networks are set as a predetermined number δt. The arrival time of the destination node is calculated as follows:

(1)

Definition 3. [Feasible Flow]. Given a TWN G = (V, A, C(ξ), W), then the feasible flow F_ij(ξ) of the arc (v_i, v_j) can be expressed as follows:

(2)

where

(3)

Considering the particularity of the departure node v_s, then the feasible flow F_sy(ξ) can be calculated by the following equation:

(4)

Definition 4. [Model of the TWMFP]. Given a time limitation T₀. Follows from (1)–(4), the model of the TWMFP is formulated by the following equation:

(5)

where

(6)

(7)

3. Time-Flow Neural Network Algorithm Description

Generally, the labeling algorithms are used to find the solution of maximum flow problems. A disadvantage of these approaches is that they usually obtain large error rate solutions due to the time-varying and wastage in TWMFPs. This paper provides a better way to solve the time-varying wastage maximum flow problem.

In this section, the proposed TFNN algorithm will be described at first. And, then the construction of path-pulse neural networks (PPNNs) and subnet-flow neural networks (SFNNs) are depicted. To show the structure and algorithm of TFNN, the description of symbols are shown in Table 1.

1. Description of the symbols used in TFNN.

Symbols	Explanation
	A pulse from neuron n to neuron i at time t1
w_xi	Wastage of arc (v_x, v_i)
U_ni	Wastage list of the path from neuron s to i, where n on the path
	The z th time window of arc (v_i, v_j)
	Capacity from neuron i to neuron j at time window
B_i	The relation neuron of neuron i
f_zi	The flow of arc (v_z, v_i)
G_o	The set of subnets without wastage arcs
G_w	The set of subnets with wastage arcs
U_ix	Pulse information of arc (v_i, v_x)

3.1. Description of TFNN

The underlying idea of using TFNN to solve TWMFP is that a neuron sends “preflows” (viz. pulses) to its successor neurons when the current neuron received pulses. With this new viewpoint, the proposed TFNN can reach a better solution of TWMFPs. There are two main parts in the design of TFNN, the first part is to find two subnet sets (viz. with wastage arcs and without) by path-pulse neural networks (PPNN), while the second part is to calculate the maximum flow of the subnets based on subnet-flow neural networks (SFNNs). The detailed steps of TFNN are shown in Algorithm 1.

Algorithm 1: Time-flow Neural Network (TFNN).

Input: Δt, T₀, G.
Output: f^∗./ ^∗ The maximum flow. ^∗/
(1)
Set t = 0, f^∗ = 0, G_o = ∅, G_w = ∅.
(2)
Do
(3)
Generate subnet sets G_o and G_w from G by PPNN.
(4)
Set t = t + Δt.
(5)
Until t > T₀./ ^∗ End step2 ^∗/
(6)
Update f^∗ of all subnets in G_o by SFNN.
(7)
Update f^∗ of all subnets in G_w by SFNN.
(8)
Report the maximum flow f^∗.

3.2. Description of PPNN

PPNN is used to generate two subnet sets (viz. with and without wastage arcs) through the following parts: first, initialize neurons by Step 1. Second, generate pulses from the departure neuron s at every time by Step 3. Third, update all nodes but s at every time by Step 4. Fourth, update subnet sets at every time by Steps 5–10. Finally, output subnet sets. The detailed steps of PPNN are shown in Algorithm 2.

Algorithm 2: Path-pulse Neural Networks (PPNN).

Input: Δt, G, t, G_o, G_w.
Output: G_o, G_w./ ^∗ Subnet sets of G. ^∗/
(1)
Set
(2)
Do
(3)
Update , and of s using (13)–(16).
(4)
Update all nodes i ∈ V/{s} using (8)–(16).
(5)
If
(6)
Set G_o = G_o ∪ R(P_nd).
(7)
End If./ ^∗ End step5 ^∗/
(8)
If
(9)
Set G_w = G_w ∪ R(P_nd).
(10)
End If./ ^∗ End step8 ^∗/
(11)
Set t1 = t1 + Δt
(12)
Until t1 > t./ ^∗ End step2 ^∗/
(13)
Report two subnet sets G_o and G_w.

All neurons in the PPNN will no longer generate pulses when the time limitation is reached. A general structure of a neuron in PPNN is shown in Figure 1.

Details are in the caption following the image — Open in figure viewer PowerPoint

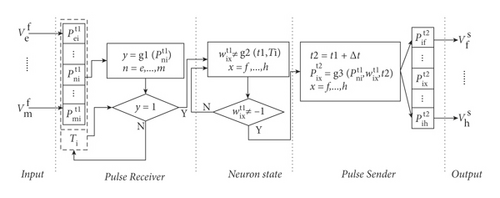
3.2.1. Input

The input part is used to receive pulses from its predecessor neurons.

3.2.2. Pulse Receiver

The pulse receiver part is used to filter the received pulses and consists of

, y and time window T_i. Time window T_i is initialized by Algorithm 2 (PPNN).

is explained as follows:

(8)

where

(9)

y is explained as follows:

(10)

where

means at least one pulse has reached at t1.

If the current neuron is the destination neuron d, the neuron no longer generates pulses and output the path

and the wastage

. Their expressions are shown as follows:

(11)

(12)

3.2.3. Neuron State

The neuron state part is used to select the time window and consists of

, x = f, …, h.

is explained in the following equation:

(13)

3.2.4. Pulse Sender

The pulse sender part is used to calculate the parameter and generates pulses and consists of t2 and

, x = f, …, h. The expression of them are shown as follows:

(14)

(15)

where

(16)

3.2.5. Output

The output part is used to send the pulse to its successor neurons.

3.3. Description of SFNN

SFNN is used to find the maximum flow of subnets through the following parts: first, initialize neurons by Step 1. Second, update all nodes, , and f^∗ by Steps 2–7. Third, update D by Steps 8–10. Final, output the maximum flow. The detailed steps of SFNN are shown in Algorithm 3.

Algorithm 3: Subnet-flow Neural Networks (SFNNs).

Input: f^∗, G^′.
Output: f^∗.
(1)
Set , B_s = s, C = C^′.
(2)
Do
(3)
Set D = 0, p = ∅, f(p) = 0.
(4)
Update all nodes using (17)–(25).
(5)
Set p = Q(P_nd), w(p) = ∑_{(i, j)∈p}w_ij, f(p) = F(P_nd)∗(1 − w(p))
(6)
Set where (i, j) ∈ p.
(7)
Set f^∗ = f^∗ + f(p).
(8)
If M(i) of all nodes are not equal to 0.
(9)
Set D = 1.
(10)
End If./ ^∗ End step8 ^∗/
(11)
Until D = = 1./ ^∗ End step2 ^∗/
(12)
Report f^∗.

Each neuron in SFNN will reserve the first pulse received in an iteration. A general structure of a neuron in subnet-flow neural networks is shown in Figure 2.

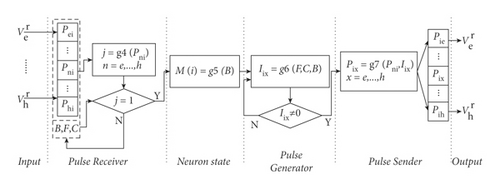
3.3.1. Input

The input part is used to receive pulses coming from its relational neurons.

3.3.2. Pulse Receiver

The pulse receiver part is used to filter the received pulses and consists of P_ni, j, B, F, and C. The value of B, F, and C are calculated by the SFNN Algorithm. P_ni is shown as follows:

(17)

where

(18)

j is explained as follows:

(19)

The value of P_ni not equals ∅ means at least one pulse has reached at current neuron i at t.

If current neuron i is the destination neuron d, the neuron no longer generates pulses and output the path Q(P_nd) and the path flow F(P_nd). Their expressions are shown as follows:

(20)

(21)

3.3.3. Neuron State

The neuron state part is used to record whether the current neuron has received a pulse and consists of M(i). It is explained as follows:

(22)

where x ∈ V_R(i). The value of M(i) is initialized as 0.

3.3.4. Pulse Generator

The pulse generator part is used to calculate the parameter for sending pulses. This part consists of I_ix, x = e, …, h. I_ix is shown as follows:

(23)

3.3.5. Pulse Sender

The pulse sender part is used to generate pulses and consists of P_ix, x = e, …, h. P_ix is explained as follows:

(24)

where

(25)

3.3.6. Output

The output part is used to send pulses to its relational neurons.

3.4. An Example

The detailed steps of TFNN for solving the TWMFPs are illustrated by an example. The topology and description of a time-varying wastage network are described as shown in Figure 3 and Table 2. The time limitation is T₀ = 3.

2. Description of a time-varying wastage network.

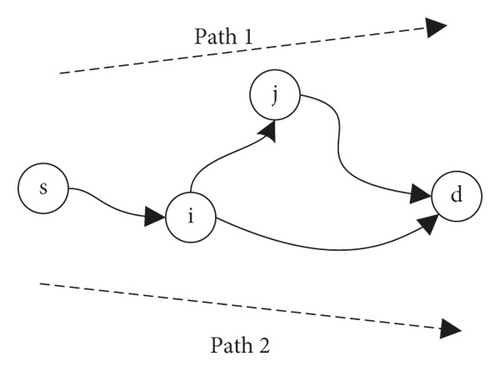
Node	Arc	Time window	Capacity	Wastage
s	s⟶i	[0,1)	10	0
s	s⟶i	[1,3]	5	0

i	i⟶j	[0,3]	10	0
i	i⟶d	[0,3]	10	0.5

j	j⟶d	[0,3]	10	0

The proposed TFNN can solve this problem by the following steps:

First, find two subnet sets (viz. with wastage arcs G_w and without G_o).
- G_o = {Path1, t = 0}, where V_o = {s, i, j, d}, W_o = {0,0,0}, C_o = {10,10,10}.
- G_w = {Path2, t = 0, and 1}, where V_w = {s, i, d}, W_w = {0,0.5}, C_w = {10,10} at t = 0, C_w = {5,10} at t = 1.
Second, calculate the maximum flow of the subnet.
- The flow of G_o is equal to f1 = 10 − 10∗0 = 10. Then, the capacity of arc (s, i) with depart time t = 0 is adjusted to 0. The flow of Path2 with depart time t = 0 is equal to 0. Therefore, the flow of G_w is equal to f2 = 5 − 5∗0.5 = 2.5.
- To sum up, the maximum flow is f^∗ = f1 + f2 = 12.5.

3.5. Time Complexity

Theorem 1. [Time Complexity of TFNN]. Given a TWN G, n represents the nodes number in G, m denotes the arcs number in G, T₀ represents the time limitation, Δt means a unit time. Then, TFNN solves the time-varying wastage maximum flow problem in time, where int denotes the top of the integral function.

Proof. The overall PPNN consists of two parts. The time complexity of the first part (viz. Steps 1–5) depends on the PPNN algorithm and the second part (viz. Steps 6–8) depends on the SFNN algorithm.

For the PPNN algorithm, there is one loop and the worst time complexity is equal to o(5 + T₀/Δt(3 + 12n + 2)) = o(5T₀/Δt(12n + 5)). Based on the time complexity of PPNN, the time complexity of the first part of TFNN is equal to o(4 + T₀/Δt(5 + T₀/Δt(12n + 5) + 1)).

For the SFNN algorithm, there is one loop and the worst time complexity is equal to o(7 + T₀/Δt(3 + 9n + 2 + m + 2)) = o(7 + T₀/Δt(9n + m + 7)). According to the number of subnetworks is less then n, the time complexity of the second part of TFNN is equal to o(2n(7 + T₀/Δt(9n + m + 7))).

To sum up, the time complexity of TFNN is equal to o(4 + T₀/Δt(5 + T₀/Δt(12n + 5) + 1) + 2n(7 + T₀/Δt(9n + m + 7))) = o(4 + 14n + (18n² + 2mn + 14n))T₀/Δt + (12n + 5)T₀/Δt². Because there are at least two nodes (viz. n ≥ 2) and one arc (viz. m ≥ 1) in a network, we have. o(4 + 14n + (18n² + 2mn + 14n)(T₀/Δt) + (12n + 5)(T₀/Δt²)) ≤ o((18n² + 40n + 2mn + 9)(T₀/Δt²)) ≤ o((43mn²)(T₀/Δt²)).

According to Δt ≥ 1, the time complexity of TFNN can be simplified as follows: , here k denotes a constant.

Theorem 1 is proven.

4. Experiments

A large transportation network (viz. New York Road) is used to test the performance of the proposed TFNN algorithm. Time-varying and wastage components are added to some arcs in the network. The Ford–Fulkerson (FF) [26], genetic algorithm (GA) [22], Edmonds–Karp (EK) [10], and the Cai–Sha (CS) algorithm [11] will be used for experimental comparison with the proposed TFNN. There are 100 generations and 50 populations preset in the genetic algorithm [27].

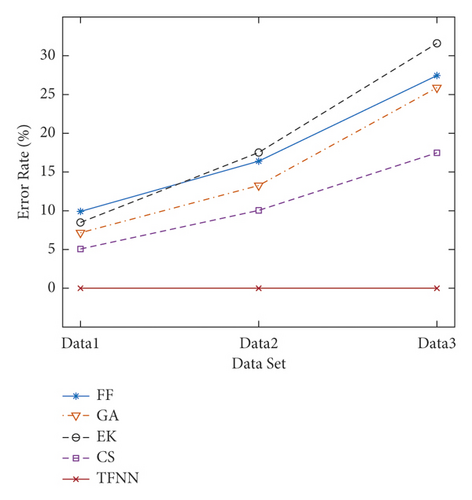
The error rate and computational time of these algorithms are compared as follows: the percentage deviation of the mean value (PDM) and the percentage deviation of the best value (PDB) are used as performance indexes (PI) to illustrate the error rate (ER) of different algorithms. PDM and PDB, respectively, are the mean and best value of ER for a set of networks. ER can be calculated as ER = (F_m − F_a)/F_m ^∗100%, where F_m is the maximum flow among these algorithms and F_a is the flow value of each algorithm.We used 1000-node, 3000-node, and 5000-node networks for experiments and analyzed the error rate and computational time of the results. Table 3 reports the experimental results of TFNN, FF, GA, EK, and CS algorithms. Compared with other algorithms, the proposed TFNN always can find the best solutions in all cases. The error rate of other algorithms increases with the increase of nodes number. The PDM of other algorithms on Data3 all exceed 17.48% and the PDM of FF and EK are 27.45% and 31.61%, while TFNN is 0.00%. This is because both of FF and EK fail to take into time-varying components. GA adopts a random search mechanism. CS algorithm always finds the shortest path first, it reduces the solution accuracy. These results show that the proposed TFNN has better performance than existing algorithms (including FF, GA, EK, and CS). The tendency of the error rate of FF, GA, EK, CS, and the proposed TFNN algorithms are shown in Figure 4(a).

3. Comparative results of the TFNN and other algorithms.

Dataset	Nodes	Arcs	PI	FF	GA	EK	CS	TFNN
Data1	1000	2067	PDM (%)	9.911	7.159	8.491	5.067	0.00
			PDB (%)	7.261	5.590	7.013	3.960	0.00
			Time (ms)	49.13	1776	52.03	57.41	60.25

Data2	3000	6106	PDM (%)	16.40	13.26	17.52	10.05	0.00
			PDB (%)	13.51	10.94	13.19	8.108	0.00
			Time (ms)	304.85	3574	317.49	436.53	240.93

Data3	5000	10095	PDM (%)	27.45	25.88	31.61	17.48	0.00
			PDB (%)	23.08	23.57	28.19	15.38	0.00
			Time (ms)	955.64	6346	915.96	1213.96	582.21

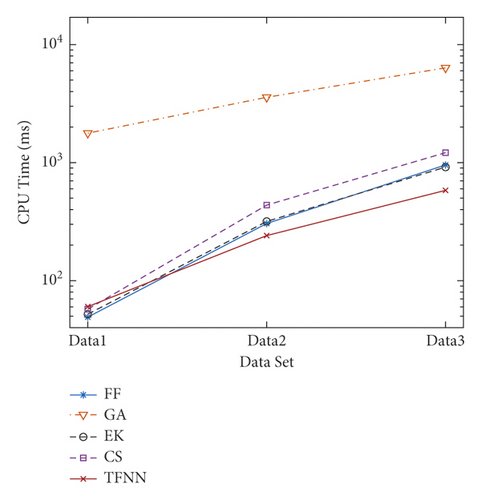
The calculation times of TFNN, FF, GA, EK, and CS algorithms are shown in Table 3. The computational time of the proposed TFNN is relatively short than other algorithms. First, GA requires more time to find a solution due to its pure random search mechanism. Second, as the number of nodes increases, the calculation time of TFNN is gradually better than the other three algorithms. The reason is that the complexity of the CS algorithm largely depends on the number of nodes, while the FF and EK algorithm will take more time to iterate as the number of nodes increases. The tendency of computational time of FF, GA, EK, CS, and the proposed TFNN algorithms are described in Figure 4(b).

5. Conclusions

In this research, we introduce the time-varying wastage maximum flow problem and propose the Time-flow Neural Network to solve the TWMFPs. The proposed TFNN does not require any training by means of a time-flow mechanism. Experimental results show that the proposed TFNN has better performance than traditional algorithms (including FF, EK, and CS) and intelligent algorithm (such as GA). The main advantages of TFNN are shown as follows.

First, compared with existing maximum flow algorithms, TFNN has higher accuracy when solving the TWMFPs. The proposed TFNN can obtain a larger flow due to its group calculation idea. The experiment results show that the error rate of TFNN is lower (17.48% lower than CS and 31.61% lower than EK) on a large network (5000 nodes and 10095 arcs).

Second, TFNN has a higher calculation speed based on its parallel computing feature. The experiment results show that the computational time of TFNN is 52% shorter than CS on a large network (5000 nodes and 10095 arcs).

In future research, more constraints can be considered when solving the time-varying wastage maximum flow problems. And, the neural network framework should be improved for the maximum flow problems under uncertain environments.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported in part by the National Science Foundation of China (Grant no. 61673295).

Open Research

Data Availability

The simulation experiment data used to support the findings of this study are available from the corresponding author upon request.

References

1 Zhao S., Sun X., Chen J., Duan Z., Yanping Y. Z., and Yiwen Y. Z., Relational granulation method based on Quotient Space Theory for maximum flow problem, Information Sciences. (2020) 507, 472–484, https://doi.org/10.1016/j.ins.2018.12.009.
10.1016/j.ins.2018.12.009
Web of Science® Google Scholar
2 Khanal D. P., Pyakurel U., and Dhamala T. N., Maximum multicommodity flow with intermediate storage, Mathematical Problems in Engineering. (2021) 2021, 11, 5063207, https://doi.org/10.1155/2021/5063207.
10.1155/2021/5063207
Web of Science® Google Scholar
3 Goodchild K. F. and Goodchild A., The isolated community evacuation problem with mixed integer programming, Transportation Research Part E: Logistics and Transportation Review. (2022) 161, 102710, https://doi.org/10.1016/j.tre.2022.102710.
10.1016/j.tre.2022.102710
Web of Science® Google Scholar
4 Fan L., Su H., Wang W., Zio E., Zhang L., Yang Z., Peng S., Yu W., Zhang L., and Zhang J., A systematic method for the optimization of gas supply reliability in natural gas pipeline network based on Bayesian networks and deep reinforcement learning, Reliability Engineering & System Safety. (2022) 225, 108613, https://doi.org/10.1016/j.ress.2022.108613.
10.1016/j.ress.2022.108613
Web of Science® Google Scholar
5 Jiang L., Liu J., Zhou D., Zhou Q., Yang X., and Yu G., Predicting the evolution of hot topics: a solution based on the online opinion dynamics model in social network, IEEE Transactions on Systems Man Cybernetics Systems. (2010) 50, no. 10, 3828–3840.
Google Scholar
6 Yuan P., Jiang L., Liu J., Zhou D., Li P., and Gao Y., Dual-level attention based on heterogeneous graph convolution network for aspect-based sentiment classification, Wireless Communications and Mobile Computing. (2021) 2021, 13, 6625899, https://doi.org/10.1155/2021/6625899.
10.1155/2021/6625899
Web of Science® Google Scholar
7 Borradaile G., Klein P. N., Mozes S., Nussbaum Y., and Wulff-Nilsen C., Multiple-source multiple-sink maximum flow in directed planar graphs in near-linear time, SIAM Journal on Computing. (2017) 46, no. 4, 1280–1303, https://doi.org/10.1137/15m1042929, 2-s2.0-85028665771.
10.1137/15M1042929
Web of Science® Google Scholar
8 Aalipour A., Kebriaei H., and Ramezani M., Analytical optimal solution of perimeter traffic flow control based on mfd dynamics: a pontryagin's maximum principle approach, IEEE Transactions on Intelligent Transportation Systems. (2019) 20, no. 9, 3224–3234, https://doi.org/10.1109/tits.2018.2873104, 2-s2.0-85055166543.
10.1109/TITS.2018.2873104
Web of Science® Google Scholar
9 Hosseini H. S. and Hosseini S. A., Maximum flow problem on dynamic generative network flows with time-varying bounds, Applied Mathematical Modelling. (2010) 34, no. 8, 2136–2147, https://doi.org/10.1016/j.apm.2009.10.026, 2-s2.0-77950019872.
10.1016/j.apm.2009.10.026
Web of Science® Google Scholar
10 Marquez J., Gutierrez I., and Sanchez E., Approach of multicasting routing with solution for network coding applying edmonds-karp, Proceedings of the 2018 IEEE international Conference on Automation/XXIII Congress of the Chilean Association of Automatic Control (ICA-ACCA), October 2018, Concepcion, Chile, 1–8, https://doi.org/10.1109/ica-acca.2018.8609753, 2-s2.0-85062167483.
10.1109/ica-acca.2018.8609753
Google Scholar
11 Cai X., Sha D., and Wong C., Time-varying universal maximum flow problems, Mathematical and Computer Modelling. (2001) 33, no. 4-5, 407–430, https://doi.org/10.1016/s0895-7177(00)00252-1, 2-s2.0-0035130078.
10.1016/S0895-7177(00)00252-1
Google Scholar
12 Bauer D., Richter G., Asamer J., Heilmann B., Lenz G., and Kolbl R., Quasi-Dynamic estimation of OD flows from traffic counts without prior OD matrix, IEEE Transactions on Intelligent Transportation Systems. (2018) 19, no. 6, 2025–2034, https://doi.org/10.1109/tits.2017.2741528, 2-s2.0-85030310735.
10.1109/TITS.2017.2741528
Web of Science® Google Scholar
13 Weir J. D., Average longest path and maximum cost network flows with multiple-criteria weights, Electronic Notes in Discrete Mathematics. (2018) 69, 181–188, https://doi.org/10.1016/j.endm.2018.07.024, 2-s2.0-85051055325.
10.1016/j.endm.2018.07.024
Google Scholar
14 Ahmed N., Das S., and Purusotham S., The problem of maximum flow with minimum attainable cost in a network, Opsearch. (2012) 50, no. 2, 197–214, https://doi.org/10.1007/s12597-012-0106-1, 2-s2.0-84878727946.
10.1007/s12597-012-0106-1
Google Scholar
15 Szymanski T. H., Max-flow min-cost routing in a future-internet with improved QoS guarantees, IEEE Transactions on Communications. (2013) 61, no. 4, 1485–1497, https://doi.org/10.1109/tcomm.2013.020713.110882, 2-s2.0-84877923748.
10.1109/TCOMM.2013.020713.110882
Web of Science® Google Scholar
16 Park G. and Song M., Prediction-based resource allocation using LSTM and minimum cost and maximum flow algorithm, Proceedings of the International Conference on Process Mining (ICPM), June 2019, Aachen, Germany, 1–9, https://doi.org/10.1109/icpm.2019.00027, 2-s2.0-85071182772.
10.1109/icpm.2019.00027
Google Scholar
17 Eboli M., A flow network analysis of direct balance-sheet contagion in financial networks, Journal of Economic Dynamics and Control. (2019) 103, 205–233, https://doi.org/10.1016/j.jedc.2019.04.007, 2-s2.0-85065526864.
10.1016/j.jedc.2019.04.007
Web of Science® Google Scholar
18 Tartibu I. O., Okwu L. K., and Okwu M. O., Prediction and modeling of traffic flow of human-driven vehicles at a signalized road intersection using artificial neural network model: a South African road transportation system scenario, Transport Engineer. (2021) 6, 100095, https://doi.org/10.1016/j.treng.2021.100095.
10.1016/j.treng.2021.100095
Google Scholar
19 Peng C. and Peng J., Models and algorithm of maximum flow problem in uncertain network, Proceedings of the International Conference on Artificial Intelligence & Computational Intelligence (AICI), September 2011, Taiyuan, China, 101–109, https://doi.org/10.1007/978-3-642-23881-9_14, 2-s2.0-80054698847.
10.1007/978-3-642-23881-9_14
Google Scholar
20 Gharehbolagh H. H., Hafezalkotob A., Makui A., and Raissi S., Cooperative strategies for maximum-flow problem in uncertain decentralized systems using reliability analysis, Security and Communication Networks. (2016) 2016, 9, 2349712.
Google Scholar
21 Li H., Zhang T., Zhang Y., Wang K., and Li J., A maximum flow algorithm based on storage time aggregated graph for delay-tolerant networks, Ad Hoc Networks. (2017) 59, no. 1, 63–70, https://doi.org/10.1016/j.adhoc.2017.01.006, 2-s2.0-85011295980.
10.1016/j.adhoc.2017.01.006
Web of Science® Google Scholar
22 Buzdalov M. and Shalyto A., Hard test generation for augmenting path maximum flow algorithms using genetic algorithms: Revisited, Proceedings of the. 2015 IEEE Congress on Evolutionary Computation (CEC), May 2015, Sendai, Japan, 2121–2128, https://doi.org/10.1109/cec.2015.7257146, 2-s2.0-84963532932.
10.1109/cec.2015.7257146
Google Scholar
23 Cai F. J. and Cai M. C., Shortest path and maximum flow problems in networks with additive losses and gains, Theoretical Computer Science. (2011) 412, no. 4-5, 391–401, https://doi.org/10.1016/j.tcs.2010.11.019, 2-s2.0-78650823446.
10.1016/j.tcs.2010.11.019
Web of Science® Google Scholar
24 Song K., Li G., Chen X., Deng L., Xiao G., Zeng F., and Pei J., Target controllability of two-layer multiplex networks based on network flow theory, IEEE Transactions on Cybernetics. (2021) 51, no. 5, 2699–2711, https://doi.org/10.1109/tcyb.2019.2906700.
10.1109/TCYB.2019.2906700
PubMed Web of Science® Google Scholar
25 Takahashi T., The simplest and smallest network on which the ford-fulkerson maximum flow procedure may fail to terminate, Journal of Information Processing. (2016) 24, no. 2, 390–394.
10.2197/ipsjjip.24.390
Google Scholar
26 Özcan M. and Ozcan E., Optimization of electricity transmission by Ford-Fulkerson algorithm, Sustainable Energy, Grids and Networks. (2021) 28, 100544, https://doi.org/10.1016/j.segan.2021.100544.
10.1016/j.segan.2021.100544
Web of Science® Google Scholar
27 Kavasseri C. and Kavasseri R., Efficient network reconfiguration using minimum cost maximum flow-based branch exchanges and random walks-based loss estimations, IEEE Transactions on Power Systems. (2011) 26, no. 1, 30–37, https://doi.org/10.1109/tpwrs.2010.2052076, 2-s2.0-79251530751.
10.1109/TPWRS.2010.2052076
Web of Science® Google Scholar

Citing Literature

All articles

[Retracted] A Novel Maximum Flow Algorithm with Neural Network for Time-Varying Wastage Networks

Retraction(s) for this article

Retracted: A Novel Maximum Flow Algorithm with Neural Network for Time-Varying Wastage Networks

Abstract

1. Introduction

2. Mathematical Formulation