The renovation and expansion of highway is a technical, comprehensive, and complex work, and the determination of its optimal scheme requires the consideration of multiple factors. In the process of highway construction, road engineers attempt to select an optimal scheme with the aim of saving cost, reducing construction difficulties, and protecting environment. It is difficult to assess because of the large number of attribute indices and the diversity of data distribution. In order to scientifically evaluate the comprehensive benefits of highway reconstruction and extension (HRE) schemes, an evaluation model of HRE scheme based on multiple attribute decision making (MADM) was established. This paper constructed the evaluation index system of HRE based on the four aspects of technology, economy, environmental impact, and landscape. This paper has made two major improvements. First, a method was proposed to determine the weight of evaluation index by coupling fuzzy analytic hierarchy process (FAHP) with difference driven principle (DDP). Then, technique for order preference by similarity to an ideal solution (TOPSIS) method was optimized by grey relational analysis (GRA) method. Finally, the MADA evaluation model is utilized to analyze the ranking of optimal scheme selection problem by relative closeness as a decision index. The results showed that the subjective intention of decision makers was considered and also fully the objective information of data itself was fully mined. The optimal scheme was scheme 3 through the analysis of five HRE schemes. This model highlighted the differences among the schemes and also avoided the problem of excessive differences. The results were consistent with the actual situation, verifying the feasibility and practicability of the model.

1. Introduction

China’s road network is developing rapidly. It effectively promoted the development of comprehensive transportation system and economy and significantly enhanced the comprehensive national power [1, 2]. As a part of road network, highway plays the role of the main channel of transportation. However, the capacity and service level of highway constructed in early can no longer adapt the needs of modernization of transportation industry [3, 4]. It was clearly pointed out that we should upgrade mainly existing routes, focus on the improvement of highway capacity and service level, and achieve green and sustainable development of roads in China’s highway network plan. In addition, HRE project has the advantages of low investments, short cycles, saving resources, and environmental protection. It is also an important reason for its wide application [5, 6].

The HRE project is a complex system engineering, which has many evaluation indexes including some qualitative indexes. It is difficult to evaluate comprehensive benefits of highway reconstruction and extension project scientifically and reasonably. A MADM is to choose optimal scheme or sort schemes when considering multiple attributes, which is gradually applied to solve the problem of HRE scheme optimization.

Yuan et al. [7] analyzed the research status and development trend of highway reconstruction in China and put forward an FAHP method used for highway expansion scheme. Wang et al. [8] used analytic hierarchy process (AHP) to determine the weight of each indexes and established the optimization model of highway route scheme based on matter-element theory. Yang et al. [9] constructed the evaluation index system of Beijing-Shanghai HRE project, determined the index weight by expert scoring method and AHP, and calculated the final score of the project. Li et al. [10] established a comprehensive evaluation index model of the influence of HRE on regional highway network. The weight was determined for uncertain AHP, and the influence of highway traffic on regional road network before and after reconstruction and expansion was analyzed. Liang et al. [11] proposed an improved fuzzy TOPSIS method for highway route optimization and verified the feasibility and rationality of this method. Yang et al. [12] analyzed and optimized the best scheme of suburban highway reconstruction by using the improved fuzzy analytic hierarchy process with 0-1 planning group decision method. Xie et al. [13] determined the index weight by AHP and recommended the best scheme by TOPSIS. An et al. [14] combined AHP and GRA method to optimize the best HRE scheme. In summary, the research on the evaluation model of HRE scheme mainly focuses on the determination of index weight and the improvement of decision-making method. About weight determination, subjective weighting methods such as AHP and FAHP are often adopted. While these method focus too much on the subjective intention of decision makers, and the objective information contained in the data itself is ignored. Referring to the improvement of decision-making methods, GRA and TOPSIS method are mainly used. However, two methods have certain limitations. The GRA method focuses on the geometric shape of data. The TOPSIS method focuses on the data distance [15–17].

Therefore, the evaluation index system of HRE is built in this paper. An evaluation model of HRE scheme based on MADM is established. A method of index weight determined by coupling FAHP and DDP has come up. This method considers both two aspects of subjective and objective. The GRA and TOPSIS methods are effectively synthesized to balance the data distance and geometric shape. Relative closeness is come up with reflecting the pros and cons of the scheme. The final evaluation value of HRE is calculated and sorted. The feasibility of the model is verified.

The structure of this paper is as follows. In Section 2, the evaluation index system of HRE is constructed. In Section 3, the multiple attribute decision-making evaluation model is established. In terms of weight, the FAHP method and the DDP method were combined. In addition, the TOPSIS method was optimized by the GRA method. Finally, the three methods are adopted and select the route scheme by relative closeness as a decision index, and the conclusions are drawn.

2. Evaluation Index System

The HRE evaluation index is the scale to evaluate the pros and cons of the reconstruction and expansion schemes. In order to effectively evaluate different reconstruction and expansion schemes, a scientific and reasonable evaluation index system should be established. The evaluation index system should scientifically and comprehensively reflect the nature of reconstruction and expansion projects, ensuring independent representation of indicators and avoiding the information overlap. According to the characteristics of indicators, quantitative and qualitative analysis should be carried out to ensure that the selected indicators are scientific, objective, and reasonable. Therefore, this study followed the principles of scientific comprehensiveness, independent representation, and the combination of quantitative and qualitative principles. The methods of survey research and frequency statistics research were adopted. The evaluation index system of HRE was constructed from four aspects of technical, economic, environmental impact, and landscape. The evaluation index system is shown in Figure 1.

Details are in the caption following the image — Open in figure viewer PowerPoint

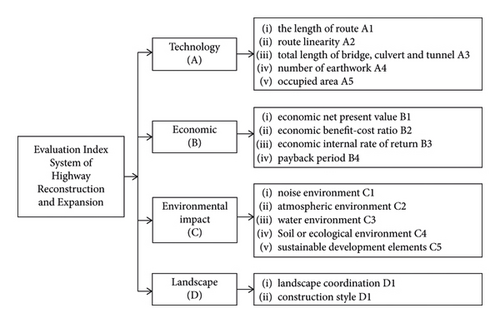
2.1. Technology Indexes

Technology indexes are the basis to ensure the technical feasibility of highway reconstruction and expansion schemes. The design parameters directly affect the road performance and comfort. According to the highway grade, function, comfort, and the design indexes are determined and meet the requirements of relevant specifications.

2.1.1. The Length of Route

Highway expansion route direction is determined, but the route lengths of different expansion schemes are different. As the most intuitive technical index, the route length has a significant effect on the engineering amount and cost of the project.

2.1.2. Route Linearity

Route linearity is the core index of technical index. Highway alignment design is to determine the spatial position, geometric shape, and size of the route. It affects the safety, comfort, and economy of highway.

2.1.3. Total Length of Bridge, Culvert, and Tunnel

As an important part of highway, total length of bridge, culvert, and tunnel is an important index in technical indexes. The longer the length is, the more difficult technology is, and the higher the cost is. But it also reduces the land occupation. So the total length of bridge, culvert, and tunnel must be reasonably considered.

2.1.4. Number of Earthwork

The HRE has a large demand for earthwork resources. Reasonable consideration of the number of earthwork can reduce unnecessary earthwork borrowing and abandonment, project cost, and ecological environment damage.

2.1.5. Occupied Area

When selecting the best reconstruction and expansion scheme, we should make full use of the original highway. It can reduce the land occupation and house demolition along the line.

2.2. Economic Indexes

Economic indexes are the basis for judging the economic feasibility of highway reconstruction and expansion projects. The scientific analysis method is applied to evaluate the financial feasibility and economic rationality of the project, which provides the basis for scientific decisions of the project.

2.2.1. Economic Net Present Value

The economic net present value is one of the important indicators for evaluating the economic analysis of the reconstruction and expansion scheme. If the net present value is greater than zero, the scheme is feasible. The greater the net present value is, the better the scheme is and the better the investment benefit is.

2.2.2. Economic Benefit-Cost Ratio

Economic benefit-cost ratio refers to the ratio of benefit present value and cost present value in the project during the calculation period. If the economic benefit-cost ratio is greater than one, it shows that the project economic analysis has reached an acceptable level.

2.2.3. Economic Internal Rate of Return

Economic internal rate of return can not only indicate economic benefits of the scheme but also show the antirisk ability of the scheme. When the economic internal return rate is greater than the benchmark return rate, it indicates that the project is feasible and the greater the better the index.

2.2.4. Payback Period

The payback period refers to the time required for the net income of the project to offset all construction costs, which reflects the ability of project recovery. The shorter the payback period, the faster the project investment recovery and the stronger the ability to resist risks.

2.3. Environmental Impact Indexes

The environment is the basic condition for human survival. The HRE have a negative impact on the environment in the construction process. When evaluating project schemes, the environmental impact should be taken into account. To minimize the impact on the environment as far as possible and achieve the harmonious development of human, highway, and natural ecological environment.

2.3.1. Noise Environment

The noise is made by the construction machinery, equipment, and transportation vehicles during the construction period. A reconstruction and expansion plan should be as far as possible away from the residents living area and put forward noise reduction measures to reduce sound pollution.

2.3.2. Atmospheric Environment

The roadbed excavation and earthwork transportation can cause the dust, increasing the content of suspended particulate matter in the atmosphere. So we need to assess this index.

2.3.3. Water Environment

The water environment mainly covers two aspects. One is the impact on the water environment along the line. The other is the domestic wastewater, sewage in the construction process, and sewage produced in the service area.

2.3.4. Soil or Ecological Environment

The HRE will occupy the land along the line. In addition, building materials, construction machinery, and earthwork excavation will cause certain damage to the surrounding soil and ecology.

2.3.5. Sustainable Development Elements

The HRE will produce a lot of construction waste. It is important to utilize solid waste, save resources, reduce environmental costs, realizing the unity of economic, environmental, and social.

2.4. Landscape Indexes

2.4.1. Landscape Coordination

In the scheme selection, the design theme is reasonably determined by local conditions, natural scenery, and tourism resources along the road. Then, the road itself becomes a scenic line.

2.4.2. Construction Style

The construction style is influenced by political, social, economic, building materials, and cultural factors of the times. Reconstruction and extension programs should be combined with folk customs along highway to enhance the ornamental value.

3. Multiple Attribute Decision-Making Evaluation Model

The multiple attribute decision-making evaluation model built in this paper is divided into three sections. First, the advantages and disadvantages of various weight methods are compared, and the weight is determined from both subjective and objective based on FAHP and DDP. Then, all schemes are evaluated by improved TOPSIS method based on GRA. Finally, the optimal solution is obtained.

3.1. Decision Matrix Standardization

There are m schemes and n evaluation indexes, described as R = {R₁,R₂, …,R_m} and U = {U₁,U₂, …,U_n}. The decision matrix denoted by

, where i = 1, 2, …, m, j = 1, 2, …, n; the symbol a_ij is the jth indicator value of the ith scheme.

(1)

The quantification of qualitative indicators is obtained according to expert scoring. The value is shown in Table 1.

1. Quantification of evaluation level.

Evaluation level	Excellent	Good	General	Bad	Not meet the requirements
Quantification of evaluation index level	>0.9	0.8∼0.9	0.7∼0.8	0.6∼0.7	Elimination

The standardized decision matrix is obtained by dimensionless standardization of indicators because of different dimensions and units of evaluation indicators.

For benefit indicators,

(2)

For cost indicators,

(3)

where the symbol

is the maximum value of the jth indicator and the symbol

is the minimum value of the jth indicator.

3.2. Index Weight Calculation

The index weight reflects the importance of an index in the index system. The determination method of weight plays a decisive role in the comprehensive evaluation. The principles of different methods are not the same, so the calculated weights are different. The weight methods are mainly divided into two categories. One is the subjective weight method that the index weights are given through the experience of decision makers, such as AHP, FAHP, and Delphi [18–20]. The other is the objective weighting method that the index weights are determined by the amount of index information in the evaluation, such as the entropy method, DDP, and variation coefficient method [21–23]. However, both the subjective weight method and the objective weight method are difficult to fully reflect the importance of the index in the actual analysis process. Therefore, the combination weight method is used to balance the subjective experience of decision makers and the objective information contained in the data itself, and the weights of the indexes are reasonably determined.

3.2.1. FAHP Method

FAHP method is an improvement of AHP method [19]. The AHP method is widely used in the evaluation of multi-index problems because of the thinking and mathematization of subjective judgment, simple and flexible. However, there are some problems in the AHP method, such as the difficulty of consistency test and thinking consistency and the lack of scientific basis for the judgment standard CR < 0.1 [26]. These problems are well solved by FAHP method. Steps are as follows.

Step 1. Construct priority relation matrix
The priority judgment matrix is established by adopting 0.1∼0.9 scale shown in Table 2.
(4)
The judgment matrix is fuzzy complementary matrix.
Step 2. Transform priority relation matrix into fuzzy consistent matrix.
(5)
where .
Step 3. Calculate weight vector by normalization method.
(6)
Step 4. Solve higher precision weight vector by power method.

2. 0.1∼0.9 Scaling method.

Scale	Definition	Explanation
0.5	Equally important	The two factors are equally important
0.6	Slightly important	Compared with the two factors, one factor is slightly more important than the other
0.7	Obviously important	Compared with the two factors, one factor is obviously more important than the other.
0.8	Strongly important	Compared with the two factors, one is strongly more important than the other
0.9	Extremely important	Compared with the two factors, one is extremely more important than the other
0.1, 0.2, 0.3, 0.4	Inverse comparison	If f_ij can be get by comparing factor a_i and a_j, f_ji can be get by f_ji = 1 − f_ij

Fuzzy consistent matrix (6) is transformed into reciprocal matrix.

(7)

where e_ij = r_ij/r_ji.

The weight vector

obtained by normalization method is as initial vector V⁽⁰⁾ and iterated by the following equations:

(8)

where

and

, k = 0, 1, 2, ….

The above iterative process is as follows. If is available, we can get , where ε is the given error and λ_max is maximum eigenvalue of fuzzy consistent matrix R. The vector obtained by normalized V^{(k + 1)} is the weight W^′ obtained by FAHP. If not, go on iteration.

3.2.2. DDP Method

The basic idea of DDP is as follows. The original information of empowerment comes directly from indexes. The weight coefficient is determined according to the variation degree of each indexes in the overall index and the influence degree on other indexes [22]. This method avoids human interference.

There are n targets and m evaluation indexes that are defined as x₁, x₂, …, x_m. The corresponding weight coefficients are defined as ω₁, ω₂, …, ω_m. All index values of the ith targets are denoted as x_i1, x_i2, …, x_im, where

. The comprehensive evaluation function is denoted as follows:

(9)

Let

and

, we can get

(10)

The sample variance of y is as follows:

(11)

where

is denoted as the mean value of y_i.

Because the original data are standardized, the value of

is 0. This is as follows:

(12)

where H = X^TX.

The maximum value in equations (12) is to make the information difference between the indexes maximum, realizing the difference driving.

(13)

When the elements of H are greater than 0, there is a unique positive maximum eigenvalue and its corresponding eigenvector. The eigenvector is calculated and normalized to obtain index weight coefficient vector w.

3.2.3. FAHF-DDP Method

The weight of both W′ obtained by FAHP and W″ obtained by DDP is combined with relative entropy principle [27]. According to relative entropy principle, the weight W should be as close as possible to the weight W′ and W′′.

(14)

The optimal solution is obtained by Lagrange multiplier method.

(15)

Coupling weight vector is denoted as W = (w₁, w₂, …, w_j).

3.2.4. Decision Value Calculation

We need to sort the schemes of decision problems comprehensively after determining the decision matrix and index weight. At present, there are many decision-making methods. The vlsekriterijumska optimizacija i kompromisno resenje (VIKOR) is that trade-off ranking of finite decision schemes by maximizing group utility and minimizing individual regret [28]. It is a compromise solution regarded as the closest to the ideal to solve the decision-making problems with noncommensurable and conflicting criteria [29, 30]. The multiattribute value theory (MAVT) allows decision makers to provide different attribute value functions for each different attribute criterion and then combine the weight calculation to obtain the utility value of each scheme [31]. The elimination and choice translating reality (ELECTRE) provide as much as possible precise and suitable set of actions or alternatives to the underlying problem by eliminating the alternatives that are outranked by others [32]. The preference ranking organization method for enrichment of evaluations (PROMETHEE) is the most appropriate approach where a committee of decision makers is working on several complex problems, especially those with some factors or criteria, including numerous judgments and perceptions with long-term impacts on decisions [33]. The TOPSIS method is to construct positive and negative ideal solutions for multiattribute problems and sort by the relative closeness of evaluation objects to positive and negative ideal solutions [34]. The GRA method is based on the similarity between the comparison sequence and reference sequence to evaluate schemes [16]. Comparing the above methods, the VIKOR and MAVT prefer to the opinions of decision makers. The ELECTRE and PROMETHEE do not need the process of nondimensionalization, which often leads to the lack of information and results [35]. In addition, fuzzy mathematics methods are also used, but there is a lot of uncertainty and subjectivity in the designing of fuzzy sets [36–39]. These methods is complex and not applicable for the evaluation of HRE schemes. The TOPSIS is selected because of simple principle, easy understanding, and strong capacity to integrate other methods [23]. It can well reflect the position distance between the alternative scheme and the positive and negative ideal scheme. In fact, only considering the maximum and minimum distance between data is not enough. The GRA method can reflect the similarity between the two sets of data sample curves [17]. The two methods are combined to make more effective evaluation and get more accurate evaluation results. Thus, an improved TOPSIS method based on GRA is came up. This method is similar to the actual situation that it has differences and linkages between HRE schemes. In this paper, the comprehensive distance is redefined, and the relative closeness of comprehensive distance is used as scheme decision-making indicators:

Step 1: determine the positive ideal scheme V⁺ and the negative ideal scheme V⁻.
(16)
Step 2: calculate the euclidean distances of each alternative to the positive ideal scheme and the negative ideal scheme.
(17)
Step 3: calculate the grey correlation degrees of each alternative to the positive ideal scheme and the negative ideal scheme.
(18)
The value of ρ takes 0.5.
Step 4: normalize the euclidean distance and grey correlation degree.
(19)
Step 5: fit the euclidean distance and grey correlation degree by linear.
(20)
The value of α takes 0.5.
Step 6: calculate the value of relative closeness .
(21)

4. Case Analysis

A HRE example is from Sayram Lake to Guozigoukou on G405 line in Xinjiang [40]. The effectiveness of the evaluation method is verified. The evaluation indexes of five most representative schemes are shown in Table 3.

3. The evaluation indexes of five schemes.

Evaluation indexes		S₁	S₂	S₃	S₄	S₅
A	A₁	9.461	9.154	10.064	9.313	9.560
	A₂	Good	General	Excellent	General	Bad
	A₃	4108	1542	5068	2194	5182
	A₄	360848	480503	91412	681274	1416183
	A₅	403.5	257.04	171.66	458.49	555.61

B	B₁	58633	40311	91610	68823	73341
	B₂	1.3	1.24	1.56	1.35	1.04
	B₃	12.48	12.07	14.42	11.25	10.33
	B₄	19	19.8	15.9	20.1	23.6

C	C₁	Good	Good	Excellent	General	Bad
	C₂	Good	Good	Excellent	General	Bad
	C₃	Good	Good	Good	General	Bad
	C₄	General	General	Good	Bad	Bad
	C₅	General	Good	Good	General	Bad

D	D₁	General	Good	Good	General	Bad
D	D₂	General	Good	Good	General	General

4.1. Standardized Decision Matrix

Obtain standardized decision matrix according to equations (1)–(3).

The columns 1 to 8 of decision matrix:

(22)

The columns 9 to 16 of decision matrix:

(23)

4.2. Evaluation Index Coupling Weight

The coupling weights of evaluation indexes are calculated according to equations (4)∼(15). The results are shown in Table 4.

4. FAHP-DDP coupling weights.

Evaluation indexes		Weights by FAHP [27]	Weights by DDP	Coupling weights
A	A₁	0.0758	0.0552	0.0666
	A₂	0.0937	0.0388	0.0616
	A₃	0.0540	0.0467	0.0516
	A₄	0.0457	0.0752	0.0603
	A₅	0.0395	0.0642	0.0518

B	B₁	0.0935	0.0500	0.0703
	B₂	0.0764	0.0614	0.0704
	B₃	0.0764	0.0570	0.0678
	B₄	0.0624	0.0639	0.0649

C	C₁	0.0347	0.0680	0.0499
	C₂	0.0347	0.0680	0.0499
	C₃	0.0425	0.0862	0.0621
	C₄	0.0520	0.0549	0.0548
	C₅	0.0520	0.0762	0.0646

D	D₁	0.0834	0.0762	0.0819
D	D₂	0.0834	0.0581	0.0715

As can be seen from the above table, there are obvious differences between the two weight determination methods. Decision makers pay more attention to indicators such as route linearity, economic net present value, landscape coordination, and architectural style. While the weights of land area, atmospheric environment, and noise environment are relatively low. Considering the objective information of the indicators, the weights of each indicator are relatively close. The difference is obvious compared with the subjective weight, which indicates that the difference-driven is realized. The weight coupling not only considers the subjective and objective but also makes the weight result more balanced.

4.3. Comparative Analysis of Different Methods

As shown in Table 5, the relative closeness degree of multiple attribute decision-making evaluation model is calculated and sorted by the data of coupling weights in Table 4 and formulas (16)∼(22).

5. Calculation results and ranking of five alternatives.

Alternatives								Ranking
A₁	0.3488	0.3806	0.6100	0.7314	0.4588	0.5041	0.4765	3
A₂	0.2129	0.7114	0.8123	0.5838	0.7133	0.3697	0.6587	2
A₃	0.2144	1.0000	1.0000	0.5025	0.9403	0.3337	0.7380	1
A₄	0.4366	0.3123	0.5677	0.7821	0.4061	0.5709	0.4157	4
A₅	1.0000	0.1356	0.4600	1.0000	0.2703	0.9509	0.2213	5

The grey target decision method is a commonly effective method in multiobjective decision analysis. The main idea of grey target decision method is to get a grey target from original data processing. The decision points are compared with the target center, and the ranking is determined by comparing the target center distances [41]. The comparison results of methods in the paper, grey relational analysis method, and grey target decision method are as shown in Table 6.

6. The results of different methods.

Evaluation methods	Alternatives
Evaluation methods	A₁	A₂	A₃	A₄	A₅
Grey relational analysis [27]	0.7505	0.8043	0.8052	0.7314	0.6051
Grey target decision [42]	0.0968	0.1050	0.0826	0.0861	0.1101
Method in the paper	0.4765	0.6587	0.7380	0.4157	0.2213

The distances of different evaluation schemes calculated by the three methods are different, but the overall trends are also different. The distinction among schemes is not high in the grey correlation analysis method, especially scheme 2and scheme 3, which is inconsistent with the actual situation. The grey target decision method pays too much attention to the distance between the indexes and does not consider the correlation between the index, so the evaluation results are A₃ > A₄ > A₁ > A₂ > A₅. The evaluation result of method in this paper is A₃ > A₂ > A₁ > A₄ > A₅, which is consistent with the result of grey correlation analysis. The relative closeness of schemes has obvious differences, which can effectively select the optimal scheme. From the three methods can be seen that the best highway reconstruction and expansion scheme is scheme 3. At the same time, the advantages of scheme 3 mainly lie in the number of earthwork, occupied area, economic net present value, and economic internal rate of return. This is consistent with the actual situation, indicating that the multiattribute model established in this paper is effective and advanced on evaluating highway reconstruction and expansion scheme.

4.4. Influence of the Linear Combination Coefficient

Linear combination coefficient α is 0.5 in this model. In order to better provide reference for decision makers, the influence of different α value on the ranking results are analyzed as shown in Table 7.

7. Ranking results of different α values.

α value	A₁		A₂		A₃		A₄		A₅
α value		Ranking		Ranking		Ranking		Ranking		Ranking
0.1	0.4586	3	0.5947	2	0.6786	1	0.4204	4	0.2995	5
0.3	0.4674	3	0.6233	2	0.7062	1	0.4199	4	0.2661	5
0.5	0.4765	3	0.6587	2	0.7380	1	0.4157	4	0.2213	5
0.7	0.4922	3	0.6958	2	0.7687	1	0.4186	4	0.1889	5
0.9	0.5104	3	0.7427	2	0.8044	1	0.4176	4	0.1438	5

It can be seen from Table 6 that when the linear combination coefficient α is 0.1, 0.3, 0.5, 0.7, and 0.9, respectively, the relative closeness values of different schemes are different, but the ranking of schemes is consistent. It indicates that the linear combination coefficient does not affect the selection of the optimal scheme and only represents the preference degree of decision makers for data distance and data similarity between decision schemes [24, 25].

5. Conclusions

(1)
This paper starts from four aspects of technology, economy, environmental impact, and landscape and selects 16 specific indexes and builds a performance evaluation index system of highway reconstruction and extension.
(2)
The evaluation index coupling weight W is determined by using combination fuzzy analytic hierarchy process and difference-driven principle. This weight method balances both the intention of the decision maker and the objective information of the data, making the index weight more scientific and reasonable.
(3)
The TOPSIS method is optimized by the GRA method. This decision-making method reflects both date distance and geometric shape. An evaluation model of HRE scheme based on MADM is established.
(4)
Combined with a case analysis, the results of GRA method and grey target decision method show that the optimal scheme is scheme 3. It proves the feasibility and superiority of the model in this paper to solve the comprehensive benefit the problem of HRE scheme.
(5)
This research study has a limitation that property indicators are specific values or can be quantified by other methods, but it is difficult to solve decision-making problems that allow for fuzziness and imprecision in the ample range. This limitation will be addressed in future work by lead-in fuzzy set and combine with multiple attribute decision making and fuzzy set.

Conflicts of Interest

The authors declare that they have no conflicts of interest regarding the publication of this paper.

Acknowledgments

This study was supported by the Natural Science Foundation of Heilongjiang Province (No. QC2014C043) and the Fundamental Research Funds for the Central Universities (No. 2572015CB31).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Xueyan W., Xu C., Wei J., and Tian Y., Development of capacity models for twelve-lane freeways in China [C], Proceedings of the Fifth International Conference on Transportation Engineering, September 2015, Dalian, China.
Google Scholar
2 Chen C., Wang C., Yu S., Song Z., Fu H., and An T., Low-temperature mechanical properties of polyurethane-modified waterborne epoxy resin for pavement coating, International Journal of Pavement Engineering. (2022) 1–13, https://doi.org/10.1080/10298436.2022.2099853.
10.1080/10298436.2022.2099853
Web of Science® Google Scholar
3 Cheng Y., Construction Technology Urumqi outer ring expressway road reconstruction project expansion, Applied Mechanics and Materials. (2014) 587-589, 965–970, https://doi.org/10.4028/www.scientific.net/amm.587-589.965, 2-s2.0-84904979303.
10.4028/www.scientific.net/AMM.587-589.965
Google Scholar
4 Wang C., Wang M., Chen Q., and Zhang L., Basic performance and asphalt smoke absorption effect of environment-friendly asphalt to improve pavement construction environment, Journal of Cleaner Production. (2022) 333, 130142, https://doi.org/10.1016/j.jclepro.2021.130142.
10.1016/j.jclepro.2021.130142
CAS Web of Science® Google Scholar
5 Xi K., Mode analysis of expressway expansion and reconstruction [C], Proceedings of the Fourteenth COTA International Conference of Transportation Professionals, July 2014, Changsha, China, ASCE.
Google Scholar
6 Yuan Y., The study on expressway reconstruction project of China, Applied Mechanics and Materials. (2012) 253-255, 1139–1146, https://doi.org/10.4028/www.scientific.net/amm.253-255.1139, 2-s2.0-84872930283.
10.4028/www.scientific.net/AMM.253-255.1139
Google Scholar
7 Yuan C. and Shi L., Study on reconstruction scheme of expressway in China and optimization within the AHP-fuzzy method [C], Proceedings of the Fourteenth COTA International Conference of Transportation Professionals, July 2014, Changsha, China, ASCE.
Google Scholar
8 Wang S., Xiong Li., Zhang C., Chen J., and Jin L., An optimization model of a highway route scheme in permafrost regions, Cold Regions Science and Technology. (2017) 138, 84–90, https://doi.org/10.1016/j.coldregions.2017.03.010, 2-s2.0-85016414374.
10.1016/j.coldregions.2017.03.010
Web of Science® Google Scholar
9 Yang Y., Xia J., Zhao R., and Chen Li., Research on evaluation index system of green highway in reconstruction and expansion projects [C], Proceedings of the Second International Academic Exchange Conference on Science and Technology Innovation, January 2020, Guangzhou, China.
Google Scholar
10 Li C., Wang J., and Wang M., The evaluation of the Traffic impact of highways’ reconstruction and extension on area highway network, Applied Mechanics and Materials. (2013) 361-363, 1937–1940, https://doi.org/10.4028/www.scientific.net/amm.361-363.1937, 2-s2.0-84883298992.
10.4028/www.scientific.net/AMM.361-363.1937
Google Scholar
11 Liang X. and Meng X., An extended FTOPSIS method for freeway route selection in the pre-feasibility study stage, Physica A: Statistical Mechanics and Its Applications. (2019) 526, 120871, https://doi.org/10.1016/j.physa.2019.04.107, 2-s2.0-85064708239.
10.1016/j.physa.2019.04.107
Web of Science® Google Scholar
12 Yang C., Liu C., and Jin C., Research on the selection of reconstruction scheme for suburban expressway [J], Journal of Railway Science and Engineering. (2018) 15, no. 1, 255–262.
Google Scholar
13 Xie C., Pu H., and Zhang T., Evaluation of mountainous highway route scheme based on AHP-TOPSIS evaluation model [J], Highway. (2016) 61, no. 8, 17–21.
Google Scholar
14 An P., Su X., and Wu Q., Research on optimization of expressway reconstruction and extension scheme based on improved AHP-grey correlation method[J], Journal of Shandong University of Technology. (2018) 32, no. 4, 45–49.
Google Scholar
15 Zhang F., Fan Yu, and Ye Z., Comprehensive evaluation of academic journals based on difference-driven and GRA-TOPSIS method [J], Modern Intelligence. (2018) 38, no. 4, 77–82.
CAS Google Scholar
16 Yang W. and Wu Y., A Novel TOPSIS method based on improved grey relational analysis for Multiattribute decision-making problem, Mathematical Problems in Engineering. (2019) 2019, 1–10, 8761681, https://doi.org/10.1155/2019/8761681, 2-s2.0-85062352018.
10.1155/2019/8761681
CAS Web of Science® Google Scholar
17 Ying Li., Guohui F., Liang Yu., Qiang Li., and Mengyun S., The research of applying TOPSIS combined with grey relational analysis approach for building energy consumption evaluation [C], Proceedings of the Eighth International Symposium on Heating, Ventilation, and Air Conditioning, October 2014, Xian, China.
Google Scholar
18 Sun Y., Liu C., Sang M., Niu H., Xu F., and Xu F., Establishment and evaluation of performance index system of electric heated solid thermal storage, Journal of Computational Methods in Science and Engineering. (2021) 21, no. 5, 1531–1547, https://doi.org/10.3233/jcm-215076.
10.3233/JCM-215076
Web of Science® Google Scholar
19 Singh M. P., Singh P., and Singh P., Fuzzy AHP-based multi-criteria decision-making analysis for route alignment planning using geographic information system (GIS), Journal of Geographical Systems. (2019) 21, no. 3, 395–432, https://doi.org/10.1007/s10109-019-00296-0, 2-s2.0-85064338777.
10.1007/s10109-019-00296-0
Web of Science® Google Scholar
20 Hayati H., Majnounian M., Abdi E., Sessions J., and Makhdoum M., An expert-based approach to forest road network planning by combining Delphi and spatial multi-criteria evaluation, Environmental Monitoring and Assessment. (2013) 185, no. 2, 1767–1776, https://doi.org/10.1007/s10661-012-2666-1, 2-s2.0-84874421633.
10.1007/s10661-012-2666-1
PubMed Web of Science® Google Scholar
21 Zheng Y., Zhong H., Fang Y., Zhang K., Liu J., and Fang J., Rockburst Prediction model based on entropy weight integrated with grey relational BP Neural network, Advances in Civil Engineering. (2019) 2019, 1–8, https://doi.org/10.1155/2019/3453614, 2-s2.0-85056699015.
10.1155/2019/2174562
Web of Science® Google Scholar
22 Ma S., Shao C., and Liu D., Road traffic safety evaluation based on difference driving principle [J], Journal of Jilin University (Engineering Edition). (2010) 40, no. 4, 981–985.
Google Scholar
23 Chen P., A Novel coordinated TOPSIS based on coefficient of variation, Mathematics. (2019) 7, no. 7, https://doi.org/10.3390/math7070614, 2-s2.0-85068837519.
10.3390/math7070614
Web of Science® Google Scholar
24 Li Z., Fan Z., and Shen S., Urban green Space Suitability evaluation based on the AHP-CV combined weight method: a case study of Fuping County, China, Sustainability. (2018) 10, no. 8, https://doi.org/10.3390/su10082656, 2-s2.0-85051060167.
10.3390/su10082656
Web of Science® Google Scholar
25 Chen C., A Novel multi-criteria decision-making model for building material Supplier selection based on entropy-AHP weighted TOPSIS, Entropy. (2020) 22, no. 2, https://doi.org/10.3390/e22020259.
10.3390/e22020259
Web of Science® Google Scholar
26 Lee S., Determination of priority weights under Multiattribute decision-making situations: AHP versus fuzzy AHP, Journal of Construction Engineering and Management. (2015) 141, no. 2, 05014015, https://doi.org/10.1061/(asce)co.1943-7862.0000897, 2-s2.0-84921417311.
10.1061/(ASCE)CO.1943-7862.0000897
Web of Science® Google Scholar
27 Wang Lu., Qingxiang S., and Wu Q., Highway reconstruction and extension scheme decision based on coupling weight and fuzzy matter element analysis [J], Statistics and decision. (2017) no. 19, 60–63.
Google Scholar
28 Akram M., Shabir M., Adeel A., and Al-Kenani A. N., A Multiattribute decision-making Framework: VIKOR method with complex Spherical fuzzy N-soft sets, Mathematical Problems in Engineering. (2021) 2021, 1–25, https://doi.org/10.1155/2021/1490807.
10.1155/2021/1490807
Web of Science® Google Scholar
29 Meysam M. S., Behnam V., and Sadigh B. S., Designing a model of intuitionistic fuzzy VIKOR in multi-attribute group decision-making problems [J], Iranian Journal of Fuzzy Systems. (2016) 13, no. 1, 45–65.
Web of Science® Google Scholar
30 Sari F., Forest fire susceptibility mapping via multi-criteria decision analysis techniques for Mugla, Turkey: a comparative analysis of VIKOR and TOPSIS, Forest Ecology and Management. (2021) 480, 118644, https://doi.org/10.1016/j.foreco.2020.118644.
10.1016/j.foreco.2020.118644
Web of Science® Google Scholar
31 Alamos R. A., Walshe F. H., and Walshe T., Accounting for uncertainty in value Judgements when applying multi-attribute value Theory, Environmental Modeling & Assessment. (2017) 23, no. 1, 87–97, https://doi.org/10.1007/s10666-017-9555-5, 2-s2.0-85017141791.
10.1007/s10666-017-9555-5
Web of Science® Google Scholar
32 Akram M., Ilyas F., and Garg H., Multi-criteria group decision making based on ELECTRE I method in Pythagorean fuzzy information, Soft Computing. (2020) 24, no. 5, 3425–3453, https://doi.org/10.1007/s00500-019-04105-0, 2-s2.0-85067312547.
10.1007/s00500-019-04105-0
Web of Science® Google Scholar
33 Mousavi M., Gitinavard H., and Mousavi S. M., A soft computing based-modified ELECTRE model for renewable energy policy selection with unknown information, Renewable and Sustainable Energy Reviews. (2017) 68, 774–787, https://doi.org/10.1016/j.rser.2016.09.125, 2-s2.0-84995518861.
10.1016/j.rser.2016.09.125
Web of Science® Google Scholar
34 Reka S. and Toth C., Revision of sustainable road rating systems: selection of the best suited system for Hungarian road construction using TOPSIS method [J], Sustainability. (2020) 12, no. 21.
Google Scholar
35 Tang J., Zhu H.-lin, Liu Z., Jia X., and Zheng X., Urban Sustainability evaluation under the modified TOPSIS based on grey relational analysis, International Journal of Environmental Research and Public Health. (2019) 16, no. 2, https://doi.org/10.3390/ijerph16020256, 2-s2.0-85060126703.
10.3390/ijerph16020256
Web of Science® Google Scholar
36 Akram M., Wasim F., and Al-Kenani A. N., A Hybrid decision-making approach under complex Pythagorean fuzzy N-soft sets, International Journal of Computational Intelligence Systems. (2021) 14, no. 1, 1263–1291, https://doi.org/10.2991/ijcis.d.210331.002.
10.2991/ijcis.d.210331.002
Web of Science® Google Scholar
37 Akram Shumaiza M., Multi-criteria decision making based on q-rung orthopair fuzzy promethee approach [J], Iranian Journal of Fuzzy Systems. (2021) 18, no. 5, 107–127.
Web of Science® Google Scholar
38 Chen Z. S., Zhang X., Rodríguez R. M., Pedrycz L., and Martínez L., Expertise-based bid evaluation for construction-contractor selection with generalized comparative linguistic ELECTRE III, Automation in Construction. (2021) 125, 103578, https://doi.org/10.1016/j.autcon.2021.103578.
10.1016/j.autcon.2021.103578
Web of Science® Google Scholar
39 Yatsalo B., Korobov A., Öztayşi B., Kahraman L., and Martínez L., Fuzzy extensions of PROMETHEE: models of different complexity with different ranking methods and their comparison, Fuzzy Sets and Systems. (2021) 422, no. 15, 1–26, https://doi.org/10.1016/j.fss.2020.08.015.
10.1016/j.fss.2020.08.015
Web of Science® Google Scholar
40 Zhu X., Fang S., and Simutula A., Comprehensive evaluation of highway route scheme [J], Highway engineering. (2008) no. 5, 85–87+113.
Google Scholar
41 Chen C., Wang C., Wen P., Sun X., and Guo T., Performance evaluation of tourmaline modified asphalt mixture based on grey target decision method, Construction and Building Materials. (2019) 205, 137–147, https://doi.org/10.1016/j.conbuildmat.2019.01.168, 2-s2.0-85061090039.
10.1016/j.conbuildmat.2019.01.168
CAS Web of Science® Google Scholar
42 Ma M., Chen Q., Wang C., Fu H., and Li T., High-performance organosilicon-refractory bauxite: coating and fundamental properties, Construction and Building Materials. (2019) 207, 563–571, https://doi.org/10.1016/j.conbuildmat.2019.02.137, 2-s2.0-85062196752.
10.1016/j.conbuildmat.2019.02.137
CAS Web of Science® Google Scholar

Citing Literature

All articles

Evaluation Model of Highway Reconstruction and Expansion Scheme Based on Multiple Attribute Decision Making

Abstract

1. Introduction

2. Evaluation Index System

2.1. Technology Indexes

2.1.1. The Length of Route

2.1.2. Route Linearity

2.1.3. Total Length of Bridge, Culvert, and Tunnel

2.1.4. Number of Earthwork

2.1.5. Occupied Area

2.2. Economic Indexes

2.2.1. Economic Net Present Value

2.2.2. Economic Benefit-Cost Ratio

2.2.3. Economic Internal Rate of Return

2.2.4. Payback Period

2.3. Environmental Impact Indexes

2.3.1. Noise Environment

2.3.2. Atmospheric Environment

2.3.3. Water Environment

2.3.4. Soil or Ecological Environment

2.3.5. Sustainable Development Elements

2.4. Landscape Indexes

2.4.1. Landscape Coordination

2.4.2. Construction Style

3. Multiple Attribute Decision-Making Evaluation Model

3.1. Decision Matrix Standardization

3.2. Index Weight Calculation

3.2.1. FAHP Method

3.2.2. DDP Method

3.2.3. FAHF-DDP Method

3.2.4. Decision Value Calculation

4. Case Analysis

4.1. Standardized Decision Matrix

4.2. Evaluation Index Coupling Weight

4.3. Comparative Analysis of Different Methods

4.4. Influence of the Linear Combination Coefficient

5. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information