Volume 2022, Issue 1 3653225

Research Article

Open Access

SR-Fuzzy Sets and Their Weighted Aggregated Operators in Application to Decision-Making

Tareq M. Al-shami,

Corresponding Author

Tareq M. Al-shami

[email protected]

orcid.org/0000-0002-8074-1102

Department of Mathematics, Sana’a University, P.O.Box 1247 Sana’a, Yemen su.edu.ye

Search for more papers by this author

Hariwan Z. Ibrahim,

Hariwan Z. Ibrahim

orcid.org/0000-0001-9417-2695

Department of Mathematics, Faculty of Education, University of Zakho, Zakho, Iraq uoz-krg.org

Search for more papers by this author

A. A. Azzam,

A. A. Azzam

orcid.org/0000-0002-1206-9326

Department of Mathematics, Faculty of Science and Humanities, Prince Sattam Bin Abdulaziz University, Alkharj 11942, Saudi Arabia psau.edu.sa

Department of Mathematics, Faculty of Science, New Valley University, Elkharga 72511, Egypt

Search for more papers by this author

Ahmed I. EL-Maghrabi,

Ahmed I. EL-Maghrabi

Department of Mathematics, Faculty of Science, Kafrelsheikh University, Kafrelsheikh, Egypt kfs.edu.eg

Search for more papers by this author

Tareq M. Al-shami,

Corresponding Author

Tareq M. Al-shami

[email protected]

orcid.org/0000-0002-8074-1102

Department of Mathematics, Sana’a University, P.O.Box 1247 Sana’a, Yemen su.edu.ye

Search for more papers by this author

Hariwan Z. Ibrahim,

Hariwan Z. Ibrahim

orcid.org/0000-0001-9417-2695

Department of Mathematics, Faculty of Education, University of Zakho, Zakho, Iraq uoz-krg.org

Search for more papers by this author

A. A. Azzam,

A. A. Azzam

orcid.org/0000-0002-1206-9326

Department of Mathematics, Faculty of Science and Humanities, Prince Sattam Bin Abdulaziz University, Alkharj 11942, Saudi Arabia psau.edu.sa

Department of Mathematics, Faculty of Science, New Valley University, Elkharga 72511, Egypt

Search for more papers by this author

Ahmed I. EL-Maghrabi,

Ahmed I. EL-Maghrabi

Department of Mathematics, Faculty of Science, Kafrelsheikh University, Kafrelsheikh, Egypt kfs.edu.eg

Search for more papers by this author

First published: 11 March 2022

https://doi.org/10.1155/2022/3653225

Citations: 26

Academic Editor: Muhammad Gulzar

Share a link

Email
Wechat
Bluesky

Abstract

An intuitionistic fuzzy set is one of the efficient generalizations of a fuzzy set for dealing with vagueness/uncertainties in information. Under this environment, in this manuscript, we familiarize a new type of extensions of fuzzy sets called square-root fuzzy sets (briefly, SR-Fuzzy sets) and contrast SR-Fuzzy sets with intuitionistic fuzzy sets and Pythagorean fuzzy sets. We discover the essential set of operations for the SR-Fuzzy sets along with their several properties. In addition, we define a score function for the ranking of SR-Fuzzy sets. To study multiattribute decision-making problems, we introduce four new weighted aggregated operators, namely, SR-Fuzzy weighted average (SR-FWA) operator, SR-Fuzzy weighted geometric (SR-FWG) operator, SR-Fuzzy weighted power average (SR-FWPA) operator, and SR-Fuzzy weighted power geometric (SR-FWPG) operator over SR-Fuzzy sets. We apply these operators to select the top-rank university and show how we can choose the best option by comparing the aggregate outputs through score values.

1. Introduction

The idea of fuzzy sets was proposed by Zadeh [1] to handle the imprecise information. The notion of rough set theory was originally introduced by Pawlak [2], and it was applied to many different domains (see [3–5]). The concept of soft sets was first defined by Molodtsov [6] as a general mathematical tool for dealing with uncertain objects. The merging between fuzzy sets and some uncertainty approaches such as rough sets and soft sets have been discussed in [7–9].

In several real-life situations, the degree of nonmembership is not obtained from the degree of membership. In these cases, the notion of intuitionistic fuzzy sets defined by Atanassov [10] worked very well. It is one of the interesting generalizations of fuzzy sets with best applicability. In various fields, the applications of intuitionistic fuzzy sets appear, including optimization problems, medical diagnosis, and decision-making [11–15]. However, there are numerous situations where the decision-maker may supply the degrees of membership and nonmembership of a specific attribute in such a way that their sum is greater than one. Therefore, Yager [16] put forward the concept of Pythagorean fuzzy sets which is a generalization of intuitionistic fuzzy sets, and it is a more powerful tool to solve uncertain problems. Ibrahim et al. [17] defined a new generalization of Pythagorean fuzzy sets called (3, 2)-Fuzzy sets. The main advantage of (3, 2)-Fuzzy sets is that they can characterize more vague cases than Pythagorean fuzzy sets, which can be exploited in many decision-making problems.

The idea of intuitionistic fuzzy weighted averaging operators was proposed by Xu [18]. Some geometric weighted, geometric ordered weighted, and geometric hybrid operators under the environment of intuitionistic fuzzy sets were introduced by Xu and Yager [19]. In Refs. [20–25], many researchers worked in the area of intuitionistic fuzzy sets and established various aggregation operators which are applied to group decision-making. After the advent of the Pythagorean fuzzy sets, the operators of Pythagorean fuzzy aggregation have also become an important and interesting field for research. Yager and Abbasov [26, 27], in 2013, introduced the concepts of weighted geometric, weighted averaging, ordered weighted geometric, and ordered weighted averaging operators in the frame of Pythagorean fuzzy environment. The essential properties of Pythagorean fuzzy aggregation operators were investigated by the authors of [28]. Shahzadi et al. [29] established some aggregation operators under Pythagorean fuzzy data for assessing the distinct preferences of the choice among the decision-making process. By using Pythagorean fuzzy values, Rahman et al. presented many aggregation operators like weighted geometric [30], hybrid geometric [31], weighted averaging [32], and ordered weighted geometric operators [33] and also discussed their practical applications.

The aims of writing this paper are (1) to present a novel extension of intuitionistic fuzzy set called SR-Fuzzy sets which is not obtained from q-rung orthopair fuzzy sets, (2) to introduce novel types of weighted aggregation operators and discuss their main properties, and (3) to investigate a MCDM methods depending on these operators.

In this paper, we define the concept of SR-Fuzzy sets and compare it with the other types of fuzzy sets in Section 2. Then, we introduce the set of operations for the SR-Fuzzy sets and explore their main features in Section 3. Also, the concepts of weighted aggregated operators for SR-Fuzzy sets are investigated. Thereafter, we describe MADM problems under these operators in Section 4. Finally, we outline the main achievements of the paper and propose some upcoming works in Section 5.

Before we present our main concepts and results, we recall the definitions of the intuitionistic fuzzy set (IFS) and Pythagorean fuzzy set (PFS).

Definition 1. Let S be a universal set such that Y_Θ : S⟶[0, 1] and Ψ_Θ : S⟶[0, 1] are mapping. Then, the intuitionistic fuzzy set (IFS) [10] (resp., Pythagorean fuzzy set (PFS) [16]) is defined by the following:

(1)

including the condition 0 ≤ Y_Θ(p) + Ψ_Θ(p) ≤ 1 (resp.,

), where Y_Θ(p) is the degree of membership and Ψ_Θ(p) is the degree of nonmembership of every p ∈ S to Θ.

2. SR-Fuzzy Sets

In this section, we initiate the notion of SR-Fuzzy sets and study its features in detail. For computations, we use only six decimal places in the whole paper.

Definition 2. Let S be a universal set such that Y_Θ : S⟶[0, 1] and Ψ_Θ : S⟶[0, 1] are mapping. Then, the SR-Fuzzy set (briefly, SR-FS) Θ is defined as following:

(2)

where Y_Θ(p) is the degree of membership and Ψ_Θ(p) is the degree of nonmembership of p ∈ S to Θ, such that

(3)

Then, there is a degree of indeterminacy of p ∈ S to Θ defined by

(4)

It is obvious that . Otherwise, π_Θ(p) = 0 whenever .

In the interest of simplicity, we shall mention the symbol Θ = (Y_Θ, Ψ_Θ) for the SR-FS Θ = {〈p, Y_Θ(p), Ψ_Θ(p)〉: p ∈ S}. The space of SR-Fuzzy membership grades is displayed in Figure 1.

Example 1. Assume that Y_Θ(p) = 0.3 and Ψ_Θ(p) = 0.8 for S = {p}. Then, Θ = (0.3,0.8) is not an intuitionistic fuzzy set because 0.3 + 0.8 = 1.1 > 1. In contrast, Θ = (0.3,0.8) is an SR-FS because .

Details are in the caption following the image — Open in figure viewer PowerPoint

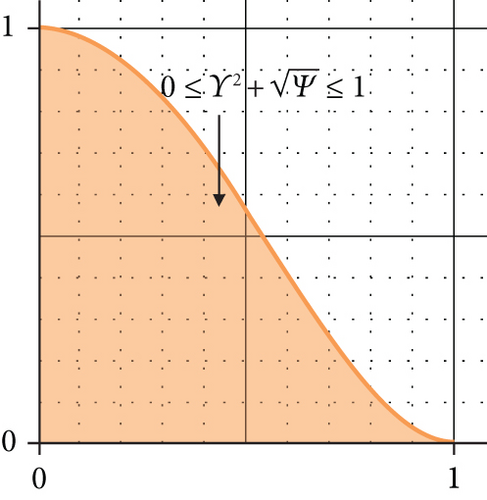
Note that π_Θ(p) ≈ 0.015573, and hence, .

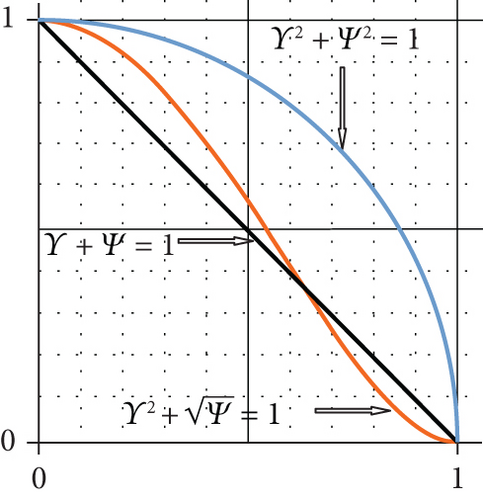
Remark 3. From Figure 2, we get that

(1)
The space of Pythagorean membership grades is larger than the space of SR-Fuzzy membership grades
(2)
The SR-Fuzzy and intuitionistic fuzzy sets intersect at the point
(3)
For and , the space of SR-Fuzzy membership grades starts to be larger than the space of intuitionistic membership grades
(4)
for and , the space of SR-Fuzzy membership grades starts to be smaller than the space of intuitionistic membership grades

Definition 4. Let and be two SR-FSs; then

(1)
Θ₁ = Θ₂ if and only if and
(2)
Θ₁ ≥ Θ₂ if and only if and

Example 2.

(1)
If Θ₁ = (0.2,0.9) and Θ₂ = (0.2,0.9) for S = {p}, then Θ₁ = Θ₂
(2)
If Θ₁ = (0.2,0.9) and Θ₂ = (0.1,0.91) for S = {p}, then Θ₂ ≤ Θ₁

Definition 5. Let and be two SR-Fuzzy sets (SR-FSs). Then

Note that , so is an SR-Fuzzy set. It is obvious that .

Example 3. Assume that and are both SR-FSs for S = {p}. Then

Theorem 6. Let and be two SR-FSs; then the following properties hold:

(1)
Θ₁∩Θ₂ = Θ₂∩Θ₁
(2)
Θ₁ ∪ Θ₂ = Θ₂ ∪ Θ₁

Proof. From Definition 5, we can obtain the following:

(1)
(2)
The proof is similar to (1)

Theorem 7. Let , and be three SR-FSs; then

(1)
Θ₁∩(Θ₂∩Θ₃) = (Θ₁∩Θ₂)∩Θ₃
(2)
Θ₁ ∪ (Θ₂ ∪ Θ₃) = (Θ₁ ∪ Θ₂) ∪ Θ₃

Proof. For the three SR-FSs Θ₁, Θ₂, and Θ₃, according to Definition 5, we obtain the following:

(1)
(2)
The proof is similar to (1)

Theorem 8. Let and be two SR-FSs. Then

(1)
(Θ₁∩Θ₂) ∪ Θ₂ = Θ₂
(2)
(Θ₁ ∪ Θ₂)∩Θ₂ = Θ₂

Proof. From Definition 5, we obtain the following:

(1)
(2)
The proof is similar to (1)

Theorem 9. Let and be two SR-FSs; then

Proof. For the two SR-FSs Θ₁ and Θ₂, according to Definition 5, we obtain the following:

(1)
(2)
The proof is similar to (1)

3. Aggregation of SR-Fuzzy Sets and Its Properties

In this section, we introduce some new operations on SR-Fuzzy sets. Besides, we study the SR-Fuzzy aggregation operators and some attracted properties are indicated in detail.

3.1. Some Operations On SR-Fuzzy Sets

Definition 10. Let Θ = (Y_Θ, Ψ_Θ), and be three SR-FSs and ρ be a positive real value (ρ > 0). Then their operations are defined as follows:

Example 4. Suppose that and are both SR-FSs for S = {p}. Then

(1)
(2)
(3)
, for ρ = 3
(4)
, for ρ = 3

Theorem 11. If and are two SR-FSs, then Θ₁ ⊕ Θ₂ and Θ₁ ⊗ Θ₂ are also SR-FSs.

Proof. For SR-FSs and , the following relations are evident:

(5)

Then, we have

(6)

which indicates that

(7)

Since and , then , and we get , and hence, .

Similarly, we get

(8)

It is obvious that

(9)

Then we get

(10)

Therefore

(11)

and

(12)

Similarly, we have

(13)

and

(14)

These indicate that both of Θ₁ ⊕ Θ₂ and Θ₁ ⊗ Θ₂ are SR-FSs.

Theorem 12. Let Θ = (Y_Θ, Ψ_Θ) be an SR-FS and ρ be a positive real value. Then, ρΘ and Θ^ρ are also SR-FSs.

Proof. Since , , and , then

(15)

It is obvious that ; then we get

(16)

Similarly, we also get

(17)

Therefore, ρΘ and Θ^ρ are SR-FSs.

Theorem 13. Let and be two SR-FSs. Then the following properties hold:

(1)
Θ₁ ⊕ Θ₂ = Θ₂ ⊕ Θ₁
(2)
Θ₁ ⊗ Θ₂ = Θ₂ ⊗ Θ₁

Proof. From Definition 10, we obtain the following:

Theorem 14. Let Θ = (Y_Θ, Ψ_Θ), and be three SR-FSs. Then

(1)
ρ(Θ₁ ⊕ Θ₂) = ρΘ₁ ⊕ ρΘ₂, for ρ > 0
(2)
(ρ₁ + ρ₂)Θ = ρ₁Θ ⊕ ρ₂Θ, for ρ₁, ρ₂ > 0
(3)
, for ρ > 0
(4)
, for ρ₁, ρ₂ > 0

Proof. For the three SR-FSs Θ, Θ₁, and Θ₂, and ρ, ρ₁, ρ₂ > 0, according to Definition 10, we obtain the following:

(1)
.

And

Theorem 15. Let and be two SR-FSs and ρ > 0. Then

(1)
ρ(Θ₁ ∪ Θ₂) = ρΘ₁ ∪ ρΘ₂
(2)

Proof. For the two SR-FSs Θ₁ and Θ₂, and ρ > 0, according to Definitions 5 and 10, we obtain the following:

(1)
.

And

(2)
The proof is similar to (1)

Theorem 16. Let Θ = (Y_Θ, Ψ_Θ), and be three SR-FSs, and ρ > 0. Then

Proof. For the three SR-FSs Θ, Θ₁ and Θ₂, and ρ > 0, according to Definitions 5(3) and 10, we obtain the following:

Theorem 17. Let , , and be three SR-FSs. Then

(1)
(Θ₁∩Θ₂) ⊕ Θ₃ = (Θ₁ ⊕ Θ₃)∩(Θ₂ ⊕ Θ₃)
(2)
(Θ₁ ∪ Θ₂) ⊕ Θ₃ = (Θ₁ ⊕ Θ₃) ∪ (Θ₂ ⊕ Θ₃)
(3)
(Θ₁∩Θ₂) ⊗ Θ₃ = (Θ₁ ⊗ Θ₃)∩(Θ₂ ⊗ Θ₃)
(4)
(Θ₁ ∪ Θ₂) ⊗ Θ₃ = (Θ₁ ⊗ Θ₃) ∪ (Θ₂ ⊗ Θ₃)

Proof. By Definitions 5 and 10, we obtain the following:

(1)
.

And .

Thus, (Θ₁∩Θ₂) ⊕ Θ₃ = (Θ₁ ⊕ Θ₃)∩(Θ₂ ⊕ Θ₃)

(2)
The proof is similar to (1)
(3)
.

And .

Thus, (Θ₁∩Θ₂) ⊗ Θ₃ = (Θ₁ ⊗ Θ₃)∩(Θ₂ ⊗ Θ₃)

(4)
The proof is similar to (3)

Theorem 18. Let , , and be three SR-FSs. Then

(1)
Θ₁ ⊕ Θ₂ ⊕ Θ₃ = Θ₁ ⊕ Θ₃ ⊕ Θ₂
(2)
Θ₁ ⊗ Θ₂ ⊗ Θ₃ = Θ₁ ⊗ Θ₃ ⊗ Θ₂

Proof.

(1)
(2)
The proof is similar to (1)

In order to rank SR-FSs, we define the score function and accuracy function of the SR-FS:

Definition 19.

(1)
The score function of an SR-FS Θ = (Y_Θ, Ψ_Θ) can be represented as
(2)
The accuracy function of an SR-FS Θ = (Y_Θ, Ψ_Θ) can be represented as

Example 5. For an SR-FS Θ = (0.3,0.8), we find that score(Θ) ≈ −0.804427 and accuracy(Θ) ≈ 0.984427. In particular, if Θ = (0, 1), then score(Θ) = −1, and if Θ = (1, 0), then score(Θ) = 1.

Theorem 20. The suggested score function of any SR-FS Θ = (Y_Θ, Ψ_Θ), denoted by score(Θ) lies in [−1, 1].

Proof. Since for any SR-FS Θ, we have , hence and . Therefore, . Hence, score(Θ) ∈ [−1, 1].

Remark 21. The suggested accuracy function of any SR-FS Θ = (Y_Θ, Ψ_Θ), denoted by accuracy(Θ), lies in [0, 1].

3.2. Aggregation of SR-Fuzzy Sets

Definition 22. Let (i = 1, 2, ⋯, m) be a value of SR-FSs and be the weight vector of Θ_i with w_i > 0 and . Then an SR-Fuzzy

(1)
Weighted average (SR-FWA) operator is a function SR-FWA : Θ^m⟶Θ, where

(18)

(2)
Weighted geometric (SR-FWG) operator is a function SR-FWG : Θ^m⟶Θ, where

(19)

(3)
Weighted power average (SR-FWPA) operator is a function SR-FWPA : Θ^m⟶Θ, where

(20)

(4)
Weighted power geometric (SR-FWPG) operator is a function SR-FWPG : Θ^m⟶Θ, where

(21)

Example 6. Suppose that Θ₁ = (0.53,0.49), Θ₂ = (0.52,0.51), Θ₃ = (0.26,0.76), Θ₄ = (0.51,0.53), Θ₅ = (0.50,0.54), and Θ₆ = (0.22,0.86) are six SR-Fuzzy sets, and let w = (0.12,0.32,0.22,0.13,0.10,0.11)^T be a weight vector of Θ_i (i = 1, 2, ⋯, 6). Then

(1)
SR − FWA(Θ₁, Θ₂, ⋯, Θ₆) = (0.53 × 0.12 + 0.52 × 0.32 + 0.26 × 0.22 + 0.51 × 0.13 + 0.50 × 0.10 + 0.22 × 0.11,0.49 × 0.12 + 0.51 × 0.32 + 0.76 × 0.22 + 0.53 × 0.13 + 0.54 × 0.10 + 0.86 × 0.11) = (0.4277,0.6067)
(2)
SR − FWG(Θ₁, Θ₂, ⋯, Θ₆) = (0.53^0.12 × 0.52^0.32 × 0.26^0.22 × 0.51^0.13 × 0.50^0.10 × 0.22^0.11, 0.49^0.12 × 0.51^0.32 × 0.76^0.22 × 0.53^0.13 × 0.54^0.10 × 0.86^0.11) ≈ (0.404460,0.593219)
(3)
(4)

Remark 23. Note that the ordered values induced from the different operators introduced in Definition 22 need not be an SR-FS. To validate this matter, take the ordered values (0.452616,0.632933) which are given in (4) of the above example. By calculating, we find that which means that SR-FWPG(Θ₁, Θ₂, ⋯, Θ₆) is not an SR-FS.

Theorem 24. Let (i = 1, 2, ⋯, m) be a value of SR-FSs, Θ = (Y_Θ, Ψ_Θ) be SR-FS, and be a weight vector of Θ_i with . Then

(1)
SR − FWA(Θ₁ ⊕ Θ, Θ₂ ⊕ Θ, ⋯, Θ_m ⊕ Θ) ≥ SR − FWA(Θ₁ ⊗ Θ, Θ₂ ⊗ Θ, ⋯, Θ_m ⊗ Θ)
(2)
SR − FWG(Θ₁ ⊕ Θ, Θ₂ ⊕ Θ, ⋯, Θ_m ⊕ Θ) ≥ SR − FWG(Θ₁ ⊗ Θ, Θ₂ ⊗ Θ, ⋯, Θ_m ⊗ Θ)
(3)
SR − FWPA(Θ₁ ⊕ Θ, Θ₂ ⊕ Θ, ⋯, Θ_m ⊕ Θ) ≥ SR − FWPA(Θ₁ ⊗ Θ, Θ₂ ⊗ Θ, ⋯, Θ_m ⊗ Θ)
(4)
SR − FWPG(Θ₁ ⊕ Θ, Θ₂ ⊕ Θ, ⋯, Θ_m ⊕ Θ) ≥ SR − FWPG(Θ₁ ⊗ Θ, Θ₂ ⊗ Θ, ⋯, Θ_m ⊗ Θ)

Proof. We will display the proof of (1) and (4). The other affirmations are proved in a similar fashion.

(1)
For any (i = 1, 2, ⋯, m) and Θ = (Y_Θ, Ψ_Θ), we get

(22)

that is

(23)

and

(24)

By Definition 10 (1) and (2), we have

(25)

Therefore, from (25), the proof is proved

(4)
For any (i = 1, 2, ⋯, m) and Θ = (Y_Θ, Ψ_Θ), we get

(26)

Similarly

(27)

Now, by (1) and (2) of Definition 10, we have

(28)

Hence, SR-FWPG(Θ₁ ⊕ Θ, Θ₂ ⊕ Θ, ⋯, Θ_m ⊕ Θ) ≥ SR-FWPG(Θ₁ ⊗ Θ, Θ₂ ⊗ Θ, ⋯, Θ_m ⊗ Θ).

Theorem 25. Let (i = 1, 2, ⋯, m) be a value of SR-FSs, Θ = (Y_Θ, Ψ_Θ) be SR-FS, and be the weight vector of Θ_i with ; then

(1)
SR-FWA(Θ₁ ⊕ Θ, Θ₂ ⊕ Θ, ⋯, Θ_m ⊕ Θ) ≥ SR-FWA(Θ₁, Θ₂, ⋯, Θ_m) ⊗ Θ
(2)
SR-FWG(Θ₁ ⊕ Θ, Θ₂ ⊕ Θ, ⋯, Θ_m ⊕ Θ) ≥ SR-FWG(Θ₁, Θ₂, ⋯, Θ_m) ⊗ Θ
(3)
SR-FWPA(Θ₁ ⊕ Θ, Θ₂ ⊕ Θ, ⋯, Θ_m ⊕ Θ) ≥ SR-FWPA(Θ₁, Θ₂, ⋯, Θ_m) ⊗ Θ
(4)
SR-FWPG(Θ₁ ⊕ Θ, Θ₂ ⊕ Θ, ⋯, Θ_m ⊕ Θ) ≥ SR-FWPG(Θ₁, Θ₂, ⋯, Θ_m) ⊗ Θ

Proof. We will display the proof of (1). The other affirmations are proved in a similar fashion.

(1)
For any (i = 1, 2, ⋯, m) and Θ = (Y_Θ, Ψ_Θ), we get

(29)

that is

(30)

Similarly,

(31)

By (1) and (2) of Definition 10, we have

(32)

Hence, the desired result is proved.

Theorem 26. Let and (i = 1, 2, ⋯, m) be two values of SR-FSs, and be a weight vector of them with . Then

(1)
SR − FWA(Θ₁ ⊕ K₁, Θ₂ ⊕ K₂, ⋯, Θ_m ⊕ K_m) ≥ SR − FWA(Θ₁ ⊗ K₁, Θ₂ ⊗ K₂, ⋯, Θ_m ⊗ K_m)
(2)
SR − FWG(Θ₁ ⊕ K₁, Θ₂ ⊕ K₂, ⋯, Θ_m ⊕ K_m) ≥ SR − FWG(Θ₁ ⊗ K₁, Θ₂ ⊗ K₂, ⋯, Θ_m ⊗ K_m)
(3)
SR − FWPA(Θ₁ ⊕ K₁, Θ₂ ⊕ K₂, ⋯, Θ_m ⊕ K_m) ≥ SR − FWPA(Θ₁ ⊗ K₁, Θ₂ ⊗ K₂, ⋯, Θ_m ⊗ K_m)
(4)
SR − FWPG(Θ₁ ⊕ K₁, Θ₂ ⊕ K₂, ⋯, Θ_m ⊕ K_m) ≥ SR − FWPG(Θ₁ ⊗ K₁, Θ₂ ⊗ K₂, ⋯, Θ_m ⊗ K_m)

Proof. We will display the proof of (1). The other affirmations are proved in a similar fashion.

(1)
For any and (i = 1, 2, ⋯, m), we get

(33)

that is

(34)

Similarly

(35)

By (1) and (2) of Definition 10, we have

(36)

Thus, SR-FWA(Θ₁ ⊕ K₁, Θ₂ ⊕ K₂, ⋯, Θ_m ⊕ K_m) ≥ SR-FWA(Θ₁ ⊗ K₁, Θ₂ ⊗ K₂, ⋯, Θ_m ⊗ K_m).

Theorem 27. Let (i = 1, 2, ⋯, m) be a value of SR-FSs, and be the weight vector of Θ_i with and ρ ≥ 1; then

Proof. We will display the proof of (1). The other affirmations are proved in a similar fashion.

(1)
For any (i = 1, 2, ⋯, m), we have

(37)

Let , and we have to show . Using the Newton generalized binomial theorem, we are able to get

(38)

Thus, , that is

(39)

Similarly,

(40)

Therefore .

Theorem 28. Let (i = 1, 2, ⋯, m) be a value of SR-FSs, Θ = (Y_Θ, Ψ_Θ) be SR-FS, and be a weight vector of Θ_i with and ρ ≥ 1. Then

Proof. We will display the proof of (1). The other affirmations are proved in a similar fashion.

(1)
For any (i = 1, 2, ⋯, m) and Θ = (Y_Θ, Ψ_Θ), we have

(41)

Let , and we have to show that . At first we indicate and take the derivative of ; then

(42)

Therefore, if , then is monotonic increasing, and if , then is monotonic decreasing, so . Since , hence

(43)

Similarly

(44)

Hence, .

To prove the following three results, we suppose that the values obtained from the introduced operators are an SR-FS (see Remark 23).

Theorem 29. Let (i = 1, 2, ⋯, m) be a value of SR-FSs, Θ = (Y_Θ, Ψ_Θ) be SR-FS, and be the weight vector of Θ_i with ; then

(1)
SR-FWA(Θ₁, Θ₂, ⋯, Θ_m) ⊕ Θ ≥ SR-FWA(Θ₁, Θ₂, ⋯, Θ_m) ⊗ Θ
(2)
SR-FWG(Θ₁, Θ₂, ⋯, Θ_m) ⊕ Θ ≥ SR-FWG(Θ₁, Θ₂, ⋯, Θ_m) ⊗ Θ
(3)
SR-FWPA(Θ₁, Θ₂, ⋯, Θ_m) ⊕ Θ ≥ SR-FWPA(Θ₁, Θ₂, ⋯, Θ_m) ⊗ Θ
(4)
SR-FWPG(Θ₁, Θ₂, ⋯, Θ_m) ⊕ Θ ≥ SR-FWPG(Θ₁, Θ₂, ⋯, Θ_m) ⊗ Θ

Proof. We will display the proof of (1). The other affirmations are proved in a similar fashion.

(1)
For any (i = 1, 2, ⋯, m) and Θ = (Y_Θ, Ψ_Θ), we get

(45)

Similarly

(46)

By (1) and (2) of Definition 10, we obtain

(47)

Hence, the desired result is proved.

Theorem 30. Let and (i = 1, 2, ⋯, m) be two values of SR-FSs and be a weight vector of them with . Then

(1)
SR − FWA(Θ₁, Θ₂, ⋯, Θ_m) ⊕ SR − FWA(K₁, K₂, ⋯, K_m) ≥ SR − FWA(Θ₁, Θ₂, ⋯, Θ_m) ⊗ SR − FWA(K₁, K₂, ⋯, K_m)
(2)
SR − FWG(Θ₁, Θ₂, ⋯, Θ_m) ⊕ SR − FWG(K₁, K₂, ⋯, K_m) ≥ SR − FWG(Θ₁, Θ₂, ⋯, Θ_m) ⊗ SR − FWG(K₁, K₂, ⋯, K_m)
(3)
SR − FWPA(Θ₁, Θ₂, ⋯, Θ_m) ⊕ SR − FWPA(K₁, K₂, ⋯, K_m) ≥ SR − FWPA(Θ₁, Θ₂, ⋯, Θ_m) ⊗ SR − FWPA(K₁, K₂, ⋯, K_m)
(4)
SR − FWPG(Θ₁, Θ₂, ⋯, Θ_m) ⊕ SR − FWPG(K₁, K₂, ⋯, K_m) ≥ SR − FWPG(Θ₁, Θ₂, ⋯, Θ_m) ⊗ SR − FWPG(K₁, K₂, ⋯, K_m)

Theorem 31. Let (i = 1, 2, ⋯, m) be a value of SR-FSs and be the weight vector of Θ_i with and ρ ≥ 1; then

4. Application of SR-FSs to Select the Top-Rank University

In this section, we apply the SR-FWA, SR-FWG, SR-FWPA, and SR-FWPG operators to select the top-rank university among different universities.

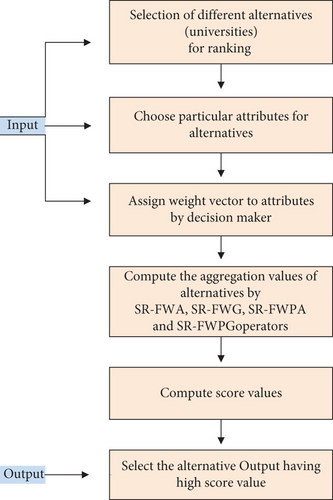
One of the following techniques to handle the multicriteria decision-making (in short, MCDM) problems is based on the different types of fuzzy weighted operators. Herein, we, first, show the steps used in the proposed methodology for MCDM:

Step 1. Represent a MCDM problem under study using the SR-Fuzzy decision matrix.

Step 2. Transmit SR-Fuzzy decision matrix into the normalized SR-Fuzzy decision matrix.

Step 3. Compute for each alternative all kinds of SR-Fuzzy weighted operators.

Step 4. Compute the scores and accuracy functions for each alternative (as we showed in Remark 23, the ordered values induced from the different operators need not be an SR-FS; however, we apply the formulas of scores and accuracy functions given in Definition 19 for those ordered values).

Step 5. Compare the given alternatives based on the score function.

Step 6. If the score functions are equal for some alternatives, then compare between them in terms of accuracy function.

Step 7. Determine the optimal ranking order of the alternatives and recognize the optimal alternative(s).

In the next example, we illustrate how the above steps are applied to select the top-rank university among different universities.

Example 7. Let U = {U₁, U₂, U₃} be a set of alternatives (universities) and P = {P₁, P₂, P₃, P₄, P₅, P₆, P₇} be a set of seven attributes for the selection of universities, where

(48)

Suppose that the weight vector of the attributes given by the decision-maker is w = (0.1,0.37, 0.14,0.03,0.27,0.06,0.03)^T. Obviously, . The SR-F values of the alternatives according to different attributes are given in Table 1, where is the positive membership degree for which alternative obeys the given attribute and is the membership degree for which alternative does not obey the given attribute such that and .

1. SR-Fuzzy values.

Universities	P₁	P₂	P₃	P₄	P₅	P₆	P₇
U₁	(0.7, 0.2)	(0.4, 0.5)	(0.4, 0.7)	(0.5, 0.5)	(0.4, 0.5)	(0.7, 0.1)	(0.8, 0.1)
U₂	(0.6, 0.3)	(0.3, 0.6)	(0.3, 0.8)	(0.6, 0.4)	(0.4, 0.7)	(0.6, 0.1)	(0.7, 0.2)
U₃	(0.8, 0.1)	(0.5, 0.4)	(0.5, 0.5)	(0.6, 0.4)	(0.7, 0.2)	(0.8, 0.1)	(1, 0)

Applying the proposed aggregation operators given in Definition 22, score and accuracy functions, we find, as demonstrated in Table 2, that the optimal ranking order of the three universities is U₃≻U₁≻U₂, and thus, the top alternative is U₃.

2. Evaluation of scores and accuracy with SR-Fuzzy aggregation operators.

	U₁	U₂	U₃	rank order
SR − FWA	(0.463, 0.462)	(0.396, 0.577)	(0.62, 0.3)
Score	-0.465337	-0.602789	-0.163323	U₃≻U₁≻U₂
Accuracy	0.894075	0.916421	0.932123	U₃≻U₂≻U₁
SR − FWG	(0.449660, 0.413739)	(0.379393, 0.521591)	(0.606024, 0)
Score	-0.441031	-0.578274	0.367265	U₃≻U₁≻U₂
Accuracy	0.845420	0.866152	0.367265	U₂≻U₁≻U₃
SR − FWPA	(0.479479, 0.440997)	(0.414970, 0.553320)	(0.634823, 0.273865)
Score	-0.434176	-0.571655	-0.120321	U₃≻U₁≻U₂
Accuracy	0.893976	0.916055	0.926321	U₃≻U₂≻U₁
SR − FWPG	(0.496476, 0.475544)	(0.425919, 0.605327)	(1, 0)
Score	-0.443109	-0.596621	1	U₃≻U₁≻U₂
Accuracy	0.936085	0.959435	1	U₃≻U₂≻U₁

Note that the score functions for the data given in Table 2 are unequal, so they are enough to determine the optimal alternative.

The method adopted in this application is illustrated in Figure 3.

5. Conclusions

This paper contributes to the fuzzy set theory in which interest in it grew since the moment Zadeh launched it. To handle some real-life issues which are difficult to solve using fuzzy set theory, some researchers extended this theory to other fuzzy models; the most important are IFSs and PFSs.

In this paper, we have proposed a new shape of fuzzy sets called an SR-Fuzzy set and revealed its relationship with other types of the generalizations of fuzzy sets. Then, some operators on SR-Fuzzy sets have been defined, and their relationships have been presented. Furthermore, we have introduced four new weighted aggregated operators over SR-Fuzzy sets and discussed their properties in detail. Moreover, we have shown this procedure with one practical fully developed example.

In future works, further applications of SR-Fuzzy sets may be investigated, and also, SR-Fuzzy soft sets may be explored. Also, we will try to generate the topology from the collection of SR-Fuzzy sets and introduce the ideas of connectedness and compactness in SR-Fuzzy topology.

Conflicts of Interest

The authors declare no conflicts of interest.

Open Research

Data Availability

No data were used to support this study.

References

1 Zadeh L. A., Fuzzy sets, Control. (1965) 8, no. 3, 338–353, https://doi.org/10.1016/S0019-9958(65)90241-X, 2-s2.0-34248666540.
10.1016/S0019-9958(65)90241-X
Web of Science® Google Scholar
2 Pawlak Z., Rough sets, International journal of information and computer sciences. (1982) 11, no. 5, 341–356, https://doi.org/10.1007/BF01001956, 2-s2.0-27744565978.
10.1007/BF01001956
Google Scholar
3 Al-shami T. M., An improvement of rough sets’ accuracy measure using containment neighborhoods with a medical application, Information Sciences. (2021) 569, 110–124, https://doi.org/10.1016/j.ins.2021.04.016.
10.1016/j.ins.2021.04.016
Web of Science® Google Scholar
4 Al-shami T. M., Improvement of the approximations and accuracy measure of a rough set using somewhere dense sets, Soft Computing. (2021) 25, no. 23, 14449–14460, https://doi.org/10.1007/s00500-021-06358-0.
10.1007/s00500-021-06358-0
Web of Science® Google Scholar
5 Al-shami T. M. and Ciucci D., Subset neighborhood rough sets, Knowledge-Based Systems. (2022) 237, https://doi.org/10.1016/j.knosys.2021.107868.
10.1016/j.knosys.2021.107868
Web of Science® Google Scholar
6 Molodtsov D., Soft set theory--first results, Computers & Mathematcs with Applications. (1999) 37, no. 4-5, 19–31, https://doi.org/10.1016/S0898-1221(99)00056-5.
10.1016/S0898-1221(99)00056-5
Web of Science® Google Scholar
7 Ahmad B. and Kharal A., On fuzzy soft sets, Advances in Fuzzy Systems. (2009) 2009, 6, 586507, https://doi.org/10.1155/2009/586507, 2-s2.0-69449088128.
10.1155/2009/586507
Google Scholar
8 Atef M., Ali M. I., and Al-shami T. M., Fuzzy soft covering-based multi-granulation fuzzy rough sets and their applications, Computational and Applied Mathematics. (2021) 40, no. 4, https://doi.org/10.1007/s40314-021-01501-x.
10.1007/s40314-021-01501-x
Web of Science® Google Scholar
9 Cagman N., Enginoglu S., and Citak F., Fuzzy soft set theory and its application, Iranian Journal of Fuzzy Systems. (2011) 8, no. 3, 137–147.
Web of Science® Google Scholar
10 Atanassov K. T., Intuitionistic fuzzy sets, Fuzzy Sets and Systems. (1986) 20, no. 1, 87–96, https://doi.org/10.1016/S0165-0114(86)80034-3, 2-s2.0-0002740725.
10.1016/S0165-0114(86)80034-3
Web of Science® Google Scholar
11 Kozae A. M., Shokry M., and Omran M., Intuitionistic fuzzy set and its application in corona Covid-19, Applied and Computational Mathematics. (2020) 9, no. 5, 146–154, https://doi.org/10.11648/j.acm.20200905.11.
10.11648/j.acm.20200905.11
Google Scholar
12 Atanassov K. T., Applications of intuitionistic fuzzy sets Intuitionistic Fuzzy Sets. Studies in Fuzziness and Soft Computing, 1999, 35, Physica, Heidelberg, https://doi.org/10.1007/978-3-7908-1870-3_5.
10.1007/978-3-7908-1870-3_5
Google Scholar
13 Al-shami T. M. and Azzam A. A., Infra soft semiopen sets and infra soft semicontinuity, Journal of Function Spaces. (2021) 2021, 11, 5716876, https://doi.org/10.1155/2021/5716876.
10.1155/2021/5716876
Web of Science® Google Scholar
14 Garg H. and Singh S., A novel triangular interval type-2 intuitionistic fuzzy set and their aggregation operators, Iranian Journal of Fuzzy Systems. (2018) 15, 69–93.
Web of Science® Google Scholar
15 Garg H. and Kumar K., An advanced study on the similarity measures of intuitionistic fuzzy sets based on the set pair analysis theory and their application in decision making, Soft Computing. (2018) 22, no. 15, 4959–4970, https://doi.org/10.1007/s00500-018-3202-1, 2-s2.0-85047786375.
10.1007/s00500-018-3202-1
Web of Science® Google Scholar
16 Yager R. R., Pythagorean fuzzy subsets, 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), 2013, Edmonton, AB, Canada, 57–61.
Google Scholar
17 Ibrahim H. Z., Al-shami T. M., and Elbarbary O. G., (3, 2)-Fuzzy sets and their applications to topology and optimal choices, Computational Intelligence and Neuroscience. (2021) 2021, 14, 1272266, https://doi.org/10.1155/2021/1272266.
10.1155/2021/1272266
PubMed Web of Science® Google Scholar
18 Xu Z., Intuitionistic fuzzy aggregation operators, IEEE Transactions on Fuzzy Systems. (2007) 15, no. 6, 1179–1187, https://doi.org/10.1109/TFUZZ.2006.890678, 2-s2.0-37249067095.
10.1109/TFUZZ.2006.890678
Web of Science® Google Scholar
19 Xu Z. and Yager R. R., Some geometric aggregation operators based on intuitionistic fuzzy sets, International Journal of General Systems. (2006) 35, no. 4, 417–433, https://doi.org/10.1080/03081070600574353, 2-s2.0-33750916532.
10.1080/03081070600574353
Web of Science® Google Scholar
20 Liao H. and Xu Z., Intuitionistic fuzzy hybrid weighted aggregation operators, International Journal of Intelligence Systems. (2014) 29, no. 11, 971–993, https://doi.org/10.1002/int.21672, 2-s2.0-85027933879.
10.1002/int.21672
Web of Science® Google Scholar
21 Rahman K., Abdullah S., Jamil M., and Khan M. Y., Some generalized intuitionistic fuzzy Einstein hybrid aggregation operators and their application to multiple attribute group decision making, International Journal of Fuzzy Systems. (2018) 20, no. 5, 1567–1575, https://doi.org/10.1007/s40815-018-0452-0, 2-s2.0-85066298694.
10.1007/s40815-018-0452-0
Web of Science® Google Scholar
22 Xu Z., Intuitionistic fuzzy aggregation and clustering, 2012, springer, Berlin.
10.1007/978-3-642-28406-9
Google Scholar
23 Xu Z. and Hu H., Projection models for intuitionistic fuzzy multiple attribute decision making, International Journal of Information Technology and Decision Making. (2010) 9, no. 2, 267–280, https://doi.org/10.1142/S0219622010003816, 2-s2.0-77951672266.
10.1142/S0219622010003816
Web of Science® Google Scholar
24 Xu Z. and Cai X. Q., Recent advances in intuitionistic fuzzy information aggregation, Fuzzy Optimization and Decision Making. (2010) 9, no. 4, 359–381, https://doi.org/10.1007/s10700-010-9090-1, 2-s2.0-78649822314.
10.1007/s10700-010-9090-1
Web of Science® Google Scholar
25 Yu D. and Liao H., Visualization and quantitative research on intuitionistic fuzzy studies, International Journal of Fuzzy Systems. (2016) 30, no. 6, 3653–3663, https://doi.org/10.3233/IFS-162111, 2-s2.0-84971455052.
10.3233/IFS-162111
Google Scholar
26 Yager R. R., Pythagorean membership grades in multicriteria decision making, IEEE Transactions on Fuzzy Systems. (2014) 22, 958–965.
10.1109/TFUZZ.2013.2278989
Web of Science® Google Scholar
27 Yager R. R. and Abbasov A. M., Pythagorean membership grades, complex numbers, and decision making, International Journal of Intelligence Systems. (2013) 28, no. 5, 436–452, https://doi.org/10.1002/int.21584, 2-s2.0-84875259751.
10.1002/int.21584
Web of Science® Google Scholar
28 Peng X. and Yuan H., Fundamental properties of Pythagorean fuzzy aggregation operators, Fundamenta Informaticae. (2016) 147, no. 4, 415–446, https://doi.org/10.3233/FI-2016-1415, 2-s2.0-84997335788.
10.3233/FI-2016-1415
Web of Science® Google Scholar
29 Shahzadi G., Akram M., and Al-Kenani A., Decision-making approach under pythagorean fuzzy yager weighted operators, Mathematics. (2020) 8, no. 1, https://doi.org/10.3390/math8010070.
10.3390/math8010070
Web of Science® Google Scholar
30 Rahman K., Abdullah S., Husain F., and Ali Khan M. S., Approaches to Pythagorean fuzzy geometric aggregation operators, International Journal of Computer Science and Information Security (IJCSIS). (2016) 14, 174–200.
Google Scholar
31 Rahman K., Abdullah S., Ali Khan M. S., and Shakeel M., Pythagorean fuzzy hybrid geometric aggregation operator and their applications to multiple attribute decision making, International Journal of Computer Science and Information Security (IJCSIS). (2016) 14, 837–854.
Google Scholar
32 Rahman K., Ali Khan M. S., and Ullah M., New approaches to Pythagorean fuzzy averaging aggregation operators, Math Lett. (2017) 3, no. 2, 29–36, https://doi.org/10.11648/j.ml.20170302.12.
10.11648/j.ml.20170302.12
Google Scholar
33 Rahman K., Abdullah S., Husain F., Ali Khan M. S., and Shakeel M., Pythagorean fuzzy ordered weighted geometric aggregation operator and their application to multiple attribute group decision making, Journal of Applied Environmental and Biological Sciences. (2017) 7, 67–83.
Google Scholar

Citing Literature

All articles

SR-Fuzzy Sets and Their Weighted Aggregated Operators in Application to Decision-Making

Abstract

1. Introduction

2. SR-Fuzzy Sets

3. Aggregation of SR-Fuzzy Sets and Its Properties

3.1. Some Operations On SR-Fuzzy Sets

3.2. Aggregation of SR-Fuzzy Sets

4. Application of SR-FSs to Select the Top-Rank University

5. Conclusions

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

SR-Fuzzy Sets and Their Weighted Aggregated Operators in Application to Decision-Making

Abstract

1. Introduction

2. SR-Fuzzy Sets

3. Aggregation of SR-Fuzzy Sets and Its Properties

3.1. Some Operations On SR-Fuzzy Sets

3.2. Aggregation of SR-Fuzzy Sets

4. Application of SR-FSs to Select the Top-Rank University

5. Conclusions

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information