A model for detecting weak pulse signals in chaotic noise was proposed. Firstly, based on the short-term predictability of chaotic signals, according to Takens’s theorem, the phase space of observed signal was reconstructed. Then, an improved brain emotional learning (BEL) model combined with PSO-AGA was proposed to predict chaotic signals, and the one-step prediction error was obtained. In order to optimize the parameters of the BEL model, an algorithm named PSO-AGA combined with particle swarm optimization and adaptive genetic algorithm was adopted to achieve the balance of global search and local search capabilities. Finally, the hypothesis testing method was used to detect whether there existed the pulse signal from the one-step prediction error. The experiments simulated the Lorenz system and the magnetic storm loop current system. In the Lorenz system, the MAD of BEL-PSO-AGA, BP-NN-PSO-AGA, and Wavelet-NN-PSO-AGA were 0.0022, 0.0142, and 0.0076; the MSE were 8.95 × 10⁻⁶, 0.00034, and 0.00016; the RMSE were 0.0029, 0.0187, and 0.0128; the running times were 410 s, 792 s, and 721 s; the ACC were 0.999, 0.972, and 0.997; the F1 were 0.984, 0.423, and 0.878. It could be seen that the BEL model had better performance, shorter running time and higher values of the ACC and F1, indicated that the BEL model ran faster and had a better predictive effect. The MAD of BEL-PSO-AGA, BEL-WOA, BEL-AGA, and BEL-PSO were 0.0022, 0.0065, 0.0135, and 0.0071; the MSE were 8.95 × 10⁻⁶, 0.00013, 0.00029, and 0.00014; the RMSE were 0.0029, 0.0115, 0.0173, and 0.0119; the ACC were 0.999, 0.992, 0.990, and 0.997; the F1 were 0.984, 0.733, 0.451, and 0.878. This indicated that the PSO-AGA also had better performance and higher prediction accuracy. In the magnetic storm loop current system, the experimental results were similar to the Lorenz experiment, which also indicated that the BEL-PSO-AGA model was better. To sum up, the detection results of simulations showed that the proposed model and algorithm could effectively detect weak pulse signals from the chaotic noise.

1. Introduction

A weak signal is a signal with low signal-to-noise ratio (SNR) that is overwhelmed by noises and is difficult to be detected by traditional methods. “Weak” is relative to the strength of the noise [1]. Chaos refers to a random or random-like phenomenon that appears in a deterministic system, which has two remarkable characteristics, the unpredictability for a long time and the predictability in a short term [2]. Due to its irregularity and long-term unpredictability, signal detection in chaotic noise has always been a difficult point in signal detection. With the development of scientific technology and the continuous maturity of chaos theory, the detection of weak signals in chaotic noise has gradually become a hot issue in signal detection. Researchers have proposed methods such as neural network, least squares support vector machine, and Duffing oscillator to extract weak signals in chaotic noise [3–5].

Pulse signal is a kind of common signal, often used in communication and fault diagnosis and other fields [6]. Improving the detection ability of pulse signal is of great practical significance [7]. The detection of weak pulse signal in chaotic noise has become a hot spot in the field of signal processing. Early detection methods include Boxcar Integrator and phase-locked amplifier, strongly coupled Duffing oscillator subsystem, Birkhoff-Shaw oscillator subsystem, and modern cross-spectrum estimation [8–11]. However, most of these methods have some defects such as low sensitivity, low adaptability, and slow operating speed. In order to improve the detection performance, some scholars have applied Jordan neural network, Elman neural network, empirical likelihood ratio method, support vector machine, local linear and Kalman filter hybrid algorithm, and double local linear model to detect pulse signal in chaotic noise [12–17].

It can be found from the above researches that the detection performances depends on the prediction effect of chaotic signal. The higher prediction accuracy of chaotic signal, the better detection effect of target signal. Therefore, it is crucial to improve the prediction accuracy of chaotic signal for the detection of weak pulse signals. In recent years, many methods such as fractional maximum correlation entropy algorithm, GRNN neural network, hybrid neural network and attention mechanism, extreme learning machine, robust extreme learning machine, support vector machine, and deep learning have been applied to the prediction model of chaotic time series, which improved the prediction accuracy of chaotic time series [18–24]. Mei et al. [25] applied the method based on brain emotion learning (BEL) model and adaptive genetic algorithm (AGA) to chaotic time series prediction, which achieved great prediction accuracy. Yang [26] applied the method proposed by [25] to detect the pulse signal, but the detection performance was poor due to the convergence instability of GA. What we do technically in this paper is to improve the detection performance of pulse signal in chaotic noise. The BEl model is improved, and the PSO-AGA is proposed to optimize the parameters of the BEL model. The algorithm inherits the characteristics of fast search speed and high efficiency of particle swarm optimization; meanwhile, it has the characteristics of strong global search ability of GA and introduces dynamic crossover and mutation parameters to make the optimization effect better.

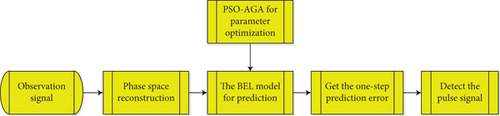
The rest of this paper is organized as follows. In Section 2, as the signal detection problem in chaotic noise has been abstracted as a hypothesis testing problem, the phase space is reconstructed. An improved BEL model is established to predict the reconstructed observation signal, and the pulse signal detection model is proposed from the one-step prediction error. In Section 3, the PSO-AGA is established and used to optimize the parameters of BEL. Then, the problem of signal detection is explained. The simulations are shown in Section 4, which validates the applicability of the proposed model and algorithm. Finally, Section 5 gives concluding remarks. The idea diagram of this paper is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flow chart of signal detection in chaotic noise.

The innovation points of this article are discussed below.

(1)
The signals in the afferent sensory cortex, orbitofrontal cortex, and amygdala are activated, and the hyperbolic tangent function is used as the activation function
(2)
On the basis of AGA algorithm, the PSO algorithm is added. Using the characteristics of PSO with fast convergence and high efficiency, then use the advantages of GA global search for population screening and improve the diversity of population
(3)
In order to verify the effectiveness of the proposed BEL-PSO-AGA model, the BEL model is compared with the BP neural network and wavelet neural network to determine the advantages of fast running and high precision. Then, on the basis of the BEL model and compared with WOA, AGA, and PSO optimization algorithms, it is found that the BEL-PSO-AGA has the best prediction effect

2. Detection of Weak Pulse Signal in Chaotic Noise

2.1. The Problem of Signal Detection in Chaotic Noise

The signal detection problem in chaotic noise can be abstracted as a hypothesis testing problem as follows:

(1)

where H₀ denotes null hypothesis and H₁ denotes the alternative hypothesis, which means that there is no target signal in the observation and there is a target signal in the observation respectively. y(t), c(t), s(t), N(t) denote observation signal, chaotic noise, target signal (impulse signal), and white noise, respectively. The target signal s(t) is independent of chaotic noise c(t) and white noise N(t).

As the target signal is submerged in the chaotic noise, the target signal could not be detected directly from the observed signal. If the chaotic signal could be isolated from the observed signal, the above hypothesis test (1) should be transformed into

(2)

Thus, the next work is to separate the chaotic noise c(t) from the observed signal y(t). Fortunately, according to Takens’s theorem [27], the chaotic signals can be predicted by phase space reconstruction.

2.2. Phase Space Reconstruction

For the observed signal, a m dimensional phase space of the original system can be constructed by introducing the embedding dimension m and the delay time τ. The reconstructed phase space is expressed as Y(t) = (y(t), y(t − τ), y(t − 2τ), ⋯,y(t − (m − 1)τ))^′, where t > (m − 1)τ. According to Takens’s theorem [27], the mapping of a phase point to the reconstructed space is an embedding and can be expressed as f : R^m⟶R, such that y(t + 1) = f(Y(t)). If the mapping f has been found and the appropriate embedding dimension m and delay time τ are selected, the next point y(t + 1) should be predicted.

According to Mei et al. [25], a BEL model has a good prediction effect in chaotic time series. Therefore, an improved BEL model is constructed to predict the reconstructed observation signals.

2.3. Improved BEL Model

Emotion is an advanced function of the brain that ensures the organism’s adaptation and survival. Emotional neuroscience research shows that the brain mechanism of emotion is mainly prefrontal cortex and limbic system. The core part of the limbic system is composed of amygdala and hippocampus, used for emotional learning and memory. After the sensory stimulation reaches the thalamus, it can be directly sent to the amygdala through the lower channel or sent to the sensory cortex first through the upper channel, where the sensory stimulation is processed carefully, and then the signal is sent to the amygdala [28].

Inspired by neurobiological studies, Balkenius and MorÉn [29] proposed a neural network-based emotional learning model of the brain, which consists of thalamus, sensory cortex, orbitofrontal cortex, and amygdala. Based on the model in [29], Mei et al. [25] proposed a BEL model combined with AGA to predict the chaotic signal. The BEL model proposed by Mei et al. is a neural network with two hidden layers, i.e., orbitofrontal cortex and amygdala. In order to improve the accuracy of the prediction of BEL model, an improved BEL model with three hidden layers, i.e., sensory cortex, orbitofrontal cortex, and amygdala, is proposed in this paper. The improved BEL model’s network structure is shown in Figure 2.

In Figure 2, S_I = [S₁, S₂, ⋯, S_n], represents the input signal received in the thalamus, where n denotes the dimension of the input signal. The input signal S_I was transmitted from thalamus to sensory cortex while the maximum value of input signal S_max = max(S_I) was transmitted from thalamus to amygdala directly.

For each input signal S_i, the sensory cortex will conduct a preliminary learning M_i, which would be transmitted to the amygdala and the orbitofrontal cortex. In the orbitofrontal cortex, the input sensory signal M_i was converted to O_i, i.e.,

(3)

where w_i represents the weights between nodes of the orbitofrontal cortex. Then, the internal output E_o of orbitofrontal cortex is expressed as

(4)

where b_o is the bias received by the orbitofrontal cortex.

As for the signal S_max from the thalamus and the signal M_i from the sensory cortex, there are also corresponding nodes A_i, i = 1, 2, ⋯, n + 1 in the amygdala, which can be expressed as

(5)

where v_i denotes the weight between nodes in the amygdala and S_max denotes the signal from the thalamus. Then, the internal output E_a of amygdala is

(6)

where b_a is the bias received by the amygdala.

The orbitofrontal cortex assists the amygdala in learning and inhibits its output. Therefore, under the mutual learning between the orbitofrontal cortex and amygdala, the final output of the brain emotional learning model is E, represented in

(7)

To sum up, the improved BEL is a neural network model between sensory cortex, orbitofrontal cortex, and amygdala. There are some parameters including weights w_i, v_i and biases b₀, b_a that need to be optimized. In the below, PSO-AGA will be introduced into the model to optimize the weights and biases.

3. PSO-AGA

The AGA has a large space of improvement in search ability, while the convergence speed is slow. The PSO algorithm has certain memory function, while it is easy to fall into local optimum. Combining AGA with PSO, it will not only improve the convergence speed but also enhances the global search ability [30]. The particle can be searched in a larger space, instead of being limited to the previous optimal position, which will improve the flexibility of the algorithm and enhance the optimization ability. The flow chart of BEL model and PSO-AGA is shown in Figure 3.

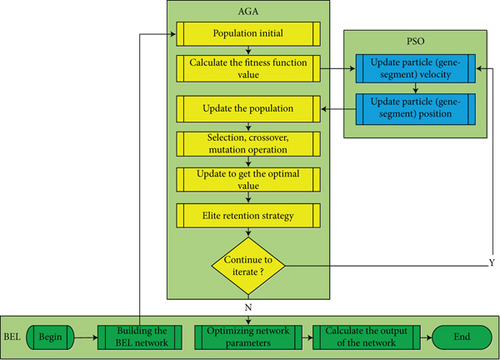
In the PSO-AGA algorithm, firstly, the genetic parameters are initialized, such as maximum and minimum crossover probability, maximum and minimum mutation probability, and iteration times. Secondly, the population and chromosomes are initialized; then, the PSO algorithm is used to update the population, and the AGA algorithm is used to further update the population. Then, the optimal chromosomes are preserved into the next generation until the maximum number of iterations is reached. Finally, the optimal chromosomes, namely, the optimal weight and threshold value, are substituted into the BEL model to output the final prediction results.

3.1. Adaptive Genetic Algorithm (AGA)

The genetic algorithm (GA) is a common intelligent optimization algorithm, which draws on the random search method of natural selection mechanism in biological world and can be applied in various fields. It has higher global performance and a more mature convergence analysis method [31]. However, the general genetic algorithms have some defects such as the crossover and mutation probability are fixed, converged slowly, and too subjective. In order to improve the flexibility and performance of GA, an adaptive genetic algorithm (AGA) is proposed in which the adaptive crossover and mutation probability are designed. The operation of AGA is shown below.

3.1.1. Chromosomal Coding

The weights w_i, v_i and biases b₀, b_a of BEL model in Figure 2 are taken as gene sequences on chromosomes. Since the weights and biases are real numbers, the method of real number coding is adopted which would improve the coding efficiency. The coding format of chromosome (CH) is presented in

(8)

where w₁, ⋯, w_n is the weights between nodes in the orbitofrontal cortex, b_o is the receiving bias in the orbitofrontal cortex, v₁, ⋯, v_{(n + 1)} is the weights between nodes in the amygdala, b_a is the bias received in the amygdala, and n denotes the input signal dimension. The number of genes per chromosome is 2n + 3.

3.1.2. Fitness Function

A fitness function is used to guide the search process. The design of fitness function is related to the convergence speed and prediction accuracy of the algorithm. In general, the fitness function is converted from the objective function. In this paper, the smaller the prediction error of BEL model, the better the adjustment of chromosome parameters. Therefore, the fitness function F(·) is defined as follows:

(9)

where m denotes the number of sample points,

denotes the output value of BEL model, and y_k denotes the actual value. According to the expression of F(CH) in (9), the chromosome that minimizes the fitness function is optimal.

3.1.3. Select Operation

In the selection operation, the roulette method is used to select better individuals to participate in the selection of the next generation. The probability of each chromosome being selected should be proportional to its individual fitness value; that is, those with large individual fitness values are more likely to be retained. Suppose the fitness value of the ith chromosome is f_i and the probability of individual selection is p_i. f_i and p_i are expressed as follows:

(10)

(11)

where M represents the number of population and F(CH_i) denotes the fitness value of the ith chromosome. According to the formula (11), p_i denotes the proportion of the ith individual fitness value in the sum of all individual fitness values. The greater the individual fitness value, the greater the probability of individual selection.

3.1.4. Crossover Operation

In this paper, the adaptive crossover probability is adopted to increase the flexibility of the algorithm. The calculation formula of crossover probability p_c is defined as follows:

(12)

where p_cmax and p_cmin are the maximum and minimum crossing probabilities set artificially, f_max and f_avg denote the maximum and average values of the fitness function of the population, and f denotes the parent of current chromosome whose value of fitness is higher.

In crossover operation, the combination of multipoint crossover and arithmetic crossover is adopted. At first, the paternal chromosomes selected randomly are divided into multiple gene segments. Then, the arithmetic crossover is performed on each segment as follows:

(13)

where gs₁ and gs₂ represent the according gene segments of the two parents,

and

represent the according gene segments of the two children, and r ∈ [0, 1] denotes a random number.

3.1.5. Mutation Operation

In the mutation operation, the adaptive variation probability p_m is adopted, which is expressed as follows:

(14)

where p_mmax and p_mmin denote the maximum and minimum variation probabilities set artificially, f_max and f_avg denote the maximum and the average fitness values of the population, and

indicates the fitness value of the individual who currently needs to mutate.

In the mutation operation, the uniform mutation strategy is adopted [32]. Every gene of chromosome has an equal chance to mutate. If the jth gene of the ith chromosome a_ij was selected for mutation, the gene a_ij would be updated as follows:

(15)

where f(g) = r^′(1 − g/G_max), a_max and a_min are the upper and lower bounds of gene a_ij, respectively, r, r^′ ∈ [0, 1] are random numbers, g is the current iteration number, and G_max is the maximum iteration number. With the increasing of iteration times, the range of individual variation will become smaller, which is beneficial to retain the optimal individuals.

3.1.6. Elite Retention Strategy

If the fitness value of the optimal individual in the current population was greater than that of the optimal individual in the next generation, the optimal individual in the next generation should be replaced by the optimal individual in the current population. This strategy, which called elite retention strategy, could effectively prevent the loss or destruction of the optimal individuals and would be a basic guarantee for the population convergence to the optimal solution [33].

AGA can improve the diversity of the population and has a large space of improvement in search ability, while the convergence speed is slow. In this paper, particle swarm optimization (PSO) is used to improve the convergence performance of AGA.

3.2. Particle Swarm Optimization (PSO)

Particle swarm optimization (PSO) is inspired and evolved from the process of birds searching for food. The characteristics of each particle in PSO algorithm are represented by fitness, position, and speed. The fitness determines the quality of the particle [34]. Suppose the dimension of the search space is d, the size of the population is k, and the position and the speed of the ith particle are x_i = (x_i1, x_i2, ⋯, x_id) and v_i = (v_i1, v_i2, ⋯, v_id), respectively, where i = 1, 2, ⋯, k. In each iteration, the updating formula of velocity and position is expressed as follows:

(16)

where p_i = (p_i1, p_i2, ⋯, p_id) denotes the optimal position of the ith particle searched in the iterative process, p_g = (p_g1, p_g2, ⋯, p_gd) denotes the optimal position searched by the whole particle swarm in the iterative process, superscript t denotes the current iteration number,

and

denote the velocity and position of the particle, respectively, at the t-th iteration, c₁ and c₂ denote learning factors, r₁, r₂ ∈ [0, 1] denote random numbers, and w denotes the inertial weight.

Particle swarm optimization is also used to optimize the parameters, which can improve the prediction ability and performance of the model [35]. However, particle swarm optimization is easy to fall into the problem of local optimization, so combining the AGA algorithm can expand the particle search space, increase the diversity of the population, and make the model performance better and the prediction accuracy higher.

3.3. Detection of the Target Signals

As the phase space was reconstructed, the BEL model is established and the PSO-AGA is used to optimize the parameters of the BEL model. The optimized BEL model would effectively approximate the mapping f : c(t) ≈ g(Y(t − 1)) which have been mentioned in the Section 2.2. The final output of the BEL model is the single-step prediction value g(Y(t − 1)). Then, the one-step prediction error e(t) is obtained as follows:

(17)

The one-step prediction error is used to determine whether there is a pulse signal. Substituting equation (17) into equation (2), the result is as follows:

(18)

When the null hypothesis in equation (18) is true, it means that the one-step prediction error only contains white noise. When the alternative hypothesis is true, it means that the one-step prediction error contains not only white noise but also weak signal. In order to prove the existence of impulse signals objectively, the z-test method is adopted. In statistics, it is usually assumed that the distribution of errors is normally distributed. According to the equation (18), because N(t) is white noise, we assume further that N(t) ~ N(μ, σ²). The detection of pulse signal for each the observation signal can be abstracted as hypothesis testing problem below.

(19)

Construct statistic , for a given 0 < α < 1, P = P(|z| ≥ z_α/2) is obtained, when P < α, the null hypothesis is rejected, and it can be considered that the observed signal contains the weak signals. Two simulation experiments are used to test the applicability of the model and algorithm.

4. Simulations

In the experiment, Intel CPU Core I5-10210U processor, main frequency 2.11GHz, 16GB memory, 64-bit Windows10 operating system, and Python programming environment are adopted.

In order to verify the feasibility and effectiveness of PSO-AGA, the prediction accuracy of the BEL model, and the pulse signal detection performance, two simulation experiments are carried out. In experiment 1, the Lorenz system is used to generate the chaotic noise signal, while geomagnetic storm loop current Index (Dst) is used in experiment 2.

4.1. Index of Performance Evaluation

In this paper, the mean absolute error (MAD), mean square error (MSE), and root mean square error (RMSE) are used to measure the prediction effect of the BEL model. SNR is used to measure the strength of the pulse signal. The accuracy rate (ACC) and the value of F1 are used to measure the detection performance of the pulse signal detection. The formula is expressed as follows:

(20)

where

(21)

and are the mean values of s(t) and c(t), respectively. is the variance of white noise N(t). is the predicted value, while y(t) is the true value of the observed signal sequence. n is the number of samples. FP, FN, TN, and TP, which come from machine learning, denote the false positive, false negative, true negative, and true positive, respectively. P is accuracy rate and R is recall rate.

4.2. Data Processing and Parameter Setting

Before the simulation experiment, it is necessary to explain the setting of the pulse signal and processing of observed signal and white noise.

4.2.1. Setting of Pulse Signals

As the frequency of the general periodic pulse signal is consistent, the regularity of the signal is too strong. In each simulation experiment, the pulse signal will be generated in a random manner. Therefore, 40 pulse signals are generated as follows. s(t) = q · s₀(t), where s₀(t) is expressed as follows:

(22)

where T = {t₁, t₂, ⋯, t₄₀}, t₁, t₂, ⋯, t₄₀ are 40 random integers. In experiment 1, 40 pulse signals are generated with q = 2.5, while 40 pulse signals are generated with q = 8 in experiment 2. The white noise with a mean value of 0 and a variance of 0.1 is used in both experiments.

4.2.2. Processing of Observed Signal

Before building the BEL model, the observed signal need to be standardized. The maximum and minimum normalization method is adopted, which is expressed as follows:

(23)

where x_t and

denote the time series of observed signal and the time series normalized, respectively, x_min and x_max denote the minimum and maximum value of x_t, respectively, and N denotes the length of time series.

In order to measure the performance of the BEL model, the optimal output of the model will be inversely normalized. The inverse normalization method is expressed as follows:

(24)

where z_t and

denote the output of the BEL model and the data inversely normalized, respectively, and z_min and z_max represents the minimum and maximum value of the output z_t.

4.2.3. Parameter Setting

In this paper, the embedding dimension m = 4 and delay time τ = 1 are determined by the method of saturated correlation dimension and mutual information function [36]. According to the phase space reconstruction method, the observed signal is reconstructed to a 4-dimensional vector which could be expressed as [y(t), y(t − 1), y(t − 2), y(t − 3)]^T. Thus, the input data of BEL model is a 4-dimensional vector. There are 9 weights, and 2 biases need to be optimized. The initial values of weights range from 0 to 1 and initial values of the biases range from -1 to 1.

In PSO-AGA, the population size, maximum iteration number, and length of chromosome (particle) are set to be 1000, 100, and 11, respectively. The learning factors are set to be c₁ = c₂ = 2. The maximum and minimum crossover probabilities are set as p_cmax = 0.8 and p_cmin = 0.5, and the maximum and minimum mutation probabilities are set as p_mmax = 0.1 and p_mmin = 0.001. PSO-AGA is carried out according parameters set above. The output data is processed by inverse normalization, and the predicted value is finally obtained.

4.3. Experiment 1: Test Pulse Signal in the Lorenz System

In experiment 1, the chaotic noise signal is generated from the Lorenz system. The equation of this model is expressed as follows:

(25)

where σ = 10, b = 8/3, r = 28, and x, y, z denote the time function. The initial points are x = 1, y = 1, and z = 1, and the step length of the integral is t = 0.01s. The four-order Runge-Kutta integral method is applied, and a simulated time series of x with 10000 data is obtained. In order to reduce the influence of transition, get rid of the first and the last 3000 data points and only keep the middle 4000 data, i.e., {c(t), t = 1, 2, ⋯4000}.

4.3.1. Prediction Result of BEL Model in the Lorenz System

In experiment 1, the observation signal y(t) is composed of c(t), N(t) and s(t), i.e., y(t) = c(t) + N(t) + s(t). The chaotic noise signal with white noise is shown in Figure 4, while the observed signal y(t) which contain pulse signal s(t) is shown in Figure 5.

Figures 4 and 5 show that the two signals are very similar. It is hard to differentiate directly. It seems that the influence of weak pulse signal in chaotic noise is very weak and has been submerged in chaotic noise. So the weak pulse signal cannot be detected directly, where SNR is -71.147 dB.

The BEL model is used to get the one-step prediction of observed signal. The PSO-AGA is used to optimize the parameters of BEL model. The performance and convergence situation of PSO-AGA determines the performance of BEL model. Figures 6 and 7 show the convergence situation of PSO-AGA and the performance of BEL model, respectively.

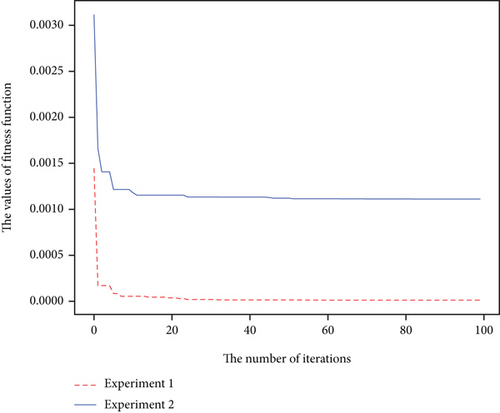
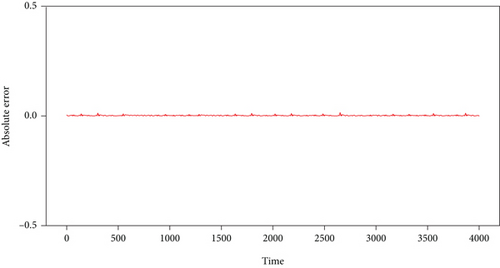
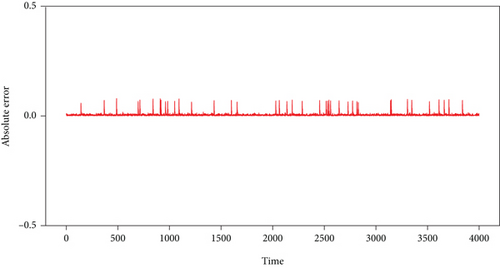
In Figure 6, it is shown that the convergence speed of PSO-AGA is fast in both experiments which means the proposed PSO-AGA is stable and effective. Figures 7(a) and 7(b) show the absolute one-step prediction error of the observation signal without and with pulse signal, respectively. The one-step prediction error of the observation signal without pulse signal is very small in Figures 7 (a). Comparing the two absolute errors, there is an obviously larger error value that appears in Figures 7(b), indicating the possible existence of pulse signals. The correlation coefficient of the predicted value and actual value is shown in Figure 8.

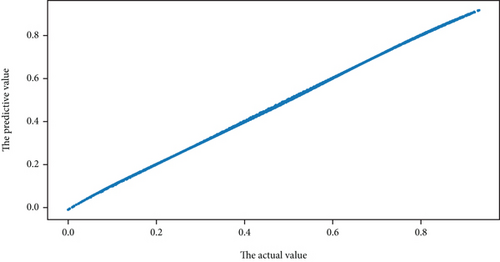
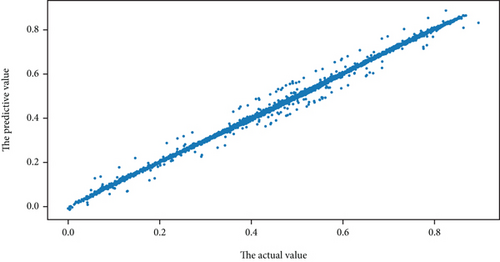
Comparing Figures 8(a) and 8(b), it can be seen that there are obviously some points deviating from the straight line in Figures 8(b), which indicates that there must be some pulse signals. The method of hypothesis testing will be used to detect the pulse signal form prediction error below.

4.3.2. Detection of Pulse Signal in the Lorenz System

Figures 7(b) and 8(b) show that there must be some pulse signals in the observation signal, which is subjective and inaccurate. As shown in Figure 7(a), it is reasonable to suppose that μ = 0 when there is no pulse signal in the observation signal. According to the Section 3.3, the z-test is applied. The variance σ² of prediction error e(t) must be given in advance in the z-test. In this paper, the sample variance is used to instead of σ². For each point of the prediction error e(t), there is a z-test for pulse signal. It is 4000 times test in total, and there are 40 pulse signals. The ACC and F1 are used to measure the performance of the test. Given significance level as α = 0.1, the detection performance of test with different q, i.e., q = 3,2.5,2, 1.5,1, 0.5, are shown in Table 1.

Table 1. Detection results of pulse signals.

q	SNR (dB)	ACC	F1
3.0	-67.501	1.000	1.000
2.5	-71.147	0.999	0.984
2.0	-75.610	0.999	0.984
1.5	-81.364	0.995	0.947
1.0	-89.473	0.990	0.139
0.5	-103.33	0.990	0.000

In Table 1 that SNR keeps decreasing with the decreasing of q. Overall, the BEL model and PSO-AGA have ideal detection performance when q ≥ 2. However, as the SNR keeps decreasing, although the accuracy rate is very high, the value of F1 keeps decreasing. When the SNR ≤ −89.473 dB, the detection ability is very poor. This is because the pulse signal is too weak; it has been completely submerged in the chaotic noise.

4.3.3. Compared with Different Models

In order to verify the effectiveness of the BEL, under the PSO-AGA algorithm, the performance of the BEL model is analyzed by comparing the traditional neural network model, such as BP neural network and wavelet neural network. The comparison results are shown in Table 2.

Table 2. Comparison results of different models.

Model	MAD	MSE	RMSE	Time (s)	ACC	F1
BP-NN	0.0142	0.00034	0.0187	792	0.972	0.423
Wavelet-NN	0.0076	0.00016	0.0128	721	0.997	0.878
BEL	0.0022	8.95 × 10⁻⁶	0.0029	410	0.999	0.984

It can be seen from the results in Table 2 that the MAD, MSE, and RMSE of the BEL model are 0.0022, 8.95 × 10⁻⁶, and 0.0029, which are the smallest. At the same significance level α = 0.1, the ACC and F1 values are the highest. Most importantly, the BEL model has shorter computation time than the traditional neural network model. In general, the BEL model has obvious advantages in prediction accuracy, running speed, and stability.

4.3.4. Compared with Different Optimization Algorithms

After comparing the different models, on the basis of the BEL model, it is compared with different optimization algorithms. The comparison results are shown in Table 3 and in Figure 9.

Table 3. Comparison results of different optimization algorithms.

Algorithm	MAD	MSE	RMSE	Time (s)	ACC	F1
WOA	0.0065	0.00013	0.0115	218	0.992	0.733
AGA	0.0135	0.00029	0.0173	302	0.990	0.451
PSO	0.0071	0.00014	0.0119	198	0.997	0.878
PSO-AGA	0.0022	8.95 × 10⁻⁶	0.0029	410	0.999	0.984

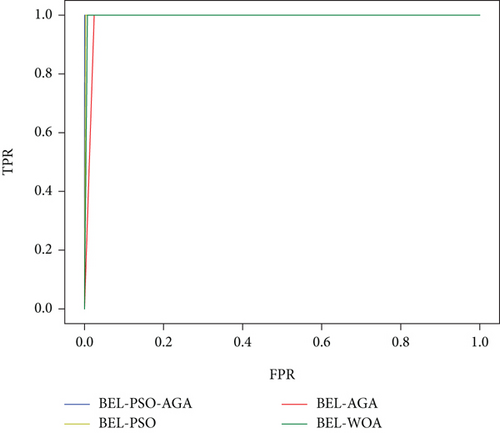
It can be seen from the results in Table 3, on the basis of BEL model, comparing with other optimization algorithms. Although the running time of the PSO-AGA algorithm is longer than other algorithms, the MAD, MSE, and RMSE of PSO-AGA are the smallest. Moreover, at the same SNR and the same significance level α = 0.1, the ACC and F1 of PSO-AGA are superior to other optimization algorithms. Figure 9 shows that the ROC curves of different optimization algorithms. It is observed that the BEL-PSO-AGA has the largest area covered by ROC curve and the value of AUC is 0.999. The AUC values of the other three optimization algorithms are 0.998, 0.987, and 0.996, respectively. Therefore, it seems that the proposed BEL-PSO-AGA model has good fitting ability and better model performance in the Lorenz system.

4.4. Experiment 2: Test Pulse Signal in Dst

Geomagnetic storm loop current Index (Dst) is a geomagnetic index that indicates the intensity of a geomagnetic storm. A geomagnetic storm is a violent movement of the earth’s magnetosphere lasting from ten to dozens of hours, which is complex and changeable. According to the level of magnetic storm, it can be divided into weak storm, medium storm, strong storm, and great storm, among which the strong storm and great storm will form serious disaster weather [37]. Therefore, signal detection in the harsh environment of magnetic storms is of great significance which would avoid disaster. Signal detection in Dst has played an important role in the research of signal processing.

The Dst indices collected in this paper are from the World Geomagnetic Data Center [38]. 2000 Dst indices occurred in 2020 are selected as chaotic noise, which is a typical chaotic time series with a time interval of 1 hour. The pulse signals are generated as in Section 4.2 with q = 8.

4.4.1. Prediction Results of BEL Model in Dst

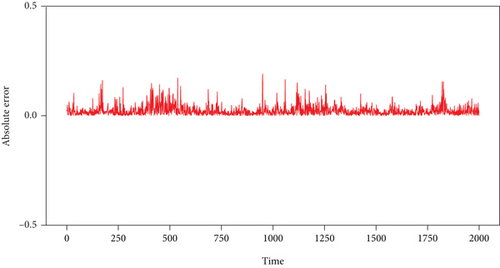
The purely magnetic storm loop current Dst signal c(t) is shown in Figure 10(a), while the observation signal y(t) which contains pulse signal s(t) is shown in Figure 10(b). Figures 10(c) and 10(d) show the absolute one-step prediction error of purely magnetic storm loop current Dst signal and the observation signal with pulse signal, respectively.

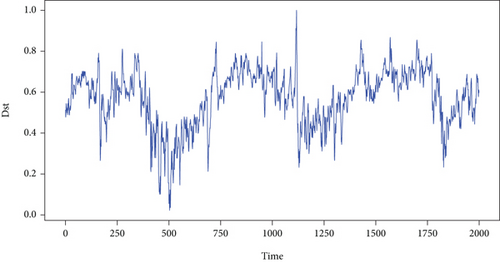
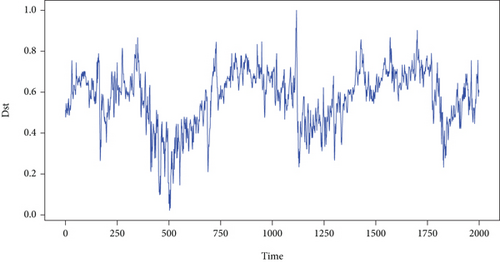
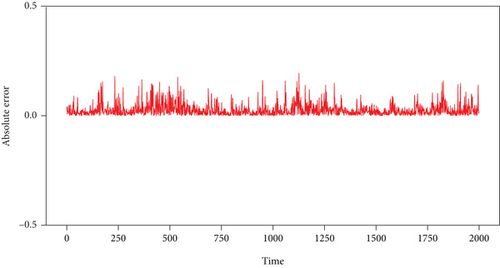
Figures 10(a) and 10(b) show that the two signals are very similar. It is hard to differentiate directly. It seems that the influence of weak pulse signal in chaotic noise is very weak and has been submerged in chaotic noise, where SNR = −55.864 dB.

In Figure 6, it is shown that the convergence speed of PSO-AGA is fast in experiment 2. Figures 10(c) and 10(d) show the absolute one-step prediction error of the observation signal without and with pulse signal, respectively. Comparing with the two errors in Figure 10, both of them fluctuate within a small range near zero. The error in Figure 10(d) seems a little greater than that in Figure 10(c). Comparing with the prediction error in Figures 7(b) and 10(d), it is more difficult to determine whether the pulse signal exist in Dst. The hypothesis testing will be used to detect the pulse signal as in the Lorenz system.

4.4.2. Detection of Pulse Signal in Dst

The detection of pulse signal for each detected error could be abstracted as hypothesis testing problem (18) just as experiment 1. The sample variance is used to instead of the variance of the population. There are 2000 times tests in total, and there are 40 pulse signal. The ACC and F1 are used to measure the performance of the test. Given the significance level as α = 0.4, the detection performance of test with different q, i.e., q = 9, 8, 7, 6, 5, 4, are shown in Table 4.

Table 4. Detection results of pulse signals.

q	SNR (dB)	ACC	F1
9	-53.509	0.978	0.933
8	-55.864	0.958	0.931
7	-58.535	0.941	0.651
6	-61.618	0.952	0.720
5	-65.264	0.966	0.823
4	-69.727	0.934	0.627

In Table 4, when SNR ≥ −55.864 dB, the values of ACC and F1 are very high, which indicates that the model has the strong signal detection ability. However, when SNR ≤ −55.864 dB, the values of ACC and F1 are relatively low, which indicates the detection ability of the model is also gradually weakened and which indicates that in the complex magnetic storm loop current system, the pulse signal is submerged and the signal is difficult to be detected.

4.4.3. Compared with Different Models

Same as the detection of pulse signals in experiment 1, under the same environment and PSO-AGA optimization algorithm, the comparison results with the traditional neural network models are as follows:

It can be seen from the results in Table 5, the MAD, MSE, and RMSE of BEL model are the smallest. Not only the computation time is less than that of the traditional neural network models, but also the value of F1 is higher. Therefore, the BEL model is better in all aspects.

Table 5. Comparison results of different models.

Model	MAD	MSE	RMSE	Time (s)	ACC	F1
BP-NN	0.0265	0.00145	0.0382	561	0.981	0.889
Wavelet-NN	0.0271	0.00151	0.0387	493	0.979	0.817
BEL	0.0242	0.00104	0.0323	374	0.958	0.931

4.4.4. Compared with Different Optimization Algorithms

Under the same experimental conditions, BEL-WOA, BEL-AGA, BEL-PSO, and the proposed BEL-PSO-AGA model are used to detect the pulse signal in Dst. The comparison results are shown in Table 6 and in Figure 11.

Table 6. Comparison results of different optimization algorithms.

Algorithm	MAD	MSE	RMSE	Time (s)	ACC	F1
WOA	0.0244	0.00118	0.0343	124	0.956	0.889
AGA	0.0292	0.00171	0.0413	211	0.952	0.816
PSO	0.0259	0.00141	0.0375	116	0.957	0.911
PSO-AGA	0.0242	0.00104	0.0323	374	0.958	0.931

In Table 6, comparing with other algorithms, the MAD, MSE, and RMSE values of PSO-AGA are the smallest, which indicates that the proposed PSO-AGA has high prediction accuracy and stability. Moreover, the ACC and F1 of the PSO-AGA algorithm are superior to other algorithms. Figure 11 shows the ROC curves of different optimization algorithms. As you can see from the picture, the BEL-PSO-AGA has the largest area covered by ROC curve and the value of AUC is 0.819. The AUC values of the other three optimization algorithm models are 0.807, 0.804, and 0.806, respectively. Thus, there are good reasons to believe that the BEL-PSO-AGA could detect the pulse signal from the complex environment of magnetic storm ring current.

5. Conclusions

Combining the characteristics of BEL model, AGA, and PSO algorithm, a new method for detecting weak pulse signals in chaotic noise is proposed. Comparing with other models, the BEL model has faster convergence speed, shorter running time, and higher accuracy than traditional neural network. The PSO-AGA improves the detection accuracy; stability as PSO-AGA could achieve the balance between global search and local search ability. Comparing with other optimization algorithms, the PSO-AGA has better performance and prediction accuracy. The experimental results show that the BEL model and PSO-AGA have wide application values and could effectively detect weak pulse signal from chaotic noise.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by Science Foundation of The Chongqing Education Commission (Grant KJQN202101125), the Natural Science Foundation of Chongqing Science and Technology Bureau (Grant No. cstc 2019jcyj-msxmX0020), the Natural Science Foundation of Chongqing (No. cstc 2021jcyj-msxmX0388), and Chongqing Postgraduate Research and Innovation Project Funding (Project No. gzlcx20222081).

Open Research

Data Availability

The Lorentz data comes from the Lorentz equation, and the magnetic storm ring’s data are from the World Geomagnetic Data Center (http://wdc.kugi.kyoto-u.ac.jp).

References

1 Hu S., Jiang X. W., and Yang G., Using of moving average filter in faint pulse signal detection, Computer and Digital Engineering. (2007) 35, no. 10, 169–171.
Google Scholar
2 Gao J. J., Study and Application of Chaotic Time Series Prediction, 2013, Shanghai Jiao Tong University.
Google Scholar
3 Haykin S. and Li X. B., Detection of signals in chaos, IEEE Proceedings. (1995) 83, no. 1, 95–122, https://doi.org/10.1109/5.362751, 2-s2.0-0029191714.
10.1109/5.362751
Web of Science® Google Scholar
4 Xing H. and Jin T., Detection of weak signal in chaotic clutter using advanced LS-SVM regression, IEEE 2009 2nd International Congress on Image and Signal Processing, 2009, Tianjin, China, 1–5, https://doi.org/10.1109/CISP.2009.5303941, 2-s2.0-73849094401.
10.1109/CISP.2009.5303941
Google Scholar
5 Jalilvand A. and Fotoohabadi H., The application of Duffing oscillator in weak signal detection, ECTI Transactions on Electrical Engineering, Electronics, and Communications. (2011) 9, no. 1, 1–6, https://doi.org/10.37936/ecti-eec.201191.172249.
10.37936/ecti-eec.201191.172249
Google Scholar
6 Liu L. S. and Zhang L., Test and analysis of the signal impulse based on MSP430, Electronic Testing. (2009) 8, 19–22.
Google Scholar
7 Shi Y. D., Wang D. S., and Chen L., Detection of weak pulse signals based on a controlled Lorenz system, Journal of Dynamics and Control. (2010) 8, no. 1, 48–52.
Google Scholar
8 Li Y., Yang B. J., and Du L. Z., Chaos-based weak periodic pulse signal detection approach under colored noise background, Journal of Electronics and Information Technology. (2003) 25, no. 2, 195–199.
Google Scholar
9 Li Y., Lu P., and Yang B. J., Applying a special kind of two coupled Duffing oscillator system to detect periodic signals under the background of strong colored noise, Acta Physica Sinica. (2006) 55, no. 4, 1672–1677, https://doi.org/10.7498/aps.55.1672.
10.7498/aps.55.1672
Web of Science® Google Scholar
10 Li J. Y., Research on Weak Signal Detection Technology Based on Chaotic Oscillator, 2010, University of Electronic Science and Technology.
Google Scholar
11 Ma Y., Shi Y. W., and Kang X. T., Harmonic retrieval in colored noisesï¼šcross-spectral SVD-LS approach with cleared false peaks of spectral estimation, Acta Electronica Sinica. (2002) 30, no. 1, 14–17.
Google Scholar
12 Ling X., Weak Pulse Signal Estimation Based on Jordan Neural Network in Chaotic Background, 2021, Chongqing University of Technology.
Google Scholar
13 Deng L., Statistical Detection and Estimation of Weak Pulse Signal under Chaotic Noise Interference Based on Deep Learning Model, 2020, 2020, Chongqing University of Technology, https://doi.org/10.1155/2020/9653586.
Google Scholar
14 Zhu W. L., Weak Harmonic Signal Detection Based on Empirical Likelihood Ratio Method in Chaotic Background, 2020, Chongqing University of Technology.
Google Scholar
15 Du J. Y. and Hou Y. B., Detection of weak harmonic signal embedded in chaotic noise using SVM, Chinese Journal of Scientific Instrument. (2007) 28, no. 3, 555–559.
Google Scholar
16 Su L. Y., Sun H. H., and Li C. L., LL-P-KF hybrid algorithm for detecting and ï¼²ecovering sinusoidal signal in strong chaotic noise, Acta Electronica Sinica. (2017) 45, no. 4, 837–843.
Google Scholar
17 Su L. Y., Sun H. H., Wang J., and Yang L. M., Detection and estimation of weak pulse signal in chaotic background noise, Acta Physica Sinica. (2017) 66, no. 9, 29–38.
Web of Science® Google Scholar
18 Wang S. Y., Shi C. F., Qian G. B., and Wang W. L., Prediction of chaotic time series based on the fractional-order maximum correntropy criterion algorithm, Acta Physica Sinica. (2018) 67, no. 1, 283–290.
Web of Science® Google Scholar
19 Lin H. B., Qi F., Deng X. Y., and Li Y., Generalization regression neural network method for detecting weak harmonic signal under background of noisy chaos, Journal of Jilin University (Information Science Edition). (2004) 3, 29–33.
Google Scholar
20 Huang W. J., Li Y. T., and Huang Y., Prediction of chaotic time series using hybrid neural network and attention mechanism, Acta Physica Sinica. (2021) 70, no. 1, 10243–10501, https://doi.org/10.7498/aps.70.20200899.
10.7498/aps.70.20200899
Web of Science® Google Scholar
21 Su L. Y. and Li X. M., Chaotic time series prediction and application based on extreme learning machine, Journal of Physics: Conference Series. (2021) 1738, no. 1.
Google Scholar
22 Shen L. H., Chen J. H., Zeng Z. G., and Jin J., Chaotic time series prediction based on robust extreme learning machine, Acta Physica Sinica. (2018) 67, no. 3, 30501–30542, https://doi.org/10.7498/aps.67.20171887, 2-s2.0-85046760934.
10.7498/aps.67.20171887
Web of Science® Google Scholar
23 Wang C., Prediction Methods of Chaotic Time Series Based on SVM, 2018, Hebei University.
Google Scholar
24 Li X., Research on Chaotic Time Series Forecasting Based on Particle Swarm Optimization Algorithm, 2020, Dalian University of Technology.
Google Scholar
25 Mei Y., Tan G. Z., Liu Z. T., and Wu H., Chaotic time series prediction based on brain emotional learning model and self-adaptive genetic algorithm, Acta Physica Sinica. (2018) 67, no. 8, 80502–80531, https://doi.org/10.7498/aps.67.20172104, 2-s2.0-85050527273.
10.7498/aps.67.20172104
Web of Science® Google Scholar
26 Yang F., Chaotic Time Series Prediction Based on Brain Emotion Learning Model and Self-Adaptive Genetic Algorithm, 2021, Chongqing University of Technology.
Google Scholar
27 Tankens F., Detecting strange attractors in turbulence, Lecture Notes in Mathematics. (1981) 898, no. 1.
10.1007/BFb0091924
Google Scholar
28 Wang X. F. and Wang S. F., Brain emotion circuit based artificial emotional intelligence model, Pattern Recognition and Artificial Intelligence. (2007) 20, no. 2, 167–172.
CAS Google Scholar
29 Balkenius C. and MorÉn J., Emotional learning: a computational model of the amygdala, Cybernetics and Systems. (2001) 32, no. 6, 611–636, https://doi.org/10.1080/01969720118947, 2-s2.0-13844265451.
10.1080/01969720118947
Web of Science® Google Scholar
30 Ji S., Li G. F., and Shu L. S., Short-term trajectory prediction based on GAPSO-Elman neural network algorithm, Aeronautical Computing Technology. (2021) 51, no. 1, 60–63.
Google Scholar
31 Li Y. X., Tang B. Z., Jiang X. R., and Yi Y. M., Bearing fault feature extraction method based on GA-VMD and center frequency, Mathematical Problems in Engineering. (2022) 2022, 19, https://doi.org/10.1155/2022/2058258.
10.1155/2022/2058258
Web of Science® Google Scholar
32 Song M. D., Short-Term Load Forecasting Based on Improved Genetic Algorithm to Optimize Elman Neural Network, 2020, University of South China.
Google Scholar
33 Ren Z. W. and San Y., Improved adaptive genetic algorithm and its application research in parameter identification, Journal of System Simulation. (2006) 18, no. 1, 41–43.
Google Scholar
34 Sun J., Cui T. T., Liu X. Y., and Xu B., Prediction of silicon content in blast furnace hot metal by PSO-GA optimized ELM, Machinery Design and Manufacture. (2021) 1–6.
Google Scholar
35 Li Y. X., Mu L. X., and Gao P. Y., Particle swarm optimization fractional slope entropy: a new time series complexity indicator for bearing fault diagnosis, Fractal and Fractional. (2022) 6, no. 7, https://doi.org/10.3390/fractalfract6070345.
10.3390/fractalfract6070345
Web of Science® Google Scholar
36 Yang F., Traffic Flow Prediction Model Based on Echo State Networks and Related Research, 2012, Beijing University of Posts and Telecommunications.
Google Scholar
37 Xie L., Pu Z. Y., Zhou X. Z., Fu S. Y., and Zong Q. G., Formation of the storm-time ring current, Chinese Science Bulletin. (2004) 49, no. 7, 716–723, https://doi.org/10.1007/BF03184271.
10.1007/BF03184271
Web of Science® Google Scholar
38 The World Geomagnetic Data Center, http://wdc.kugi.kyoto-u.ac.jp.
Google Scholar

Citing Literature

All articles

Detection of Weak Pulse Signal in Chaotic Noise Based on Improved Brain Emotional Learning Model and PSO-AGA

Abstract

1. Introduction

2. Detection of Weak Pulse Signal in Chaotic Noise

2.1. The Problem of Signal Detection in Chaotic Noise

2.2. Phase Space Reconstruction

2.3. Improved BEL Model

3. PSO-AGA

3.1. Adaptive Genetic Algorithm (AGA)

3.1.1. Chromosomal Coding

3.1.2. Fitness Function

3.1.3. Select Operation

3.1.4. Crossover Operation

3.1.5. Mutation Operation

3.1.6. Elite Retention Strategy

3.2. Particle Swarm Optimization (PSO)

3.3. Detection of the Target Signals

4. Simulations

4.1. Index of Performance Evaluation

4.2. Data Processing and Parameter Setting

4.2.1. Setting of Pulse Signals

4.2.2. Processing of Observed Signal

4.2.3. Parameter Setting

4.3. Experiment 1: Test Pulse Signal in the Lorenz System

4.3.1. Prediction Result of BEL Model in the Lorenz System

4.3.2. Detection of Pulse Signal in the Lorenz System

4.3.3. Compared with Different Models

4.3.4. Compared with Different Optimization Algorithms

4.4. Experiment 2: Test Pulse Signal in Dst

4.4.1. Prediction Results of BEL Model in Dst

4.4.2. Detection of Pulse Signal in Dst

4.4.3. Compared with Different Models

4.4.4. Compared with Different Optimization Algorithms

5. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information