Automatic Control of Food Machinery Based on Neural Network and Computational Torque Compounding
Abstract
In order to improve the effect of automatic control of food machinery, this paper combines neural network and computational torque compounding to study the automatic control system of food machinery to improve the effect of automatic control of food machinery. Moreover, this paper studies the problem of strong time-varying nonlinear friction disturbance in the servo motion system, and analyzes the friction nonlinearity at low speed and commutation motion of the system. In addition, this paper introduces the application requirements for the nonlinear friction compensation control method, and proves that the designed controller can maintain the stability of the system under the condition of strong nonlinear time-varying friction through the Lyapunov stability principle. The experimental study shows that the control strategy given in this paper can not only effectively improve the tracking speed of the joints, but also effectively alleviate the later tremor, and the automatic control effect of food machinery based on neural network and computational torque compounding has certain effects.
1. Introduction
At this stage, the overall economic situation is a global economic integration environment under the market economy. Under the influence of this big environment, food processing enterprises can only continuously improve the technical level and management level of food processing only by continuously carrying out technological reform and innovation, and continuously applying new technologies, new materials and new processes to food processing. Moreover, continuously improving the quality and safety of products and building the competitive advantage of brands play an important role in improving the international market competitiveness of food processing enterprises [1]. Based on this, food processing enterprises need to continuously apply new technologies in food machinery to improve the safety, intelligence, automation and so on of food processing. Therefore, the application of new technologies in food machinery is inevitable for social development, economic development, and technological development. It is very necessary to fight the invasion of foreign enterprises [2].
Product packaging is one of the important ways to achieve brand innovation, rapidly increase market share, and achieve sustainable development [3]. Packaging machinery refers to the mechanical equipment that can realize the packaging of all or part of products and commodities [4]. This packaging process mainly includes the steps of forming packaging materials, filling materials, wrapping and sealing, as well as pre- and post-packaging processes such as cleaning, drying, sterilization, and labeling, as well as other auxiliary processes such as transfer and sorting. The use of packaging machinery can not only improve production efficiency, reduce labor intensity of workers, save costs to achieve large-scale high-speed production needs, but also meet the needs of modern industrial green environmental protection [5]. A country's level of development and degree of development in the packaging industry has become one of the important indicators of the country's economic life and civilization. The packaging industry includes many industrial fields, including the design and production of packaging products, the development, printing and supply of packaging materials, the improvement and manufacture of packaging machinery, etc. The fields involved range from primary to tertiary industries, goods circulation, industrial agriculture Business to every aspect of people's lives. As a “sunrise industry” recognized by the world today, the packaging industry is bound to play an immeasurable role in promoting the development of the global manufacturing industry and accelerating the regional circulation of products [6]. The control system is one of the important components of packaging machinery. It realizes the control, adjustment and monitoring of the entire working process, including: making various processes follow the set order; Control; product quality monitoring, production safety protection, the realization of automatic measurement and counting in the packaging process; the realization of functions such as supply and stop of materials, and automatic alarm in the event of a fault [7]. Nowadays, most of the control systems of packaging machinery also use relay control methods, and more components will inevitably lead to greatly reduced reliability and life of the control system and equipment, and occupy a large physical space. If a PLC control system is used, the traditional intermediate relay can be replaced by programming its internal auxiliary relay. Since it is only a virtual internal register of PLC, as long as the program is written within the range permitted by the capacity, various complex control functions can be realized, which greatly simplifies the mechanical and electrical structure [8]. PLC is the programmable controller, which is the product of the combination of computer and relay control technology. It is one of the most rapidly developed and widely used automation control equipment in the past ten years. It has the characteristics of small size, easy programming, rich modules and powerful functions, and is very suitable for automatic packaging machine control systems. In addition, PLC also has the advantages of changing the control function only by modifying the program without adjusting the hardware configuration; the program can be copied, which is easy to mass produce; it can realize various control functions that cannot be achieved by relays and other advantages. Although the cost is slightly higher than that of relay control, in view of the many advantages mentioned above, PLC control begins to gradually replace traditional relay control [9].
Electronic information technology has played a pivotal role in the development of the industry, triggered another technological change in the industry, and realized the dynamic tracking control of industrial production. The application of electronic information technology in food machinery has played the same role. Application of electronic information technology. The running state of food machinery can be controlled online from time to time. It also plays a precise control role in the rapid location and recovery of faults. The application of electronic information technology to food machinery is mainly realized by the information processing system [10]. In the information system processing system. The parameters of food machinery operation, operation status, and mechanical and electrical equipment can be monitored online from time to time. And the system can provide an extensible platform. The ability to incorporate any connectable new technology system into it. Realize the control of the quality, technical level and safety of food processing. After the information processing system is integrated into electronic automatic control, it can control the automatic production of food processing through the operation portal, and realize the integration of automatic production of food machinery [11].
Membrane separation technology is a kind of bionic technology, which achieves selective separation through molecular semipermeable membrane according to cross-flow. This enables the separation of high-quality products. The application of membrane separation technology in food machinery is a new bright spot in the reform of food machinery. Application of Membrane Separation Technology. Greatly improve the quality and safety of products produced and processed by food machinery. Improve the technical level of food processing enterprises. Membrane separation technology has been widely used in the production and processing of food machinery in the production of fresh draft beer, mineral water filtration and sterilization, food factory wastewater treatment, desalination of seawater and brackish water, and air filtration and sterilization. Product quality and reducing production costs play an important role [12].
The application of frequency conversion control technology greatly improves the scientific and technological content of food machinery, ensures the quality stability of food processing, improves the production efficiency of food machinery, reduces the energy consumption of food machinery, thereby reducing the production cost of food enterprises. The long-term development of enterprises plays an important role. The application of frequency conversion control technology in food machinery mainly depends on the frequency converter to change the working frequency of the machinery. Thereby, the precise control of the machine is realized, and its application effect is outstanding in the food conveying system and the food mixing system. In the food conveying system, through the control of the frequency converter, the transmission system can perform speed regulation and synchronization within a certain range, fine-tune as needed, etc., and at the same time, the advantages of the asynchronous motor can be fully utilized [13]. The use of a frequency converter for speed regulation does not require an additional mechanical speed regulating mechanism, so the transmission system will be more compact and lightweight, and the geared asynchronous motor will operate more efficiently. Similarly, variable frequency speed regulation avoids the tedious maintenance work of replacing carbon brushes or commutators similar to DC motor speed regulation [14]. Of course, for some asynchronous motor transmission systems that used to run at a constant speed, the application of variable frequency speed regulation is also very simple and effective, and the transformation can be completed only by adding a frequency converter [15].
Intelligent control technology is to use programmable intelligent chips to build an intelligent control system. The intelligent control system can collect and process information on the operation of food machinery, reducing the workload of the human brain. The application of intelligent control system in food machinery can improve the calculation accuracy of electrical system [16]. Thereby promoting the efficiency of system and equipment operation and reducing labor costs. The application of intelligent control technology in food machinery is mainly reflected in the electrical control process, including neural network control, fuzzy control and effective control of expert systems. As for the application in AC drive. It mainly works by replacing some conventional speed control controllers with fuzzy controllers. It can be seen that intelligent control technology can solve complex problems that cannot be solved by traditional methods, and has great application value [17].
This paper combines neural network and computational torque compounding to study the automatic control system of food machinery, so as to improve the automatic control effect of food machinery and improve the efficiency of food production.
2. Torque compounding calculation
2.1. Immersion invariant control theoretical basis
Different from the nonlinear control method based on Lyapunov stability theory, this method does not need to design the Lyapunov function, which greatly simplifies the realization difficulty of the control system. The immersion invariant control method first designs a low-order target system that can be asymptotically stable, and then designs the immersion mapping and control law. This ensures that on an invariant attracting manifold, the dynamic trajectory of the controlled system under the action of the control law is consistent with the image of the low-order target system under immersion mapping, and makes the system closed-loop and bounded, thereby ensuring the stability of the entire system.
The basic principle of immersion invariance is as follows:
- (1)
The following systems exist in the target system:
- (2)
Immersion conditions
- (3)
Implicit manifold
- (4)
Manifold attractiveness and trajectory boundedness
If all state variables are bounded, that is, all trajectories of the system are bounded, the asymptotically stable equilibrium point of the closed-loop system is x∗. At this time, the corresponding control law u = ψ(x, z) satisfies the initial assumption, and the system is said to be immersed and stable.
To sum up, the stabilization of nonlinear systems using the immersion invariant method can be roughly implemented in two steps. First, a local asymptotically stable system with lower dimension than the original real system is selected as the target system, and an immersion map x = π(ξ) is found such that the immersion condition holds. Secondly, the control law of the system is designed so that the implicit attracting manifold M is invariant and the system is closed-loop and bounded. When applying the immersion invariant method, it is necessary to determine the immersion map by solving the partial differential equation according to the target system, which is often difficult in actual calculation. However, in most cases, the target system can be selected according to the principles and theories related to the original system and the control target, so as to solve the problem that it is difficult to design the target system due to the difficulty in solving partial differential equations. Because the implicit manifold is endowed with invariance and attractive shape, the target system can well describe the restriction on M of the closed-loop system. However, the control input u that makes the implicit manifold invariant is not unique, simply because it is uniquely defined on M.
According to the immersion invariance theory, when the original system is an n-order system, the target system can choose any one-order system from 1 to n − 1. The method is to immerse a low-order target system that is asymptotically stable at the origin into a high-order original system. The Figure 1 below is a schematic illustration of the immersion invariant method, where n is 3. The method of designing the controller based on Lyapunov function can be regarded as a specialization of the immersion invariant method, but when designing the control law, it is necessary to select an appropriate Lyapunov function V(x) and make the function positive definite and satisfy . That is, the target system state quantity ξ is replaced by the designed Lyapunov function V(x).
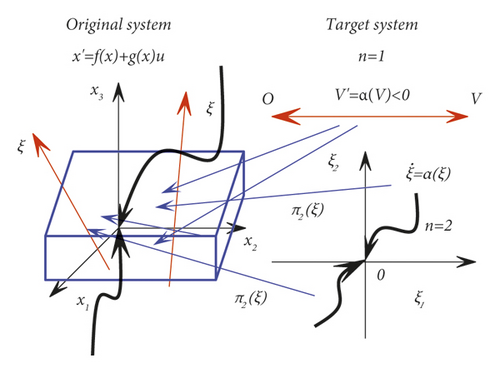
From the analysis and conclusion of the dynamic model of the passive force/torque composite servo loading platform, it can be seen that the dynamic characteristics of the position loop of the loading platform are significantly affected by the static friction and the friction nonlinearity of the preparatory slip section and the boundary lubrication section when moving at low speed. The serious low-speed climbing phenomenon, hysteresis response and even difficult tracking will further affect the high precision and high dynamic response of passive force-torque servo loading, so it is extremely important to accurately estimate and compensate for friction disturbances. The expression form of the system state space function including nonlinear friction disturbance is known, and the state quantity of the system itself and the friction dynamic state quantity z can be obtained. Therefore, adopting the control strategy based on the immersion invariance theory can transform the design problem of the compensation control law for disturbance into the parameter estimation problem of the nonlinear characteristic term of the system. Compared with model reference adaptation, the immersion invariant method requires less prior knowledge, and the control performance is not affected by the system order and initial values of model parameters. Furthermore, the controller design is simpler and increases the flexibility and adaptability of the controller. For the LuGre friction system with strong time-varying nonlinearity, the immersion invariant strategy can theoretically effectively estimate the dynamic and static parameters of friction and then compensate for its disturbance to the loading platform at low speed. As shown in Figure 2
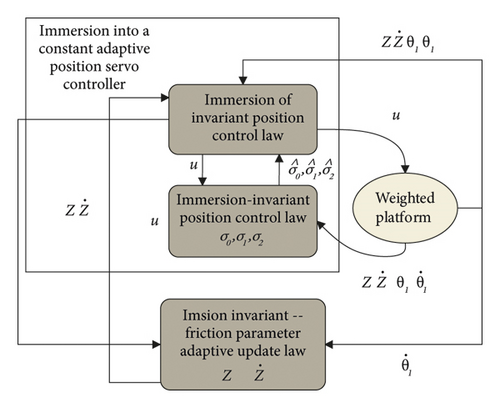
2.2. Nonlinear immersion invariant disturbance compensation control algorithm
Among them, m ∈ R is the number of state variables of the system disturbance term, that is, the number of disturbance model parameters.
We assume that the disturbance term has m state quantities, and the estimation problem of disturbance can be transformed into an adaptive control problem with m unknown parameters. Moreover, we assume that there exists a suitable state feedback control law, namely a parameterized function u = v(x, φ, α1), that makes the above system globally asymptotically stable at the equilibrium point x1 = x∗.
- (1)
First, the algorithm designs the following system as the target system:
- (2)
Secondly, the algorithm considers the system immersion mapping, so that the immersion conditions are established as follows:
- (3)
The algorithm derives the implicit manifold and obtains the control law.
- (4)
The algorithm ensures manifold attractiveness and trajectory boundedness.
According to the actual system, the above control law can be modified to make the dimensions unified and ensure the meaning of mathematical calculation.
We set Δx = x1 − x∗. In order to meet the system stability requirements, namely, , it is necessary to ensure that , that is, the selection of the constant c needs to satisfy c ∈ [0.5, 1].
Therefore, after selecting the appropriate auxiliary compensation function β1(x), the adaptive update law w1 of the interference parameters, and the constants c and λ, it can be seen from the above system that both z1 and s can converge to zero at this time, is the only global asymptotically stable equilibrium, and x1 converges to x∗. That is, it is proved that the above system has a globally asymptotically stable equilibrium point at the desired point.
2.3. Design and analysis of nonlinear immersion invariant adaptive position controller
In view of the nonlinear dynamic disturbance in the following system, the parameters of the system friction model are unknown, and the control input um(t) is designed to make the servo platform track the desired rotation angle command and ensure that all closed-loop signals are bounded. Furthermore, an immersion-invariant nonlinear disturbance compensation control law is proposed in this paper. As shown in Figure 3.The controller consists of immersion and invariant parameter estimation combined with the system dynamic nonlinear composite function term to form an adaptive control law.
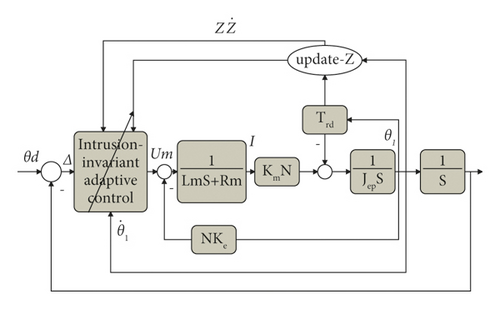
- (1)
The algorithm design target system:
- (2)
The algorithm designs an immersion map that satisfies the immersion conditions:
- (3)
The algorithm derives the implicit manifold and obtains the control law:
- (4)
The algorithm ensures manifold attractiveness and trajectory boundedness:
Selecting β1 according to the above solution can ensure that z1 can converge to 0.
In the formula, k1 is a positive coefficient greater than zero.
Therefore, when β1(x) is selected according to formula 52 and w1 is selected according to formula 53, and the constants c and λ are determined, both z1 and s can converge to zero, and x1 converges to θd . Finally, we can infer that the above system has a globally asymptotically stable equilibrium point at the desired position point, that is, the proof is complete, and the control law um can guarantee the stability of the system shown in formula 34.
Among them, is a time-varying nonlinear function with disturbance state variables.
The above parameter (kp, ki, kd) is changed by the update and change of the time-varying nonlinear adaptive function f(⋅) composed of the state variables affecting the disturbance, so that the control output of the control law changes in real time. The adaptive feedforward control combined with the feedback control can quickly eliminate the position deviation caused by friction and realize the high-precision position servo of the loading platform.
3. Automatic control of food machinery based on neural network and computational torque compounding
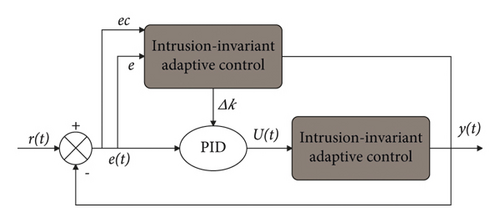
The controller takes the error e and the error rate ec between the actual measured and set parameters of temperature and humidity as input variables. Through the combined operation of fuzzy control and neural network, the real-time tuning PID control factor variation △K (△KP, △KI, △KD) is output. Then, the sum of the initial K0 and △K of the PID control factor is used as the control factor K(t) of the PID input variable e(t) to calculate the output control value u(t). After that, the execution unit is controlled to achieve the purpose of real-time regulation of the temperature control system. As shown in Figure 4.
This paper takes the plane two-degree-of-freedom manipulator system as shown in Figure 5 as the research object. The system consists of a satellite base and a two-degree-of-freedom manipulator.
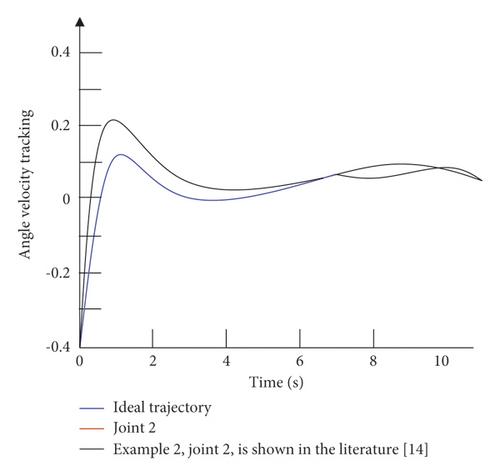
The simulation time is set to 10 s, and the simulation step size is 0.001 s. The simulation results are divided into two parts: the first is the comparison between the control strategy of this paper and the control strategy of the example without external interference; the second is the comparison of the control strategy of this paper and the control strategy of the example under the condition of external interference. The angular displacement and angular velocity simulation curves of the double-joint manipulator are shown in Figure 6 and Figure 7.
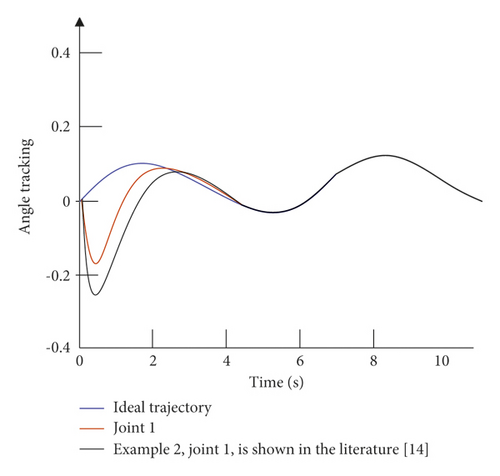
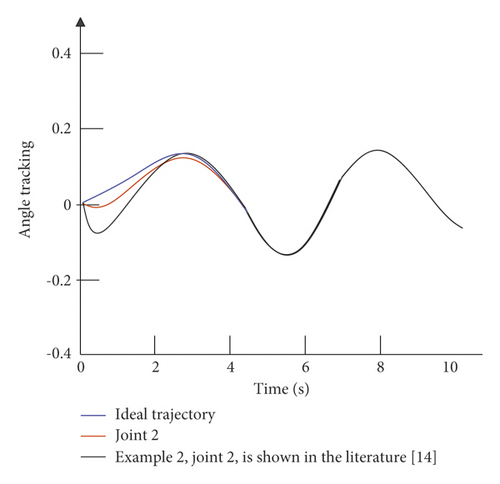
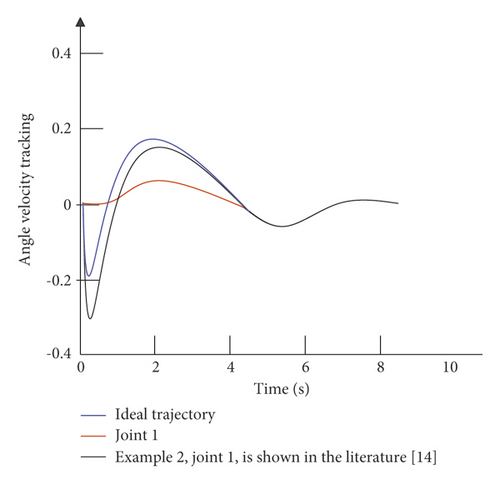
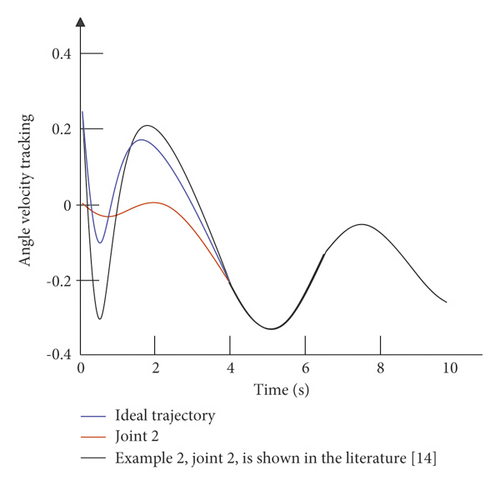
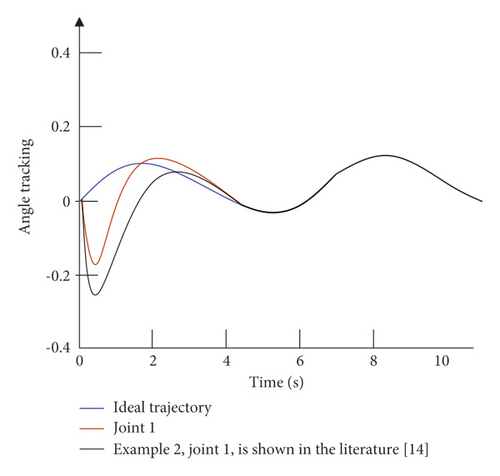
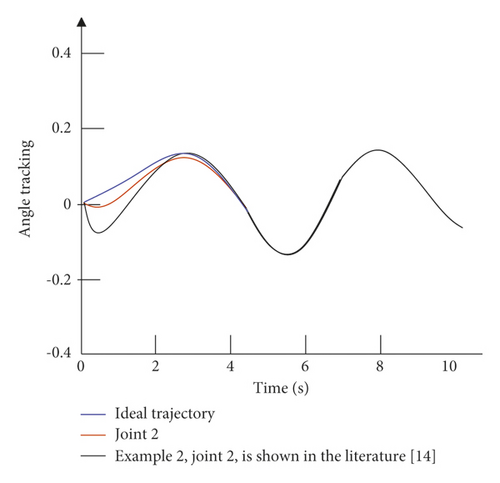
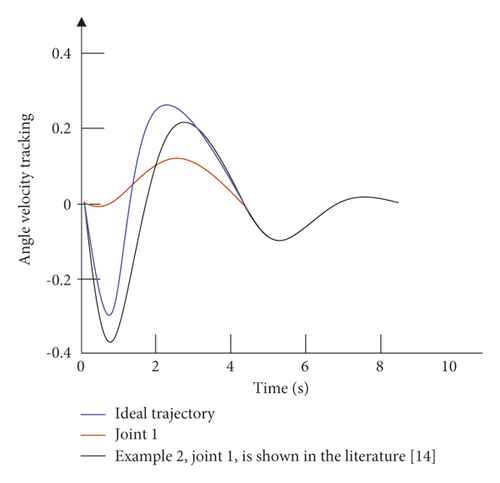
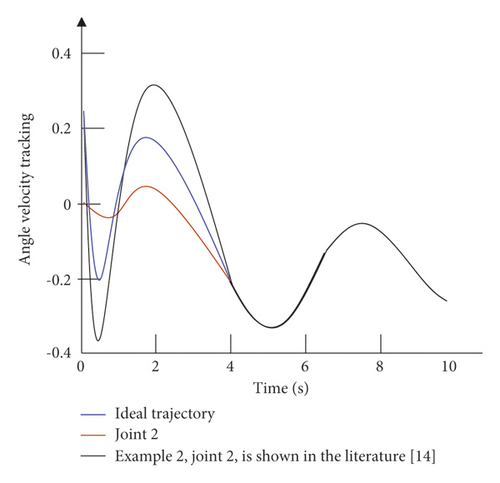
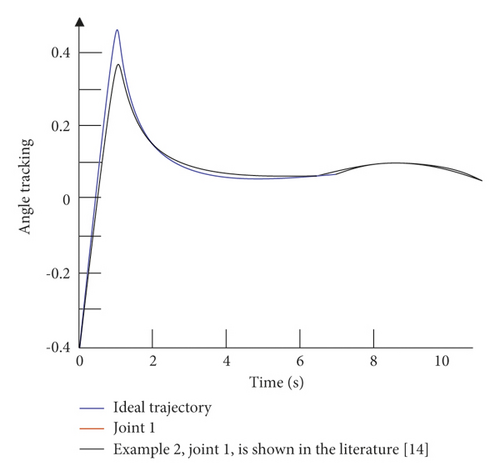
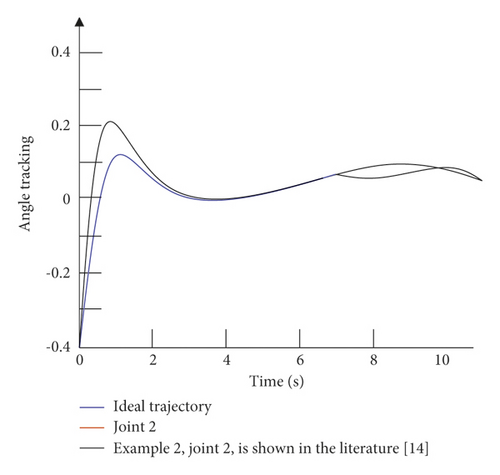
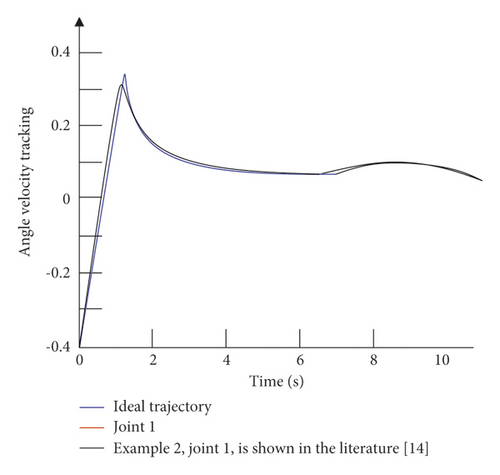
It can be seen from Figure 6 that in the absence of external interference, the control strategy of the example is relatively slow in the control tracking speed of joint 1 and joint 2. Although the ideal curve can be roughly tracked in the later stage, the effect is not optimal, and there is a small amount of jitter in the later stage of tracking. The control strategy given in this paper can not only effectively improve the tracking speed of the joints, but also effectively alleviate the tremor in the later stage. It can be seen from Figure 7 that in the case of external disturbances, there is a certain error in the tracking of the trajectory by the control strategy of the example. Moreover, in the early tracking process, the speed is slow and the fluctuation is large, and in the late tracking period, there is obvious jitter. The control strategy given in this paper can still track the ideal trajectory faster in the presence of external disturbance, and there is no obvious jitter in the later stage. Figure 8 is a graph of the control input of each joint of the dual-joint manipulator in the interference state and the non-interference state.
It can be seen from the above research that the automatic control effect of food machinery based on neural network and computational torque compounding has a certain effect.
4. Conclusion
With the continuous improvement of social productivity, the continuous enrichment of agricultural and animal husbandry products has brought new development opportunities for food processing enterprises. In order to occupy a certain brand position in the market economy, food processing enterprises not only continuously update management technology, but also continuously introduce new technologies into food processing. This lays a technical foundation for the efficient operation of food processing machinery and provides technical support for the long-term development of food enterprises. This paper combines neural network and computational torque compounding to study the automatic control system of food machinery to improve the automatic control effect of food machinery. The experimental study shows that the control strategy given in this paper can not only effectively improve the tracking speed of the joint, but also effectively alleviate the later tremor. Therefore, the automatic control effect of food machinery based on neural network and computational torque compounding has a certain effect.
Conflicts of Interest
The author declare no competing interests.
Acknowledgments
This work was supported by Zhejiang University.
Open Research
Data Availability
The labeled dataset used to support the findings of this study are available from the corresponding author upon request.




