Volume 2022, Issue 1 2376289

Research Article

Open Access

[Retracted] Multiplicative Topological Properties on Degree Based for Fourth Type of Hex-Derived Networks

Retraction(s) for this article

Haidar Ali,

Haidar Ali

orcid.org/0000-0002-9815-7158

Department of Mathematics, Riphah International University, Faisalabad, Pakistan riphah.edu.pk

Search for more papers by this author

Ghulam Dustigeer,

Ghulam Dustigeer

Department of Mathematics and Statistics, University of Agriculture, Faisalabad, Pakistan uaf.edu.pk

Search for more papers by this author

Yong-Min Li,

Corresponding Author

Yong-Min Li

[email protected]

orcid.org/0000-0001-6645-5356

Department of Mathematics, Huzhou University, Huzhou 313000, China zjhu.edu.cn

Institute for Advanced Study Honoring Chen Jian Gong, Hangzhou Normal University, Hangzhou 311121, China hznu.edu.cn

Search for more papers by this author

Muhammad Kashif Shafiq,

Muhammad Kashif Shafiq

Department of Mathematics, University of Management and Technology, Sialkot Campus, Pakistan umt.edu.pk

Search for more papers by this author

Parvez Ali,

Parvez Ali

orcid.org/0000-0001-7363-4563

Department of Mechanical Engineering, College of Engineering, Qassim University, Unaizah, Saudi Arabia qu.edu.sa

Search for more papers by this author

Haidar Ali,

Haidar Ali

orcid.org/0000-0002-9815-7158

Department of Mathematics, Riphah International University, Faisalabad, Pakistan riphah.edu.pk

Search for more papers by this author

Ghulam Dustigeer,

Ghulam Dustigeer

Department of Mathematics and Statistics, University of Agriculture, Faisalabad, Pakistan uaf.edu.pk

Search for more papers by this author

Yong-Min Li,

Corresponding Author

Yong-Min Li

[email protected]

orcid.org/0000-0001-6645-5356

Department of Mathematics, Huzhou University, Huzhou 313000, China zjhu.edu.cn

Institute for Advanced Study Honoring Chen Jian Gong, Hangzhou Normal University, Hangzhou 311121, China hznu.edu.cn

Search for more papers by this author

Muhammad Kashif Shafiq,

Muhammad Kashif Shafiq

Department of Mathematics, University of Management and Technology, Sialkot Campus, Pakistan umt.edu.pk

Search for more papers by this author

Parvez Ali,

Parvez Ali

orcid.org/0000-0001-7363-4563

Department of Mechanical Engineering, College of Engineering, Qassim University, Unaizah, Saudi Arabia qu.edu.sa

Search for more papers by this author

First published: 10 May 2022

https://doi.org/10.1155/2022/2376289

Citations: 2

Academic Editor: Hanan Alolaiyan

Share a link

Email
Wechat
Bluesky

Abstract

Chemical graph theory is a subfield of graph theory that uses a molecular graph to describe a chemical compound. When there is at least one connection between the vertices of a graph, it is said to be connected. Topology of graph has been expressed by numerical quantity which is known as topological index. Cheminformatics is a product field that combines chemistry, mathematics, and computer science. The graph plays a key role in modelling and coming up with any chemical arrangement. In this paper, we computed the multiplicative degree-based indices like Randić, Zagreb, Harmonic, augmented Zagreb, atom-bond connectivity, and geometric-arithmetic indices for newly developed fourth type of hex-derived networks and also present the graphical representations of results.

1. Introduction

Graph theory has provided chemists with a number of useful methods, such as topological indices. A molecular graph is often used to represent molecules and molecular compounds. A molecular graph is a graph theory definition of a compound’s molecular formula, the vertices that correspond to the compound’s atoms, and hence the edges that correspond to chemical bonds. Cheminformatics may be a trendy subject that would be a mix of chemistry, arithmetic, and data science. Topological indices, given by graph theory, square measure a vital tool. The topology index could be a quantity associated with a graph that unambiguously characterizes that graph. The chemical graph theory could be a combination of chemistry and graph theory. It is the mathematical chemistry branch that applies the graph hypothesis for modelling chemical structure. A graph will acknowledge a network, a meeting of numbers, a numeric variety, and a polynomial that speaks to the structure of that chart. The vertices and the edges of any chart moreover speak to the topological records. Cheminformatics is a modern scholarly field that brings together the fields of chemistry, mathematics, and information science. It examines the relationships between QSAR and QSPR, which are used to estimate biological activities and chemical compound properties. Wiener is the pioneer of TIs; he developed this theory in 1947, when he was working on the boiling points of Paraffins. Wiener called it a path number but afterwards; it is introduced by Wiener [1]. It is the first distance-based topological index. Topological indices are valuable in QSAR and QSPR studies, as they can alter the chemical structure into numerical values. More than 100 topological descriptors evaluated to get the connection between the atoms. There are a few strategies for evaluating atomic structures, the topological index of which is the most common since it can be derived specifically from atomic structures and measured effectively for a huge number of atoms.

1.1. Method for Drawing HDN4 Networks

Step 1. Let take a benzene network with dimension r.

Step 2. Place benzene graph in each K₃ subgraph of hexagonal network.

Step 3. Connect alternating vertices of each benzene graph to every corner of triangle.

Step 4. At the end, the derived result of the graph is called the fourth type of hex-derived network HDN4 (see Figure 1). In this way, we can also construct THDN4 (see Figure 2) and RHDN4 (see Figure 3).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Fourth type of the hex-derived network (HDN4 (4)).

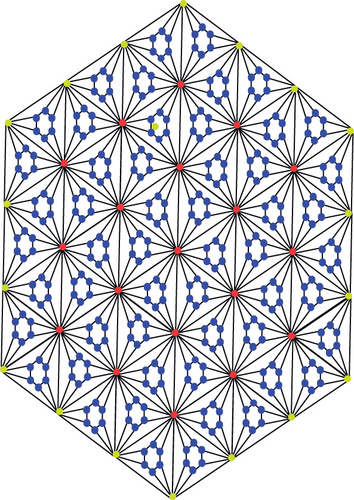
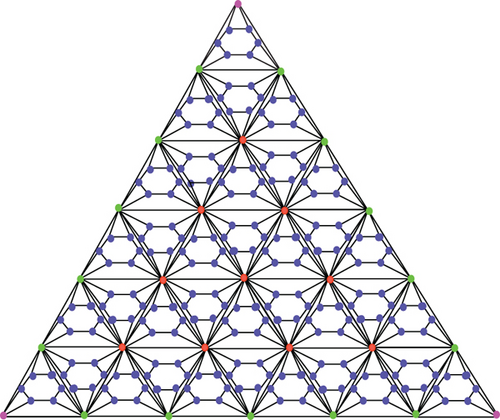
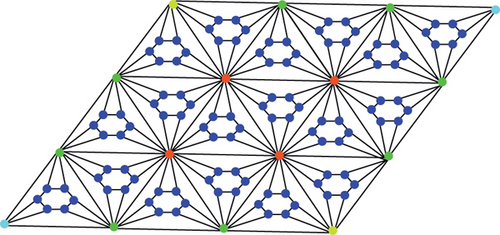
On the newly developed graphs, the degree-based TIs have been calculated in this paper. First of all, Randić index computes on the fourth type of hex-derived network.

Let Y be e simple graph. The general form of the Randić index R_γ(Y), where γ ∈ ℝ is the sum of

over all edges

, defined as follows:

(1)

The Zagreb index, denoted by M₁(Y), introduced by Gutman and Das [2] was familiar, and mathematically, it can be written as follows:

(2)

Zhong [3] calculated the harmonic index, and it can be written as follows:

(3)

Furtula et al. [4] calculated the augmented Zagreb index, and this index is defined as follows:

(4)

The mathematical form of ABC-index has been computed by Estrada et al. [5] and defined as follows:

(5)

The mathematical form of GA-index has been developed by Vukičević and Furtula [6] and defined as follows:

(6)

2. Main Results

In this research article, we introduced the different kinds of fourth type of hex-derived networks. The degree-based topological indices have been calculated in this research on the above networks. Currently, there is exhaustive study on the topological indices and with different kinds, see [7–9].For the basic definitions about graph theory and notations, see [10, 11].

2.1. Results for Fourth Type of the Hex-Derived Network HDN4(r)

For the first time, we compute the exact result on the above mentioned indices in Section 1 for newly developed graphs in this section.

Theorem 1. Consider the fourth type of hex-derived network HDN4(r), the general form of the Randić index is equal to:

(7)

Proof. The Y₁≅HDN4(r) is shown in Figure 1, where condition r ≥ 4. Thus, by using equation (1), it follows that

(8)

For γ = 1, the general form of the Randić index R_γ(Y₁) has been computed as follows:

(9)

Using Table 1, we get

(10)

Table 1. Degree-based edge partition of HDN4(r) of the end vertices on each edge.

where	Number of edges	where	Number of edges
(3, 3)	36r² − 72r + 36	(7, 18)	12m − 18
(3, 7)	36r − 48	(18, 18)	9r² − 33r + 30
(3, 18)	36r² − 108r + 84
(7, 7)	6r − 6

Forγ = 1/2, we apply the formula ofR_γ(Y₁):

(11)

Using Table 1, we get

(12)

Forγ = −1, by using formula ofR_γ(Y₁):

(13)

Forγ = −1/2, we apply the formula ofR_γ(Y₁):

(14)

Theorem 2. For fourth type of hex-derived network Y₁, the first form of the Zagreb index is equal to:

(15)

Proof. Let Y₁≅HDN4(r) be the hex-derived network. The below is the result of using the Table 1. Equation (2) can be used to calculate the Zagreb index as follows:

(16)

By doing some calculations, we get:

(17)

The H-index, AZI-index, ABC-index, and GA-index have been computed for the fourth type of hex-derived network Y₁.

Theorem 3. Let Y₁ be the fourth form of the hex-derived network, then:

(i)
H(Y₁) = (223/14)r² − (28961/1050)r + 5507/525
(ii)
AZI(Y₁) = (4865917013307/539172272)r² − (35453987024262256/1230020443767)r + 88794905734397152/3690061331301
(iii)
ABC(Y₁) = 8r² − 92r + 43
(iv)
GA(Y₁) = 70r² − 131r + 59

Proof. Using Table 1 and equation (3) to calculate the Harmonic index.

(18)

By doing some calculations, we get

(19)

By using equation (4) to calculate the augmented Zagreb index is equal to:

(20)

By doing some calculations, we get

(21)

By using equation (5) to calculate the ABC-index:

(22)

By doing some calculations, we get

(23)

By using equation (6) to calculate the geometric arithmetic index

(24)

By doing some calculations, we get

(25)

2.2. Results for Fourth Type of Triangular Hex-Derived Network THDN4(r)

The degree-based TIs have been computed for the fourth form of the triangular hex-derived network in this portion. We calculate general form of Randić index R_γ with γ = {1, −1, 1/2, −1/2}, M₁-index, H-index, AZI-index, ABC-index, and GA-index in the coming theorems.

Theorem 4. Consider the THDN4(r), then general form of the Randić index is equal to:

(26)

Proof. Let Y₂≅(THDN4(r)), using Table 2 and equation (1), we have

(27)

Table 2. Edge partition of a THDN4(r) based on degrees of end vertices of each edge.

where	Number of edges	where	Number of edges
(3, 3)	6r² − 12r + 6	(4, 10)	6
(3, 4)	6	(10, 10)	3(r − 2)
(3, 10)	9(2r − 4)	(10, 18)	6(m − 3)
(3, 18)	2(3r² − 15r + 18)	(18, 18)

Forγ = 1, the general form of the Randić indexR_γ(Y₂)can be computed as follows:

(28)

Using Table 2, we get

(29)

Forγ = 1/2, we apply the formula ofR_γ(Y₂):

(30)

Using Table 2, we get

(31)

Forγ = −1, by using the formula ofR_γ(Y₂):

(32)

Forγ = −1/2, by using the formula ofR_γ(Y₂):

(33)

Theorem 5. The first form of the Zagreb index for fourth type of triangular hex-derived network Y₂ is equivalent to:

(34)

Proof. Let Y₂≅THDN3(r). Using Table 2 and equation (2), the first Zagreb index is equal to

(35)

By doing some calculations, we get:

(36)

Theorem 6. Let Y₂ be the THDN4, then:

(i)
H(Y₂) = (223/84)r² − (21527/5460)r + 717/455
(ii)
AZI(Y₂) = (1203267/800)r² − (2816367/400)r + 325590119/36000
(iii)
ABC(Y₂) = 8r² − 15r + 7
(iv)
GA(Y₂) = 12r² − 19r + 7

Proof. Using Table 2 to calculate the Harmonic index and using equation (3):

(37)

By doing some calculations, we get

(38)

Using equation (5) to calculate the augmented Zagreb index.

(39)

By doing some calculations, we get

(40)

By using equation (6) to calculate the atom bond connectivity index

(41)

By doing some calculations, we get

(42)

By using equation (7) to calculate the geometric arithmetic index:

(43)

By doing some calculations, we get

(44)

2.3. Result for Fourth Type of Rectangular Hex-Derived Network RHDN4(r, s)

Some topological indices which based on the degree of the RHDN4(r, s) with condition r = s have been computed in this portion. We evaluate the general form Randić index R_γ(RHDN4(r)) for the γ = {1, −1, 1/2, −1/2}, M₁-index, H-index, AZI-index, ABC-index, and GA-index in the forward theorems of RHDN4(r, s).

Theorem 7. For the fourth type of rectangular hex-derived network RHDN4(r), the general Randić index is equal to

(45)

Proof. Let Y₃≅RHDN4(r) be seen in Figure 3, with condition r = s ≥ 4. The edge partition as seen in the table is as follows:

(46)

For γ = 1, the general form of the Randić index R_γ(Y₃) can be calculated as follows:

(47)

Using Table 3, we get

(48)

Table 3. The edge partition of fourth type of rectangular hex-derived network.

where	Number of edges	where	Number of edges
(3, 3)	12r² − 24r + 12	(7, 10)	4
(3, 4)	4	(7, 18)	2
(3, 7)	8	(10, 10)	2(2r − 5)
(3, 10)	6(4r − 8)	(10, 18)	4(2r − 5)
(3, 18)	6(2r² − 8r + 8)	(18, 18)	3r² − 16r + 21
(4, 10)	4

Forγ = 1/2, we apply the formula ofR_γ(Y₃):

(49)

Using Table 3, we get

(50)

Forγ = −1, by using the formula ofR_γ(Y₃):

(51)

Forγ = −1/2, using formula ofR_γ(Y₃):

(52)

Theorem 8. The first Zagreb index for the RHDN4(r) is equivalent to

(53)

Proof. Let Y₃≅RHDN4(r). Using Table 3 and equation (2) to calculate the Zagreb index:

(54)

By doing some calculations, we get

(55)

Now, we calculate the H-index, AZI-index, ABC-index, and GA-index for RHDN4(r).

Theorem 9. Let Y₃ be the fourth type of rectangular hex-derived network, then:

(i)
H(Y₃) = (439/84)r² − (4886/585)r + 1525241/464100
(ii)
AZI(Y₃) = (240663/80)r² − (2278779/200)r + 268079839/24000
(iii)
ABC(Y₃) = 2(8r − 7)(r − 1)
(iv)
GA(Y₃) = 23r² − 42r + 18

Proof. Using Table 3 and equation (3) to calculate the Harmonic index:

(56)

By doing some calculations, we get

(57)

Using equation (4) to calculate the augmented Zagreb index:

(58)

By doing some calculations, we get

(59)

Using equation (5) to calculate the atom bond connectivity index:

(60)

By doing some calculations, we get

(61)

Using equation (6) to geometric arithmetic index:

(62)

By doing some calculations, we get

(63)

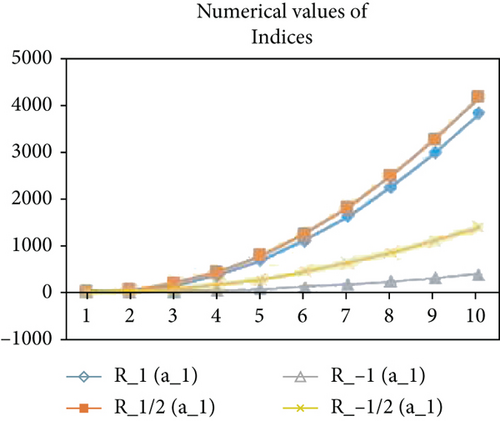
For comparison through graphs, the comparison of the different topological indices for the HDN4, THDN4, and RHDN4, a newly developed fourth type of hex-derived networks has been evaluated for the different values. The graphical representation shows the correctness of the results as shown in Figures 4–9.

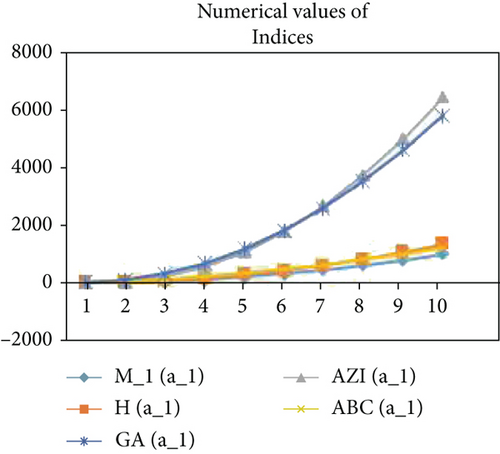
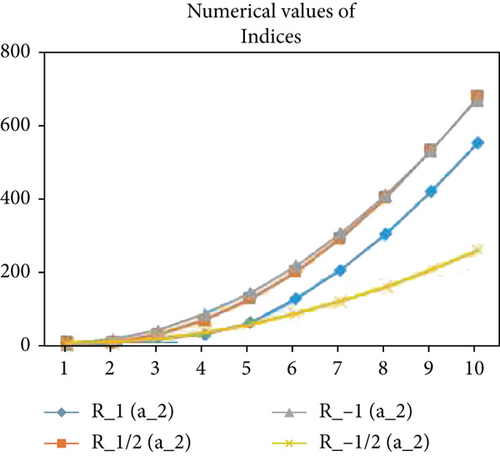
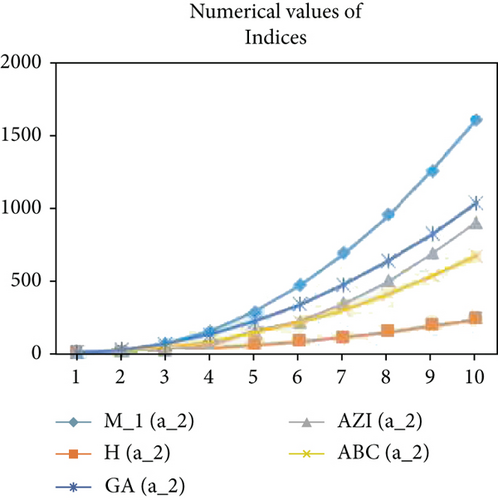
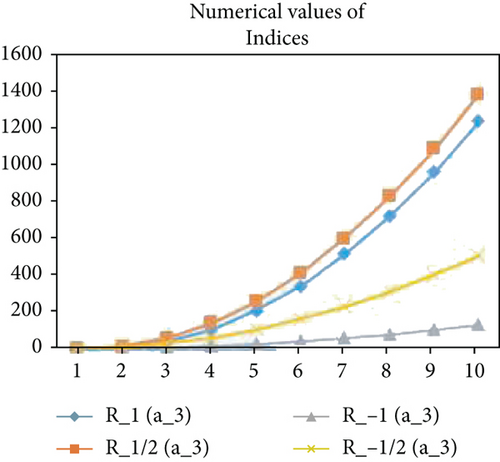
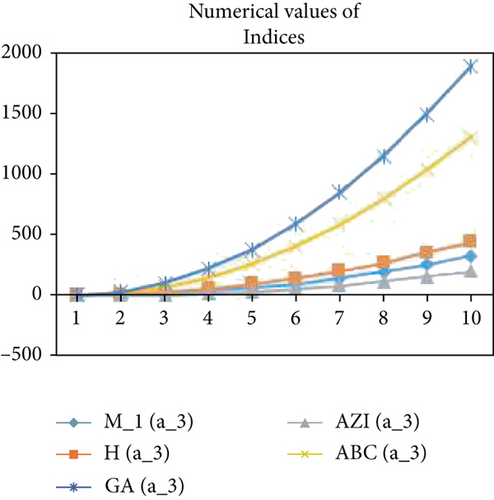
3. Conclusion

In this paper, certain degree-based topological indices, namely, the Randić, Zagreb, Harmonic, augmented Zagreb, atom-bond connectivity, and geometric-arithmetic indices for the HDN4, THDN4, and RHDN4 networks, were studied for the first time, and analytical closed formulas for these networks were determined that will help the people working in network science to understand the underlying topologies of these networks. In future, we are interested in designing some new architectures/networks and then studying their topological indices, which will be quite helpful in understanding their underlying topologies.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

No data were used to support this study.

References

1 Wiener H., Structural determination of paraffin boiling points, Journal of the American Chemical Society. (1947) 69, no. 1, 17–20, https://doi.org/10.1021/ja01193a005, 2-s2.0-8544254107, 20291038.
10.1021/ja01193a005
CAS PubMed Web of Science® Google Scholar
2 Gutman I. and Das K. C., The first Zagreb index 30 years after, MATCH Communications in Mathematical and in Computer Chemistry. (2004) 50, no. 1, 83–92.
CAS Google Scholar
3 Zhong L., The harmonic index for graphs, Applied Mathematics Letters. (2012) 25, no. 3, 561–566, https://doi.org/10.1016/j.aml.2011.09.059, 2-s2.0-80955166259.
10.1016/j.aml.2011.09.059
Web of Science® Google Scholar
4 Furtula B., Graovac A., and Vukićevixcx D., Augmented Zagreb index, Journal of Mathematical Chemistry. (2010) 48, no. 2, 370–380, https://doi.org/10.1007/s10910-010-9677-3, 2-s2.0-77954457136.
10.1007/s10910-010-9677-3
CAS Web of Science® Google Scholar
5 Estrada E., Torres L., Rodríguez L., and Gutman I., An atom-bond connectivity index: modelling the enthalpy of formation of alkanes, Indian Journal of Chemistry. (1998) 37, 849–855.
Web of Science® Google Scholar
6 Vukičević D. and Furtula B., Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges, Journal of Mathematical Chemistry. (2009) 46, no. 4, 1369–1376, https://doi.org/10.1007/s10910-009-9520-x, 2-s2.0-70350166990.
10.1007/s10910-009-9520-x
CAS Web of Science® Google Scholar
7 Liu J. B., Ali H., Shafiq M. K., Dustigeer G., and Ali P., On topological properties of planar octahedron networks, Polycyclic Aromatic Compounds. (2021) 1–17.
Web of Science® Google Scholar
8 Qi R., Ali H., Babar U., Liu J. B., and Ali P., On the sum of degree-based topological indices of rhombus-type silicate and oxide structures, Journal of Mathematics. (2021) 2021, 16, https://doi.org/10.1155/2021/1100024.
10.1155/2021/1100024
Web of Science® Google Scholar
9 Ali H., Binyamin M. A., Shafiq M. K., and Gao W., On the degree-based topological indices of some derived networks, Mathematics. (2019) 7, no. 7, https://doi.org/10.3390/math7070612, 2-s2.0-85068853338.
10.3390/math7070612
Web of Science® Google Scholar
10 Diudea M. V., Gutman I., and Lorentz J., Molecular Topology, 2001, Nova Science Publishers, Huntington, NY, USA.
Google Scholar
11 Gutman I., Topological properties of benzenoid systems, Topics in Current Chemistry. (1992) 162, 21–28.
Web of Science® Google Scholar

Citing Literature

All articles

[Retracted] Multiplicative Topological Properties on Degree Based for Fourth Type of Hex-Derived Networks

Retraction(s) for this article

Retracted: Multiplicative Topological Properties on Degree Based for Fourth Type of Hex-Derived Networks

Abstract

1. Introduction

1.1. Method for Drawing HDN4 Networks

2. Main Results

2.1. Results for Fourth Type of the Hex-Derived Network HDN4(r)

2.2. Results for Fourth Type of Triangular Hex-Derived Network THDN4(r)

2.3. Result for Fourth Type of Rectangular Hex-Derived Network RHDN4(r, s)

3. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

[Retracted] Multiplicative Topological Properties on Degree Based for Fourth Type of Hex-Derived Networks

Retraction(s) for this article

Retracted: Multiplicative Topological Properties on Degree Based for Fourth Type of Hex-Derived Networks

Abstract

1. Introduction

1.1. Method for Drawing HDN4 Networks

2. Main Results

2.1. Results for Fourth Type of the Hex-Derived Network HDN4(r)

2.2. Results for Fourth Type of Triangular Hex-Derived Network THDN4(r)

2.3. Result for Fourth Type of Rectangular Hex-Derived Network RHDN4(r, s)

3. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information