Computational Intelligence and Neuroscience

Volume 2022, Issue 1 2006574

Research Article

Open Access

Computing the Entropy Measures for the Line Graphs of Some Chemical Networks

Muhammad Farhan Hanif,

Muhammad Farhan Hanif

orcid.org/0000-0002-2439-3967

Abdus Salam School of Mathematical Sciences, Government College University, Lahore, Pakistan gcu.edu.pk

Search for more papers by this author

Hasan Mahmood,

Hasan Mahmood

Abdus Salam School of Mathematical Sciences, Government College University, Lahore, Pakistan gcu.edu.pk

Department of Mathematics, Government College University, Lahore, Pakistan gcu.edu.pk

Search for more papers by this author

Shazia Manzoor,

Shazia Manzoor

orcid.org/0000-0001-9867-7148

Department of Mathematics, COMSATS University Islamabad, Lahore Campus, Pakistan comsats.edu.pk

Search for more papers by this author

Fikre Bogale Petros,

Corresponding Author

Fikre Bogale Petros

[email protected]

orcid.org/0000-0003-4270-8114

Department of Mathematics, Addis Ababa University, Addis Ababa, Ethiopia aau.edu.et

Search for more papers by this author

Muhammad Farhan Hanif,

Muhammad Farhan Hanif

orcid.org/0000-0002-2439-3967

Abdus Salam School of Mathematical Sciences, Government College University, Lahore, Pakistan gcu.edu.pk

Search for more papers by this author

Hasan Mahmood,

Hasan Mahmood

Abdus Salam School of Mathematical Sciences, Government College University, Lahore, Pakistan gcu.edu.pk

Department of Mathematics, Government College University, Lahore, Pakistan gcu.edu.pk

Search for more papers by this author

Shazia Manzoor,

Shazia Manzoor

orcid.org/0000-0001-9867-7148

Department of Mathematics, COMSATS University Islamabad, Lahore Campus, Pakistan comsats.edu.pk

Search for more papers by this author

Fikre Bogale Petros,

Corresponding Author

Fikre Bogale Petros

[email protected]

orcid.org/0000-0003-4270-8114

Department of Mathematics, Addis Ababa University, Addis Ababa, Ethiopia aau.edu.et

Search for more papers by this author

First published: 06 October 2022

https://doi.org/10.1155/2022/2006574

Citations: 1

Academic Editor: Gohar Ali

Share a link

Email
Wechat
Bluesky

Abstract

Chemical Graph entropy plays a significant role to measure the complexity of chemical structures. It has explicit chemical uses in chemistry, biology, and information sciences. A molecular structure of a compound consists of many atoms. Especially, the hydrocarbons is a chemical compound that consists of carbon and hydrogen atoms. In this article, we discussed the concept of subdivision of chemical graphs and their corresponding line chemical graphs. More preciously, we discuss the properties of chemical graph entropies and then constructed the chemical structures namely triangular benzenoid, hexagonal parallelogram, and zigzag edge coronoid fused with starphene. Also, we estimated the degree-based entropies with the help of line graphs of the subdivision of above mentioned chemical graphs.

1. Introduction

Mathematical chemistry is a field of theoretical chemistry that uses mathematical approaches to discuss molecular structure without necessarily referring to quantum mechanics [1]. Chemical Graph Theory is a branch of mathematical chemistry where a chemical phenomenon is theoretically described using graph theory [2, 3]. The growth of organic disciplines has been aided by Chemical Graph Theory [4, 5]. In mathematical chemistry, graph invariants or topological indices are numeric quantities that describe various essential features of organic components and are produced from an analogous molecular graph [6, 7]. Degree-based indices are among the topological indices used to predict bioactivity, boiling point, draining energy, stability, and physico-chemical properties of certain chemical compounds [8, 9]. Due to their chemical applications, these indices have significant role in theoretical chemistry. Zhang et al. [10–12] discuss the topological indices of generalized bridge molecular graphs, Carbon Nanotubes and product of chemical graphs. Zhang et al. [13–15] provided the physical analysis of heat for formation and entropy of Ceria Oxide. For further study about indices, see [16, 17].Shannon [18] originated the conception of information entropy in communication theory. However, it was later discovered as a quantity that applied to all things with a set nature [19, 20], including molecular graphs [21–23]. In chemistry, information entropy is now used in two modes. Firstly, it is a structural descriptor for assessing the complexity of chemical structures [24]. Information entropy is useful in this regard for connecting structural and physico-chemical features [25], numerically distinguishing isomers of organic molecules [26], and classifying natural products and synthetic chemicals [27, 28]. The physico-chemical sounding of information entropy is a different mode of application. As a result, Terenteva and Kobozev demonstrated its utility in analyzing physico-chemical processes that simulate information transmission [29]. Zhdanov [30] used entropy values to study organic compound chemical processes. The information entropy is defined as:

(1)

Here, the logarithm is considered to be with base e while

and Λ(lm) represent the vertex set, the edge set and the edge weight of the edge (lm) in Λ. Many graph entropies have been calculated in the literature utilising characteristic polynomials, vertices degree, and graph order [31–34]. Graph entropies, which are based on independent sets, matchings, and the degree of vertices [35], have been estimated in recent years. Dehmer and Mowshowits proposed several graph complexity and Hosoya entropy relationships [23, 32, 36, 37]. For further study, see [19, 21, 38–42, 59, 60].The graph

is structured into ordered pairs, with one object being referred to as a vertex set

and the other as an edge set

, and these vertices and edges being connected. When two vertices of

share an edge, they are said to be neighboring. The sum of the degrees of all neighboring vertices of l is denoted by A_l, and the degree of a vertex l is represented by

. By replacing each of

’s edges with a path of length two, the subdivision graph

is formed. The line graph is denoted by the symbol

in which

and two vertices of

are adjacent iff their corresponding edges share a common end points in

1.1. Randić Entropy [43, 44]

, then

(2)

Now (1) represent the Randi

Entropy.

(3)

1.2. Atom Bond Connectivity Entropy [45]

, then

(4)

Thus (1) is converted in the following form:

(5)

1.3. The Geometric Arithmetic Entropy [43, 44]

, then

(6)

Now (1) takes the form as given below.

(7)

1.4. The Fourth Atom Bond Connectivity Entropy [35]

, then

(8)

Now (1) converted in the following form as:

(9)

1.5. The Fifth Geometric Arithmetic Entropy [35]

, then

(10)

Equation (1) is now changed to the following form, which is known as fifth geometric arithmetic entropy.

(11)

See [35, 44] for further information on these entropy measures.

2. Formation of Triangular Benzenoid

Triangular benzenoids are a group of benzenoid molecular graphs and are denoted by T_x, where x characterizes the number of hexagons at the bottom of the graph and 1/2x(x + 1) represents the total number of hexagons in T_x. Triangular benzenoids are a generalization of the benzene molecule C₆H₆, with benzene rings forming a triangular shape. In physics, chemistry, and nanosciences, the benzene molecule is a common molecule. Synthesizing aromatic chemicals is quite fruitful [46]. Raut [47] calculated some toplogical indices for the triangular benzenoid system. Hussain et al. [48] discussed the irregularity determinants of some benzenoid systems. Kwun [49] calculated degree-based indices by using M polynomials. For further details, see [50, 51]. The hexagons are placed in rows, with each row increasing by one hexagon. For T₁, there are only one type of edges e₁ = (2,2) and |e₁| = 6. Therefore, V(T₁) = 6 and E(T₁) = 6 while three kinds of edges are there in T₂ e.g. e₁ = (2,2), e₂ = (2,3), e₃ = (3,3) and |e₁| = 6, |e₂| = 6, |e₃| = 3. Therefore, V(T − 2) = 13 and E(T₂) = 15. Continuing in this way, |V(T_x)| = x² + 4x + 1 and |E(T_x)| = 3/2x(x + 3). The subdivision graph of T_x and its line graph are demonstrated in Figure 1. It is to be noted that |V(L(S(T_x)))| = 3x(x + 3) and |E(L(S(T_x)))| = 3/2(3x² + 7x − 2).

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

(a) Triangular benzenoid T₅, (b) Subdivision of T₅, (c) The line graph of subdivision graph of T₅.

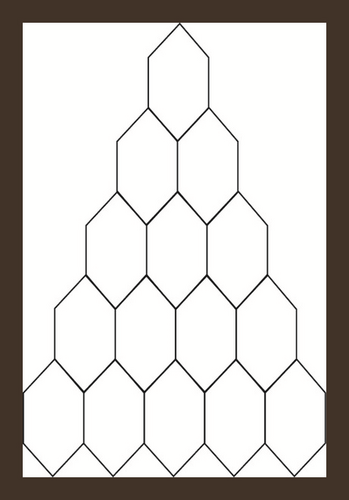
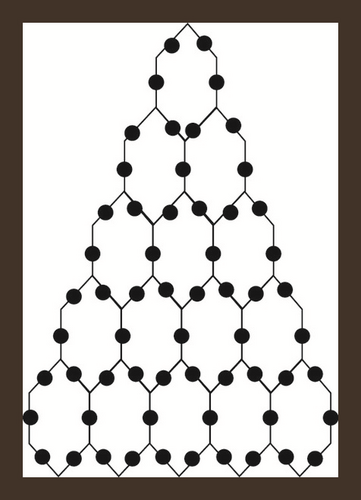
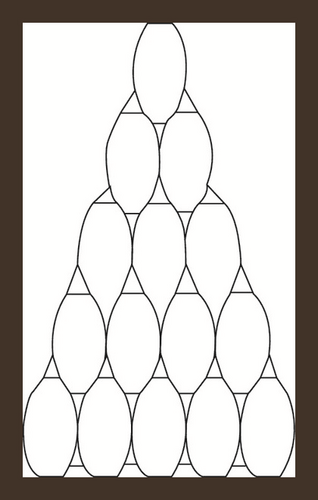
Let . i-e. is the line graph of the subdivision graph of triangular benzenoid T_x. We will use the edge partition and vertices counting technique to compute our abstracted indices and entropies. The degree of each edge’s terminal vertices is used in the edge partitioning of . It is easy to see that there are only three types of edges shown in Table 1.

Table 1. Edge partition of L(S(T_x)).

	N_i	Set of Edges
(2,2)	2(x + 3)	E₁
(2,3)	6(x − 1)	E₂
(3,3)	3/2(3x² + x − 4)	E₃

2.1. Entropy Measure for L(S(T_x))

We’ll calculate the entropies of in this section.

2.1.1. Randi Entropy of L(S(T_x))

The Randi

index and entropy for α = 1, −1, 1/2, −1/2, with the help of Table 1, and equation (3) is:

(12)

By putting α = 1, −1, 1/2, −1/2, in (3), we get the Randi

entropies as given below:

(13)

2.1.2. The ABC Entropy of L(S(T_x))

The ABC index and entropy measure with the help of Table 1 and equation (5) is:

(14)

2.1.3. The Geometric Arithmetic Entropy of L(S(T_x))

The GA index and entropy measure with the help of Table 1 and equation (7) is:

(15)

2.1.4. The ABC₄ Entropy of L(S(T_x))

The edge partition of the graph L(S(T_x)) is grounded on the degree addition of terminal vertices of every edge, as shown in Table 2.

Table 2. Edge partition of L(S(T_x)).

(A_l, A_m)	N_i	Set of Edges
(4, 4)	9
(4, 5)	6
(5, 5)	3(x − 2)
(5, 8)	6(y − 1)
(8, 8)	3(x − 1)
(8, 9)	6(x − 1)
(9, 9)	3/2(3x² + 2 − 5x)

After simple calculations, by using Table 2 subject to the condition that x ≠ 1, we get

(16)

By using (9), the ABC₄ entropy as follows:

(17)

If we consider x = 1, Then , and .

2.1.5. The GA₅ Entropy of L(S(T_x))

After some simple calculations, the GA₅ index may be calculated using Table 2 under the constraint that x ≠ 1.

(18)

Therefore, (11), with Table 2 converted in the form:

(19)

3. Formation of Hexagonal Parallelogram Nanotubes H(x, y),

Hexagonal parallelogram nanotubes are formed by arranging hexagons in a parallelogram fashion. Baig et al. [52] computed counting polynomials of benzoid carbon nanotubes. Also, see [53]. We will denote this structure by , in which x and y represent the quantity of hexagons in any row and column respectively. Also, the order and size of H(x, y) is 2(x + y + xy) and 3xy + 2x + 2y − 1 respectively. The subdivision graph of H(x, y) and its line graph is shown in Figure 2, see [46]. Let , then and . To compute our results, we will use edge partition technique which is grounded on the degree of terminal vertices of every edge. It is to be noted that there are only three types of edges, see Figure 2. The edge partition of chemical graph L(S(H(x, y))) depending on the degree of terminal vertices is presented in Table 3.

Table 3. Edge partition of L(S(H(x, y))).

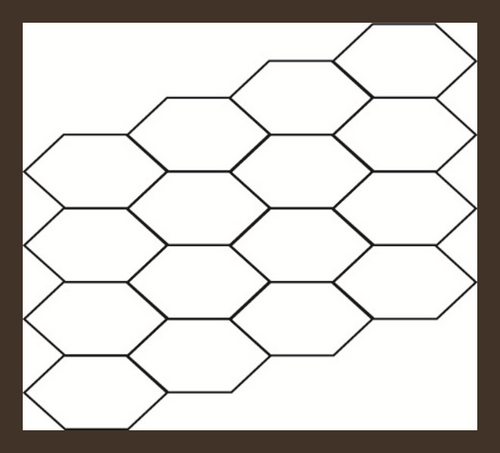
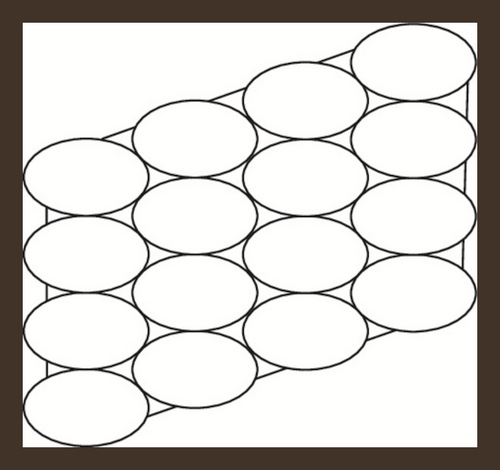
	N_i	Kinds of Edges
(2, 2)	2(4 + y + x)
(2, 3)	4(−2 + y + x)
(3, 3)	9xy − 2m − 2n − 5

3.1. Entropy Measure for L(S(H(x, y)))

We will enumerate the entropies of in this section.

3.1.1. Randić Entropy of

The Randi

index for α = 1, −1, 1/2, −1/2, by using Table 3 is:

(20)

So the (3) with Table 3 gives the Randi

entropy and is converted in the form:

(21)

Now substitute α = 1, −1, 1/2, −1/2, in (20), we get the Randi

entropies as given below:

(22)

3.1.2. The ABC Entropy of

With the use of Table 3 and equation (5), we can calculate the ABC index and entropy measure as follows:

(23)

Therefore, the equation (5), with Table 3 becomes as following and is called the atom bond connectivity entropy.

(24)

3.1.3. The Geometric Arithmetic Entropy of

We can calculate the GA index and entropy measure using Table 3 and equation (7) as follows:

(25)

3.1.4. The ABC₄ Entropy of

Case 1. when x > 1, y ≠ 1

The edge partition of L(S(H(x, y))) is shown in Table 4.

Therefore, the ABC₄ index and entropy measure with the help of Table 4 and equation (9) yield as:

(26)

Since has seven kinds of edges, So (9) by using Table 4 is converted in the form:

(27)

Table 4. Edge partition of L(S(H(x, y))).

(A_l, A_m)	N_i	Kinds of edges
(4, 4)	8
(4, 5)	8
(5, 5)	2(−4 + y + x)
(5, 8)	4(−2 + y + x)
(8, 8)	2(−2 + x + y)
(8, 9)	2(−2 + x + y)
(9, 9)	9xy − 8x − 8y + 7

Case 2. when x = 1, y ≠ 1

By using the same process, we get the closed expressions for the ABC₄ index and ABC₄ entropy as:

(28)

3.1.5. The Fifth Geometric Arithmetic Entropy of

Case 3. when x > 1, y ≠ 1The fifth geometric arithmetic entropy can be estimated by using (11), and Table 4 in the following manner:

(29)

So the (11), with Table 4 can be written as:

(30)

Case 4. when x = 1, y ≠ 1By using Table 5 and using (11) we get the closed expressions for the GA₅ index and GA₅ entropy as:

(31)

Table 5. Edge partition of L(S(H(x, y))), for x = 1.

(A_l, A_m)	N_i	Kinds of edges
(4, 4)	10
(4, 5)	4
(5, 5)	2(y − 2)
(5, 8)	4(y − 1)
(8, 8)	2(y − 1)
(8, 9)	2(y − 1)
(9, 9)	y − 1

4. Formation from Fusion of Zigzag-Edge Coronoid with Starphene ZCS(x, y, z) Nanotubes

If a zigzag-edge coronoid ZC(x, y, z) is fused with a starphene St(x, y, z), then we will obtain a composite benzenoid. It is to b noted that |V(ZCS(x, y, z))| = 36x − 54 and |E(ZCS(x, y, z))| = −63 + 15(z + y + x). The subdivision graph of ZCS(x, y, z) and its line graph are illustrated in Figure 3. We can see from figures that the order and the size in the line graph of the subdivision graph of ZCS(x, y, z) are −126 + 30(z + y + x) and −153 + 39(z + y + x) respectively [46]. Let represents the subdivision graph of ZCS(x, y, z)’s line graph. The edge division is determined by the degree of each edge’s terminal vertices. Table 6 illustrates this.

Table 6. Edge partition of L(S(ZCS)).

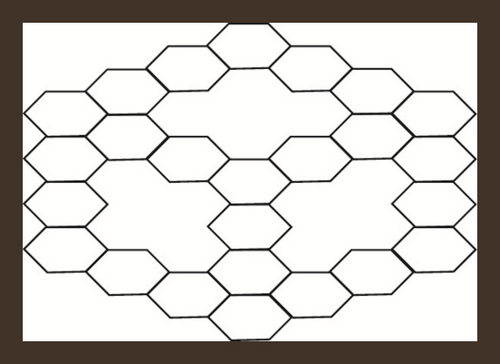
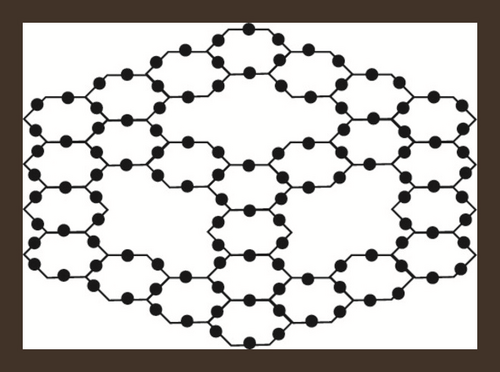
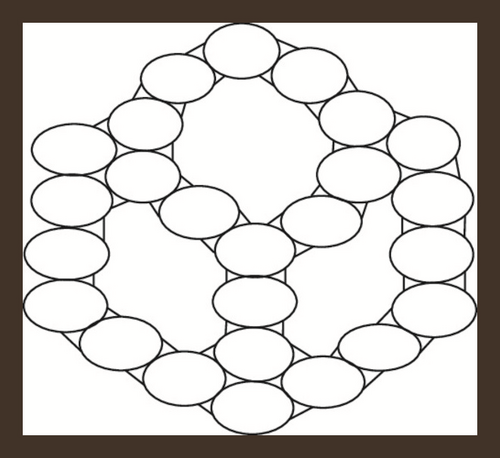
	N_i	Kinds of Edges
(2,2)	6(−5 + z + y + x)
(2,3)	12(−7 + z + y + x)
(3,3)	−39 + 21(z + y + x)

4.1. Entropy Measure for L(S(ZCS(x, y, z)))

We’ll calculate the entropies of in this section.

4.1.1. Randi Entropy of

For α = 1, −1, 1/2, −1/2, the Randi

index with the help of Table 1 is

(32)

Using (3) Randi

entropy is:

(33)

By putting α = 1, −1, 1/2, −1/2, in (32), we get the Randi

entropies as given below:

(34)

4.1.2. The ABC Entropy of

The ABC index and entropy measure with the help of Table 6 and equation (5) are:

(35)

4.1.3. The Geometric Arithmetic Entropy of

The GA index and corresponding entropy with the help of Table 6 and equation (7) are:

(36)

4.1.4. The ABC₄ entropy of

Table 7 shows the graph L(S(ZCS(x, y, z)))’s edge partition, which is based on the degree addition of each edge’s terminal vertices.

Table 7. Edge partition of L(S(ZCS(x, y, z))) established on degree sum of terminal vertices, for every x = y = z ≥ 4

(A_l, A_m)	N_i	Kinds of Edges
(4, 4)	6
(4, 5)	12
(5, 5)	6(x + y + z − 8)
(5, 8)	12(x + y + z − 7)
(8, 8)	6(x + y + z − 9)
(8, 9)	12(x + y + z − 5)
(9, 9)	3(x + y + z + 25)

After simple calculations, the ABC₄ index and entropy measure with the help of Table 7 and equation (9) subject to the condition that x = y = z ≥ 41

(37)

4.1.5. The GA₅ Entropy of

After some simple calculations, the GA₅ index and corresponding entropy measure with the help of Table 7 and equation (11) subject to the condition that x = y = z ≥ 4.

(38)

5. Concluding remarks for Computed Results

The applications of information-theoretic framework in many disciplines of study, such as biology, physics, engineering, and social sciences, have grown exponentially in the recent two decades. This phenomenal increase has been particularly impressive in the fields of soft computing, molecular biology, and information technology. As a result, the scientists may find our numerical and graphical results useful [54, 55]. The entropy function is monotonic, which means that as the size of a chemical structure increases, so does the entropy measure, and as the entropy of a system increases, so does the uncertainty regarding its reaction.

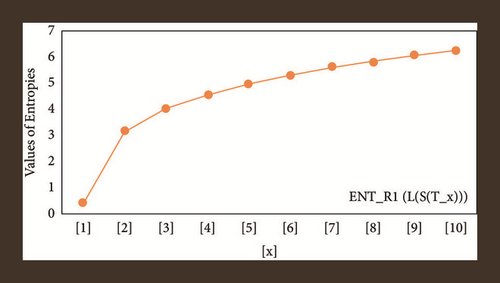
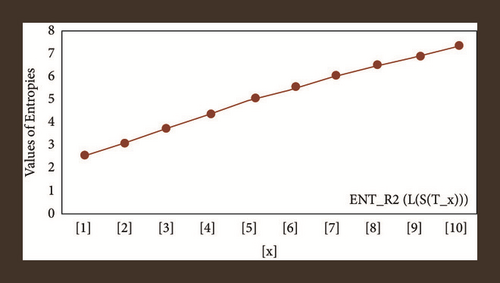
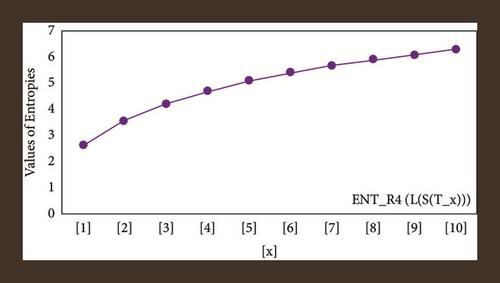
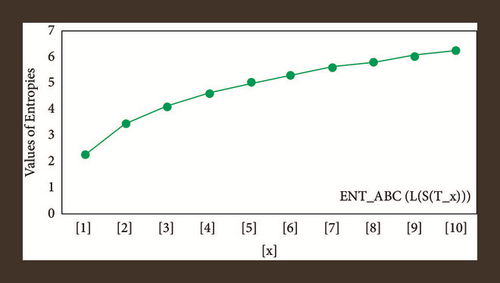
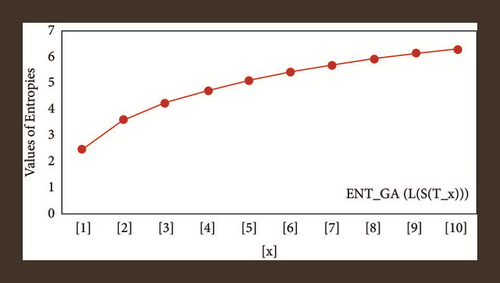
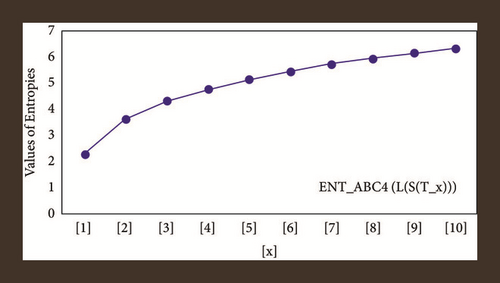
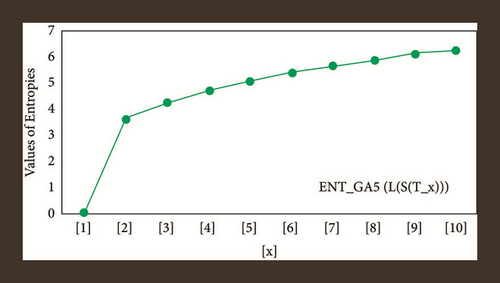
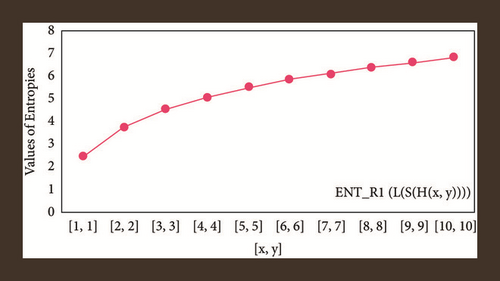
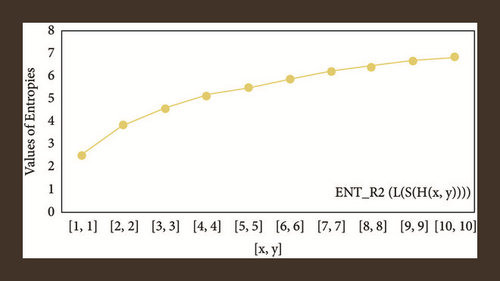
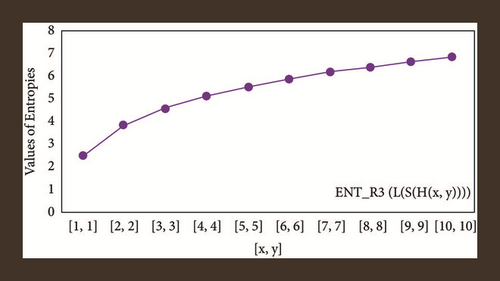
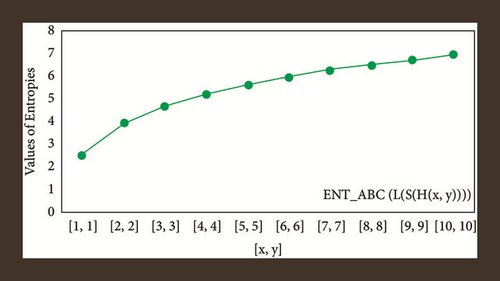
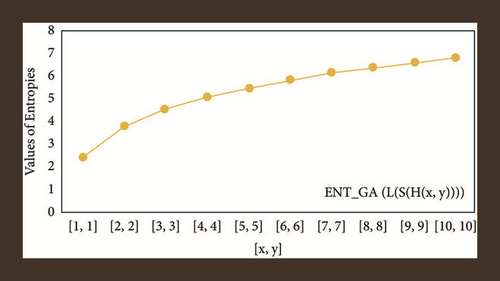
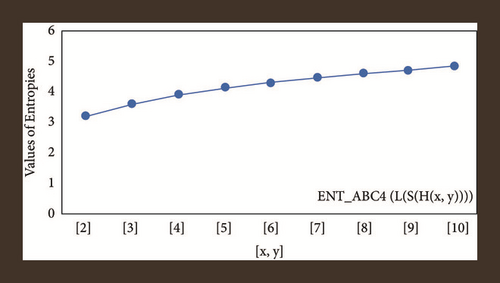
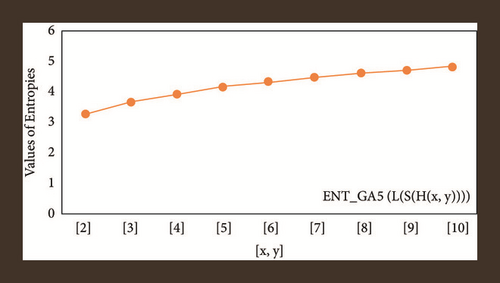
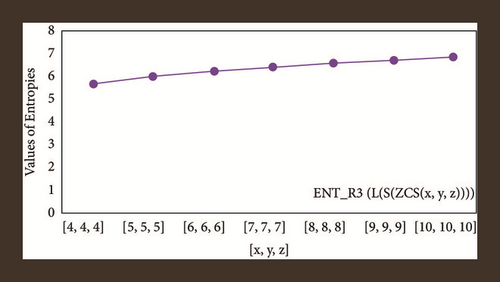
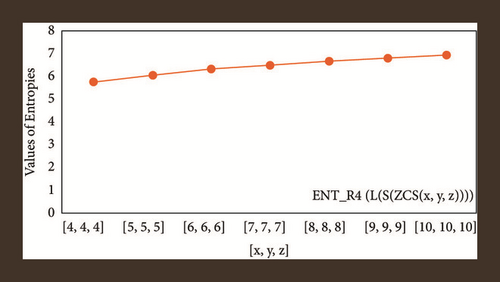
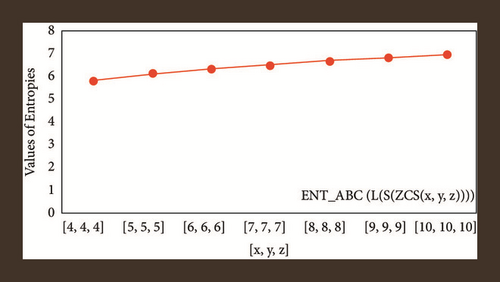
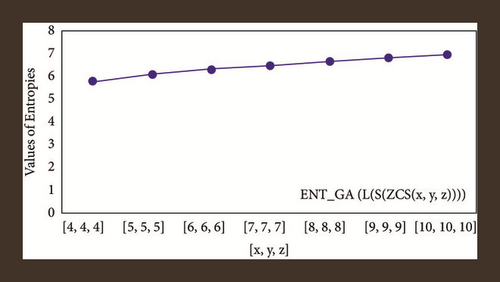
For L(S(T_x)), the numerical and graphical results are shown in Tables 8 and 9 and Figures 4–7. In Table 9, the fifth arithmetic geometric entropy is zero which shows that the process is deterministic for x = 1. When the chemical structure L(S(T_x)) expands, the Randi entropy for α = 1/2 develops more quickly than other entropy measurements of L(S(T_x)), whereas the Randi entropy for α = −1/2 develops more slowly. This demonstrates that different topologies have varied entropy characteristics. For L(S(H(x, y))), the numerical and graphical results are shown in Tables 10–13 and Figures 8–12. When the chemical structure L(S(H(x, y))) expands, the geometric arithmetic entropy develops more quickly than other entropy measurements of L(S(H(x, y))), whereas the ABC₄ entropy develops more slowly. Finally, for L(S(ZCS(x, y, z))), the numerical and graphical results are shown in Table 14 and Figures 13–16. When the chemical structure L(S(ZCS(x, y, z))) expands, the geometric arithmetic entropy develops more quickly than other entropy measurements of L(S(ZCS(x, y, z))), whereas the Randi entropy for α = −1 develops more slowly.

Table 8. Comparison of randic entropies for L(S(T_x)).

[x]
[46]	0.4055	2.5590	2.4849	2.6263
[52]	3.1863	3.0463	3.5667	3.5970
[25]	4.0316	3.6767	4.2203	4.2280
[26]	4.5797	4.2928	4.6981	4.6991
[24]	4.9945	4.8714	5.0779	5.0764
[23]	5.3312	5.4107	5.3942	5.3918
[27]	5.6159	5.9131	5.6658	5.6631
[2]	5.8632	6.3820	5.9041	5.9013
[56]	6.0820	6.8208	6.1164	6.1136
[31]	6.2785	7.2325	6.3080	6.3053

Table 9. Comparison of ENT_ABC, ENT_GA,

, and

for L(S(T_x)).

[x]	ENT_ABC	ENT_GA
[46]	2.3116	2.4849	2.1972	0
[52]	3.5239	3.5835	3.5749	3.5835
[25]	4.2025	4.2341	4.2263	4.2341
[26]	4.6897	4.7095	4.7028	4.7095
[24]	5.0739	5.0876	5.0817	5.0876
[23]	5.3926	5.4027	5.3975	5.4026
[27]	5.6655	5.6733	5.6687	5.6733
[2]	5.9046	5.91087	5.9066	5.9108
[56]	6.1174	6.1225	6.1187	6.1225
[31]	6.3093	6.3135	6.3100	6.3135

Table 10. Comparison of randic entropies for L(S(H(x, y))).

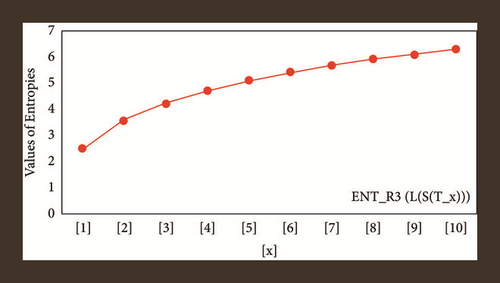
[x, y]
[1,1]	2.4849	2.4849	2.4849	2.4849
[2,2]	3.7917	3.7830	3.8344	3.8332
[3,3]	4.5635	4.5428	4.5933	4.5906
[4,4]	5.1096	5.0872	5.1323	5.1294
[5,5]	5.5345	5.5129	5.5530	5.5502
[6,6]	5.8833	5.8630	5.8988	5.8962
[7,7]	6.1794	6.1615	6.1928	6.1904
[8,8]	6.4368	6.4194	6.4486	6.4464
[9,9]	6.6646	6.6483	6.6751	6.6731
[10,10]	6.8688	6.5370	6.8783	6.8822

Table 11. Comparison of ENT_ABC and ENT_GA entropies for L(S(H(x, y))).

[x, y]	ENT_ABC	ENT_GA
[1,1]	2.4849	2.4849
[2,2]	3.8497	3.8501
[3,3]	4.6048	4.6051
[4,4]	5.1413	5.1416
[5,5]	5.5604	5.5607
[6,6]	5.9051	5.9053
[7,7]	6.1982	6.1985
[8,8]	6.4534	6.4536
[9,9]	6.6794	6.6796
[10,10]	6.8822	6.8824

Table 12. Comparison of

and

Entropies for L(S(H(x, y))), x > 1 and y ≠ 1.

[x, y]
[2,2]	3.7879	3.4822
[3,3]	4.5387	2.2596
[4,4]	5.0783	4.8387
[5,5]	5.5018	5.2952
[6,6]	5.8509	5.6704
[7,7]	6.1481	5.9882
[8,8]	6.4068	6.2636
[9,9]	6.6360	6.5064
[10,10]	6.8417	6.7234

Table 13. Comparison of

and

entropies for L(S(H(x, y))), x = 1 and y ≠ 1.

[y]
[52]	3.1846	3.2958
[25]	3.5933	3.6888
[26]	3.8884	3.9702
[24]	4.1184	4.1896
[23]	4.3064	4.3694
[27]	4.4653	4.5217
[2]	4.6027	4.6539
[56]	4.7238	4.7706
[31]	4.8319	4.8751

Table 14. Comparison of randic entropies for L(S(ZCS(x, y, z))).

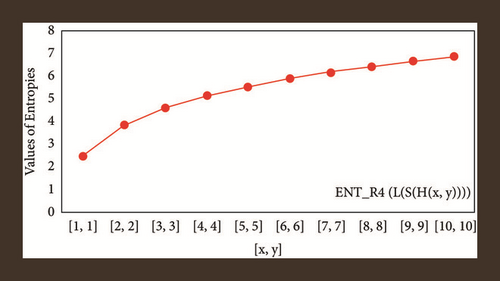
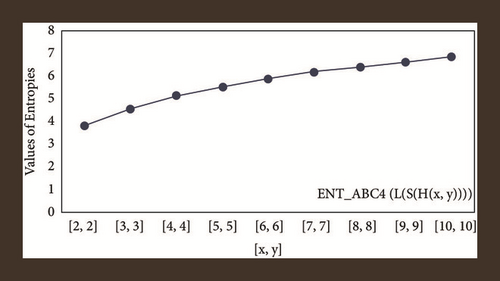
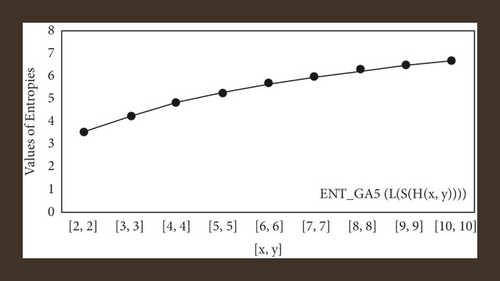
[x, y, z]
[4,4,4]	5.7200	5.70060	5.7432	5.7407
[5,5,5]	6.0342	6.0165	6.0587	6.0565
[6,6,6]	6.2730	6.2564	6.2982	6.2961
[7,7,7]	6.4657	6.4497	6.4913	6.4893
[8,8,8]	6.6272	6.6117	6.6531	6.6511
[9,9,9]	6.7662	6.7511	6.7923	6.7904
[10,10,10]	6.8883	6.8734	6.9145	6.9126

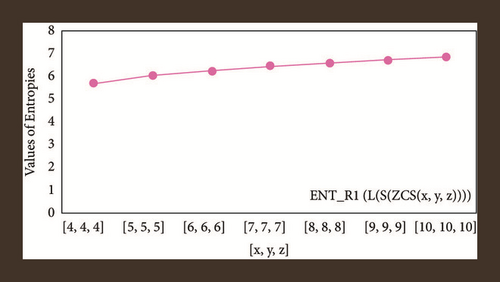
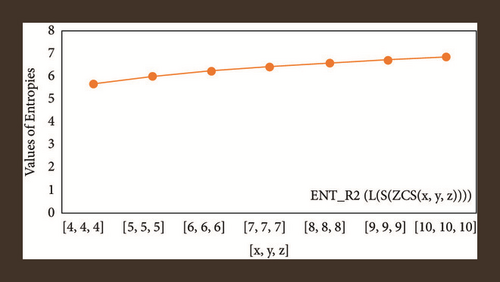
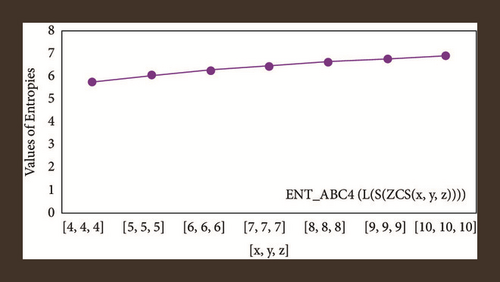
The novelty of this article is that entropies are computed for three types of benzenoid systems. These entropy measures are useful in estimating the heat of formation and many Physico-chemical properties. In statistical analysis of benzene structures, entropy measures showed more significant results as compared to topological indices. Therefore, we can say that the entropy measure is a newly introduced topological descriptor.

6. Conclusion

Using Shanon’s entropy and Chen et al. [31] entropy definitions, we generated graph entropies associated to a new information function in this research. Between indices and information entropies, a relationship is created. Using the line graph of the subdivision of these graphs, we estimated the entropies for triangular benzenoids T_x, hexagonal parallelogram H(x, y) nanotubes, and ZCS(x, y, z). Thermodynamic entropy of enzyme-substrate complexions [57, 58] and configuration entropy of glass-forming liquids [56] are two examples of thermodynamic entropy employed in molecular dynamics studies of complex chemical systems. Similarly, using information entropy as a crucial structural criterion could be a new step in this direction.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Authors’ Contributions

This work was equally contributed by all writers.

Open Research

Data Availability

The data used to support the findings of this study are cited at relevant places within the text as references.

References

1 Chu Z. Q., Siddiqui M. K., Manzoor S., Kirmani S. A. K., Hanif M. F., and Muhammad M. H., On rational curve fitting between topological indices and entropy measures for graphite carbon nitride, Polycyclic Aromatic Compounds. (2022) 5, 1–18, https://doi.org/10.1080/10406638.2022.2048034.
10.1080/10406638.2022.2048034
Google Scholar
2 Gao W. and Farahani M. R., Degree-based indices computation for special chemical molecular structures using edge dividing method, Applied Mathematics and Nonlinear Sciences. (2016) 1, no. 1, 99–122, https://doi.org/10.21042/amns.2016.1.00009.
10.21042/AMNS.2016.1.00009
Google Scholar
3 Estrada E., Torres L., Rodríguez L., and Gutman I., An atom-bond connectivity index. Modelling the enthalpy of formation of alkanes, Indian Journal of Chemistry. (1998) 37A, 849–855.
CAS Google Scholar
4 Estrada E. and Hatano N., Statistical-mechanical approach to subgraph centrality in complex networks, Chemical Physics Letters. (2007) 439, no. 1-3, 247–251, https://doi.org/10.1016/j.cplett.2007.03.098.
10.1016/j.cplett.2007.03.098
CAS Web of Science® Google Scholar
5 Estrada E., Generalized walks-based centrality measures for complex biological networks, Journal of Theoretical Biology. (2010) 263, no. 4, 556–565, https://doi.org/10.1016/j.jtbi.2010.01.014.
10.1016/j.jtbi.2010.01.014
PubMed Web of Science® Google Scholar
6 Gao W., Siddiqui M. K., Naeem M., and Rehman N. A., Topological characterization of carbon graphite and crystal cubic carbon structures, Molecules. (2017) 22, no. 9, 1496–1507, https://doi.org/10.3390/molecules22091496.
10.3390/molecules22091496
PubMed Web of Science® Google Scholar
7 Imran M., Siddiqui M. K., Naeem M., and Iqbal M. A., On topological properties of symmetric chemical structures, Symmetry. (2018) 10, no. 5, 173–221, https://doi.org/10.3390/sym10050173.
10.3390/sym10050173
Web of Science® Google Scholar
8 Randic M., On characterization of molecular branching, Journal of the American Chemical Society. (1975) 97, no. 23, 6609–6615.
10.1021/ja00856a001
CAS Web of Science® Google Scholar
9 Siddiqui M. K., Imran M., and Ahmad A., On Zagreb indices, Zagreb polynomials of some nanostar dendrimers, Applied Mathematics and Computation. (2016) 280, 132–139, https://doi.org/10.1016/j.amc.2016.01.041.
10.1016/j.amc.2016.01.041
Web of Science® Google Scholar
10 Zhang X., Wu X., Akhter S., Jamil M. K., Liu J. B., and Farahani M. R., Edge-version atom-bond connectivity and geometric arithmetic indices of generalized bridge molecular graphs, Symmetry. (2018) 10, no. 12, 751–786, https://doi.org/10.3390/sym10120751.
10.3390/sym10120751
CAS Web of Science® Google Scholar
11 Zhang X., Awais H. M., Javaid M., and Siddiqui M. K., Multiplicative Zagreb indices of molecular graphs, Journal of Chemistry. (2019) 2019, 19, 5294198, https://doi.org/10.1155/2019/5294198.
10.1155/2019/5294198
Web of Science® Google Scholar
12 Zhang X., Rauf A., Ishtiaq M., Siddiqui M. K., and Muhammad M. H., On degree based topological properties of two carbon nanotubes, Polycyclic Aromatic Compounds. (2020) 42, no. 3, 866–884, https://doi.org/10.1080/10406638.2020.1753221.
10.1080/10406638.2020.1753221
Web of Science® Google Scholar
13 Zhang X., Jiang H., Liu J. B., and Shao Z., The cartesian product and join graphs on edge-version atom-bond connectivity and geometric arithmetic indices, Molecules. (2018) 23, no. 7, 1731–1817, https://doi.org/10.3390/molecules23071731.
10.3390/molecules23071731
PubMed Web of Science® Google Scholar
14 Zhang X., Naeem M., Baig A. Q., and Zahid M. A., Study of hardness of superhard crystals by topological indices, Journal of Chemistry. (2021) 2021, 10, 9604106, https://doi.org/10.1155/2021/9604106.
10.1155/2021/9604106
Web of Science® Google Scholar
15 Zhang X., Siddiqui M. K., Javed S., Sherin L., Kausar F., and Muhammad M. H., Physical analysis of heat for formation and entropy of Ceria Oxide using topological indices, Combinatorial Chemistry & High Throughput Screening. (2022) 25, no. 3, 441–450, https://doi.org/10.2174/1386207323999201001210832.
10.2174/1386207323999201001210832
CAS PubMed Web of Science® Google Scholar
16 Siddiqui M. K., Naeem M., Rahman N. A., and Imran M., Computing topological indicesof certain networks, Journal of Optoelectronics and Advanced Materials. (2016) 18, no. 9-10, 884–892.
Web of Science® Google Scholar
17 Vukicevic D. and Furtula B., Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges, Journal of Mathematical Chemistry. (2009) 46, no. 4, 1369–1376, https://doi.org/10.1007/s10910-009-9520-x.
10.1007/s10910-009-9520-x
CAS Web of Science® Google Scholar
18 Shannon C. E., A mathematical theory of communication, Bell System Technical Journal. (1948) 27, no. 3, 379–423, https://doi.org/10.1002/j.1538-7305.1948.tb01338.x.
10.1002/j.1538-7305.1948.tb01338.x
Web of Science® Google Scholar
19 Trucco E., A note on the information content of graphs, Bulletin of Mathematical Biophysics. (1956) 18, no. 2, 129–135, https://doi.org/10.1007/bf02477836.
10.1007/BF02477836
Google Scholar
20 Mowshowitz A., Entropy and the complexity of graphs: I. An index of the relative complexity of a graph, Bulletin of Mathematical Biophysics. (1968) 30, no. 1, 175–204, https://doi.org/10.1007/bf02476948.
10.1007/BF02476948
CAS PubMed Web of Science® Google Scholar
21 Rashevsky N., Life, information theory, and topology, Bulletin of Mathematical Biophysics. (1955) 17, no. 3, 229–235, https://doi.org/10.1007/bf02477860.
10.1007/BF02477860
CAS Google Scholar
22 Karreman G., Topological information content and chemical reactions, Bulletin of Mathematical Biophysics. (1955) 17, no. 4, 279–285, https://doi.org/10.1007/bf02477754.
10.1007/bf02477754
CAS Google Scholar
23 Bonchev D., Complexity in Chemistry, Introduction and Fundamentals, 2003, 2, Taylor & Francis, Boca Raton, FL, USA, 1–100.
Google Scholar
24 Bonchev D. G., Kolmogorov’s information, shannon’s entropy, and topological complexity of molecules, Bulgarian Chemical Communications. (1995) 28, no. 3-4, 567–582.
CAS Google Scholar
25 Bonchev D. and Trinajstic N., Information theory, distance matrix, and molecular branching, The Journal of Chemical Physics. (1977) 67, no. 10, 4517–4533, https://doi.org/10.1063/1.434593.
10.1063/1.434593
CAS Web of Science® Google Scholar
26 Bonchev D., Mekenyan O. V., and Trinajstić N., Isomer discrimination by topological information approach, Journal of Computational Chemistry. (1981) 2, no. 2, 127–148, https://doi.org/10.1002/jcc.540020202.
10.1002/jcc.540020202
CAS Web of Science® Google Scholar
27 Castellano G. and Torrens F., Information entropy-based classification of triterpenoids and steroids from Ganoderma, Phytochemistry. (2015) 116, 305–313, https://doi.org/10.1016/j.phytochem.2015.05.008.
10.1016/j.phytochem.2015.05.008
CAS Web of Science® Google Scholar
28 Dehmer M., Varmuza K., Borgert S., and Emmert-Streib F., On entropy-based molecular descriptors: statistical analysis of real and synthetic chemical structures, Journal of Chemical Information and Modeling. (2009) 49, no. 7, 1655–1663, https://doi.org/10.1021/ci900060x.
10.1021/ci900060x
CAS PubMed Web of Science® Google Scholar
29 Terenteva Z. and Kobozev N. I., Possible relation between entropy of information-theory and thermodynamic entropy, Zhurnal Fizicheskoi Khimii. (1976) 50, no. 4, 877–881.
CAS Google Scholar
30 Zhdanov Y. A., Information Entropy in Organic Chemistry, 1979, 1, Rostov University, Rostov Oblast, Russia, in Russian.
Google Scholar
31 Chen Z., Dehmer M., and Shi Y., A note on distance based graph entropies, Entropy. (2014) 16, no. 10, 5416–5427, https://doi.org/10.3390/e16105416.
10.3390/e16105416
Web of Science® Google Scholar
32 Cao S., Dehmer M., and Shi Y., Extremality of degree-based graph entropies, Information Sciences. (2014) 278, 22–33, https://doi.org/10.1016/j.ins.2014.03.133.
10.1016/j.ins.2014.03.133
Web of Science® Google Scholar
33 Dehmer M., Information processing in complex networks: graph entropy and information functionals, Applied Mathematics and Computation. (2008) 201, no. 1-2, 82–94, https://doi.org/10.1016/j.amc.2007.12.010.
10.1016/j.amc.2007.12.010
Web of Science® Google Scholar
34 Dehmer M. and Mowshowitz A., A history of graph entropy measures, Information Sciences. (2011) 181, no. 1, 57–78, https://doi.org/10.1016/j.ins.2010.08.041.
10.1016/j.ins.2010.08.041
Web of Science® Google Scholar
35 Manzoor S., Siddiqui M. K., and Ahmad S., On entropy measures of molecular graphs using topological indices, Arabian Journal of Chemistry. (2020) 13, no. 8, 6285–6298, https://doi.org/10.1016/j.arabjc.2020.05.021.
10.1016/j.arabjc.2020.05.021
CAS Web of Science® Google Scholar
36 Cao S. and Dehmer M., Degree-based entropies of networks revisited, Applied Mathematics and Computation. (2015) 261, 141–147, https://doi.org/10.1016/j.amc.2015.03.046.
10.1016/j.amc.2015.03.046
Web of Science® Google Scholar
37 Dehmer M., Sivakumar L., and Varmuza K., Uniquely discriminating molecular structures using novel eigenvalue-based descriptors, MATCH Communications in Mathematical. (2012) 67, 147–172.
CAS Web of Science® Google Scholar
38 Morowitz H. J., Some order-disorder considerations in living systems, Bulletin of Mathematical Biophysics. (1955) 17, no. 2, 81–86, https://doi.org/10.1007/bf02477985.
10.1007/BF02477985
CAS Google Scholar
39 Rashevsky N., Information theory in biology, Bulletin of Mathematical Biophysics. (1954) 16, no. 2, 183–185, https://doi.org/10.1007/bf02478375.
10.1007/bf02478375
Google Scholar
40 Shannon C. E., A mathematical theory of communication, ACM SIGMOBILE - Mobile Computing and Communications Review. (2001) 5, no. 1, 3–55, https://doi.org/10.1145/584091.584093.
10.1145/584091.584093
Google Scholar
41 Sol R. V. and Valverde S. I., Information theory of complex networks: on evolution and architectural constraints, Complex Networks Lectures Notes in Physics. (2004) 650, 189–207.
Google Scholar
42 Tan Y. J. and Wu J., Network structure entropy and its application to scale-free networks, Systems Engineering - Theory & Practice. (2004) 6, 1–3.
Google Scholar
43 Manzoor S., Siddiqui M. K., and Ahmad S., On physical analysis of degree-based entropy measures for metal–organic superlattices, The European Physical Journal Plus. (2021) 136, no. 3, 287–322, https://doi.org/10.1140/epjp/s13360-021-01275-5.
10.1140/epjp/s13360-021-01275-5
CAS Web of Science® Google Scholar
44 Manzoor S., Siddiqui M. K., and Ahmad S., Degree-based entropy of molecular structure of hyaluronic acid–curcumin conjugates, The European Physical Journal Plus. (2021) 136, no. 1, 15–21, https://doi.org/10.1140/epjp/s13360-020-00976-7.
10.1140/epjp/s13360-020-00976-7
CAS Web of Science® Google Scholar
45 Rashid M. A., Ahmad S., Siddiqui M. K., Manzoor S., and Dhlamini M., An Analysis of Eccentricity-Based Invariants for Biochemical Hypernetworks, Complexity. (2021) 2021, 14, 1974642, https://doi.org/10.1155/2021/1974642.
10.1155/2021/1974642
Google Scholar
46 Akhter S. and Imran M., On molecular topological properties of benzenoid structures, Canadian Journal of Chemistry. (2016) 94, no. 8, 687–698, https://doi.org/10.1139/cjc-2016-0032.
10.1139/cjc-2016-0032
CAS Web of Science® Google Scholar
47 Raut N. K., Topological indices and topological polynomials of triangular benzenoid system, International Journal of Mathematics Trends and Technology. (2021) 67, no. 6, 90–96, https://doi.org/10.14445/22315373/ijmtt-v67i6p511.
10.14445/22315373/ijmtt-v67i6p511
Google Scholar
48 Hussain Z., Rafique S., Munir M., Athar M., Chaudhary M., Ahmad H., and Min Kang S., Irregularity molecular descriptors of hourglass, jagged-rectangle, and triangular benzenoid systems, Processes. (2019) 7, no. 7, https://doi.org/10.3390/pr7070413.
10.3390/pr7070413
Web of Science® Google Scholar
49 Kwun Y. C., Ali A., Nazeer W., Ahmad Chaudhary M., and Kang S. M., M-polynomials and degree-based topological indices of triangular, hourglass, and jagged-rectangle benzenoid systems, Journal of Chemistry. (2018) 2018, 8, 8213950, https://doi.org/10.1155/2018/8213950.
10.1155/2018/8213950
Web of Science® Google Scholar
50 Kulli V. R., Chaluvaraju B., and Boregowda H. S., Connectivity Banhatti indices for certain families of benzenoid systems, Journal of Ultra Chemistry. (2017) 13, no. 04, 81–87, https://doi.org/10.22147/juc/130402.
10.22147/juc/130402
CAS Google Scholar
51 Ghorbani M. and Ghazi M., Computing some topological indices of Triangular Benzenoid, Digest Journal of Nanomaterials and Biostructures. (2010) 5, no. 4, 1107–1111.
Web of Science® Google Scholar
52 Baig A. Q., Imran M., and Ali H., Computing Omega, Sadhana and PI polynomials of benzoid carbon nanotubes, Optoelectronics and advanced materials-rapid communications. (2015) 9, 248–255.
CAS Web of Science® Google Scholar
53 Mirajkar K. G. and Pooja B., On Gourava indices of some chemical graphs, International Journal of Applied Engineering Research. (2019) 14, no. 3, 743–749.
Google Scholar
54 Mehler A., Lücking A., and Weib P., A network model of interpersonal alignment in dialog, Entropy. (2010) 12, no. 6, 1440–1483, https://doi.org/10.3390/e12061440.
10.3390/e12061440
Web of Science® Google Scholar
55 Mowshowitz A. and Dehmer M., Entropy and the complexity of graphs revisited, Entropy. (2012) 14, no. 3, 559–570, https://doi.org/10.3390/e14030559.
10.3390/e14030559
Web of Science® Google Scholar
56 Champion Y. and Thurieau N., The sample size effect in metallic glass deformation, Scientific Reports. (2020) 10, no. 1, 10801, https://doi.org/10.1038/s41598-020-67813-w.
10.1038/s41598-020-67813-w
CAS Web of Science® Google Scholar
57 Graf M. M. H., Bren U., Haltrich D., and Oostenbrink C., Molecular dynamics simulations give insight into d-glucose dioxidation at C2 and C3 by Agaricus meleagris pyranose dehydrogenaseC-2and C3by Agaricus meleagris pyranose dehydrogenase, Journal of Computer-Aided Molecular Design. (2013) 27, no. 4, 295–304, https://doi.org/10.1007/s10822-013-9645-7.
10.1007/s10822-013-9645-7
CAS PubMed Web of Science® Google Scholar
58 Putz M. V., Lacrama A. M., and Ostafe V., Full analytic progress curves of enzymic reactions in vitro, International Journal of Molecular Sciences. (2006) 7, no. 11, 469–484, https://doi.org/10.3390/i7110469.
10.3390/i7110469
CAS Web of Science® Google Scholar
59 Dehmer M. and Graber M., The discrimination power of molecular identification numbers revisited, MATCH Communications in Mathematical. (2013) 69, 785–794.
Web of Science® Google Scholar
60 Ulanowicz R. E., Quantitative methods for ecological network analysis, Computational Biology and Chemistry. (2004) 28, no. 5-6, 321–339, https://doi.org/10.1016/j.compbiolchem.2004.09.001.
10.1016/j.compbiolchem.2004.09.001
CAS PubMed Web of Science® Google Scholar

Citing Literature

All articles

Computing the Entropy Measures for the Line Graphs of Some Chemical Networks

Abstract

1. Introduction

1.1. Randić Entropy [43, 44]

1.2. Atom Bond Connectivity Entropy [45]

1.3. The Geometric Arithmetic Entropy [43, 44]

1.4. The Fourth Atom Bond Connectivity Entropy [35]

1.5. The Fifth Geometric Arithmetic Entropy [35]

2. Formation of Triangular Benzenoid

2.1. Entropy Measure for L(S(Tx))

2.1.1. Randi Entropy of L(S(Tx))

2.1.2. The ABC Entropy of L(S(Tx))

2.1.3. The Geometric Arithmetic Entropy of L(S(Tx))

2.1.4. The ABC4 Entropy of L(S(Tx))

2.1.5. The GA5 Entropy of L(S(Tx))

3. Formation of Hexagonal Parallelogram Nanotubes H(x, y),

3.1. Entropy Measure for L(S(H(x, y)))

3.1.1. Randić Entropy of

3.1.2. The ABC Entropy of

3.1.3. The Geometric Arithmetic Entropy of

3.1.4. The ABC4 Entropy of

3.1.5. The Fifth Geometric Arithmetic Entropy of

4. Formation from Fusion of Zigzag-Edge Coronoid with Starphene ZCS(x, y, z) Nanotubes

4.1. Entropy Measure for L(S(ZCS(x, y, z)))

4.1.1. Randi Entropy of

4.1.2. The ABC Entropy of

4.1.3. The Geometric Arithmetic Entropy of

4.1.4. The ABC4 entropy of

4.1.5. The GA5 Entropy of

5. Concluding remarks for Computed Results

6. Conclusion

Conflicts of Interest

Authors’ Contributions

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information

2.1. Entropy Measure for L(S(T_x))

2.1.1. Randi Entropy of L(S(T_x))

2.1.2. The ABC Entropy of L(S(T_x))

2.1.3. The Geometric Arithmetic Entropy of L(S(T_x))

2.1.4. The ABC₄ Entropy of L(S(T_x))

2.1.5. The GA₅ Entropy of L(S(T_x))

3.1.4. The ABC₄ Entropy of

4.1.4. The ABC₄ entropy of

4.1.5. The GA₅ Entropy of