1. Introduction

With the increasing frequency of human space launch activities and the continuous deterioration of the space environment, space debris has become an important factor threatening the safe operation and normal function of spacecraft in orbit [1]. Space is an important part of space resources, and it is also the main reason for spacecraft in-orbit failure or even failure [2]. Space debris is one of the most hazardous environments in the space environment, and there have been several collisions between spacecraft in orbit for many years. Once the space debris meets the spacecraft, there will be a serious collision. This kind of collision belongs to the category of hypervelocity collision, and the consequences are extremely serious [3]. This may lead to the failure of some functions of the spacecraft or even the termination of the mission. For manned spaceflight, it also poses a serious threat to the personal safety of the crew. Space debris protection design is a key technology that must be broken through by large spacecraft in near-earth orbit, especially manned spacecraft [4]. For the spacecraft protection structure, the ballistic limit equation is the main standard to characterize the protection capability. At present, the ballistic limit research of the protection structure mostly adopts the experimental method, and the ballistic limit equation is obtained by fitting the experimental data. The method needs a lot of experiments and cannot explain the deep physical process of high-speed impact well. The establishment of ballistic limit equation is an important content in the research and development of protective structure [5]. Accurate ballistic limit equation is one of the first conditions for developing and applying the software of space debris/micrometeoroid impact risk assessment. In addition, when designing specific protective structures, it is necessary to revise the original ballistic limit equation according to the actual situation [6].

Because of the public’s interest in manned aircraft’s nuclear defense systems, research into the dangers of space debris and the possibility of a meteor colliding with the earth or other stars has greatly increased our understanding of hypervelocity collisions [7]. Through passive protection design, space debris protection engineering primarily addresses the risk of spacecraft damage caused by hypervelocity impact of space debris and possible functional failure. Its main goal is to solve the technology of spacecraft protection structure design and development of protection materials [8]. The relative collision velocity of space debris is extremely high, and the material density is almost identical to that of aluminum alloy. As a result, when space debris collides with a spacecraft in orbit, the massive collision kinetic energy is sufficient to cause structural damage, functional failure, and even catastrophic spacecraft accidents. The optimization design of various materials and protection structure configurations is a multiparameter and multiconstraint condition for spacecraft debris protection design. Its primary goal is to design a cost-effective and safe space debris protection structure for spacecraft, as well as to make layout recommendations [9]. The impact limit equation was developed using a hypervelocity impact test and its analysis, and it has since been applied to spacecraft protection design and material analysis. There are two parts to the equation: a general equation and a special equation [10]. The ballistic limit equations used in engineering today are all semiempirical and semianalytical equations derived through experimental methods. Fractal theory has been widely studied as a new research method in a variety of fields [11]. It has its own set of benefits when it comes to solving complex nonlinear problems. The numerical simulation of the ballistic limit of a protective structure is investigated using fractal theory in this paper.

The hypervelocity collision between space debris and orbiting spacecraft is a complex nonlinear dynamic process with significant deformation [12]. The trajectory limit equation is commonly used as an engineering method of failure judgment in spacecraft space debris impact risk assessment to determine the damage probability or failure probability of spacecraft impacted by M/OD hypervelocity and to serve as the foundation for the design and optimization of spacecraft protection structures [13]. There is no right or wrong in the semiempirical ballistic limit equation, only differences in accuracy [14]. The prediction accuracy of the rear wall failure in the hypervelocity impact experiment describes the accuracy of the limit equation. The ballistic limit equation will be revised on a regular basis as more hypervelocity impact experimental data and analysis methods become available [15]. This paper investigates the numerical simulation of the ballistic limit of a protective structure using fractal theory. The numerical simulation method can overcome experimental conditions’ limitations and conduct numerical experimental research on the impact of Whipple protective structures in high-speed areas. The critical diameter is calculated based on the hypervelocity collision problem of some Whipple shield structures, and then, the numerical simulation of plate damage beyond the critical diameter is used to verify the accuracy of the results. The impact experiment of simulating the damage of space temperature environment, including the impact of mixed multiscreen protective structure at extreme temperature, and the impact experiment of target made of thermal cycling target at high temperature, normal temperature, and low temperature, was carried out on the basis of the benchmark limit speed. In order to verify the consistency of critical failure kinetic energy of different diameter projectiles impacting the same single-layer target, this paper uses different diameter projectiles to carry out high-speed impact verification experiments and obtains satisfactory results. The research in this paper can provide a new idea for the design of spacecraft protective structure.

2. Related Work

The development technology of the ballistic limit equation was discussed in the literature [16], and both experiment and numerical simulation were used as methods of ballistic limit modeling. Numerical simulation is thought to be useful in supplementing experimental data, particularly in obtaining impact data that cannot be obtained at the experimental speed. According to literature [17], the role of numerical simulation in ballistic limit equation modeling will become more apparent as the hypervelocity impact simulation algorithm improves and the accuracy of material models improves. Literature [18] provides a typical ballistic limit equation, calculates the critical diameter of some Whipple shield structures for hypervelocity collision problems, and then uses an engineering algorithm to numerically simulate the damage of the rear plate beyond the critical diameter to ensure that the results are accurate. Based on the ballistic limit of protective structures, literature [19] established a performance evaluation method for protective structures from an energy standpoint. Numerical simulation of hypervelocity collisions of various shielding screens is carried out in literature [20], with the goal of preliminary research on how to obtain the ballistic limit parameters of spacecraft through numerical simulation. Literature [21] uses ultrahigh-speed impact experimental technology and experimental methods of data calibration and comparative analysis to investigate the effect of accumulated damage on the impact resistance of basalt, Kevlar, and other woven fabric protective materials against high-speed projectiles, with the goal of determining the influence of accumulated damage on the impact resistance of basalt, Kevlar, and other woven fabric protective materials against high-speed projectiles. The ballistic limit equations of various types of protective structures are introduced in literature [22], as well as the method for establishing the ballistic limit equations and the ballistic limit equation models of three ballistic zones. The experimental scheme of the impact limit equation of Whipple protective structure was designed based on literature [23]. The main advantage of Lagrange numerical technology, according to literature [24], is that it can clearly describe the action behavior of material interfaces. However, when the material is deformed greatly, mesh entanglement will inevitably occur, resulting in a decrease in calculation efficiency and even the inability to continue the calculation. At this point, the grid must be subdivided using the erosion algorithm. Literature [25] used the high-speed impact characteristics and fatigue characteristics of Whipple protection structure with defects were studied by combining numerical simulation with ground simulation experiment, based on the mechanical response background of spacecraft protection structure with defects in space debris environment and temperature environment. Literature [26] proposes a method for modeling the ballistic limit equation of typical spacecraft structures based on dimensional theory, hypervelocity impact experiments, and numerical simulation, as well as concrete implementation steps. Literature [27] numerically simulated the penetration of thick targets and the impact of Whipple protective structure at high speed by substituting the GRAY three-phase equation of state, which can deal with the phase change effect of materials, into the self-made calculation program of material point method.

By numerical simulation, the shape change of the projectile, the propagation of stress wave in the projectile and the shield, the change of the velocity of the projectile, and the transformation of the system energy composed of the projectile and the shield are compared, and the mechanism of the influence of the defects on the performance of the spacecraft shield structure is analyzed. Then, the accuracy of the results is verified. The results show that the numerical simulation results are basically consistent with those calculated by ballistic limit equation, which shows that the algorithm can better simulate the damage of hypervelocity collision and qualitatively describe the phenomenon of hypervelocity collision. This method is feasible. This shows the feasibility and effectiveness of the ballistic limit modeling method. It is hoped that it can provide a general and efficient modeling method for numerical simulation of ballistic limit of typical structures of various spacecraft in China.

3. Methodology

3.2. Numerical Simulation of Protective Ballistic Limit of Structure

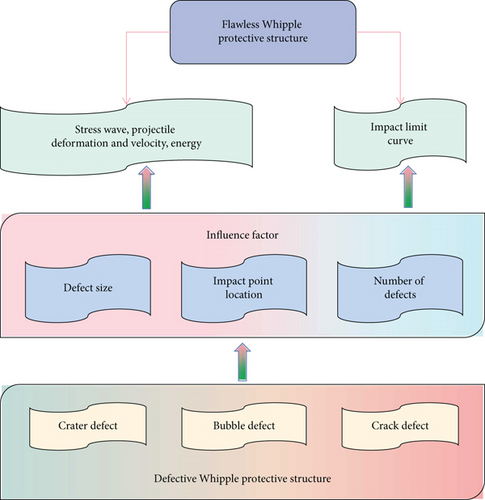
In order to ensure the safe operation of spacecraft in orbit, the commonly adopted method is to set up passive protection structures. Whipple protective structure is the most basic protective configuration. The principle is to set a layer of aluminum protective screen at a certain distance in front of the bulkhead of spacecraft, which makes the kinetic energy of incident objects highly dispersed after hitting the protective screen, reduces the energy flow density acting on the bulkhead, and realizes the protection of the bulkhead. According to the impact speed, the impact of aluminum projectile on aluminum alloy protective front screen can be divided into ballistic section characteristics, crushing section characteristics and gasification section characteristics. Under the ground laboratory conditions, the high speed required by the gasification section is difficult to achieve, so this paper does not consider the gasification section but only studies the ballistic section and the crushing section. The research scheme of numerical simulation of high-speed impact of protective structure is shown in Figure 1.

The basic idea of the material point method is to discretize the continuum into a group of particles and establish a background grid in the material movement area. The particles carry material information such as mass, velocity, stress, strain, and internal energy. The grid is only used to solve the momentum equation and calculate the spatial derivative, and the grid nodes do not store any material information. There is neither the mesh distortion problem of Lagrangian method nor the convection term of Euler method. Moreover, its computational efficiency is better than that of the smooth particle fluid dynamics method, which is very suitable for analyzing the hypervelocity collision problems with large deformation and breakage of materials. Based on the observation of the experimental process and the summary of experience, for thin plate perforation, when the speed is not high, the edge of the hole will be accompanied by plastic deformation, forming convex edges. When the speed increases, the perforation diameter of the sheet increases, the flange tends to be flat, and the perforation diameters of the front and back of the sheet are almost the same. Since the development of autocorrelation research, there have been many empirical and semiempirical formulas for the hole diameter of spherical projectiles impacting thin plates. When V_n ≤ 2 km (V_n is normal speed),

$$ (1)

When 2 km/s < V_n < 8 km/S,

$$ (2)

When V_n ≥ 8 km/S,

$$ (3)

In the formula, d_c is the limit diameter, t_w is the thickness of the rear target, t_b is the thickness of the shielding plate, S is the distance between the shielding plate and the rear target, and the unit is cm. σ is the failure stress of the rear target in ksi. θ is the projectile incident angle in deg. V is the incident velocity of the projectile, and the unit is km/s; ρ_p is the density of the projectile, and ρ_b is the density of the shielding plate, and the unit is g/cm³.

Determine dimensionless variables by selecting major physical quantities. There should have in-depth examination of the main physical quantities in each velocity zone, evaluation of their impact on hypervelocity impact characteristics, and rational selection of physical quantities in conjunction with ballistic limit modeling requirements. The basic physical quantities are correctly and reasonably selected on this basis, and dimensionless variables are determined through dimensional analysis. The particle is completely connected to the grid in each time step, and the shape function establishes the information mapping between the particle and the grid node. Interpolating the information from the grid node yields the derivative of the displacement, stress, and other information carried by the particle. At the end of the time step, toss the distorted background grid away. The numerical simulation flow is shown in Figure 2.

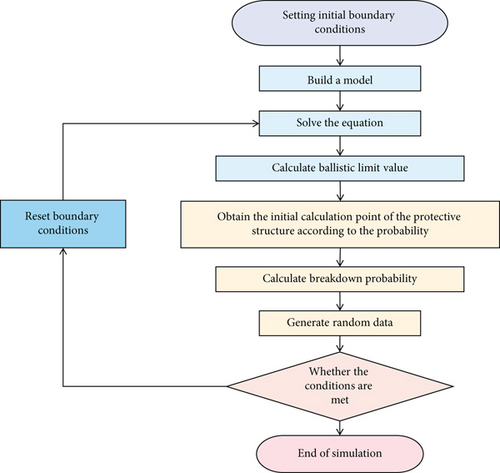
In the process of protection structure design, the designer first determines the protection structure configuration parameters that can meet the initial protection requirements according to the design equation and then iterates with the performance equation to verify whether the protection requirements are met. In the development of ballistic limit equation, it is generally required that the rear wall of protective structure can at least resist perforation, that is, the failure criterion is no perforation. The material model describes the response of the material under external force. Materials include constitutive model, failure model, and equation of state. Considering the types of protective materials, the design range of structural dimensions, the impact velocity and diameter distribution of M/OD particles, typical hypervelocity impact experiments, and numerical simulations are designed, and a certain number of effective impact parameters are obtained, that is, those under critical penetration of the rear wall of the protective structure.

When studying the perforation law of a plate, the object of study is a thin plate, which means that there is no gradient change of the physical field along the thickness direction of the plate, and the plate whose thickness is less than the characteristic dimension of the incident projectile can also be called a thin plate. As shown in formula (4), the aperture D_c has a linear relationship with the projectile impact velocity v_p.

$$ (4)

In the formula, d_p is the diameter of the projectile, and t_b is the thickness of the target plate. Consider the effect of material properties:

$$ (5)

where ρ_p and ρ_t are the densities of the projectile and the thin plate, respectively, and c_p and c_t are the speed of sound in the projectile and the thin plate, respectively. The model considers physical quantities relatively complete, but it can be seen from the exponential coefficient in the model that the model formula is obtained through data calibration, so the scope of application and accuracy is limited. Considering the effect of temperature, put the temperature term into the expression, and get the following form:

$$ (6)

In the formula, T_b is the temperature of the impact sheet, and T_r is the outdoor ambient temperature.

Under the combined action of incident wave and sparse wave, the projectile is broken into small pieces after impacting the protective screen at ultrahigh speeds. Because the size of secondary debris is much smaller than the thickness of the bulkhead, studying the penetration of thick targets for the design of spacecraft protection structures is essential. The impact limit curve, as opposed to the ballistic limit equation, more intuitively reflects the protective structure’s performance characteristics. Because the ballistic limit equations are all empirical, the impact limit curves obtained from the ballistic limit equations have certain errors, so in practical engineering applications, appropriate safety factors must be introduced. The verification board technology is used to assess the quality of cloud centers. The relevant parameters of the particles can be obtained by placing the verification plate in direct contact with the debris cloud and measuring the damage caused by debris particles to the verification plate. The impact crater reflects the energy of the fragments, and the holes formed on the verification plate are closely related to the quality of the fragments.

Fixing the launching speed and changing the diameter of the projectile are ways to get the critical impact parameters. The impact parameters at this time are considered critical impact parameters if the difference between the minimum diameter of the projectile in the case of penetration and the maximum diameter of the projectile in the case of nonpenetration is less than 0.2 mm. Define the impact limit parameters, such as the critical projectile diameter, and fix other variables in the impact limit equation to determine the relationship between the impact limit parameters and the selected variables. We get the functional formula of the impact limit parameters and all other variables, which is the impact limit equation, after many experiments. The remaining undetermined indices and all undetermined coefficients are solved using critical impact parameters. The critical impact parameters equal to the undetermined constant must be obtained only in theory, and the values of the undetermined constant can be obtained by simultaneously solving the equations and substituting them into the general formula of the ballistic limit equation. Formula (1) depicts the partial stress updating algorithm:

$$ (7)

In the formula, $$ is the deformation rate tensor; Ω_jk = 0.5(v_j,k + v_k,j); G is the shear modulus, i = r, z, θ, j = r, z, θ, and k = r, z, θ. The yield stress of a material during a hypervelocity collision can be represented by the Johnson-Cook model:

$$ (8)

where ε^p is the equivalent plastic strain; $$ is the dimensionless equivalent plastic strain rate; T^∗ is the dimensionless temperature; A, B, C, n, and m are the material constants.

The traditional hypervelocity impact simulation experiment involves using spherical projectiles to simulate space debris to impact various configurations of protective structures, with the protective structure’s rear wall representing the spacecraft’s bulkhead, and the impact process taking place in a high vacuum environment. To account for experimental and simulation data errors and improve the equation’s generality, multiply the number of critical impact parameters by the number of undetermined constants, substitute them into the general formula of the ballistic limit equation, list several equations, solve them individually, and then calculate the mean value and deviation of each undetermined constant. If the deviation value is excessively large, it means that the general formula for the ballistic limit equation cannot accurately describe the hypervelocity impact dynamic characteristics of the protective structure and needs to be corrected. Take the obtained mean value as the value of each undetermined constant if the deviation value is small. The bulkhead breakdown depth is used to describe the damage to the protective structure when the projectile does not penetrate the bulkhead. When a projectile punctures the bulkhead, the thickness of the bulkhead and the puncture depth of the observation plate are used to describe the protective structure’s damage.

The debris cloud created by the high-speed impact in the crushing section is divided into two parts: projectile fragments and fragments falling off the front screen. The distribution of secondary debris formed after the projectile strikes the shield has a direct impact on the bulkhead’s damage level. The particles formed after the collision between the projectile and the buffer screen contain solid and liquid states, which belong to the middle of the ballistic zone and the melting/gasification zone, when the collision velocity is in the crushing zone. As a result, the ballistic limit equation model of the crushing zone can be derived from the ballistic and melting/gasification zone ballistic limit equations. The wave fronts of the nondefective shield, the shield with crater defects, and the shield with bubble defects are all symmetrical about the impact point when the shield is impacted by the projectile, resulting in a circular perforation shape. However, because the stress wave cannot propagate from one side of the crack to the other, the protective screen’s perforation shape with crack defects is not a regular circle. Take its equivalent diameter into account in the calculation.

4. Result Analysis and Discussion

In order to obtain the numerical simulation of ballistic limit for a class of protective configurations, various protective structures are usually combined with different protective structure parameters and different protective screen materials. Projectiles with different materials and diameters are used to carry out hypervelocity impact experiments in groups at different speeds with different sizes and collision angles. The most important difference between the high-speed impact process of the fragment segment and the ballistic segment is the generation of the debris cloud, so the influence of the energy distribution caused by the debris cloud should be considered in the process of energy analysis. In the process of impacting the protective front screen, the initial velocity of the projectile reaches or exceeds the critical crushing velocity of the projectile, and the projectile is broken. In the process of penetration, similar to the ballistic section, the energy consumed in the process of penetration mainly comes from the same residual velocity of the peeling part of the front screen material, and the energy consumption of doing work in this process can be ignored. According to the particle characteristics of the projectile after hitting the protective screen, the experiment is divided into three sections according to the speed range: the first section is low speed, at which time the debris particles are not liquefied or gasified. The second stage is medium speed, when the debris particles are liquefied or gasified. The third stage is of high speed, when the debris particles are completely liquefied or gasified. The ballistic limit curve is shown in Figure 3.

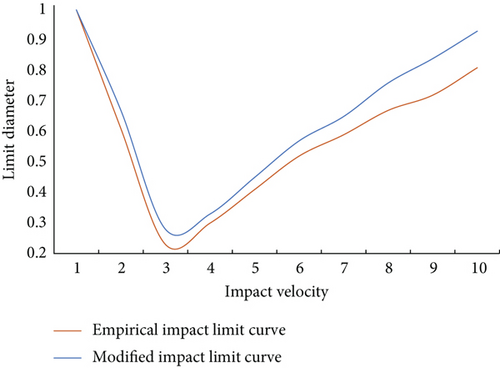
By changing the protective materials and geometric dimensions of the protective structure, different protective structures are constructed, and different projectile diameters, projectile materials, collision speeds, and collision angles are set, and a large number of hypervelocity impact numerical simulations are carried out, so as to analyze the main influencing factors of two critical speeds and establish the relationship between each critical speed and these influencing factors and finally verify it with a few typical hypervelocity impact experiments. Considering the energy consumption caused by the fragmentation of the projectile, although the projectile is broken in the process of penetrating the front screen, the overall quality does not change, and the fragmentation of the projectile does not affect the velocity of the projectile, so there is no obvious energy loss, but the fragmentation leads to the energy dispersion after penetrating, so it is very important to find out the energy that can effectively damage and destroy the rear panel after penetrating the front screen. The modified impact limit curves of trajectory section and crushing section are shown in Figure 4.

Because determining the critical diameter of the projectile that simply causes the protective structure to fail in a hypervelocity impact experiment is difficult, the data analysis first creates the ballistic limit curve corresponding to each group of protective structures and then fits the specific ballistic limit equation under specific impact conditions. The specific ballistic limit equations are then combined to produce a general ballistic limit equation suitable for a particular type of protective structure. The damage to the bulkhead when it is penetrated by projectile can be accurately described by observation plate in the method of placing observation plate in a double-deck structure with projectile impact. There is no need to measure intermediate variables in comparison to single-layer board. Because the momentum of debris after penetrating through the bulkhead is smaller than with a single-layer observation plate, the multilayer observation plate can describe the damage more precisely than the single-layer observation plate. Under the same collision conditions, the comparison between numerical simulation and experimental results of ballistic limit of Whipple protective structure is shown in Figure 5.

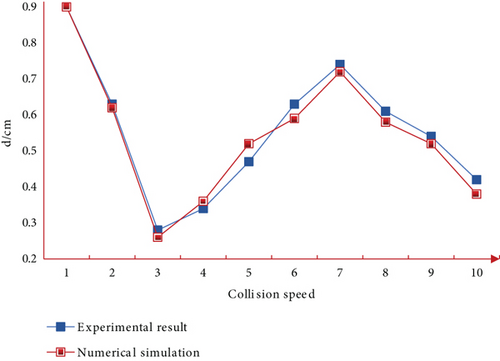
As can be seen from Figure 3, the numerical simulation results of the ballistic limit of Whipple protective structure are in good agreement with the experimental values, and the ballistic limit shows three trends with the increase of collision speed. Moreover, the deviation between the numerical simulation results of ballistic limit and the experimental values increases with the increase of collision speed.

In the crushing stage, the decline of the projectile’s ability to penetrate the target plate is mainly caused by energy dispersion. In this paper, it is reasonable to ignore the energy required by the projectile’s own crushing. For brittle materials, the energy consumption of material crushing deformation is very small. For aluminum projectiles, this energy neglect has little effect on the high-speed impact energy. Through numerical simulation, the critical impact velocity of different spacecraft protective structures with defects is calculated, and then, the ballistic segment of the impact limit curve is fitted, and compared with the impact limit curve of projectiles impacting the protective structures of nondefective spacecraft, the influence of defects on the protective performance of the protective structures of spacecraft is analyzed. This paper makes a preliminary theoretical analysis from the angle of empirical ballistic limit and damage law of woven materials, puts forward quantitative evaluation parameters of damage degree, and uses these parameters to modify the empirical curve of ballistic limit. In order to verify the accuracy of this method, we carry out experiments. Comparing the method proposed in reference [18], the method proposed in reference [20], and the method in this paper, the accuracy results of different algorithms are obtained, as shown in Figure 6.

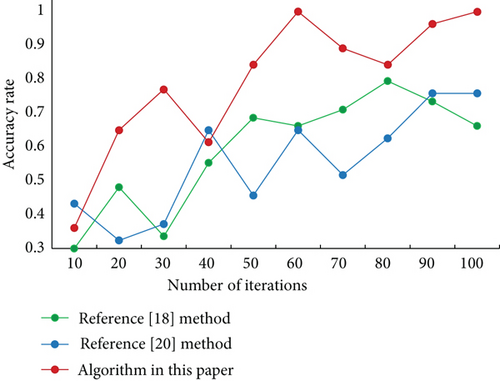
By analyzing the trend in Figure 6, we can see that the accuracy of the algorithms in literature [18] and literature [20] is low, and the accuracy of this method is the highest. The superiority of this method is verified.

Typical hypervelocity impact experiments and numerical simulations are designed to verify the prediction accuracy of the ballistic limit equation. If the accuracy does not meet the requirements, the value of the coefficient or index to be determined should be revised. The accuracy of verification and correction mainly depends on the following two points: ① accuracy of experimental data of hypervelocity impact, especially the measurement and processing accuracy of critical penetration diameter data and ② accuracy of material model used in numerical simulation of hypervelocity impact, including accuracy of main parameters related to material characteristics in constitutive model and equation of state. The research methods of theoretical analysis, empirical formula, and numerical simulation are adopted to simulate the generation of debris cloud and the destruction process of structure, and the velocity of debris flying is preliminarily obtained. The debris cloud continues to act on the back plate, leaving a lot of craters on the back plate. Because the shape of the debris cloud is approximately ellipsoid, the impact crater damage on the back plate is distributed circularly. However, in the cross section of the debris cloud, the debris is not uniformly distributed, and the closer to the central axis, the denser the mass distribution of the debris cloud. Therefore, the impact crater of the rear plate can be divided into several parts according to the ring shape. The generation of debris cloud is decoupled from the response and damage of the model. The generation of debris cloud adopts engineering algorithm, and then, its expansion process is used as an input parameter to simulate the response and damage of the model structure. In order to verify the practicability of the method proposed in this paper, we use different methods for experimental comparison. The prediction accuracy result is shown in Figure 7.

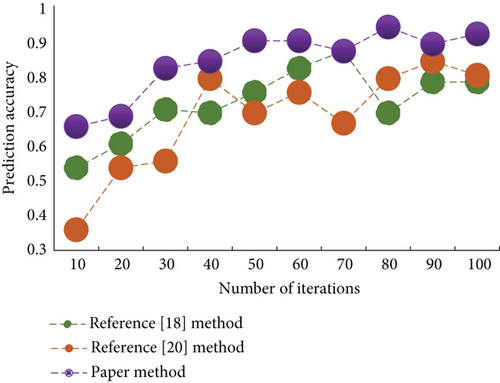
The results show that this method has the best prediction accuracy, while the other two methods have the worst. As a result, this method has a high level of prediction accuracy. The impact limit curve, which includes the critical projectile diameter impact limit curve and the critical bulkhead thickness impact limit curve, is commonly used to evaluate the performance of protective structures. The critical projectile diameter impact limit curve is used in this paper to assess the performance of protective structures. In the deformation zone, the structure’s ballistic limit curve decreases nonlinearly, increases linearly in the crushing zone, and then decreases nonlinearly in the melting/vaporization zone. When the collision velocity is in the ballistic zone, the projectile does not break after colliding with the buffer screen, causing significant damage to the protective screen, and the protective performance of the protective structure is less affected by the spacing, so spacing is not taken into account in this zone. Because the area of the debris cloud interacting with the target plate is much larger than the cross-sectional area of the largest main mass debris, only a portion of the debris cloud’s kinetic energy is used to determine the target plate’s penetration process.

According to the results of comparative analysis in this chapter, the impact limit curves of the mixed protective structure in ballistic section and crushing section under the experimental configuration parameters are revised. The influence of the magnitude and distribution area of residual stress on the limit of aluminum alloy shield is analyzed. From the experiment, it is concluded that the damage of the largest main debris to the rear plate is the main influence during the high-speed impact of the crushing section, and the ballistic limit curve of the crushing section is approximately a straight line when the largest main debris is considered separately. With the increase of impact velocity, the damage of each screen generally increases, especially in the crushing section, which increases sharply after the impact limit, while the damage of each screen shows obvious fluctuation near the critical velocity of ballistic section and crushing section. In addition, compared with the ballistic limit empirical curve, the protective performance of the experimental calibrated mixed protective structure has been improved. The feasibility and effectiveness of the numerical simulation modeling method of ballistic limit in this paper are verified.

5. Conclusions

The numerical simulation of the ballistic limit of a protective structure is investigated using fractal theory in this paper. The perforation of thin plate, the characteristics of debris cloud, the pit formation of medium plate, and the impact characteristics of double-layer plate were all investigated in-depth using hypervelocity impact characteristic analysis. The variation rules of perforation diameter of thin aluminum plate with three parameters of projectile impact velocity, projectile diameter, and thickness of thin aluminum plate are obtained, respectively, through numerical simulation of perforation characteristics of thin plate. When the aluminum spherical projectile strikes the aluminum double-layer plate protection structure in the crushing section, the fact that the crushing section’s ballistic limit curve is an approximate straight line is demonstrated. The point where the straight reverse extension line intersects the coordinate axis is also close to the origin. The kinetic energy of a single fragment decreases as projectile fragments, and the damage to the target plate or bulkhead can be attributed to the combined action of the largest main fragment and other debris clouds.

Dimension theory is used to model dimensionless variables of the ballistic limit equation in this paper, making it easier to obtain a general relation that accurately reflects the characteristics of hypervelocity impact. Only a few typical hypervelocity impact experiments are used, and the high-efficiency and low-cost hypervelocity impact numerical simulation is fully utilized to solve and verify the undetermined constants, significantly lowering the development cost and improving the development efficiency of the ballistic limit equation. The Whipple protective structure of aluminum plate with craters and cracks was studied for high-speed impact damage. High-speed impact with craters and cracks has different damage characteristics than a nondefective Whipple protective structure. The high-speed impact protection performance of the hybrid protection structure in the ballistic and crushing sections is better than the predicted results of the existing ballistic limit empirical equation under the experimental parameters. The failure speed interval has been shortened, and the performance index has gone negative. It can be seen that when it comes to concrete engineering practice, it is necessary to check the protective structure against the protective design parameters in order to ensure performance reliability. Despite the fact that this paper has some accomplishments, however, given the author’s limited research time and ability, some aspects can still be improved. The concrete relationship between the experimental effects of a multilayer observation plate and a one-layer observation plate, for example, and the problem of protective spacing when the protective structure is studied separately will be investigated further in the future.

Conflicts of Interest

The authors do not have any possible conflicts of interest.