Wireless Communications and Mobile Computing

Volume 2022, Issue 1 1932708

Research Article

Open Access

Uplink Multiple Access for Reconfigurable Intelligent Surface-Aided Wireless Systems

Nhan Duc Nguyen

orcid.org/0000-0002-1561-7914

Faculty of Mechanical-Electrical and Computer Engineering, School of Engineering and Technology, Van Lang University, 69/68 Dang Thuy Tram Street, Ward 13, Binh Thanh District, Ho Chi Minh City 70000, Vietnam vanlanguni.edu.vn

Search for more papers by this author

Chi-Bao Le,

Chi-Bao Le

orcid.org/0000-0002-3175-5698

Faculty of Electronics Technology, Industrial University of Ho Chi Minh City (IUH), Ho Chi Minh City, Vietnam hui.edu.vn

Search for more papers by this author

Munyaradzi Munochiveyi,

Corresponding Author

Munyaradzi Munochiveyi

[email protected]

orcid.org/0000-0001-7114-8609

Electrical and Electronic Engineering Department, University of Zimbabwe, Mount Pleasant, Harare, Zimbabwe uz.ac.zw

Search for more papers by this author

Nhan Duc Nguyen,

Nhan Duc Nguyen

orcid.org/0000-0002-1561-7914

Search for more papers by this author

Chi-Bao Le,

Chi-Bao Le

orcid.org/0000-0002-3175-5698

Faculty of Electronics Technology, Industrial University of Ho Chi Minh City (IUH), Ho Chi Minh City, Vietnam hui.edu.vn

Search for more papers by this author

Munyaradzi Munochiveyi,

Corresponding Author

Munyaradzi Munochiveyi

[email protected]

orcid.org/0000-0001-7114-8609

Electrical and Electronic Engineering Department, University of Zimbabwe, Mount Pleasant, Harare, Zimbabwe uz.ac.zw

Search for more papers by this author

First published: 21 July 2022

https://doi.org/10.1155/2022/1932708

Academic Editor: A.H. Alamoodi

Share a link

Email
Wechat
Bluesky

Abstract

The integration of reconfigurable intelligent surface- (RIS-) aided wireless communication and multiple access is an attractive and promising scheme for next-generation wireless networks. In this research work, separate uplink RIS-aided nonorthogonal multiple access (NOMA) and uplink relay-assisted NOMA schemes are studied, where the RIS and relay devices are deployed to enhance the coverage of an obstructed single-antenna far user by assisting it to communicate with a single-antenna base station. In each scenario, both perfect successive interference cancellation (pSIC) and imperfect successive interference cancellation (ipSIC) operations are considered in the proposed multiple access network. To characterize the system performance, the associated residual interference caused by ipSIC and relay loop self-interference is characterized using the Rayleigh fading model; subsequently, new channel statistics are derived based on the Gauss-Laguerre polynomial. Consequently, the closed-form approximate outage probability expressions are derived for each scenario in the high signal-to-noise ratio (SNR) regime. To gain further insight, the system throughput in the delay-limited transmission is also obtained for each scenario. The formulated expressions are validated via Monte-Carlo simulations. Finally, the obtained simulation results demonstrate and validate the superiority of the RIS system over the relay device under several system parameters of interest despite the limitation of ipSIC.

1. Introduction

The prospect of large low-power machine-type communications (mMTC), very low-delay communication, Tbps data rates, massive connectivity, and other extraordinary services and applications in 5G and beyond networks has created renewed research interest in new multiple access schemes [1, 2]. In 5G and beyond, multiple access technologies require a redesign due to the combination of low-energy Internet of Things (IoT) and massive connectivity [2]. Existing carrier sense multiple access (CSMA) and noncontention orthogonal multiple access (OMA) techniques found in 1G-4G cellular networks do not scale well in massive connectivity scenarios where a massive number of devices are aimed at accessing a single base station (BS) simultaneously [2]. Thus, new multiple access techniques that enhance scale and reliability need to be considered [2].

Recently, nonorthogonal multiple access (NOMA) is a promising approach to address the aforementioned challenges by serving many users within the same resource block [3–5]. Several recent research works such as [6–9] have demonstrated via numerical results the significant enhancement obtained by NOMA over OMA under certain channel conditions. However, this is not necessarily the case as the authors in [6] showed that at low signal-to-noise ratios (SNRs) in finite blocklength schemes, OMA-based users with good channel conditions outperform users relying on NOMA, albeit, at high SNRs, the reverse is true as the overall link-layer rate of NOMA outperforms OMA when the delay exponent is loose. In [7], the authors investigated cooperative NOMA networks by considering generic α − μ fading channel under the impact of residual transceiver hardware impairments (RTHIs). To be practical, imperfect channel state information (CSI) and imperfect successive interference cancellation (SIC) are taken into account. More particularly, two representative NOMA scenarios are proposed, namely, noncooperative NOMA and cooperative NOMA. The authors in [8] investigated the physical layer security (PLS) of the ambient backscatter NOMA systems to raise problems of reliability and security. They considered the realistic scenarios of channel estimation errors (CEEs) and imperfect successive interference cancellation (ipSIC) and residual hardware impairments (RHIs) and how these parameters affect system performance. In [9], the authors considered downlink NOMA over fading channels under full and partial channel state information at the transmitter (CSIT). Furthermore, the authors showed that NOMA is more effective than OMA in terms of average sum rate while maintaining user fairness in fading channels.

There are two ways of implementing NOMA which are power domain or code domain [3–5]. In this article, we focus on power-domain NOMA (PD-NOMA). In PD-NOMA, the users’ receiver has additional complexity from the successive interference cancellation (SIC) technique employed to mitigate interference among users [3–5]. However, as indicated in [10], despite PD-NOMA achieving user fairness via power allocation, this improvement in the performance of users with poor channel conditions may end up impacting users with good channel conditions. The integration of reconfigurable intelligent surfaces (RISs)—also known as intelligent reflecting surfaces (IRS)—and PD-NOMA [11] has been proposed as a way to address this disadvantage of PD-NOMA. RIS devices are made up of massive passive/active low-cost reflecting elements capable of smartly configuring the phase shift of incident electromagnetic signals via a RIS controller [11]. Hence, RIS-assisted NOMA systems can provide additional channel paths which are useful in providing PD-NOMA gain in unfavorable scenarios such as when the channel strengths of the far and near user are similar or mutually orthogonal as in downlink multiple-input-single-output (MISO) networks [10]. In such scenarios, NOMA may not be beneficial or offer many advantages over OMA [12]. Another benefit of the additional channel paths provided by RIS is in blockage impacted communication such as in mmWave networks [13] where mmWave communications are vulnerable to blockages caused by vehicles, buildings, pedestrians, and trees. Further, in [14], the authors demonstrated via simulation results that the proposed downlink RIS-aided mmWave-NOMA system outperforms the traditional mmWave-NOMA without RIS in terms of achievable sum rate.

1.1. Related Works on Downlink RIS-NOMA Systems

Recently, research into RIS-aided NOMA communication systems has gained considerable attention. However, most of the research works are focused on the performance of downlink transmission in RIS-NOMA systems. In [15], the authors studied a downlink multicluster MISO RIS-NOMA system with a joint beamforming design. In this system, the authors demonstrated that using second-order cone programming- (SOCP-) based algorithm obtains a locally optimal solution for the total power minimization problem subject to base station beamforming matrices and RIS reflection amplitude and phase shift constraints. This enables the proposed RIS-NOMA system with 32 RIS elements to achieve a 2.5 dB gain over traditional MIMO systems with 64 transmit antennas. In [16], the authors demonstrated that RIS devices are a promising technology for improving NOMA systems in downlink RIS-assisted multicell NOMA networks, as RIS enables blocked users to transmit information. Using stochastic geometry, the authors were able to show the benefits of integrating RIS with NOMA by deriving closed-form and asymptotic coverage probability expressions for paired NOMA users. Simulation results proved that networks aided by RIS significantly outperform conventional networks without RIS. Additionally, the SIC order can be modified as RISs can alter the channel quality of NOMA users.

Differently, in [17], the authors considered the downlink of RIS-aided cooperative nonorthogonal multiple access (C-NOMA) systems. Here, the authors via simulation results showed that the RIS-assisted C-NOMA systems empowered by iterative penalty function-based semidefinite programming (SDP) and the successive refinement approach-based algorithm outperformed traditional C-NOMA systems without RIS. Similarly, in [18], the authors considered the downlink transmission RIS-assisted C-NOMA system with half-duplex (HD) and full-duplex (FD) relay modes under consideration. Here, the system is comprised of a BS, two NOMA users, and a RIS device. The motivation of the authors was to minimize the total transmit power of the BS and user-cooperating relay by jointly optimizing the BS power allocation coefficients, the relay user transmit power coefficient, and the RIS passive beamforming while subject to power budget, SIC, and the cellular user minimum required quality of service (QoS). The authors proposed an alternating optimization method to solve the highly coupled optimization variables. Simulation results showed that RIS introduces total transmit power gain in C-NOMA networks.

Moreover, in terms of artificial intelligence (AI) empowered downlink RIS systems, the authors in [19] investigated the benefits of deep learning (DL) and reinforcement learning (RL) approaches in empowering both RIS-NOMA and RIS-OMA multiuser downlink communication systems over fading channels. The authors also considered the time overhead required for configuring the RIS elements at the start of each fading channel. Moreover, the authors maximized the effective throughput by jointly optimizing the RIS phase shift and the access point (AP) power allocation for each channel block. Numerical results highlighted that for the proposed scheme, NOMA achieves about 42% gain over OMA; additionally, RL and DL agents achieve similar performance in Rician channels; however, in Rayleigh channels, RL is the best. However, we should refer to uplink to look at how NOMA works under the case RIS is enabled as the consideration in the next section.

1.2. Related Works on Uplink RIS-NOMA Systems

In terms of uplink RIS-NOMA systems, there have been several recent research works written on this topic. In [20], the authors considered the benefits of integrating RIS into UAV-assisted multiuser NOMA networks to enhance energy efficiency. The authors also proposed a single-leader multiple-follower Stackelberg Game to jointly design the UAV received signal strength and NOMA users’ achieved energy efficiency. Simulation results demonstrated significant energy efficiency with the introduction of RIS. Differently, in [21], the authors studied the spectral and energy efficiency of RIS-NOMA-enabled simultaneous wireless information and power transfer (SWIPT) techniques in the Internet of Things (IoT) networks. The authors also utilized the single-leader multiple-follower Stackelberg Game to jointly optimize the RIS phase shifts, IoT devices’ downlink allocated powers, and their harvested energy. Numerical results demonstrated the gain obtained by the introduction of RIS to the NOMA-enabled SWIPT network of IoT devices.

Furthermore, in [22], the authors considered security concerns when the design of RIS at downlink exhibits beneficial to security improvement by jointly designing the transceivers and RIS phase shifts. The authors also proposed performance analysis to confirm the role of the number of metasurface in RIS for security improvement. Numerical results demonstrated that in terms of total transmit power, the framework outdid different frameworks. Differently, the authors in [23] considered the uplink and how the system deals with downlink and uplink when we have different requirements of services at both sides. Simulation results showed the benefits of the proposed scheme in enhancing the performance at base station and mobile users.

On the other hand, in [24], the authors considered both downlink and uplink IRS-assisted NOMA and OMA networks. Here, the IRS is deployed to assist cell-edge users to communicate with a BS. The authors characterized the system performance by investigating new channel statistics of the BS-IRS-user links under Nakagami-m fading conditions. Furthermore, the authors also formulated outage probability and ergodic capacity closed-form expressions for each scenario. For further insights, the authors also obtained the diversity order and high SNR slope based on the approximations in the high-SNR regime. Simulation results showed that IRS reflecting elements and Nakagami-m fading parameters impacted the diversity order but did not impact the high-SNR slope. Numerical results showed that the IRS is superior to FD decode-and-forward relays.

1.3. Motivations and Contributions

Motivated by the above benefits of the addition of RIS in uplink NOMA networks, this article considers the impact on outage probability when RIS is introduced into uplink NOMA systems and explores the benefits of RIS under blocking, different from the works in [20–24] which lacked a detailed study on imperfect SIC (ipSIC) operation in uplink RIS-aided NOMA.

In this article, we consider the scenario of both perfect SIC (pSIC) and ipSIC uplink RIS-aided NOMA and uplink relay-assisted NOMA loop self-interference scenarios, where the RIS and relay devices are deployed to enhance the coverage of an obstructed far user by assisting it to communicate with a BS. Furthermore, to characterize the system performance of each scenario, we adopt the Rayleigh fading model for both the residual interference caused by ipSIC and relay loop self-interference. Afterward, we formulate new channel statistics of these interferences based on the Gauss-Laguerre integration. Subsequently, the closed-form outage expressions are determined for each scenario. To gain further insight, the system throughput in the delay-limited transmission is also obtained for each scenario.

Our main contributions can be written as follows:

(i)
We provide an analytical study on outage probability and throughput of RIS-aided uplink multiple access transmissions under blocking conditions
(ii)
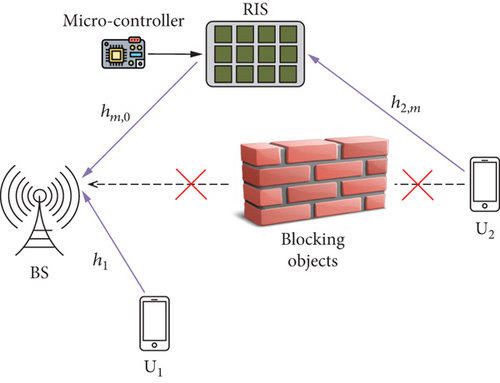
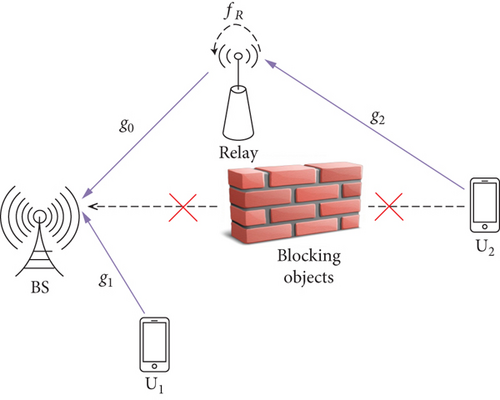
To confirm the strong contribution of RIS in enhancing the performance of a distant user-facing obstruction, we compare it against traditional relaying technology facing similar obstruction conditions as seen in Figures 1 and 2
(iii)
We consider the scenario of both pSIC and ipSIC operations in the NOMA system. To characterize the system performance, we adopt the Rayleigh fading model for both the residual interference caused by ipSIC and relay loop self-interference. Subsequently, new channel statistics of these interferences based on the Gauss-Laguerre integration are derived
(iv)
We focus on outage probability and throughput for the above two mentioned practical situations. To further provide insights into such RIS and relay-aided systems, we derive closed-form approximations for both RIS and relay schemes at a high SNR utilizing the Gauss-Laguerre parameter T = 40 to yield close approximate equations. The derived equations are validated by Monte Carlo simulations
(v)
Finally, we analyze and compare the outage probability and throughput expressions of the two schemes. In particular, we find that ipSIC and relay loop self-interference are the main limitations on both system outage and throughput performance. Furthermore, we observe that based on these impacts, an error floor is imposed on the system outage probability and conversely, a ceiling is placed on the system throughput. Despite these limitations, our numerical results showed that the proposed RIS-aided NOMA scheme can still outperform the relay-aided scheme in the high-SNR regime

Details are in the caption following the image — Open in figure viewer PowerPoint

1.4. Organization

The rest of this paper is organized as follows: Section 2 presents the system models and channel statistics of the RIS-aided and relay-aided systems in the presence of a blockage. In Section 3, we analyze the outage probability of the proposed uplink systems. Section 4 provides the closed-form outage probability approximations of both systems as well as the throughput performance. Section 5 provides numerical simulations. Section 6 concludes the paper.

2. System Models and the Channel Models

2.1. Scheme I: Uplink RIS

Figure 1 shows the uplink RIS-aided multiple access systems under blocking. The proposed system consists of a single-antenna BS, two NOMA single-antenna users—U₁ and U₂—a RIS device, and a blocking object obstructing the direct transmission between the far-user U₂ and the BS. The following transmit power constraint is imposed at BS in [24]

(1)

where P_U denotes each of the two users’ transmit power;

is the RIS reflection coefficient produced by the mth reflector; ϖ_m(ϕ_m) = 1 is the ideal phase shifts (m = 1, 2, 3, ⋯, M);

and

denote the U₁ and U₂ transmitted signals, respectively;

denotes the AWGN at the BS with variance N₀; and ϕ_m ∈ [0, 2π) is the RIS phase-shift variable of the mth element ∀m ∈ M. Moreover, we have

, and

. According to [25], we assume that RIS knows perfectly ϑ_m and θ_m.

The BS decodes U₁ first by regarding the signal from U₂ as interference, and the corresponding signal to interference and noise ratio (SINR) is written as

(2)

As in [26], we obtain the maximal SINR using ϕ_m = ϑ_m + θ_m. Then, we can rewrite (2) as

(3)

where ρ = P_U/N₀ is the transmit SNR of each two users,

, and

with

, and

After implementing SIC, U₂’s signal is detected with the SNR given by

(4a)

(4b)

where

and

represent the pSIC and ipSIC operations. We assume that the residual ipSIC interference is characterized as Rayleigh fading, with h_I ~ CN(0, λ_I) being the associated complex channel coefficient with λ_I representing the level of residual interference caused by ipSIC in [27].

2.2. Scheme II: Uplink Relay

Figure 2 depicts the uplink relay-aided multiple access systems under blocking. The proposed system consists of a single-antenna BS, two NOMA single-antenna users—U₁ and U₂, a relay device, and a blocking object obstructing the direct transmission between the far-user U₂ and the BS. The following transmit power constraint is imposed at the BS.

(5)

where P₂ and P_R are the transmission powers for U₂ and relay, respectively, and

denotes the AWGN with mean power N₀. Moreover, the loop self-interference is expressed as a Rayleigh fading channel with coefficient f_R, and λ_R is the corresponding average power. For simplicity, it could be assumed that P₂ = P_R as well as ρ = P₂/N₀ = P_R/N₀. Hence, the received SINR for

at the relay is given by

(6)

At the BS, the received signal is written as

(7)

where

is the normalized transmission power at U₁ and

stands for AWGN with mean power N₀. Similarly, we assume

and

Therefore, the received SINR at the BS is given by

(8)

Next, the BS cancels the signal U₁ by utilizing SIC. Hence, the received SNR at the BS is given by

(9a)

(9b)

2.3. Channel Statistics

Before computing outage probability, the probability distribution function (PDF) of channel

in which

, is given by [28].

(10)

In terms of the corresponding cumulative distribution function (CDF) of channel h_p,

is given as

(11)

Based on [29], the PDF and CDF of the cascade channel gain from U₂ to RIS and then to the BS are

(12)

(13)

3. Outage Probability

3.1. Scheme I: Performance Analysis for Uplink Transmission with RIS

3.1.1. Outage Probability of U₁

The outage probability of U₁ in the uplink phase can be given as

(14)

where

, and

, i ∈ {1, 2}, with R_i being the target rate at U_i.

Using (11) and (12) into (14), P₁ is calculated as

(15)

Let

; then, P₁ can be rewritten as

(16)

Using Equation (6.631.3), P₁ is given as

(17)

where W_a,b(c) is a Whittaker function.

3.1.2. Outage Probability of U₂

We assume that in the first time slot, the BS successfully processes messages at U_1.

can be formulated by

(18)

Proposition 1. The closed-form approximation of outage probability at user U₂ can be given by

(19)

Proof. The details are given in the appendix.

Similarly, if , can be first transformed into

(20)

Based on formula (13), The outage probability of U₂ with ipSIC for the uplink is presented in the following:

(21)

3.2. Scheme II: Performance Analysis for Uplink Transmission with Relay

3.2.1. Outage Probability of U₁

The outage probability of U₁ in the uplink phase can be given as

(22)

Furthermore, substituting (10) and (11) to (22), A₁ can be calculated as

(23)

Same as A₁ and after some algebraic manipulations, A₂ is calculated as

(24)

Substituting (23) and (24) into (22), we can obtain the outage probability of U₁ by

(25)

3.2.2. Outage Probability of U₂

Based on (9a), if

, then the outage probability of U₂ for uplink NOMA with ipSIC is given by

(26)

And by a series of calculations, we can figure out B is given by

(27)

So, we substitute (27) and (23) into (26); we can get (28).

(28)

Finally, if

, then the outage probability of U₂ with pSIC is calculated as

(29)

4. The Approximation of Outage Probability

4.1. Scheme I: The Approximation for Uplink Transmission with RIS

As ρ⟶∞, according to (3) and (4a), we have and .

First, the asymptotic expression for U₁ is calculated by

(30)

In (30), we pay attention on K_a(·) which can be expressed in terms of the Meijer-G function as in [30], Equation (9.34.3).

(31)

Then,

can be reformulated as below:

(32)

Applying [30], Equation (7.813.1) from the table of integrals, (32) can be reformulated by

(33)

Next, the asymptotic expression for U₂ with ipSIC is calculated by

(34)

By using Equation (7.813.1) of [30], the asymptotic outage probability of U₂ with ipSIC at high SNRs can be claimed by

(35)

Finally, the asymptotic outage probability of U₂ with pSIC at high SNRs for the situations M = 1 and M ≥ 2 is given by the following equations:

(36a)

(36b)

Proof. To make the computation easier, we use the series form of the Bessel function K_n(x) to approximate the high SNR. K_n(x) can be approximated when n = 1 and n ≥ 2 as

(37a)

(37b)

Equations (36a) and (36b) can be obtained by putting (37a) and (37b) into (21), respectively. The proof is finished.

4.2. Scheme II: The Approximation for Uplink Transmission with Relay

The results can be obtained easily by using three approximate equations, namely,

, and

. Thereby at high SNRs, we can write the approximate expression for the U₁, U₂ with ipSIC, and U₂ with pSIC as follows:

(38a)

(38b)

(38c)

4.3. Consideration on System Throughput Performance

Although outage probability plays an important role, another metric is also necessary to evaluate system performance which is given by [31] (Equation (42))

(39)

We expect to evaluate outage performance, and then, throughput can be used to provide useful guidelines for design of such RIS-aided system. More importantly, key parameters can be determined to control the quality as expected.

5. Numerical Results

In this section, we simulate the obtained outage probability and further verify with Monte Carlo simulation. The main parameters used are summarized in Table 1, where BPCU stands for a bit per channel use and we set the Gauss-Laguerre parameter as T = 40 to yield a close approximation; the variances of complex channel coefficients are set to be λ₀ = 1, λ₁ = 1, λ₂ = 1, and λ_I = 0.001, respectively.

1. Main system parameters.

Monte Carlo simulations	10⁷ iterations
The targeted data rates for users	R₁ = 0.5, R₂ = 1 (BPCU)
The distance from U₂ to RIS	d₂ = 20 m
The distance from RIS to BS	d₀ = 30 m
The distance from U₁ to BS	d₁ = 10 m
The path loss exponent	α = 2

Figure 3 depicts the outage probability versus transmit SNR in decibels in uplink RIS-aided NOMA when the residual interference caused by ipSIC is λ_I = −30 dB. Paying special attention to the outage performance of RIS-assisted uplink transmission from U₂, we observe that the best outage performance is achieved when the SIC operation is perfect and the RIS phase shifts are set at M = 32. On the other hand, when the SIC operation is imperfect, the outage performance approaches a floor in the high-SNR region. Similarly, the uplink outage probability from U₁ experiences the same effect of approaching a floor in the high SNR region. The main reason is that both floors of the RIS-aided NOMA network are also determined by the efficiency of the SIC.

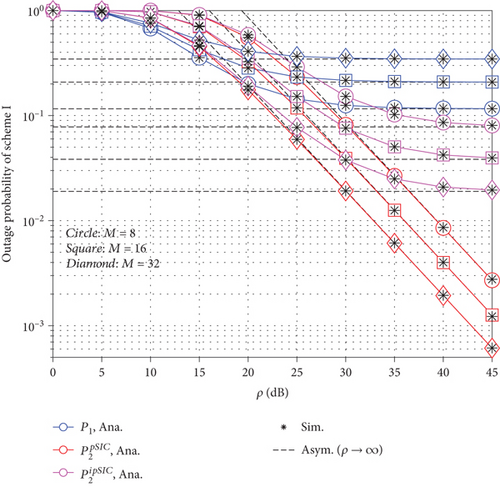
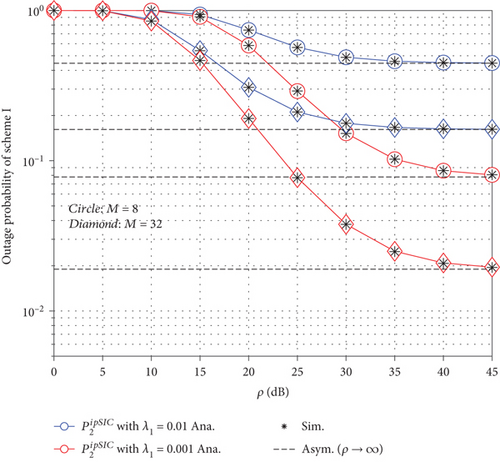
The impact of residual interference is observed in Figure 4. Particularly, the worst performance is observed for the case of λ_I = 0.01. This means that pSIC allows the system to work at acceptable outage performance levels. We can also see the performance could be better by adjusting the RIS phase shifts reasonably and the outage performance becomes suitable for continuous work of this system.

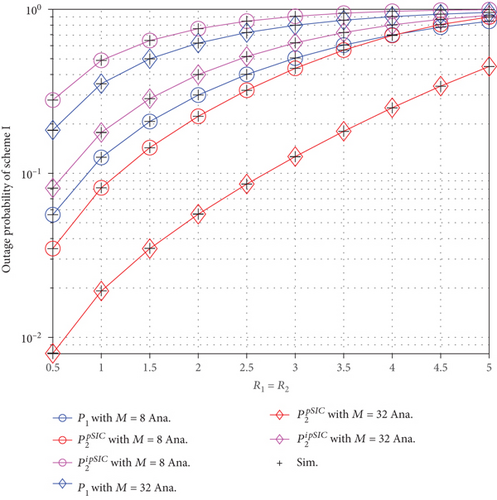
In Figure 5, we analyze the outage probability versus targeted data rates R₁ = R₂ with residual interference λ_I = 0.001 and transmit SNR ρ = 30 (dB). Here again, we can see the impact of ipSIC and RIS phase shifts with increasing throughput. The best outage performance is achieved by lower R₁ = R₂ rates. It is important to note that for uplink RIS-NOMA systems, both Figures 3–5 highlight the contribution of RIS phase shifts to outage probability.

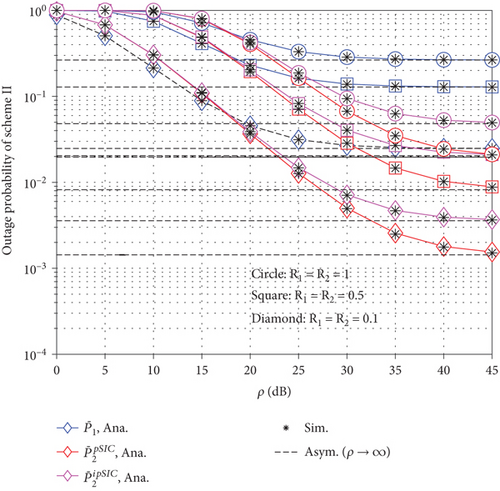
In Figure 6, we can observe the outage probability versus SNR in decibels for the uplink relay-aided NOMA system with and λ_I = 0.01 representing the relay loop self-interference and ipSIC residual interference, respectively. All the outage probability curves approach a floor in the high-SNR region. Similar to the findings in Figure 5, the best outage performance in the proposed relay-aided NOMA system is achieved by lower R₁ = R₂ rates.

Similarly, as in Figure 4, we can see the impact of residual interference on outage performance in relay-aided NOMA systems in Figure 7. We can observe the best outage performance is obtained with both lower R₁ = R₂ rates as well as lower residual interference λ_I.

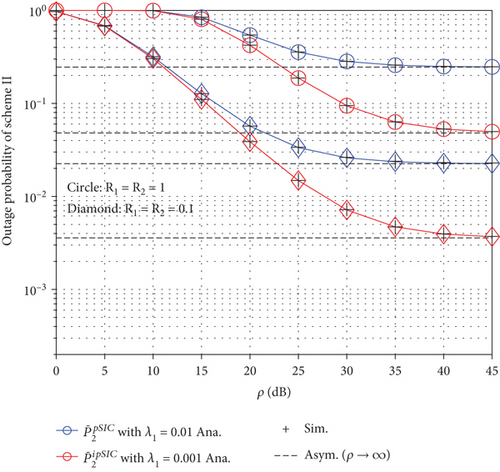
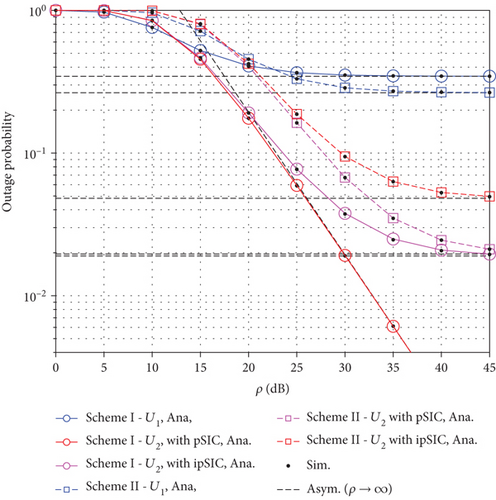
Figure 8 compares the outage probability of the two proposed schemes versus SNR in dB with and M = 32. This figure confirms the superiority of the RIS-aided system over the relay-aided system.

In Figure 9, we can see the trend of throughput between the two schemes. The curves approach an error ceiling in the high-SNR region due to the residual and loop interference.

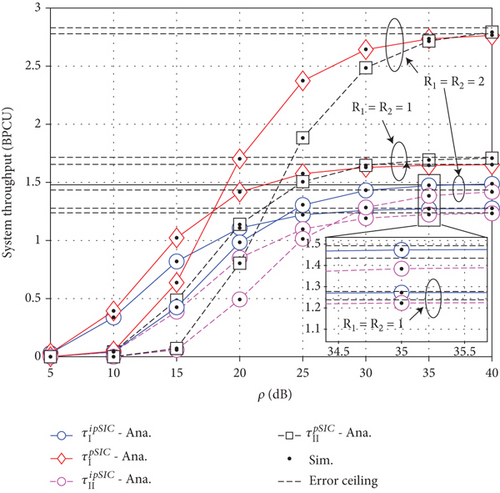
Finally, we can observe for all Figures 3–9 that the simulated curves and asymptotic curves closely match in the high SNR region thus, confirming the validity of the derived high-SNR approximations.

6. Conclusion

We have investigated the system outage and throughput performance of uplink RIS-assisted multiple access systems by exploring the impact of pSIC and ipSIC. To gain further insights into the benefits of including RIS in uplink multiple access systems, we compared it to an uplink relay-aided multiple access system. In each scenario, the RIS and relay devices are deployed to enhance the coverage of an obstructed far user by assisting it to upload information to a BS. To provide system performance analysis, we adopted the Gauss-Laguerre integration to achieve the closed-form approximate outage expressions in the high-SNR regime. We evaluate the derived expressions to understand whether the outage and throughput can be improved. Numerical results of ipSIC scenarios indicate that the RIS-NOMA system can still perform despite the impact of ipSIC. Furthermore, the results demonstrate the superiority of RIS over the relay in the high-SNR region. However, it is important to note the existence of outage error floors and throughput ceilings in a high-SNR region. Therefore, this regard could be target outage and throughput performance once we improve other system parameters. In future work, we will investigate the impact of introducing multiple RIS devices in the system to further enhance the system uplink performance.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work has been supported by Van Lang University, Ho Chi Minh City, Vietnam under the Project 1000.

Appendix

Proof of Proposition 1

The outage of U₂ under ipSIC is given as

(A.1)

where

is the Meijer G-function given in [30], Equation (9.301),

, where H_t is the weight of the Gauss-Laguerre integration [32] and q_t is the q-th zero of Laguerre polynomial L_T(q_t). The parameter T is to ensure a complexity-accuracy tradeoff.

With the help of the [30], Equation (9.34.3) and after some manipulation, we have

(A.2)

where

is the Meijer G-function given in [30], Equation (9.301). Specifically, we let q = x/λ_I and with the help of Gauss-Laguerre integration [33], Equation (25.4.45). The closed-form approximation of the

can be given as

(A.3)

where

, where H_t is the weight of the Gauss-Laguerre integration and q_t is the q-th zero of Laguerre polynomial L_T(q_t).

The proof of Proposition 1 is completed.

Open Research

Data Availability

No data were used to support this study.

References

1 Gupta A. and Jha R. K., A survey of 5G network: architecture and emerging technologies, IEEE Access. (2015) 3, 1206–1232, https://doi.org/10.1109/ACCESS.2015.2461602, 2-s2.0-84959851913.
10.1109/ACCESS.2015.2461602
Web of Science® Google Scholar
2 Tataria H., Shafi M., Molisch A. F., Dohler M., Sjöland H., and Tufvesson F., 6G wireless systems: vision, requirements, challenges, insights, and opportunities, Proceedings of the IEEE. (2021) 109, no. 7, 1166–1199, https://doi.org/10.1109/JPROC.2021.3061701.
10.1109/JPROC.2021.3061701
Web of Science® Google Scholar
3 Liu Y., Qin Z., Elkashlan M., Ding Z., Nallanathan A., and Hanzo L., Nonorthogonal multiple access for 5G and beyond, Proceedings of the IEEE. (2017) 105, no. 12, 2347–2381, https://doi.org/10.1109/JPROC.2017.2768666, 2-s2.0-85040546588.
10.1109/JPROC.2017.2768666
Web of Science® Google Scholar
4 Van Nguyen M.-S., Dinh-Thuan D., Al-Rubaye S., Mumtaz S., Al-Dulaimi A., and Dobre O., Exploiting impacts of antenna selection and energy harvesting for massive network connectivity, IEEE Transactions on Communications. (2021) 69, no. 11, 7587–7602, https://doi.org/10.1109/TCOMM.2021.3106099.
10.1109/TCOMM.2021.3106099
Web of Science® Google Scholar
5 Do D.-T., Anh-Tu L., Liu Y., and Jamalipour A., User grouping and energy harvesting in UAV-NOMA system with AF/DF relaying, IEEE Transactions on Vehicular Technology. (2021) 70, no. 11, 11855–11868, https://doi.org/10.1109/TVT.2021.3116101.
10.1109/TVT.2021.3116101
Web of Science® Google Scholar
6 Do D. T., Van Nguyen M. S., Voznak M., Kwasinski A., and de Souza J. N., Souza, "Performance analysis of clustering car-following V2X system with wireless power transfer and massive connections,", IEEE Internet of Things Journal. (2021) https://doi.org/10.1109/JIOT.2021.3070744.
10.1109/JIOT.2021.3070744
Web of Science® Google Scholar
7 Li X., Li J., Liu Y., Ding Z., and Nallanathan A., Residual transceiver hardware impairments on cooperative NOMA networks, IEEE Transactions on Wireless Communications. (2020) 19, no. 1, 680–695, https://doi.org/10.1109/TWC.2019.2947670.
10.1109/TWC.2019.2947670
Web of Science® Google Scholar
8 Li X., Zhao M., Zeng M., Mumtaz S., Menon V. G., Ding Z., and Dobre O. A., Hardware impaired ambient backscatter NOMA systems: reliability and security, IEEE Transactions on Communications. (2021) 69, no. 4, 2723–2736, https://doi.org/10.1109/TCOMM.2021.3050503.
10.1109/TCOMM.2021.3050503
Web of Science® Google Scholar
9 Do D. T., Van Nguyen M. S., Le A. T., Rabie K. M., and Zhang J., Joint fullduplex and roadside unit selection for NOMA-enabled V2X communications: ergodic rate performance, IEEE Access. (2020) 8, 140348–140360.
10.1109/ACCESS.2020.3012976
Web of Science® Google Scholar
10 Yang G., Xu X., Liang Y. -C., and Renzo M. D., Reconfigurable intelligent surface-assisted non-orthogonal multiple access, IEEE Transactions on Wireless Communications. (2021) 20, no. 5, 3137–3151, https://doi.org/10.1109/TWC.2020.3047632.
10.1109/TWC.2020.3047632
Web of Science® Google Scholar
11 Munochiveyi M., Pogaku A. C., Do D. -T., Le A. -T., Voznak M., and Nguyen N. D., Reconfigurable intelligent surface aided multi-user communications: state-of-the-art techniques and open issues, IEEE Access. (2021) 9, 118584–118605, https://doi.org/10.1109/ACCESS.2021.3107316.
10.1109/ACCESS.2021.3107316
Web of Science® Google Scholar
12 Fu M., Zhou Y., Shi Y., and Letaief K. B., Reconfigurable intelligent surface empowered downlink non-orthogonal multiple access, IEEE Transactions on Communications. (2021) 69, no. 6, 3802–3817, https://doi.org/10.1109/TCOMM.2021.3066587.
10.1109/TCOMM.2021.3066587
Web of Science® Google Scholar
13 Pan C., Ren H., Wang K., Kolb J. F., Elkashlan M., Chen M., di Renzo M., Hao Y., Wang J., Swindlehurst A. L., You X., and Hanzo L., Reconfigurable intelligent surfaces for 6G systems: principles, applications, and research directions, IEEE Communications Magazine. (2021) 59, no. 6, 14–20, https://doi.org/10.1109/MCOM.001.2001076.
10.1109/MCOM.001.2001076
Web of Science® Google Scholar
14 Xiu Y., Zhao J., Sun W., Renzo M. D., Gui G., Zhang Z., and Wei N., Reconfigurable intelligent surfaces aided mmWave NOMA: joint power allocation, phase shifts, and hybrid beamforming optimization, IEEE Transactions on Wireless Communications. (2021) 20, no. 12, 8393–8409, https://doi.org/10.1109/TWC.2021.3092597.
10.1109/TWC.2021.3092597
Web of Science® Google Scholar
15 Li Y., Jiang M., Zhang Q., and Qin J., Joint beamforming design in multi-cluster MISO NOMA reconfigurable intelligent surface-aided downlink communication networks, IEEE Transactions on Communications. (2021) 69, no. 1, 664–674, https://doi.org/10.1109/TCOMM.2020.3032695.
10.1109/TCOMM.2020.3032695
Web of Science® Google Scholar
16 Zhang C., Yi W., Liu Y., Yang K., and Ding Z., Reconfigurable intelligent surfaces aided multi-cell NOMA networks: a stochastic geometry model, IEEE Transactions on Communications. (2021) 70, no. 2, 951–966, https://doi.org/10.1109/TCOMM.2021.3126598.
10.1109/TCOMM.2021.3126598
Web of Science® Google Scholar
17 Zuo J., Liu Y., and Al-Dhahir N., Reconfigurable intelligent surface assisted cooperative non-orthogonal multiple access systems, IEEE Transactions on Communications. (2021) 69, no. 10, 6750–6764, https://doi.org/10.1109/TCOMM.2021.3098684.
10.1109/TCOMM.2021.3098684
Web of Science® Google Scholar
18 Elhattab M., Arfaoui M. A., Assi C., and Ghrayeb A., Reconfigurable intelligent surface enabled full-duplex/half-duplex cooperative non-orthogonal multiple access, IEEE Transactions on Wireless Communications. (2021) 21, no. 5, 3349–3364, https://doi.org/10.1109/TWC.2021.3120989.
10.1109/TWC.2021.3120989
Web of Science® Google Scholar
19 Zhong R., Liu Y., Mu X., Chen Y., and Song L., AI empowered RIS-assisted NOMA networks: deep learning or reinforcement learning?, IEEE Journal on Selected Areas in Communications. (2022) 40, no. 1, 182–196, https://doi.org/10.1109/JSAC.2021.3126068.
10.1109/JSAC.2021.3126068
Web of Science® Google Scholar
20 Diamanti M., Tsampazi M., Tsiropoulou E. E., and Papavassiliou S., Energy efficient multi-user communications aided by reconfigurable intelligent surfaces and UAVs, 2021 IEEE International Conference on Smart Computing (SMARTCOMP), August 2021, Irvine, CA, USA, 371–376, https://doi.org/10.1109/SMARTCOMP52413.2021.00075.
10.1109/SMARTCOMP52413.2021.00075
Google Scholar
21 Diamanti M., Tsiropoulou E. E., and Papavassiliou S., The joint power of NOMA and reconfigurable intelligent surfaces in SWIPT networks, 2021 IEEE 22nd International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), September 2021, Lucca, Italy, 621–625, https://doi.org/10.1109/SPAWC51858.2021.9593111.
10.1109/SPAWC51858.2021.9593111
Google Scholar
22 Dinh-Thuan D. and Le A.-T., Physical layer security for Internet of Things via reconfigurable intelligent surface, Future Generation Computer Systems. (2022) 126, 330–339, https://doi.org/10.1016/j.future.2021.08.012.
10.1016/j.future.2021.08.012
Web of Science® Google Scholar
23 Do D. T., Nguyen T. T. T., Nguyen T. N., Li X., and Voznak M., Uplink and downlink NOMA transmission using full-duplex UAV, IEEE Access. (2020) 8, 164347–164364.
10.1109/ACCESS.2020.3023163
Web of Science® Google Scholar
24 Cheng Y., Li K. H., Liu Y., Teh K. C., and Vincent Poor H., Downlink and uplink intelligent reflecting surface aided networks: NOMA and OMA, IEEE Transactions on Wireless Communications. (2021) 20, no. 6, 3988–4000, https://doi.org/10.1109/TWC.2021.3054841.
10.1109/TWC.2021.3054841
Web of Science® Google Scholar
25 Yang L., Yang Y., Hasna M. O., and Alouini M. -S., Coverage, probability of SNR gain, and DOR analysis of RIS-aided communication systems, IEEE Wireless Communications Letters. (2020) 9, no. 8, 1268–1272.
10.1109/LWC.2020.2987798
Web of Science® Google Scholar
26 Basar E., Di Renzo M., De Rosny J., Debbah M., Alouini M. S., and Zhang R., Wireless communications through reconfigurable intelligent surfaces, IEEE Access. (2019) 7, 116753–116773.
10.1109/ACCESS.2019.2935192
Web of Science® Google Scholar
27 Yue X. and Liu Y., Performance analysis of intelligent reflecting surface assisted NOMA networks, IEEE Transactions on Wireless Communications. (2022) 21, no. 4, 2623–2636, https://doi.org/10.1109/TWC.2021.3114221.
10.1109/TWC.2021.3114221
Web of Science® Google Scholar
28 Le C.-B. and Do D.-T., Joint evaluation of imperfect SIC and fixed power allocation scheme for wireless powered D2D-NOMA networks with multiple antennas at base station, Wireless Networks. (2019) 25, no. 8, 5069–5081, https://doi.org/10.1007/s11276-019-02116-1, 2-s2.0-85071275978.
10.1007/s11276-019-02116-1
Web of Science® Google Scholar
29 Le C.-B., Do D.-T., Li X., Huang Y.-F., Chen H.-C., and Voznak M., Enabling NOMA in backscatter reconfigurable intelligent surfaces-aided systems, IEEE Access. (2021) 9, 33782–33795, https://doi.org/10.1109/ACCESS.2021.3061429.
10.1109/ACCESS.2021.3061429
Web of Science® Google Scholar
30 Gradshteyn I. S. and Ryzhik I. M., Table of Integrals, Series, and Products, 2007, Elsevier, Amsterdam, The Netherlands.
Google Scholar
31 Do D.-T., Le C.-B., and Afghah F., Enabling full-duplex and energy harvesting in uplink and downlink of small-cell network relying on power domain based multiple access, IEEE Access. (2020) 8, 142772–142784, https://doi.org/10.1109/ACCESS.2020.3013912.
10.1109/ACCESS.2020.3013912
Web of Science® Google Scholar
32 Yue X., Liu Y., Yao Y., Li X., Liu R., and Nallanathan A., Secure communications in a unified non-orthogonal multiple access framework, IEEE Transactions on Wireless Communications. (2020) 19, no. 3, 2163–2178, https://doi.org/10.1109/TWC.2019.2963181.
10.1109/TWC.2019.2963181
Web of Science® Google Scholar
33 Abramowitz M. and Stegun I., Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 1972, Dover, New York, NY, USA.
Google Scholar

All articles

Uplink Multiple Access for Reconfigurable Intelligent Surface-Aided Wireless Systems

Abstract

1. Introduction

1.1. Related Works on Downlink RIS-NOMA Systems

1.2. Related Works on Uplink RIS-NOMA Systems

1.3. Motivations and Contributions

1.4. Organization

2. System Models and the Channel Models

2.1. Scheme I: Uplink RIS

2.2. Scheme II: Uplink Relay

2.3. Channel Statistics

3. Outage Probability

3.1. Scheme I: Performance Analysis for Uplink Transmission with RIS

3.1.1. Outage Probability of U₁

3.1.2. Outage Probability of U₂

3.2. Scheme II: Performance Analysis for Uplink Transmission with Relay

3.2.1. Outage Probability of U₁

3.2.2. Outage Probability of U₂

4. The Approximation of Outage Probability

4.1. Scheme I: The Approximation for Uplink Transmission with RIS

4.2. Scheme II: The Approximation for Uplink Transmission with Relay

4.3. Consideration on System Throughput Performance

5. Numerical Results

6. Conclusion

Conflicts of Interest

Acknowledgments

Appendix

Proof of Proposition 1

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Uplink Multiple Access for Reconfigurable Intelligent Surface-Aided Wireless Systems

Abstract

1. Introduction

1.1. Related Works on Downlink RIS-NOMA Systems

1.2. Related Works on Uplink RIS-NOMA Systems

1.3. Motivations and Contributions

1.4. Organization

2. System Models and the Channel Models

2.1. Scheme I: Uplink RIS

2.2. Scheme II: Uplink Relay

2.3. Channel Statistics

3. Outage Probability

3.1. Scheme I: Performance Analysis for Uplink Transmission with RIS

3.1.1. Outage Probability of U1

3.1.2. Outage Probability of U2

3.2. Scheme II: Performance Analysis for Uplink Transmission with Relay

3.2.1. Outage Probability of U1

3.2.2. Outage Probability of U2

4. The Approximation of Outage Probability

4.1. Scheme I: The Approximation for Uplink Transmission with RIS

4.2. Scheme II: The Approximation for Uplink Transmission with Relay

4.3. Consideration on System Throughput Performance

5. Numerical Results

6. Conclusion

Conflicts of Interest

Acknowledgments

Appendix

Proof of Proposition 1

Open Research

Data Availability

References

Figures

References

Related

Information

3.1.1. Outage Probability of U₁

3.1.2. Outage Probability of U₂

3.2.1. Outage Probability of U₁

3.2.2. Outage Probability of U₂