Current-Sensorless Control Strategy for the MPPT of a PV Cell: An Energy-Based Approach
Abstract
A novel energy-based modelling and control strategy is developed and implemented to solve the maximum power point tracking problem when a photovoltaic cell array is connected to consumption loads. A mathematical model that contains key characteristic parameters of an energy converter stage connected to a photovoltaic cell array is proposed and recast using the port-Hamiltonian framework. The system consists of input-output power port pairs and storage and dissipating elements. Then, a current-sensorless control loop for a maximum power point tracking is designed, acting over the energy converter stage and following an interconnection and damping assignment passivity-based strategy. The performance of the proposed strategy is compared to a (classical) sliding mode control law. Our energy-based strategy is implemented in a hardware platform with a sampling rate of 122 Hz, resulting in lower dynamic power consumption compared to other maximum power point tracking control strategies. Numerical simulations and experimental results validate the performance of the proposed energy-based modelling and the novel control law approach.
1. Introduction
The emerging advances in photovoltaic (PV) cell panel manufacturing processes have pushed forward the technology. It is considered a feasible option for energy production instead of fossil fuels due to its safe, sustainable, and clean supply capabilities. The feasibility is reflected in the advancement of installed solar capacity by at least ten times from 2010 to 2018 [1]. However, the current PV panel technology forfeits up to 25% of its generated energy due to a deficient performance and dependence on climatic conditions [2]. Thus, the maximum power point tracking (MPPT) problem should be addressed in order to enhance the PV cell arrays’ energy generation. By having an adequate MPPT strategy, the power transfer efficiency from the PV cell arrays to consumption loads is improved. The MPPT focuses on matching the PV panel’s output load by controlling a DC voltage converter stage, ensuring the maximum power transfer [2–4].
Different approaches for the MPPT techniques based on application requirements and system constraints define the scope and objective of the control technique [5]. A first approach is focused on the maximum power point (MPP) of a single stage of PV cells, where the objective of the control is the extraction of the maximum power of a specific block of PV cells (or a single PV cell) of the whole array, under any environmental condition. The stage is generally governed by a control on a DC-DC converter from a microcontroller and works specifically over the block independently from the rest of the PV cell array [2, 6–16]. Since the objective of this strategy relies on the local control of the MPPT on a low area of PV cells, the robustness of the solution relies on the control capability to reach the MPP under disturbances over the whole controlled stage, i.e., disturbances on radiation or output load. Consequently, the shading issue is neglected from our scope, and later improvements on the PV arrays could be required to cover shading issues for more extensive areas. Traditional methods, such as constant voltage tracking, open-circuit voltage tracking, short-circuit current tracking, lookup table, current scanning, and curve fitting, are recommended when addressing the shading issues. Although the effectiveness of intelligent control strategies such as genetic algorithms, fuzzy logic algorithms, artificial neural networks, and upgraded P&O has been verified by experiments in many cases, such algorithms still have the disadvantages of high complexity and slow convergence speed [13]. Furthermore, the local MPPT approach is helpful in applications such as space satellites, solar vehicles, and solar water-pump systems [4].
A second approach is focused on the global MPP of the whole PV cell array or a big block of the array, where partial shading (PS) has an appreciable effect due to the area of the array. The PS distorts the global MPPT of the PV cell array due to the reflection of the power-voltage characteristics of any single shaded stage of PV cells over the characteristics of the whole PV cell array. It results in multiple peaks that could distract the MPPT control unit, while it may remain into a local MPP instead of a global one; see for instance [3, 17–26]. These techniques attain a balance of the power distribution between shaded, partially shaded, and fully illuminated stages of PV cells over the area of the whole array. The strategy is based on the flexibility to modify the architecture of the array [3]. Intelligent techniques, such as fuzzy logic control, artificial neural networks, and particle swarm optimization, have the advantage of working with imprecise inputs, becoming more suitable methods for applications where PS is a critical issue [5].
Robust controllers have been previously proposed to improve the performance of the PV cell arrays on the local MPP. For example, the sliding mode controller (SMC) represents a robust algorithm that efficiently responds to environmental changes and load variations, [7, 8, 19, 27]. The stability and robustness of the SMC have been verified through simulations and experiments, reported in [7, 8, 19, 28]. The SMC nonlinear control strategy proposes differential mapping algorithms that require constant and simultaneous sensing of voltage and current at the output of the PV cell array to perform the MPPT, [9, 20]. Such a nonlinear strategy includes extra steps to determine future states from previous ones based on historical data [7, 19].
On the other hand, in [10], an interconnection and damping assignment passivity-based control (IDA-PBC) is proposed to address the local MPPT problem. Their IDA-PBC method provides a strategy that brings the system to the desired energy equilibrium by sensing the instantaneous current/voltage responses from the PV cell, avoiding the estimation of future and past states.
The strategies mentioned above, based on “electrical current monitoring”, presents several inconveniences thoroughly discussed in [29, 30]. Examples of such inconveniences are the loss of connections, replacement complexity, inconsistent sensibility and resolution at low current, parasitic magnetic energy remanence in the cores, periodical calibration requirements, and erratic frequency responses. Moreover, external current sensors are usually expensive, which increases the inherent cost of the PV power system [11, 29, 31]. Finally, implementing algorithms of future-step prediction required a higher operating frequency and memory from the controller.
Consequently, the elimination of current sensors to track the MPP has been proposed as a counterpart to increase the cost benefits of PV systems [31]. Previous surveys have classified the so-called current-sensorless techniques according to their features and type of MPPT control strategies. See, for instance, [4, 5, 31] and the references therein. Specifically, the temperature/radiation monitoring (TRM) technique demonstrates a lower dependency on the topology and direct sensing connections. Controllers based on sensing radiation are seen as a more effective solution due to their economic advantage, fast response, and noninvasive characteristics [4]. Hence, the radiation parameter might be familiar to any PV cell connected to the same array, allowing a single sensor for control purposes.
In this paper, we propose an energy-based modelling approach for a PV cell array system connected to a DC-DC boost converter, based on the port-Hamiltonian formalism of [32–34]. The formalism is adopted here since the system has energy storage and dissipating elements (inter)connected with input-output power port-pairs. The port-Hamiltonian framework is the natural selection modelling approach because it allows a clear physical interpretation of the system’s energy flow towards a robust and scalable control design. Thus, inspired by [35, 36], a novel current-sensorless control algorithm in the framework of an IDA-PBC strategy is able to track the local MPP under variations of solar irradiance and output loads. The inputs for the control are the output voltage of the PV cell array and the sensed solar irradiance. The control objective is reached by setting the impedance matching between two stages: the PV cell array and a DC-DC boost converter system.
Since the control is based on sensing irradiation as a control input, the strategy allows connecting several PV cell stages to the same irradiation sensor with a separated control per stage. Our proposed strategy is effective since it ensures the extraction of the maximum power from any PV cell or stage. Nonetheless, the strategy requires that environmental conditions and disturbances remain homogeneously over the PV cell stages interconnected to the same radiation sensor. Furthermore, the proposed strategy demands lower frequency and power consumption than other robust control laws such as the SMC strategy, requiring noncomplex hardware to implement the control algorithm. The controller could be extended to several independent MPPT stages interconnected to a single solar irradiance sensor, decreasing the cost of sensing devices. Such an extension implementation is left out of the current work. The outline of this paper is as follows. Section 2 recapitulates the port-Hamiltonian modelling framework. In the same section, we summarize the IDA-PBC technique of [35, 36] and the SMC strategy of [8, 12]. In Section 3, we have proposed a novel port-Hamiltonian modelling approach for the PV cell array connected to a solar irradiance sensor and a DC-DC boost converter system. From our port-Hamiltonian modelling approach, we have developed a sensorless control loop in Section 4, ruled by a control algorithm designed under the IDA-PBC strategy, that avoids the current monitoring as in [10]. Furthermore, in Section 5, simulation results are given to demonstrate the performance of the proposed IDA-PBC compared to the SMC. The system is characterized, implemented, and controlled with a noncomplex hardware platform, and the experimental results are presented in Section 6. Finally, in Section 7 key concluding remarks and future work are provided.
2. Mathematical Modelling and Control Strategies
Firstly, it is necessary to cover the bases of the port-Hamiltonian modelling framework, as a preamble to develop a useful mathematical model to design a IDA-PBC strategy, for a further comparison with the well-known SMC strategy.
Notation 1. The time differential and the gradient of a scalar vector are given by
Furthermore, all vectors are considered as column vectors.
2.1. Port-Hamiltonian Framework
We first recapitulate the port-Hamiltonian (pH) framework for a general class of (non)linear physical systems, which is based on the description of their energy (Hamiltonian) function, interconnection structure, dissipating elements, and power port pairs (inputs and outputs) [32–34]. A characteristic of the pH framework is how the energy transfer between the physical system and the environment is modelled via the energy storage and dissipation elements together with their power preserving ports [34].
Next, we recapitulate the main control strategy developed to our PV cell and DC-DC boost converter system based on passivity.
2.2. Interconnection and Damping Assignment Passivity-Based Control (IDA-PBC)
The IDA-PBC strategy is a well-established technique that has demonstrated high efficiency and robustness for the control design of nonlinear systems. The strategy was firstly described in the Euler-Lagrange equations of motion and, more recently, extended to the pH approach, as seen in [35–37]. Generally speaking, IDA-PBC focuses on changing the potential energy shape by employing a closed-loop energy function equal to the difference between the energy of the system and the energy supplied by the controller. The energy shaping is performed while the interconnecting and structural properties of the system are preserved. Therefore, the system reaches its equilibrium point through energy stabilization [35–37]. The system structure is transformed to obtain the new desired interconnection and damping matrices with key parameters obtained from solving a partial differential equation (PDE). The solution of the PDE characterizes all the energy functions that can be assigned [33, 36, 37]. Finally, one of the solutions is chosen such that minimum requirements are satisfied by which the static state feedback control function u in (2) is obtained. The feedback control renders a closed-loop dynamics with a structured preserved pH system with dissipation. The proposed fully controlled system and the statements to satisfy the mathematical coherence of the structure are described in the following proposition.
Proposition 2 (see [36].)Assuming the functions β(x), , , and a vector function that satisfy
It follows that the vector function should be found in order to obtain a controller function β(x)+.
- (i)
Structure preservation
(14) - (ii)
Integrability
(15) - (iii)
Equilibrium assignment (where x∗: state values at (locally) stable equilibrium)
(16) - (iv)
Lyapunov stability
(17)
Once having introduced the IDA-PBC design strategy, it follows in the next section the recapitulation of the well-known sliding mode control of [8, 12] which is applied to achieve stabilization of nonlinear systems.
2.3. Sliding Mode Control (SMC)
The SMC strategy considers the dynamics of the solar irradiance sensor DC-DC transfer system and the output load. It consists of two operation modes. The first one is the approach mode, where the states of the system converge to a predefined domain known as the finite time sliding function σ1. The second one is the so-called sliding mode σ2, where the state of the system is restricted to a sliding surface that approaches the origin of the system, as in [7, 8, 12].
In the next section, the system of the PV cell connected to the DC-DC boost converter has been described following the pH framework.
3. A Port-Hamiltonian Modelling Approach to a PV Cell Connected to a DC-DC Boost Converter System
We first defined a pH approach to the PV cell modelling problem. Such an energy-based modelling strategy is previously introduced in [38] where we have proposed a model of a pumped hydro storage system powered by solar radiation. Also, in [38] we have simulated the system’s open-loop model in order to evaluate its performance where a control strategy is not yet designed and implemented to attain MPPT. Instead, in [38] we have applied a conveniently fixed frequency square signal to activate the switch of the DC-DC buck converter system.
3.1. PV Cell Modelling Approach
The equivalent circuit of the PV stage shown in Figure 1 is based on the model of [39–41]. The PV cell electrical performance follows the five-parameter model approach as in [42–44]. Into the PV cell structure represented by the dashed rectangle, the current iph is generated by the solar irradiance, while the diode D1 represents the equivalent model of the p-n join semiconductor layers. Furthermore, an equivalent resistor Rp is connected in a shunt configuration, followed by a serial resistor RS at the system’s output power. Meanwhile, the output of the the PV cell is linked to the next stage across the DC-link capacitor Cpv.
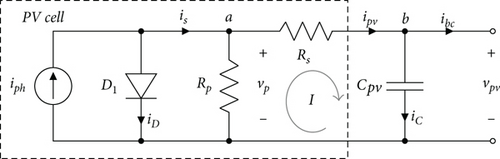
Based on the dynamics of (39) with an input-output port pair (upv, ypv) = (is, vp) and the Hamiltonian (35), and since Rp + Rs ≥ 0, we see how the power balance (9) clearly holds.
For control design purposes, it is now necessary to find an expression to track the amplitude of vpv according to the solar irradiance in order to obtain the so-called current-sensorless control strategy. Such expression is developed in the following subsection.
3.2. Equilibrium Trajectory of the PV Cell State Variables over the MPP
The following section presents the mathematical modelling approach to the DC-DC boost converter stage under the pH framework. Such a stage has been interconnected with the PV cell subsystem in Section 3.4.
3.3. DC-DC Boost Converter Modelling Approach
A boost configuration is selected here to achieve a DC-DC voltage step-up conversion which is regulated by a switching device. The converter is able to draw the MPP from the PV cell by adjusting its duty cycle for given solar radiance levels. For further details regarding the working principles of the model, we refer to [45, 46] and the references therein.
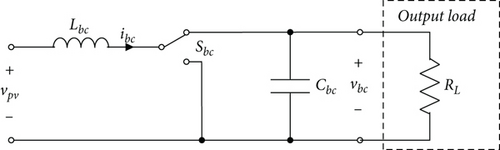
Based on the dynamics of (47) with its input-output port pair (ubc, ybc) = (vpv, ibc) and the Hamiltonian (46), and since RL > 0, the power balance (9) clearly holds.
The following subsection provides the resulting interconnected system containing the PV cell and the DC-DC boost converter.
3.4. A PV Cell Array and the Boost Converter: An Energy-Based Approach
Clearly, the power balance (9) also holds for (49) since . In the follow-up, we presented our passivity-based control design to the MPPT problem. Furthermore, we compared its performance with respect to an SMC strategy previously introduced in Section 2.3. We finally support our main findings with simulation results in Section 5, together with experimental results in Section 6.
4. Proposed Control Approach
We have formulated in Section 2.3 a specific type of SMC strategy for our PV cell plus the DC-DC boost converter system for the MPPT problem according to [8, 12]. Now, we introduce our novel IDA-PBC design to the interconnected system (49), and the Hamiltonian function (50). Our IDA-PBC strategy is inspired by the work of [10, 35, 36], whose main design steps are recapitulated in Section 2.2.
First, we develop the IDA-PBC method of Section 2.2 to the interconnected pH system Σ as in (49). The feedback function β(x) in (10) is obtained in order to control the system (49). We compute below the requirements on structure preservation (14), integrability (15), equilibrium assignment (16), and Lyapunov stability (17) [label = ( )].
4.1. Structure Preservation
4.2. Integrability
C1 in (56) is a term to be defined to accomplish the equilibrium assignment and Lyapunov stability forward. Equation (56) meets the requirement on (52) and complies the integrability condition.
4.3. Equilibrium Assignment at Stable Equilibrium x∗
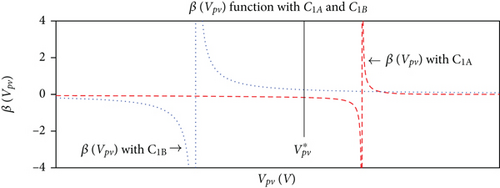
Notice how C1B in (59) depends on the equilibrium state , which also depends on iph and Gsun.
4.4. Lyapunov Stability
The inequality (60) meets the stability statement, leading the system to satisfy the MPP in the equilibrium trajectory described in (44).
4.5. IDA-PBC Control Law
The converter can be considered as a lossless stage controlled by the discrete set Sbc = {0, 1}, as introduced by [47]. Each element of Sbc represents a mode, where the exerted control law β(qp) over the switch in Figure 2 drives the state of Sbc on a mode 0 or 1, adjusting the controller to the desired trajectory of the MPP. The trajectory follows the solar irradiance Gsun, requiring a feedback reference to adjust the switching to a threshold dynamic level. Furthermore, to define this dynamic threshold level, the scalar function β(qpv) is evaluated on the desired equilibrium point over the MPP trajectory, i.e., , with as the state value that reaches the MPP. Notice how the voltage at the desired MPP depends also on the charge, i.e., as in (44). In addition to this, the current iph as in (25) depends on the solar irradiance, then becomes a control parameter dynamically adjusted by the radiation power.
We finally define our main control law in the following proposition and remark.
Proposition 3. Main result given a PV cell connected to a DC-DC boost converter represented in the pH system (50), with a duty cycle for the switch Sbc that lies between two modes, such that 0 ≤ Sbc ≤ 1, as in [8], then the MPPT control objective is obtained via a scalar function β(x) in (56) which solves the PDE in (11). Inspired by [12, 47], the proposed control signal is given by
Proof. The closed-loop pH system in (13) has a Hamiltonian function Hd(x, β(x)) given by
In the following section, we compare the performance of our IDA-PBC control law (62) with the SMC strategy of Section 2.3 via numerical simulations and an experimental setup.
5. Simulation Results
We simulate here the behaviour of the terms C1A and C1B from the control function β(vpv), the transfer and power functions of the PV cell, and the response of the PV cell output power at different solar irradiance and output impedance levels. The simulation integrates the control action of our IDA-PBC and the SMC strategies over the pH system (50). Then, a behavioural multi-physics numerical model is developed, fed with the key parameters of Table 1 from Section 6. In order to get accurate simulation results, the sampling of the states for the control strategies ({vpv, Gsun} in IDA-PBC and {vpv, ipv} in SMC) is restricted in frequency into the programming code.
| Parameter description | Magnitude |
|---|---|
| Environment temperature T | 30 |
| PV cell temperature Tv | 30 |
| PV nominal irradiation Gnom | 1000 kW/m2 |
| PV cell output short circuit ISC,noma | 1.95 A |
| PV cell output open circuit VOC,noma | 6.5 V |
| PV cell output Inom@MPPa | 1.42 A |
| PV cell output Vnom@MPPa | 4.0 V |
| Saturation current i0b | 745 μA |
| Simplified constant ab | 0.711 V |
| PV cell series resistor Rsb | 43m Ω |
| PV cell shunt resistor Rpb | 11.28 Ω |
| PV cell DC-link capacitor Cpv | 470 μF |
| DC-DC boost capacitor Cbc | 14.1 mF |
| DC-DC boost inductor Lbc | 2 mH |
From (56) and (59), it can be demonstrated that the function β(vpv) has a discontinuous behaviour at the right and left sides of a given equilibrium state , respectively, in terms of C1A and C1B, as shown in Figure 3. Therefore, C1A must be aplied to the control law (61) when the instant value of and C1B in the case to ensure the continuity of the control law over the whole tracking trajectory.
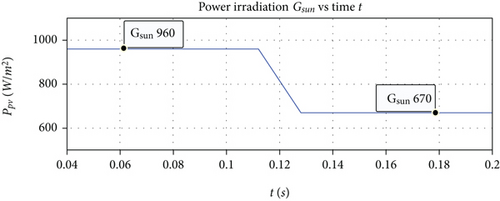
In Figure 4, the responses of the PV cell output power Ppv for the strategies IDA-PBC and SMC in (b) are compared under level changes on the solar irradiance as shown in (a), from 960 W/m2 to 670 W/m2. Here, the PV cell’s output power Ppv of both the IDA-PBC as in (61), and the SMC as in (23), shows no perceptible differences. The sample rate of the simulation for both control strategies is set to 10 MHz, in order to ensure an SMC suitable performance due to the extra-computation requirements for the differential equation calculation.
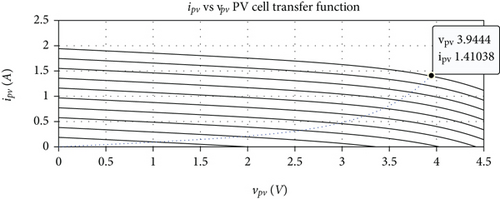
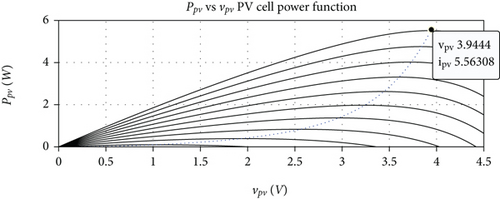
In Figure 5, we show the transfer functions ipv vs vpv in (a) and Ppv vs vpv in (b) of a PV cell, in order to determine the MPP of the array. Such characteristic curves of the PV cell are based on the dynamics of (26) to (28), with the key parameters given in Table 1. The figure also shows the values of vpv, ipv, and Ppv at the MPP for a solar irradiance Gsun = 1000. We test and evaluate here the capacity of the control laws (61) and (23) to follow the PV cell functions’ behaviour.
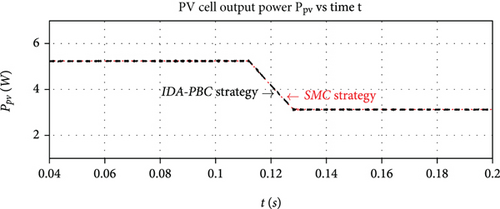
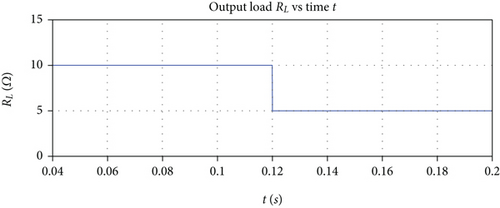
In order to further compare the performance of the IDA-PBC and the SMC strategies, the DC-DC boost converter load RL is simulated as a time function, following a step perturbation from 10Ω to 5Ω (Figure 6(a)). As a result, the power signal Ppv remains unmovable for both the IDA-PBC and the SMC (Figure 6(b)). Once again, the sample rate of the simulation for both control strategies is set to 10 MHz, due to the extra-computation requirements for the differential equation calculation required by the SMC.
The radiation is represented by 100 W/m2 steps from 100 to 1000 W/m2 for both (a) and (b).
6. Experimental Results
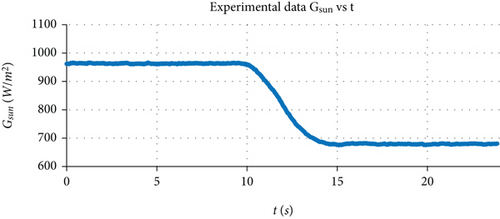
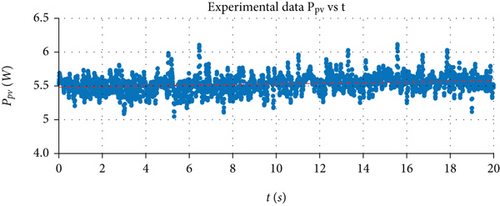
The experimental setup used to measure the radiation and control of the MPP is shown in Figure 7. The setup consists of (a) commercial PV cell JD-7 W; (b) an open-source electronic prototyping platform Arduino UNO; (c) an Adafruit data logger shield; (d) irradiance sensor Spectrum 210; (d) hall current sensor module ACS712 5A; (e) multimeter BK Precision 393; (f) oscilloscope BK Precision 2540C; (g) laptop DELL Latitude 5491; (h) generic electronic components (resistors, capacitors, inductors, semiconductors); (i) protective boxes [48]. We have used real-time data from a sensor of the Costa Rican’s National Meteorological Institute (https://www.imn.ac.cr/web/imn/inicio), to calibrate our irradiance sensor Spectrum323 210. The experimental set up from Figure 7 allows to track the physical parameters vpv and ipv under constant solar irradiance of ≈1000 W/m2, ≈850 W/m2, and ≈700 W/m2. Meanwhile, a variable resistance load connected at the output of the PV cell induced different impedance matching conditions. Hence, the experimental PV cell output power function was determined by fitting the PV cell output power Ppv at the MPP, as shown in Figure 8. An MPP is determined from the experimental data for Ppv ≈ 5.7 W when the voltage vpv ≈ 4.0 V and ipv ≈ 1.41 A. In addition to this, the values ISC,nom ≈ 1.95 A and VOC,nom ≈ 6.5 V are calculated at the top end and bottom end of the impedance matching. These aforementioned parameters allow the characterization of the PV cell as explained in the follow-up.

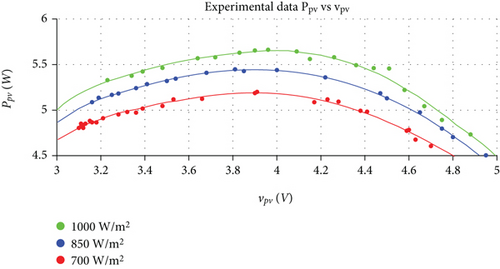
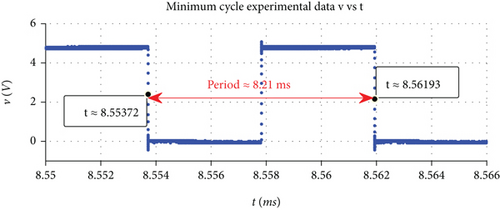
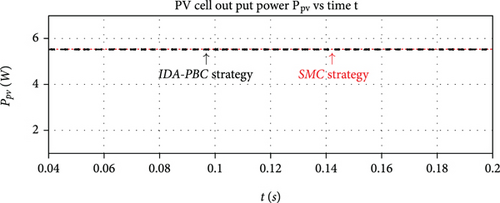
In order to evaluate the response of IDA-PBC strategy, the system setup in Figure 7 is firstly exposed to a constant solar irradiance. Then, the PV cell device is rotated, generating an irradiance step from GSun ≈ 960 W/m2 to GSun ≈ 670 W/m2, as shown in Figure 10(a). Consistently, the response of the output power Ppv to this irradiance step is measured. It is experimentally demonstrated that the IDA-PBC strategy implemented into the hardware platform tracks the MPP (Figure 10(b)), according to the Ppv experimental trend lines of Figure 8.

Finally, Figure 11(a) shows an output impedance step from 10 Ω to 5 Ω that is induced at the output of the boost DC-DC converter at a constant solar irradiance of GSun ≈ 960 W/m2. Once again, the implemented IDA-PBC strategy controls the system and keeps the PV cell output power Ppv unmovable around 5.5 W (Figure 11(b)). Such result is consistent with the MPP reported on the Ppv experimental functions of Figure 8.
Remark 4. The proposed IDA-PBC requires to monitor the PV cell output voltage vp and the radiation power GSun as input parameters. Such strategy is a noninvasive approach since it operates without electrical current sensors, contrary to the SMC law in (22) and the IDA-PBC law of [10] that require to monitor electrical currents at the output of the PV cell.

7. Concluding Remarks and Future Work
We have proposed a novel control law for the local MPPT problem in an energy-based setting, which takes advantage of the structure preservation properties of the system under study. The simplicity in the calculations allows an adequate response under uncertainties in radiation inputs. We have also simulation results on an SMC control law strategy. Our novel control law and the SMC are simulated, and we demonstrated that both strategies are able to reach the addressed MPPT problem. However, for the physical implementation, our IDA-PBC approach requires no direct electrical current measurements, being, in this case, less invasive and requiring less monitoring sensors than the SMC strategy.
The control strategy is tested for a single PV cell’s MPPT. However, the solution can be extended to applications where PS is not critical. For instance, an application with PV cell arrays governed with separated DC-DC converters, exposed to the same radiation level or localized far away from PS sources. It means that several PV cell arrays could be controlled with a single sensor. Since the sensor is externally connected, its installation does not depend on a specific place. Moreover, a single sensor requires a single connection line. Such installation simplicity reduces implementation costs, e.g., wiring over the array, in applications such as low power production PV farms and roof PV cell arrays.
The IDA-PBC strategy is physically implemented in a prototype governed by a hardware platform, with a maximum switching rate on the control signal of 122 Hz. The sense sampling time in our control strategy is faster than the SMC strategy. Such an advantage is due to the algorithm’s simplicity, resulting in a low-cost implementation and a low dynamic-power consumption. Moreover, the PV cell is characterized to obtain the MPP at several solar irradiance inputs. The prototype’s performance is tested by setting step changes in the dynamics of the system: firstly, in the solar irradiance input over the PV cell, and secondly, in the impedance output of the boost DC-DC converter. In both cases, the output power remains over the MPP of the PV cell, according to the characterization of the PV cell. Our control law requires the PV cell’s parameter identification. Such identification follows mainly from the manufacturer’s datasheet. The parameter identification procedure should be made once if the PV array is homogeneous in terms of PV cells.
Future work will consider the design and implementation of the proposed control law in a higher power physical system and under reactive output loads conditions.
Conflicts of Interest
The authors declare that there is no conflict of interest regarding the publication of this paper.
Acknowledgments
The authors thank the Instituto Tecnológico de Costa Rica (ITCR), Cartago, and the Centro Académico de Alajuela for providing the necessary infrastructure and resources to carry out this work.
Open Research
Data Availability
All the data that supports this research is available under request at the authors’ email addresses.




