Volume 2022, Issue 1 1541486

Research Article

Open Access

A Modified Algorithm Based on Haar Wavelets for the Numerical Simulation of Interface Models

Gule Rana,

Gule Rana

Department of Mathematics, Shaheed Benazir Bhutto Women University, Peshawar, Pakistan sbbwu.edu.pk

Search for more papers by this author

Muhammad Asif,

Muhammad Asif

Department of Mathematics, University of Peshawar, Peshawar, Khyber Pakhtunkhwa, Pakistan uop.edu.pk

Search for more papers by this author

Nadeem Haider,

Nadeem Haider

Department of Mathematics, University of Peshawar, Peshawar, Khyber Pakhtunkhwa, Pakistan uop.edu.pk

Search for more papers by this author

Rubi Bilal,

Rubi Bilal

Department of Mathematics, Shaheed Benazir Bhutto Women University, Peshawar, Pakistan sbbwu.edu.pk

Search for more papers by this author

Muhammad Ahsan,

Muhammad Ahsan

Department of Mathematics, University of Swabi, Swabi, Khyber Pakhtunkhwa, Pakistan uoswabi.edu.pk

Search for more papers by this author

Qasem Al-Mdallal,

Qasem Al-Mdallal

orcid.org/0000-0002-2853-9337

Department of Mathematical Sciences, UAE University, P.O. Box, 15551 Al Ain, UAE uaeu.ac.ae

Search for more papers by this author

Fahd Jarad,

Corresponding Author

Fahd Jarad

[email protected]

orcid.org/0000-0002-3303-0623

Department of Mathematics, Çankaya University, Ankara 06790, Turkey cankaya.edu.tr

Department of Medical Research, China Medical University, Taichung 40402, Taiwan cmu.edu.cn

Search for more papers by this author

Gule Rana,

Gule Rana

Department of Mathematics, Shaheed Benazir Bhutto Women University, Peshawar, Pakistan sbbwu.edu.pk

Search for more papers by this author

Muhammad Asif,

Muhammad Asif

Department of Mathematics, University of Peshawar, Peshawar, Khyber Pakhtunkhwa, Pakistan uop.edu.pk

Search for more papers by this author

Nadeem Haider,

Nadeem Haider

Department of Mathematics, University of Peshawar, Peshawar, Khyber Pakhtunkhwa, Pakistan uop.edu.pk

Search for more papers by this author

Rubi Bilal,

Rubi Bilal

Department of Mathematics, Shaheed Benazir Bhutto Women University, Peshawar, Pakistan sbbwu.edu.pk

Search for more papers by this author

Muhammad Ahsan,

Muhammad Ahsan

Department of Mathematics, University of Swabi, Swabi, Khyber Pakhtunkhwa, Pakistan uoswabi.edu.pk

Search for more papers by this author

Qasem Al-Mdallal,

Qasem Al-Mdallal

orcid.org/0000-0002-2853-9337

Department of Mathematical Sciences, UAE University, P.O. Box, 15551 Al Ain, UAE uaeu.ac.ae

Search for more papers by this author

Fahd Jarad,

Corresponding Author

Fahd Jarad

[email protected]

orcid.org/0000-0002-3303-0623

Department of Mathematics, Çankaya University, Ankara 06790, Turkey cankaya.edu.tr

Department of Medical Research, China Medical University, Taichung 40402, Taiwan cmu.edu.cn

Search for more papers by this author

First published: 09 August 2022

https://doi.org/10.1155/2022/1541486

Citations: 3

Academic Editor: Anna Napoli

Share a link

Email
Wechat
Bluesky

Abstract

In this paper, a new numerical technique is proposed for the simulations of advection-diffusion-reaction type elliptic and parabolic interface models. The proposed technique comprises of the Haar wavelet collocation method and the finite difference method. In this technique, the spatial derivative is approximated by truncated Haar wavelet series, while for temporal derivative, the finite difference formula is used. The diffusion coefficients, advection coefficients, and reaction coefficients are considered discontinuously across the fixed interface. The newly established numerical technique is applied to both linear and nonlinear benchmark interface models. In the case of linear interface models, Gauss elimination method is used, whereas for nonlinear interface models, the nonlinearity is removed by using the quasi-Newton linearization technique. The L_∞ errors are calculated for different number of collocation points. The obtained numerical results are compared with the immersed interface method. The stability and convergence of the method are also discussed. On the whole, the numerical results show more efficiency, better accuracy, and simpler applicability of the newly developed numerical technique compared to the existing methods in literature.

1. Introduction

Interface models play an important role in many disciplines including electromagnetic wave propagation, material science, fluid dynamics, and biological systems. The shared boundary between the two intervals in case of one-dimensional domains or between two regions in case of higher-dimensional domains is known as an interface. These domains (intervals or regions) are kept together with the help of suitable jump constraints. These phenomena can be modeled by using partial differential equations (PDEs) or ordinary differential equations (ODEs), where the parameters in these differential equations across the interface separating the two materials or states are discontinuous. Interface model is a mathematical model which considers two identical or different materials at different states having a shared boundary. The example of interface models with same materials in different states is water and ice, while water and oil is an example of interface models with different materials [1, 2]. These models frequently arise in heat conduction, Navier-Stokes flows, crystal growth, wave propagation through nonhomogeneous media, and models of solidification. Most of the interface model equations consist of highly varying coefficients [1, 3, 4]. The approximations of various physical and biomedical models often consist of highly varying coefficients or heterogeneous ODE or PDE models [5].

The solution of these models is a challenge for many standard numerical methods such as finite element method, finite volume method, and finite difference method. These methods have either poor performance or unable to catch the discontinuity in the solution. Due to the numerous applications of such type of models, several numerical methods have been introduced for the solution of these models with regular and irregular geometries in literature. Some of the numerical methods are immersed boundary method (IBM) [6, 7], immersed interface method (IIM) [1, 8], ghost fluid method (GFM) [9], matched interface and boundary method (MIBM) [10–12], the method based on the integral equations approach [13], and finite element methods [14–17].

Recently, wavelet analysis has got much popularity in the approximation theory. Different wavelets and approximating functions are introduced for approximation purpose. Wavelets have simple and fast algorithms, which result better approximation. Among all these wavelets, Haar wavelet has got great importance due to their simplicity and applications. Haar wavelet contains piecewise constant box functions. The Haar wavelet collocation method (HWCM) got attention of many authors due their simple nature, properties of orthogonality, and compact support. The Haar wavelet contains piecewise constant functions; therefore, complicated models can be approximated very easily using these wavelets. Besides, several types of boundary conditions including local and nonlocal conditions can be utilized. Various applications of HWCM in the approximation theory can be seen in [18–27]. Some of the recent work using Haar wavelets is given in [28–36].

In this article, a new approach based on Haar wavelet and finite difference method is developed for the numerical solution of advection-diffusion-reaction type elliptic and parabolic interface models.

The article is organized as follow. In Section 3, definition of the Haar wavelet and their integrals are presented. In Section 4, construction of the newly proposed numerical method based on Haar wavelet and FDM is given. The convergence and stability analysis of the proposed numerical method are discussed in Sections 5 and 6. In Section 7, numerical validation of the method is given. In the last section, conclusion is presented.

2. Governing Models

2.1. Elliptic Interface Model

Consider the following forms of linear and nonlinear elliptic interface models:

(1)

(2)

At the interface point η = ζ, the interval I = [a, b] is divided into two subintervals I₁ = [a, ζ] and I₂ = [ζ, b]. The functions involved in Equations (1) and (2) are of the form

(3)

The Dirichlet boundary conditions at boundary points η = a and η = b are given by

(4)

The following interface conditions are considered at the interface point η = ζ:

(5)

(6)

where f₁(η), α₁(η) > 0, β₁(η) > 0, and σ₁(η) ≥ 0 and f₂(η), α₂(η) > 0, β₂(η) > 0, and σ₂(η) ≥ 0 are known functions defined on I₁ and I₂, respectively.

2.2. Parabolic Interface Model

The following forms of linear and nonlinear parabolic interface models are considered:

(7)

(8)

The interface point η = ζ divides the interval I into two subintervals I₁ and I₂, where I, I₁, and I₂ are the same as given in the above elliptic problem. The functions involved in Equations (7) and (8) are of the following form:

(9)

Subject to the following initial and Dirichlet boundary conditions points η = a and η = b,

(10)

The following interface conditions are considered at the interface point η = ζ:

(11)

(12)

The functions f₁(η), α₁(η) > 0, β₁(η) > 0, and σ₁(η) ≥ 0 and f₂(η), α₂(η) > 0, β₂(η) > 0, and σ₂(η) ≥ 0 are smooth functions defined on I₁ and I₂, respectively.

3. Haar Wavelets

The i^th wavelet of the Haar family over [0, 1) is defined as [37]

(13)

where

(14)

In the above equations, m and k are integers such that m = 2^j, j = 0, 1, ⋯, and k = 0, 1, ⋯, m − 1. The level of the resolution of the Haar wavelet and the translation parameter are represented by the integers j and k, respectively. For approximation purposes, we consider a maximal value J of the integer j. The integer J is then called maximal level of resolution. We also define

. The equation i = m + k + 1 shows the relation among i, m, and k. The minimal and maximal values of i can be obtained from the equation i = m + k + 1. If m = 1, k = 0, then minimal value is i = 2 and the maximal value is

. For i = 1, we get h₁(η), which is known as scaling function for Haar wavelet family and is defined as

(15)

Any square integrable function f(η) over the interval (0, 1) can be expressed as infinite sum of functions of the Haar wavelet family as

(16)

For approximation purpose, the above series is truncated to a finite sum in the following manner:

(17)

where

is the maximal resolution defined above. All other members of the Haar family can be obtained from Equation (13) by the process of dilation and translation. The following notations are introduced for Haar integrals:

(18)

These integrals can be calculated utilizing Equation (13) and are given below.

(19)

where i = 2, 3, ⋯. For i = 1, we have

(20)

4. Numerical Procedure

In this section, formulation of numerical technique both for elliptic and parabolic advection-diffusion-reaction type interface models is discussed. The interval of study is considered to be [a, b] = [0, 1].

4.1. HWCM for Elliptic Model with Single Interface

In this technique, the higher-order spatial derivative is approximated by truncated Haar series; the approximate expressions for the lower order derivatives and for the unknown function are calculated by integration process. The details of the procedure are given below:

(21)

Integrating Equation (21), from η to ζ, we get

(22)

Again integrating from 0 to η, we have

(23)

Similarly, we can approximate the second function v₂(η) over the second subinterval I₂ = [ζ, 1] as follows:

(24)

Integrating Equation (24), we get the expressions v₂(η) and v_2η(η) as follows:

(25)

(26)

After substituting the Haar expression, Equations (5) and (6) become

(27)

(28)

The remaining procedure will be explained separately for both linear and nonlinear cases.

4.1.1. Linear Case

Substituting the values of v₁(η), v_1η(η), and v_1ηη(η) in Equation (1) and simplifying, we have

(29)

Similarly, substituting the values of v₂(η), v_2η(η), and v_2ηη(η) in Equation (1), we get

(30)

The following discrete points are used for single interface problem:

(31)

After discretization, we get the subsequent forms of Equations (29) and (30):

(32)

(33)

Equations (32) and (33) combined with Equations (27) and (28) give a linear system of

equations with

unknowns

, v_1η(ζ), and v_2η(ζ). We can write the above system in matrix form as follows:

(34)

where

(35)

(36)

(37)

The entries of the matrix S are given by

(38)

Finally, we obtained the following entries of the matrix Q:

(39)

Equation (34) can be solved by any linear solver in order to get the unknown Haar coefficients. Now utilizing these unknown Haar coefficients in Equations (23) and (26), we can easily obtain the approximate solution of the problem.

4.1.2. Nonlinear Case

In nonlinear case, first we linearize Equation (2) by using the following quasi-Newton linearization technique [38]:

(40)

After linearizing Equation (2), substituting the Haar approximations for v and its derivatives and then discretizing, we get

(41)

(42)

Equations (41) and (42) along with Equations (27) and (28) give a linear system of size with the unknown Haar coefficients and the values v_1η(ζ) and v_2η(ζ). The above linear system can be solved by using any linear solver.

4.2. HWCM for Parabolic Model with Single Interface

This is a parabolic interface model. The time derivative is approximated by using the following forward difference formula:

(43)

Now approximating the highest order spatial derivative v_1ηη(η, t) over the first subinterval I₁ = [0, ζ] by truncated Haar series,

(44)

Integrating Equation (44), we get the approximate expressions for v_1η(η, t) and v₁(η, t) as follows:

(45)

(46)

Similarly, approximating v_2ηη(η, t) over the second subinterval I₂ = [ζ, 1] as follows,

(47)

Integrating Equation (47), we obtain the approximate expressions for v_2η(η, t) and v₂(η, t) as follows:

(48)

(49)

Substituting the values of v₁(ζ, t), v₂(ζ, t), α₁(ζ, t), α₂(ζ, t), β₁(ζ, t), and β₂(ζ, t) in Equations (11) and (12), the interface conditions imply that

(50)

(51)

The remaining procedure is explained for linear and nonlinear cases separately in the upcoming section.

4.2.1. Linear Case

Substituting Equations (43) and (46) in Equation (7) and simplifying, we have

(52)

Similarly by using Equation (43) and Equations (47)–(49) in Equation (7) and simplifying, we have

(53)

The following nodes are defined for interface conditions at η = ζ:

(54)

Discretizing, we get the following systems of linear equations:

(55)

(56)

Equations (55) and (56) combined with Equations (50) and (51) give a linear system of size

with

unknown coefficients

, v_1η(ζ, t), and v_2η(ζ, t). In matrix form, the above system can be written as

(57)

where S and Q are given in Equations (35) and (37), respectively, and

(58)

The entries of the matrix S are given by

(59)

Finally, we can write the elements of the matrix Q as follows:

(60)

From Equation (57), we get

(61)

Solving system (61) by any linear solver, we obtained the values of the unknown Haar coefficients , , v_1η(ζ, t), and v_2η(ζ, t). By utilizing these unknown Haar coefficients in Equations (46) and (49), we can easily obtain the approximate solution of the problem.

4.2.2. Nonlinear Case

In nonlinear interface models first, we linearize problem (8) by using the following quasi-Newton Linearization technique [38]:

(62)

Now substituting the approximate expressions for higher-order derivatives, unknown function v, and temporal derivative in the linearized equation and discretizing, we obtain the following systems of equations.

(63)

(64)

Equations (63) and (64) together with Equations (50) and (51) give a linear system of size . Solving the system by any linear solver, we can get the unknown Haar coefficients. Using these unknown Haar coefficients, we can easily obtain the approximate solution.

5. Convergence

Lemma 1 [39]. Assume that v ∈ C²(−∞, ∞) with |v^′| ≤ K, ∀η ∈ (a, b), K > 0, and , and then, |λ_i| ≤ K2^{−(3j − 2)/2}.

Lemma 2 [39]. Let v ∈ C²(−∞, ∞) be continuous on (a, b). Then, the error norm at J^th level satisfies

(65)

where |v^′| ≤ K, ∀η ∈ (a, b) and K > 0, and

is a positive real number related to the J^th level resolution of the wavelet given by

Theorem 3. If v(η) is the exact solution and is the approximate solution of Equation (1), the error norm at J^th level resolution is given by

(66)

Proof. The error estimate of the proposed method at J^th level resolution is given as

(67)

which implies that

(68)

where

. Now, Equation (68) can be written as

(69)

Now, using Lemmas 1 and 2, inequality (69) can be written as

(70)

in which on further simplification and taking squire root, we get

(71)

It is concluded that error norm is inversely proportional to level of the Haar wavelet resolution J. Hence, the error of the HWCM decreases as J increases, i.e.,

(72)

Theorem 4. If v(η, t_p) is the exact solution and is the approximate solution of Equation (7) and if p = 0, 1, 2 ⋯ P, where P is a positive integer, then the error norm at J-th level resolution is given by

(73)

Proof. For p = 0, 1, 2 ⋯ P,

(74)

see Theorem 3.

For time derivatives, we have used first-order finite difference approximation in Equation (43), so

(75)

Hence,

(76)

6. Stability

In this section, we study the computational stability of the proposed technique. For this purpose, we have observed the maximum eigenvalues of matrix S at every time step, which represent the corresponding Haar weights. All the maximum eigenvalues of matrix S stay away from zero (see Figure 1), and this leads to a sufficient condition for the proposed technique to be stable. We can write Equations (1) and (2) in the form

(77)

where

is the operator.

(78)

(79)

(80)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The stability analysis of the proposed method for different examples at N = 64, Δt = 0.01/32, t = 1, a = 0, and b = 1.

Here, t is the next time level and t₀ is the previous time level. After introducing the Haar wavelet, Equation (80) can be written as

(81)

where

is the weight Haar matrix for operator

and I is the identity matrix. If the maximum eigenvalue of

is λ, then from Equation (81), the stability condition will be [23, 24]

(82)

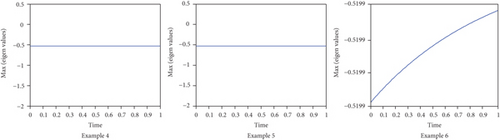
Here, δt is the time step which is always positive, i.e., δt > 0. We have discussed the following three different cases related to Equation (82).

Case 1. If λ = 0, then Equation (82) gives

(83)

which is identically satisfied.

Case 2. If λ < 0, i.e., λ = −ξ², where ξ ∈ ℝ, then Equation (82) gives

(84)

The inequality holds because the denominator is greater than the numerator.

Case 3. If λ > 0, i.e., λ = ξ², then Equation (82) gives

(85)

which is does not holds as the denominator is smaller than the numerator.

Thus, Equation (82) is valid for Cases 1 and 2, which are verified computationally in Figure 1.

Furthermore, examples (1) and (2) are linear and nonlinear steady problems. Therefore, we have found their eigenvalues and listed them in Tables 1 and 2. From the tables, we can observe that all the eigenvalues lie on the left half of the complex plane. Therefore, systems (34) and (42) are stable, because we have a result that state that “A system AX = B will be stable if and only if the real part of all eigenvalues of the matrix A lie on the left half of the complex plane” [40].

Table 1. Analysis of errors for Example 1.

J	N	E_c(N) proposed technique	CPU time in sec	Eigenvalues	N	IIM	R_c(N)
2	16	2.7551 × 10⁻⁴	0.454092	-1.7826	20	6.1 × 10⁻³	1.8275
3	32	7.3171 × 10⁻⁵	0.492690	-2.1337	40	1.4 × 10⁻³	1.9128
4	64	1.8859 × 10⁻⁵	0.582250	-2.4974	80	3.2779 × 10⁻⁴	1.9560
5	128	4.7873 × 10⁻⁶	1.096531	-2.8811	160	7.9702 × 10⁻⁵	1.9780
6	256	1.2060 × 10⁻⁶	2.806679	-3.2862	320	1.9644 × 10⁻⁵	1.9890

Table 2. Analysis of errors for Example 2.

J	N	E_c(N) proposed technique	CUP time in sec	Eigenvalues	No. of iterations	R_c(N)
1	8	7.1012 × 10⁻⁴	0.009185	-3.2264	4
2	16	1.9064 × 10⁻⁴	0.031301	-3.2264	4	1.8972
3	32	4.9514 × 10⁻⁵	0.097082	-3.3663	4	1.9449
4	64	1.2626 × 10⁻⁵	0.392260	-3.2264	4	1.9714
5	128	3.1885 × 10⁻⁶	1.514269	-3.3663	4	1.9854
6	256	8.0118 × 10⁻⁷	6.019626	-3.3577	4	1.9927
7	512	2.0081 × 10⁻⁷	23.903250	-3.2264	4	1.9962

7. Examples and Discussion

This section is devoted to apply HWCM on some benchmark test models. These problems include parabolic and elliptic advection-diffusion-reaction type linear and nonlinear models with single interface conditions. In nonlinear test models, the quasi-Newton linearization technique given in [41] is utilized. The initial guess for nonlinear elliptic problem is taken 0.1 and stopped the iterations when the criterion of convergence 10⁻⁵ is satisfied. For calculating experimental convergence rates, we have used the following formula:

(86)

where

is the maximum absolute error at

collocation points.

Example 1. Consider the following initial-boundary value linear elliptic interface model equation [41]:

(87)

with boundary conditions:

(88)

and interface conditions:

(89)

The exact solution of the test problem is given by

(90)

Example 2. Consider the following initial-boundary value nonlinear elliptic interface problem:

(91)

with boundary conditions:

(92)

and interface conditions:

(93)

The exact solution of the test problem is given by

(94)

Example 3. Suppose the following initial-boundary value linear parabolic problem with single interface conditions [41]:

(95)

subject to the following initial and boundary conditions:

(96)

and interface conditions:

(97)

The exact solution of the test problem is given by

(98)

Example 4. Consider another initial-boundary value linear parabolic interface problem [41]:

(99)

with the following initial and boundary conditions:

(100)

and interface conditions:

(101)

The exact solution of the test problem is given by

(102)

Example 5. Consider another linear parabolic interface model:

(103)

with the subsequent initial conditions and boundary conditions:

(104)

and interface conditions:

(105)

The exact solution of the test problem is given by

(106)

Example 6. Consider the following nonlinear parabolic interface model:

(107)

subject to the following initial and boundary conditions:

(108)

and interface conditions:

(109)

The exact solution of the test problem is given by

(110)

In this section, some numerical experiments comprising linear and nonlinear elliptic and parabolic advection-diffusion-reaction type interface models have been carried out, in order to check the efficiency and better accuracy of the newly proposed numerical technique for these types of models. First, we have discussed elliptic interface models and then parabolic interface models.

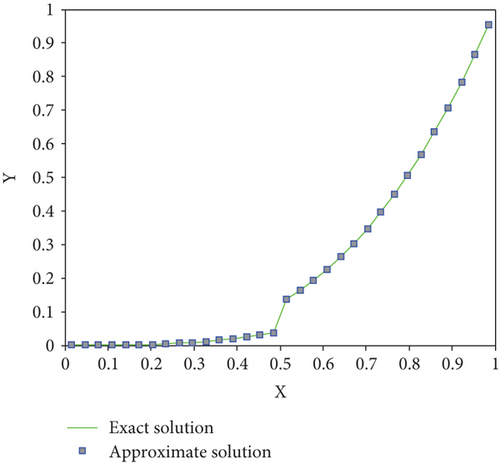
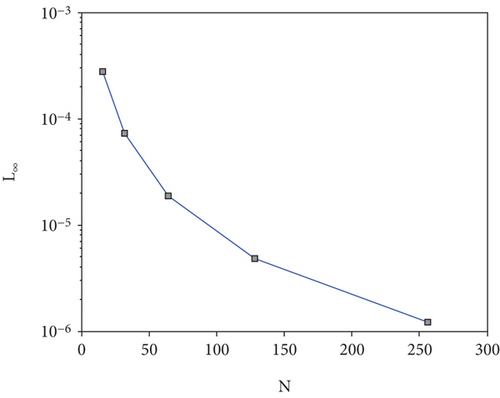
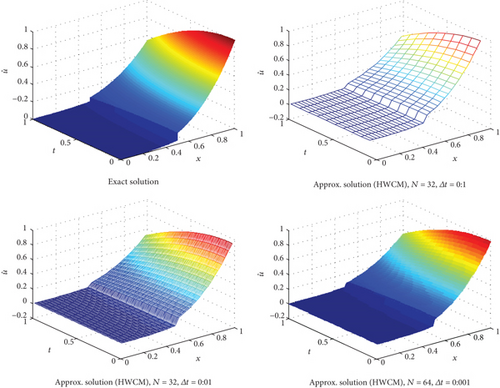
In the first two linear and nonlinear elliptic interface models, the errors are decreased to 10^-6 and 10^-7 even for small number of grid points. It is worth mentioning that more accurate numerical results can be obtained if we increase the number grid points. In Table 1, the absolute errors for distinct collocation points are listed. The graph given in Figure 2 also demonstrates that the proposed technique captures the discontinuity very well, where the other methods failed to do so. The computational rate of convergence of the proposed method is approaching to 2, which is theoretically confirmed by Majak et al. [42, 43]. The obtained results are compared with the immersed interface method from literature. The comparability shows that the newly proposed technique is efficient and more accurate for elliptic type interface models than the existing methods. The newly proposed numerical technique is also tested on advection-diffusion-reaction type parabolic interface models, comprising of three linear and one nonlinear models. The obtained point wise absolute errors are mentioned in Tables 3–6. The numerical results are also demonstrated through 3D visualization of the graphs listed in Figures 3 and 4. From the aforementioned figures, it is clear that the newly proposed technique handled the jump discontinuity at 0.5 and 0.7 very well. The approximate results are compared with the immersed interface method from the existing literature. The comparability shows that the proposed technique has better accuracy with simple implementation.

Table 3. Analysis of errors for Example 3.

J	N	Δt	E_c(N) proposed technique	CPU time in sec	N	IIM
1	8	1/8	1.8394 × 10⁻³	0.279452	8	3.7 × 10⁻²
2	16	1/16	7.7251 × 10⁻⁴	0.345287	16	7.1 × 10⁻³
3	32	1/32	3.5115 × 10⁻⁴	0.612788	32	1.5 × 10⁻³
4	64	1/64	1.6775 × 10⁻⁴	2.966826	64	3.0 × 10⁻⁴
5	128	1/128	8.1976 × 10⁻⁵	20.057056	128	1.0 × 10⁻⁴

Table 4. Analysis of errors for Example 4.

J	N	Δt	E_c(N) proposed technique	CPU time in sec	N	IIM
1	8	0.1/8	1.5 × 10⁻³	0.395921	8	1.02 × 10⁻²
2	16	0.1/16	7.5054 × 10⁻⁴	0.748104	16	2.4 × 10⁻³
3	32	0.1/32	3.7709 × 10⁻⁴	3.148897	32	6.0 × 10⁻⁴
4	64	0.1/64	1.8867 × 10⁻⁴	25.324517	64	1.0 × 10⁻⁴
5	128	0.1/128	9.4324 × 10⁻⁵	194.237104	128	1.0 × 10⁻⁴

Table 5. Analysis of errors for Example 5.

J	N	Δt	E_c(N) proposed technique	CPU time in sec	N	IIM
2	16	0.001/16	3.6548 × 10⁻⁶	34.662755	20	2.9061 × 10⁻⁵
3	32	0.001/32	1.8282 × 10⁻⁶	272.116930	40	6.6497 × 10⁻⁶
4	64	0.001/64	9.1465 × 10⁻⁷	2460.769702	80	1.6343 × 10⁻⁶
5	128	0.001/128	4.5753 × 10⁻⁷	35500.767379	160	4.0802 × 10⁻⁷

Table 6. Analysis of errors Example 6.

J	N	Δt	E_c(N) proposed technique	CPU time in sec
1	8	0.1/8	6.0232 × 10⁻⁴	0.157302
2	16	0.1/16	1.4666 × 10⁻⁴	1.147091
3	32	0.1/32	3.3345 × 10⁻⁵	11.147277
4	64	0.1/64	6.8252 × 10⁻⁶	81.104287
5	128	0.1/128	1.3904 × 10⁻⁶	588.111313

8. Conclusion

In this article, Haar wavelet collocation technique is utilized to solve interface models comprising advection-diffusion-reaction type elliptic and parabolic models with discontinuous coefficients. The newly proposed numerical technique is applicable to both linear and nonlinear interface models. The errors are decreased up to 10^-6 and 10^-7 for small number of collocation points, which is supposed to be better accuracy for practical problems. The 3D graphs of the estimated and exact solutions also demonstrate that the newly proposed technique handle the jump discontinuity very well, while the other existing techniques failed to capture it. The stability and convergence of the said numerical technique are also proved in the convergence and stability sections, which made the method more powerful. The obtained results are compared with the immersed interface method. The comparability shows that the newly proposed technique is efficient and has better accuracy than immersed interface method.

Conflicts of Interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

Open Research

Data Availability

No data were used to support this study.

References

1 Li Z. and Ito K., The immersed interface method: numerical solutions of PDEs involving interfaces and irregular domains, Society for Industrial and Applied Mathematics, (SIAM). (2006) 33, 3665–3673.
Google Scholar
2 Li Z. and Ito K., Maximum principle preserving schemes for interface problems with discontinuous coefficients, SIAM Journal of Scientific Computing. (2001) 23, 1225–1242.
10.1137/S1064827500370160
Web of Science® Google Scholar
3 Li Z. and Soni B., Fast and accurate numerical approaches for Stefan problems and crystal growth, Numerical Heat Transfer, Part B: Fundamentals. (1999) 35, 461–484.
10.1080/104077999275848
CAS Web of Science® Google Scholar
4 Bell J. B., Colella P., and Glaz H. M., A second-order projection method for the incompressible Navier-Stokes equations, Journal of Computational Physics. (1989) 85, no. 2, 257–283, https://doi.org/10.1016/0021-9991(89)90151-4, 2-s2.0-0001608079.
10.1016/0021-9991(89)90151-4
Web of Science® Google Scholar
5 Liu X. D. and Sideris T., Convergence of the ghost fluid method for elliptic equations with interfaces, Mathematics of Computation. (2003) 72, no. 244, 1731–1747, https://doi.org/10.1090/S0025-5718-03-01525-4, 2-s2.0-0141872535.
10.1090/S0025-5718-03-01525-4
Web of Science® Google Scholar
6 Peskin C. S., Numerical analysis of blood flow in the heart, Journal of Computational Physics. (1977) 3, no. 25, 220–252.
10.1016/0021-9991(77)90100-0
Google Scholar
7 Peskin C. S., The Immersed Boundary Method. Acta Numerica, 2002, 11, Cambridge University Press.
Google Scholar
8 Leveque J. R. and Li Z., The immersed interface method for elliptic equations with discontinuous coefficients and singular sources, SIAM Journal on Numerical Analysis. (1994) 31, no. 4, 1019–1044, https://doi.org/10.1137/0731054, 2-s2.0-0028485385.
10.1137/0731054
Web of Science® Google Scholar
9 Fedkiw R. P., Aslam T., Merriman B., and Osher S., A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method), Journal of Computational Physics. (1999) 152, no. 2, 457–492, https://doi.org/10.1006/jcph.1999.6236, 2-s2.0-0346837922.
10.1006/jcph.1999.6236
CAS Web of Science® Google Scholar
10 Yu S., Zhou Y., and Wei G. W., Matched interface and boundary (MIB) method for elliptic problems with sharp- edged interfaces, Journal of Computational Physics. (2007) 224, no. 2, 729–756, https://doi.org/10.1016/j.jcp.2006.10.030, 2-s2.0-34248596727.
10.1016/j.jcp.2006.10.030
Web of Science® Google Scholar
11 Zhou Y. C., Liu J., and Harry D. L., A matched interface and boundary method for solving multi-flow Navier-Stokes equations with applications to geodynamics, Journal of Computational Physics. (2012) 231, no. 1, 223–242, https://doi.org/10.1016/j.jcp.2011.09.010, 2-s2.0-80054866166.
10.1016/j.jcp.2011.09.010
Web of Science® Google Scholar
12 Zhou Y., Zhao S., Feig M., and Wei G. W., High order matched interface and boundary method for elliptic equations with discontinuous coefficients and singular sources, Journal of Computational Physics. (2006) 1, no. 213, 1–30, https://doi.org/10.1016/j.jcp.2005.07.022, 2-s2.0-31744448526.
10.1016/j.jcp.2005.07.022
CAS Google Scholar
13 Mayo A., The fast solution of Poisson’s and the biharmonic equations on irregular regions, SIAM Journal on Numerical Analysis. (1984) 21, no. 2, 285–299, https://doi.org/10.1137/0721021, 2-s2.0-0021417514.
10.1137/0721021
Web of Science® Google Scholar
14 Feng W., He X., Lin Y., and Zhang X., Immersed finite element method for interface problems with algebraic multigrid solver, Communications in Computational Physics. (2014) 15, no. 4, 1045–1067, https://doi.org/10.4208/cicp.150313.171013s, 2-s2.0-84894116332.
10.4208/cicp.150313.171013s
Web of Science® Google Scholar
15 Gong Y., Li B., and Li Z., Immersed-interface finite-element methods for elliptic interface problems with nonhomogeneous jump conditions, SIAM Journal on Numerical Analysis. (2008) 46, no. 1, 472–495, https://doi.org/10.1137/060666482, 2-s2.0-55549138751.
10.1137/060666482
Web of Science® Google Scholar
16 Yang Q. and Zhang X., Discontinuous Galerkin immersed finite element methods for parabolic interface problems, Journal of Computational and Applied Mathematics. (2016) 299, 127–139, https://doi.org/10.1016/j.cam.2015.11.020, 2-s2.0-84956629901.
10.1016/j.cam.2015.11.020
Web of Science® Google Scholar
17 Lehrenfeld C. and Reusken A., Analysis of a high-order unfitted finite element method for elliptic interface problems, IMA Journal of Numerical Analysis. (2017) 38, 1351–1387, https://doi.org/10.1093/imanum/drx041, 2-s2.0-85054526227.
10.1093/imanum/drx041
Web of Science® Google Scholar
18 Hsiao C. H. and Wang W. J., Haar wavelet approach to nonlinear stiff systems, Mathematics and Computers in Simulation. (2001) 57, no. 6, 347–353, https://doi.org/10.1016/S0378-4754(01)00275-0, 2-s2.0-0034857840.
10.1016/S0378-4754(01)00275-0
Web of Science® Google Scholar
19 Hsiao C. H., Haar wavelet approach to linear stiff systems, Mathematics and Computers in Simulation. (2004) 64, no. 5, 561–567, https://doi.org/10.1016/j.matcom.2003.11.011, 2-s2.0-1242276106.
10.1016/j.matcom.2003.11.011
Web of Science® Google Scholar
20 Lepik U., Numerical solution of differential equations using Haar wavelets, Mathematics and Computers in Simulation. (2005) 68, no. 2, 127–143, https://doi.org/10.1016/j.matcom.2004.10.005, 2-s2.0-17444421176.
10.1016/j.matcom.2004.10.005
Web of Science® Google Scholar
21 Lepik U., Numerical solution of evolution equations by the Haar wavelet method, Applied Mathematics and Computation. (2007) 185, 695–704, https://doi.org/10.1016/j.amc.2006.07.077, 2-s2.0-33846929829.
10.1016/j.amc.2006.07.077
Web of Science® Google Scholar
22 Ahsan M., Islam S., and Hussain I., Haar wavelets multi-resolution collocation analysis of unsteady inverse heat problems, Inverse Problems in Science and Engineering. (2019) 27, no. 11, 1498–1520, https://doi.org/10.1080/17415977.2018.1481405, 2-s2.0-85048748471.
10.1080/17415977.2018.1481405
Web of Science® Google Scholar
23 Islam S., Ahsan M., and Hussain I., A multi-resolution collocation procedure for time-dependent inverse heat problems, International Journal of Thermal Sciiences. (2018) 128, 160–174, https://doi.org/10.1016/j.ijthermalsci.2018.01.001, 2-s2.0-85042066402.
10.1016/j.ijthermalsci.2018.01.001
Web of Science® Google Scholar
24 Ahsan M., Ahmad I., Ahmad M., and Hussian I., A numerical Haar wavelet-finite difference hybrid method for linear and non-linear Schrdinger equation, Mathematics and Computer in Simulation. (2019) 165, 13–25, https://doi.org/10.1016/j.matcom.2019.02.011, 2-s2.0-85062963358.
10.1016/j.matcom.2019.02.011
Web of Science® Google Scholar
25 Amin R., Shah K., Asif M., Khan I., and Ullah F., An efficient algorithm for numerical solution of fractional integro-differential equations via Haar wavelet, Journal of Computational and Applied Mathematics. (2020) 73, article 113028, 1–17, https://doi.org/10.1016/j.cam.2020.113028.
10.1016/j.cam.2020.113028
Google Scholar
26 Aziz I., Islam S., and Asif M., Haar wavelet collocation method for three-dimensional elliptic partial differential equations, Computers and Mathematics with Applications. (2017) 73, no. 9, 2023–2034, https://doi.org/10.1016/j.camwa.2017.02.034, 2-s2.0-85015660640.
10.1016/j.camwa.2017.02.034
Web of Science® Google Scholar
27 Majak J., Karjust K., Eermea M., Kurnitskia J., and Shvartsman B. S., New higher order Haar wavelet method: application to FGM structures, Composite Structures. (2018) 201, 72–78, https://doi.org/10.1016/j.compstruct.2018.06.013, 2-s2.0-85048279527.
10.1016/j.compstruct.2018.06.013
Web of Science® Google Scholar
28 Zhi S., Yan-Hua X., and Jun-Ping Z., Haar wavelets method for solving Poisson equations with jump conditions in irregular domain, Advances in Computational Mathematics. (2016) 42, no. 4, 995–1012, https://doi.org/10.1007/s10444-015-9450-z, 2-s2.0-84953438763.
10.1007/s10444-015-9450-z
Web of Science® Google Scholar
29 Oruc O., An efficient meshfree method based on Pascal polynomials and multiple-scale approach for numerical solution of 2-D and 3-D second order elliptic interface problems, Journal of Computational Physics. (2021) 428, article 110070, https://doi.org/10.1016/j.jcp.2020.110070.
10.1016/j.jcp.2020.110070
Web of Science® Google Scholar
30 Bulut F., Oruc O., and Esen A., Higher order Haar wavelet method integrated with strang splitting for solving regularized long wave equation, Mathematics and Computers in Simulation. (2022) 197, 277–290, https://doi.org/10.1016/j.matcom.2022.02.006.
10.1016/j.matcom.2022.02.006
Web of Science® Google Scholar
31 Oruc O., Esen A., and Bulut F., Numerical investigation of dynamic Euler-Bernoulli equation via 3-scale Haar wavelet collocation method, Hacettepe Journal of Mathematics and Statistics. (2021) 50, 159–179.
10.15672/hujms.610834
Web of Science® Google Scholar
32 Oruc O., Bulut F., and Esen A., Numerical solution of the KdV equation by Haar wavelet method, Pranama Journal of Physics. (2016) 87, no. 6, https://doi.org/10.1007/s12043-016-1286-7.
10.1007/s12043-016-1286-7
Google Scholar
33 Oruc O., A non-uniform Haar wavelet method for numerically solving two-dimensional convection-dominated equations and two-dimensional near singular elliptic equations, Computers and Mathematics with Applications. (2019) 7, no. 77, 1799–1820, https://doi.org/10.1016/j.camwa.2018.11.018, 2-s2.0-85057505772.
10.1016/j.camwa.2018.11.018
Google Scholar
34 Ratas M., Majak J., and Salupere A., Solving nonlinear boundary value problems using the higher order Haar wavelet method, Mathematics. (2021) 9, no. 21, https://doi.org/10.3390/math9212809.
10.3390/math9212809
Google Scholar
35 Mehrparvar M., Majak J., Karjust K., and Arda M., Free vibration analysis of tapered Timoshenko beam with higher order Haar wavelet method, Proceedings of the Estonian Academy of Sciences. (2022) 1, no. 71, 77–83.
10.3176/proc.2022.1.07
Google Scholar
36 Ratas M., Salupere A., and Majak J., Solving nonlinear PDEs using the higher order Haar wavelet method on nonuniform and adaptive grids, Mathematical Modelling and Analysis. (2021) 1, no. 26, 147–169.
10.3846/mma.2021.12920
Google Scholar
37 Asif M., Haider N., Mdallal Q. A., and Khan I., A Haar wavelet collocation approach for solving one and two-dimensional second-order linear and nonlinear hyperbolic telegraph equations, Numerical Methods for Partial Differential Equations. (2020) 36, no. 6, 1962–1981, https://doi.org/10.1002/num.22512.
10.1002/num.22512
Web of Science® Google Scholar
38 Bellman R. E. and Kalaba R. E., Quasilinearization and Nonlinear Boundary Value Problems, 1965, American, Elsevier, New York.
Google Scholar
39 Kumar M. and Pandit S., A composite numerical scheme for the numerical simulation of coupled Burgers equation, Computer Physics Communications. (2014) 185, no. 3, 809–817, https://doi.org/10.1016/j.cpc.2013.11.012, 2-s2.0-84893814338.
10.1016/j.cpc.2013.11.012
CAS Web of Science® Google Scholar
40 Zada A., Asymptotic Behavior of Solutions for a Class of Semi-Linear Differential Systems in Finite Dimensional Spaces, 2010, Abdus Salam School of Mathematical Sciences GC University Lahore, Pakistan.
Google Scholar
41 Aljahdaly N., The immersed interface method for elliptic and parabolic problems with discontinuous coefficients, American Journal of Numerical Analysis. (2014) 2, 152–166.
Google Scholar
42 Majak J., Shvartsman B., Kirs M., Pohlak M., and Herranan H., Convergence theorem for the Haar wavelet based discretization method, Composite Structures. (2015) 126, 227–232, https://doi.org/10.1016/j.compstruct.2015.02.050, 2-s2.0-84924854821.
10.1016/j.compstruct.2015.02.050
Web of Science® Google Scholar
43 Majak J., Shvartsman B., Karjust K., Mikola M., Haavajoe A., and Pohlak M., On the accuracy of the Haar wavelet discretization method, Composits B. (2015) 80, 321–327, https://doi.org/10.1016/j.compositesb.2015.06.008, 2-s2.0-84933045258.
10.1016/j.compositesb.2015.06.008
Web of Science® Google Scholar

Citing Literature

All articles

A Modified Algorithm Based on Haar Wavelets for the Numerical Simulation of Interface Models

Abstract

1. Introduction

2. Governing Models

2.1. Elliptic Interface Model

2.2. Parabolic Interface Model

3. Haar Wavelets

4. Numerical Procedure

4.1. HWCM for Elliptic Model with Single Interface

4.1.1. Linear Case

4.1.2. Nonlinear Case

4.2. HWCM for Parabolic Model with Single Interface

4.2.1. Linear Case

4.2.2. Nonlinear Case

5. Convergence

6. Stability

7. Examples and Discussion

8. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Modified Algorithm Based on Haar Wavelets for the Numerical Simulation of Interface Models

Abstract

1. Introduction

2. Governing Models

2.1. Elliptic Interface Model

2.2. Parabolic Interface Model

3. Haar Wavelets

4. Numerical Procedure

4.1. HWCM for Elliptic Model with Single Interface

4.1.1. Linear Case

4.1.2. Nonlinear Case

4.2. HWCM for Parabolic Model with Single Interface

4.2.1. Linear Case

4.2.2. Nonlinear Case

5. Convergence

6. Stability

7. Examples and Discussion

8. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information