Distance based topological indices (TIs) play a vital role in the study of various structural and chemical aspects for the molecular graphs. The first distance-based TI is used to find the boiling point of paraffin. The connection distance (CD) index is a latest developed TI that is defined as the sum of all the products of distances between pair of vertices with the sum of their respective connection numbers . In this paper, we computed CD indices of the different derived graphs (subdivision graph S(G), vertex-semitotal graph R(G), edge-semitotal graph Q(G) and total graph T(G) obtained from the graph G under various operations of subdivision in the form of degree distance (DD) and CD indices of the basic graphs including some other algebraic expressions.

1. Introduction

A topological index (TI) is a function from the set of simple graphs to the set of real numbers that assigns a unique number to each graph G belonging to . More importantly, it remains constant for the isomorphic graphs that is if G₁≅G₂ then TI(G₁) = TI(G₂). Many topological indices have been introduced for the molecular graphs in the chemical graph theory to predict the certain structural and chemical properties such as vaporization, freezing point, boiling point, volume, density, weight and physicochemical properties of chemical bound [1]. Moreover, most rapidly growing fields of science such as chemistry, mathematics and information sciences provide effective research achievements in the last decade and one of the combinations of these subjects is called by cheminformatics which studies two relationships techniques quantitative structures property relationships (QSPR) and quantitative structure activity relationships (QSAR) for the different molecular structures, see [2–4].

Wiener (1947) [5] was first scientist who laid the foundation of chemical graph theory. In chemical graph theory, atoms and bounds are taken as vertices and edges. He discovered through his research work that there is a close correlation between the sums of the distances among pairs of vertices and the boiling points of paraffine. Almost, after passage of three quarters of the 20th century (1972) [6] discovered degree-based indices, (First and Second Zagreb indices), which were utilized to calculate the total π-electron energy of molecules. After these developments, many TIs were introduced which are found to be highly useful for the study of different physicochemical properties of chemical compounds. Degree distance index [7] and Gutman index [8] are the most important distance-degree based TIs. Ali and Trinajstic [9] (2018) restudied the first Zagreb connection index (ZC₁), second Zagreb connection index (ZC₂) and the modified first Zagreb connection index . Recently, Javaid et al. [10] defined a new distance-based TI called by connection distance index as the sum of all the products of distances between pair of vertices with the sum of their respective connection numbers.

Yan et al. [11] defined the new graphs called as subdivided graph S(G), vertex-total graph R(G), edge-total graph Q(G) and total graph T(G) with the help of the subdivision-related operations S, R, Q and T respectively. Xu et al. [12] have determined the degree distance index of the derived graphs. Bahadur et al. [13] have determined Gutman index of derived graphs. In particular, on different families of graphs for the result about degree based TIs, see [14, 15] (line graph), [16, 17] (sum-graphs), [18, 19] (derived graphs), [20, 21] (extremal graphs), [22, 23] (generalized sum graphs), [24] (nanotube) and distance based TIs, see [25–27].

In this paper, firstly, we have determined the exact values of connection numbers of old (black) vertices and new (white) for derived graph S(G) and bounded values of connection numbers for {C₃, C₄}− graph of R(G), Q(G) and T(G) were determined. Then, finally, bounded and exact values of connection distance (CD) of derived graphs {S(G), R(G), Q(G), T(G)} are determined by Theorems and Corollaries. Section 2 consists of applications, Section 3 comprises some related definitions, Section 4 covers the main results of connection distance index (CD) for the derived graphs and Section 5 sum up our findings.

2. Applications

From the last two decades, the worth investing problem of finding out the physicochemical properties of the molecular structures is attracting the attention of chemists and mathematicians continuously. The TIs have been used to: predict the solubility of fullerene C₆₀ [28], find the ionic liquids densities [1], optimize QSPR models (Simplex optimisation of generalized TIs) [29], manufacture the anticancer drugs [30, 31], calculate molecular van der Waals areas or volumes [32] and measure the vaporisation, sublimation, formation & combustion for the monocarboxylic acids (C₂H₄O₂ − C₂₀H₄₀O₂) [4]. Recently, International Academy of Mathematical Chemistry checked thirteen physicochemical properties of octane isomers (heat capacity at T constant, heat capacity at P constant, density, boiling point, entropy, acentric factor, enthalpy of formation, octanol-water partition coefficient, enthalpy of vaporisation, standard enthalpy of formation, molar volume and total surface tension) with the help of the connection number-based TIs and declared that the chemical capability of the Zagreb connection indices is better than the ordinary Zagreb indices for the entropy and acentric factor of the octane isomers, for detail see [9]. In addition, Javaid et al. [33] presents comparison of correlation coefficients between different TIs and eleven physicochemical properties of octane isomers (boiling point, heat capacity, entropy, density,mean radius, change in heat of vaporization, standard heat of formation, acentric factor, enthalpy of vaporization and standard enthalpy of vaporization) which shows that Gutman connection index is a very useful TI for the prediction of entropy, acentric factor, enthalpy of vaporization and standard enthalpy of vaporization.

3. Preliminaries

Throughout in this research paper, we take a simple and connected graphs G with V(G) = {u_i : 1 ≤ i ≤ n} and E(G) = {e_i : 1 ≤ i ≤ m} such that |V(G)| = n and |E(G)| = m. For more basic notations of graphs, see [34, 35]. Now, we define some most frequent used definition as follows

•
The number of vertices at distance one from a vertex u_i is called its degree and it is denoted by δ(u_i).
•
Degree of an edge e_i = u_ju_k is given by δ(e_i) = δ(u_j) + δ(u_k) − 2, where 1 ≤ i ≤ m for some 1 ≤ j, k ≤ n.
•
The distance between two vertices u_i, u_j ∈ V(G) is denoted by d(u_i, u_j) and defined as the length of the shortest path between both the vertices u_i and u_j for 1 ≤ i, j ≤ n.
•
The distance between two edges e_i = u_pu_q and e_j = u_ru_s is defined as d_G(e_i, e_j) = min{d_G(u_p, u_r), d_G(u_p, u_s), d_G(u_q, u_r), d_G(u_q, u_s)}, where 1 ≤ i, j ≤ m and 1 ≤ p, q, r, s ≤ n.
•
The distance between one vertex u_i and one edge e_j = u_pu_q is defined as d_G(u_i, e_j) = min{d_G(u_i, u_p), d_G(u_i, u_q)}, where 1 ≤ j ≤ m and 1 ≤ i, p, q ≤ n.
•
The number of vertices at distance two from a vertex u_i is called its connection number of u_i and it is denoted by τ(u_i) for 1 ≤ i ≤ n .

More details about aforesaid definitions can be obtained from [9, 36, 37].

Some important and related TIs are the following:

Definition 1 (see [5].)Let G be a connected graph of order n, then its Wiener index is

(1)

where 1 ≤ i, j ≤ n.

Definition 2 (see [6].)Let G be a connected graph of order n, then first and second Zagreb index are defined as

(2)

(3)

where 1 ≤ i, j ≤ n.

Definition 3 (see [38].)Let G be a connected graph of order n, then first and second Zagreb coindex are defined as

(4)

(5)

where 1 ≤ i, j ≤ n.

Definition 4 (see [6].)Let G be a connected graph of order n and size m, then edge version of Wiener index is defined as

(6)

where 1 ≤ i, j ≤ m.

Definition 5 (see [35].)Let G be a connected graph of order n, then the degree distance index of G is

(7)

where 1 ≤ i, j ≤ n.

Definition 6 (see [12].)Let G be a connected graph of order n and size m, then the edge version of degree distance index of G is

(8)

where 1 ≤ i, j ≤ m.

Definition 7 (see [8].)Let G be a connected graph, then the Gutman index of G is

(9)

where 1 ≤ i, j ≤ n.

Definition 8 (see [10].)Connection Distance index of a graph G (denoted by C D(G)) is defined as

(10)

where 1 ≤ i, j ≤ n or

(11)

Definition 9 (see [10].)Gutman Connection index of a graph G (denoted by G C(G)) is defines as

(12)

where 1 ≤ i, j ≤ n or

(13)

Yan et al. [11] defined the four operations S, R, Q and T on the graph G and obtained the four new graphs from G as follows:

•
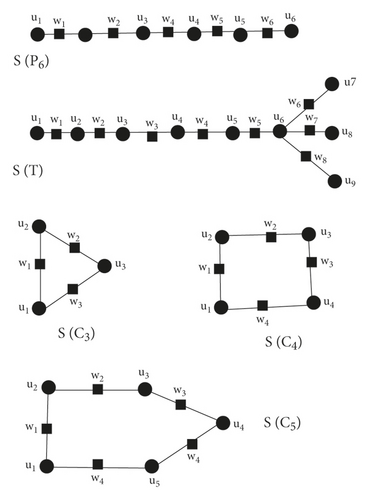
S(G) is obtained from G if a new vertex w_i is inserted in every edge e_i of G. The already existing vertices u_i of G are named as old or black vertices while new vertices w_i are also named new or white vertices.
•
R(G) is formed by assigning a new vertex w_i corresponding to each edge e_i of G and this new vertex w_i is connected with the end vertices of the respective edge e_i.
•
Q(G) is formed from S(G) if two white vertices w_i and w_j are further joined together when corresponding edges e_i and e_j have one common end vertex.
•
T(G) is formed from R(G) if two white vertices w_i and w_j are further joined together when corresponding edges e_i and e_j have one common end vertex.

4. Relation Between Connection Numbers and Degrees

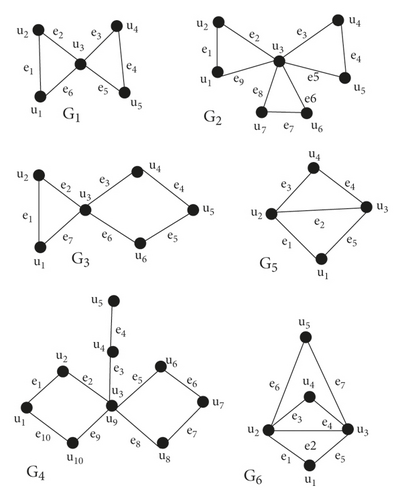
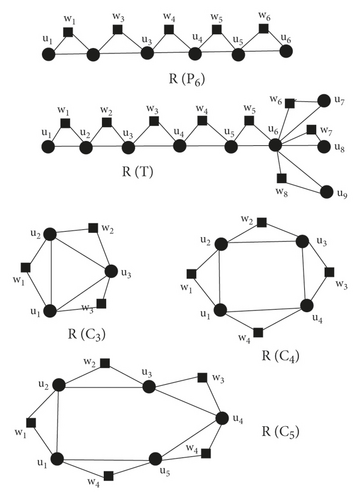
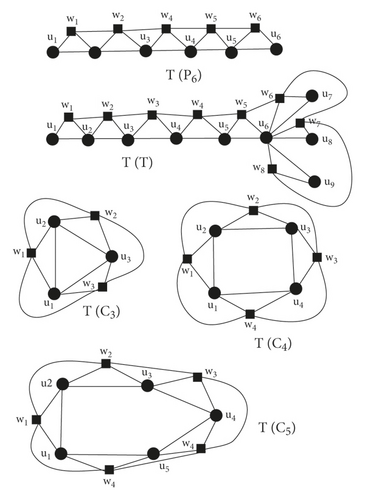
In order to determine connection numbers or bounded values of connection numbers of derived graphs S(G), R(G), Q(G) and T(G), we will develop Lemma 1 to Lemma 4. Before to the proofs of these results, in particular we consider Figure 1 and Figure 2 to present some trees, cycles and graphs consisting of cycles of order 3 and 4.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Some trees and cycles.

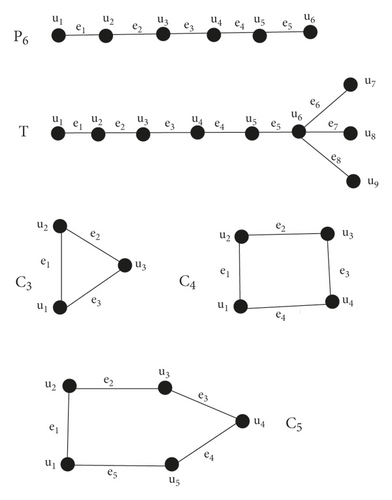
Lemma 1. For a simple and connected graph G (i) τ_S(G)(u_i) = δ_(G)(u_i) and (ii) τ_S(G)(w_i) = δ_(G)(u_j) + δ_(G)(u_k) − 2 = δ(e_i) where w_i is a new vertex corresponding to edge e_i = u_ju_k.

Proof 1. On applying S-operation, subdivision graph S(G), each vertex u_i is connected with δ_(G)(u_i) = d_i new (white) vertices. So, δ_(G)(u_i) = d_i new (white) vertices w_i are at distance one from old vertices u_i. Further d_i old vertices u_j are at distance two from u_i in S(G) (which are at distance one in G)

Also, each new vertex (white) w_i corresponds to each edge e_i = u_ju_k is at distance one from u_j and u_k. So, number of vertices at distance 2 from w_i are δ_(G)(u_j) − 1 + δ_(G)(u_k) − 1 (see Figure 3 and Figure 4). Therefore τ_S(G)(w_i) = δ_(G)(u_j) + δ_(G)(u_k) − 2 = δ_(G)(e_i).

Lemma 2. Let G be a simple and connected graph

(a)
If G is a {C₃, C₄}− free graph, then
- (i)
  τ_R(G)(u_i) = 2τ_(G)(u_i) and
- (ii)
  τ_R(G)(w_i) = 2[δ_(G)(u_j) + δ_(G)(u_k)] − 4 = 2[δ_(G)(e_i)].
(b)
If G is a {C₃, C₄}− graph, then
- (i)
  τ_R(G)(u_i)⩽2τ_(G)(u_i) + r, where r = max{r_i} and r_i are number of C₃ and C₄ cycles connected with u_i in G.
- (ii)
  τ_R(G)(w_i)⩽2[δ_(G)(u_j) + δ_(G)(u_k)] − 4 − s = 2[δ_(G)(e_i)] − s, where s = max{s_i} and s_i are number of C₃ cycles connected with u_i in G.

Proof 2. On applying R − operation, a new vertex w_i is joined with the corresponding vertices of edge e_i = u_ju_k.

Case (a)

If G is a {C₃, C₄}− free graph, then the degree of each vertex u_i in R(G) is twice the degree u_i in G i.e. δ_R(G)(u_i) = 2δ_G(u_i) (see Figure 5) . Then their connection number of each vertex u_i in R(G) is twice the connection number u_i in G i.e. τ_R(G)(u_i) = 2τ_(G)(u_i). Also u_j and u_k are at distance one from w_i, but in R(G), degree of u_j and u_k are also doubled, then number of vertices at distance 2 of w_i are 2[δ_(G)(u_j) − 1 + δ_(G)(u_k) − 1] = 2[δ_(G)(u_j) + δ_(G)(u_k)] − 42δ_G(e_i) = 2δ_G(e_i). Also for n ≥ 5, , , , , and = , i = 1,2 … n.

Case (b)

If G is a {C₃, C₄}− graph, then consider , , and ,= 2δ_G(e_i) − 1 i = 1,2,3.

, , , and = , i = 1,2,3,4.

Consider R(G₁) graph in which two C₃ are connected by a common vertex u₃ as shown in Figure 6, then , ⇒ for i = 1,2,4,5 and , as u₃ lies in two C₃ graphs. Also = 2δ_G(e_i) − 1 for i = 1,4 and = 2δ_G(e_i) − 1, for i = 2,3,5,6.

Consider R(G₂) graph in which three C₃ are connected by a common vertex u₃ as shown in Figure 6, then , ⇒ for i = 1,2,4,5,6,7 and , as u₃ lies in three C₃ graphs. Also = 2δ_G(e_i) − 1 for i = 1,4,7 and = 2δ_G(e_i) − 1, for i = 2,3,5,6,8,9.

Consider R(G₃) in which one C₃ and one C₄ are connected by a common vertex u₃ as shown in Figure 6, then for i = 1,2,4,5,6, for for for , for , as u₃ lies in one C₃ and one C₄ graphs, , for , Also = 2δ_G(e_i) − 1, = 2δ_G(e_i) − 1, = 2δ_G(e₃), = 2δ_G(e₄).

Consider R(G₄) graph in which two C₄ graphs and one path are connected by vertex u₃ as shown in Figure 6. As for i = 1,2,4,6,8, and , , , , , , , = 2δ_G(e₁), = = = .

Consider a graph R(G₅), in which one edge u₂u₃ is common in two C₃ − graphs as shown in Figure 6. and , as N(u₁) ∈ two C₃ graphs, for i = 1,4, and as N(u_i) ∈ C₃ graphs, for i = 2,3, = , similarly we can get w₂, w₃ and w₄, = , as u₂u₃ ∈ two C₃ graph.

Now consider a graph R(G₆) in which one edge u₂u₃ is common in three C₃ − graphs as shown in Figure 6, and , as N(u₁) ∈ three C₃ graphs, for i = 1,4,5, and , as N(u₁) ∈ three C₃ graphs, for i = 2,3, = . Similarly, we can get w₃, w₄, w₅, w₆, and w₇, = , as u₂u₃ ∈ three C₃ graph.

Now, we close our discussion by taking r = max{r_i} and s = max{s_i}, then upper bound for connection number is taken is taken as τ_R(G)(u_i) = 2τ_(G)(u_i) + r and τ_R(G)(w_i) = 2[δ_(G)(x_i) + δ_(G)(y_i)] − 4 = 2[δ_(G)(e_i)]. And lower bound for connection number is taken as τ_R(G)(u_i) = 2τ_(G)(u_i) and τ_R(G)(w_i) = 2[δ_(G)(x_i) + δ_(G)(y_i)] − 4 − s = 2[δ_(G)(e_i)] − s.

Lemma 3. For a simple and connected graph G,

(a)
If G is a {C₃, C₄}− free graph, then
- (i)
  τ_Q(G)(u_i) = δ_(G)(u_i) + τ_(G)(u_i) and
- (ii)
  τ_Q(G)(w_i) = τ_(G)(x_i) + τ_(G)(y_i).
(b)
If G is a {C₃, C₄}− graph, then
- (i)
  τ_Q(G)(u_i)⩽δ_(G)(u_i) + τ_(G)(u_i) + r where r = max{r_i} and r_i is the number of C₃ and C₄ cycles connected with vertex u_i .
- (ii)
  τ_Q(G)(w_i)⩽τ_(G)(u_j) + τ_(G)(u_k) + s where s = max{s_i} and s_i is the number of C₃ cycles in graph G connected with edge e_i.

Proof 3. Case (a)

If G is a {C₃, C₄}− free graph, On applying first S-operation, the connection number of u_i becomes equal to . Then for Q-operation, further two new (white) vertices of S(G) are also joined if their corresponding edges have a common vertex between them. So connection number of u_i in Q(G) becomes equal to the sum of and τ_G(u_i).

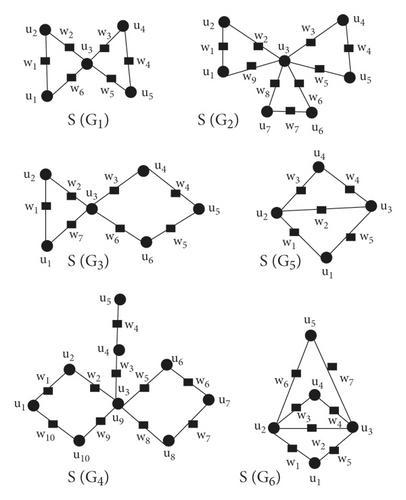
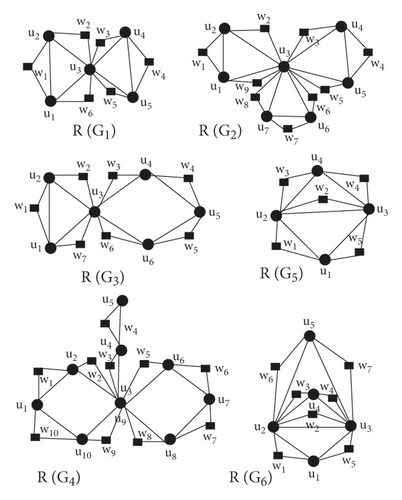
(For explanation from Figure 7, first consider a tree T with nine vertices in which δ_(T)(u_i) = 1 for i = 1,7,8,9, δ_(T)(u_i) = 2 for i = 2,3,4,5. δ_(T)(u₆) = 4, τ_(G)(u_i) = 1 i = 1,2,6, τ_(T)(u_i) = 3 i = 3,4, τ_(T)(u₅) = 4, τ_(G)(u_i) = 3 i = 7,8,9. Then τ_Q(T)(u₁) = 2 = δ_(T)(u₁) + τ_(T)(u₁), τ_Q(T)(u₂) = 3 = δ_(T)(u₂) + τ_(T)(u₂), τ_Q(T)(u₃) = 4 = δ_(T)(u₃) + τ_(T)(u₃) = τ_Q(T)(u₄), τ_Q(T)(u₅) = 6 = δ_(T)(u₅) + τ_(T)(u₅), τ_Q(T)(u₆) = 5 = δ_(T)(u₆) + τ_(G)(u₆), τ_Q(T)(u₇) = 4 = δ_(T)(u₇) + τ_(T)(u₇) = τ_Q(T)(u₈) = τ_Q(T)(u₉), τ_Q(T)(w₁) = 2 = τ_(T)(u₁) + τ_(T)(u₂), τ_Q(T)(w₂) = 3 = τ_(T)(u₂) + τ_(T)(u₃), τ_Q(T)(w₃) = τ_(T)(u₃) + τ_(T)(u₄), , here we conclude τ_Q(T)(u_i) = δ_(T)(u_i) + τ_(T)(u_i) and τ_Q(G)(T_i) = τ_(G)(u_j) + τ_(T)(u_k)).

Also for n ≥ 5, , , , , and τ_Q(G)(w_i) = τ_(G)(u_j) + τ_(G)(u_k).

Case(b)

Consider , , and , i = 1,2,3.

, , and τ_Q(G)(w_i) = τ_(G)(u_j) + τ_(G)(u_k), i = 1,2,3,4.

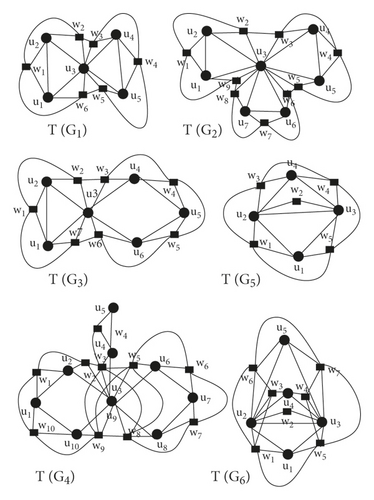
Consider Q(G₁) graph in which two C₃ are connected by a common vertex u₃ as shown in Figure 8, then , ⇒ for i = 1,2,4,5 and , as u₃ lies in two C₃ graphs. Also , but when u₁ and u₂ is of same degree and u₃ is their third vertex in C₃, Also for i = 1,4 and , for i = 2,3,5,6.

Consider Q(G₂) graph in which three C₃ are connected by a common vertex u₃ as shown in Figure 8, then , ⇒ for i = 1,2,4,5,6,7 and , as u₃ lies in three C₃ graphs. Also for i = 1,4,7 but when u₁ and u₂ is of same degree and u₃ is their third vertex in C₃, Also for i = 1,4,7 and , for i = 2,3,5,6,8,9.

Consider Q(G₃) graph in which one C₃ and one C₄ are connected by a common vertex u₃ as shown in Figure 8, then for i = 1,2,4,5,6, for for for , , as u₃ lies in one C₃ and one C₄ graphs, . Also when u₁ and u₂ is of same degree and u₃ is their third vertex in C₃, Also , , .

Consider Q(G₄) graph in which two C₄ graphs and one path are connected by vertex u₃ as shown in Figure 8. As for i = 1,2,4, and , , , , , , , , , , .

Now we consider a graph Q(G₅), in which one edge u₂u₄ is common in two C₃ − graphs as shown in Figure 8 . and , as N(u₁) ∈ two C₃ graphs, for i = 1,3, and as N(u_i) ∈ C₃ graphs, for i = 2,4, . Similarly, we can get w₂, w₃ and w₄, , as u₂u₄ ∈ two C₃ graph.

Now we consider a graph Q(G₆) in which one edge u₂u₄ is common in three C₃ − graphs as shown in Figure 8, and , as N(u₁) ∈ three C₃ graphs, for i = 1,3,5, and , as N(u_i) ∈ three C₃ graphs, for i = 2,4, =6. Similarly, we can get w₂, w₃, w₄, w₆, and w₇, , as u₂u₄ ∈ three C₃ graph.

Now, we close our discussion by taking, r = max{r_i} and s = max{s_i}, τ_Q(G)(u_i)⩽δ_(G)(u_i) + τ_(G)(u_i) + r and τ_Q(G)(w_i)⩽τ_(G)(u_j) + τ_(G)(u_k) + s.

Lemma 4. For a simple, connected graph G,

(a)
If G is a {C₃, C₄}− free graph, then
- (i)
  τ_T(G)(u_i) = 2τ_(G)(u_i) and
- (ii)
  τ_T(G)(w_i) = τ_(G)(u_j) + τ_(G)(u_k).
(b)
If G is a {C₃, C₄}− graph, then
- (i)
  τ_T(G)(u_i)⩽2τ_(G)(u_i) + r where r = max{r_i} and vertex u_i is connected with r_i number of C₃ and C₄ cycles and
- (ii)
  τ_T(G)(w_i)⩽τ_(G)(u_j) + τ_(G)(u_k) + s where s = max{s_i} and edge e_i is connected with the s_i number of C₃ cycles in graph G.

Proof 4. After applying T-operation on G, we get m new vertices w_i corresponding to each edge e_i = u_ju_k = x_iy_i for u_j = x_i, u_k = y_i.

Case (a)

If G is a {C₃, C₄}− free graph, on applying first R-operation, the connection number of u_i becomes equal to . Then for T-operation, further two new (white) vertices of R(G) are also joined if their corresponding edges have a common vertex between them. So connection number of u_i in T(G) becomes equal to the twice of .

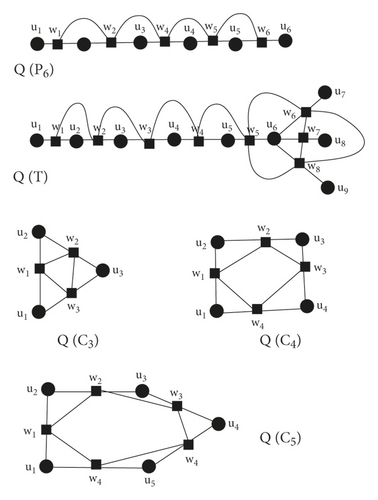
(For explanation from Figure 9, first consider for i = 1,6, for for , , here we conclude and

Also for , , , , and τ_T(G)(w_i) = τ_(G)(u_j) + τ_(G)(u_k)).

Case (b)

Now consider , , and , i = 1,2,3.

, , and , i = 1,2,3,4.

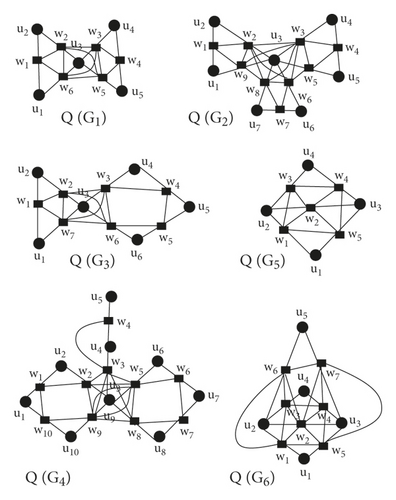
Consider T(G₁) in which two C₃ are connected by a common vertex u₃ as shown in figure 10, then , ⇒ for i = 1,2,4,5 and , as u₃ lies in two C₃ cycles. Also , but when u₁ and u₂ is of same degree 2 and u₃ is their third vertex in C₃, Also for i = 1,4 and , for i = 2,3,5,6.

Consider T(G₂) in which three C₃ are connected by a common vertex u₃ as shown in Figure 10, then , ⟶ for i = 1,2,4,5,6,7 and , as u₃ lies in three C₃ graphs. Also for i = 1,4,7 but when u₁ and u₂ is of same degree 2 and u₃ is their third vertex in C₃,moreover for i = 1,4,7 and , for i = 2,3,5,6,8,9.

Consider T(G₃) in which one C₃ and one C₄ are connected by a common vertex u₃ as shown in Figure 10, then for i = 1,2,4,5,6, for for , , as u₃ lies in one C₃ and one C₄ graphs, , . Also when u₁ and u₂ are of same degree and u₃ is their third vertex in C₃, Also , , .

Consider G₄ graph in which two C₄ graphs and one path are connected by vertex u₃ as shown in Figure 10. As for i = 1,2,4, and , , , , , , , , , , .

Now we consider a graph G₅, in which one edge u₂u₄ is common in two C₃ − graphs . and , , for i = 1,3, and as u_i∈ two C₃ cycles, for i = 2,4, . Similarly, we can get w₂, w₃ and w₄, , as u₂u₄∈ two C₃ graph.

Now we consider a graph G₆ in which one edge u₂u₃ is common in three C₃ − graphs as shown in Figure 10, and , as N(u₁)∈ three C₃ graphs, for i = 1,4,5, and as N(u_i)∈ three C₃ graphs, for i = 2,4, . Similarly, we can get w₂, w₃, w₄, w₆, and w₇, , as u₂u₄∈ three C₃ graph.

Now, we close our discussion by taking r = max{r_i} and s = max{s_i}, τ_T(G)(u_i)⩽δ_(G)(u_i) + τ_(G)(u_i) + r and τ_T(G)(w_i)⩽τ_(G)(u_j) + τ_(G)(u_k) + s.

5. Connection Distance Indices of derived graphs

Now, we will determine degree connection sum of derived graphs S(G), R(G), Q(G) and S(G) by the following theorems.

Theorem 1. If S(G) is subdivision graph of G, then

(14)

Proof 5. By

lemma 5. τ_S(G)(u_i) = δ_(G)(u_i) and τ_S(G)(w_i) = δ_(G)(u_j) + δ_(G)(u_k) − 2 = τ_S(G)(e_i)

Also

(15)

Theorem 2. If G be a {C₃, C₄}− graph and R(G) is an vertex-semitotal graph of G, then

(16)

Proof 6.

(a)
For upper bounds, we take by lemma 2, τ_R(G)(u_i) = 2τ_(G)(u_i) + r and τ_R(G)(w_i) = δ_(G)(u_j) + δ_(G)(u_k) − 2 = δ_G(e_i).

Also d_R(u_i, u_j) = d_G(u_i, u_j), for u_i, u_j ∈ V(G). d_R(w_i, w_j) = d_G(e_i, e_j) + 2, for e_i, e_j ∈ E(G). d_R(u_i, w_j) = d_G(u_i, e_j) + 1, for u_i ∈ V(G) and e_j ∈ E(G).

(17)

For lower bounds, by

lemma 6. τ_R(G)(u_i) = 2τ_(G)(u_i) and τ_R(G)(w_i) = [δ_(G)(u_j) + δ_(G)(u_k) − 2] − s = δ_G(e_i) − s.

(18)

If G is {C₃, C₄}− free graph, then connection distance index (CD)of R(G) can also be determined by taking r = 0 and s = 0 in Theorem 2.

Corollary 1. If G be a {C₃, C₄}− free graph,then

(19)

Theorem 3. If Q(G) is an edge-semitotal graph of G, then

(20)

Proof 7. By

lemma 7. τ_Q(G)(u_i)⩽δ_G(u_i) + τ_G(u_i) + r and τ_Q(G)(w_i)⩽τ_(G)(u_j) + τ_(G)(u_k) + s.

To avoid confusion, we take edge e_i = x_iy_i = u_ju_k for some j and k, then τ_Q(G)(w_i)⩽τ_(G)(x_i) + τ_(G)(y_i) + s. Also

(21)

If G is {C₃, C₄}− free graph, then connection distance index (CD) of Q(G) can also be determined by taking r = 0 and s = 0 in Theorem 3.

Corollary 2. If G is a {C₃, C₄}− free graph, then

(22)

Theorem 4. If T = T(G) is an total graph of G, then

(23)

Proof 8. To avoid confusion, we take edge e_i = x_iy_i = u_ju_k for some j and k. By lemma 4, τ_T(G)(w_i)⩽τ_(G)(x_i) + τ_(G)(y_i) + s and τ_T(G)(u_i) = 2τ_G(u_i) + r

Also

(24)

If G is {C₃, C₄}− free graph, then connection distance index (CD) of T(G) can also be determined by taking r = 0 and s = 0 in Theorem 4.

Corollary 3. If G is a {C₃, C₄}− free graph, then

(25)

6. Conclusion

In previous section, first of all, connection numbers of old (black) vertices and new (white) were determined for derived graph F(G) where F ∈ {S, R, Q, T} (by Lemma 1, Lemma 2,Lemma 3 and Lemma 4 ) . It was found that exact values of connection numbers for {C₃, C₄}− free graph and S(G) were determined. Bounded values of R(G), Q(G) and T(G) for {C₃, C₄}− graphs were determined. Then, finally, exact and bounded values of connection distance (CD) of derived graphs {S(G), R(G), Q(G), T(G)} were determined by Theorems and Corollaries. International Academy of Mathematical Chemistry declared better reports for the chemical capability of the Zagreb connection indices than the ordinary Zagreb indices for the entropy and acentric factor of the octane isomers.

Conflicts of Interest

The authors declare no conflicts of interest.

Open Research

Data Availability

The whole data are included within this article. However, the reader may contact the corresponding author for more details on the data.

References

1 Yan F., Shang Q., Xia S., Wang Q., and Ma P., Application of topological index in predicting ionic liquids densities by the quantitative structure property relationship method, Journal of Chemical & Engineering Data. (2015) 60, no. 3, 734–739, https://doi.org/10.1021/je5008668, 2-s2.0-84924591017.
10.1021/je5008668
CAS Web of Science® Google Scholar
2 Devillers J. and Balaban A. T., Topological Indices and Related Descriptors in QSAR and QSPR, 1999, Gordon & Breach, Amsterdam, The Netherlands.
Google Scholar
3 Diudea M. V., QSPR/QSAR Studies by Molecular Descriptors, 2001, NOVA, New York, NY, USA.
Google Scholar
4 Shafiei F., Relationship between topological indices and thermodynamic properties and of the monocarboxylic acids applications in QSPR, Iranian Journal of Mathematical Chemistry. (2015) 6, no. 1, 15–28.
Web of Science® Google Scholar
5 Wiener H., Structural determination of paraffin boiling points, Journal of the American Chemical Society. (1947) 69, no. 1, 17–20, https://doi.org/10.1021/ja01193a005, 2-s2.0-8544254107.
10.1021/ja01193a005
CAS PubMed Web of Science® Google Scholar
6 Gutman I. and Trinajstic N., Graph theory and molecular orbitals: total π-electron energy of alternant hydrocarbons, Chemical Physics Letters. (1972) 17, 535–538.
10.1016/0009-2614(72)85099-1
CAS Web of Science® Google Scholar
7 Dobrynin A. A. and Kochetova A. A., Degree distance of a graph: a degree analog of the wiener index, Journal of Chemical Information and Computer Sciences. (1994) 34, no. 5, 1082–1086, https://doi.org/10.1021/ci00021a008, 2-s2.0-0028499619.
10.1021/ci00021a008
CAS Web of Science® Google Scholar
8 Gutman I., Selected properties of the Schultz molecular topological index, Journal of Chemical Information and Computer Sciences. (1994) 34, no. 5, 1087–1089, https://doi.org/10.1021/ci00021a009, 2-s2.0-0028498920.
10.1021/ci00021a009
CAS Web of Science® Google Scholar
9 Ali A. and Trinajstic N., A novel/old modification of the first Zagreb index, Mol. Inf.(2018) 37, no. 6-7, 1800008, https://doi.org/10.1002/minf.201800008, 2-s2.0-85043690255.
10.1002/minf.201800008
Web of Science® Google Scholar
10 Javaid M., Khubab Siddique M., and Ali U., Novel connection based indices of several wheel-ralated graph, Compu. J. Combin. Math.(2020) 2, 31–58.
Google Scholar
11 Yan W., Yang B. Y., and Yeh Y. N., The behavior of Wiener indices and polynomials of graphs under five graph decorations, Applied Mathematics Letters. (2007) 20, no. 3, 290–295, https://doi.org/10.1016/j.aml.2006.04.010, 2-s2.0-33751162621.
10.1016/j.aml.2006.04.010
Web of Science® Google Scholar
12 Xu J., Liu J. B., Bilal A., Ahmad U., Siddiqui H. M. A., Ali B., and Farahani M. R., Distance degree index of some derived graphs, Mathematics. (2019) 7, no. 3, https://doi.org/10.3390/math7030283, 2-s2.0-85063888908.
10.3390/math7030283
Web of Science® Google Scholar
13 Ali B., Imran M., Malik M. A., Saddiqui H. M. A., Bilal A., and Farhani M. R., Gutman Index of some derived graphs, Advances and Applications in Discrete Mathematics. (2019) 20, no. 1, 165–184, https://doi.org/10.17654/dm020010165.
10.17654/DM020010165
Google Scholar
14 Ahmad A., Elahi K., Hasni R., and Nadeem M. F., Computing the degree based topological indices of line graph of benzene ring embedded in P-type-surface in 2D network, Journal of Information and Optimization Sciences. (2019) 40, no. 7, 1511–1528, https://doi.org/10.1080/02522667.2018.1552411.
10.1080/02522667.2018.1552411
Web of Science® Google Scholar
15 Nadeem M. F., Zafar S., and Zahid Z., On topological properties of the line graphs of subdivision graphs of certain nanostructures, Applied Mathematics and Computation. (2016) 273, 125–130, https://doi.org/10.1016/j.amc.2015.10.010, 2-s2.0-84945151432.
10.1016/j.amc.2015.10.010
Web of Science® Google Scholar
16 Ahmad M., Saeed M., Javaid M., and Hussain M., Exact formula and improved bounds for general sum-connectivity index of graph operations, IEEE Access. (2019) 7, 167290, https://doi.org/10.1109/access.2019.2953338.
10.1109/ACCESS.2019.2953338
Google Scholar
17 Awais H. M., Javaid M., and Jamal M., Forgotten Index of generalized F-sum graphs, J Prime Res Math. (2019) 15, 115–128.
Google Scholar
18 Akhter S. and Imran M., The sharp bounds on general sum-connectivity index of four operations on graphs, Journel of Inequalities and Applications. (2016) 241, 1–10.
Google Scholar
19 Liu J. B., Javaid M., and Awais H. M., Computing Zagreb indices of the subdivision-related generalized operations of graphs, IEEE Access. (2019) 7, 105479, https://doi.org/10.1109/access.2019.2932002, 2-s2.0-85071198790.
10.1109/ACCESS.2019.2932002
Web of Science® Google Scholar
20 Du Z., Ali A., and Trinajstic N., Alkanes with the first three maximal/minimal modified first Zagreb connection indices, Mol. Inf.(2019) 38, no. 4, 1800116, https://doi.org/10.1002/minf.201800116, 2-s2.0-85059672318.
10.1002/minf.201800116
Web of Science® Google Scholar
21 Noureen S., Bhatti A. A., and Ali A., Extremal trees for the modified first Zagreb connection index with fixed number of segments or vertices of degree 2, JOURNAL OF TAIBAH UNIVERSITY FOR SCIENCE. (2020) 14, no. 1, 31–37, https://doi.org/10.1080/16583655.2019.1699227.
10.1080/16583655.2019.1699227
Google Scholar
22 Awais H. M., Javaid M., and Raheem A., Hyper-Zegreb index of graph based on generalized subdivision-related operations, Punjab University Journal of Mathematics. (2020) 52, no. 5, 89–103.
Web of Science® Google Scholar
23 Liu J. B., Javed S., Javaid M., and Shabbir K., Computing first general Zagreb index of operations on graphs, IEEE Access. (2019) 7, 47494, https://doi.org/10.1109/access.2019.2909822, 2-s2.0-85065090345.
10.1109/ACCESS.2019.2909822
Web of Science® Google Scholar
24 Javaid M., Liu J. B., Rehman M. A., and Wang S., On the certain topolgical indices of titania nanotube TiO₂[m, n], Zeitschrift für Naturforschung. (2017) 72, no. 7, 647–654.
10.1515/zna-2017-0101
CAS Google Scholar
25 Das K. C. and Gutman I., On Wiener and multiplicative Wiener indices of graphs, Discrete Applied Mathematics. (2016) 206, 9–14, https://doi.org/10.1016/j.dam.2016.01.037, 2-s2.0-84976217069.
10.1016/j.dam.2016.01.037
Web of Science® Google Scholar
26 Das K. C., Gutman I., and Nadjafi Arani M. J., Relations between distance based and degree based topological indices, Applied Mathematics and Computation. (2015) 270, 142–147, https://doi.org/10.1016/j.amc.2015.08.061, 2-s2.0-84940399436.
10.1016/j.amc.2015.08.061
Google Scholar
27 Dobrynin A. A., Entringer R., and Gutman I., Wiener index of trees, theory and applications, Acta Applicandae Mathematica. (2001) 66, no. 3, 211–249, https://doi.org/10.1023/a:1010767517079, 2-s2.0-0035329265.
10.1023/A:1010767517079
Web of Science® Google Scholar
28 Petrova T., Rasulev B. F., Toropov A. A., Leszczynska D., and Leszczynski J., Improved model for fullerene C60 solubility in organic solvents based on quantum-chemical and topological descriptors, Journal of Nanoparticle Research. (2011) 13, no. 8, 3235–3247, https://doi.org/10.1007/s11051-011-0238-x, 2-s2.0-80051588636.
10.1007/s11051-011-0238-x
CAS Web of Science® Google Scholar
29 Matamala A. R. and Estrada E., Simplex optimization of generalized topological index (GTI-Simplex): a unified approach to optimize QSPR models, The Journal of Physical Chemistry A. (2005) 109, no. 43, 9890–9895, https://doi.org/10.1021/jp053408x, 2-s2.0-27744526372.
10.1021/jp053408x
CAS PubMed Web of Science® Google Scholar
30 Gao W., Siddiqui M. K., Imran M., Jamil M. K., and Farahani M. R., Forgotten topological index of chemical structure in drugs, Saudi Pharmaceutical Journal. (2016) 24, no. 3, 258–264, https://doi.org/10.1016/j.jsps.2016.04.012, 2-s2.0-84969674666.
10.1016/j.jsps.2016.04.012
PubMed Web of Science® Google Scholar
31 Gonzalez-Diaz H., Vilar S., Santana L., and Uriarte E., Medicinal chemistry and bioinformatics - current trends in drugs discovery with networks topological indices, Current Topics in Medicinal Chemistry. (2007) 7, no. 10, 1015–1029, https://doi.org/10.2174/156802607780906771, 2-s2.0-34447254270.
10.2174/156802607780906771
CAS PubMed Web of Science® Google Scholar
32 Labanowski J. K., Motoc I., and Dammkoehler R. A., The physical meaning of topological indices, Computers & Chemistry\&. (1991) 15, no. 1, 47–53.
10.1016/0097-8485(91)80023-F
CAS Web of Science® Google Scholar
33 Javaid M., Siddique M. K., and Bonyah E., Computing gutman connection index of thorn graphs, Journal of Mathematics. (2021) 2021, 1–13, 2289514, https://doi.org/10.1155/2021/2289514.
10.1155/2021/2289514
Google Scholar
34 Flapan E., When Topology Meets Chemistry, 2000, Cambridge University Press and the Mathematical Association of America, Cambridge, CA, USA.
10.1017/CBO9780511626272
Google Scholar
35 Todeschini R., Consonni V., Mannhold R., Kubinyi H., and Timmerman H., Handbook of Molecular Descriptors, 2002, Wiley VCH, Weinheim; Germany.
Google Scholar
36 Diestel R., Graph Theory, 2000, Springer-Verlag, New York, NY, USA.
10.1007/b100033
Google Scholar
37 West D. B., Introduction to Graph Theory, 1996, Prentice-Hall, New Jersery, NY, USA.
Google Scholar
38 Doslic T., Vertex-weighted Wiener polynomials for composite graphs, Ars Math. Contemp. (2008) 1, 66–80, https://doi.org/10.26493/1855-3974.15.895.
10.26493/1855-3974.15.895
Web of Science® Google Scholar

Citing Literature

All articles

Computing Connection Distance Index of Derived Graphs

Abstract

1. Introduction

2. Applications

3. Preliminaries

4. Relation Between Connection Numbers and Degrees

5. Connection Distance Indices of derived graphs

6. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Computing Connection Distance Index of Derived Graphs

Abstract

1. Introduction

2. Applications

3. Preliminaries

4. Relation Between Connection Numbers and Degrees

5. Connection Distance Indices of derived graphs

6. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information