Volume 2022, Issue 1 1285552

Research Article

Open Access

Analysis of Tire-Pavement Contact Morphology Characteristics during the Virtual Track Train Maneuvering

Chengping Wang,

Chengping Wang

Institution of Rail Transit, Tongji University, Shanghai 201804, China tongji.edu.cn

Search for more papers by this author

Jimin Zhang,

Corresponding Author

Jimin Zhang

[email protected]

orcid.org/0000-0001-7445-9381

Institution of Rail Transit, Tongji University, Shanghai 201804, China tongji.edu.cn

Search for more papers by this author

Hechao Zhou,

Hechao Zhou

orcid.org/0000-0003-2722-922X

Institution of Rail Transit, Tongji University, Shanghai 201804, China tongji.edu.cn

State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, Sichuan, China swjtu.edu.cn

Search for more papers by this author

Chengping Wang,

Chengping Wang

Institution of Rail Transit, Tongji University, Shanghai 201804, China tongji.edu.cn

Search for more papers by this author

Jimin Zhang,

Corresponding Author

Jimin Zhang

[email protected]

orcid.org/0000-0001-7445-9381

Institution of Rail Transit, Tongji University, Shanghai 201804, China tongji.edu.cn

Search for more papers by this author

Hechao Zhou,

Hechao Zhou

orcid.org/0000-0003-2722-922X

Institution of Rail Transit, Tongji University, Shanghai 201804, China tongji.edu.cn

State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, Sichuan, China swjtu.edu.cn

Search for more papers by this author

First published: 11 October 2022

https://doi.org/10.1155/2022/1285552

Citations: 2

Academic Editor: Donato Ciampa

Share a link

Email
Wechat
Bluesky

Abstract

The tire-pavement contact morphology during the virtual track train maneuvering has an essential function in assessing vehicle performance and pavement damage. The longitudinal tread tire and viscoelastic asphalt pavement were developed based on the finite element method. Then, the tire-pavement contact model was developed according to the Euler–Lagrange algorithm and validated. Contact area and stress distribution under uniform, braking, and cornering conditions are explored with the dynamic tire force of the virtual track train as the external load. Also, the effect factors were analyzed. The results indicate that vertical stress distribution is symmetrical along the length and width directions, and contact area is rectangular under uniform condition. Vertical and longitudinal stresses have similar distributions under braking condition, with a wide front and a narrow back along the length direction. Under cornering condition, the closer to the inside of the cornering, the larger the contact area. Vertical stress is similar to the lateral stress distribution, and the larger stress value is concentrated on the inner side of each tread. Load, tire pressure, slip rate, and slip angle have significant effects on contact morphology, while velocity has little effect. Contact area increases with the increase of load and slip rate and decreases with the increase of tire pressure and slip angle. Vertical stress increases gradually with the increase of load. Higher tire pressure makes stress distribution more concentrated. The increase in slip rate increases vertical and longitudinal stresses and gradually moves in the running direction. Vertical and lateral stresses increase with the slip angle and are mainly distributed on the inside of the turn. This research can be used to evaluate and analyze the response and damage of the virtual track train to asphalt pavement under uniform, braking, and cornering conditions. It can be used as a reference for the design and paving of asphalt pavement.

1. Introduction

The interaction between the vehicle and pavement is transmitted through the tire. Therefore, the contact problem between tire and pavement not only affects vehicle performance but also affects pavement service time. Normally, based on the geometric and mechanical parameters of tire and pavement, researchers constructed the tire-pavement contact model to study contact characteristics during vehicle maneuverings, such as static, free-rolling, traction, braking, and cornering.

The tire-pavement contact model was developed to simulate contact stress distribution under static, free-rolling, acceleration, and braking. The results demonstrated that running conditions have a marked effect on contact stress [1]. A truck radial tire was used to analyze the tire-pavement contact stress distribution under static, free-rolling, braking, camber, and cornering by H. Zhou et al. It is found that running conditions have a direct effect on contact stress distribution [2]. Oubahdou et al. [3] studied the contact shape and stress distribution between tire and pavement. The tire-pavement contact model was built by Yu et al. to discuss contact stress distribution under static, steady-state rolling, and braking conditions [4]. According to the Lagrange method, the tire-pavement contact model was built to investigate contact characteristics under static and antilock system conditions. Contact stress increased by 8.4% and contact area decreased by 7.7% under antilock system condition [5]. M. Guo et al. [6] developed a bus tire-pavement contact model to analyze the vertical, longitudinal, and lateral contact stress distribution under uniform, acceleration, and braking conditions. The 11.00R20 radial heavy-duty tire-viscoelastic asphalt pavement contact model was constructed to simulate contact characteristics under static, dynamic, and braking conditions [7].

The contact relationship between tire and pavement is described through contact morphology characteristics [8–10]. Generally, methods for studying contact morphology mainly include experimental and analytical methods. The experimental method can truly reflect contact area and stress, but the operation process is complicated [11]. The analytical method (the finite element method) has been widely accepted because of its ease of operation [12]. Consequently, based on the finite element method, tire and pavement finite element models were built to analyze the geometric characteristics and three-dimensional stress distribution. Simultaneously, factors including tire types (radial, diagonal, wide base, and dual), tire characteristics (tread pattern, rubber material, and inflation pressure), vehicle running conditions (static, uniform, acceleration, braking, and cornering), vehicle loads (unload, full-load, and overload), pavement (type, material, and texture), and temperature were investigated [13–19].

In previous studies, tire load was considered static, and the dynamic tire load under the interaction of vehicle and road was less considered. Compared to the tire model, the pavement model was considered rigid, ignoring the viscoelasticity and laminarity of asphalt pavement. In addition, the virtual rail train (VTT), as a new mode of transportation, runs on asphalt pavement. Therefore, it is necessary to develop a tire-viscoelastic asphalt pavement contact model for VTT under dynamic tire load to explore contact morphology under different running conditions and then evaluate the vehicle performance and pavement damage.

The objective of this study is to analyze and compare the contact morphology between the tire and pavement under typical running conditions. The method of Euler–Lagrange was applied to develop the longitudinal tread tire-viscoelastic asphalt pavement contact model, and the stiffness was verified. Based on the dynamic tire force calculated by the virtual track train dynamics model, the contact area and stress distribution under uniform, braking, and cornering conditions were explored. The influence of load, tire pressure, velocity, slip rate, and slip angle on the contact morphology was also analyzed.

2. Tire-Pavement Contact Model

The structure and material of tire and pavement are all important factors that affect contact morphology.

2.1. Tire Finite Element Model

The tire specification used for VTT is 385-65-R22.5 radial tire. According to the Chinese standard [19], tire parameters are shown in Table 1. It is mainly composed of rubber and reinforcement in different directions. The rubber includes tread, sidewall, and bead. The reinforcement includes belt ply 0-degree, belt ply 1, belt ply 2, belt ply 3, bead wire, and ply.

1. Parameters of radial tire 385/65R22.5

Tire parameter	Section width (mm)	Maximum overall diameter (mm)	Static load radius (mm)	Load capacity (kg)	Inflation pressure (kPa)
Values	389	1091	494	4500	900

Since the stress-strain of rubber material exhibits a strong nonlinearity relationship, the Yeoh model, which can characterize the large deformation capacity of rubber material, was chosen to describe its properties. The expression of strain energy function is as follows:

(1)

where U denotes the rubber strain energy density, J is the elastic volume ratio, C_ij and D_i represent the material constants (the value of D_i is close to zero), and I₁ is the first strain invariant its expression is as follows:

(2)

where λ₁, λ₂, and λ₃ are the primary elongation.

The linear elastic model was used to represent reinforcement, which was embedded in the corresponding rubber as a rebar element. Tire parameters were provided by Kasaike Tire Company, as illustrated in Table 2 and Table 3.

2. Yeoh model parameters of rubber.

Rubber	Yeoh model
Rubber	C₁₀(×10⁵Pa)	C₂₀(×10⁴Pa)	C₃₀(×10⁴Pa)
Tread	7.7	−6.71	9.55
Sidewall	9.35	−1.90	18.4
Bead	9.26	−8.60	8.29

3. Rebar parameter setting.

Rebar	Tensile modulus (MPa)	Poisson’s ratio	Cross-sectional area (mm²)	Spacing (mm)	Density (kg/m³)	Angle (∘)
Belt ply 0-degree	19025	0.3	1.50	2.22	7800	90
Belt ply 1	19025	0.3	2.06	2.08	7800	66
Belt ply 2	19025	0.3	2.06	2.08	7800	105
Belt ply 3	19025	0.3	1.02	2.50	7800	75
Bead wire	19025	0.3	1.50	1.65	7800	90
Ply	19025	0.3	2.06	2.08	7800	0

The 3D finite element model of the tire could be rotated from a 2D model due to its pronounced symmetry, as depicted in Figure 1. CGAX4H, CGAX3H, and SFMGAX1 element types were selected in the 2D model. In the 3D model, the corresponding transformations were C3D8H, C3D6H, and SFM3D4R. The number of elements in the 3D tire finite element model was 104828.

Details are in the caption following the image — Open in figure viewer PowerPoint

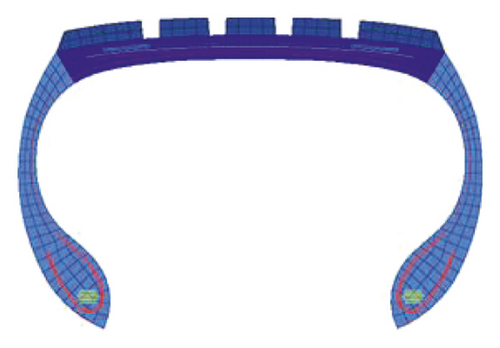
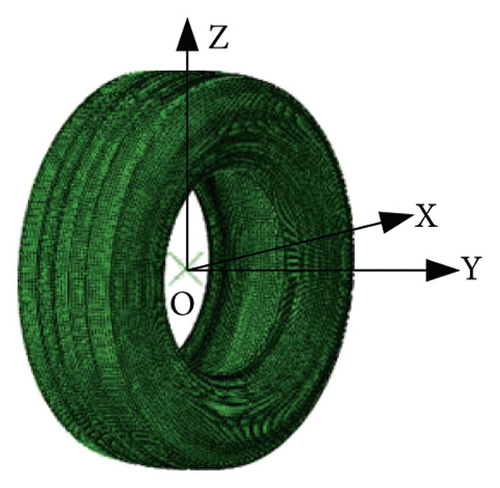
2.2. Asphalt Pavement Finite Element Model

Asphalt pavement is a typical semirigid base asphalt pavement. Its main structure includes the upper layer (modified SMA-13), middle layer (modified AC-20), lower layer (AC-25), base layer (cement-stabilized crushed stone), subgrade layer (lime soil), and soil layer, as illustrated in Figure 2.

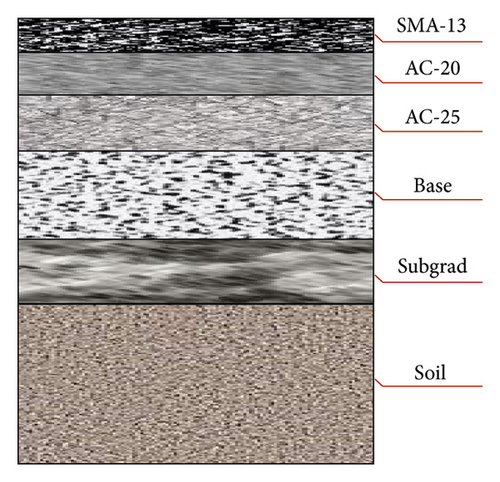
The upper layer, middle layer, and lower layer are viscoelastic. The base layer, sub-base layer, and soil layer are linear elastic. The parameters of each layer are listed in Table 4.

4. Asphalt pavement structure and parameters [20].

Structural layer	Thickness (mm)	Dynamic modulus (MPa)	Poisson’s ratio	Density (kg/m³⁾
SMA-13	4	—	0.3	2300
AC-20	6	—	0.3	2300
AC-25	8	—	0.3	2300
Base	40	1200	0.2	2200
Subgrade	20	300	0.3	2100
Soil	—	45	0.4	1800

Viscoelastic material is described by the generalized Maxwell model and expression is as follows:

(3)

(4)

(5)

where E(t) is the relaxation modulus, E_e is the equilibrium modulus, E_i is the relaxation strength, p_i is the relaxation time, G(t)is the shear modulus, μ is Poisson’s ratio, g(t) is obtained by normalizing G(t) by transient shear modulus, g_i is the constant material, τ_i is the delayed time, and N is number of the Prony series.

Viscoelastic parameters of asphalt mixtures can be obtained by the dynamic modulus test. Reference [21] was tested according to dynamic modulus test in the Chinese standard JTG E20-2011 [22]. Dynamic modulus was carried out for three asphalt mixtures (SMA-13, AC-20, and AC-25) by the simple performance tester (SPT). During the test, the temperature was set to 4.4^∘C, 15^∘C, 20^∘C, 40^∘C, and 54.5^∘Cand the load frequency was set to 0.1 Hz, 0.5 Hz, 1 Hz, 5 Hz, 10 Hz, and 20 Hz. The order of load frequency and the temperature were from low to high. Dynamic modulus and phase angle were automatically obtained by SPT. More details for test results can be found in Reference [21]. Dynamic modulus was transformed to the Prony series based on Equations (3)-(5). Table 5 provides the Prony series of viscoelastic materials at a reference temperature of 20^∘C.

5. Prony series of viscoelastic materials (20^∘C).

τ_i	g_i
τ_i	SMA-13	AC-20	AC-25
0.0001	0.06505	0.051952	0.028045
0.001	0.27209	0.222824	0.162232
0.01	0.27277	0.271189	0.258214
0.1	0.19323	0.216740	0.265024
1	0.10649	0.127760	0.177240
10	0.04989	0.061263	0.074611
100	0.01839	0.021408	0.021880
1000	0.00789	0.009682	0.004920
10000	0.01393	0.016890	0.007655
100000	0.00026	0.000291	0.000178

For the three-dimensional asphalt pavement finite element model, the plane geometric ranges from 1.12 m to 12 m, and the depth direction range is within 0.74 m to 12 m [23]. The contact length and width between the tire and asphalt pavement are 0.24 m and 0.32 m, respectively. Considering the load influence range and improving the calculation efficiency, the length, width, and depth of the asphalt pavement finite element model are set as 3 m, 2 m, and 2 m, respectively, where X-axis is tire running direction (longitudinal), Y-axis is asphalt pavement width direction (lateral), and Z-axis is asphalt pavement depth direction (vertical). Asphalt pavement was completely restrained at the bottom and symmetrically restrained in lateral and longitudinal directions. The interlayer contact of asphalt pavement was completely continuous. The element type was C3D8R, and the number of elements was 146899.

2.3. Development and Verification of Tire-Asphalt Pavement Contact Model

Tire-asphalt pavement contact model was developed using Abaqus software, as shown in Figure 3. In the finite element analysis, a hybrid Lagrange/Eulerian approach was used to realize the steady-state rolling of tire on asphalt pavement [24], where normal contact adopted the “hard contact” attribute, which is usually described by a penalty function (see (6)). Tangential contact is defined by Coulomb friction model (see (7)).

(6)

(7)

where f_n is the normal interaction force, K_n is the normal contact stiffness, C is the gap value of the contact node relative to the target surface, f_s is the tangential interaction force, K_t is the tangential stiffness, η^e is the elastic deformation of the contact node with respect to the target surface, and μ is the sliding friction coefficient.

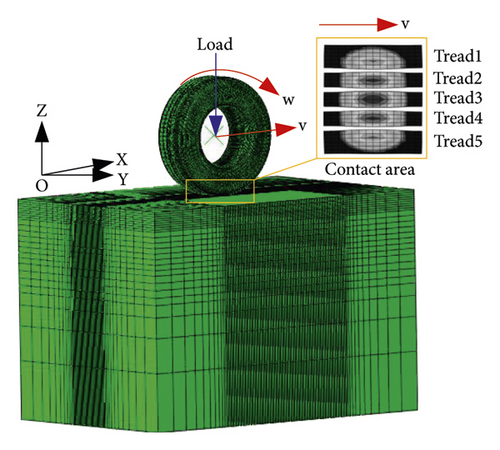
Contact morphology is directly related to the amount of tire deformation caused by load. Therefore, tire stiffness is an important indicator to measure the accuracy of tire-asphalt pavement contact model. The longitudinal, lateral, and vertical stiffness test datum were provided by the Kasaike Tire Company. They carried out the tire stiffness experiment in strict accordance with the Chinese standard [25].

It can be observed from Table 6 that the errors of tire stiffness simulation results were within the permissible range compared with experiment results (all less than 20%) [26]. Thus, the accuracy of tire-asphalt pavement contact model was verified.

6. Experiment and simulation tire stiffness results.

Result	Longitudinal stiffness (N/mm)	Lateral stiffness (N/mm)	Vertical stiffness (N/mm)
Simulation	823.95	551.33	1170.02
Experiment	813.62	513.17	1208.33
Error	1.27%	7.44%	3.17%

3. Tire Load

3.1. VTT Dynamics Model

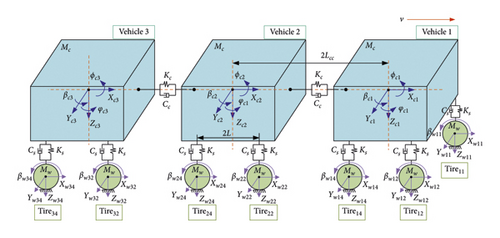
The VTT dynamics model considering was established (see Figure 4) to obtain tire load during the VTT maneuvering. It consisted of three vehicles, which were connected by a coupler device with stiffness and damping. Each vehicle was connected to its corresponding wheel by an independent suspension device with stiffness and damping. The magic formula model was used to describe the dynamic response of the rubber wheels.

3.2. Tire Load of the VTT

To adequately reflect contact morphology during the VTT maneuvering, tire dynamic load under typical running conditions was calculated, including uniform, braking, and cornering.

Vertical tire load is defined as follows:

(8)

Horizontal tire load is defined as follows:

(9)

where F_VDL and F_HDL represent vertical and horizontal (longitudinal and lateral) tire loads, respectively. F_vs and F_hs denote the static vertical and horizontal tire load, separately.

and

are the root mean square of the dynamic vertical and horizontal tire loads, respectively.

Running conditions were set as follows: (1) vehicle load was rated load. (2) Pavement grade was B. (3) Velocity under uniform and cornering conditions was 30 km/h. (4) Under braking condition, deceleration was −4m/s² and velocity changed from 60 km/h to 0 km/h. (5) Curve radius was 30 m. Vertical, longitudinal, and lateral tire loads (left tire, along velocity direction) under different running conditions are displayed in Tables 7-9, respectively.

7. Vertical tire load under different running conditions (kN).

Condition	Tire number
Condition	11	13	21	23	31	33
Static	35	31	33	33	31	35
Uniform	39.2	34.4	35.5	35.3	34.6	38.5
Braking	32.7	36.2	36.9	35.8	33.5	45.2
Cornering	48.1	42.8	45.0	44.8	42.2	48.2

8. Longitudinal tire load under different running conditions (N).

Condition	Tire number
Condition	11	13	21	23	31	33
Static	≈0	≈0	≈0	≈0	≈0	≈0
Uniform	793	695	719	716	701	778
Braking	14498	14533	14547	14529	14526	14558
Cornering	791	693	709	704	690	763

9. Lateral tire load under different running conditions (N).

Condition	Tire number
Condition	11	13	21	23	31	33
Static	≈0	≈0	≈0	≈0	≈0	≈0
Uniform	182	152	174	179	185	226
Braking	182	184	200	122	197	150
Cornering	9977	7974	8185	9489	4970	10399

It can be noted from Table 7 that the direction and magnitude of tire load under uniform, braking, and cornering conditions are more complex than those under static condition, which is closely related to running conditions (road grade, velocity, deceleration, curve radius, etc.,).

4. Results and Discussion

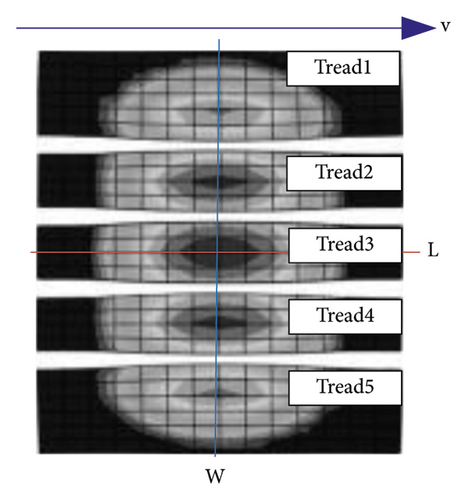
Due to the complex running conditions of the VTT and the large number of tires, it is difficult to analyze the contact morphology of each tire under each running condition. Therefore, tire load under typical running conditions was selected to analyze the variation law of contact morphology. This section analyzed contact morphology around contact stress and contact area. Figure 5 shows the schematic diagram of contact area.

4.1. Contact Morphology Analysis under Uniform Condition

Under uniform condition, no additional driving/braking torque was applied on tire. So, angular velocity was equal to velocity divided by free-rolling radius. Velocity was set to 30 km/h, tire pressure was set to 900 kPa, and tire load was set to 30 kN.

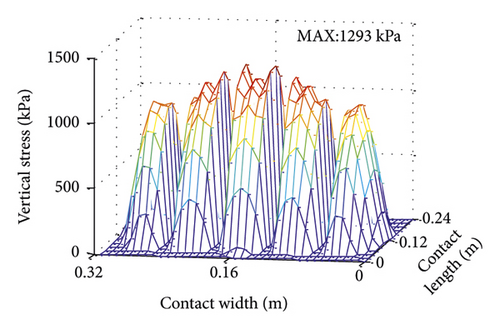
3D contact stress filed simulated from the tire-asphalt pavement contact model under uniform condition is shown in Figure 6. It can be seen that contact area presents rectangular. Vertical stress distribution is symmetrical along length and width directions, respectively. Vertical stress is concentrated in Tread 2, Tread 3, and Tread 4, with a maximum of 1293 kPa (in Tread 3). Longitudinal stress distribution is symmetrical along the width direction. The front side is positive and the rear side is negative along the length direction, with little difference in magnitude. Lateral stress distribution is symmetrical along the length direction. It alternates positive and negative along the width direction.

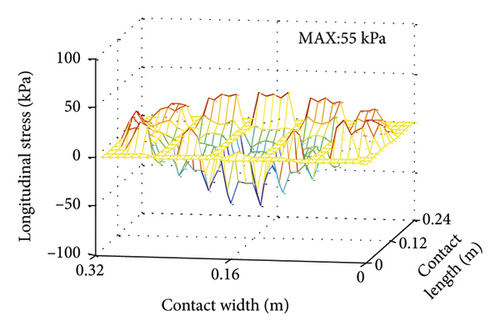
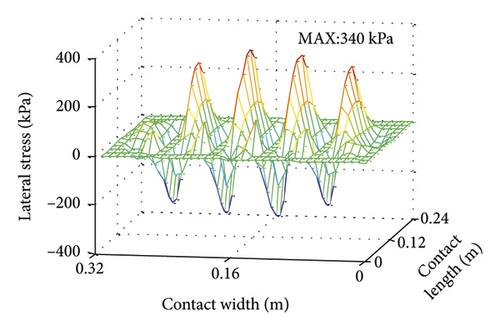
Under uniform condition, longitudinal and lateral stresses are smaller than vertical stresses. Therefore, longitudinal and lateral stresses are neglected in subsequent analysis of influencing factors.

4.1.1. Effect of Load on Contact Morphology

To analyze the effect of load on contact morphology, load was set to 20 kN, 30 kN, 40 kN, and 50 kN. Tire pressure and velocity were set to 900 kPa and 30 km/h, respectively.

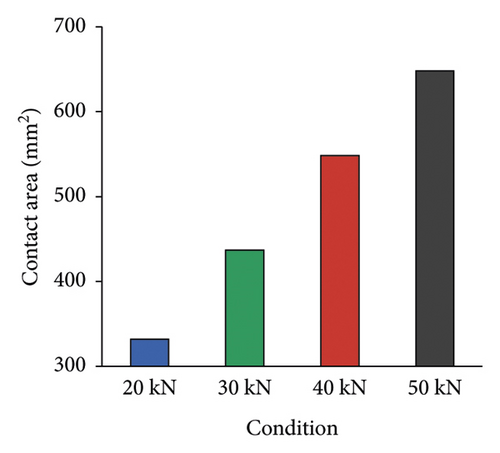
Contact area under different loads is shown in Figure 7. It can be seen that the contact area increases with the increase of load, where contact area under 50 kN is about 2 times larger than that of 20 kN.

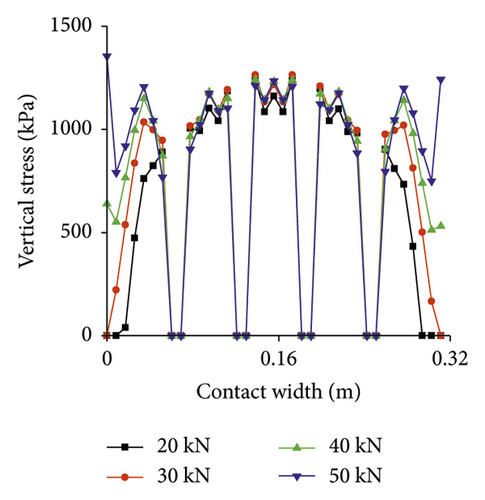
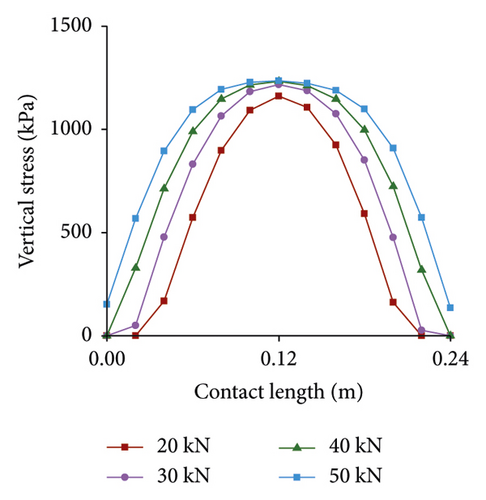
Vertical stress distribution under different loads is presented in Figure 8. Stress maximum increases with increasing load, but growth rate becomes slower, which is due to hyperelasticity of rubber material. As load increases, stress near the tire center increases less, while the edge tread increases significantly, especially Tread 1 and Tread 5. Stress appears as a “convex” shape along the length direction.

4.1.2. Effect of Tire Pressure on Contact Morphology

To analyze the effect of tire pressure on contact morphology, tire pressure was set to 720 kPa, 900 kPa, and 1080 kPa, corresponding to low pressure, rated pressure, and high pressure, respectively. Load and velocity were set to 30 kN and 30 km/h, respectively.

Contact area under different tire pressures is shown in Figure 9. Contact area decreases with the increase of tire pressure, in which contact area under high pressure decreases about 1.3 times than that of low pressure.

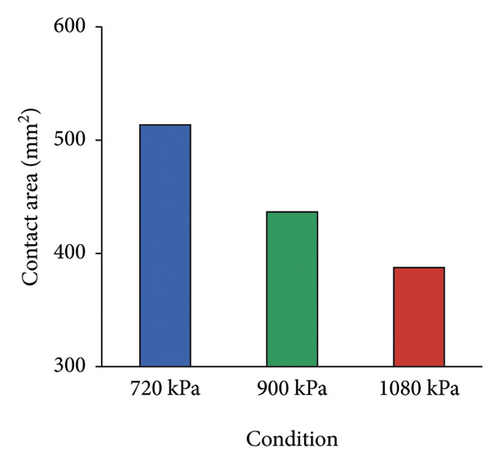
Vertical stress under different tire pressures is presented in Figure 10. It can be found that the distribution of stress is mainly concentrated in the tire center under high pressure, while it is more evenly distributed under low pressure. Overall, stress increases with the increase of tire pressure, and maximum under high pressure is 48% higher than that under low pressure.

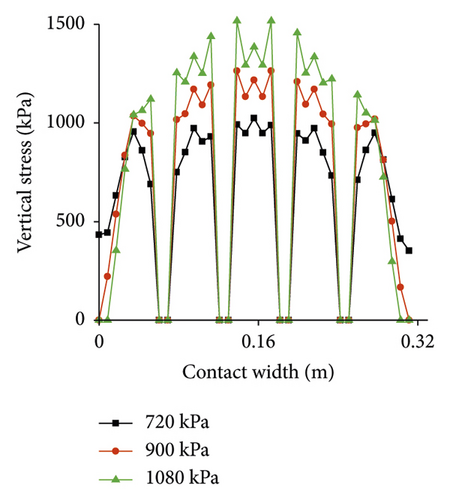
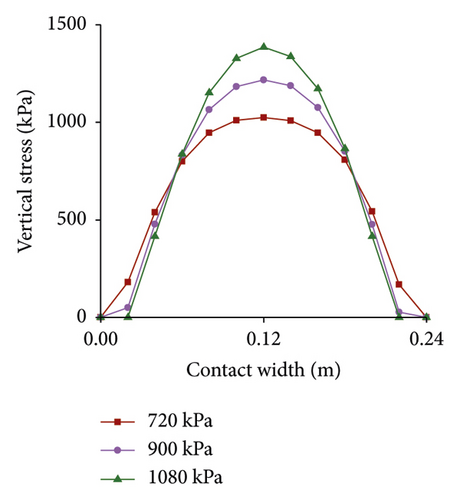
4.1.3. Effect of Velocity on Contact Morphology

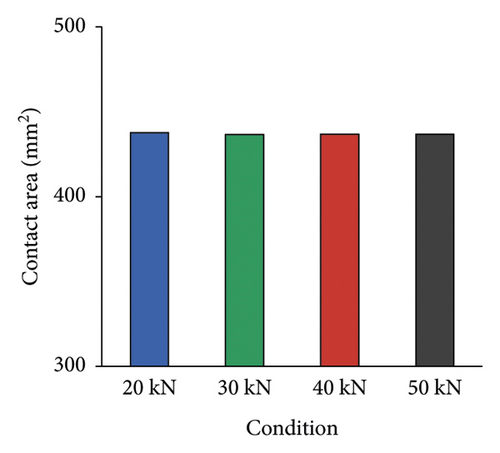
To analyze the effect of velocity on contact morphology, velocity was set to 10 km/h, 30 km/h, 50 km/h, and 70 km/h. Load and tire pressure were set to 30 kN and 900 kPa, respectively.

Contact area under different velocities is shown in Figure 11. There is basically no difference in contact area under different velocities.

Vertical stress under different velocities is presented in Figure 12. It can be found that the effect of velocity on stress is limited.

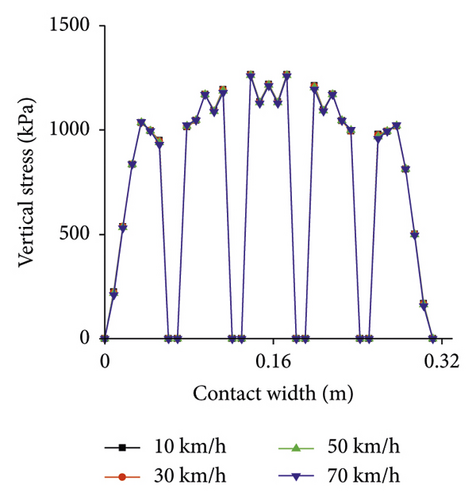
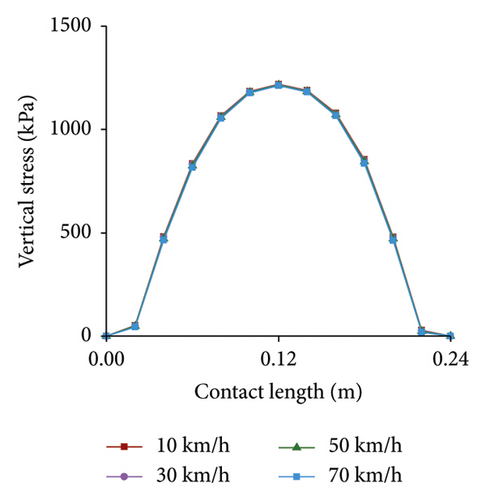
4.2. Contact Morphology Analysis under Braking Condition

Tire motion under driving or braking condition can be described using the relationship between velocity and angular velocity. Hence, slip rate s was introduced and its expression is as follows:

(10)

where v is the velocity, w is the angular velocity, and r is the rolling radius under uniform condition.

After calculation, it is found that when the slip rate reaches 0.08, the tire can have a relatively large braking effect. 3D contact stress field under full braking condition (s = 0.08) is presented in Figure 13. Vertical and longitudinal stresses have similar distribution rules, both symmetrical along the width direction. Due to the influence of longitudinal friction, the overall distribution of vertical and longitudinal stress is front and rear (along the length direction). The maximum values are evenly distributed in Tread 3, which are 1611 kPa and 1044 kPa, separately. Lateral stress distribution is the same as that under uniform condition.

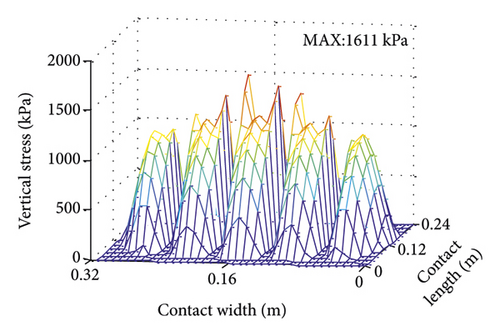
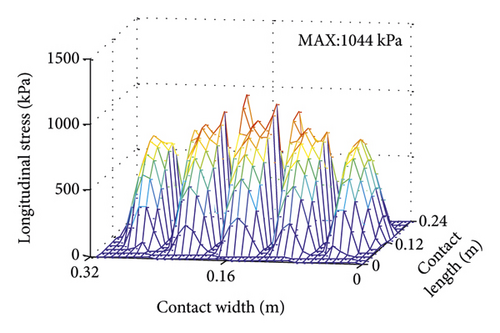
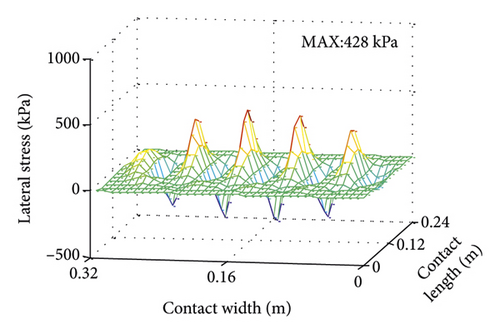
4.2.1. Effect of Slip Rate on Contact Morphology

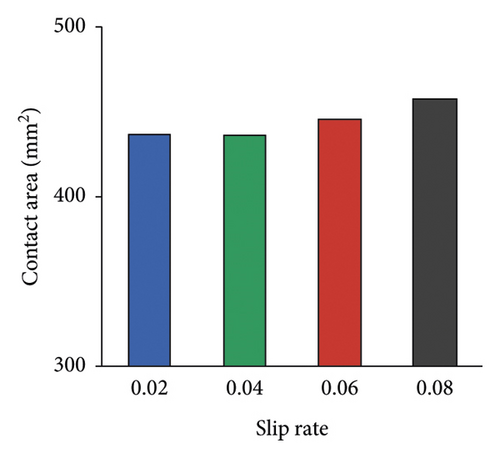
Contact area under different slip rates is shown in Figure 14. As slip rate increases, contact area tends to increase in general, but the change is small. Compared with 0.02, contact area at 0.08 only increases by about 4.8%.

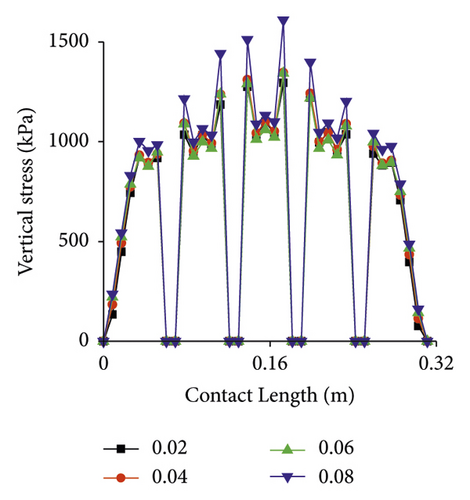
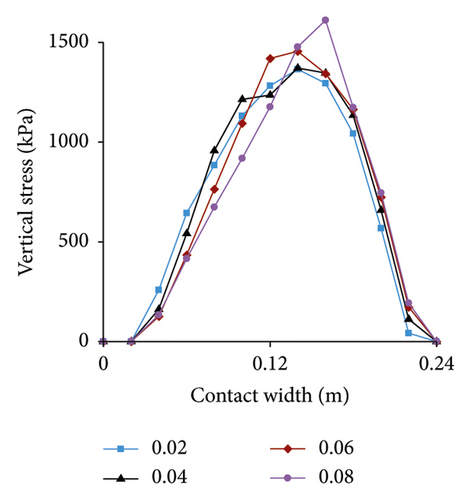
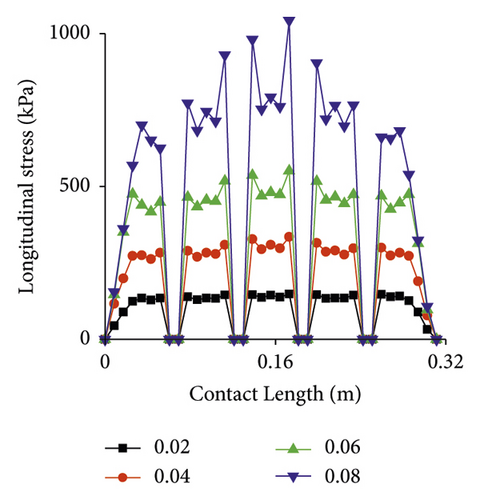
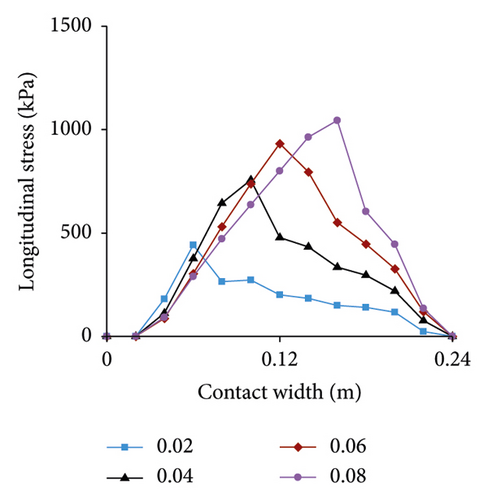
Vertical stress under different slip rates is presented in Figure 15. Vertical stress distribution is significantly affected by slip rate. As slip rate increases, the larger stress gradually moves toward the front side of contact area (along the length direction). The maximum value at 0.08 is a 25% increase compared to slip rate at 0.02.

Longitudinal stress under different slip rates is displayed in Figure 16. Similar to vertical stress, lateral stress is also greatly affected by slip rate, but more significantly than vertical stress. The maximum stress at 0.08 is 600% higher than at 0.02.

4.3. Contact Morphology Analysis under Cornering Condition

When a vehicle is passing through a curve, tire is subjected to lateral friction of pavement to balance the centrifugal force generated by the vehicle. Thus, slip angle occurs as tire corner.

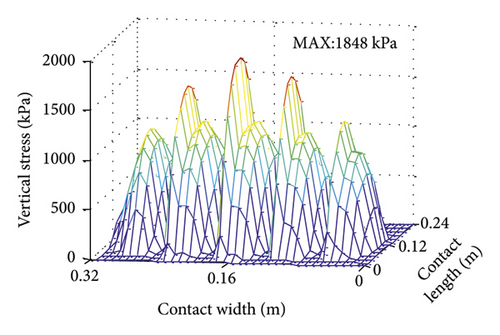
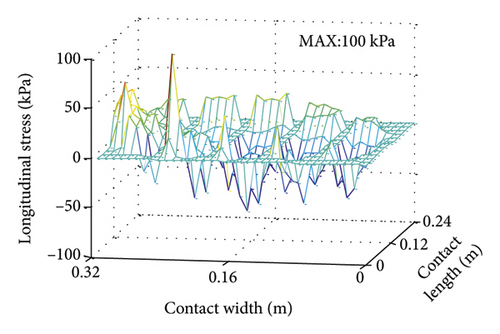
3D contact stress filed under cornering condition (slip angle is 2°) is presented in Figure 17. The distribution trends of vertical and longitudinal stress are consistent, and both are symmetrical along the length direction. Contact area is larger on the cornering inside and smaller on the cornering outside. Vertical and lateral stresses are concentrated on the inner side of the cornering, and the maximum stress appears at the edge of Tread 3 near the inner side of the cornering. Longitudinal stress distribution is approximately the same as under uniform condition.

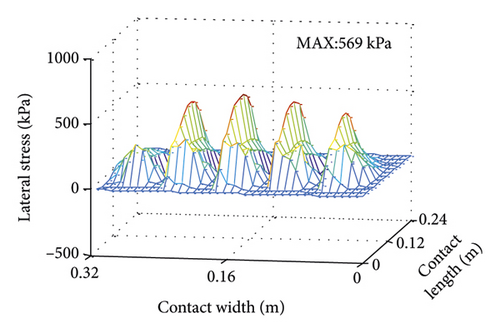
4.3.1. Effect of Slip Angle on Contact Morphology

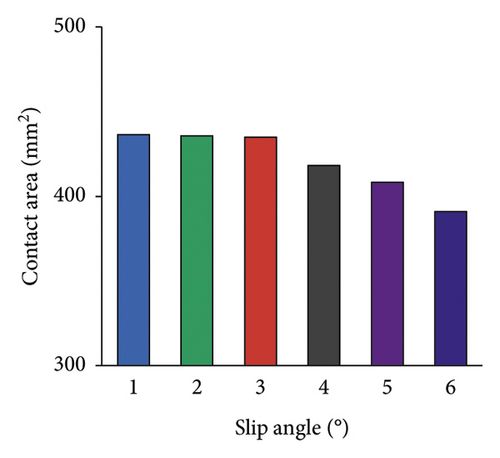
Contact area under different slip angles is shown in Figure 18. Contact area decreases with the increase of slip angle, and it reduces 1.1 times at 6° than at 1°.

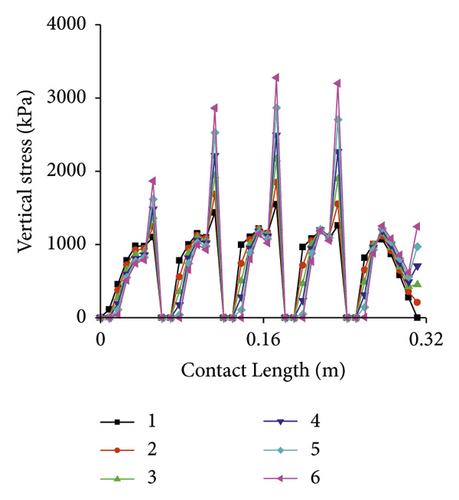
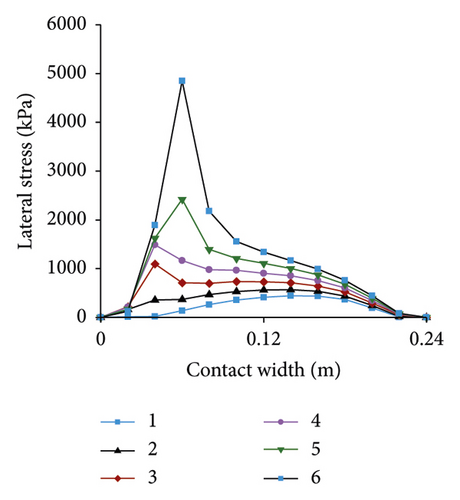
Vertical stress under different slip angles is presented in Figure 19. With the increase of slip angle, contact area decreases and lateral friction increases. Vertical stress is gradually concentrated mainly in each tread near the inner side of cornering and increases accordingly. The maximum stress value at 1° is 384% higher than that at 6°.

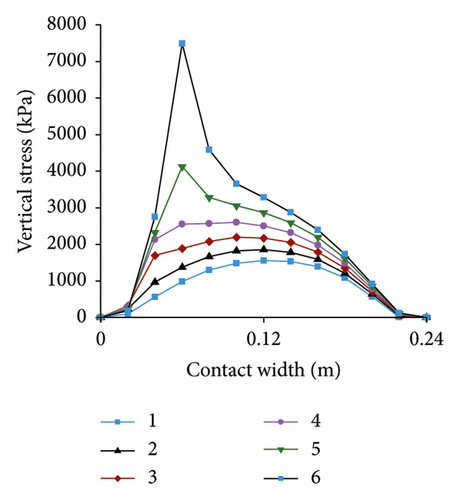
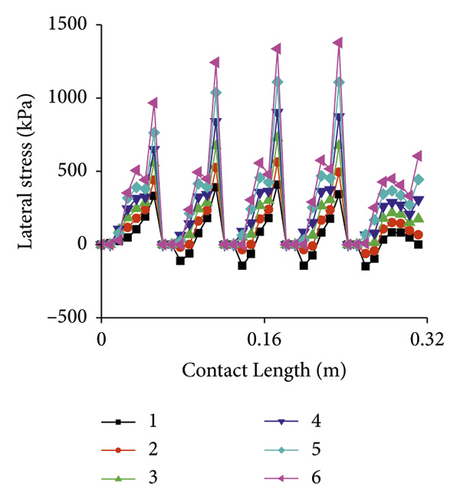
Lateral stress under different slip angles is displayed in Figure 20. The trend of lateral stress is similar to that of vertical stress. Lateral stress is mainly distributed in each tread near the inner side of the cornering. As slip angle increases, lateral stress gradually becomes positive and increases continuously.

5. Conclusions

To analyze contact area and contact stress under uniform, braking, and cornering conditions, the tire-asphalt pavement contact model was developed based on the Euler–Lagrange method. The contact morphology of the VTT during maneuvering was simulated and compared. The main conclusions are as follows:

Under uniform condition, vertical stress is symmetrical along the length. The larger stresses are concentrated on both sides of each tread along the width direction. Longitudinal stress is positive on the front side and negative on the back side along the length direction. Lateral stress alternates positive and negative along the width direction.

Under braking condition, the distribution of vertical and longitudinal stresses is similar. By the action of friction, both are wide in front and narrow in the rear along the length direction. Lateral stress distribution is basically the same as that of the uniform condition.

Under cornering condition, contact area on the inside of the cornering is larger, and vice versa is smaller. The distribution of vertical and lateral stresses is similar, and the larger values of both are concentrated on the tread on the inside of the cornering.

Contact area increases with the increase of load and decreases with the increase of tire pressure. The increase in load causes an increase in vertical stress, but the growth rate becomes slower. Higher tire pressure causes vertical stress to be concentrated mainly in tire center, while lower tire pressure results in a more uniform distribution. Velocity has a limited effect on contact morphology.

The increase of slip rate makes the distribution of vertical and lateral stresses change, and the larger stress increases with the increase of slip rate and moves to the front side of running direction. Longitudinal stress is more significantly affected by slip rate, which is 600% higher at 0.08 than at 0.02.

When slip angle gradually increases, contact area of the cornering inner side increases, and the cornering outer side decreases. Both vertical and lateral stresses increase, and the larger stresses are mainly distributed on the inner side of the cornering.

It can be clear from the analysis results that the contact morphology of the tire-asphalt pavement is significantly affected by the running conditions and related factors (load, tire pressure, slip rate, and slip angle). The analysis of contact area and stress distribution between tire and asphalt pavement during VTT maneuvering in this paper can be used to analyze pavement response and damage under typical running conditions. Furthermore, asphalt pavement is considered for the commonly used semirigid asphalt pavement structures. The design of materials, structures, and other conditions can be further developed in future research.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the Open Project Program of the State Key Laboratory of Traction Power of Southwest Jiaotong University (TPL2107), the National Key Research and Development Program of China (Research on the train load and rutting evolution of the virtual track train 2018YFB1201603-08), and the Shanghai Collaborative Innovation Center for Multi-Network and Multi-Mode Rail Transit (28002360012).

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 He H., Li R., Yang Q., Pei J., and Guo F., Analysis of the tire-pavement contact stress characteristics during vehicle maneuvering, KSCE Journal of Civil Engineering. (2021) 25, no. 7, 2451–2463, https://doi.org/10.1007/s12205-021-1306-0.
10.1007/s12205-021-1306-0
Web of Science® Google Scholar
2 Zhou H., Wang G., Ding Y., Yang J., Liang C., and Fu J., Effect of friction model and tire maneuvering on tire-pavement contact stress, Advances in Materials Science and Engineering. (2015) 2015, 11, https://doi.org/10.1155/2015/632647, 2-s2.0-84934325392, 632647.
10.1155/2015/632647
Web of Science® Google Scholar
3 Oubahdou Y., Wallace E. R., Reynaud P., Picoux B., Dopeux J., Petit C., and Nelias D., Effect of the tire-pavement contact at the surface layer when the tire is tilted in bend, Construction and Building Materials. (2021) 305, 124765, https://doi.org/10.1016/j.conbuildmat.2021.124765.
10.1016/j.conbuildmat.2021.124765
Web of Science® Google Scholar
4 Yu L., Hu J., Li R., Yang Q., Guo F., and Pei J., Tire-pavement contact pressure distribution analysis based on ABAQUS simulation, Arabian Journal for Science and Engineering. (2021) 47, no. 4, 4119–4132, https://doi.org/10.1007/s13369-021-05903-1.
10.1007/s13369-021-05903-1
Web of Science® Google Scholar
5 Zheng B., Chen J., Zhao R., Tang J., Tian R., Zhu S., and Huang X., Analysis of contact behaviour on patterned tire-asphalt pavement with 3-D FEM contact model, International Journal of Pavement Engineering. (2020) 23, no. 2, 171–186, https://doi.org/10.1080/10298436.2020.1736294.
10.1080/10298436.2020.1736294
Web of Science® Google Scholar
6 Guo M. and Zhou X., Tire-pavement contact stress characteristics and critical slip ratio at multiple working conditions, Advances in Materials Science and Engineering. (2019) 2019, 11, 5178516, https://doi.org/10.1155/2019/5178516, 2-s2.0-85071141399.
10.1155/2019/5178516
Web of Science® Google Scholar
7 Han D., Zhu G., Hu H., and Li L., Dynamic simulation analysis of the tire-pavement system considering temperature fields, Construction and Building Materials. (2018) 171, 261–272, https://doi.org/10.1016/j.conbuildmat.2018.03.071, 2-s2.0-85044459092.
10.1016/j.conbuildmat.2018.03.071
Web of Science® Google Scholar
8 Cao P., Zhou C., Jin F., Feng D., and Fan X., Tire–pavement contact stress with 3D finite-element model—Part 1: semi-steel radial tires on light vehicles, Journal of Testing and Evaluation. (2016) 44, no. 2, 20150234, https://doi.org/10.1520/jte20150234, 2-s2.0-84962798310.
10.1520/jte20150234
Web of Science® Google Scholar
9 Wang H., Al-Qadi I. L., and Stanciulescu I., Simulation of tyre–pavement interaction for predicting contact stresses at static and various rolling conditions, International Journal of Pavement Engineering. (2012) 13, no. 4, 310–321, https://doi.org/10.1080/10298436.2011.565767, 2-s2.0-84862664359.
10.1080/10298436.2011.565767
Web of Science® Google Scholar
10 Ivanov V., Analysis of tire contact parameters using visual processing, Advances in Tribology. (2010) 2010, 11, 491723, https://doi.org/10.1155/2010/491723, 2-s2.0-77955388570.
10.1155/2010/491723
Google Scholar
11 Hernandez J. A. and Al-Qadi I. L., Contact phenomenon of free-rolling wide-base tires: effect of speed and temperature, Journal of Transportation Engineering. (2016) 142, no. 12, 04016060, https://doi.org/10.1061/(asce)te.1943-5436.0000893, 2-s2.0-84997096252.
10.1061/(ASCE)TE.1943-5436.0000893
Google Scholar
12 Zhang A. Q. and Yao Z. Y., Tire contact pressure distribution and its test method, ’ Rubber Industry. (2001) 48, 368–374.
Google Scholar
13 Wu C., Wang H., Zhao J., Jiang X., Yanjun Q., and Yusupov B., Prediction of viscoelastic pavement responses under moving load and nonuniform tire contact stresses using 2.5-D finite element method, Mathematical Problems in Engineering. (2020) 2020, 18, 1029089, https://doi.org/10.1155/2020/1029089.
10.1155/2020/1029089
Web of Science® Google Scholar
14 Dong Z. and Ma X., Analytical solutions of asphalt pavement responses under moving loads with arbitrary non-uniform tire contact pressure and irregular tire imprint, Road Materials and Pavement Design. (2017) 19, no. 8, 1887–1903, https://doi.org/10.1080/14680629.2017.1354776, 2-s2.0-85025475158.
10.1080/14680629.2017.1354776
Web of Science® Google Scholar
15 Du Z., Wen X., Zhao D., Xu Z., and Chen L., Numerical analysis of partial abrasion of the straddle-type monorail vehicle running tyre, Transactions of FAMENA. (2017) 41, no. 1, 99–112, https://doi.org/10.21278/tof.41109, 2-s2.0-85018748426.
10.21278/TOF.41109
Web of Science® Google Scholar
16 Hernandez J. A. and Al-Qadi I. L., Tire–pavement interaction modelling: hyperelastic tire and elastic pavement, Road Materials and Pavement Design. (2016) 18, no. 5, 1067–1083, https://doi.org/10.1080/14680629.2016.1206485, 2-s2.0-84978726707.
10.1080/14680629.2016.1206485
Web of Science® Google Scholar
17 Wollny I., Behnke R., Villaret K., and Kaliske M., Numerical modelling of tyre–pavement interaction phenomena: coupled structural investigations, Road Materials and Pavement Design. (2015) 17, no. 3, 563–578, https://doi.org/10.1080/14680629.2015.1094399, 2-s2.0-84945217509.
10.1080/14680629.2015.1094399
Web of Science® Google Scholar
18 Wang H., Al-Qadi I. L., and Stanciulescu I., Effect of surface friction on tire–pavement contact stresses during vehicle maneuvering, Journal of Engineering Mechanics. (2014) 140, no. 4, 04014001, https://doi.org/10.1061/(asce)em.1943-7889.0000691, 2-s2.0-84896267069.
10.1061/(ASCE)EM.1943-7889.0000691
Web of Science® Google Scholar
19 Gb/T2977-2016, Specification, Size, Air Pressure and Load of Truck Tires, 2016, National Technical Committee for Tire and Rim Standardization, Beijing, China.
Google Scholar
20 Liao G. Y. and Huang X. M., Application of ABAQUS Finite Element Software in Pavement Engineering, 2014, Southeast University Press, Nanjing, China.
Google Scholar
21 You Y. J., Research on Dynamic Modulus of Asphalt Mixtures, 2017, Shandong Jianzhu University, Master.
Google Scholar
22 JTG E20-2011, Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering, 2011, Beijing, China.
Google Scholar
23 Xiao C., Study on Dynamic Behavior of Typical Asphalt Pavement and its Structural Combination Optimization, 2014, Southwest Jiaotong University, Ph.D.
Google Scholar
24 Wang Y., Research on Mechanical Behavior of Asphalt Pavement under Complex Tire Force, 2017, Beijing Jiaotong University, Ph.D.
Google Scholar
25 Gb/T 23663-2009, Test Method of Automobile Tyre Longitudinal and Lateral Stiffness, 2009, Beijing, China.
Google Scholar
26 Liu P., Ravee V., Wang D., and Oeser M., Study of the influence of pavement unevenness on the mechanical response of asphalt pavement by means of the finite element method, Journal of Traffic and Transportation Engineering. (2018) 5, no. 3, 169–180, https://doi.org/10.1016/j.jtte.2017.12.001, 2-s2.0-85048896051.
10.1016/j.jtte.2017.12.001
Google Scholar
27 Wang C. P., Zhang J. M., Zhou H. C., and Lu H., Analysis of the running quality and road friendliness of the virtual track train in multiple running stages between stations, Journal of Mechanical Science and Technology. (2022) 36, no. 2, 593–605, https://doi.org/10.1007/s12206-022-0107-9.
10.1007/s12206-022-0107-9
Web of Science® Google Scholar

Citing Literature

All articles

Analysis of Tire-Pavement Contact Morphology Characteristics during the Virtual Track Train Maneuvering

Abstract

1. Introduction