With the widespread use of intelligent teaching, data containing student performance information continues to emerge, and artificial intelligence technology based on big data has made a qualitative leap. At present, the prediction of college students’ sports performance is only based on the past performance, and it does not reflect the student’s training effect very well. In order to solve these problems, this paper puts forward the analysis and simulation of college sports performance fusion with adaptive federated deep learning algorithm, aiming to study the influencing factors of student sports performance and suggestions for improvement. This paper uses an adaptive federated learning method and a personalized federated learning algorithm based on deep learning and then proposes a student performance prediction method. These methods integrate the quantitative methods of motor skill assessment and establish standards for college students, which are good standards for evaluating college students’ sports skills. This paper adopts the performance prediction framework and then establishes the sports performance prediction model. Through the analysis of sports performance analysis examples, it is concluded that the model proposed in this paper can accurately predict the student’s sports performance, and the average accuracy rate of each sports item has reached 91.7%.

1. Introduction

1.1. Background

The contradiction between the demand for physical and mental health in today’s society and the continuous decline in the physical and mental health of young people is attracting attention from all walks of life. Physical health is the basis for a person’s all-round development, and physical fitness is an important part of health and an important content of quality education. Federated learning is essentially a distributed machine learning technology and a machine learning framework. The rapid development of university informatization and the continuous advancement of software engineering technology have promoted the process of education informatization in China. Teachers have accumulated a large amount of student learning data in the education process, but these data are currently only stored in the system’s database and have no real effect. Through data mining technology, users can obtain useful knowledge and discover relevant laws from these data and information. These data can provide good decision-making basis for optimizing all links of education and improving the quality of education.

1.2. Significance

The performance prediction warning is to predict the student’s final grade through various data reflecting the student’s learning situation during the learning process and to give early warning to those who may fail in their academic performance. Therefore, studying the prediction model of curriculum performance has important practical significance in improving the quality of education and reducing the dropout rate of students. Aiming at physical education in a Chinese university, this paper studies a performance prediction model based on adaptive correlation deep learning algorithm and uses this model to build a course performance early warning system. This article focuses on the issue of college sports, will strengthen the work of college sports, enhance the quality of students, promote the overall development of students, and further emphasize the value and importance of research, so as to better play the leading role of the evaluation mechanism. This research establishes a scientific and reasonable student quality evaluation index system, which has specific theoretical and practical significance for effectively promoting the health of students.

1.3. Related Work

Federated learning and deep learning are currently hot research topics, and there are more and more application fields. Liu et al. introduced a privacy protection machine learning technology called federated learning and proposed a gated recurrent unit neural network algorithm based on federated learning for traffic prediction. The algorithm he proposed is different from the current centralized learning method. In the security parameter mechanism, data privacy can be effectively guaranteed [1]. Manias and Shami proposed federated learning and deployed a joint model on the transportation infrastructure through ITS case studies to improve the ability of automobiles to recover from failures using smart technology, while reducing recovery time and improving compatibility [2]. Ahmed et al. proposed an embedding model based on federated learning for transaction classification tasks, which can learn low-dimensional continuous vectors through high-frequency trading commodities. They conducted in-depth experimental analysis on the amount of high-dimensional transaction data to verify the performance of the development model based on the attention mechanism and federated learning [3]. Alguliyev et al. proposed a deep learning method for big data privacy protection analysis, which converts the sensitive part of personal information into nonsensitive data. In order to reduce the loss in data conversion, they added the sparsity parameter to the objective function of the autoencoder through the Kullback-Leibler divergence function [4]. Khan et al. proposed a two-stage calculation model based on deep neural networks, which uses standard learning methods to automatically extract information features from RNA sequences. The method they proposed does not require a lot of ergonomics and professional knowledge to design an accurate recognition model [5]. The deep learning model proposed by Farooq and Bazaz can intelligently adapt to the new ground reality in real time. Every time a new data set is received from evolving training data, there is no need to retrain the model from scratch. The model was validated with historical data, and a 30-day forecast of disease transmission was given in the five states most severely affected by the new coronavirus in India [6]. Voegele et al. proposed a performance prediction method, which aims to automatically extract and convert workload specifications for load testing and model-based performance prediction of session-based application systems. This method (WESSBAS) includes three main components, hierarchical modeling of workload specifications that are not related to systems and tools and converting instances into executable workload specifications for load generation tools and model-based performance evaluation tools [7].

1.4. Innovation

The prediction model proposed in this paper has a certain impact on the cultivation of students’ comprehensive physical quality and overall development. Experimental results show that a variety of strategy selection methods based on deep learning algorithms can allow quantitative models to help schools formulate strategies. In this article, the author will train neural networks by creating samples to innovate performance prediction models.

2. Adaptive Federated Deep Learning Algorithm

2.1. Adaptive Federated Learning Method

Federated learning is a distributed machine learning method. The training data used for model learning is scattered on each mobile device, and all training of the model is realized through iterative global aggregation and update. Considering an actual distributed data training scenario, there are currently N scattered clients, and the whole composed of these clients is represented as a user set P, that is, ∣P | = N. Each client n has a local data set S_n that is kept and controlled by itself, and the amount of data contained in it is D_n, that is, ∣S_n | = D_n, the total amount of data in the client set P is denoted as

. Assuming that these data are collected together in a centralized manner to train a neural network model, the weight parameter W of the model obeys an m-dimensional real number space. Then, the expression of the loss caused by the model fitting the ith sampled data point (x_i, y_i) is shown in

(1)

In the process of model learning, this paper continuously optimizes the loss function through optimization algorithms [8]. In order to find the optimal model parameters, the value of the loss function is minimized, and the training process of the neural network is regarded as an optimization problem. The definition of neural network optimization goal is shown in

(2)

Now, considering the scattered form of data, for each client n, all data on the device can be regarded as a partition of global data, and the loss caused by this data partition is shown in

(3)

Then, the global optimization goal defined in formula (2) can be rewritten into the form shown in

(4)

If the data partition S_n is formed by uniformly randomly distributing the global training samples on the client set P, this means that all global samples obey an implicitly unknown distribution. The training data on the client is equivalent to being sampled independently from this distribution, so the data of each client in the set P can be regarded as subject to independent and identical distribution (IID) [9]. In probability theory and statistics, IID data collection means that the random variable represented by each data has the same probability distribution as other variables, and all variables are independent of each other. In this case, the optimization training of the model conforms to the independent and identical distribution assumption of the traditional distributed optimization problem. Then, the value of the global loss function f(W) is equivalent to the expectation of the local loss function on each data partition S_n, that is, formula (5) holds. In contrast to this, if the data partitions S_n on the set P are not formed by the uniform random distribution of the global training samples, then the data of each client in the set P does not obey the independent and identical distribution (non-IID) [10].

(5)

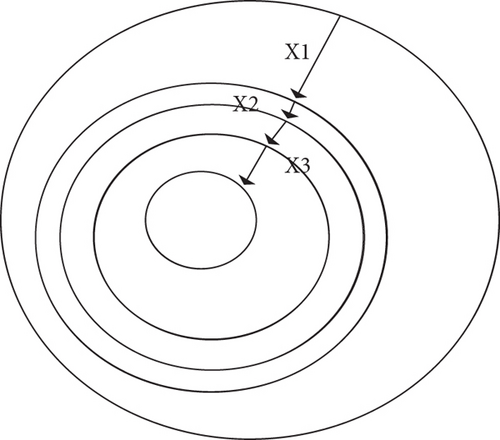
In summary, for training data scattered on multiple clients, the global optimization problem in the learning process of the model can be transformed into the sum of multiple local problems and distributed to each client for joint solution. This is also the prototype of the idea of federated learning. The calculation process of federated learning can be described with reference to Figure 1. Assuming that a certain function as an optimization target is defined on a plane, and its graph has a bowl shape, the blue curve is a contour line, that is, this line represents a constant value of the function.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Principle of gradient descent.

In order to optimize the communication cost of federated learning and improve its efficiency, it is necessary to analyze and elaborate its communication process in detail [11]. The network protocol of the federated learning architecture is shown in Figure 2. The participants of the protocol are client devices and servers, and the latter provides a cloud-based distributed service platform.

In the process of federated average Fed Avg, the algorithm adds a complete gradient descent step to each device to improve communication efficiency. The specific implementation is that in each round of global training, each client performs a complete gradient update calculation and then implements the gradient descent process, thereby calculating the local model parameter update

, as shown in

(6)

because the parameter update of the global model performed on the server can be expressed in the form shown in.

(7)

Therefore, combining formulas (6) and (7), the parameters of the global model can be calculated by the method shown in

(8)

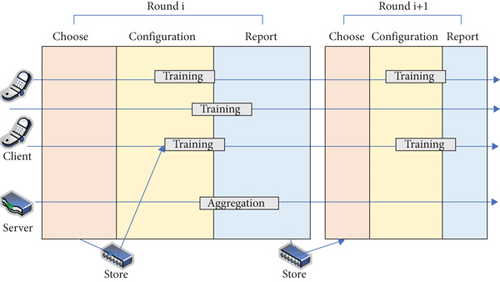
Therefore, after each client n calculates the parameter update of its own local model, it uploads it to the server for global aggregation to obtain the parameter update of the global model. Then, the server starts the next round of iteration and distributes the model obtained from the previous round of training to the device to train the next round of updates. through the implementation of a complete gradient descent and model update operations on the device. The Fed Avg algorithm provides better performance than Fed SGD and reduces communication overhead. Therefore, this algorithm is regarded as a standard algorithm for federated learning, has a high degree of recognition, and is widely used [12].

2.2. Personalized Federated Learning Algorithm Based on Deep Learning

In federated learning, it is assumed that there are N clients Ci, i = 1 ⋯ N, which jointly learn together under the scheduling of the central server. Define the data set on all clients as D = {D1, ⋯Di}, i = 1, ⋯N and the corresponding data set on each client as Di. Assume that the data set on each client obeys a distribution Pi, and the size of each data set is ∣Di∣. For each data set, each item is (x, y), where x ∈ R is the corresponding input feature. Define the loss function on each client as

. Assuming that wi is a model parameter corresponding to each client, the model on each client can be expressed as

, and the optimization goal for each client is:

(9)

Putting

into the above formula, it can get the following expression:

(10)

The federated average algorithm is an algorithm under the classic federated framework. The algorithm obtains the final model by optimizing the aggregate value of the loss function on the client side [13]. The federated average algorithm is a learning algorithm for the global model, so the model parameters on each client are the same, that is, w = w₀ = w₁ = ⋯ = w_i. The optimization goals of the federated average algorithm are:

(11)

where N represents the number of clients, B represents the size of the local training batch, E represents the local training round, T represents the entire representative round [14], and β represents the rate of learning. Figure 3 shows a schematic diagram of independent identically distributed and nonindependently identically distributed sampling when the number of clients is 4, the overall data category is 3, and the data category sampled on each client is 2.

After determining the setting of the calculation parameters, this article compares the parameter settings in Table 1.

Table 1. Federated averaging algorithm exploration operation parameters.

Numbering	Data set	Data distribution	Calculation	Total client	Number of categories	Number of training sets
3-1-1	MNIST	IID	Independent calculation	9	9	2600
3-1-2	MNIST	IID	Federated computing	9	9	2600
3-1-3	MNIST	NIID	Independent calculation	9	9	2600
3-1-4	MNIST	NIID	Federated computing	9	9	2600
3-1-5	EMNIST	IID	Independent calculation	9	18	3600
3-1-6	EMNIST	IID	Federated computing	9	18	3600
3-1-7	EMNIST	NIID	Independent calculation	9	18	3600
3-1-8	EMNIST	NIID	Federated computing	9	18	3600

The method used in the comparison operation is the federated average learning algorithm (FedAvg). The main purpose of computational exploration is to explore the influence of personalized federated data sets constructed by different data sets on the algorithm, explore the influence of different data distributions on the results of the algorithm, and explore the difference between the results of local independent calculation methods and the use of federated average calculation methods [15]. For any two clients C_i and C_j, suppose they receive the model parameter w at the same time. After the partial update procedure of the client, the updated parameters on the two clients are w_i and w_j. Then, the update of the corresponding gradient for each client is:

(12)

The correlation between the two clients based on the model parameter w is defined by the cosine similarity of the gradients uploaded by two clients, as shown in the following formula:

(13)

Specifically, the randomly initialized global model is sampled, and the number of samples in this paper is 100. The global initialization model for each sampling can calculate the similarity value sim(i, j) between any two clients. The mean value of the similarity of 100 samples is counted as E[sim(i, j)]. Through the analysis of these calculation results, some important factors related to personalization can be discovered. Table 2 shows the corresponding calculation results.

Table 2. Federal average experimental results (%).

Numbering	c1	c2	c3	c4	Average
3-1-1	88	82.5	84.9	83.4	84.7
3-1-2	80.2	81.2	84.5	82	81.975
3-1-3	81.4	86.5	83.5	89.3	85.175
3-1-4	81.9	87.7	81.6	81.7	83.225
3-1-5	83.3	85	85.7	84.3	84.575
3-1-6	85.2	80.9	80.9	87.7	83.675
3-1-7	87.9	86.2	89.7	87.3	87.775
3-1-8	85.5	80.2	80.8	83.5	82.5

The analysis of the calculation results can be considered that if each client can obtain a positive gain in a nonindependent and identically distributed scenario, then personalized learning can be well realized [16].

Generally, assuming that the parameter of the model is w, define a model based on this parameter, denoted as fw. When the initialization parameters are applied to a new task T_i, based on the stochastic gradient descent algorithm, the parameters of the model will change from w to

, then the change of the parameters can be represented by formula (14), where L represents the loss function and β represents the learning rate on the task, which is a hyperparameter.

(14)

Through the federated average learning algorithm, the key factors related to personalization in federated learning are explored. This section proposes a personalized federated learning algorithm based on deep learning. The core is to model the correlation between clients [17]. The algorithm includes personalized algorithms for the client and server, and different weights are assigned to the client through correlation, and a personalized integration strategy is realized.

2.3. Methods of Predicting Student Performance

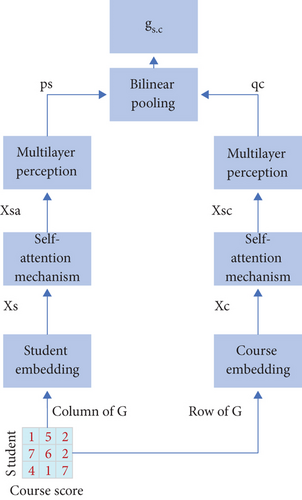
In the input layer, construct the grade matrix of T semester student-course data as G, G⁽ⁿ⁾ is the row vector of the student’s score for each course, and G_j is the column vector of each student’s score in different courses. In the formula, (i, j) ∈ Ω, this article uses G⁽ⁿ⁾ and G_j as the prediction model input [18].

This article maps and projects the rows and columns of the performance matrix and summarizes the hidden features of athletes and courses. Since the constructed score matrix is very sparse, embedding layer mapping can be used to reduce the dimensionality of the data and reduce the sparseness of the data. It uses formula (15) to perform nontraditional operations. For the hypothetical score formula G_nj, there are:

(15)

Among them, xs, xc ∈ G^k are the potential special factors of the students and the potential special factors of the course, respectively. Ws ∈ G^m×k, Wc ∈ G^k×n is the characteristic corresponding ratio matrix of athletes and sports items. The noncalculated result uses the commonly used activation function Tanh function. Different weight values are added to the student potential feature vector and the curriculum potential feature vector. Each student’s performance and each sport’s characteristics have different importance, which can be transformed according to the following formula:

(16)

Among them, W_sa and W_ca are proportional factors, xsa, xca is divided into student potential feature vector and course potential feature vector [19]. Among them, multilayer perception is transformed according to formula (17). Its purpose is to simulate the special structure of the data and perform two-layer nonlinear mapping of the hidden personality of students and the hidden characteristics of sports items:

(17)

The result of the performance deduction in this article is expressed as the result of the product. This article uses bilinear pooling to obtain the predicted value of the performance. Its main function is to reduce the amount of calculation while reducing the dimensionality, prevent the model from overfitting, and improve the generalization ability of the model. The output value is converted in the bilinear pooling layer as follows:

(18)

Among them, K is the proportional factor, ∗ in the formula represents Hadamard, and Q is the activation formula. Simulate T academic year’s sports performance, specifically expressed as:

(19)

Among them, W is the set of unknown parameters in the model, and

is the deduction result of the formula output by the nonlinear pooling layer [20]. Use ps(ps ∈ G^k), qc(qc ∈ G^k) to represent the potential k dimension characteristics of students s and courses c. The deduction performance of the athlete s in the sports project c can be calculated as:

(20)

This formula can predict students’ grades in the T semester. The structure of student performance prediction method based on deep learning is shown in Figure 4.

3. Performance Prediction Model Experiment and Analysis

3.1. Performance Prediction Framework

In order to verify the accuracy of the performance prediction model proposed in this paper, this paper designs two experiments: (1) multisource small sample, focusing on the fusion of multispatial data and the impact of multidimensional behavior on academic performance [21]; (2) single-source large sample, focusing model’s prediction accuracy for large sample and the difference in behavior patterns of different groups of students in liberal arts and sciences. The research framework of this article is shown in Figure 5.

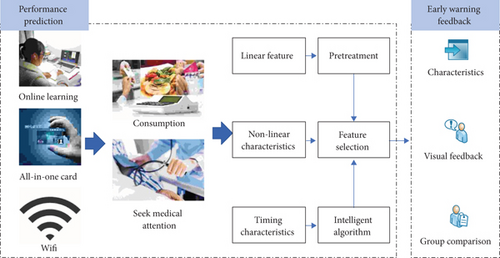
It can be seen from Figure 5 that this research framework is mainly composed of academic prediction and early warning feedback. The main data sources of this research include digital educational administration system, all-in-one card, and cloud classroom online learning data. In this article, the experiment attempts to build a multidimensional behavioral quantitative calculation system to ensure the protection of secret data, encrypt key personal information, and divide the academic performance into various intervals based on the average score [22]. The early warning feedback part includes providing feedback and early warning to high-risk students based on the predicted results.

This article establishes a classification model based on machine learning algorithms to predict academic performance and builds classification models based on five machine learning algorithms: RF random forest, GBRT gradient boosting decision tree, KNN nearest neighbor, SVM support vector machine, and extreme gradient boosting XGBoost. Table 3 shows the experiments and experimental results to verify the prediction results.

Table 3. Experimental classification results.

Data	Feature	Algorithm	Accuracy	Precision	Recall	AUC
D1 (SPOC)	C-1	RF	0.114	0.502	0.459	0.533
		GBRT	0.439	0.343	0.909	0.604
D2 (all-in-one card)	C-2	KNN	0.606	0.542	0.230	0.702
		SVM	0.018	0.534	0.615	0.527
D3 (WiFi)	C-3	XGBoost	0.723	0.906	0.128	0.181

RF (random forest), GBDTm and XGBoost all belong to the ensemble learning model. The purpose of ensemble learning is to improve the generalization ability and robustness of a single learner by combining the prediction results of multiple base learners. That is, there is a strong dependency between individual learners and a serialization method that must be generated serially, and there is no strong dependency between individual learners and a parallelization method that can be generated at the same time. The former is represented by boosting, and the latter is represented by bagging and “random forest.”

Although the five machine learning algorithms have their own performance advantages, in general, the classification performance of the five machine learning algorithms has a small gap on this data set [23]. The experimental result is that more data sources can make the prediction results more accurate. In order to better illustrate this point, this study considered the performance prediction model based on SVM and also compared the performance of three different feature combinations, as shown in Figure 6.

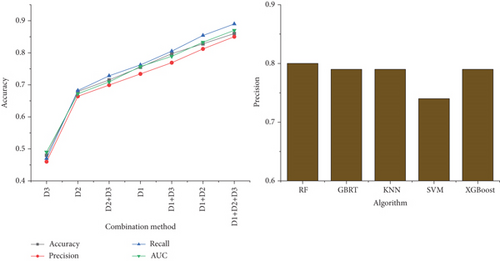
As shown in Figure 6, from DI to D1+D2 and DI+D2+D3, all five classification evaluation indicators increase significantly with the increase of data source types. This experiment proves that richer data sources help to explore the deep-level mechanism of student behavior. All five evaluation indicators of C-3 (accuracy, accuracy, recall, f, and AUC) are significantly higher than C-1 and C-2. This result shows that the multifeature combination (namely, C-3) proposed in this research can significantly improve the predictive ability of academic performance.

In addition, this article calculates and supplements six other indicators and also calculates the Pearson correlation r between these indicators and academic performance. The closer the absolute value of r is to 1 or -1, the stronger the correlation between the two, and the closer r is to 0, the weaker the correlation between the two. The index evaluation is shown in Figure 7.

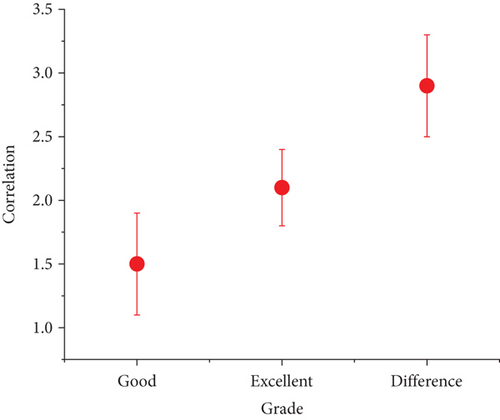
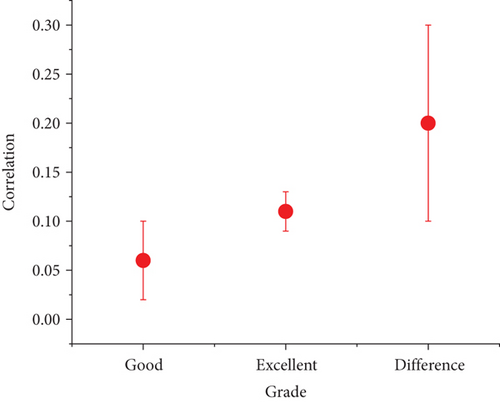
In the smart campus environment, this study collected student behavior data noninvasively, established a high-precision sports performance prediction model, and provided a basis for decision-making for college administrators [24]. This research has obtained conclusions on the behavior patterns of students with different liberal arts backgrounds and their impact on academic performance, which will help managers to further guide and optimize students’ daily behaviors.

3.2. Establishment of Sports Performance Prediction Model

The research of performance prediction model is to predict the specific aspects of specific students. Now, by predicting specific physical abilities and specific abilities, we can comprehensively improve sports performance and create more economic value. This article has achieved this goal. In the process of modern sports training, coaches conduct regular assessments and evaluations of students, estimate their specific performance based on the results of the assessment items, and adjust their regular training plans. These data need to provide a basis for students’ training. Over the years, coaches and scholars have continued to study, provide scientific improvement programs for student training, clarify students’ sports training goals, and cultivate many outstanding sports talents through the establishment of performance prediction models. Therefore, the research of sports performance prediction model is a highly scientific and practical research.

This article will survey 100 students aged 18 to 21 from a sports school in China. Scientific index selection is the prerequisite for establishing an evaluation model. Through a variety of mathematical statistical methods and scientific selection of parameter indicators, this article can provide a reliable basis for formulating students’ training goals. Therefore, this article needs a mathematical analysis of whether the special performance and various special fitness indicators are normally distributed. After the scientific data test, the special performances and the special fitness indexes investigated are normal, which is enough to show that the method of screening indexes through factor analysis has scientific hypothesis for this topic. In order to clarify the degree of closeness between the variables, this article first conducts a correlation analysis and establishes a correlation coefficient matrix.

There are many physical factors that affect sports performance. Through research and statistics, this article classifies and sorts out the indicators that can accurately reflect the physical fitness level and the typical indicators closely related to the development of specific performance and obtains the four-element regression equation of the student’s specific physical fitness indicator system, that is, a special performance prediction model. Among them, the prediction model includes 30-meter running with a gun (continuous), 3-step approach and 5-step jump, and a ball with a weight of 300 grams on the shoulder during the full approach, dependent variable: specific performance.

The purpose of the evaluation system established is to enable students to obtain objective and quantitative evaluations of the training and development level of various indicators. According to the individual development characteristics of the students and the development requirements of special sports events, the main special physical fitness that affects the performance is grasped as a whole. Therefore, the establishment of an evaluation system is the basis and prerequisite for quantitative monitoring of model training and an important link in the implementation of system control. The system has a good reference for training planning and implementation, as well as the evaluation and feedback of training effects.

In order to explain the differences between the four special physical fitness sensitive indicators that influence youth sports performance extracted by factor analysis, this study adopted the standard percentage method to evaluate the individual indicators of the main influencing factors. According to the relevant statistical analysis described above, it is shown that the normal distribution of various indicators of specific performance and specific physical fitness is better, as shown in Figure 8.

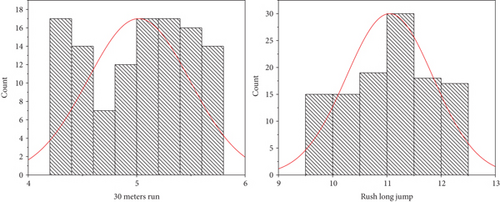
Using factor analysis and other mathematical statistical methods to analyze, in order to make the special physical fitness training of these students truly scientific, optimize the special physical fitness training system and other factors that may affect the special performance. Physical education teachers can comprehensively consider factors such as general abilities, special skills, and body shape in the process of adopting modular special physical fitness training to achieve the best results of scientific training.

3.3. Examples of Sports Performance Analysis

The basic process of establishing a special motor skill evaluation system in this paper is to screen out all the difficult movements that can reflect the level of motor skills, establish an effective technical level evaluation index system, and construct a scoring scale one by one. Sports index testing is actually testing and scoring students in accordance with the scoring standards, and the accuracy of the evaluation results is evaluated by a dedicated coach. Table 4 shows the test results of the subject’s body type and fitness index.

Table 4. Test results of physical fitness indicators.

Index	Average	Standard deviation	Lowest value	Highest value
Height	172	3.6	154	186
Weight	60	2.7	41	76
Shoulder width	35	2.9	30	40
Chest circumference	84	2.5	79	89
Waistline	67	2.8	62	72
Hips	91	3.5	86	96
Upper limb length	71	4.7	66	76
Arm length	46	4.1	41	51
Tight upper arm circumference	29	2.8	24	34
Relax upper arm	30	2.5	25	35
Thigh circumference	54	3.3	49	59
Standing long jump	2.04	2.3	-2.96	7.04
Seated pregenus	29	4.9	24	34
Minute push-ups	87	2.2	82	92
Cross jump test	8	4.3	3	13
1 minute skipping rope	143	4.6	138	148
800 m run	193	5	188	198
30-meter run	5	2	4	6

From the results of the cluster analysis, it can be seen that among the indicators selected for the second time, the 1-minute push-up and the right-angle support are classified into one category, indicating that there is a very high degree of correlation between these two indicators. For a sports student, if the performance of 1-minute push-ups is excellent, then his performance of right angle support must be excellent, and vice versa, so this article only needs to select representative indicators.

Existing predictive models for student specific performance generally use multiple regression methods and gray models. This paper establishes the functional relationship between specific performance and quality training level and then predicts performance through student performance recognition. These predictive models reflect the relationship between special performance and training indicators to a certain extent and provide corresponding guidance for trainees’ training. However, the decisions of these models are based on certain assumptions, so formulas for special performance prediction models must be set in advance. In fact, the functional relationship between special performance and various related factors is very complicated, and the presumed formula does not fit these relationships well.

After a lot of training and prediction tests, this article found that adding some test data will affect the convergence speed and prediction accuracy of the model. For example, due to some special circumstances, the training time is not long enough, or there is a deviation in certain index tests. Therefore, this kind of data was excluded in the test. Federated learning algorithms have high requirements for computer configuration, especially memory, due to the huge amount of calculation. The entire training prediction process consists of 6 modules, as shown in Figure 9.

This article uses body shape, physical function, physical strength, ontology knowledge, operational knowledge, basic skills, technical combination, sports learning experience, sports competition participation experience, etc. as secondary indicators, reflecting the diversification of sports quality evaluation. On this basis, this article subdivides 25 three-level indicators, which are easy to operate and quantify, and scientifically assign weights to the above indicators.

According to the prediction model proposed in this article, 100 students’ 9 sports performances were predicted and compared with their actual scores. The comparison results are shown in Figure 10.

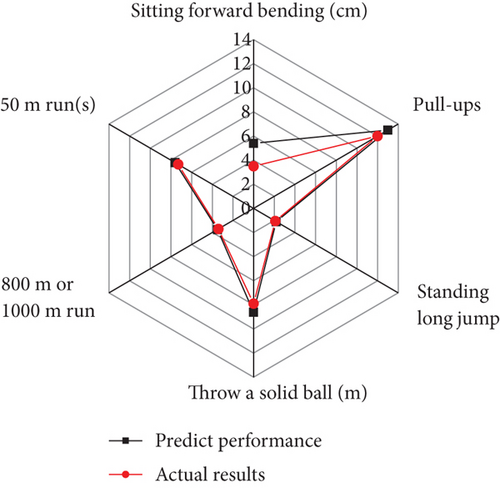
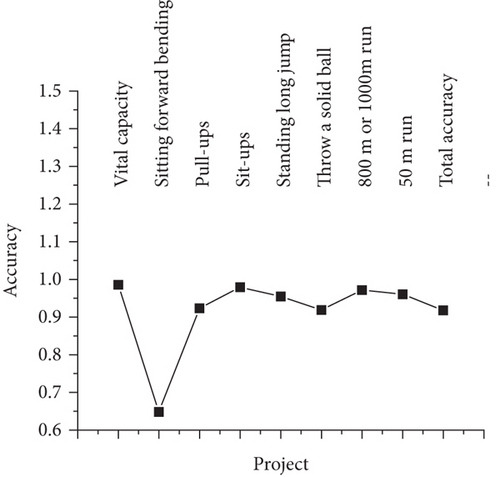
It can be seen from Figure 10 that there is not much difference between the predicted result and the actual score, and the overall accuracy rate has reached 91.7%. The experimental results show that the model can provide relatively accurate prediction results for teachers and students.

4. Discussion

The above are the main research results of this article. Although the algorithm proposed in this paper can better improve the problems caused by the average aggregation method of the classic federated learning algorithm, there are still some problems that have not been considered. In terms of privacy protection, this article adopts a privacy protection method consistent with the classic Fed Avg, that is, to protect privacy by transferring model parameters while retaining the original data locally. However, this level of privacy protection cannot meet the requirements of higher levels. In the future, more secure privacy protection technologies can be explored to empower federated learning. This paper is based on the performance prediction model constructed by federated learning and deep learning algorithms, which can provide teachers and students with relatively accurate prediction results. However, the accuracy of the stage performance prediction model to predict the final score interval is not good, so the next work needs to optimize the construction of the stage performance prediction model.

5. Conclusions

This paper studies a performance prediction model based on federated learning and deep learning algorithms and uses this model to implement a sports performance early warning system. In this article, the author will use a deep learning algorithm to predict the performance of 100 students based on a real-world application of improved algorithms, investigate the impact of physical learning on physical performance, and analyze the classification rules generated for students in various basic courses. This model can provide teachers with real-time understanding of the training situation of class students, the results of course performance prediction, and early warning to notify students in crisis, so that the quality of class teaching can be improved by guiding students in crisis in advance. It can provide students with real-time understanding of personal learning situation, sports performance prediction results, and viewing early warning reasons and learning suggestions, so that they can avoid missed courses through strengthened training.

Conflicts of Interest

The author declares no conflicts of interest.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Liu Y., Yu J., Kang J., Niyato D., and Zhang S., Privacy-preserving traffic flow prediction: a federated learning approach, IEEE Internet of Things Journal. (2020) 7, no. 8, 7751–7763, https://doi.org/10.1109/JIOT.2020.2991401.
10.1109/JIOT.2020.2991401
Web of Science® Google Scholar
2 Manias D. M. and Shami A., Making a case for federated learning in the internet of vehicles and intelligent transportation systems, IEEE Network. (2021) 35, no. 3, 88–94, https://doi.org/10.1109/MNET.011.2000552.
10.1109/MNET.011.2000552
Web of Science® Google Scholar
3 Ahmed U., Srivastava G., and Lin C. W., A federated learning approach to frequent itemset mining in cyber-physical systems, Journal of Network and Systems Management. (2021) 29, no. 4, 1–17, https://doi.org/10.1007/s10922-021-09609-5.
10.1007/s10922-021-09609-5
Web of Science® Google Scholar
4 Alguliyev R. M., Aliguliyev R. M., and Abdullayeva F. J., Privacy-preserving deep learning algorithm for big personal data analysis, Journal of Industrial Information Integration. (2019) 15, 1–14, https://doi.org/10.1016/j.jii.2019.07.002, 2-s2.0-85068544522.
10.1016/j.jii.2019.07.002
Web of Science® Google Scholar
5 Khan S., Khan M., Iqbal N., Hussain T., Khan S. A., and Chou K. C., A two-level computation model based on deep learning algorithm for identification of piRNA and their functions via Chou's 5-steps rule, International Journal of Peptide Research and Therapeutics. (2020) 26, no. 2, 795–809, https://doi.org/10.1007/s10989-019-09887-3, 2-s2.0-85068879320.
10.1007/s10989-019-09887-3
CAS Web of Science® Google Scholar
6 Farooq J. and Bazaz M. A., A deep learning algorithm for modeling and forecasting of COVID-19 in five worst affected states of India, Alexandria Engineering Journal. (2021) 60, no. 1, 587–596, https://doi.org/10.1016/j.aej.2020.09.037.
10.1016/j.aej.2020.09.037
Web of Science® Google Scholar
7 Voegele C., Hoorn A. V., Schulz E., Hasselbring W., and Krcmar H., WESSBAS: extraction of probabilistic workload specifications for load testing and performance prediction—a model-driven approach for session-based application systems, Software & Systems Modeling. (2018) 17, no. 2, 443–477, https://doi.org/10.1007/s10270-016-0566-5, 2-s2.0-84991818131, 29706857.
10.1007/s10270-016-0566-5
PubMed Web of Science® Google Scholar
8 Wang Y., Tian Y., Yin X., and Hei X., A trusted recommendation scheme for privacy protection based on federated learning, CCF Transactions on Networking. (2020) 3, no. 3-4, 218–228, https://doi.org/10.1007/s42045-020-00045-8.
10.1007/s42045-020-00045-8
Google Scholar
9 Qi Y., Hossain M. S., Nie J., and Li X., Privacy-preserving blockchain-based federated learning for traffic flow prediction, Future Generation Computer Systems. (2021) 117, no. 2946, 328–337, https://doi.org/10.1016/j.future.2020.12.003.
10.1016/j.future.2020.12.003
Web of Science® Google Scholar
10 Giles A. B., Davies J. E., Ren K., and Kelaher B., A deep learning algorithm to detect and classify sun glint from high- resolution aerial imagery over shallow marine environments, ISPRS Journal of Photogrammetry and Remote Sensing. (2021) 181, no. 4, 20–26, https://doi.org/10.1016/j.isprsjprs.2021.09.004.
10.1016/j.isprsjprs.2021.09.004
Web of Science® Google Scholar
11 Wang F., Xing L., Bagshaw H. P., Buyyounouski M. K., and Han B., Automated needle digitization in ultrasound-based prostate high dose-rate brachytherapy using a deep learning algorithm, International Journal of Radiation Oncology • Biology • Physics. (2020) 108, no. 3, S129–S130, https://doi.org/10.1016/j.ijrobp.2020.07.857.
10.1016/j.ijrobp.2020.07.857
CAS Web of Science® Google Scholar
12 Sudha D. and Priyadarshini J., An intelligent multiple vehicle detection and tracking using modified vibe algorithm and deep learning algorithm, Soft Computing. (2020) 24, no. 22, 17417–17429, https://doi.org/10.1007/s00500-020-05042-z.
10.1007/s00500-020-05042-z
Web of Science® Google Scholar
13 Liu C. and Zheng X., Exploring resource management for innovation power network based on deep learning algorithm, Neural Computing and Applications. (2021) 33, no. 9, 4013–4025, https://doi.org/10.1007/s00521-020-05446-w.
10.1007/s00521-020-05446-w
Web of Science® Google Scholar
14 Agarwal G. and Om H., Performance of deer hunting optimization based deep learning algorithm for speech emotion recognition, Multimedia Tools and Applications. (2021) 80, no. 7, 9961–9992, https://doi.org/10.1007/s11042-020-10118-x.
10.1007/s11042-020-10118-x
Web of Science® Google Scholar
15 Jiang X. W., Yan T. H., Zhu J. J., He B., Li W. H., du H. P., and Sun S. S., Densely connected deep extreme learning machine algorithm, Cognitive Computation. (2020) 12, no. 5, 979–990, https://doi.org/10.1007/s12559-020-09752-2.
10.1007/s12559-020-09752-2
Web of Science® Google Scholar
16 Struyvenberg M. R., Groof J. D., Putten J., van der Sommen F., Baldaque-Silva F., Bisschops R., Schoon E., Curvers W., de With P. H. N., and Bergman J., 297 - deep learning algorithm for characterization of Barrett's neoplasia demonstrates high accuracy on Nbi-zoom images, Gastroenterology. (2019) 156, no. 6, https://doi.org/10.1016/S0016-5085(19)36929-X.
10.1016/S0016-5085(19)36929-X
Web of Science® Google Scholar
17 Dong S., Zhang Y., He Z., Deng N., Yu X., and Yao S., Investigation of support vector machine and back propagation artificial neural network for performance prediction of the organic Rankine cycle system, Energy. (2018) 144, 851–864, https://doi.org/10.1016/j.energy.2017.12.094, 2-s2.0-85038958056.
10.1016/j.energy.2017.12.094
Web of Science® Google Scholar
18 Tirupathinaidu C., Jain N., Renganathan T., and Pushpavanam S., Unified thermodynamic model for performance prediction of adiabatic feedstock gasifiers, Industrial and Engineering Chemistry Research. (2020) 59, no. 44, 19751–19769, https://doi.org/10.1021/acs.iecr.0c03703.
10.1021/acs.iecr.0c03703
CAS Web of Science® Google Scholar
19 Dang D. D., Pham X. T., and Nguyen C. C., Thermal performance prediction in the air gap of a rotor-stator configuration: effects of numerical models, Journal of Thermal Science. (2020) 29, no. 1, 206–218, https://doi.org/10.1007/s11630-019-1096-6, 2-s2.0-85066897306.
10.1007/s11630-019-1096-6
Web of Science® Google Scholar
20 Armaghani D. J., Faradonbeh R. S., Momeni E., Fahimifar A., and Tahir M. M., Performance prediction of tunnel boring machine through developing a gene expression programming equation, Engineering with Computers. (2017) 34, no. 1, 129–141, https://doi.org/10.1007/s00366-017-0526-x, 2-s2.0-85021189190.
10.1007/s00366-017-0526-x
Web of Science® Google Scholar
21 Zhao Z., Quan Q., and Cai K. Y., A health performance prediction method of large-scale stochastic linear hybrid systems with small failure probability, Reliability Engineering and System Safety. (2017) 165, 74–88, https://doi.org/10.1016/j.ress.2017.03.014, 2-s2.0-85016459384.
10.1016/j.ress.2017.03.014
Web of Science® Google Scholar
22 Woodman S., Hiden H., and Watson P., Applications of provenance in performance prediction and data storage optimisation, Future Generation Computer Systems. (2017) 75, 299–309, https://doi.org/10.1016/j.future.2017.01.003, 2-s2.0-85011256374.
10.1016/j.future.2017.01.003
Web of Science® Google Scholar
23 López-Plaza D., Alacid F., Muyor J. M., and López-Miñarro P. Á., Sprint kayaking and canoeing performance prediction based on the relationship between maturity status, anthropometry and physical fitness in young elite paddlers, Journal of Sports Sciences. (2017) 35, no. 11, 1083–1090, https://doi.org/10.1080/02640414.2016.1210817, 2-s2.0-84978732416.
10.1080/02640414.2016.1210817
PubMed Web of Science® Google Scholar
24 Al-Faifi A. M., Song B., Hassan M. M., Alamri A., and Gumaei A., Performance prediction model for cloud service selection from smart data, Future Generation Computer Systems. (2018) 85, 97–106, https://doi.org/10.1016/j.future.2018.03.015, 2-s2.0-85044281603.
10.1016/j.future.2018.03.015
Web of Science® Google Scholar

Citing Literature

All articles

Predictive Analysis and Simulation of College Sports Performance Fused with Adaptive Federated Deep Learning Algorithm

Abstract

1. Introduction

1.1. Background

1.2. Significance

1.3. Related Work

1.4. Innovation

2. Adaptive Federated Deep Learning Algorithm

2.1. Adaptive Federated Learning Method

2.2. Personalized Federated Learning Algorithm Based on Deep Learning

2.3. Methods of Predicting Student Performance

3. Performance Prediction Model Experiment and Analysis

3.1. Performance Prediction Framework

3.2. Establishment of Sports Performance Prediction Model

3.3. Examples of Sports Performance Analysis

4. Discussion

5. Conclusions

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley