A topological index (TI) is a numerical descriptor of a molecule structure or graph that predicts its different physical, biological, and chemical properties in a theoretical way avoiding the difficult and costly procedures of chemical labs. In this paper, for two connected (molecular) graphs G₁ and G₂, we define the generalized total-sum graph consisting of various (molecular) polygonal chains by the lexicographic product of the graphs T_k(G₁) and G₂, where T_k(G₁) is obtained by applying the generalized total operation T_k on G₁ with k ≥ 1 as some integral value. Moreover, we compute the different degree-based TIs such as first Zagreb, second Zagreb, forgotten Zagreb, and hyper-Zagreb. In the end, a comparison among all the aforesaid TIs is also conducted with the help of certain statistical tools for some particular families of generalized total-sum graphs under lexicographic product.

1. Introduction

Chemical graph theory is a fascinating branch of mathematical chemistry in which the structural formulas of the different chemicals or chemical compounds are modelled as chemical structures or graphs such as the vertices correspond to the atoms and edges represent the chemical bonds between them. Topological indices (TIs) are graph-theoretic tools which are widely used in chemical graph theory to study the various structural and chemical characteristics (critical temperature, heat formation, density, extremal connectivity, unique classifications, and symmetric behaviours) of the chemical graphs. In the subject of cheminformatics, these indices also play a key role in the studies of the quantitative structure-property and quantitative structure-activity relationships which mathematically correlate the chemical properties with the physical structures of their chemical compounds. Moreover, TIs remain constant for the isomorphic structures.

In 1947, the very first TI is introduced by Wiener to check the critical temperature of paraffin [1]. Gutman and Trinajsti (1972) [2] defined the 1st and 2nd Zagreb indices that are used to compute the different structure base characteristics of the molecular graphs. These Zagreb indices are also used to measure the extent of branching of the carbon-atom skeleton of the various underlying chemical structures. After that, many degree-, distance-, and polynomial-based TIs came into existence, but the degree-based indices received more attention from the researchers (see [3–5]). For various results of the TIs on different chemical graphs, we refer to [6–8].

Li and Zheng and Bollobas and Erdos [9, 10] generalized the first and second Zagreb indices by the name of first general Zagreb index and general Randic index, respectively. In 2015, Furtula and Gutman redefined the concept of a F-index (forgotten index) with its basic properties [11]. It also measures the branching of the different atoms with predictive ability quite similar to the first Zagreb index. In the case of entropy and acentric factor, both first Zagreb and F-indices gain the correlation coefficients larger than 0.95. In addition, their linear combination yields a highly accurate mathematical model of certain physicochemical properties of alkanes. A significant improvement with the above model was obtained in the case of octanol-water partition coefficient. It is worth noting that this paper [11] has been cited more than 300 times so far. Moreover, in 2013, Shirdel et al. introduced another degree-based TI called by the hyper-Zagreb index [12]. For further study of different results on Zagreb indices, we refer to [13–15].

On the other hand, in the studies of the complex graphs, the operations on graphs (subdivision, union, intersection, switching, sum, complement, and product) play an important role to dissolve this complexity by constructing the new graphs where old graphs are distinguished by the name of the factor graphs. Yan et al. [16] defined the total operation T₁ and obtained the total graph T₁(G) by applying the operation T₁ on graph G. They also computed the Wiener indices of this newly derived graph. Liu et al. defined the extended version of this operation called generalized total operation for any integral value of k ≥ 1 and obtained the generalized total graph T_k(G) [17]. Eliasi and Taeri [18] defined the total-sum graph (T₁-sum graph) with the help of the total operation and Cartesian product of graphs. They also computed the Wiener index of this total sum graph. Moreover, Deng et al. [19], Akhter and Imran [20], Chu et al. [21], and Liu et al. [22] computed the various indices of the T₁-sum graph based on the Cartesian product. The results related to Zagreb indices for T₁-sum graph under strong product can be found in [7, 23]. For further study, we refer to [24, 25].

Moreover, Sarala et al. [26], De [27], Pattabiraman et al. [28, 29], and Suresh et al. [30] computed first, second, forgotten, and hyper- and reformulated Zagreb indices for the total sum (T₁-sum) graph, respectively, where the T₁-sum graph is obtained with the help of the total operation and lexicographic product of graphs.

In this note, we defined the concept of the generalized total-sum graphs under the operation of generalized total operation and lexicographic product of two connected graphs. Moreover, we computed the different Zagreb indices such as first, second, forgotten, and hyper for the generalized total-sum graphs in terms of different TIs of factor graphs. A computing analysis among all the aforesaid TIs is also conducted with the help of the certain statistical tools for some particular families of lexicographic product and generalized total-sum graphs. The rest of the paper is distributed in Sections 2, 3, 4, and 5 which cover the methodology, construction of graphs, main results, and regression modelling and conclusion, respectively.

2. Methodology

Let G = (V(G), E(G)) be a simple, finite, and undirected graph with a vertex set V(G) and edge set E(G)⊆V(G) × V(G), where |V(G)| and |E(G)| are called the order and size of the graph G, respectively. For a vertex or node v ∈ V(G), the number of incident edges on v or the adjacent vertices with v is called its degree, where the set of these adjacent vertices is known by the neighborhood set of v in G (denoted by N_G(v)). For more basic terminologies, we refer to [31]. Now, we defined some TIs which are frequently used in the main developments of the present study.

Definition 1 (see [2], [11].)The first, second, and forgotten Zagreb indices of a graph G are

(1)

Definition 2 (see [9].)The first general Zagreb index of a graph G is

(2)

Definition 3 (see [10].)The general Randi index (GRI) of a graph G is

(3)

For α = 2 and 3, the first Zagreb index and forgotten topological index are two special cases of the first general Zagreb index, respectively. Similarly, the first general Randi index becomes second Zagreb index for α = 1.

Definition 4 (see [12].)The hyper-Zagreb index of a graph G is

(4)

For further study of TIs, we refer [32, 33]. Now, if we assume X = G₁[G₂] and as dependent and independent variables, respectively, where G₁[G₂] is the simple lexicographic product graph of the graphs G₁ and G₂ and ) is the generalized total-sum graph that is a lexicographic product graph of the generalized total graphs and G₂, then the simple linear regression modelling is described with H₀ : Y = b₀ and H₁ : Y = b₀ + b₁X.

3. Construction of Graphs

In this section, we define different families of graphs as follows:

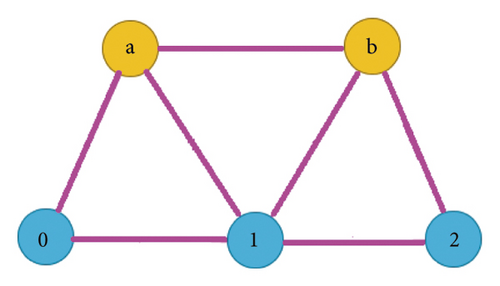
Definition 5 (see [16].)For a connected graph G = (V(G), E(G)), a total graph T₁(G) is defined with vertex set {V(G) ∪ E(G)} and two vertices m and n in T₁(G) are adjacent if either

m and n are in V(G) and m is adjacent to n in G or
m and n are in E(G) and m and n are adjacent in G or
m is in V(G), n is in E(G), and m and n are incident in G (for more details, see Figure 1)

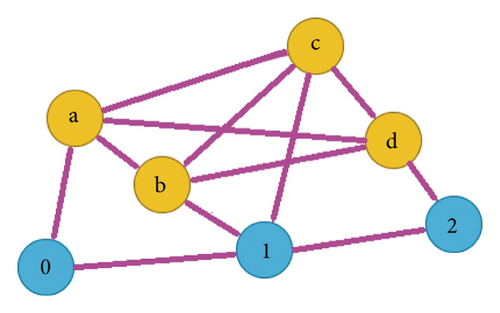
Liu et al. [17] defined the generalized total graph T_k(G) with vertex set V(G) ∪ kE(G) and edge set with same conditions on the vertices as defined in Definition 5, where k ≥ 1 is some integral value. For more explanation, we refer to Figures 2 and 3.

The composition or lexicographic product of two connected graphs G₁ and G₂ (denoted by G₁[G₂]) is a graph such that the set of vertices is V(G₁) × V(G₂) and two vertices (x₁, y₁) and (x₂, y₂) will be adjacent in G₁[G₂] iff: [x₁ = x₂ and y₁ is adjacent to y₂] or [x₁ is adjacent to x₂ and y₁ is adjacent to y₂] [31]. Now, we define the generalized total sum graph under the operations of generalized total operation and lexicographic product of graphs as follows.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Total graph T₁(G), where G₁≅P₃.

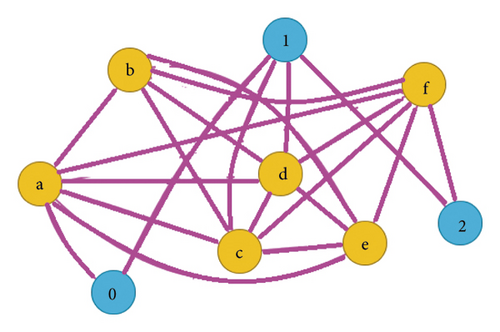
Definition 6. Let G₁ and G₂ be two connected graphs; the generalized T-sum graph is a graph having vertex set = V(T_k(G₁)) × V(G₂) = (V(G₁) ∪ k(E(G₁))) × V(G₂) and edge set such as two vertices (x₁, y₁) and (x₂, y₂) of are adjacent iff [x₁ = x₂ in V(G₁) and y₁ is adjacent to y₂ in E(G₂)] or [x₁ is adjacent to x₂ in E((T_k(G₁))) and y₁ is adjacent to y₂ in E(G₂)], where k ≥ 1 is a positive integer. For more explanation, we refer to Figure 4.

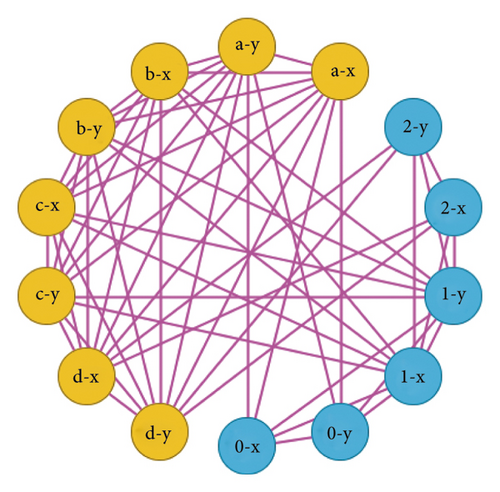
4. Computational Results of Zagreb Indices

This section covers the main computational results.

Theorem 1. For two connected graphs G₁ and G₂ with |V(G₁)|, |V(G₂)| ≥ 4, and k ≥ 1, we have

(5)

Proof. Consider

(6)

Now, we take

(7)

and

(8)

where s₁ and s₂ are the vertices that are inserted into the edges uv of G₁ and vw of G₁, respectively.

(9)

Consequently, we obtained our required result.

Theorem 2. For two connected graphs G₁ and G₂ with |V(G)₁|, |V(G₂)| ≥ 4, and k ≥ 1, we have

(10)

Proof.

(11)

Consider

(12)

where s₂ is the vertex inserted into the edge s₁w₁ of G₁,

(13)

where

is the set of neighbor vertices of s₁ in G₁,

(14)

and

(15)

where s₁ is the added vertex in the edge uv and s₂ is the added vertex in the edges vw of G₁. Also,

(16)

where r is the number of neighbors which are common vertices of u and v in G₁.

Hence proved.

Theorem 3. For two connected graphs G₁ and G₂ with |V(G₁)|, |V(G₂)| ≥ 4, and k ≥ 1, we have

(17)

Proof. Consider be the degree of a node (s, t) in the molecular graph .

(18)

Now,

(19)

and

(20)

where s₁ and s₂ are the nodes that are introduced into the edge set of uv and vw of G₁.

(21)

Hence proved.

Theorem 4. For two connected graphs G₁ and G₂ with |V(G₁)|, |V(G₂)| ≥ 4, and k ≥ 1, we have

(22)

Proof. Let be the degree of a node (s, t) in the molecular graph .

(23)

Now, consider

(24)

(25)

and

(26)

Here, W and X are the nodes of L(G₁), so we have

(27)

Hence, we obtain our required result.

5. Comparison and Conclusion

To check the correlation between the predefined lexicographic product of two simple graphs and newly defined generalized total-sum graphs via understudy Zagreb indices, we apply the linear regression model on the obtained formulas (Theorem 1–Theorem 4) of the first, second, forgotten, and hyper-Zagreb indices. For the purpose, we consider two simple path graphs P_n and P_m and construct their lexicographic product graph P_n[P_m] and generalized total-sum graph based on the lexicographic product, where m, n ≥ 1. By using Theorem 1 to Theorem 4, the first, second, forgotten, and hyper-Zagreb indices of these graphs for different values of m and n are shown in Tables 1 and 2.

Table 1. Zagreb indices of P_n[P_m].

[m, n]	\|V\|	\|E\|	M₁	M₂	F(G)	H(G)
(3, 3)	9	24	276	764	1704	3232
(4, 4)	16	60	968	3868	8280	16 016
(5, 5)	25	120	2460	12 576	26 460	51 612
(6, 6)	36	210	5196	32 132	66 948	131 212
(7, 7)	49	336	9716	70 276	145 488	286 040

Table 2. Zagreb indices of

[m, n, k]	\|V\|	\|E\|	M₁	M₂	F(G)	H(G)
(3, 3, 3)	27	207	6948	58989	122616	240594
(4, 4, 4)	64	992	71232	1293596	2787376	5374568
(5, 5, 5)	125	3275	397920	1.235160 8 × 10⁷	2.595604 × 10⁷	5.0659256 × 10⁷
(6, 6, 6)	216	8604	1574856	7.357629 6 × 10⁷	1.52609976 × 10⁸	2.99762568 × 10⁸
(7, 7, 7)	343	19355	496452	3.24253988 × 10⁸	6.67171624 × 10⁸	1.315679 6 × 10⁹

By using Tables 1 and 2, we construct the following linear regression lines:

(i)
First Zagreb Index. For and Y = M₁(P_n[P_m]), we have Y = 2260.3506 + 0.002871X with a value of correlation coefficient 0.471 1
(ii)
Second Zagreb Index. For and Y = M₂(P_n[P_m]), we have Y = 1548.9242 + 0.00002654X with a value of correlation coefficient 0.953
(iii)
Forgotten Topological Index. For and Y = F(P_n[P_m]), we have Y = 7355.407 + 0.0002013X with a value of correlation coefficient 0.9738 (see Table 3).
(iv)
Hyper-Zagreb Index. For and Y = HZ(P_n⌊P_m⌋), we have Y = 30154.5419 + 0.0002018X with a value of correlation coefficient 0.973 7

Now, we present these values in Table 3 more precisely.

Table 3. Correlation coefficient between

and P_n[P_m].

TI’s	Value of correlation coefficient	Relationship between X and Y
First Zagreb index	0.471 1	Very strong direct relationship
Second Zagreb index	0.953	Very strong direct relationship
Forgotten Zagreb index	0.9738	Very strong direct relationship
Hyper-Zagreb index	0.973 7	Very strong direct relationship

In this paper, we computed different Zagreb indices for the generalized total-sum graphs. To compute the correlation values, we considered certain families of graphs that belong to lexicographic product graphs and the generalized total-sum graphs under the lexicographic product for their regression lines and values of the correlation coefficients as given in Table 3. From Table 3, we obtain the following two conclusions.

Firstly, there exists a strong correlation between the lexicographic product graphs and the generalized total-sum graphs under lexicographic product via all the understudy Zagreb indices. More clearly, we can state that by increasing the number of atoms and bonds in lexicographic product graphs to obtain the generalized total-sum graphs under the lexicographic product, the chemical properties do not change their strength. Secondly, hyper-Zagreb index shows the strong correlation among all the understudy Zagreb indices by attaining value 0.9738 as shown in Table 3.

Now, we close this section with the comment that the problem is still open to investigate the comparison among the other TIs for different operations on graphs.

Conflicts of Interest

The authors declare that there are no conflicts of interest.

Open Research

Data Availability

All the data are included within this paper. However, more details of the data are available from the corresponding author upon request.

References

1 Wiener H., Structural determination of paraffin boiling points, Journal of the American Chemical Society. (1947) 69, no. 1, 17–20, https://doi.org/10.1021/ja01193a005, 2-s2.0-8544254107.
10.1021/ja01193a005
CAS PubMed Web of Science® Google Scholar
2 Gutman I. and Trinajstić N., Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbonsπ-electron energy of alternant hydrocarbons, Chemical Physics Letters. (1972) 17, no. 4, 535–538, https://doi.org/10.1016/0009-2614(72)85099-1, 2-s2.0-33845352210.
10.1016/0009-2614(72)85099-1
CAS Web of Science® Google Scholar
3 Gutman I., Degree-based topological indices, Croatica Chemica Acta. (2013) 86, no. 4, 351–361, https://doi.org/10.5562/cca2294, 2-s2.0-84897584934.
10.5562/cca2294
CAS Web of Science® Google Scholar
4 Cheng R., Ali G., Rahmat G., Khan M. Y., Semanicova-Fenovcikova A., and Liu J.-B., Investigation of general power sum-connectivity index for some classes of extremal graphs, Complexity. (2021) 2021, 8, 6623277, https://doi.org/10.1155/2021/6623277.
10.1155/2021/6623277
Web of Science® Google Scholar
5 fang J., Ahmed I., Mehboob A., Nazar K., and Ahmad H., Irregularity of block shift networks and Hierarchical Hypercube networks, Journal of Chemistry. (2019) 2019, 12, https://doi.org/10.1155/2019/1042308, 1042308.
10.1155/2019/1042308
Web of Science® Google Scholar
6 Gutman I. and Polansky O., Mathematical Concepts in Organic Chemistry, 1986, Springer-Verlag, Berlin, Germany.
10.1007/978-3-642-70982-1
Google Scholar
7 Afzal Siddiqui H. M., Nadeem M. F., Azeem M., Arshad M. A., Haider A., and Malik M. A., Topological properties of supramolecular chain of different complexes of N-Salicylidene-L-Valine, Polycyclic Aromatic Compounds. (2021) 1–14, https://doi.org/10.1080/10406638.2021.1980060.
10.1080/10406638.2021.1980060
Google Scholar
8 Rafiullah M., Siddiqui H. M. A., Siddiqui M. K., and Dhlamini M., On degree-based topological indices for strong double graphs, Journal of Chemistry. (2021) 2021, 12, https://doi.org/10.1155/2021/4852459, 4852459.
10.1155/2021/4852459
Google Scholar
9 Li X. and Zheng J., A unified approach to the extremal trees for different indices, MATCH Communications in Mathematical and in Computer Chemistry. (2005) 54, 195–208.
CAS Web of Science® Google Scholar
10 Bollobas B. and Erdos P., Graphs of extremal weights, Ars Combinatoria. (1998) 50, 225–233.
Web of Science® Google Scholar
11 Furtula B. and Gutman I., A forgotten topological index, Journal of Mathematical Chemistry. (2015) 53, no. 4, 1184–1190, https://doi.org/10.1007/s10910-015-0480-z, 2-s2.0-84925541764.
10.1007/s10910-015-0480-z
CAS Web of Science® Google Scholar
12 Shirdel G. H., Rezapour H., and Sayadi A. M., Hyper-Zagreb index of graph operations, Iranian Journal of Mathematical Chemistry. (2013) 4, 213–220.
Google Scholar
13 Song P., Ali H., Binyamin M. A., Ali B., and Liu J.-B., On computation of entropy of hex-derived network, Complexity. (2021) 2021, 18, 9993504, https://doi.org/10.1155/2021/9993504.
10.1155/2021/9993504
Web of Science® Google Scholar
14 Imran M., Baig A. Q., and Ali H., On molecular topological properties of hex-derived networks, Journal of Chemometrics. (2016) 30, no. 3, 121–129, https://doi.org/10.1002/cem.2785, 2-s2.0-84959566673.
10.1002/cem.2785
CAS Web of Science® Google Scholar
15 Gutman I., Ruscic B., Trinajstic N., and Wilcox C. F., Graph theory and molecular orbitals. XII. Acyclic polyenes, The Journal of Chemical Physics. (1975) 62, no. 9, 3399–3405, https://doi.org/10.1063/1.430994, 2-s2.0-36749120371.
10.1063/1.430994
CAS Web of Science® Google Scholar
16 Yan W., Yang B.-Y., and Yeh Y.-N., The behavior of Wiener indices and polynomials of graphs under five graph decorations, Applied Mathematics Letters. (2007) 20, no. 3, 290–295, https://doi.org/10.1016/j.aml.2006.04.010, 2-s2.0-33751162621.
10.1016/j.aml.2006.04.010
Web of Science® Google Scholar
17 Liu J.-B., Javaid M., and Awais H. M., Computing Zagreb Indices of the Subdivision-Related Generalized Operations of Graphs, IEEE Access. (2019) 7, 105479–105488, https://doi.org/10.1109/access.2019.2932002, 2-s2.0-85071198790.
10.1109/ACCESS.2019.2932002
Web of Science® Google Scholar
18 Eliasi M. and Taeri B., Four new sums of graphs and their Wiener indices, Discrete Applied Mathematics. (2009) 157, no. 4, 794–803, https://doi.org/10.1016/j.dam.2008.07.001, 2-s2.0-59749099397.
10.1016/j.dam.2008.07.001
Web of Science® Google Scholar
19 Deng H., Sarala D., Ayyaswamy S. K., and Balachandran S., The Zagreb Indices of Four Operations on Graphs, Applied Mathematics and Computation. (2016) 275, 422–431, https://doi.org/10.1016/j.amc.2015.11.058, 2-s2.0-84955486256.
10.1016/j.amc.2015.11.058
Web of Science® Google Scholar
20 Akhter S. and Imran M., Computing the forgotten topological index of four operations on graphs, AKCE International Journal of Graphs and Combinatorics. (2017) 14, no. 1, 70–79, https://doi.org/10.1016/j.akcej.2016.11.012, 2-s2.0-85009381987.
10.1016/j.akcej.2016.11.012
Google Scholar
21 Chu Y.-M., Javed S., Javaid M., and Kamran Siddiqui M., On bounds for topological descriptors of φ-sum graphsϕ-sum graphs, Journal of Taibah University for Science. (2020) 14, no. 1, 1288–1301, https://doi.org/10.1080/16583655.2020.1819026.
10.1080/16583655.2020.1819026
Google Scholar
22 Liu J.-B., Javed S., Javaid M., and Shabbir K., Computing first general zagreb index of operations on graphs, IEEE Access. (2019) 7, 47494–47502, https://doi.org/10.1109/access.2019.2909822, 2-s2.0-85065090345.
10.1109/ACCESS.2019.2909822
Web of Science® Google Scholar
23 Javaid M., Javed S., Alanazi A. M., and Alotaibi M. R., Computing analysis of Zagreb indices for generalized sum graphs under strong product, Journal of Chemistry. (2021) 2021, 20, 6663624, https://doi.org/10.1155/2021/6663624.
10.1155/2021/6663624
Web of Science® Google Scholar
24 Ahmad U. and Hameed S., Study of topological indices in a class of benzenoid graphs, Journal of Combinatorial Mathematics and Combinatorial Computing. (2020) 1, 19–30.
Google Scholar
25 Ejaz F. and Hussain M., Penta beryllium phosphate: a novel two dimensional network with its topological aspects, compu, Journal of Combinatorial Mathematics and Combinatorial Computing. (2020) 1, 76–87.
Google Scholar
26 Sarala D., Deng H., Ayyaswamy S. K., and Balachandran S., The Zagreb indices of graphs based on four New Operations Related to the Lexicographic Product, Applied Mathematics and Computation. (2017) 309, 156–169, https://doi.org/10.1016/j.amc.2017.04.002, 2-s2.0-85017574924.
10.1016/j.amc.2017.04.002
Web of Science® Google Scholar
27 De N., F-index of graphs based on four operations related to the lexicographic product, 2017, https://arxiv.org/abs/1706.00464.
Google Scholar
28 Pattabiraman K., Four new operations related to composition and their Hyper-Zagreb Index, Southeast Asian Bulletin of Mathematics. (2019) 43, no. 6.
Web of Science® Google Scholar
29 Pattabiraman K. and Santhakumar A., Four new operations related to composition and their reformulated Zagreb index, Indonesian Journal of Combinatorics. (2018) 2, no. 1, 35–49, https://doi.org/10.19184/ijc.2018.2.1.5.
10.19184/ijc.2018.2.1.5
Google Scholar
30 Suresh M. and Devi G. S., Some operations in hyper Zagreb indices, 2277, Proceedings of the 1st International Conference on Mathematical Techniques and Applications: ICMTA2020, November 2020, no. 1, https://doi.org/10.1063/5.0025242.
10.1063/5.0025242
Google Scholar
31 West D. B., Introduction to Graph Theory, 2001, 2nd edition, Prentice Hall, Hoboken, NJ, USA.
Google Scholar
32 Todeschini R., Consonni V., Mannhold R., Kubinyi H., and Timmerman H., Handbook of Molecular Descriptors, 2002, Wiley-VCH, Weinheim, Germany.
Google Scholar
33 Awais H. M., Javaid M., and Raheem A., Hyper-Zagreb index of graphs based on generalized subdivision related operations, Punjab University Journal of Mathematics. (2019) 52, no. 5, 89–103.
Web of Science® Google Scholar

Citing Literature

All articles

[Retracted] Computing Correlation among the Graphs under Lexicographic Product via Zagreb Indices

Retraction(s) for this article

Retracted: Computing Correlation among the Graphs under Lexicographic Product via Zagreb Indices

Abstract

1. Introduction

2. Methodology

3. Construction of Graphs

4. Computational Results of Zagreb Indices

5. Comparison and Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

[Retracted] Computing Correlation among the Graphs under Lexicographic Product via Zagreb Indices

Retraction(s) for this article

Retracted: Computing Correlation among the Graphs under Lexicographic Product via Zagreb Indices

Abstract

1. Introduction

2. Methodology

3. Construction of Graphs

4. Computational Results of Zagreb Indices

5. Comparison and Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information