Graph invariants provide an amazing tool to analyze the abstract structures of networks. The interaction and interconnection between devices, sensors, and service providers have opened the door for an eruption of mobile over the web applications. Structure of web sites containing number of pages can be represented using graph, where web pages are considered to be the vertices, and an edge is a link between two pages. Figuring resolving partition of the graph is an intriguing inquest in graph theory as it has many applications such as sensor design, compound classification in chemistry, robotic navigation, and Internet network. The partition dimension is a graph parameter akin to the concept of metric dimension, and fault-tolerant partition dimension is an advancement in the line of research of partition dimension of the graph. In this paper, we compute fault-tolerant partition dimension of alternate triangular cycle, mirror graph, and tortoise graphs.

1. Introduction and Basic Terminologies

Graph theory is an intense region of arithmetic that has capacious variety of implementations in numerous regions of science, such as chemistry, biology, software engineering, and electrical and hardware engineering. Graphing is a powerful tool for representing and understanding objects and their relationships. Currently, online social networks are considered as an essential element for interpersonal relationships where people and smart objects are connected together in smart environments. Theoretical principles of graph theory are applied to practical fields, by determining graph invariants such as vertices, edges, diameter, and degree and mapping them to real-time problems. These invariants are the supporting tools between science and engineering or computational techniques in the fields of chemical, electrical, computer, and telecommunication engineering. One concept that pervades all the graph theory is that of distance and is used in isomorphism testing, graph operations, maximal and minimal problems on connectivity, and diameter. Metric dimension is one of the distance related parameter in graphs that has attracted the attention of several researchers. The generalized version of metric dimension of the graph is unique and an important parameter of graph theory called partition dimension of the graph. It is considered as an applied topic of graph theory and has applications in structure-activity issues in drug design, network discovery and verification [5], pattern recognition and image processing [16], and modelling of chemical substances [14].

In 2000, the concept of partition dimension of graph was initiated by Chartrand et al. as an extension of metric dimension of the graph [6]. Let Ω be a connected graph of order n with vertex set V(Ω) and edge set E(Ω). If two vertices w, z ∈ V(Ω), then the length of shortest path between w and z in Ω is distance between these vertices and is denoted by d(w, z). The distance between a vertex z and J⊆V(Ω) is defined as min{d(z, y)|y ∈ J} and is denoted by d(z, J). For a vertex z ∈ V(Ω), N(z) will denote the open neighbourhood of z in Ω, i.e., N(z) = {q ∈ V(Ω) : qis adjacent to z}, and closed neighbourhood of z will be denoted by N[z] = N(z) ∪ {z} [18]. Let μ = {z₁, z₂, …, z_p} be an ordered subset of vertex set of Ω. The representation of z with respect to μ is p tuple (d(z, z₁), d(z, z₂), …, d(z, z_p)) and is denoted by r(z|μ). The subset μ is called a resolving set of Ω if distinct vertices of Ω have distinct representations with respect to μ. The metric dimension of Ω is defined as min{|μ| : μ is resolving set of Ω} and is denoted by β(Ω). Ali et al. discussed that path-related graphs have constant metric dimension [1]. Zuo et al. computed constant metric dimension of some generalized convex polytopes [27]. Rehman et al. computed the metric dimension of arithmetic graph of a composite number [20]. In 2021, metric dimension of windmill graph was computed by Singh et al. [24].

In 2008, Hernando et al. initiated the concept of fault-tolerant metric dimension of graphs [10]. If, for every pair of distinct vertices q, z ∈ V(Ω), there exists at least two vertices α₁, α₂ ∈ μ such that d(q, δ_i) ≠ d(z, δ_i) for i ∈ {1,2}, then the resolving set μ of V(Ω) is called fault tolerant. The fault-tolerant metric dimension of Ω is the minimum cardinality of fault-tolerant resolving set μ and is denoted by β^′(Ω). Ahmad et al. computed fault-tolerant metric dimension of P(n, 2)⊙K₁ graph [3]. Hayat et al. discussed fault-tolerant metric dimension of interconnection networks [9].

Let ξ = {ξ₁, ξ₂, …, ξ_p} be a partition with p partition classes of vertex set of connected graph Ω. The representation of vertex z with respect to partition set ξ is p vector (d(z, ξ₁), d(z, ξ₂), …, d(z, ξ_p)) denoted by r(z|ξ). The partition ξ is called resolving partition of Ω if representation of all the vertices in Ω is different. We define the partition dimension of graph Ω as min{|ξ| : ξ is resolving partition of Ω} and is denoted by pd(Ω). Chartrand et al. [6] characterised the graphs having pd(Ω) to be 2 or n. For various classes of connected graphs, the partition dimension has been obtained. For instance, Ayesha et al. computed the partition dimension of trihexagonal α boron nanotube [23]. Mehreen et al. computed the partition dimension of the fullerene graph [15]. Hussain et al. provided the bounds on partition dimension of generalized Mobius ladder [11]. Monica et al. studied the partition dimension problem for certain classes of the series-parallel graph [17]. Chu et al. calculated the sharp bounds for partition dimension of convex polytopes [7]. Wei et al. studied the partition dimension problem for cycle-related graphs [25]. Yero et al. studied the partition dimension of strong product graphs and Cartesian product graphs [26].

Gary et al. and Khuller et al. mentioned the computational complexity of metric dimension of general graphs [8, 13]. Computation of pd(Ω) is more complex as it is more harder than computing metric dimension of a graph.

The concept of fault-tolerant partition dimension of the graph was initiated by Salman et al. [22]. Let ξ = {ξ₁, ξ₂, …, ξ_p} be a partition with p partition classes of the vertex set of connected graph Ω. The partition ξ is called fault-tolerant resolving partition of Ω if for every pair of distinct vertices y, z ∈ V(Ω), and r(y|ξ) and r(z|ξ) differ by at least two places. The fault-tolerant partition dimension of Ω is defined as min{|ξ| : ξ is fault − tolerant resolving partition of Ω} and is denoted by ℱ(Ω). Imran et al. characterised that ℱ(Ω) of all the graphs of order n is n − 1 [12]. Kamran et al. computed the ℱ(Ω) of homogeneous caterpillar, tadpole, and necklace graphs [2, 4]. Asim et al. computed ℱ(Ω) of circulant graphs with connection set {1,2} in [19]. In this paper, we extend this study by considering alternate triangular cycle, mirror graph, and tortoise graphs and show that they have constant fault-tolerant partition dimension.

Chartrand et al. revealed the following basic results on pd(Ω).

Proposition 1 (see [6].)Let Ω be a graph; then,

(1)
pd(Ω) ≤ β(Ω) + 1
(2)
pd(Ω) = 2 if Ω = P_n, where P_n is a path
(3)
pd(Ω) = n if Ω = K_n, where K_n is the complete graph

Salman et al. revealed the following basic results on ℱ(Ω).

Proposition 2 (see [21].)For n ≥ 2,

(1)
pd(Ω) ≤ ℱ(Ω)
(2)
ℱ(Ω) = n if Ω≅K_n or Ω≅K_n − e

Proposition 3 (see [22].)

(1)
For n ≥ 2, ℱ(Ω) ≤ β^′(Ω) + 1
(2)
For n ≥ 3, 3 ≤ ℱ(Ω) ≤ n

The remaining part of the paper is structured in the following manner. In Section 2, we are concerned with the computation of ℱ(A(C_2n)), ℱ(Mr(P_n)), and ℱ(T_n), where A(C_2n), Mr(P_n), and T_n are alternate triangular cycle, mirror graph, and tortoise graphs, respectively. Finally, we conclude the paper in Section 3, by giving future research direction.

2. Fault-Tolerant Partition Dimension of Alternate Triangular Cycle

In this section, we compute ℱ(A(C_2n)), where A(C_2n) is alternate triangular cycle. Vertices of A(C_2n), for n ≥ 3, are divided into three sets, D = {d_ϱ : 1 ≤ ϱ ≤ n}, E = {e_ϱ : 1 ≤ ϱ ≤ n}, and F = {f_ϱ : 1 ≤ ϱ ≤ n}. An alternate triangular cycle A(C_2n) is obtained by replacing alternate edge of an even cycle C_2n by C₃. The set V(A(C_2n)) = D ∪ E ∪ F and E(A(C_2n)) = {d_ϱe_ϱ : 1 ≤ ϱ ≤ n} ∪ {e_ϱd_ϱ+1 : 1 ≤ ϱ ≤ n − 1} ∪ {d₁e_n} ∪ {d_ϱf_ϱ : 1 ≤ ϱ ≤ n} ∪ {e_ϱf_ϱ : 1 ≤ ϱ ≤ n} are vertex set and edge set of alternate triangular cycle, respectively. Order of A(C_2n) is 3n. The alternate triangular cycle A(C₁₂) is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Alternate triangular cycle A(C₁₂).

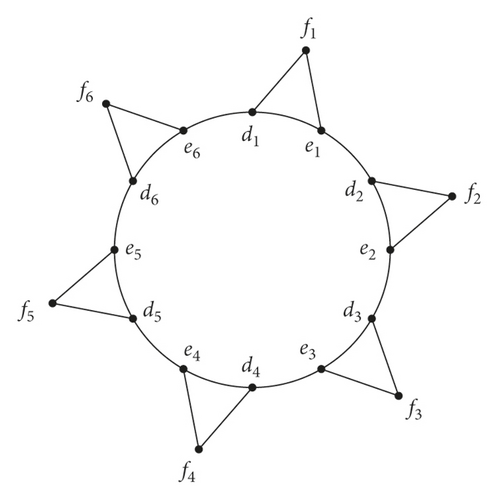
We compute pd(A(C_2n)) and (HTML translation failed) in the following theorems.

Theorem 1. The partition dimension of alternate triangular cycle A(C_2n), for n ≥ 2, is 3.

Proof. Let ξ = {ξ₁, ξ₂, ξ₃} be a partition with 3 partition classes of vertex set of A(C_2n) for n ≥ 2. For n = 2, we consider ξ₁ = {d₁}, ξ₂ = {e₁}, and ξ₃ = {d₂, e₂, f₁, f₂}. It can easily be observed that ξ is resolving partition.

Case 1: for n = 3δ, δ ≥ 1, r(w|ξ), where ξ₁ = {d_ϱ : 1 ≤ ϱ ≤ n} ∪ {e_ϱ : 1 ≤ ϱ ≤ n} ∪ {f_ϱ : 1 ≤ ϱ ≤ δ}, ξ₂ = {f_ϱ : δ + 1 ≤ ϱ ≤ 2δ}, and ξ₃ = {f_ϱ : 2δ + 1 ≤ ϱ ≤ n} are shown as follows:
(1)
Case 2: for n = 3δ + 1, δ ≥ 1, r(w|ξ), where ξ₁ = {d_ϱ : 1 ≤ ϱ ≤ n} ∪ {e_ϱ : 1 ≤ ϱ ≤ n} ∪ {f_ϱ : 1 ≤ ϱ ≤ δ + 1}, ξ₂ = {f_ϱ : δ + 2 ≤ ϱ ≤ 2δ + 1}, and ξ₃ = {f_ϱ : 2δ + 2 ≤ ϱ ≤ n} are shown as follows:
(2)
Case 3: for n = 3δ + 2, δ ≥ 1, r(w|ξ), where ξ₁ = {d_ϱ : 1 ≤ ϱ ≤ n} ∪ {e_ϱ : 1 ≤ ϱ ≤ n} ∪ {f_ϱ : 1 ≤ ϱ ≤ δ + 1}, ξ₂ = {f_ϱ : δ + 2 ≤ ϱ ≤ 2δ + 2}, and ξ₃ = {f_ϱ : 2δ + 3 ≤ ϱ ≤ n} are shown as follows:

(3)

It is obvious from the above distinct representations that ξ is resolving partition of A(C_2n); therefore, pd(A(C_2n)) ≤ 3. It follows from Proposition 1(b) that pd(A(C_2n)) ≥ 3. This completes the proof.

Theorem 2. The fault-tolerant partition dimension of alternate triangular cycle A(C_2n), for n ≥ 2, is 4.

Proof. In order to prove that ℱ(A(C_2n)) = 4, first, we show that ℱ(A(C_2n)) ≤ 4. In this regard, consider ξ = {ξ₁, ξ₂, ξ₃, ξ₄} be a partition with 4 partition classes of vertex set of A(C_2n), for n ≥ 2. For n = 2, consider ξ₁ = {d₁}, ξ₂ = {e₁, d₂}, ξ₃ = {e₂}, and ξ₄ = {f₁, f₂}. It is easy to observe that ξ is fault-tolerant resolving partition.

(1)
Case 1: for n = 3δ, δ ≥ 1, r(w|ξ), where ξ₁ = {d_ϱ : 1 ≤ ϱ ≤ n} ∪ {e_ϱ : 1 ≤ ϱ ≤ n}, ξ₂ = {f_ϱ : 1 ≤ ϱ ≤ δ}, ξ₃ = {f_ϱ : δ + 1 ≤ ϱ ≤ 2δ}, and ξ₄ = {f_ϱ : 2δ + 1 ≤ ϱ ≤ n} are shown as follows:
(4)
(2)
Case 2: for n = 3δ + 1, δ ≥ 1, r(w|ξ), where ξ₁ = {d_ϱ : 1 ≤ ϱ ≤ n} ∪ {e_ϱ : 1 ≤ ϱ ≤ n − 1}, ξ₂ = {e_n} ∪ {f_ϱ : 1 ≤ ϱ ≤ δ}, ξ₃ = {f_ϱ : δ + 1 ≤ ϱ ≤ 2δ}, and ξ₄ = {f_ϱ : 2δ + 1 ≤ ϱ ≤ n} are shown as follows:
(5)
(3)
Case 3: for n = 3δ + 2, δ ≥ 1, r(w|ξ), where ξ₁ = {d_ϱ : 1 ≤ ϱ ≤ n} ∪ {e_ϱ : 1 ≤ ϱ ≤ n} ∪ {f₁}, ξ₂ = {f_ϱ : 2 ≤ ϱ ≤ δ + 1}, ξ₃ = {f_ϱ : δ + 2 ≤ ϱ ≤ 2δ + 2}, and ξ₄ = {f_ϱ : 2δ + 3 ≤ ϱ ≤ n} are shown as follows:
(6)

It is obvious from the above distinct representations that ξ is fault-tolerant resolving partition of A(C_2n), so ℱ(A(C_2n)) ≤ 4.

Now, we prove that ℱ(A(C_2n)) ≥ 4. For this, we show that ℱ(A(C_2n)) ≠ 3. For a contradiction, suppose ξ = {ξ₁, ξ₂, ξ₃} be a fault-tolerant partition basis of A(C_2n). There will be at least one vertex of degree 3 in one of the partition set ξ₁, ξ₂, or ξ₃. Without loss of generality, we assume that d_ϱ is a vertex of degree 3 that belongs to ξ₁, and N(d_ϱ) = {e_ϱ, e_ϱ+j, f_ϱ}. Suppose that |ξ₁| = 1, and N(d_ϱ)⊆ξ₂ ∪ ξ₃, |N(d_ϱ)∩ξ₂| ≥ 2, or |N(d_ϱ)∩ξ₃| ≥ 2. Without loss of generality, we assume that, at least two vertices, s, t ∈ N(d_ϱ)∩ξ₂. As r(s|ξ) = (1,0, k₁) and r(t|ξ) = (1,0, k₂) are identical at two places, hence, it is a contradiction.

We consider the following cases when |ξ₁| ≥ 2 and d_ϱ ∈ ξ₁.

(1)
Case 1: if N(d_ϱ)∩ξ₁ = {e_ϱ, e_ϱ+j, f_ϱ}, then r(d_ϱ|ξ) = (0, b₀, c₀), r(e_ϱ|ξ) = (0, b₁, c₁), r(e_ϱ+j|ξ) = (0, b₂, c₂), and r(f_ϱ|ξ) = (0, b₃, c₃). As b₀ − 1 ≤ b₁, b₂, b₃ ≤ b₀ + 1, so using Pigeonhole principle, there will be similarity in the representation of two vertices at two places; hence, it is a contradiction.
(2)
Case 2: if two neighbours of d_ϱ ∈ ξ₁ and one neighbour of d_ϱ belongs to ξ₂, then following cases will arise:
(1)
Case 2(a): if N(d_ϱ)∩ξ₁ = {e_ϱ, e_ϱ+j} and one vertex f_ϱ ∈ ξ₂, then r(d_ϱ|ξ) = (0,1, c₀) and r(e_ϱ|ξ) = (0,1, c₁). As representation of two vertices has two identical coordinates, hence, it is a contradiction.
(2)
Case 2(b): if N(d_ϱ)∩ξ₁ = {e_ϱ, f_ϱ} and one vertex e_ϱ+j ∈ ξ₂, then, r(d_ϱ|ξ) = (0,1, c₀), r(e_ϱ|ξ) = (0, b₁, c₁), and r(f_ϱ|ξ) = (0,2, c₂). Since 1 ≤ b₁ ≤ 2, so representation of two vertices will have two identical coordinates, hence, it is a contradiction.
(3)
Case 2(c): if N(d_ϱ)∩ξ₁ = {e_ϱ+j, f_ϱ} and one vertex e_ϱ ∈ ξ₂, then r(d_ϱ|ξ) = (0,1, c₃), r(e_ϱ+j|ξ) = (0, b₂, c₄), and r(f_ϱ|ξ) = (0,2, c₅). Since 1 ≤ b₂ ≤ 2, so representation of two vertices have two identical coordinates; hence, it is a contradiction.
(3)
Case 3: if N(d_ϱ)∩ξ₁ = {e_ϱ} and two vertices e_ϱ+j, f_ϱ ∈ ξ₂, then, r(d_ϱ|ξ) = (0,1, c₀), r(e_ϱ|ξ) = (0,1, c₁), r(e_ϱ+j|ξ) = (1,0, c₂), and r(f_ϱ|ξ) = (1,0, c₃). Since representation of two vertices has two identical coordinates, thus, it is a contradiction.
(4)
Case 4: when each of ξ₁, ξ₂, and ξ₃ contains one neighbour of d_ϱ, then we have following cases:
(1)
Case 4(a): if N(d_ϱ)∩ξ₁ = {e_ϱ}, e_ϱ+j ∈ ξ₂, and f_ϱ ∈ ξ₃, then r(d_ϱ|ξ) = (0,1,1) and r(e_ϱ|ξ) = (0, c₁, 1), which leads to a contradiction.
(2)
Case 4(b): if N(d_ϱ)∩ξ₁ = {e_ϱ+j}, e_ϱ ∈ ξ₂ and f_ϱ ∈ ξ₃, then r(d_ϱ|ξ) = (0,1,1) and r(e_ϱ+j|ξ) = (0,2,2). Since N(e_ϱ+j) = {d_ϱ, d_ϱ+j, f_ϱ+j}, so let d_ϱ+j, f_ϱ+j ∈ ξ₁. Now, r(f_ϱ+j|ξ) = (0, a₁, b₁), where 2 ≤ a₁, b₁ ≤ 3, and r(d_ϱ+j|ξ) = (0, a₂, b₂), where 1 ≤ a₂ and b₂ ≤ 3. It is obvious that representation of two vertices is identical at two places, so a contradiction.
(5)
Case 5: if N(d_ϱ)∩ξ₁ = ∅, at least two vertices from N(d_ϱ) belong to ξ₂. Without loss of generality, we suppose that e_ϱ, e_ϱ+j ∈ ξ₂; then, r(d_ϱ|ξ) = (0,1, c₀), r(e_ϱ|ξ) = (1,0, c₁), and r(e_ϱ+j|ξ) = (1,0, c₂). It is again a contradiction.

This discussion concludes the proof; hence, ℱ(A(C_2n)) ≥ 4.

Example 1. Consider the alternate triangular cycle A(C₁₂), as shown in Figure 1. If ξ = {ξ₁, ξ₂, ξ₃, ξ₄}, where ξ₁ = {d_ϱ : 1 ≤ ϱ ≤ 6} ∪ {e_ϱ : 1 ≤ ϱ ≤ 6}, ξ₂ = {f₁, f₂}, ξ₃ = {f₃, f₄}, and ξ₄ = {f₅, f₆} is a partition of V(A(C₁₂)), then the representations of vertices of A(C₁₂) are as follows: r(d₁|ξ) = (0,1,5,2), r(d₂|ξ) = (0,1,3,4), r(d₃|ξ) = (0,2,1,5), r(d₄|ξ) = (0,4,1,3), r(d₅|ξ) = (0,5,2,1), r(d₆|ξ) = (0,3,4,1), r(e₁|ξ) = (0,1,4,3), r(e₂|ξ) = (0,1,2,5), r(e₃|ξ) = (0,3,1,4), r(e₄|ξ) = (0,5,1,2), r(e₅|ξ) = (0,4,3,1), r(e₆|ξ) = (0,2,5,1), r(f₁|ξ) = (1,0,5,3), r(f₂|ξ) = (1,0,3,5), r(f₃|ξ) = (1,3,0,5), r(f₄|ξ) = (1,5,0,3), r(f₅|ξ) = (1,5,3,0), and r(f₆|ξ) = (1,3,5,0).

It can be seen from the above representations that ξ is a fault-tolerant resolving partition of A(C₁₂).

2.1. Fault-Tolerant Partition Dimension of Mirror Graph

Mirror graph Mr(P_n) is defined as the disjoint union of graph Ω and its copy with additional edges joining each vertex of Ω to its corresponding vertex in . The set V(Mr(P_n)) = {w₁, w₂, …, w_2n} and E(Mr(P_n)) = {w_lw_l+1 : 1 ≤ l ≤ n − 1} ∪ {w_n+lw_n+l+1 : 1 ≤ l ≤ n − 1} ∪ {w_lw_n+l : 1 ≤ l ≤ n} are vertex set and edge set of mirror graph, respectively. Mirror graph Mr(P₄) is shown in Figure 2.

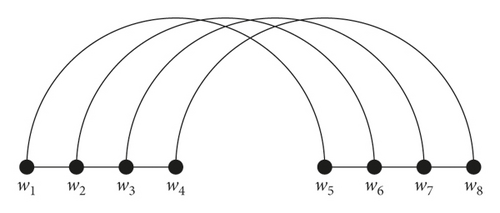
Yero et al. computed the partition dimension of the mirror graph in the following lemma.

Lemma 1 (see [26].)Let G be the mirror graph Mr(P_n); then, pd(Mr(P_n)) = 3.

The following theorem allows us to compute ℱ(Mr(P_n)).

Theorem 3. For every n ≥ 2,

(7)

Proof. Let ξ = {ξ₁, ξ₂, ξ₃} be a partition set of vertices of Mr(P_n) for n = 2. Considering ξ₁ = {w₁, w₂}, ξ₂ = {w₃}, and ξ₃ = {w₄}, it is easy to observe that ξ is fault-tolerant resolving partition of Mr(P_n).

Now, for n ≥ 3, consider ξ = {ξ₁, ξ₂, ξ₃, ξ₄} be a partition with 4 partition classes of vertices of Mr(P_n). r(w|ξ), considering ξ₁ = {w_j : 1 ≤ j ≤ n − 1}, ξ₂ = {w_n}, ξ₃ = {w_j : n + 1 ≤ j ≤ 2n − 1}, and ξ₄ = {w_2n}, are as follows:

(8)

As all the above representations are different, so ξ is fault-tolerant resolving partition of Mr(P_n); therefore, ℱ(Mr(P_n)) ≤ 4.

Now, we prove that ℱ(Mr(P_n)) ≥ 4; for this, we show that ℱ(Mr(P_n)) ≠ 3. For contradiction, let ξ = {ξ₁, ξ₂, ξ₃} be a fault-tolerant partition basis of Mr(P_n). One of the partition sets contains at least one vertex of degree 3. Without loss of generality, we assume that w_τ is a vertex of degree 3 that belongs to ξ₁, and N(w_τ) = {w_p, w_q, w_r}. Suppose that |ξ₁| = 1 and N(w_τ)⊆ξ₂ ∪ ξ₃, |N(w_τ)∩ξ₂| ≥ 2, or |N(w_τ)∩ξ₃| ≥ 2. Without loss of generality, we assume that at least two vertices e₁, e₂ ∈ N(w_τ)∩ξ₂. As r(e₁|ξ) = (1,0, k₁) and r(e₂|ξ) = (1,0, k₂) have two identical coordinates, so it is a contradiction. Now, we discuss the following cases when |ξ₁| ≥ 2 and w_τ ∈ ξ₁.

(1)
Case 1: if N(w_τ)∩ξ₁ = {w_p, w_q, w_r}, then r(w_τ|ξ) = (0, b₀, c₀), r(w_p|ξ) = (0, b₁, c₁), r(w_q|ξ) = (0, b₂, c₂), and r(w_r|ξ) = (0, b₃, c₃). As b₀ − 1 ≤ b₁, b₂, b₃ ≤ b₀ + 1, so using Pigeonhole principle, representation of two vertices have two identical coordinates; therefore, it is a contradiction.
(2)
Case 2: if N(w_τ)∩ξ₁ = {w_p, w_q} and one vertex w_r ∈ ξ₂, then r(w_τ|ξ) = (0,1, c₀), r(w_p|ξ) = (0, b₁, c₁), r(w_q|ξ) = (0, b₂, c₂), and r(w_r|ξ) = (1,0, c₃). Since 1 ≤ b₁, b₂ ≤ 2, so there will be similarity in the representation of two vertices at two places from ξ₁ and ξ₂; hence, it is a contradiction.
(3)
Case 3: if N(w_τ)∩ξ₁ = {w_p} and two vertices w_q, w_r ∈ ξ₂, then r(w_τ|ξ) = (0,1, c₀), r(w_p|ξ) = (0, b₁, c₁), r(w_q|ξ) = (1,0, c₂), and r(w_r|ξ) = (1,0, c₃). Since r(w_q|ξ) and r(w_r|ξ) have two identical coordinates, therefore, it is a contradiction.
(4)
Case 4: if N(w_τ)∩ξ₁ = {w_p}, w_q ∈ ξ₂, and w_r ∈ ξ₃, then N(w_p) = {w_τ, s₁}, N(w_q) = {w_τ, s₁, s₂}, and N(w_r) = {w_τ, s₂, s₃}. Let s₁ ∈ ξ₁, s₂ ∈ ξ₂ and s₃ ∈ ξ₃, then r(w_τ|ξ) = (0,1,1) and r(s₁|ξ) = (0,1, c₁), which leads to a contradiction. Now, let s₁ ∈ ξ₁, s₃ ∈ ξ₂, and s₂ ∈ ξ₃; then, r(w_τ|ξ) = (0,1,1) and r(s₁|ξ) = (0,1, c₁), which leads to a contradiction.
(5)
Case 5: if N(w_τ)∩ξ₁ = ∅ and at least two vertices from N(w_τ) belong to ξ₂, without loss of generality, we suppose that w_p, w_q ∈ ξ₂; then, r(w_τ|ξ) = (0,1, c₀), r(w_p|ξ) = (1,0, c₁), and r(w_q|ξ) = (1,0, c₂). Again r(w_p|ξ) and r(w_q|ξ) have two identical coordinates, a contradiction.

The above discussions show that ℱ(Mr(P_n)) ≥ 4, which completes the proof.

Example 2. Consider the mirror graph Mr(P₄), as shown in Figure 2. If ξ = {ξ₁, ξ₂, ξ₃, ξ₄}, where ξ₁ = {w₁, w₂, w₃}, ξ₂ = {w₄}, ξ₃ = {w₅, w₆, w₇}, and ξ₄ = {w₈} is a partition of V(Mr(P₄)), then the representations of vertices of Mr(P₄) are as follows: r(w₁|ξ) = (0,3,1,4), r(w₂|ξ) = (0,2,1,3), r(w₃|ξ) = (0,1,1,2), r(w₄|ξ) = (1,0,2,1), r(w₅|ξ) = (1,4,0,3), r(w₆|ξ) = (1,3,0,2), r(w₇|ξ) = (1,2,0,1), and r(w₈|ξ) = (2,1,1,0). It is obvious from the above representations that ξ is a fault-tolerant resolving partition of Mr(P₄).

2.2. Fault-Tolerant Partition Dimension of Tortoise Graph

The tortoise graph, denoted by T_n, has vertex set V(T_n) = {w₁, w₂, …, w_n} and edge set E(T_n) = {w_jw_j+1 : 1 ≤ j ≤ n − 1} ∪ {w_jw_n−j+1 : 1 ≤ j ≤ ⌊n/2⌋}. Tortoise graph T₇ is shown in Figure 3.

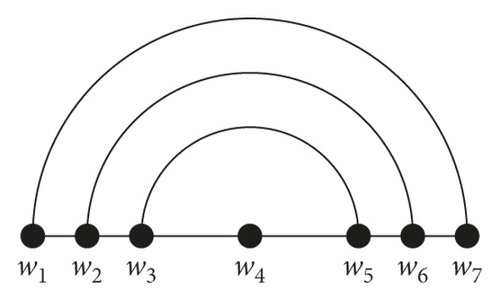
The following theorems allow us to compute pd(T_n) and ℱ(T_n).

Theorem 4. For every n ≥ 3, where n = 2δ + 1 and δ ≥ 1, pd(T_n) = 3.

Proof. Let ξ = {ξ₁, ξ₂, ξ₃} be a partition set of V(T_n) for n ≥ 3. r(w|ξ) with respect to ξ₁ = {w_i : 1 ≤ i ≤ n − 1/2}, ξ₂ = {w_{n + 1/2}}, and ξ₃ = {w_i : n + 3/2 ≤ i ≤ n} are as follows:

(9)

It is obvious from the above distinct representations that ξ is resolving partition of T_n; therefore, pd(T_n) ≤ 3. It follows by Proposition 1(b) that pd(T_n) ≥ 3. Hence, pd(T_n) = 3.

Theorem 5. For every n ≥ 3, where n = 2δ + 1 and δ ≥ 1,

(10)

Proof. Let ξ = {ξ₁, ξ₂, ξ₃} be a partition set of V(T_n) for n = 3. Considering ξ₁ = {w₁}, ξ₂ = {w₂}, and ξ₃ = {w₃}, it is easy to see that ξ is fault-tolerant resolving partition of T_n. Now, consider ξ = {ξ₁, ξ₂, ξ₃, ξ₄} be a partition with 4 partition classes of vertex set of T_n for n = 2δ + 1, where δ ≥ 2. r(w|ξ) considering ξ₁ = {w_i : 1 ≤ i ≤ n − 1/2}, ξ₂ = {w_i : n + 1/2 ≤ i ≤ n − 2}, ξ₃ = {w_n−1} and ξ₄ = {w_n} are as follows:

(11)

Distinct representations given above show that ξ is fault-tolerant resolving partition of T_n; therefore, ℱ(T_n) ≤ 4.

Now, we prove that ℱ(T_n) ≥ 4. For this, we show that ℱ(T_n) ≠ 3. For contradiction, suppose ξ = {ξ₁, ξ₂, ξ₃} be a fault-tolerant partition basis of T_n. One of the partition sets contains at least one vertex of degree 3. Without loss of generality, we assume that w_τ is a vertex of degree 3 that belongs to ξ₁, and N(w_τ) = {w_p, w_q, w_r}. Suppose that |ξ₁| = 1, and N(w_τ)⊆ξ₂ ∪ ξ₃, |N(w_τ)∩ξ₂| ≥ 2, or |N(w_τ)∩ξ₃| ≥ 2. Without loss of generality, we assume at least two vertices f₁, f₂ ∈ N(w_τ)∩ξ₂. As r(|f₁|ξ) = (1,0, k₁) and r(f₂|ξ) = (1,0, k₂) has two identical coordinates, therefore, it is a contradiction. Now, we consider the following cases when |ξ₁| ≥ 2 and w_τ ∈ ξ₁.

(1)
Case 1: if N(w_τ)∩ξ₁ = {w_p, w_q, w_r}, then r(w_τ|ξ) = (0, b₀, c₀), r(|w_p|ξ) = (0, b₁, c₁), r(w_q|ξ) = (0, b₂, c₂), and r(w_r|ξ) = (0, b₃, c₃). As b₀ − 1 ≤ b₁, b₂, b₃ ≤ b₀ + 1, so using Pigeonhole principle, there will be similarity in the representation of two vertices at two places, hence a contradiction.
(2)
Case 2: if N(w_τ)∩ξ₁ = {w_p, w_q} and one vertex w_r ∈ ξ₂, then r(w_τ|ξ) = (0,1, c₀), r(w_p|ξ) = (0, b₁, c₁), r(w_q|ξ) = (0, b₂, c₂), and r(w_r|ξ) = (1,0, c₃). Since 1 ≤ b₁, b₂ ≤ 2, so representation of two vertices will have two identical coordinates, hence a contradiction.
(3)
Case 3: if N(w_τ)∩ξ₁ = {w_p} and two vertices w_q, w_r ∈ ξ₂, then r(w_τ|ξ) = (0,1, c₀), r(w_p|ξ) = (0, b₁, c₁), r(w_q|ξ) = (1,0, c₂), and r(w_r|ξ) = (1,0, c₃). Since, representation of two vertices has two identical coordinates, thus, it is a contradiction.
(4)
Case 4: if N(w_τ)∩ξ₁ = {w_p}, w_q ∈ ξ₂ and w_r ∈ ξ₃.
(1)
For n = 5, N(w_p) = {w_τ, s₁}, N(w_q) = {w_τ, w_r}, and N(w_r) = {w_τ, w_q, s₁}. Let s₁ ∈ ξ₁; then r(w_τ|ξ) = (0,1,1), r(w_p|ξ) = (0,2,2), and r(s₁|ξ) = (0, q₁, 1), which leads to a contradiction.
(2)
For n ≥ 7, N(w_p) = {w_τ, s₁, s₂}, N(w_q) = {w_τ, s₃}, and N(w_r) = {w_τ, s₂, s₃}. Let, s₁, s₂ ∈ ξ₁ and s₃ ∈ ξ₂; then, r(w_τ|ξ) = (0,1,1), r(w_p|ξ) = (0,2,2), r(s₁|ξ) = (0, q₁, g₁), and r(s₂|ξ) = (0, q₂, 1), which leads to a contradiction. Now, let s₁, s₂ ∈ ξ₁ and s₃ ∈ ξ₃; then, r(w_τ|ξ) = (0,1,1), r(w_p|ξ) = (0,2,2), r(s₁|ξ) = (0, q₁, g₁), and r(s₂|ξ) = (0, q₂, 1), which leads to a contradiction.
(5)
Case 5: if N(w_τ)∩ξ₁ = ∅, ξ₂ contains at least two neighbours of w_τ. Without loss of generality, we suppose that w_p, w_q ∈ ξ₃; then, r(w_τ|ξ) = (0, c₀, 1), r(w_p|ξ) = (1, c₁, 0), and r(w_q|ξ) = (1, c₂, 0). Again r(w_p|ξ) and r(w_q|ξ) have two identical coordinates; hence, it is a contradiction.

The above discussion follows that ℱ(T_n) ≥ 4. Thus, ℱ(T_n) = 4.

Example 3. Consider the tortoise graph T₇, as shown in Figure 3. If ξ = {ξ₁, ξ₂, ξ₃, ξ₄}, where ξ₁ = {w₁, w₂, w₃}, ξ₂ = {w₄, w₅}, ξ₃ = {w₆}, and ξ₄ = {w₇} is a partition of V(T₇), then r(w|ξ) are as follows: r(w₁|ξ) = (0,3,2,1), r(w₂|ξ) = (0,2,1,2), r(w₃|ξ) = (0,1,2,3), r(w₄|ξ) = (1,0,2,3), r(w₅|ξ) = (1,0,1,2), r(w₆|ξ) = (1,1,0,1), and r(w₇|ξ) = (1,2,1,0). The above distinct representations verify that ξ is a fault-tolerant resolving partition of T₇.

3. Conclusion

In this paper, authors conclude that pd(Ω) of alternate triangular cycle and tortoise graph for n ≥ 2 is 3. ℱ(Ω) of alternate triangular cycle, mirror graph, and tortoise graph for n ≥ 2 is between 3 and 4. The obtained results led us to the conclusion that the discussed cyclic networks have constant partition and fault-tolerant partition dimension. pd(Ω) and ℱ(Ω) of these graphs are independent of the number of vertices of the graph. Future research can focus on computing the fault-tolerant partition dimension of alternate square and alternate pentagonal cycle.

The significance of the current work can be seen in optimization related to resource management, routing problem, and supply chain problem. These require to group certain nodes in the network to optimally approach the whole network. The least number of grouping required in such scenario can be realised as partition dimension problem. Also, the least number of grouping required to approach the whole network in case of inaccessibility of one of the group relates to fault-tolerant partition dimension of the graph.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Open Research

Data Availability

All data used to support the findings of the study are included within this article and can be obtained from the corresponding author upon request.

References

1 Ali M., Rahim M. T., and Ali G., On path related graphs with constant metric dimension, Utilitas Mathematica. (2012) 88, 203–209.
Web of Science® Google Scholar
2 Azhar K., Zafar S., and Kashif A., On fault-tolerent partition dimension of homogeneous caterpillar graphs, Mathematical Problems in Engineering. (2021) 2021, 7282245, https://doi.org/10.1155/2021/7282245.
10.1155/2021/7282245
Web of Science® Google Scholar
3 Ahmad Z., Chaudhary M. A., Baig A. Q., and Zahid M. A., Fault-tolerant metric dimension of P(n, 2)ʘK1 graph, Journal of Discrete Mathematical Sciences and Cryptography. (2021) 24, no. 2, 647–656, https://doi.org/10.1080/09720529.2021.1899209.
10.1080/09720529.2021.1899209
Web of Science® Google Scholar
4 Azhar K., Zafar S., Kashif A., and Zahid Z., On fault-tolerant partition dimension of graphs, Journal of Intelligent and Fuzzy Systems. (2021) 40, no. 1, 1129–1135, https://doi.org/10.3233/jifs-201390.
10.3233/JIFS-201390
Web of Science® Google Scholar
5 Beerliová Z., Eberhard F., Erlebach T., Hall A., Hoffmann M., Mihal’ak M., and Ram L. S., Network discovery and verification, IEEE Journal on Selected Areas in Communications. (2006) 24, no. 12, 2168–2181, https://doi.org/10.1109/jsac.2006.884015, 2-s2.0-33845653104.
10.1109/JSAC.2006.884015
Web of Science® Google Scholar
6 Chartrand G., Salehi E., and Zhang P., The partition dimension of a graph, Aequationes Mathematicae. (2000) 59, no. 1, 45–54, https://doi.org/10.1007/pl00000127, 2-s2.0-17844400423.
10.1007/PL00000127
Google Scholar
7 Chu Y.-M., Nadeem M. F., Azeem M., and Siddiqui M. K., On sharp bounds on partition dimension of convex polytopes, IEEE Access. (2020) 8, 224781–224790, https://doi.org/10.1109/ACCESS.2020.3044498.
10.1109/ACCESS.2020.3044498
Web of Science® Google Scholar
8 Garey M. R. and Johnson D. S., Computers and Intractability, A Guide to the Theory of NP-Completeness, 1979, Freeman, New York, NY, USA.
Google Scholar
9 Hayat S., Khan A., Malik M. Y. H., Imran M., and Siddiqui M. K., Fault-tolerant metric dimension of interconnection networks, IEEE Access. (2020) 8, 145435–145445, https://doi.org/10.1109/ACCESS.2020.3014883.
10.1109/ACCESS.2020.3014883
Web of Science® Google Scholar
10 Hernando C., Mora M., Slater P. J., and Wood D. R., Fault-tolerant metric dimension of graphs, Proceedings of the International Conference on Convexity in Discrete Structures, January 2008, Tiruchirappalli, India, 81–85.
Google Scholar
11 Hussain Z., Khan J. A., Munir M., Saleem M. S., and Iqbal Z., Sharp bounds for partition dimension of generalized Möbius ladders, Open Mathematics. (2018) 16, no. 1, 1283–1290, https://doi.org/10.1515/math-2018-0109, 2-s2.0-85056857628.
10.1515/math-2018-0109
Web of Science® Google Scholar
12 Javaid I., Salman M., and Chaudhry M. A., Graphs of order n with fault-tolerant partition dimension n − 1, UPB Scientific Bull. Series A. (2014) 76, no. 3.
Google Scholar
13 Khuller S., Raghavachari B., and Rosenfeld A., Landmarks in graphs, Discrete Applied Mathematics. (1996) 70, no. 3, 217–229, https://doi.org/10.1016/0166-218x(95)00106-2, 2-s2.0-0013510156.
10.1016/0166-218X(95)00106-2
Web of Science® Google Scholar
14 Khuller S., Raghavachari B., and Rosenfeld A., Location in Graphs, 1994, University of Maryland at Colleg Park, College Park, MD, USA, Technical Report CS-TR-3326.
Google Scholar
15 Mehreen N., Farooq R., Farooq R., and Akhter S., On partition dimension of fullerene graphs, AIMS Mathematics. (2018) 3, no. 3, 343–352, https://doi.org/10.3934/math.2018.3.343, 2-s2.0-85073327984.
10.3934/Math.2018.3.343
Web of Science® Google Scholar
16 Melter R. A. and Tomescu I., Metric bases in digital geometry, Computer Vision, Graphics, and Image Processing. (1984) 25, no. 1, 113–121, https://doi.org/10.1016/0734-189x(84)90051-3, 2-s2.0-0021643887.
10.1016/0734-189X(84)90051-3
Google Scholar
17 Mohan C. M., Santhakumar S., Arockiaraj M., and Liu J.-B., Partition dimension of certain classes of series parallel graphs, Theoretical Computer Science. (2019) 778, 47–60, https://doi.org/10.1016/j.tcs.2019.01.026, 2-s2.0-85061636803.
10.1016/j.tcs.2019.01.026
Web of Science® Google Scholar
18 Estrada-Moreno A., On the k-partition dimension of graphs, Theoretical Computer Science. (2020) 806, 42–52, https://doi.org/10.1016/j.tcs.2018.09.022, 2-s2.0-85054009753.
10.1016/j.tcs.2018.09.022
Web of Science® Google Scholar
19 Nadeem A., Kashif A., Zafar S., and Zahid Z., On 2-partition dimension of the circulant graphs, Journal of Intelligent and Fuzzy Systems. (2021) 40, no. 5, 9493–9503, https://doi.org/10.3233/jifs-201982.
10.3233/JIFS-201982
Web of Science® Google Scholar
20 Rehman S. u., Imran M., and Javaid I., On the metric dimension of arithmetic graph of a composite number, Symmetry. (2020) 12, no. 4, 607, https://doi.org/10.3390/sym12040607.
10.3390/sym12040607
Web of Science® Google Scholar
21 Salman M., Javaid I., and Chaudhry M., Fault-tolerant metric and partition dimension of graphs, Utilitas Mathematica. (2010) 83, 187–199.
Web of Science® Google Scholar
22 Salman M., Javaid I., Chaudhry M., and Shokat S., Fault-tolerance in resolvability, Utilitas Mathematica. (2009) 80, 263–275.
Web of Science® Google Scholar
23 Shabbir A. and Azeem M., On the partition dimension of tri-hexagonal α-boron nanotube, IEEE Access. (2021) 9, 55644–55653, https://doi.org/10.1109/ACCESS.2021.3071716.
10.1109/ACCESS.2021.3071716
Web of Science® Google Scholar
24 Singh P., Sharma S., Sharma S., Sharma S. K., and Bhat V. K., Metric dimension and edge metric dimension of windmill graphs, AIMS Mathematics. (2021) 6, no. 9, 9138–9153, https://doi.org/10.3934/math.2021531.
10.3934/math.2021531
Web of Science® Google Scholar
25 Wei C., Nadeem M. F., Siddiqui H. M. A., Azeem M., Liu J. B., and Khalil A., On partition dimension of some cycle-related graphs, Mathematical Problems in Engineering. (2021) 2021, 4046909, https://doi.org/10.1155/2021/4046909.
10.1155/2021/4046909
Web of Science® Google Scholar
26 González Yero I., Jakovac M., Kuziak D., and Taranenko A., The partition dimension of strong product graphs and Cartesian product graphs, Discrete Mathematics. (2014) 331, 43–52, https://doi.org/10.1016/j.disc.2014.04.026, 2-s2.0-84901001223.
10.1016/j.disc.2014.04.026
Web of Science® Google Scholar
27 Zuo X., Ali A., Ali G., Siddiqui M. K., Rahim M. T., and Asare-Tuah A., On constant metric dimension of some generalized convex polytopes, Jurnal Matematika. (2021) 2021, https://doi.org/10.1155/2021/6919858.
10.1155/2021/6919858
Google Scholar

Citing Literature

All articles

Fault-Tolerant Partition Resolvability of Cyclic Networks

Abstract

1. Introduction and Basic Terminologies

2. Fault-Tolerant Partition Dimension of Alternate Triangular Cycle

2.1. Fault-Tolerant Partition Dimension of Mirror Graph

2.2. Fault-Tolerant Partition Dimension of Tortoise Graph

3. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Fault-Tolerant Partition Resolvability of Cyclic Networks

Abstract

1. Introduction and Basic Terminologies

2. Fault-Tolerant Partition Dimension of Alternate Triangular Cycle

2.1. Fault-Tolerant Partition Dimension of Mirror Graph

2.2. Fault-Tolerant Partition Dimension of Tortoise Graph

3. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information