Topological indices (TIs) transform a molecular graph into a number. The TIs are a vital tool for quantitative structure activity relationship (QSAR) and quantity structure property relationship (QSPR). In this paper, we constructed two classes of Benes network: horizontal cylindrical Benes network HCB(r) and vertical cylindrical Benes network obtained by identification of vertices of first rows with last row and first column with last column of Benes network, respectively. We derive analytical close formulas for general Randić connectivity index, general Zagreb, first and the second Zagreb (and multiplicative Zagreb), general sum connectivity, atom-bond connectivity (VCB(r)), and geometric arithmetic (ABC) index of the two classes of Benes networks. Also, the fourth version of GA and the fifth version of ABC indices are computed for these classes of networks.

1. Introduction

The processing nodes in an interconnection network are the multiprocessor used to build a network of homogeneously same processor memory pairs. Programs are compiled and executed through message sending. Considerable importance to the architecture and utilization of multiprocessor interconnection network is due to low cost, more efficient microprocessors, and chips [1]. Interconnection networks resembled the communication pattern of the natural scenario, which make it more valuable and important. Most of the networks are interconnected and dependent on each other which need to be reviewed for the future work.

Graphs are used to design interconnected networks in a very natural way, in which the processors or components represent vertices and edges represent the communication links, e.g., fiber optic cables. The way in which all these components work will be carried out by incidence functions. Graphs show the topological properties of the networks. Therefore, the graph and networks are basically the same in a sense; that is, when we are considering networks, components, and links, we actually speak of graphs, vertices, and edges.

In Fourier transform networks, butterfly graphs are the basic graphs that can accomplish FFT very proficiently. There are series of interconnection patterns and switching stages in a butterfly network that permits n inputs to be linked to n outputs. The Benes network consists of butterflies connected back to back. The Benes network is known for permutation routing [2]. They are significant multistage interconnection networks, which enjoy striking topologies for communication networks [3]. The use of Benes network is in parallel computing systems such as SP1/SP2, IBM, NEC Cenju-3, and MIT Transit Project. It is also used in the internal structures of optical couplers [4, 5]. There are 2r + 1 levels in an r-dimensional Benes network where every level has 2r nodes. An r-dimensional butterfly is formed between the level 0 to level r nodes. The back to back butterflies share the middle level to form a Benes network. We denote an r-dimensional Benes by B(r). Figure 1 shows the graph 3-dimensional Benes network B(3).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

3-dimensional Benes network.

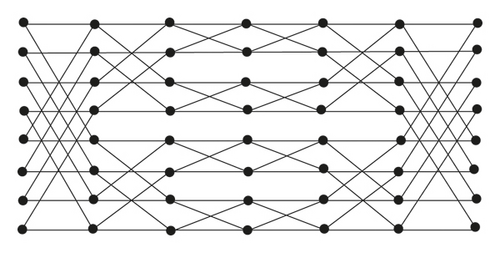
From now onward, we denote by a connected, simple graph with vertex and edge set by and . Moreover, for , d_a, N(a), and S_a present its degree, neighbors, and sum of degrees. For more details on undefined terminology, we refer the readers to [6–8].

Several invariants assigned to graphs (or molecular structure) establish correlations between its structure and chemical/physical aspects. These graph invariants are named as topological indices. Several degree-dependent TIs have been formulated so far and are found to be useful in predicting the physical/chemical properties of an underlying molecular structure. For instance, there is a virtuous correlation among the Randi index (RI) and numerous physicochemical features of alkanes including chromatographic retention times, boiling points, and surface areas. The Zagreb indices (ZIs) and its different variants contribute to understand the complexity of (molecular) structures [9–13], chirality [14], ZE isomerism [15], and heterosystems [16], whilst the overall ZIs show a latent applicability to derive multilinear regression models. The ABC index offers a good model for the strain energy of cycloalkanes and stability of linear and branched alkanes [17, 18]. In this respect, computing different forms of TIs has provided the indicators of such medicinal conduct of numerous compounds and drugs. The mathematical forms of degree-based topological descriptors, which we discuss in this article, are depicted in Table 1. For more details on computation of TIs of different chemical structures, the readers can see [29–36].

Table 1. Degree-based topological descriptors.

Topological descriptors	Mathematical form
General RI [19]
General ZI [20]
General sum-connectivity index [21]
RI [22, 23]
First ZI [7]
Second ZI [7]
Hyper ZI [24]
First multiplicative ZI [25]
Second multiplicative ZI [25]
ABC index [26]
Geometric arithmetic [27]
Fourth version of ABC index [14]
Fifth version of geometric-arithmetic index [28]

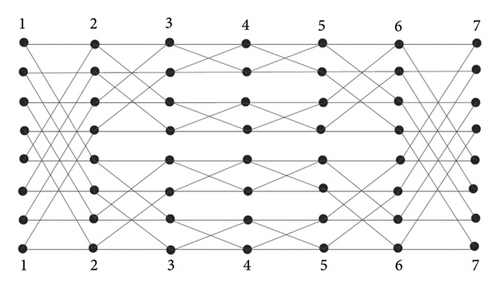
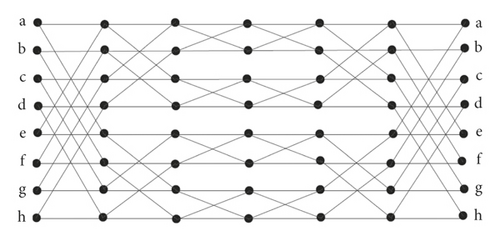
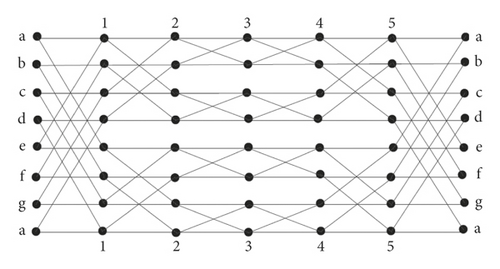
In this paper, we constructed two classes of Benes network, i.e., horizontal cylindrical Benes network HCB(r) and vertical cylindrical Benes network VCB(r) obtained by identification of vertices of first rows with last row and first column with last column of Benes network, respectively. Also, we embed the Benes network on torus denoted by TB(r). Figures 2 and 3 show the graph of horizontal and vertical Benes networks, respectively. The graph of embedding of Benes network on torus is shown in Figure 4. We compute R_α, M_α, χ_α, M₁, M₂, PM₁, PM₂, HM, ABC, and GA indices of these networks. Also, the explicit formula of ABC₄ and GA₅ indices is computed for these networks.

2. Results for Cylindrical Representation of Benes Network

In this section, we construct two types of cylindrical Benes network by identifying its vertices. First, we identify the vertices of top row to the vertices of bottom row of Benes network B(r). This will result in a cylindrical network, and we call it a horizontal cylindrical Benes network and denote it by HCB(r). Following the construction, a 3-dimensional horizontal cylindrical Benes network HCB(3) is presented in Figure 2, where the same label to the vertices represents identification of vertices. Clearly, |V(HCB(r))| = (2r + 1)(2^r − 1) and |E(HCB(r))| = 2r(2^r+1 − 1), respectively. Now, we compute the R_α, M_α, and χ_α of horizontal cylindrical Benes network HCB(r).

Theorem 1. Let ℋ be the graph of horizontal cylindrical Benes network (HCB(r)), then

(1)

Proof. In graph ℋ, we have (2r + 1)(2^r − 1) vertices among which 2(2^r − 2) vertices are of degree 2, 2 vertices are of degree 3, (2r − 1)(2^r − 2) vertices are of degree 4, and the remaining (2r − 1) vertices are of degree 6. Now, by using the formula of general Zagreb index, we get

(2)

To compute the R_α and χ_α indices, we need the partition of the edges of G based on the degree of the end vertices. This partition is given in Table 1. Using the values from Table 1, we can compute the R_α and χ_α indices as follows:

(3)

The values of first Zagreb, second Zagreb, and hyper-Zagreb indices can be computed from the Theorem 6 by taking the value of α = (−1/2), 1,2.

Corollary 1. Let ℋ be the graph of horizontal cylindrical Benes network, then

(4)

Next, we compute the PM₁, PM₂, ABC, and GA indices of horizontal cylindrical Benes network.

Table 2. The partition of edge set of HCB(r) built on the degree of end vertices of each edge.

(d_a, d_b),where	(2, 6)	(3, 4)	(3, 6)	(4, 2)	(4, 4)
Number of edges	4	4	2	2^r+2 − 12	4(r − 1)(2^r − 3)
(d_a, d_b), where	(4, 6)	(6, 6)
Number of edges	8(r − 1)	2(r − 1)

Theorem 2. Let ℋ be the graph of horizontal cylindrical Benes network, then

(5)

Proof. The result follows by using the values of the edge partition given in Table 2 to the formulas of the PM₁, PM₂, ABC, and GA indices presented in Table 1.

Now, we compute the values ABC₄ and GA₅ indices of HCB(r), where r ≥ 4. This requires the partition of its edges based on the sum of degree of neighboring vertices of end vertices of each edge. This partition is given in Table 3.

Table 3. Partition of edge set of HCB(r), r ≥ 4, built on degree sum of neighbor vertices of end vertices of each edge.

(S_a, S_a), where uv ∈ E(ℋ)	Number of edges
(8, 12)	2(2^r+1 − 1)
(12, 16)	2(2^r+1 − 1)
(16, 16)	2(2^r+1 − 1)(r − 2)

Theorem 3. Let ℋ be the graph of Horizontal cylindrical Benes network HCB(r), r ≥ 4, then

(6)

Proof. Let m_i,j denotes the number of edges of ℋ with i = S_a and j = S_b. Then, by using Table 3, ABC₄ and GA₅ indices can be computed as follows:

(7)

This completes the proof.

Next, we consider the vertical identification of the vertices. We identify the vertices on the left column with the corresponding vertices on the right column to form a cylindrical network. We name this network as the vertical cylindrical Benes network and denote it by VCB(r). The graph of VCB(3) is shown in Figure 3, where the arcs from vertical sides represent vertical sides identification. The r-dimensional vertical cylindrical Benes network has r2^r+1 vertices and r2^r+2 edges. One can see that VCB(r) is a 4-regular graph. Therefore, the computation of TIs for VCB(r) is straightforward and is presented in the following theorem.

Theorem 4. Let be the graph of vertical cylindrical Benes network, then

(8)

3. Results for Toroidal Representation of Benes Network TB(r)

If we identify the vertices in the top row of VCB(r) to the corresponding vertices of the bottom row, we get a toroidal network. We call this network Toroidal Benes network and denote it by TB(r). Figure 4 shows the graph of toroidal Benes network TB(3). Clearly, |V(TB(r))| = (2r + 1)(2^r − 1) and |E(TB(r))| = 2r(2^r+1 − 1), respectively. Now, we compute the R_α, χ_α, and M_α of toroidal Benes network TB(r).

Theorem 5. Let ℒ be the graph of toroidal cylindrical Benes network, then

(9)

Proof. In graph ℒ, we have (2r + 1)(2^r − 1) vertices among which 2r(2^r − 2) vertices are of degree 4 and the remaining 2r vertices are of degree 6. By using the formula of general Zagreb index, we get

(10)

To compute the general Randic and general sum connectivity indices, we need the partition of the edges of ℒ based on the degree of the end vertices. This partition is given in Table 4. Using the values from Table 4, we can compute the Randic and general sum connectivity indices as follows:

(11)

The values of first Zagreb, second Zagreb, and hyper-Zagreb indices can be computed from the Theorem 6 by taking value of α = (−1/2), 1 and 2.

Table 4. Partition of edge set of TB(r) built on the degree of end vertices of each edge.

(d_a, d_b),where uv ∈ E(ℒ)	Number of edges
(4, 4)	2r(2^r+1 − 6)
(4, 6)	8r
(6, 6)	2r

Corollary 2. Let ℒ be the graph of toroidal Benes network, then

(12)

Next, we compute the exact values of first multiple Zagreb, second multiple Zagreb, and ABC and GA indices of horizontal cylindrical Benes network.

Theorem 6. Let ℒ be the graph of toroidal Benes network, then

(13)

Proof. The result follows by using the values of the edge partition given in Table 4 to the formulas of the PM₁, PM₂, ABC, and GA indices presented in Table 1.

Now, we compute the values of ABC₄ and GA₅ indices of TB(r), where r ≥ 4. This requires the partition of its edges based on the sum of degree of neighboring vertices of end vertices of each edge. This partition is given in Table 5.

Table 5. The edge partition of graph TB(r), r ≥ 4, based on degree sum of neighbor vertices of end vertices of each edge.

(S_a, S_b), where ab ∈ E(ℒ)	Number of edges
(8, 12)	2(2^r+1 − 1)
(12, 16)	2(2^r+1 − 1)
(16, 16)	2(2^r+1 − 1)(r − 2)

Theorem 7. Let ℒ be the graph of toroidal Benes network TB(r), r ≥ 4, then

(14)

Proof. Let m_i,j denote the number of edges of G with i = S_a and j = S_b. Then, by using Table 5, ABC₄ and GA₅ indices can be computed as follows:

(15)

This completes the proof.

4. Conclusion and General Remarks

Designing new network structure always attract and open ways for the researchers in the networking and other structural sciences. In this paper, we constructed new classes of Benes networks embedded on the surface of cylinder and torus called horizontal cylindrical Benes network HCB(r), vertical cylindrical Benes network VCB(r), and toroidal Benes network TB(r). Then, some degree-based TIs are studied for the abovementioned networks. In future, it will help to those who are interested in problems related to interconnected networks and will be able to deal with the complex networks and their topological properties.

Disclosure

This research was carried out as a part of the employment of the authors.

Conflicts of Interest

The authors declare that there are no conflicts of interest.

Open Research

Data Availability

No additional data set has been used to support the study.

References

1 Chen M.-S., Shin K. G., and Kandlur D. D., Addressing, routing, and broadcasting in hexagonal mesh multiprocessors, IEEE Transactions on Computers. (1990) 39, no. 1, 10–18, https://doi.org/10.1109/12.46277, 2-s2.0-0025260272.
10.1109/12.46277
Web of Science® Google Scholar
2 Benes V. E., Mathematical Theory of Connecting Networks and Telephone Traffic, 1965, Academic Press, Cambridge, MA, USA.
Google Scholar
3 Manuel P. D., Abd-El-Barr M. I., Rajasingh I., and Rajan B., An efficient representation of Benes networks and its applications, Journal of Discrete Algorithms. (2008) 6, no. 1, 11–19, https://doi.org/10.1016/j.jda.2006.08.003, 2-s2.0-39149130349.
10.1016/j.jda.2006.08.003
Google Scholar
4 Liu X. and Gu Q. P., Multicasts on WDM all-optical butterfly networks, Journal of Information Science and Engineering. (2002) 18, 1049–1058.
CAS Web of Science® Google Scholar
5 Xu J., Topological Structure and Analysis of Interconnection Networks, 2001, Kluwer Academic Publishers, Amsterdam, Netherlands.
10.1007/978-1-4757-3387-7
Google Scholar
6 Diudea M. V., Gutman I., and Lorentz J., Molecular Topology, 2001, Nova, Huntington, CA, USA.
Google Scholar
7 Gutman I. and Polansky O. E., Mathematical Concepts in Organic Chemistry, 1986, Springer-Verlag, New York, NY, USA.
10.1007/978-3-642-70982-1
Google Scholar
8 Xu J., Topological Structure and Analysis of Interconnection Networks, 2001, Kluwer Academic, Amsterdam, Netherlands.
10.1007/978-1-4757-3387-7
Google Scholar
9 Bertz S. H. and Wright W. F., Graph Theory Notes of New York, 1998, New York Academy of Sciences, New York, NY, USA.
Google Scholar
10 Nikolic S., Tolic I. M., and Trinajstic N., Relations between three topological indices, MATCH Communications in Mathematical and in Computer Chemistry. (1999) 40, 187–201.
CAS Google Scholar
11 Nikolic S., Trinajstic N., and Tolic I. M., Complexity of molecules, Journal of Chemical Information and Modeling. (2000) 40, 920–926, https://doi.org/10.1021/ci9901183, 2-s2.0-0000226215.
10.1021/ci9901183
CAS Google Scholar
12 Nikolic S., Tolic I. M., Trinajstic N., and Bau i I., Complexity of some interesting (chemical) graphs, Croatica Chemica Acta. (2000) 69, no. 3, 883–897.
Google Scholar
13 Nikolic S., Trinajstic N., Tolic I. M., Rucker G., and Rucker C., D. Bonchev and D. H. Rouvray, On Molecular Complexity Indices, Complexity in Chemistry, 2003, London, UK.
Google Scholar
14 Ghorbani M. and Hosseinzadeh M. A., Computing ABC4 index of nanostar dendrimers, Optoelectronics and Advanced Materials-Rapid Communications. (2010) 4, 1419–1422.
CAS Web of Science® Google Scholar
15 Golbraikh A., Bonchev D., and Tropsha A., Novel ZE-isomerism descriptors derived from molecular topology and their application to QSAR analysis, Journal of Chemical Information and Computer Sciences. (2002) 42, no. 4, 769–787, https://doi.org/10.1021/ci0103469, 2-s2.0-0036628546.
10.1021/ci0103469
CAS PubMed Web of Science® Google Scholar
16 Milicevic A. and Nikolic S., Graphical matrices in Chemistry, Croatica Chemica Acta. (2004) 77, 97–101, In press.
CAS Web of Science® Google Scholar
17 Estrada E., Torres L., Rodriguez L., and Gutman I., Modelling the enthalpy of formation of alkanes, Indian Journal of Chemistry. (1998) 37A, 849–855.
CAS Google Scholar
18 Estrada E., Generalization of topological indices, Chemical Physics Letters. (2001) 336, no. 3-4, 248–252, https://doi.org/10.1016/s0009-2614(01)00127-0, 2-s2.0-0000645097.
10.1016/S0009-2614(01)00127-0
CAS Web of Science® Google Scholar
19 Bollobǎs B. and Erdos P., Graphs of extremal weights, Ars Combinatoria. (1998) 50, 225–233.
Web of Science® Google Scholar
20 Li X. and Zhao H., Trees with the first three smallest and largest generalized topological indices, MATCH Communications in Mathematical and in Computer Chemistry. (2004) 50.
Google Scholar
21 Zhou B. and Trinajstić N., On general sum-connectivity index, Journal of Mathematical Chemistry. (2010) 47, no. 1, 210–218, https://doi.org/10.1007/s10910-009-9542-4, 2-s2.0-72949100341.
10.1007/s10910-009-9542-4
CAS Web of Science® Google Scholar
22 Perc M. and Szolnoki A., Coevolutionary games-a mini review, Biosystems. (2010) 99, no. 2, 109–125, https://doi.org/10.1016/j.biosystems.2009.10.003, 2-s2.0-73449112588.
10.1016/j.biosystems.2009.10.003
PubMed Web of Science® Google Scholar
23 Randic M., On characterization of molecular branching, Biosystems. (1975) 99, no. 2, 6609–6615, https://doi.org/10.1016/j.biosystems.2009.10.003, 2-s2.0-73449112588.
10.1016/j.biosystems.2009.10.003
Google Scholar
24 Shirdel G. H., Pour H. R., and Sayadi A. M., The hyper-Zagreb index of graph operations, Iran, Journal of Mathematical Chemistry. (2013) 4, 213–220.
Google Scholar
25 Ghorbani M. and Azimi N., Note on multiple Zagreb indices, Iran, Journal of Mathematical Chemistry. (2012) 3, no. 2, 137–143.
Google Scholar
26 Estrada E., Torres L., Rodríguez L., and Gutman I., An atom-bond connectivity index: modelling the enthalpy of formation of alkanes, Indian Journal of Chemistry. (1998) 37A, 849–855.
CAS Google Scholar
27 Du Z., Zhou B., and Trinajsti N., On geometric-arithmetic indices of (molecular) trees, unicyclic graphs and bicyclic graphs, MATCH Communications in Mathematical and in Computer Chemistry. (2011) 66, 681–697.
CAS Web of Science® Google Scholar
28 Gravovac A., Ghorbani M., and Hosseinzadeh M. A., Computing Fth geometric-arithmatic index ABC4 index of nanostar dendrimers, Optoelectron, Advanced Materials–Rapid Communications. (2010) 4, no. 9, 1419–1422.
Web of Science® Google Scholar
29 Das K. C. and Ali A., On a conjecture about the second Zagreb index, Discrete Mathematics Letters. (2019) 2, 38–43.
Google Scholar
30 Gao W., Iqbal Z., Iqbal Z., Akhter S., Ishaq M., and Aslam A., On irregularity descriptors of derived graphs, AIMS Mathematics. (2020) 5, no. 5, 4085–4107, https://doi.org/10.3934/math.2020262.
10.3934/math.2020262
Web of Science® Google Scholar
31 Iqbal Z., Ishaq M., Aslam A., and Gao W., On eccentricity based topological descriptors of water soluble dendrimers, Zeitschrift für Naturforschung C. (2018) 74, no. 1-2, https://doi.org/10.1515/znc-2018-0123, 2-s2.0-85058809785.
10.1515/znc-2018-0123
Google Scholar
32 Aslam A., Ahmad S., Binyamin M. A., and Gao W., Calculating topological indices of certain OTIS interconnection networks, Open Chemistry. (2019) 17, no. 1, 220–228, https://doi.org/10.1515/chem-2019-0029, 2-s2.0-85064967435.
10.1515/chem-2019-0029
CAS Web of Science® Google Scholar
33 Aslam A., Nadeem M. F., Zahid Z., Zafar S., and Gao W., Computing certain topological indices of the line graphs of subdivision graphs of some rooted product graphs, Mathematics. (2019) 7, no. 5, https://doi.org/10.3390/math7000393.
10.3390/math7050393
Web of Science® Google Scholar
34 Gutman I. and Das K. C., The first Zagreb index 30 years after, MATCH Communications in Mathematical and in Computer Chemistry. (2004) 50, 83–92.
CAS Google Scholar
35 Das K. C., Akgunes N., Togan M., Yurttas A., Cangul I. N., and Cevik A. S., On the first Zagreb index and multiplicative Zagreb coindices of graphs, Analele Universitatii “Ovidius” Constanta-Seria Matematica. (2016) 24, no. 1, 153–176, https://doi.org/10.1515/auom-2016-0008, 2-s2.0-84962731881.
10.1515/auom-2016-0008
Google Scholar
36 Akgunes N., Das K. C., and Cevik A. S., I. Gutman, Topological indices on a graph of monogenic semigroups, Topics in Chemical Graph Theory, Mathematical Chemistry Monographs, 2014, University of Kragujevac and Faculty of Science Kragujevac, Kragujevac, Serbia.
Google Scholar

Citing Literature

All articles

On Topological Indices for New Classes of Benes Network

Abstract

1. Introduction

2. Results for Cylindrical Representation of Benes Network

3. Results for Toroidal Representation of Benes Network TB(r)

4. Conclusion and General Remarks

Disclosure

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On Topological Indices for New Classes of Benes Network

Abstract

1. Introduction

2. Results for Cylindrical Representation of Benes Network

3. Results for Toroidal Representation of Benes Network TB(r)

4. Conclusion and General Remarks

Disclosure

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information