1. Introduction

Low-dimensional semiconductor structures, which are the core of many semiconductor devices, have been studied for new applied fields thanks to the inventions of advanced technologies [1–12]. These devices play important roles in the fields of medicine, military, telecommunication, and many others [13–17]. The semiconductor quantum wires, one of the low-dimensional structures that possess many special properties, have drawn the attention of scientists [18–22]. These structures could be applied to create high-speed lasers [23, 24], quantum electron waveguides [25], resonant tunneling field-effect transistors [26, 27], or telecommunication networks [28]. Recently, studies of movement and interaction among electrons in the quantum wires have shown the quantum effects that can lead to various applications in the new quantum technology [29]. Nonetheless, many new physical properties of these structures, which are expected to have more breakthrough applications in the future, have been little known to researchers.

In low-dimensional semiconductor systems, scientists have observed the excitonic optical Stark effect when irradiating a strong pump laser pulse in [30, 31]. This effect resulted from the interaction between exciton states, displayed through splitting and shifting the absorption spectrum of the exciton [32–35]. Based on these properties, the researchers proposed a number of prospective applications of the excitonic optical Stark effect, such as making optical switching devices [33, 34], optical modulators [35], mesoporous hybrid multifunctional system [36], or optically controlled field-effect transistors [37]. So far, the excitonic optical Stark effect has been primarily studied on quantum wells and quantum dots [30, 31]. The existence of this effect in quantum wire structures is still under investigation.

The excitonic optical Stark effect is divided into two types. The first type is the consequence of a coupling of the exciton ground state and an exciton-excited state, e.g., the first exciton state under the effect of a strong pump laser beam called a two-level Stark effect [38]. The second type is due to a coupling of two exciton-excited states under the effect of a pump laser beam of lower intensity, known as a three-level Stark effect [38, 39]. The latter has more applicability because it is more likely to occur. The excitonic optical Stark effect can be experimentally studied by the pump-probe technique [40, 41]. For theoretical research, methods to be deployed can be the renormalized wave function theory [42], the density matrix approach [43, 44], the finite difference method [45], the photoemission theory [46], or the nonequilibrium many body perturbation theory [47]. In our viewpoint, the renormalized wave function formulation has many advantages such as it only renormalizes the wave function of exciton, or it is easy to confirm the existence of the effect as well as to reveal its physical properties.

In this study, we investigate the three-level excitonic optical Stark effect in GaAs cylindrical quantum wires utilizing the renormalized wave function formulation. We have also successfully applied that formulation to study the excitonic quantum beats [48], a phenomenon that occurs as the consequence of the three-level excitonic optical Stark effect in the same structures of quantum wires. Therefore, both the recent report and Ref. [48] share the same starting point. Hence, we can expect to successfully study the three-level excitonic optical Stark effect in those structures. This paper is organized into three main sections, with the present section justifying the rationale and introducing the stated problem. Section 2 provides the formulation and basic equations. Section 3 presents and discusses the findings of the study, based on which, conclusions are arrived at.

2. Formulation

2.1. Wave Functions and Quantized Levels of Electron and Hole in a Cylindrical Quantum Wire

Let consider a circular cylindrical quantum wire in the cylindrical coordinates (r, φ, z). Suppose that the quantum wire is of the radius R and stays along the Oz axis, and the particles are confined in the plane Oxy by an infinite cylindrical symmetric potential,

$$ (1)

where r is the length from the wire axis to the considered position. The envelope wave functions describing the states of the electron and hole in the confined plane can be written as [48, 49]

$$ (2)

where $$ is the position vector of the particle, J_m(r) are the Bessel functions of the first kind of order m (m = 0, 1, 2, ⋯), and χ_mn are its nth zero points (n = 1, 2, ⋯). The full wave functions of the electron and hole are presented as

$$ (3)

where $$ is the periodic Bloch function in the first Brillouin zone and c and v signify the conduction and valence band, respectively.

The quantized levels of the electron and hole are determined as

$$ (4)

where m_e and m_h are the effective masses of the electron and hole, respectively, and E_g is the energy gap of the wire material. Here, we set the top of the valence band as the origin for calculating the energy of the particles.

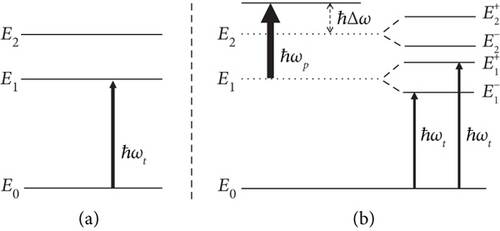
In this paper, we use a three-level energy diagram to study the excitonic optical Stark effect in the quantum wire. Therefore, we investigate a three-level model in which E₀ is the first hole level, while E₁ and E₂ are the first two electron ones (as shown in Figure 1(a)).

The energies of the particles are determined as follows [48]:

$$ (5)

with the compatible time-dependent wave functions

$$ (6)

in which $$(j = 0, 1, 2) are the stationary wave functions of the particles in the quantum wire and are defined by [48]

$$ (7)

3. Results and Discussion

In this section, we study the exciton absorption spectrum in GaAs/Al_0.7Ga_0.3As cylindrical quantum wires in the absence and in the presence of the pump laser to reveal the excitonic optical Stark effect. Of course, the band offset between GaAs and Al_0.7Ga_0.3As is finite, but here, in our very first work related to quantum wires, we assume quantum wires being surrounded by an infinite potential for the sake of simplicity. Therefore, we do not mention the effect of the barrier layer in the later discussion but leave it for future work. The parameters are used as follows. The pump laser is assigned an amplitude of about A_p = 8 × 10⁶ V/m and has a very small detuning, ℏΔω ≪ ℏω_p. The linewidth of the absorption peak is assumed to be Γ = 0.1 meV; here, we use a monochrome probe laser. The effective masses of the electron and hole of the wire material, GaAs, are m_e = 0.067m₀ and m_h = 0.51m₀, respectively [53]; the energy gap of GaAs is E_g = 1424 meV [54].

First, we plot the absorption spectra of excitons in the quantum wire of the radius R = 50 Å in the absence and in the presence of a strong pump laser that resonates accurately with two levels of the electron (ℏΔω = 0 meV), Figure 2. The results show that, before the pump laser operates, the absorption spectra of excitons include only one absorption peak (dashed line). By contrast, after turning on the pump laser, two distinct peaks (solid lines) arise in the exciton absorption spectra as convincing evidence of the existence of the excitonic optical Stark effect in the system. These results can be explained as follows.

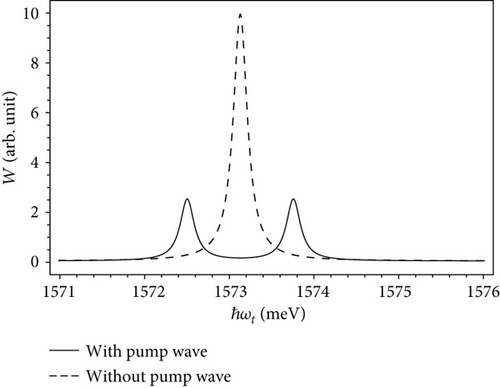
Before the pump laser is switched on, according to the selection rules for the quantum wire structures, there is only one transition between the hole level and the first electron level in the absorption spectrum of excitons (the thin arrow in Figure 1(a)). Therefore, we see only one peak in the absorption spectrum. On the contrary, if there exists a resonant pump laser that can excite the intraband transition between two electron levels (as illustrated by the thick arrow in Figure 1(b)), and if the intensity of the pump laser is very strong, then it can merge those two electron levels into a single level. According to the Pauli exclusion principle, this single level allows a maximum of two states of electron, while two initial electron levels allow up to four states. In order to ensure that the system still includes the four permitted states and still satisfies the Pauli exclusion principle, each initial electron level needs to be split into two sublevels. Fortunately, under the strong electric field of the pump laser, the symmetry of the state of this single level is broken as seen in the Stark effect. Therefore, both initial electron levels are split. Consequently, when we irradiate a proper probe laser into the system, we can find two interband transitions from the hole level to two sublevels of electron (as indicated by the two thin arrows in Figure 1(b)), and thus, we can see two distinct peaks in the exciton absorption spectrum. Obviously, due to the selection rules, it is impossible that the interband transitions from the hole level to the electron sublevels split from the second quantized level of the electron will occur. Moreover, due to the symmetry between the sublevels with reference to the position of the initial electron level, the two obtained peaks have the same height (or the same transition rate) and stay symmetrical on both sides of the initial peak, which satisfies the energy conservation law. We also found that, in Figure 2, the intensity of the exciton absorption spectra in the case of without pump wave (dashed line) appears much higher than that in the presence of the pump wave (solid line). This reduction is due to the act of the conservation of the transition rate [55]. We realize that, by turning the pump laser on or off, this effect can control the system to work as an optical switching by letting the probe laser beam of certain frequency propagate through it or not.

Now, we will thoroughly study the excitonic optical Stark effect in the quantum wires by examining the dependence of the exciton absorption spectrum on the pump laser detuning and the wire radius. First, we plot the exciton absorption spectra in the quantum wire with radius R = 50 Å with different detuning in both cases with and without the pump laser (Figure 3). We observe that in the presence of the pump laser, all excitonic absorption spectra contain two distinct spectral peaks, which implies that the optical Stark effect occurs. Moreover, as we increase the detuning, the height of one peak increases and that peak moves closer to the position of the initial peak, while the other peak gets farther from the position of the initial peak and lowered, and it almost disappears when the detuning is too large (as in the case ℏΔω = 1.2 meV, dashed line). The higher the difference in height of the two spectral peaks is, the greater the difference in the transition rate. Despite this, in all the cases under investigation, we can see that the total transition rate is conserved.

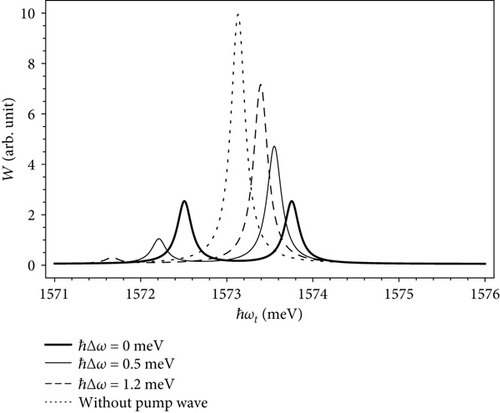
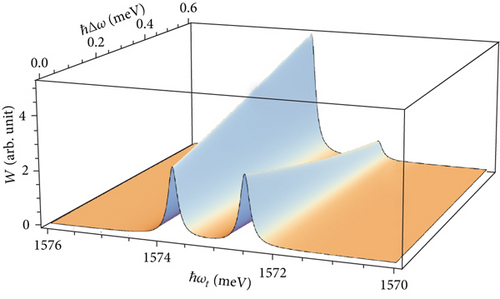
Figure 4 shows more clearly the change in height and position of the absorption peaks when the pump laser detuning is increased from 0 meV to 0.6 meV. It is obvious that when the detuning increases, then one peak raises its height while the other lowers to the zero value.

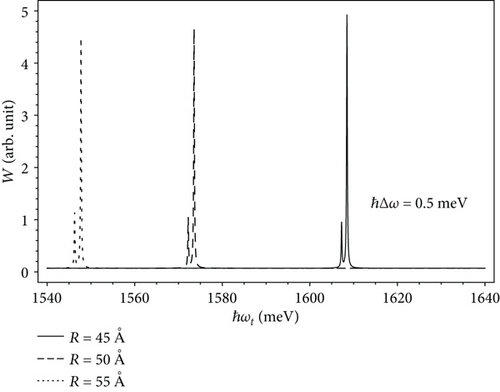
Next, we investigate the influence of the quantum wire radius on the excitonic optical Stark effect. Figure 5 shows the exciton absorption spectra in the quantum wires of radii R = 45 Å (solid line), R = 50 Å (dashed line), and R = 55 Å (dotted line) in the presence of the pump laser with the detuning ℏΔω = 0.5 meV. In all three cases, we observe the appearance of two exciton absorption peaks, which again confirmed the existence of the optical Stark effect. We can see that as the wire radius increases, the absorption spectra of excitons shift very fast to the lower energy region. This can be explained as follows. According to Equation (4), as the quantum wire radius increases, the quantized levels of the electron and hole have smaller values and they stay closer to each other. Therefore, a smaller photon energy is needed to excite the transition from the hole level to the splitting electron levels. As a result, we see that the absorption spectra of the excitons shift to a lower energy region as the wire radius becomes larger. It is worth mentioning that we have applied our theory for the other low-dimensional structures such as quantum dots and quantum wells and we have obtained the similar results [55, 56].

As an effort to provide a brief guidance for experimental verification of our results, in Figures 6 and 7, the dependence of the wavelength of pump laser λ_p and that of probe laser λ_t on the wire radius are plotted. We see that both the wavelengths increase with the wire radius as a result of the quantum size effect. However, while one curve describes a parabolic function (Figure 6), the other shows a square root one (Figure 7).

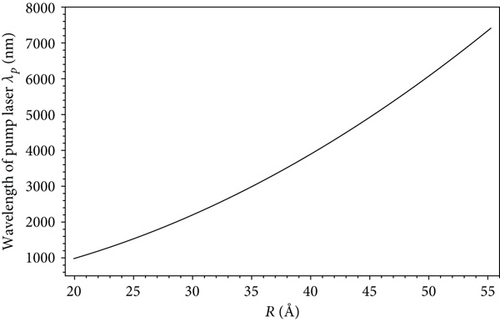
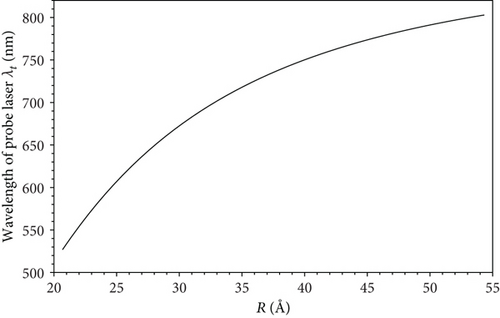
After fabricating quantum wires, by looking at these figures, experimentalists can find the proper wavelengths of lasers and set up verification experiments. By controlling the laser’s powers to fit values, the excitonic optical Stark effect is expected to occur. Also, by adjusting the other parameters, we can find the properties of the excitonic optical Stark effect.

4. Conclusions

In this work, we have studied the three-level excitonic optical Stark effect in GaAs circular cylindrical quantum wires by means of the renormalized wave function theory. The results show that, while the pump laser operates, there appear two separated spectral peaks in the excitonic absorption spectra as the indication of the excitonic optical Stark effect. Moreover, the absorption spectra of excitons shift sharply with the wire radius. Also, the heights of the two absorption peaks are very sensitive to the detuning of the pump laser.

Additionally, we have proposed an explanation for the splitting of the energy levels of the electron under the effect of the strong resonant pump laser, which leads to the formation of two new absorption peaks of the exciton. We have also tried to explain the shift of the excitonic absorption spectra as the wire radius varies. Finally, we have tried to provide a brief guidance for experimental verification of our results. We expect that these results could be confirmed by proper experiments and could have some contribution to the related fields such as making ultrafast switching devices for quantum computers.

For the sake of simplicity, here, we consider circular cylindrical quantum wires surrounded by an infinite potential. However, we believe that our model can be expanded to other quantum wires of different shapes under various potentials as long as we can determine the wave functions and energy levels of particles.

Conflicts of Interest

The authors declare that they have no conflicts of interest.