Thermal Radiation Effects on Unsteady Stagnation Point Nanofluid Flow in View of Convective Boundary Conditions
Abstract
The present communication particularizes nonlinear convective non-Newtonian stagnation point flow and heat transference effects in stretchable flow of nanofluid. Magnetohydromagnetic steady viscous flow of nanofluid is examined. Heat transfer attributes of nanofluids are addressed via a numerical algorithm. Conductivity and diffusivity characteristics of fluid are depending on temperature and concentration and furthermore, on mass conservation, momentum, energy, and concentration yield partial differential equations (PDEs). The boundary layer flow concept pioneered by Prandtl has been employed to simplify the nonlinear constitutive flow laws which are then changed to ordinary differential equations. A built-in bvp4c algorithm in Mathematica software yields convergent outcomes of nonlinear (ODEs) systems. A comprehensive analysis has been made elucidating the physical significance of various governing parameters effects presented graphically. Additionally, the flow nature was confirmed versus streamlines.
1. Introduction
The low thermal conductivity features of various non-Newtonian fluids have serious problems with heat transport mechanisms in different scientific and practical engineering applications. Several attempts have been made by researchers and engineers to address the low thermal behavior of the base fluids. Different tools and mechanisms have been adopted for the enhancement of thermal conductivity issues. Out of these suggested mechanisms, incorporating small nanosized metallic particles into base fluid yields potential results. The word nanofluid was adopted by Choi and Eastman [1]. Khan et al. [2] discussed fluid thermal conductivity features by utilizing nanofluid for the development of heat transportation analysis for various applications in different heat exchanger equipment. There are many important applications and narrative characteristics of nanofluids in various applications in engineering and industrial units. These nanofluid applications include heat exchange processes such as chillers, nuclear power stations, car engines, microelectronics, fuel cells, coolant, and many more engineering utilization as discussed by Turkyilmazoglu [3]. The nanofluid has significant advantages and applications in manufacturing industries. A great number of mathematicians, researchers, and scientists addressed such utilizations of nanofluid for development in [4–10]. For the first time, Hiemenz [11] conducted extensive research and discussed the exact solution to stagnation point flow by Navier–Stokes’s equation. Furthermore, stagnation point flow was investigated, which can be steady or unsteady, normal or oblique, two or more dimensional, onward or opposite, and viscous or inviscid. Khan et al. [12] elucidated different aspects of unsteady non-Newtonian stagnation point nanofluid flow and multiple solutions analyzed and furthermore, added the enhancement of thermal behavior of the base fluid by incorporating the nanofluid. A potential investigation has been made to analyze three-dimensional stagnation point hybrid nanofluid flow over a slip surface by Abbas et al. [13]. Serious attention has been given in recent times by researchers, engineers, and mathematicians to explore non-Newtonian stagnation point flow nanofluid flow [14–17]. The viscoelastic nanofluids have a variety of practical usage in daily life and large-scale applications. Such important utilizations of non-Newtonian fluids are foods, multiphase mixtures molecular weight systems, and various solutions. Abbas et al. [18] studied stagnation point MHD flow and thermal radiation effects on micropolar flow past through a round cylinder with sinusoidal radius variation. Furthermore, porosity influence and velocity slip jump are evaluated. Akbar et al. [19] explored hydromagnetic convective condition along with slip effects on stagnation point nanofluid by incorporation of CNT particles past a stretchable surface, and thermal radiations have been analyzed. Moreover, the convective boundary conditions with slip flow and incorporated CNT nanofluid vied in a stretchable plane surface. Those materials showing non-Newtonian fluid flow features contain the natural products, food products, polymer melts and solutions, biological fluids, multiphase mixtures, and personal care products including investigated toiletries and cosmetics and by Ijaz et al. [20]. The non-Newtonian fluids have a great number of significant utilizations in industrial units, medical technologies, and engineering application. The expanding uses of these nanofluids describe petroleum drilling, steel substances, blasting of glasses, and extrusion of polymers. Some of the polymers employed in telecommunication appliances, agriculture, and medical are analyzed by Hussain et al. [21]. Muhammad et al. [22] investigated nonlinear thermal radiation in three-dimensional Eyring–Powell nanofluid flow with activation energy. Hussain and Muhammad [23] discussed convective heat transfer at the boundaries is incorporated by employing effective thermal conductivity of nanoliquid. Muhammad et al. [24] studied Carreau nanofluid under the influence of slip over a wedge with motile microorganisms and thermal radiation effects. Besides, these many scientists carried to analyze the stagnation point flow and other non-Newtonian fluids with aspect to the following citations, provided a detailed view of flows [25–33].
2. Mathematical Formulation
-
Mass conservation expression:
(1) -
Momentum expression:
(2) -
Energy expression:
(3) -
Concentration of nanoparticles:
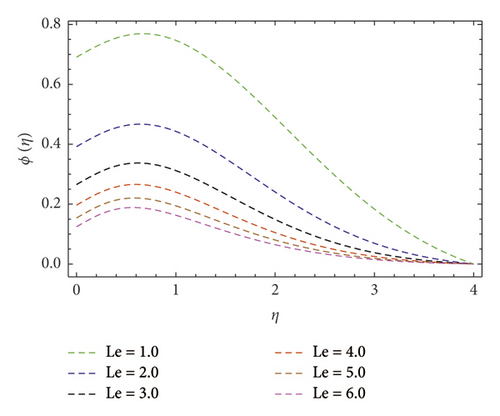
(4) -
Subject to flow conditions are as follows:
(5) -
Herein, u and v velocity components are in coordinates axes, along and normal to flow direction
-
The kinematics viscosity is υ, inside boundary layer temperature is T, nanoparticles effective heat capacity is (ρc)p, thermal capacity of fluid is (ρc)f, fluid density is (ρ), Γ = ((ρc)p/(ρc)f), and T∞ is the ambient temperature away from stretchable surface.
-
Introducing dimensionless parameters,
(6) -
Here, the stream function ψ(x, y) is defined by
(7) -
Equation (1) is justified automatically, and equations (2)–(4) take the following forms by employing equation (6):
(8)(9)(10) -
Transformed conditions:
(11) -
Variables seeming in constitutive flow laws (8)–(11) are defined as follows:
-
the magnetic parameter; Le = (α/DB), Lewis number; Pr = (υ/α), Prandtl number; A = (b/a), velocity ratio parameter; Nb = ((ρc)pDBC∞/(ρc)fυ), Brownian motion parameter; Nt = ((ρc)pDT(Tf − T∞)/(ρc)fυT∞), thermophoresis parameter; and Biot number, respectively.
-
Expressions of physical quantities (Cfx, Nux) are defined by
(12)(13) -
By substituting (13) in (12), we have
(14)
3. Numerical Solution and Convergence Analysis
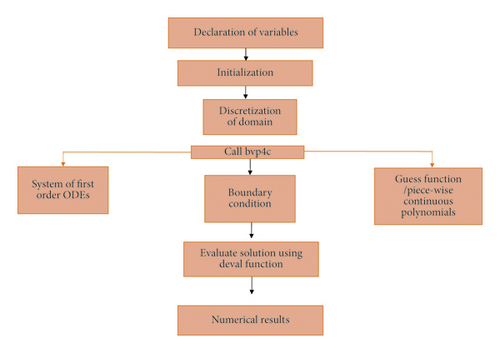
A suitable step size Δη = 0.001 is selected for the entire numerical computation work. A possible convergence limit has been adopted as 10−6. Furthermore, the boundary conditions given in (11) value at infinity is chosen as η∞ = 4; after selecting the appropriate value for η∞, all numerical solutions converge to it and are satisfied correctly. Finally, residual error analysis has been evaluated. Dwindles in error perceive for higher order deformations as shown in Figure 2. Furthermore, the algorithm of bvp4c routine calculation is shown in Figure 3.

4. Results and Discussion
The constative flow laws of nonlinear differential systems consisting of (8)–(10) subjected to specified boundary are solved numerically by employing the bvp4c algorithm. The attributes of affective pertinent flow factors on velocity field, thermal field, and nanoparticles volume are evaluated graphically and discussed in Figures 4–25.
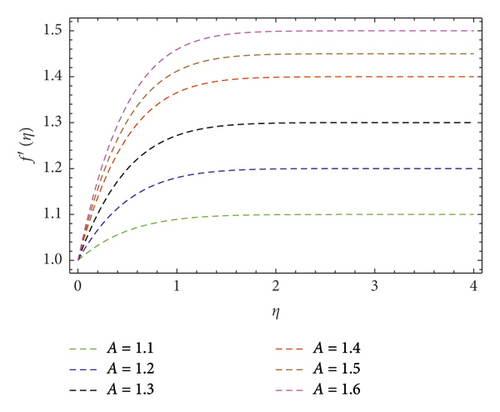
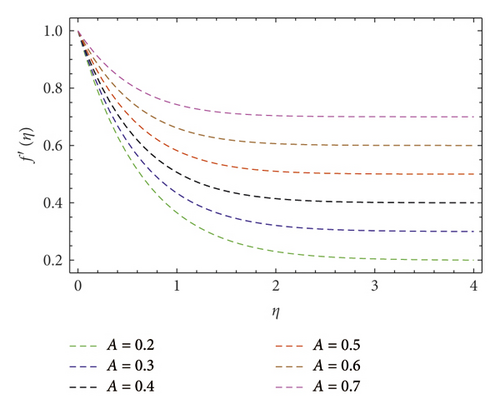
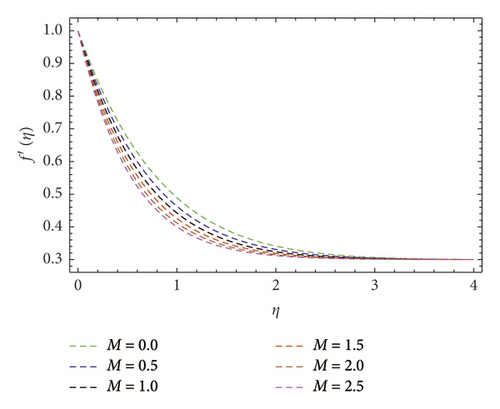
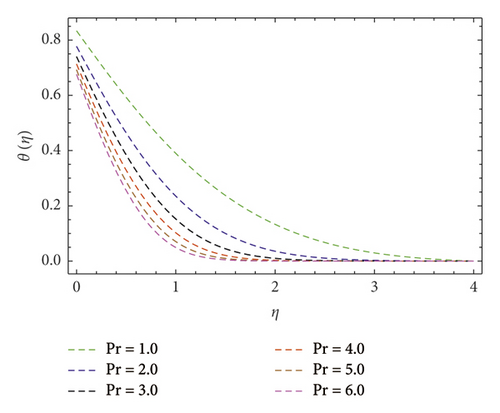
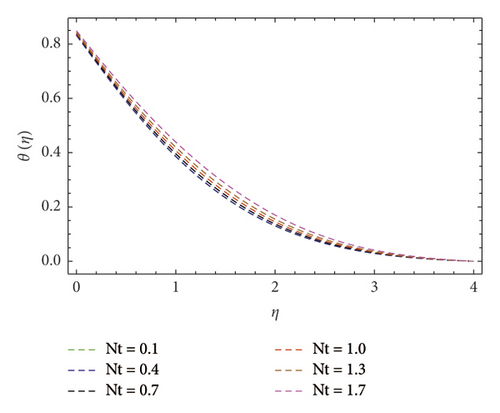
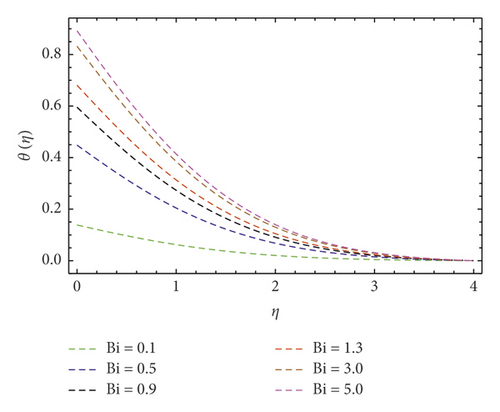
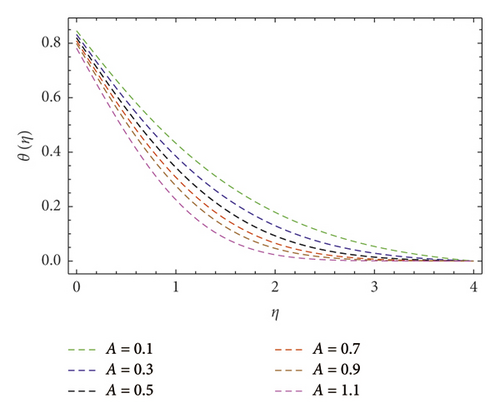
Figures 4 and 5 depict variations in f′(η) velocity subjected to velocity ratio parameter (A). These figures unveil enhancement in boundary layer thickness for higher (A), perceive when (A > 1), and diminish the hydromagnetic boundary layer thickness for lower values of (A) when (A < 1). In reality, stretching velocity is less than the free stream velocity, due to which the ratio of stretching velocity to free stream velocity is less than unity; consequently, decreasing force vanishes, and clearly, f′(η) profile is augmented. Attributes of (M) are shown in Figure 6. Herein, we noticed f′(η) is lower subjected to increment in magnetic field. Such scenario found due to higher (M) implies strong resistance force came into existence called Lorentz force. In consequence, dwindles in velocity f′(η) profile perceived. The contribution of the Prandtl number (Pr) on thermal field θ(η) is evaluated as shown in Figure 7. The thermal diffusivity diminishes when (Pr) boosts through larger values. Hence, θ(η) decays. Consequently, thermal boundary layer thickness escalates. Figure 8 explains variations in θ(η) thermal field curves for the thermophoresis (Nt) parameter. This figure unveils enhancement in θ(η) when (Nt) is enlarged. In fact, nanoparticles attain extra heat subject to the (Nt) factor. In consequence, θ(η) upsurges. The temperature field θ(η) curves for the Biot number (Bi) also called convective heating are shown in Figure 9. One can clearly perceive that θ(η) is a growing function of (Bi). In reality, heat transference at surface boosts through larger (Bi). Consequently, θ(η) upsurges. Hence, thermal boundary layer thickness escalates. Variations in temperature field θ(η) against (A) are interprets as shown in Figure 10. Clearly, larger velocity ratio factor diminishes thermal boundary layer thickness.
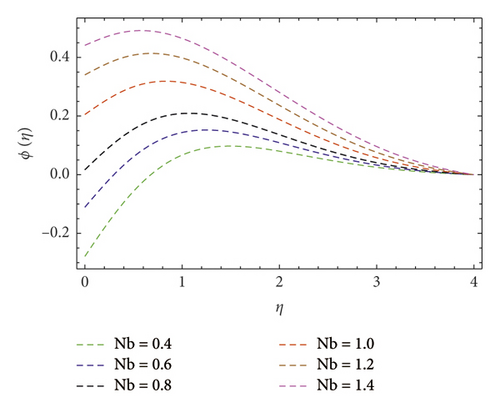
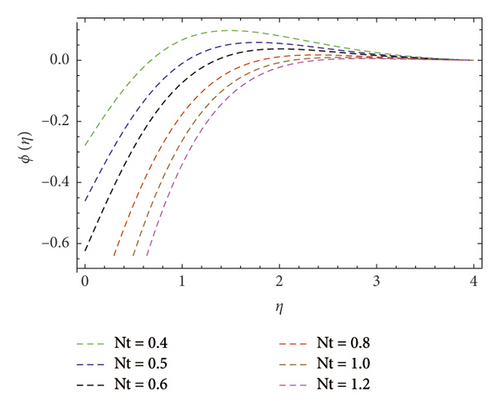
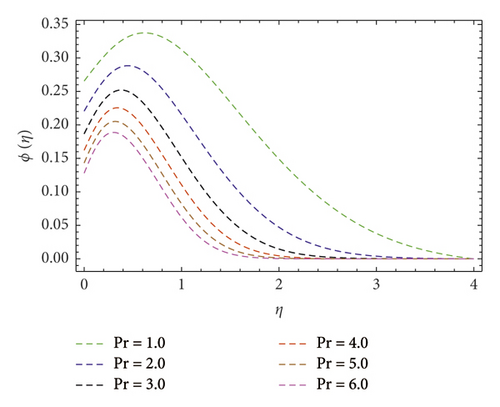
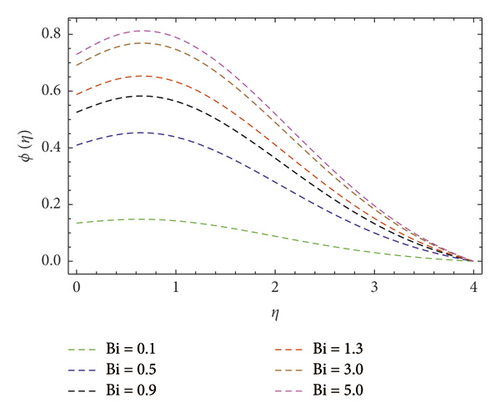
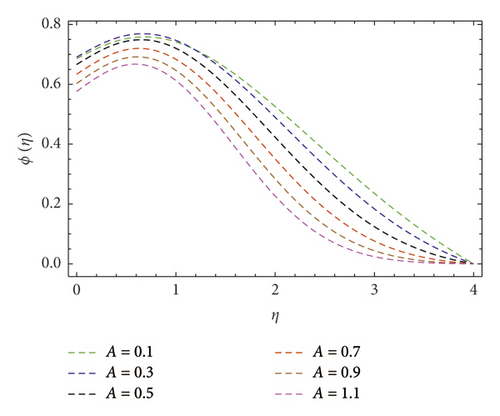
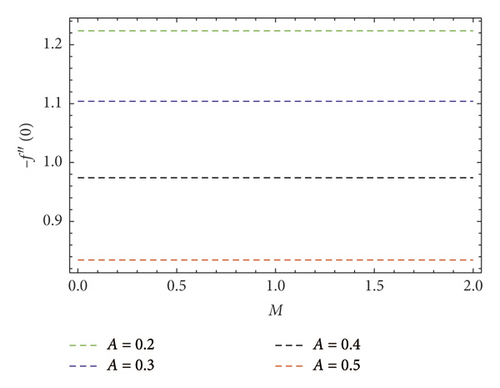
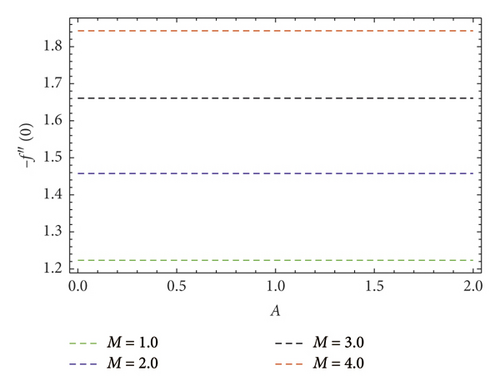
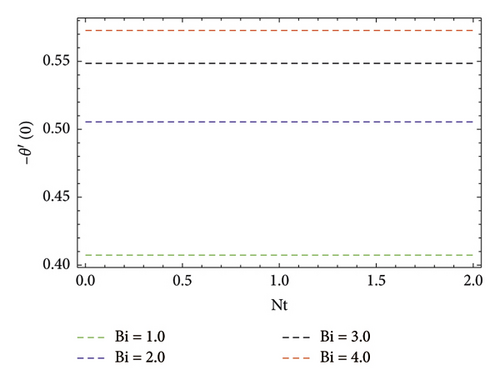
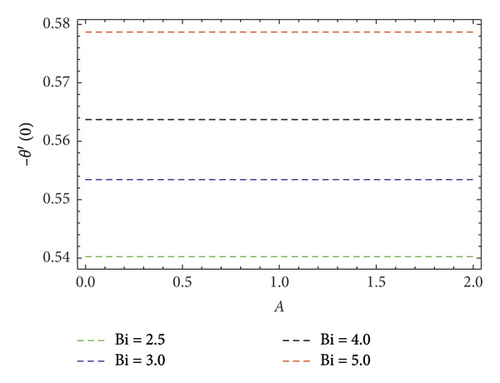
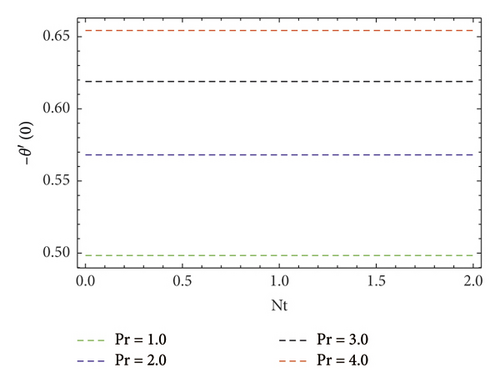
Impact of concentration ϕ(η) profile against the (Nb) parameter is portrayed as shown in Figure 11. This figure witnesses enhancement in ϕ(η). Clearly, ϕ(η) is an augmenting function of the Brownian motion parameter. In reality, one can observe heat transference boosts through larger (Nb). Consequently, ϕ(η) augments. Figure 12 discloses contribution of the (Nt) parameter on ϕ(η) profile. Clearly, dwindles ϕ(η) subject to increment in (Nt). Figure 13 shows the effects of Prandtl number (Pr) on concentration gradient. As the influence of the (Pr) parameter increases, nanoparticles diffuse outside which reduced the concentration at the surface. The contribution of Lewis number (Le) on the concentration profile is shown in Figure 14. An increasing value of the (Le) parameter shows a poor (Nb) diffusion coefficient as a result of small penetration depth observed for ϕ(η) and displays decreasing trends in the concentration profile. The contribution of Boit number (Bi) parameter via ϕ(η) is shown in Figure 15. Clearly, larger estimations correspond to upsurges in the ϕ(η) profile. Figure 16 unveils (A) velocity ratio factor influences on ϕ(η). It is viewed that the concentration ϕ(η) profile is a decreasing function of (A). Such scenario is noticed because augmentation in (A) yields reduction in fluid thermal conductivity. Consequently, ϕ(η) vanishes. Figures 17 and 18 emphasize A, M, Nt , and Bi influences on −f″(0). Here, skin friction diminishes for A and M are augmented. However, opposite appearances noticed for Nt and Bi enlarged. The attributes of Bi, Nt, A, and Pr interpreted on −θ′(0) are shown in Figures 19–21. These figures confirm that −θ′(0) Nusselt number upsurges subject to augmented in Bi, Nt, A, and Pr parameters. Figures 22–25 explain the impression of magnetic and velocity ratio parameters on streamlines.
5. Conclusions
-
We found lower −f″(0) when A velocity ratio factor incremented and −f″(0) upsurges for a higher magnetic field value
-
An augmentation in Nb and Nt yields an opposite report for the solutal ϕ(η) boundary layer
-
Larger velocity parameter A and Boit number Bi yields −θ′(0) escalates
-
An increment in thermal boundary is noticed for higher Nt and diminishes for larger Pr values
-
Both parameters Nb and Nt yield higher thermal θ(η) field
-
The solutal ϕ(η) boundary layer thickness is near stretching sheet negative and zero elsewhere
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at Majmaah University for funding this work under the project number (RGP-2019-6).
Open Research
Data Availability
The data used to support the findings of this study are included within the article.




