Volume 2021, Issue 1 5322548

Research Article

Open Access

Prototype Test and Numerical Analysis of a Shallow Cable with Novel Viscous Inertial Damper

Jing Liu,

Jing Liu

orcid.org/0000-0002-4254-911X

School of Civil Engineering and Transportation, Hebei University of Technology, Tianjin 300401, China hebut.edu.cn

Search for more papers by this author

Dong Liang,

Corresponding Author

Dong Liang

[email protected]

orcid.org/0000-0003-3990-3293

School of Civil Engineering and Transportation, Hebei University of Technology, Tianjin 300401, China hebut.edu.cn

Search for more papers by this author

Liu Yang,

Liu Yang

orcid.org/0000-0003-2747-5121

School of Civil Engineering and Transportation, Hebei University of Technology, Tianjin 300401, China hebut.edu.cn

Search for more papers by this author

Lida Wang,

Lida Wang

orcid.org/0000-0002-8363-3350

School of Civil Engineering and Transportation, Hebei University of Technology, Tianjin 300401, China hebut.edu.cn

Search for more papers by this author

Xiaowei Zhang,

Xiaowei Zhang

orcid.org/0000-0001-9016-4540

School of Civil Engineering and Transportation, Hebei University of Technology, Tianjin 300401, China hebut.edu.cn

Search for more papers by this author

Jing Liu,

Jing Liu

orcid.org/0000-0002-4254-911X

School of Civil Engineering and Transportation, Hebei University of Technology, Tianjin 300401, China hebut.edu.cn

Search for more papers by this author

Dong Liang,

Corresponding Author

Dong Liang

[email protected]

orcid.org/0000-0003-3990-3293

School of Civil Engineering and Transportation, Hebei University of Technology, Tianjin 300401, China hebut.edu.cn

Search for more papers by this author

Liu Yang,

Liu Yang

orcid.org/0000-0003-2747-5121

School of Civil Engineering and Transportation, Hebei University of Technology, Tianjin 300401, China hebut.edu.cn

Search for more papers by this author

Lida Wang,

Lida Wang

orcid.org/0000-0002-8363-3350

School of Civil Engineering and Transportation, Hebei University of Technology, Tianjin 300401, China hebut.edu.cn

Search for more papers by this author

Xiaowei Zhang,

Xiaowei Zhang

orcid.org/0000-0001-9016-4540

School of Civil Engineering and Transportation, Hebei University of Technology, Tianjin 300401, China hebut.edu.cn

Search for more papers by this author

First published: 2021

https://doi.org/10.1155/2021/5322548

Citations: 2

Academic Editor: Kaiming Bi

Share a link

Email
Wechat
Bluesky

Abstract

As an essential component of offshore bridges, stay cables are prone to vibrations due to their low inherent damping characteristics. Various dampers have been used for cable vibration control; however, the experimental research and theoretical study of inertial dampers on real cables have not been conducted sufficiently. This study aims to investigate the damping performance of a novel viscous inertial damper (VID) and focuses on the frequency-dependent and displacement amplification phenomena of a cable-damper system. Tests were first conducted to verify the energy consumption capacity of a prototype damper. A shallow cable-VID system was established. Theoretically, complex-valued modes were analyzed to determine the influence of the inertial and viscous coefficients on the cable’s frequency and mode damping ratio. The test results and numerical analysis show that the VID has a good damping effect on the shallow cable. Considering multiple adjacent cable modes, the inertial and viscous coefficients can be optimized. After optimizing, the VID can simultaneously maximize both adjacent symmetric and antisymmetric modes’ damping ratios. The two frequencies are almost the same. The displacement amplification of the VID shows that a VID can overcome the shortcomings of displacement loss caused by traditional oil dampers. The implications of these findings of the VID on shallow cable are discussed, which will guide future research and applications of the VID or other inerter dampers.

1. Introduction

As an essential component of the offshore cable-stayed bridge, cables have high flexibility and low inherent damping. Vibration problems can be frequently encountered in these bridges, such as vortex-induced vibrations, parametric resonance, wake galloping, buffeting, and wind-and rain-induced vibrations [1–9]. These problems affect the public’s confidence in the bridge’s structural safety and shorten the cables’ service life. Long-span cable-stayed bridges adopt various cable vibration control measures. The additional external viscous damper can directly increase the cable’s mode damping ratio, which is the most common cable vibration control method. The design theory and vibration control methods of stayed cables have been extensively studied [10–16]. Passive viscous dampers solve the vibration problem of cables to some extent, but the installation location restricts the damper’s damping effect. The installation location does not exceed 5% of the cable length [17, 18], so the additional damping ratio provided may be limited. Additionally, parameters such as the sag, bending stiffness, damper support stiffness, internal stiffness, and the coupled vibration between the cable and the beam will reduce the damping effect [15, 19]. Besides, external viscous dampers only achieve the optimal damping ratio for a specific vibration mode of cables. Generally, many factors dramatically limit the viscous damper’s damping effect.

In the process of studying active and semiactive dampers, researchers have found that negative stiffness can make the damper move with greater displacement, consume more energy, and achieve a higher damping ratio [20–25]. By using mechanical amplification mechanisms (such as ball screws, gears, and lever pendulums), inertial devices can provide a larger apparent mass, and inertial force is gradually used for structural vibration control. Lazar et al. [26–28] replaced the mass part of a tuned mass damper with an inertial mass and constructed a tuned inertial damper (TID). Vibration control analysis of the cable’s first vibration mode showed that the TID makes the cable obtain a higher mode damping ratio than the traditional viscous damper. Chen et al. [29] applied a passive negative stiffness device for the cable-damper system to overcome the problem of insufficient additional damping and discussed the influence of the nonlinear control force caused by negative stiffness. Shi et al. [30–33] proposed a negative stiffness damper composed of magnets that provides negative stiffness and an oil damper. Numerical analysis and experiments verified that the damper’s damping performance for the first vibration mode of the cable is much better than that of the traditional viscous damper. Nakamura et al. [34] and Wang et al. [35] developed an electromagnetic inertial mass damper (EIMD) using a rotary electromagnetic damper and ball screw inertial devices, respectively. Through the displacement enhancement mechanism of the ball screw, EIMD makes the flywheel produce larger inertial mass than its physical mass. Simultaneously, it has an acceleration effect on the rotary electromagnetic damper’s rotational speed, and the inertial coefficient and damping coefficient work synergistically. At present, the research on using inertial mass to reduce cable vibration is still in its infancy, and most scholars have only conducted theoretical research.

This study aimed to undertake more diversified vibration system research to realize cable vibration control using viscous and inertial devices. Both numerical and experimental solutions were obtained for a shallow cable with a viscous inertial damper (VID) installed close to a cable end. The understanding gained will help with interpreting cable vibration control using VIDs or other inertial devices, which can provide outstanding damping performance and understand the frequency-dependent and displacement amplification mechanism of the shallow cable-VID system. Subsequently, three different cases of inertial devices were established to experimentally verify the accuracy of the numerical analysis and validate the superior vibration mitigation performance of the VID. Finally, the most practical motivation of this study was to conduct a refined investigation and construct an achievable method for vibration control on cable structures.

2. Novel Viscous Inertial Damper

2.1. Composition and Mechanical Parameters of VID

As shown in Figure 1, the viscous inertial damper (VID) consists of two parts: inertial and viscous devices. In terms of movement, the cable and rack are connected by a ball hinge. The cable’s vibration causes the rack to reciprocate up and down in a straight line, and the pinion converts the rack’s linear reciprocating motion into the disk’s rotating motion. At the same time, it makes a rotating motion in the damping fluid to achieve a damping effect. The rack and pinion convert the cable’s vertical vibration into the shaft’s rotation, so the shaft’s rotation angle θ and torque T can be expressed as [36, 37]

\begin{matrix} θ = \frac{2 π}{l} v, \end{matrix}

(1)

\begin{matrix} T = T_{i} + T_{c}, \end{matrix}

(2)

where l denotes the pinion’s circumference, v is the displacement of the cable that drives the rack to move up and down, and T_i and T_c are the inertia torque and viscous torque, respectively. The force at the end of the rack can be expressed as

\begin{matrix} F = \frac{2 π}{l} T + M \ddot{v}, \end{matrix}

(3)

F is the force at the moving end of the VID, and M is the mass of the translation motion part of the VID.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Anatomy diagram of the cable-VID system.

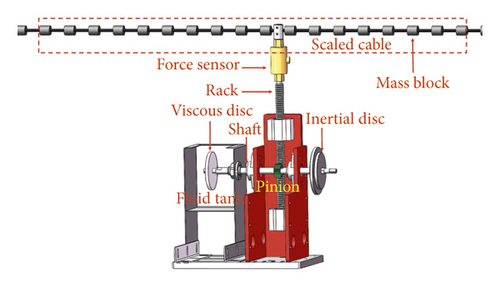
2.2. Inertial Coefficient

The rotating and translational parts of the VID generate inertial force during the movement. In equation (2), the torque T_i on the shaft can be expressed as

\begin{matrix} T_{i} = (J_{1} + J_{2} + J_{3} + J_{n}) \ddot{θ} . \end{matrix}

(4)

By converting the torque obtained in equation (4) into rack’s damping force, the damping force generated by the inertia of the damper can be expressed as

\begin{matrix} F_{i} = {(\frac{2 π}{l})}^{2} (J_{1} + J_{2} + J_{3} + J_{n}) \ddot{v} + M_{4} \ddot{v}, \\ = {(\frac{2 π}{l})}^{2} (M_{1} γ_{1}^{2} + M_{2} γ_{2}^{2} + M_{3} γ_{3}^{2} + M_{n} γ_{n}^{2}) \ddot{v} + M_{4} \ddot{v}, \end{matrix}

(5)

where J₁, γ₁, and M₁ denote the pinion’s moment of inertia, the radius of rotation, and mass, respectively; J₂, γ₂, and M₂ represent the shaft’s moment of inertia, the radius of rotation, and mass, respectively; J₃, γ₃, and M₃ reflect the viscous disc’s moment of inertia, the radius of rotation, and mass, respectively; J_n, γ_n, and M_n are the inertial disc’s moment of inertia, the radius of rotation, and mass, respectively; and M₄ is the rack’s mass. By introducing these parameters, the amplification factor n₁ ~ n₅ can be obtained.

\begin{matrix} n_{1} = {(\frac{2 π}{l})}^{2} γ_{1}^{2}; n_{2} = {(\frac{2 π}{l})}^{2} γ_{2}^{2}; n_{3} = {(\frac{2 π}{l})}^{2} γ_{3}^{2}; n_{4} = 1; n_{n} = {(\frac{2 π}{l})}^{2} γ_{n}^{2} . \end{matrix}

(6)

2.3. Viscous Coefficient

In this study, the viscous damping fluid was comprised of lithium-based grease with a higher viscosity and hydraulic oil with a lower viscosity. The damping torque T_c can be expressed as

\begin{matrix} T_{c} = \iint τ (γ) r d s = \iint τ (\frac{γ \dot{θ}}{h}) r d s = \frac{\sqrt{2}}{2} \frac{η}{h} π r_{3}^{4} \dot{θ} . \end{matrix}

(7)

In equation (7), the shear force is expressed as τ = ηγ, where η is the damping fluid’s dynamic viscosity; γ is the shear strain rate, and h is the distance between the viscous disc and the side-wall of the fluid tank. Then, the damping force equation produced by the viscous devices of the damping fluid can be expressed as

\begin{matrix} F_{c} = \frac{2 π}{l} T_{c} = {(\frac{2 π}{l})}^{2} \frac{\sqrt{2}}{2} \frac{η}{h} π r_{3}^{4} \dot{v} . \end{matrix}

(8)

At the same time, the correction of the damping term caused by bearing’s rolling friction should be considered in the test. The damping term is corrected as follows:

\begin{matrix} F_{c} = {(\frac{2 π}{l})}^{2} \frac{\sqrt{2}}{2} \frac{η}{h} π r_{3}^{4} \dot{v} + C_{b} \dot{v} = [{(\frac{2 π}{l})}^{2} \frac{\sqrt{2}}{2} \frac{η}{h} π r_{3}^{4} + C_{b}] \dot{v}, \end{matrix}

(9)

where C_b is the equivalent viscous coefficient of the bearing, and the value should be determined through prototype experiment.

2.4. Calculation of Damping Force

The movement displacement at both ends of the damper is expressed as

v (t) = {\tilde{v}}_{d} e^{i ω t}

, merging equations (5) and (9). The calculation equation of the damping force is

\begin{matrix} F = {\tilde{F}}_{i} + {\tilde{F}}_{c} = (- b_{d} ω^{2} + c_{d} i ω) \tilde{v} e^{i ω t}, \end{matrix}

(10)

\begin{matrix} b_{d} = {(\frac{2 π}{l})}^{2} (M_{1} γ_{1}^{2} + M_{2} γ_{2}^{2} + M_{3} γ_{3}^{2} + M_{n} γ_{n}^{2}) + M_{4}, \end{matrix}

(11)

\begin{matrix} C_{d} = {(\frac{2 π}{l})}^{2} \frac{\sqrt{2}}{2} \frac{η}{h} π r_{3}^{4} + C_{b}, \end{matrix}

(12)

where b_d is the inertial coefficient generated by the inertial devices, and c_d is the viscous coefficient provided by the viscous devices.

3. Mechanical Properties of VID

At present, the main method to understand the mechanical properties of dampers is the force-displacement curve. In this study, the mechanical performance of the damper under different cases (different inertial mass and different frequency) is studied through the vibration signal measured by the force sensor and the laser displacement sensor equipment on the end of the rack.

3.1. Damper’s Parameters

The parameters of the damper’s pinion, shaft, damping disc, rack, and inertial disc are calculated according to equations (4)–(6) and summarized in Tables 1 and 2.

Table 1. Damper’s parameters.

Component	Physical mass, M (kg)	Amplification factor, n	Inertial mass, b_d (kg)
Pinion, n₁	0.2387	0.5017	0.1198
Shaft, n₂	1.1098	0.1037	0.1150
Viscous disc, n₃	0.6045	2.6421	1.5976
Rack, n₄	2.4010	1	2.4010
Inertial disc 1, n₅₁	1.6350	3.5376	5.7839
Inertial disc 2, n₅₂	2.7250	5.9340	16.1701

Table 2. Damper’s inertial parameters.

Damper part	Pinion + Shaft + Rack + Damping disc	Pinion + Shaft + Rack + Damping disc + Inertial disc 1	Pinion + Shaft + Rack + Damping disc + Inertial disc 2
Inertial mass b_d	4.2334	10.0173	20.4035

3.2. Test Results and Analysis

This study added damping fluid to the tank and installed the damping disc on the shaft. The rotation of the damping disc in the damping fluid plays the role of shearing the fluid, since the disc has certain inertia. Simultaneously, it also plays a role in providing negative stiffness. If it is necessary to increase the inertia, the inertial disc can be added on the other end of the shaft outside the tank.

When the vibration frequencies are 1.92 Hz, 1.77 Hz, and 1.55 Hz, inertial mass b_d of the damper is 4.2334 kg, 10.0173 kg, and 20.4035 kg, respectively, which are named Case 1, case 2, and case 3, respectively. Force-displacement curves obtained from tests under Case 1 and corresponding theoretical force-displacement curves are shown in Figure 2(a). Force-displacement curves obtained from tests under case 2 and corresponding theoretical force-displacement curves are shown in Figure 2(b). Force-displacement curves obtained from tests under case 3 and corresponding theoretical force-displacement curves are shown in Figure 2(c). The theoretical force-displacement curves are calculated according to equation (10), nearly equal to the envelope areas and negative slope of the test force-displacement curves.

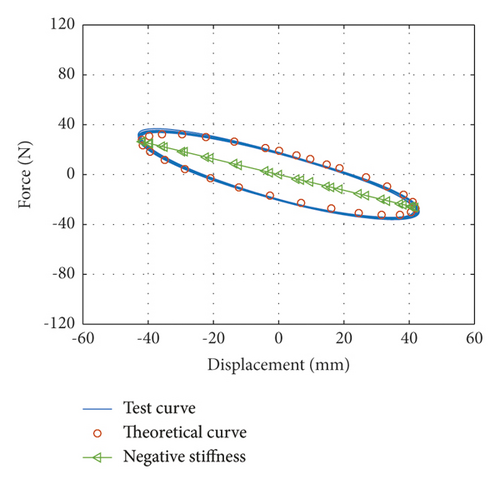
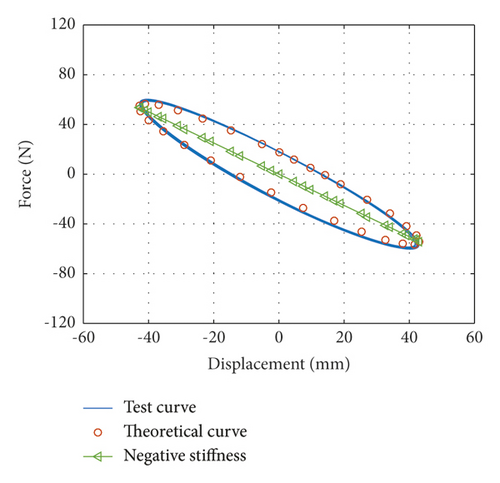
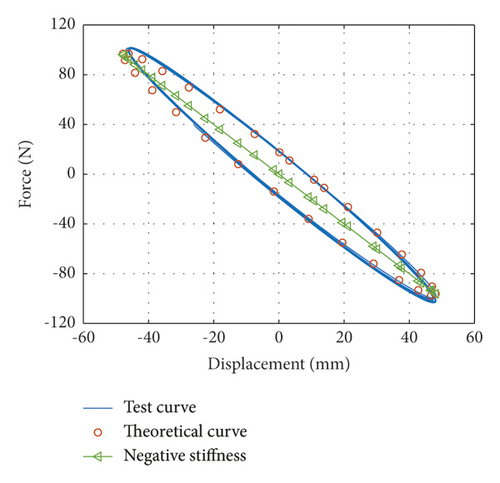
When the vibration frequencies are 3.17 Hz, 2.77 Hz, and 2.59 Hz, inertial mass b_d of the damper is 4.2334 kg, 10.0173 kg, and 20.4035 kg, respectively, which are named case 4, case 5, and case 6, respectively. Force-displacement curves obtained from tests under case 4 and corresponding theoretical force-displacement curves are shown in Figure 3(a). Force-displacement curves obtained from tests under case 5 and corresponding theoretical force-displacement curves are shown in Figure 3(b). Force-displacement curves obtained from tests under case 6 and corresponding theoretical force-displacement curve are shown in Figure 3(c). The theoretical force-displacement curves are calculated according to equation (10), which are nearly equal to the envelope areas and negative slopes of the test force-displacement curves.

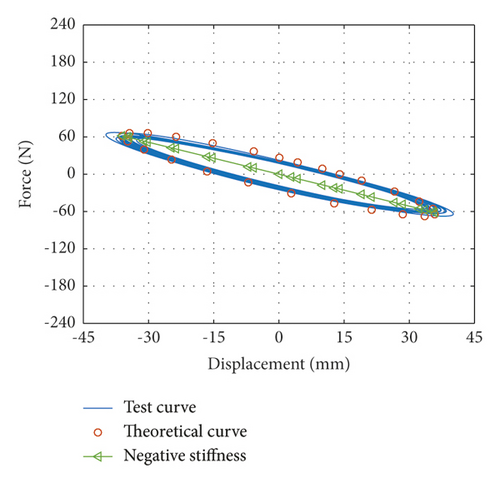
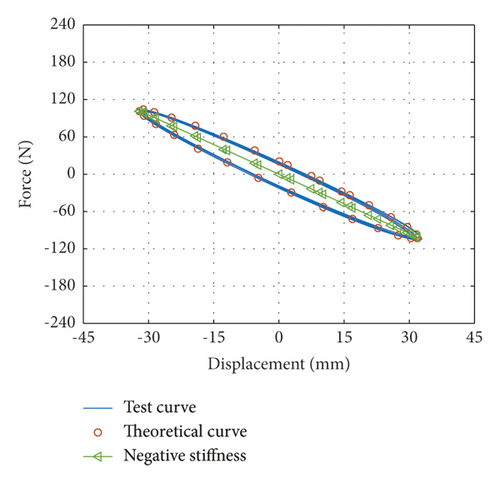
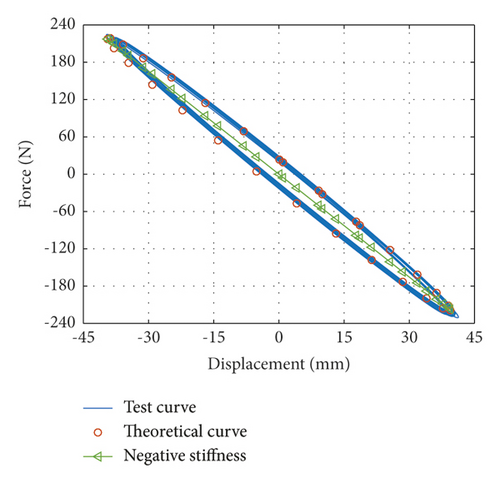
According to force-displacement curves mentioned above, the viscous coefficient c_d of the VID can be determined using equations (7)–(9) and (12). The viscous coefficient is c_d = 66.0079 N · s/m.

4. Theoretical Analysis of Cable-VID System for Vibration Control

The following theoretical analysis model was established to study the damping effect of the VID on the cable.

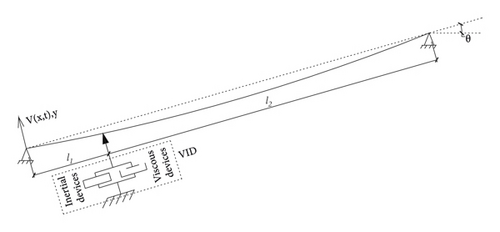
4.1. In-Plane Vibration of a Shallow Cable with a VID

This study installed one end of the VID on the cable and the other end on the bridge deck, as shown in Figure 4. The relative displacement, relative speed, and relative acceleration of the two ends of the VID were considered in the calculation. The following parameters were introduced: the cable force in the static state H, the cable’s mass per unit length ρ, the chord length of the cable L = l₁ + l₂, and the location of the damper l₁. The sag of the cable was considered. In the cable’s free vibration, the cable’s vertical displacement, additional tension, and the damping force can be expressed as a time-dependent function, which are

v = \tilde{v} (x) e^{i ω t},

h = \tilde{h} (x) e^{i ω t}

, and

F = \tilde{F} e^{i ω t}

, respectively. The cable’s vibration equation can be written as [11, 12, 14]

\begin{matrix} H \frac{\partial^{2} v (x, t)}{\partial x^{2}} + h \frac{\partial^{2} y (x, t)}{\partial x^{2}} = ρ \frac{\partial^{2} v (x, t)}{\partial t^{2}} + F δ (x - l_{1}), \end{matrix}

(13)

where h is determined by

\begin{matrix} h = \frac{E A}{L_{e}} \int_{0}^{L} \frac{d y (x)}{d x} \frac{\partial v (x, t)}{\partial x} d x = \frac{ρ g \cos^{2} θ}{H} \frac{E A}{L_{e}} \int_{0}^{L} v (x, t) d x, \end{matrix}

(14)

where y(x) = 4f(1 − x/L)x/L = ρg cos θ/2H(Lx − x²) is the cable’s static configuration, and f = ρgL²cos θ/8H is the stay cable’s mid-span sag. Restricted by experimental conditions, the test cable is horizontally tensioned, and the inclination angle θ should be set as zero.L_e ≈ [1 + 8(f/L)²] is the static (stretched) length of the cable. The Irvin parameter is

\begin{matrix} λ^{2} = \frac{E A}{L_{e} / L} \cdot \frac{{(ρ g L \cos θ)}^{2}}{H^{3}} . \end{matrix}

(15)

By substituting equations (14) and (15) into equation (13), they can be simplified into

\begin{matrix} \frac{\partial^{2} v (x, t)}{\partial x^{2}} - \frac{λ^{2}}{L^{3}} \int_{0}^{L} v (x, t) d x = \frac{ρ}{H} \frac{\partial^{2} v (x, t)}{\partial t^{2}} + \frac{F}{H} δ (x - l_{1}) . \end{matrix}

(16)

Since the displacement continuity of the shallow cable at the damper location is considered, the solution of equation (16) can be expressed as

\begin{matrix} \tilde{v} (x) = \{\begin{cases} \tilde{v} (l_{1}) \frac{\sin (β x)}{\sin (β l_{1})} + \frac{8 f}{{(β L)}^{2}} \frac{\tilde{h}}{H} \cdot [1 - \cos (β x) - \tan (\frac{β l_{1}}{2}) \sin (β x)], 0 \leq x \leq l_{1} \\ \tilde{v} (l_{1}) \frac{\sin (β x^{'})}{\sin (β l_{2})} + \frac{8 f}{{(β L)}^{2}} \frac{\tilde{h}}{H} \cdot [1 - \cos (β x^{'}) - \tan (\frac{β l_{2}}{2}) \sin (β x^{'})], 0 \leq x^{'} \leq l_{2} \end{cases}), \end{matrix}

(17)

where

β = ω \sqrt{ρ / H}

\tilde{v} (l_{1})

is the cable vibration amplitude at the damper installation location. Substitute the two terms of equation (17) into (16), eliminate the time term, and add them together to obtain

\begin{matrix} \frac{8 f}{{(β L)}^{2}} \frac{\tilde{h}}{H} [22 \tan (\frac{β l_{1}}{2}) + \tan (\frac{β l_{2}}{2}) - β L + \frac{{(β L)}^{3}}{λ^{2}}] = \tilde{v} (l_{1}) [\tan (\frac{β l_{1}}{2}) + \tan (\frac{β l_{2}}{2})] . \end{matrix}

(18)

From the force balance condition at the damper location, equation (19) can be obtained:

\begin{matrix} H \frac{\partial v (l_{1}^{+}, t)}{\partial x} - H \frac{\partial v (l_{1}^{-}, t)}{\partial x} = F . \end{matrix}

(19)

Substitute equation (17) into equation (19) and remove the time term to obtain

\begin{matrix} \frac{8 f}{{(β L)}^{2}} \frac{\tilde{h}}{H} [\tan (\frac{β l_{1}}{2}) + \tan (\frac{β l_{2}}{2})] = - \tilde{v} (l_{1}) [\cot (β l_{1}) + \cot (β l_{2}) + \frac{1}{H β} \frac{\tilde{F}}{\tilde{v} (l_{1})}] . \end{matrix}

(20)

Considering the displacement compatibility of equation (18) and the force equilibrium of equation (20) at the VID location, the wave number equation can be obtained as

\begin{matrix} \cot (β l_{1}) + \cot (β l_{2}) + \frac{{[\tan (β l_{1} / 2) + \tan (β l_{2} / 2)]}^{2}}{[22 \tan (β l_{1} / 2) + \tan (β l_{2} / 2) - β L + ({(β L)}^{3} / λ^{2})]} = - \frac{1}{H β} \frac{\tilde{F}}{\tilde{v} (l_{1})} . \end{matrix}

(21)

Considering λ² = 0, the third term of equation (21) is also zero, which is consistent with the wave number equation of the taut cable [38–40]. The tangent sum is expressed using equation (22), while the cotangent sum is expressed using equation (23):

\begin{matrix} \tan (\frac{1}{2} β l_{1}) + \tan (\frac{1}{2} β l_{2}) = \frac{\sin ((12 /) β L)}{\cos ((12 /) β l_{1}) \cos ((12 /) β l_{2})}, \end{matrix}

(22)

\begin{matrix} \cot (β l_{1}) + \cot (β l_{2}) = \frac{\sin (β L)}{\sin (β l_{1}) \sin (β l_{2})} . \end{matrix}

(23)

The following normalized parameters are defined:

\begin{matrix} \begin{matrix} \begin{matrix} \bar{v} (\bar{x}) = \frac{\tilde{v} (x)}{L} & \bar{F} = \frac{\tilde{F}}{π^{2} H} & \begin{matrix} \bar{δ} (\bar{x} - \bar{l_{1}}) = L δ (x - l_{1}) & ω_{0} = \frac{π}{L} \sqrt{\frac{H}{ρ}} \end{matrix} \end{matrix} \\ \begin{matrix} \bar{t} = ω_{0} t & \bar{x} = \frac{x}{L} & \begin{matrix} \bar{ω} = \frac{ω}{ω_{0}} & \bar{β} = \frac{L β}{π} \end{matrix} & {\bar{b}}_{d} = \frac{b_{d} L ω_{0}^{2}}{π^{2} H} & {\bar{c}}_{d} = \frac{c_{d} L ω_{0}}{π^{2} H} \end{matrix} \end{matrix}\} . \end{matrix}

(24)

Among them, the variables whose superscripts are wavy lines represent the amplitude of the variables, and those whose superscripts are straight lines are the normalized variables. According to above derivation, the wave number equation can be normalized as

\begin{matrix} \begin{matrix} \sin (\frac{\bar{β} π}{2}) \{\sin (\frac{\bar{β} π}{2}) - \cos (\frac{\bar{β} π}{2}) [\frac{\bar{β} π}{2} - \frac{4}{λ^{2}} {(\frac{\bar{β} π}{2})}^{3}]\} \\ = - 2 [\frac{π}{\bar{β}} \frac{\bar{F}}{\bar{v}}] \sin (\frac{\bar{β} π {\bar{l}}_{1}}{2}) \sin (\frac{\bar{β} π {\bar{l}}_{2}}{2}) \cdot \{\sin (\frac{\bar{β} π}{2}) - \cos (\frac{\bar{β} π {\bar{l}}_{1}}{2}) \cos (\frac{\bar{β} π {\bar{l}}_{2}}{2}) [\frac{\bar{β} π}{2} - \frac{4}{λ^{2}} {(\frac{\bar{β} π}{2})}^{3}]\} \end{matrix} . \end{matrix}

(25)

4.2. Normalized Wave Number of Symmetric Mode

The solution of the normalized wave number, equation (25), can be expressed as two solution branches: one is related to symmetric modes, and the other is related to antisymmetric modes. In symmetric mode, cable vibration is associated with the second term in equation (25). Therefore, dividing

\sin (\bar{β} π / 2)

eliminates the influence of the antisymmetric mode. The normalized wave number equation for the symmetric mode is obtained as

\begin{matrix} \begin{matrix} \tan (\frac{\bar{β} π}{2}) - [\frac{\bar{β} π}{2} - \frac{4}{λ^{2}} {(\frac{\bar{β} π}{2})}^{3}] \\ = - 2 Φ \frac{\sin (\bar{β} π {\bar{l}}_{1} / 2) \sin (\bar{β} π {\bar{l}}_{2} / 2)}{\sin (\bar{β} π / 2)} \cdot \{\tan (\bar{β} π / 2) - \frac{\cos (\bar{β} π l_{1} / 2) \cos (\bar{β} π l_{2} / 2)}{\cos (\bar{β} π / 2)} [(\bar{β} π / 2) - (4 / λ^{2}) {(\bar{β} π / 2)}^{3}]\} \end{matrix} . \end{matrix}

(26)

To simplify equation (26), equation (27) is introduced.

\begin{matrix} \frac{\cos (\bar{β} π {\bar{l}}_{1} / 2) \cos (\bar{β} π {\bar{l}}_{1} / 2)}{\cos (\bar{β} π / 2)} = \frac{\sin (\bar{β} π {\bar{l}}_{1} / 2) \sin (\bar{β} π {\bar{l}}_{1} / 2)}{\cos (\bar{β} π / 2)} + 1. \end{matrix}

(27)

After simplifying, equation (26) can be expressed as

\begin{matrix} \{\tan (\frac{\bar{β} π}{2}) - [\frac{\bar{β} π}{2} - \frac{4}{λ^{2}} {(\frac{\bar{β} π}{2})}^{3}]\} (12 + Φ Θ) = 2 Φ Θ^{2} \tan (\frac{\bar{β} π}{2}) [\frac{\bar{β} π}{2} - \frac{4}{λ^{2}} {(\frac{\bar{β} π}{2})}^{3}] . \end{matrix}

(28)

The parameters of the damper’s inertial coefficient and viscous coefficient are normalized as mentioned in equation (24), and then Φ and Θ in equation (28) can be defined as

\begin{matrix} Φ = \frac{π (- {\bar{b}}_{d} ω^{2} + {\bar{c}}_{d} i ω)}{\bar{β}}, \\ Θ = \frac{\sin (\bar{β} π {\bar{l}}_{1} / 2) \sin (\bar{β} π l_{2} / 2)}{\sin (\bar{β} π / 2)} . \end{matrix}

(29)

According to the above, the normalized wave number of symmetric mode is defined as

\begin{matrix} \tan (\frac{\bar{β} π}{2}) = [\frac{\bar{β} π}{2} - \frac{4}{λ^{2}} {(\frac{\bar{β} π}{2})}^{3}] + \frac{2 Φ Θ^{2} {[(\bar{β} π / 2) - (4 / λ^{2}) {(\bar{β} π / 2)}^{3}]}^{2}}{12 + Φ Θ \{1 - Θ [(\bar{β} π / 2) - (4 / λ^{2}) {(\bar{β} π / 2)}^{3}]\}} . \end{matrix}

(30)

4.3. Normalized Wave Number of Antisymmetric Mode

In antisymmetric mode, divide the wave number equation (25) by

\cos (\bar{β} π / 2)

to eliminate the symmetric mode’s influence on the wave number equation.

\begin{matrix} \begin{matrix} \tan (\frac{\bar{β} π}{2}) \{\sin (\frac{\bar{β} π}{2}) - \cos (\frac{\bar{β} π}{2}) [\frac{\bar{β} π}{2} - \frac{4}{λ^{2}} {(\frac{\bar{β} π}{2})}^{3}]\} \\ = - 2 Φ \frac{\sin (\bar{β} π {\bar{l}}_{1} / 2) \sin (\bar{β} π {\bar{l}}_{2} / 2)}{\cos (\bar{β} L / 2)} \cdot \{\sin (\frac{\bar{β} π}{2}) - \cos (\frac{\bar{β} π {\bar{l}}_{1}}{2}) \cos (\frac{\bar{β} π {\bar{l}}_{2}}{2}) [\frac{\bar{β} π}{2} - \frac{4}{λ^{2}} {(\frac{\bar{β} π}{2})}^{3}]\} \end{matrix} . \end{matrix}

(31)

To simplify equation (31), the following Equation is introduced:

\begin{matrix} \frac{\sin (\bar{β} π {\bar{l}}_{2} / 2)}{\cos (\bar{β} π / 2)} = \cos (\frac{\bar{β} π {\bar{l}}_{1}}{2}) \tan (\frac{\bar{β} π}{2}) - \sin (\frac{\bar{β} π {\bar{l}}_{1}}{2}) . \end{matrix}

(32)

The normalized wave number of antisymmetric mode is defined in equation (33), and equation (34) is introduced for convenience.

\begin{matrix} \tan (\frac{\bar{β} π}{2}) = \frac{2 Φ \sin^{2} (\bar{β} π {\bar{l}}_{1} / 2)}{Ψ + 2 Φ \sin (\bar{β} π {\bar{l}}_{1} / 2) \cos (\bar{β} π {\bar{l}}_{1} / 2)}, \end{matrix}

(33)

\begin{matrix} Ψ = \frac{\sin (\bar{β} π / 2) - \cos (\bar{β} π / 2) [(\bar{β} π / 2) - (4 / λ^{2}) {(\bar{β} π / 2)}^{3}]}{\sin (\bar{β} π / 2) - \cos ((\bar{β} π {\bar{l}}_{1} / 2)) \cos (\bar{β} π {\bar{l}}_{2} / 2) [(\bar{β} π / 2) - (4 / λ^{2}) {(\bar{β} π / 2)}^{3}]} . \end{matrix}

(34)

Equations (30) and (33) are solved by Newton’s iteration method. Analytical solutions can be obtained. In this study, through the numerical calculation software Matlab, the normalized wave number is obtained, and then the mode damping ratios are calculated by the following equations:

\begin{matrix} {\bar{β}}_{j} = |{\bar{β}}_{j}| (i ξ_{j} \pm \sqrt{1 - ξ_{j}^{2}}), \\ ξ_{j} = \frac{Im ({\bar{β}}_{j})}{|{\bar{β}}_{j}|}, (j = 1,2, \dots, n) . \end{matrix}

(35)

5. Cable-VID System Testing and Analysis

5.1. Experimental Setup of Scaled Cable-VID System

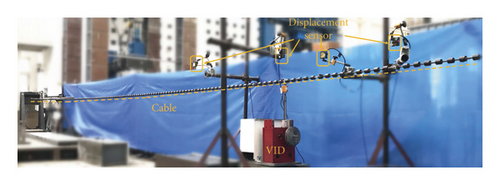
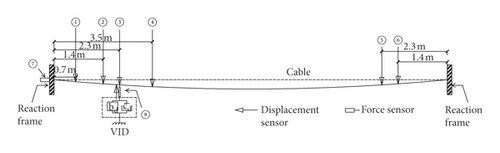
To experimentally evaluate the vibration control performance of the VID, determine the frequency variation characteristics of the cable-VID system, and validate the theoretical analysis results, prototype dampers with three different inertial coefficients and shallow cable were established in the laboratory. Considering the experimental conditions, this study chose a wire rope with a diameter of 9.3 mm as the cable, which was horizontally anchored to the reaction frame and increased the wire rope’s weight by installing a small mass block. Figure 5 shows the cable-VID system. The main parameters of the cable are listed in Table 3. Figure 6 illustrates a schematic diagram of the cable vibration control. The VID was attached to the cable 2.3 m away from the anchor, incorporating a load cell and a displacement sensor to monitor the mechanical performance of the VID. Six laser displacement sensors were installed 0.7 m, 1.4 m, 2.3 m, and 3.5 m away from the left anchor, and 1.4 m and 2.3 m away from the right anchor. Displacement sensors were adopted to identify the mode damping ratios of the cable. The DH5956 data acquisition system collected all the signals with a 1000 Hz sampling frequency.

Table 3. Physical parameters of the scaled cable.

Item	Value
Cable force (N)	7170
Cable length (m)	14
Mass per unit length (kg/m)	2.402
Cross-sectional area (m²)	5.02 E − 5
Irvin parameters (λ²)	3.316

5.2. Analysis of Vibration Control Effect

At present, analyzing the attenuation speed of the cable’s free vibration can help determine the damper’s influence on the vibration of the cable. The evaluation index is the mode damping ratio. It was found that the cable could be excited easily by just one human at the antinode of the vibration mode shape with the excitation frequency tuned to the natural cable frequency. When the vertical vibration amplitude reached a certain value, the man stopped excitation and allowed the cable to continue freely decaying the vibration. The time history of the decay of the vertical vibration was then recorded [15, 41, 42]. In this experiment, under the cable’s controlled vibration condition, the time history curve collected in the experiment was fitted by the exponential function. The free vertical vibration data were filtered by a bandpass filter to eliminate the influence of other modes.

At the same time, the parameters of the VID are normalized according to equation (24), the normalized parameters are brought into equations (30) and (33), and the mode damping ratios can be obtained through equation (35). The normalized values of each parameter are shown in Table 4.

Table 4. The normalized parameters of the damper.

	Cases 1 and 4	Cases 2 and 5	Cases 3 and 6	Cases 1∼6
Inertial coefficient, b_d (kg)	4.2334	10.0136	20.4042	Viscous coefficient, c_d (N·s/m)	66.0079
Normalized inertial coefficient, ${\bar{b}}_{d}$	0.13	0.30	0.61	Normalized viscous coefficient, ${\bar{c}}_{d}$	0.16

The normalized inertial coefficients of case 1, case 2, and case 3 are 0.13, 0.3, and 0.61, respectively. The attenuation curves of the first symmetric mode vibration are shown in Figures 7(a)–7(c), respectively. The normalized inertial coefficients of case 4, case 5, and case 6 are 0.13, 0.3, and 0.61, respectively. The attenuation curves of the first antisymmetric mode vibration are shown in Figures 8(a)–8(c), respectively. By fitting the time history curve at the cable damper’s installation location, the damping ratios of the first symmetric and antisymmetric modes were obtained. Simultaneously, the symmetric point curve at the other end of the cable was obtained. By comparing the amplitude at damper’s installation location and its symmetric point at the other end of the cable, the displacement amplification effect of the cable-VID system can be observed.

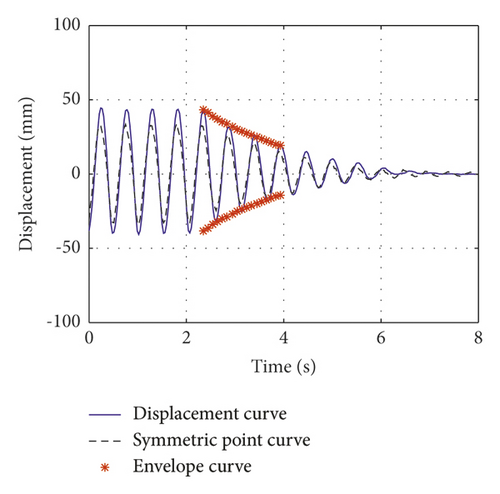
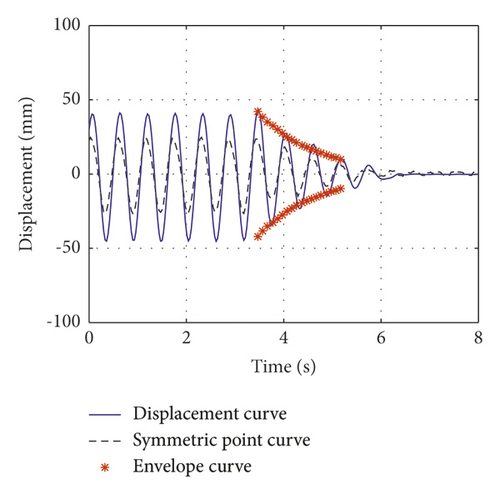
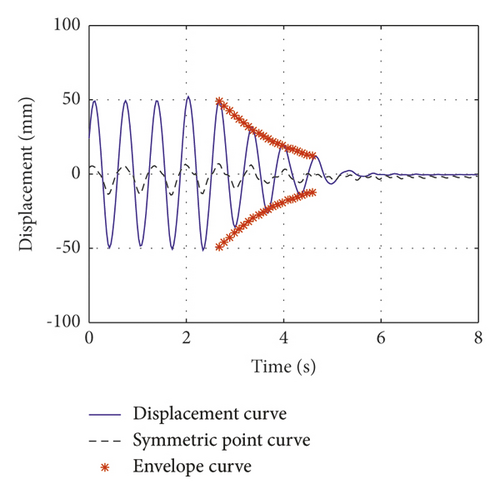
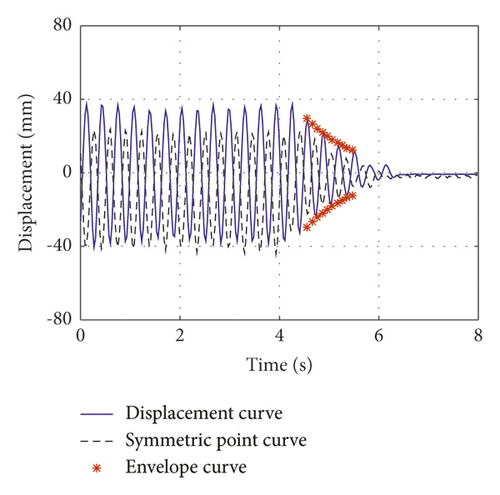
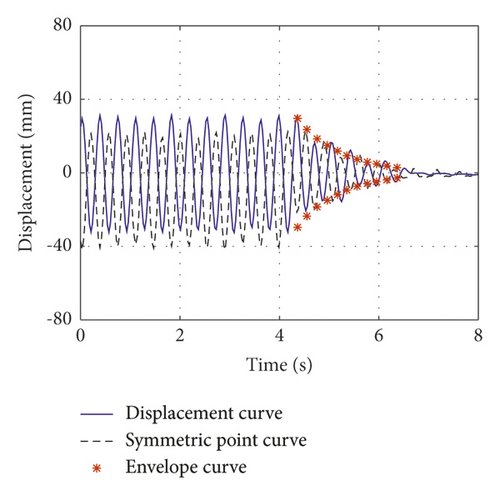
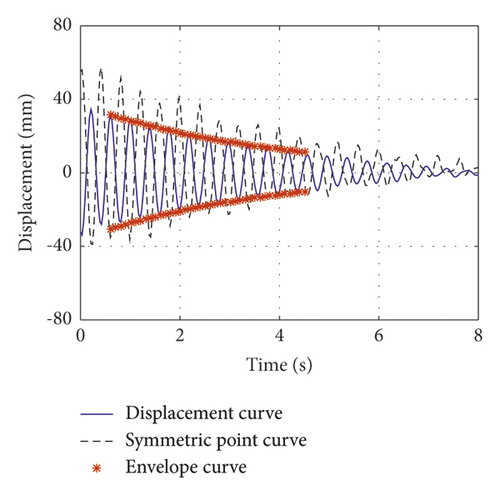
This study presents the measured damping ratio and the theoretically damping ratio at the damper’s installation location. Simultaneously, the normalized frequency calculated by the theory was deduced and compared with the measured frequency, which verified the accuracy of the theoretical calculation; it can also explain the change in the cable frequency with the additional VID. The test results, theoretical results, and deviations are summarized in Tables 5–7.

Table 5. Damping ratio results summary and deviation.

${\bar{b}}_{d} = 0.13$	First symmetric mode	First antisymmetric mode
Test damping ratio, ξ₁ (%)	4.23	6.72
Theoretical damping ratio, ξ₂ (%)	4.42	6.88
Deviation, (ξ₁ − ξ₂)/ξ₂ (%)	−4.30	−2.32
Test frequency, f₁(Hz)	1.92	3.17
Deduced frequency, f₂ (Hz)	1.92	3.15
Deviation, (f₁ − f₂)/f₂ (%)	0	0.63

Table 6. Damping ratio results summary and deviation.

${\bar{b}}_{d} = 0.3$	First symmetric mode	First antisymmetric mode
Test damping ratio, ξ₁ (%)	6.38	6.24
Theoretical damping ratio, ξ₂ (%)	6.17	6.17
Deviation, (ξ₁ − ξ₂)/ξ₂ (%)	3.40	1.13
Test frequency, f₁ (Hz)	1.77	2.77
Deduced frequency, f₂ (Hz)	1.77	2.73
Deviation, (f₁ − f₂)/f₂ (%)	0	1.47

Table 7. Damping ratio results summary and deviation.

${\bar{b}}_{d} = 0.61$	First symmetric mode	First antisymmetric mode
Test damping ratio, ξ₁ (%)	7.51	2.02
Theoretical damping ratio, ξ₂ (%)	7.51	2.17
Deviation, (ξ₁ − ξ₂)/ξ₂ (%)	0.00	−6.91
Test frequency, f₁ (Hz)	1.55	2.59
Deduced frequency, f₂ (Hz)	1.55	2.47
Deviation, (f₁ − f₂)/f₂ (%)	0	4.85

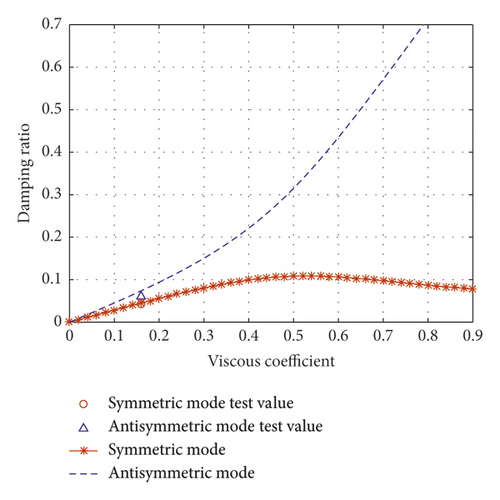
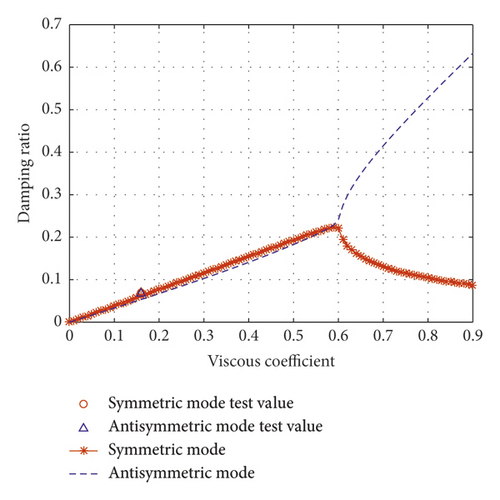
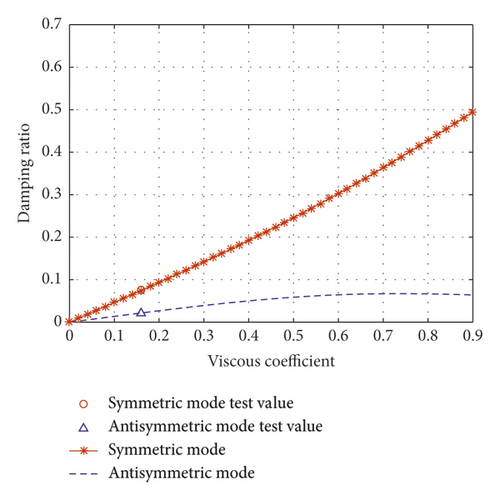
Figures 9(a)–9(c) show the comparison of theoretical results and experimental results for the different normalized inertial coefficients. The figure shows that the test results are in good agreement with the theoretical results. The theoretical analysis method described in this study is accurate, and the mode damping ratio of the cable can be analyzed by this theoretical method.

5.3. Optimal VID Design Method

This study uses an iterative method to solve equations (29) and (32). With the pure inertial device’s contribution, the viscous coefficient ${\bar{C}}_{d}$ is zero. Adding inertial coefficient generally reduces normalized wave numbers. All wave numbers decrease with an increasing inertial coefficient. In general, higher modes are associated with faster decreasing rates than lower modes. Finally, the decreasing wave numbers approach asymptotic lower bounds. This situation is shown in Figure 10. These wave numbers should be used as the initial value of the iteration in the VID optimization calculation [30].

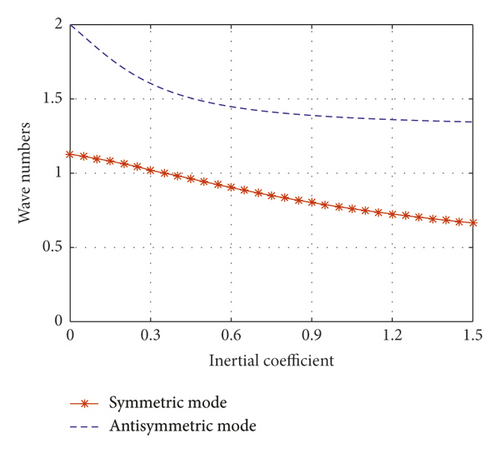
Figure 10 shows that, in both symmetric and antisymmetric modes, the lower limit of the frequency can be approximated as the adjacent lower mode of an uncontrolled cable with a length of l₂ (equivalent to the cable being clamped in the damper installation location). The shallow cable’s theoretical results in this study are approximately the same as those previously reported in [30, 35].

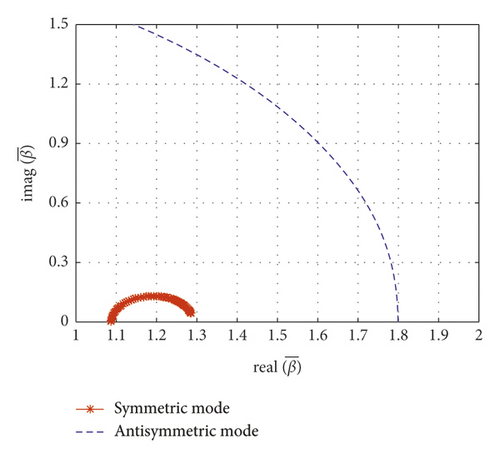
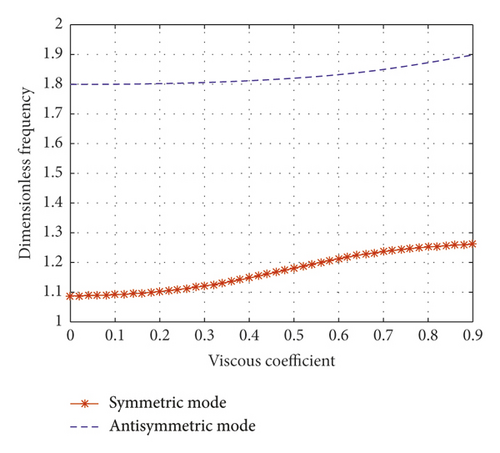
When the normalized inertial coefficient is 0.13, Figure 11(a) shows a clear schematic drawing of wave number loci. The wave number of the first symmetric mode moves toward the right with an increasing viscous coefficient. As the viscous coefficient approaches infinity (c = ∞), the first symmetric mode approaches the real axis. This finding implies that the cable is prone to the locking-like effect at the damper location. The first antisymmetric mode’s wave number moves along a quarter-circle with an increasing damping coefficient. In Figure 11(a), when the normalized viscous coefficient increases, the first antisymmetric mode’s wave number will reach the imaginary axis. The first antisymmetric mode is overdamped after the locus reaches an imaginary axis. This reveals the reason why the damping ratio of the antisymmetric mode increases with the increase of the viscous coefficient when the normalized inertial coefficient is 0.13 in Figure 9(a). As shown in Figure 11(d), when the viscous coefficient increases, the first symmetric mode frequency and the first antisymmetric mode frequency both increase.

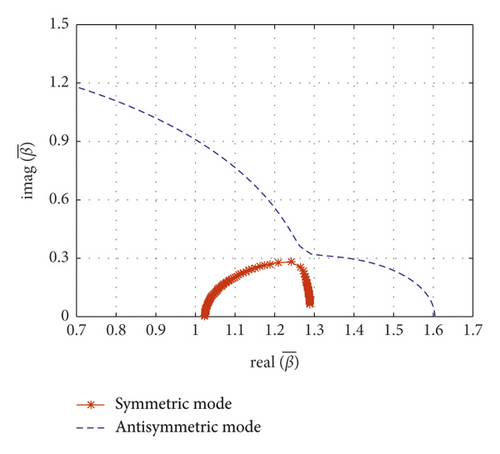
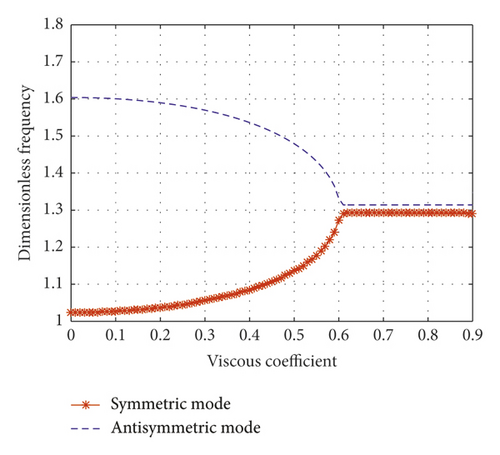
When the normalized inertial coefficient is 0.3, Figure 11(b) shows a schematic drawing of wave number loci. The wave number of the first symmetric mode moves toward the right with an increasing viscous coefficient. As the damping coefficient approaches infinity, the first symmetric mode approaches the real axis. The first antisymmetric mode’s wave number still moves along a nearly quarter-circle with increasing viscous coefficient when approaching the imaginary axis. As shown in Figure 11(b), the wave numbers of the symmetric mode and the antisymmetric mode have an intersection point at a certain viscous coefficient ( ${\bar{c}}_{d} = 0.6$ ). Also shown in Figure 9(b), before reaching this certain normalized viscous coefficient, the damping ratios of the first symmetric mode and the first antisymmetric mode of the cable are almost the same. However, after exceeding this certain viscous coefficient, the damping ratio of the first symmetric mode decreases, and the damping ratio of the first antisymmetric mode continues to increase. This study defines this viscous coefficient ( ${\bar{c}}_{d} = 0.6$ ) and the corresponding inertial coefficient ( ${\bar{b}}_{d} = 0.3$ ) as optimal value. Because, after exceeding this value, the damping ratio of the symmetric mode will gradually decrease, this value can obtain optimal damping ratio of the two adjacent vibration modes. As shown in Figure 11(e), as the viscous coefficient increases, the first symmetric mode’s frequency and the first antisymmetric mode’s frequency tend to be consistent.

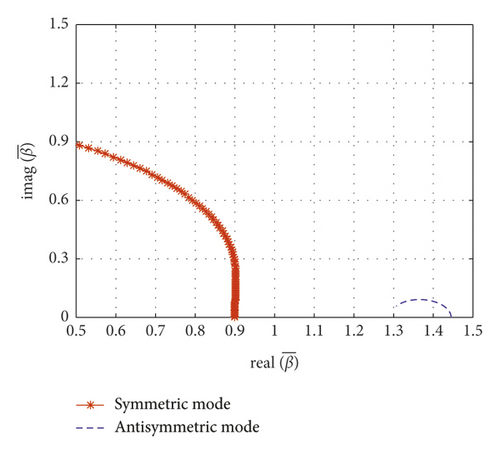
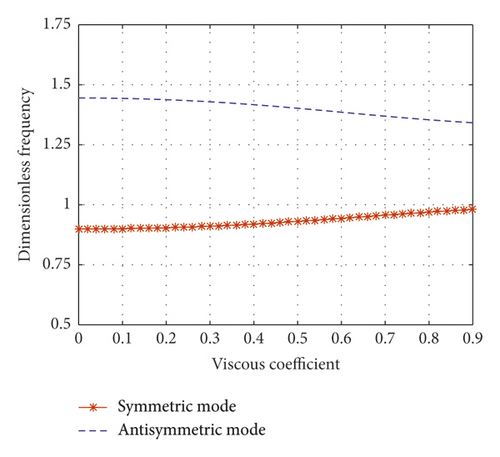
Figure 11(c) shows a schematic drawing of the wave number loci when the normalized inertial coefficient is 0.61. The first symmetric mode’s frequency moves along a quarter-circle with an increasing viscous coefficient. The first symmetric mode is overdamped after the locus reaches an imaginary axis. The wave number of the first antisymmetric mode moves toward the left with an increasing viscous coefficient. As the damping coefficient increases in Figure 11(c), the first symmetric mode approaches the imaginary axis. This reveals the reason why the damping ratio of the symmetric mode increases with the increase of the viscous coefficient when the normalized inertial coefficient is 0.61 in Figure 9(c). As shown in Figure 11(f), the symmetric mode frequency and the antisymmetric mode frequency get close to each other, but they do not converge.

5.4. Mode Shape Analysis

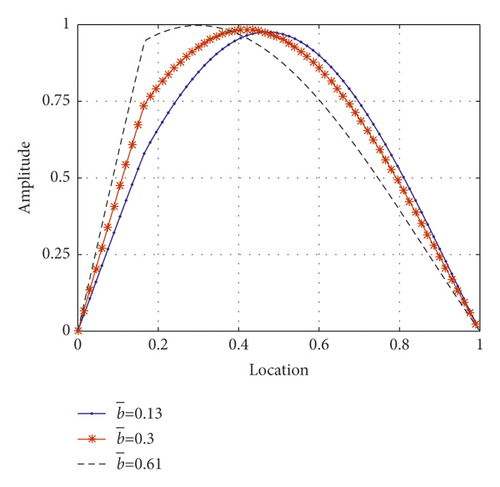
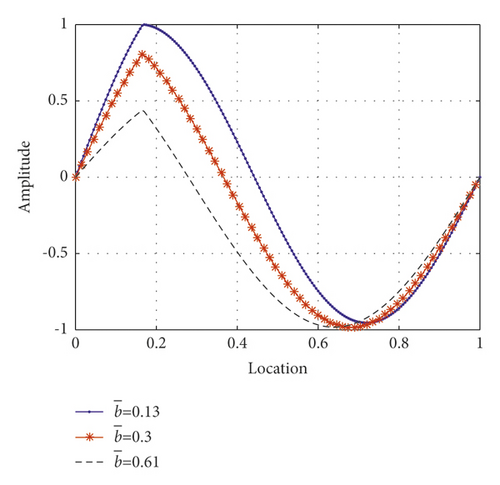
Figures 12(a) and 12(b) show the normalized mode shapes of the first symmetric mode and first antisymmetric mode of the cable under different inertial coefficients, respectively. The figure accurately explains the displacement amplification observed in the experiment. For the symmetric mode, after the inertial coefficient is optimized ( ${\bar{b}}_{d} = 0.3$ ), the VID can increase the displacement of the cable at the installation location of the damper and consumes more energy. The vibration can be quickly attenuated. The effect of the VID on the displacement amplification of the damper can be intuitively understood as improving the installation location of the damper. For the first symmetric mode, the larger the normalized inertial coefficient, the better the damping effect. However, for the first antisymmetric mode, the amplification phenomenon can also be understood as improving the damper’s installation location. However, when the inertial coefficient exceeds the optimal value ( ${\bar{b}}_{d} = 0.3$ ), it is equivalent to the fact that VID has been installed near the node of the antisymmetric mode shape. The mode damping will be reduced due to the excessive inertial coefficient.

6. Conclusions

In this study, we conducted normalized complex-valued modes analysis and experimental research on a novel viscous inertial damper. The numerical and experimental results agree well, demonstrating the accuracy of the proposed method for cable vibration control. The mechanical properties of the cable-VID system were analyzed in detail. The main conclusions of this study are summarized as follows:

(1)
The novel viscous inertial damper constructed in this study can effectively suppress cable vibration, improve the cable’s mode damping ratio, and more quickly attenuate cable vibration.
(2)
Compared with the traditional complex-valued modes analysis, after the parameters are normalized according to the method described in this article, the frequency-dependent phenomena and the damping ratio of the symmetric and antisymmetric modes of the cable were discussed in detail.
(3)
When the normalized inertial coefficient and the normalized viscous coefficient are optimal, the optimal damping ratio of the two adjacent vibration modes is obtained simultaneously. For example, the first symmetric mode and the first antisymmetric mode are optimal at the same time, or the first antisymmetric mode and the second symmetric mode are optimal at the same time. However, the frequencies of the two modes are the same.
(4)
According to the numerical method and the test method proposed in this study, the parameters of the damper can be designed according to the target mode of vibration. After theoretical calculations, the method proposed in this study can be used to precisely obtain the viscous and inertial coefficients.
(5)
In the symmetric and antisymmetric modes, the displacement amplification phenomena of the VID were verified by theoretical analysis and experimental observation. This finding proves that the VID provides superior vibration reduction performance when the inertial coefficient is optimal. The VID fabricated in this study can overcome the disadvantages of displacement loss caused by the traditional oil damper.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This research was funded by the National Science Foundation of China (Grant number 51978236). The authors are grateful for the support.

Open Research

Data Availability

All the data generated or analyzed during this study are included within this article.

References

1 Ni Y. Q., Wang X. Y., Chen Z. Q., and Ko J. M., Field observations of rain-wind-induced cable vibration in cable-stayed Dongting Lake Bridge, Journal of Wind Engineering and Industrial Aerodynamics. (2007) 95, no. 5, 303–328, https://doi.org/10.1016/j.jweia.2006.07.001, 2-s2.0-33947309244.
10.1016/j.jweia.2006.07.001
Web of Science® Google Scholar
2 Jakobsen J. B., Andersen T. L., Macdonald J. H. G. et al., Wind-induced response and excitation characteristics of an inclined cable model in the critical Reynolds number range, Journal of Wind Engineering and Industrial Aerodynamics. (2012) 110, 100–112, https://doi.org/10.1016/j.jweia.2012.04.025, 2-s2.0-84867214219.
10.1016/j.jweia.2012.04.025
Web of Science® Google Scholar
3 Nikitas N., Macdonald J. H. G., Jakobsen J. B., and Andersen T. L., Critical Reynolds number and galloping instabilities: experiments on circular cylinders, Experiments in Fluids. (2012) 52, no. 5, 1295–1306, https://doi.org/10.1007/s00348-011-1255-3, 2-s2.0-84861657414.
10.1007/s00348-011-1255-3
Web of Science® Google Scholar
4 Nikitas N. and Macdonald J. H. G., Aerodynamic forcing characteristics of dry cable galloping at critical Reynolds numbers, European Journal of Mechanics-B: Fluids. (2015) 49, 243–249, https://doi.org/10.1016/j.euromechflu.2014.09.005, 2-s2.0-84908408805.
10.1016/j.euromechflu.2014.09.005
Web of Science® Google Scholar
5 Mao J. X., Wang H., Feng D. M., Tao T. Y., and Zheng W. Z., Investigation of dynamic properties of long-span cable-stayed bridges based on one-year monitoring data under normal operating condition, Struct Control Hlth. (2018) 25, https://doi.org/10.1002/stc.2146, 2-s2.0-85041653487.
10.1002/stc.2146
Google Scholar
6 Gu M., Du X. Q., and Li S. Y., Study on rain-wind induced vibration of 3 DOF continuous cables in cable-stayed bridges, Journal of Vibration Engineering. (2007) 20, 473–479.
Google Scholar
7 Chen R. L. and Zeng Q. Y., Rain-wind induced chaotic vibration of cable on cable-stayed bridge, Journal of Vibration and Shock. (2008) 27, 42–46.
Google Scholar
8 Li J., Mao K., Yu W., Guan H., and Chen S., Preliminary analysis on the influence of raindrop impact loads on the cable rain-wind-induced vibration of cable-stayed bridges, Journal of Vibration and Shock. (2019) 38, 177–184.
Google Scholar
9 Chen J., Chen M. Z. Q., and Hu Y., Vortex-induced vibration suppression of bridges by inerter-based dynamic vibration absorbers, Shock and Vibration. (2021) 2021, 1–18, https://doi.org/10.1155/2021/4431516.
10.1155/2021/7726779
CAS Web of Science® Google Scholar
10 Krenk S. and Nielsen S. R. K., Vibrations of a shallow cable with a viscous damper, Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences. (2001) 458, no. 2018, 339–357, https://doi.org/10.1098/rspa.2001.0879, 2-s2.0-0041694978.
10.1098/rspa.2001.0879
Web of Science® Google Scholar
11 Johnson E. A., Christenson R. E., and Spencer B. F., Semiactive damping of cables with sag, Computer-Aided Civil and Infrastructure Engineering. (2003) 18, no. 2, 132–146, https://doi.org/10.1111/1467-8667.00305, 2-s2.0-0037296803.
10.1111/1467-8667.00305
Web of Science® Google Scholar
12 Krenk S. and Høgsberg J. R., Damping of cables by a transverse force, Journal of Engineering Mechanics. (2005) 131, no. 4, 340–348, https://doi.org/10.1061/(asce)0733-9399(2005)131:4(340), 2-s2.0-16344372490.
10.1061/(ASCE)0733-9399(2005)131:4(340)
Web of Science® Google Scholar
13 Wang X. Y., Ni Y. Q., Ko J. M., and Chen Z. Q., Optimal design of viscous dampers for multi-mode vibration control of bridge cables, Engineering Structures. (2005) 27, no. 5, 792–800, https://doi.org/10.1016/j.engstruct.2004.12.013, 2-s2.0-15944426125.
10.1016/j.engstruct.2004.12.013
Web of Science® Google Scholar
14 Johnson E. A., Baker G. A., Spencer B. F., and Fujino Y., Semiactive damping of stay cables, Journal of Engineering Mechanics. (2007) 133, no. 1, 1–11, https://doi.org/10.1061/(asce)0733-9399(2007)133:1(1), 2-s2.0-33845642737.
10.1061/(ASCE)0733-9399(2007)133:1(1)
Web of Science® Google Scholar
15 Zhou H., Sun L., and Xing F., Damping of full-scale stay cable with viscous damper: experiment and analysis, Advances in Structural Engineering. (2014) 17, no. 2, 265–274, https://doi.org/10.1260/1369-4332.17.2.265, 2-s2.0-84897427833.
10.1260/1369-4332.17.2.265
PubMed Web of Science® Google Scholar
16 Shi X. and Zhu S. Y., Nonlinear impact of negative stiffness dampers on stay cables, Structural Monitoring and Maintenance. (2018) 5, 15–38, https://doi.org/10.12989/smm.2018.5.1.015, 2-s2.0-85044342706.
10.12989/smm.2018.5.1.015
Google Scholar
17 Chen L., Sun L., Xu Y., Di F., Xu Y., and Wang L., A comparative study of multi-mode cable vibration control using viscous and viscoelastic dampers through field tests on the Sutong Bridge, Engineering Structures. (2020) 224, 111226, https://doi.org/10.1016/j.engstruct.2020.111226.
10.1016/j.engstruct.2020.111226
Web of Science® Google Scholar
18 Chen L., Di F., Xu Y., Sun L., Xu Y., and Wang L., Multimode cable vibration control using a viscous-shear damper: case studies on the Sutong Bridge, Structural Control and Health Monitoring. (2020) 27, https://doi.org/10.1002/stc.2536.
10.1002/stc.2536
Web of Science® Google Scholar
19 Liang D., Di F. D., Chen H. X., Duan W. B., and Li Z. S., Cable’s compound vibration reduction method under cable-girder coupled vibration, Journal of Vibration and Shock. (2018) 37, 240–247.
Google Scholar
20 Iemura H. and Pradono M. H., Advances in the development of pseudo-negative-stiffness dampers for seismic response control, Structural Control and Health Monitoring. (2009) 16, 784–799, https://doi.org/10.1002/stc.345, 2-s2.0-72649088722.
10.1002/stc.345
Web of Science® Google Scholar
21 Ou J. and Li H., Analysis of capability for semi-active or passive damping systems to achieve the performance of active control systems, Structural Control and Health Monitoring. (2010) 17, no. 7, 778–794, https://doi.org/10.1002/stc.408, 2-s2.0-78349256707.
10.1002/stc.408
Web of Science® Google Scholar
22 Pasala D. T. R., Sarlis A. A., Nagarajaiah S., Reinhorn A. M., Constantinou M. C., and Taylor D., Adaptive negative stiffness: new structural modification approach for seismic protection, Journal of Structural Engineering. (2013) 139, no. 7, 1112–1123, https://doi.org/10.1061/(asce)st.1943-541x.0000615, 2-s2.0-84878937738.
10.1061/(ASCE)ST.1943-541X.0000615
Web of Science® Google Scholar
23 Sarlis A. A., Pasala D. T. R., Constantinou M. C., Reinhorn A. M., Nagarajaiah S., and Taylor D. P., Negative stiffness device for seismic protection of structures, Journal of Structural Engineering. (2013) 139, no. 7, 1124–1133, https://doi.org/10.1061/(asce)st.1943-541x.0000616, 2-s2.0-84878931537.
10.1061/(ASCE)ST.1943-541X.0000616
Web of Science® Google Scholar
24 Krenk S., Resonant inerter based vibration absorbers on flexible structures, Journal of the Franklin Institute. (2019) 356, no. 14, 7704–7730, https://doi.org/10.1016/j.jfranklin.2018.11.038, 2-s2.0-85063096414.
10.1016/j.jfranklin.2018.11.038
Web of Science® Google Scholar
25 Hu Y. and Chen M. Z. Q., Performance evaluation for inerter-based dynamic vibration absorbers, International Journal of Mechanical Sciences. (2015) 99, 297–307, https://doi.org/10.1016/j.ijmecsci.2015.06.003, 2-s2.0-84934946840.
10.1016/j.ijmecsci.2015.06.003
Web of Science® Google Scholar
26 Lazar I. F., Neild S. A., and Wagg D. J., Performance analysis of cables with attached tuned-inerter-dampers, Conference Proceedings of the Society for Experimental Mechanics Series, 2, Proceedings of the Dynamics of Civil Structures, 2015, Cham, Switzerland, 433–441, https://doi.org/10.1007/978-3-319-15248-6_44, 2-s2.0-84945975652.
10.1007/978-3-319-15248-6_44
Google Scholar
27 Lazar I. F., Neild S. A., and Wagg D. J., Using an inerter-based device for structural vibration suppression, Earthquake Engineering & Structural Dynamics. (2014) 43, no. 8, 1129–1147, https://doi.org/10.1002/eqe.2390, 2-s2.0-84899928314.
10.1002/eqe.2390
Web of Science® Google Scholar
28 Lazar I. F., Neild S. A., and Wagg D. J., Vibration suppression of cables using tuned inerter dampers, Engineering Structures. (2016) 122, 62–71, https://doi.org/10.1016/j.engstruct.2016.04.017, 2-s2.0-84969850924.
10.1016/j.engstruct.2016.04.017
Web of Science® Google Scholar
29 Chen L., Nagarajaiah S., and Sun L., A unified analysis of negative stiffness dampers and inerter-based absorbers for multimode cable vibration control, Journal of Sound and Vibration. (2021) 494, https://doi.org/10.1016/j.jsv.2020.115814.
10.1016/j.jsv.2020.115814
Web of Science® Google Scholar
30 Shi X. and Zhu S., Dynamic characteristics of stay cables with inerter dampers, Journal of Sound and Vibration. (2018) 423, 287–305, https://doi.org/10.1016/j.jsv.2018.02.042, 2-s2.0-85045753481.
10.1016/j.jsv.2018.02.042
Web of Science® Google Scholar
31 Shi X., Zhu S., and Nagarajaiah S., Performance comparison between passive negative-stiffness dampers and active control in cable vibration mitigation, Journal of Bridge Engineering. (2017) 22, 1–15, https://doi.org/10.1061/(asce)be.1943-5592.0001088, 2-s2.0-85021648409.
10.1061/(ASCE)BE.1943-5592.0001088
Web of Science® Google Scholar
32 Shi X., Zhu S., and Spencer B. F., Experimental study on passive negative stiffness damper for cable vibration mitigation, Journal of Engineering Mechanics. (2017) 143, 04017070, https://doi.org/10.1061/(asce)em.1943-7889.0001289.
10.1061/(ASCE)EM.1943-7889.0001289
Web of Science® Google Scholar
33 Shi X., Zhu S., Li J.-Y., and Spencer B. F., Dynamic behavior of stay cables with passive negative stiffness dampers, Smart Materials and Structures. (2016) 25, 075044, https://doi.org/10.1088/0964-1726/25/7/075044, 2-s2.0-85011840628.
10.1088/0964-1726/25/7/075044
Web of Science® Google Scholar
34 Nakamura Y., Fukukita A., Tamura K. et al., Seismic response control using electromagnetic inertial mass dampers, Earthquake Engineering & Structural Dynamics. (2014) 43, no. 4, 507–527, https://doi.org/10.1002/eqe.2355, 2-s2.0-84896728883.
10.1002/eqe.2355
Web of Science® Google Scholar
35 Wang Z.-H., Gao H., Fan B.-q., and Chen Z.-Q., Inertial mass damper for vibration control of cable with sag, Journal of Low Frequency Noise, Vibration and Active Control. (2018) 39, no. 3, 749–760, https://doi.org/10.1177/1461348418814967, 2-s2.0-85059662909.
10.1177/1461348418814967
Web of Science® Google Scholar
36 Shen W. A., Zhu S. Y., and Zhu H. P., Experimental study on using electromagnetic devices on bridge stay cables for simultaneous energy harvesting and vibration damping, Smart Materials and Structures. (2016) 25, 1–17, https://doi.org/10.1088/0964-1726/25/6/065011, 2-s2.0-84969754503.
10.1088/0964-1726/25/6/065011
CAS Web of Science® Google Scholar
37 Zhu H., Li Y., Shen W., and Zhu S., Mechanical and energy-harvesting model for electromagnetic inertial mass dampers, Mechanical Systems and Signal Processing. (2019) 120, 203–220, https://doi.org/10.1016/j.ymssp.2018.10.023, 2-s2.0-85055549731.
10.1016/j.ymssp.2018.10.023
Web of Science® Google Scholar
38 Vibrations K.., Of a taut cable with an external damper, Journal of Applied Mechanics. (2000) 67, 772–776, https://doi.org/10.1115/1.1322037, 2-s2.0-0001264543.
10.1115/1.1322037
Web of Science® Google Scholar
39 Main J. A. and Jones N. P., Free vibrations of taut cable with attached damper. I: linear viscous damper, Journal of Engineering Mechanics. (2002) 128, no. 10, 1062–1071, https://doi.org/10.1061/(asce)0733-9399(2002)128:10(1062), 2-s2.0-0036794216.
10.1061/(ASCE)0733-9399(2002)128:10(1062)
PubMed Web of Science® Google Scholar
40 Main J. A. and Jones N. P., Free vibrations of taut cable with attached damper. II: nonlinear damper, Journal of Engineering Mechanics. (2002) 128, no. 10, 1072–1081, https://doi.org/10.1061/(asce)0733-9399(2002)128:10(1072), 2-s2.0-0036795386.
10.1061/(ASCE)0733-9399(2002)128:10(1072)
Web of Science® Google Scholar
41 Shi W., Wang L., Lu Z., and Wang H., Experimental and numerical study on adaptive-passive variable mass tuned mass damper, Journal of Sound and Vibration. (2019) 452, 97–111, https://doi.org/10.1016/j.jsv.2019.04.008, 2-s2.0-85064222018.
10.1016/j.jsv.2019.04.008
Web of Science® Google Scholar
42 Li Y., Shen W., and Zhu H., Vibration mitigation of stay cables using electromagnetic inertial mass dampers: full-scale experiment and analysis, Engineering Structures. (2019) 200, 1–18, https://doi.org/10.1016/j.engstruct.2019.109693, 2-s2.0-85072755489.
10.1016/j.engstruct.2019.109693
CAS Web of Science® Google Scholar

Citing Literature

All articles

Prototype Test and Numerical Analysis of a Shallow Cable with Novel Viscous Inertial Damper

Abstract

1. Introduction

2. Novel Viscous Inertial Damper

2.1. Composition and Mechanical Parameters of VID

2.2. Inertial Coefficient

2.3. Viscous Coefficient

2.4. Calculation of Damping Force

3. Mechanical Properties of VID

3.1. Damper’s Parameters

3.2. Test Results and Analysis

4. Theoretical Analysis of Cable-VID System for Vibration Control

4.1. In-Plane Vibration of a Shallow Cable with a VID

4.2. Normalized Wave Number of Symmetric Mode

4.3. Normalized Wave Number of Antisymmetric Mode

5. Cable-VID System Testing and Analysis

5.1. Experimental Setup of Scaled Cable-VID System

5.2. Analysis of Vibration Control Effect

5.3. Optimal VID Design Method

5.4. Mode Shape Analysis

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Prototype Test and Numerical Analysis of a Shallow Cable with Novel Viscous Inertial Damper

Abstract

1. Introduction

2. Novel Viscous Inertial Damper

2.1. Composition and Mechanical Parameters of VID

2.2. Inertial Coefficient

2.3. Viscous Coefficient

2.4. Calculation of Damping Force

3. Mechanical Properties of VID

3.1. Damper’s Parameters

3.2. Test Results and Analysis

4. Theoretical Analysis of Cable-VID System for Vibration Control

4.1. In-Plane Vibration of a Shallow Cable with a VID

4.2. Normalized Wave Number of Symmetric Mode

4.3. Normalized Wave Number of Antisymmetric Mode

5. Cable-VID System Testing and Analysis

5.1. Experimental Setup of Scaled Cable-VID System

5.2. Analysis of Vibration Control Effect

5.3. Optimal VID Design Method

5.4. Mode Shape Analysis

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information