International Journal of Mathematics and Mathematical Sciences
Volume 2021, Issue 1 4273851
Research Article
Open Access

An Iterative Method for Solving Split Monotone Variational Inclusion Problems and Finite Family of Variational Inequality Problems in Hilbert Spaces

Wanna Sriprad, 

Corresponding Author

Wanna Sriprad

Department of Mathematics and Computer Science, Faculty of Science and Technology, Rajamangala University of Technology, Thanyaburi, Pathum Thani 12110, Thailand rmuti.ac.th

Search for more papers by this author
Somnuk Srisawat, 

Somnuk Srisawat

Department of Mathematics and Computer Science, Faculty of Science and Technology, Rajamangala University of Technology, Thanyaburi, Pathum Thani 12110, Thailand rmuti.ac.th

Search for more papers by this author
First published: 31 December 2021
https://doi.org/10.1155/2021/4273851
Citations: 1
Academic Editor: Narendra K. Govil

Abstract

The purpose of this paper is to study the convergence analysis of an intermixed algorithm for finding the common element of the set of solutions of split monotone variational inclusion problem (SMIV) and the set of a finite family of variational inequality problems. Under the suitable assumption, a strong convergence theorem has been proved in the framework of a real Hilbert space. In addition, by using our result, we obtain some additional results involving split convex minimization problems (SCMPs) and split feasibility problems (SFPs). Also, we give some numerical examples for supporting our main theorem.

1. Introduction

Let H1 and H2 be real Hilbert spaces whose inner product and norm are denoted by 〈·, ·〉 and ‖·‖, respectively, and let C, Q be nonempty closed convex subsets of H1 and H2, respectively. For a mapping S : C⟶C, we denoted by F(S) the set of fixed points of S (i.e., F(S) = {x ∈ C : Sx = x}). Let A : C⟶H be a nonlinear mapping. The variational inequality problem (VIP) is to find x∗ ∈ C such that
(1)
and the solution set of problem (1) is denoted by VI(C, A). It is known that the variational inequality, as a strong and great tool, has already been investigated for an extensive class of optimization problems in economics and equilibrium problems arising in physics and many other branches of pure and applied sciences. Recall that a mapping A : C⟶C is said to be α-inverse strongly monotone if there exists α > 0 such that
(2)
A multivalued mapping is called monotone if for all x, y ∈ H1, 〈x − y, u − v〉 ≥ 0, for any u ∈ Mx and v ∈ My. A monotone mapping is maximal if the graph G(M) for M is not properly contained in the graph of any other monotone mapping. It is generally known that M is maximal if and only if for (x, u) ∈ H1 × H1, 〈x − y, u − v〉 ≥ 0 for all (y, v) ∈ G(M) implies u ∈ Mx. Let be a multivalued maximal monotone mapping. The resolvent mapping associated with M is defined by
(3)
where I stands for the identity operator on H1. We note that for all λ > 0, the resolvent is single-valued, nonexpansive, and firmly nonexpansive.
In 2011, Moudafi [1] introduced the following split monotone variational inclusion problem (SMVI):
(4)
(5)
where θ is the zero vector in H1 and H2, and are multivalued mappings on H1 and H2, A1 : H1⟶H1 and A2 : H2⟶H2 are two given single-valued mappings, and T : H1⟶H2 is a bounded linear operator with adjoint T∗ of T. We note that if (4) and (5) are considered separately, we have that (4) is a variational inclusion problem with its solution set VI(H1, A1, M1) and (5) is a variational inclusion problem with its solution set VI(H1, A2, M2). We denoted the set of all solutions of (SMVI) by Ω = {x∗ ∈ VI(H1, A1, M1) : Tx∗ ∈ VI(H2, A2, M2)}.

It is worth noticing that by taking M1 = NC and M2 = NQ normal cones to closed convex sets C and Q, then (SMVI) (4) and (5) reduce to the split variational inequality problem (SVIP) that was introduced by Censor et at. [2]. In [1], they mentioned that (SMVI) (4) and (5) contain many special cases, such as split minimization problem (SMP), split minimax problem (SMMP), and split equilibrium problem (SEP). Some related works can be found in [1, 3–10].

For solving (SMVI) (4) and (5), Modafi  [1] proposed the following algorithm.

Algorithm 1. Let λ > 0, x0 ∈ H1, and the sequence {xn} be generated by

(6)
where γ ∈ (1, 1/L) with L being the spectral radius of the operator T∗T.

He obtained the following weak convergence theorem for algorithm (6).

Theorem 1. (see [1]). Let H1, H2 be real Hilbert spaces. Let T : H1⟶H2 be a bounded linear operator with adjoint T∗. For i = 1,2, let Ai : Hi⟶Hi be αi-inverse strongly monotone with α = min{α1, α2} and let be two maximal monotone operators. Then, the sequence generated by (6) converges weakly to an element x∗ ∈ Ω provided that Ω ≠ ∅, λ ∈ (0,2α), and γ ∈ (1, 1/L) with L being the spectral radius of the operator T∗T.

Since then, because of a lot of applications of (SMVI), it receives much attention from many authors. They presented many approximation methods for solving (SMVI) (4) and (5). Also the iterative methods for solving (SMVIP) (4) and (5) and fixed-point problems of some nonlinear mappings have been investigated (see [11–19]).

On the other hand, Yao et al. [20] presented an intermixed Algorithm 1.3 for two strict pseudo-contractions in real Hilbert spaces. They also showed that the suggested algorithms converge strongly to the fixed points of two strict pseudo-contractions, independently. As a special case, they can find the common fixed points of two strict pseudo-contractions in Hilbert spaces (i.e., a mapping S : C⟶C is said to be κ-strictly pseudo-contractive if there exists a constant κ ∈ [0,1) such that ‖Sx − Sy‖2 ≤ ‖x − y‖2 + k‖(I − S)x − (I − S)‖,  0.3 cm ∀ x, y ∈ C).

Algorithm 2. For arbitrarily given x0, y0 ∈ C, let the sequences {xn} and {yn} be generated iteratively by

(7)
where {αn} and {βn} are two sequences of the real number in (0,1), T, S : C⟶C are λ-strictly pseudo-contractions, f : C⟶H is a ρ1-contraction, g : C⟶H is a ρ2-contraction, and k ∈ (0,1 − λ) is a constant.

Under some control conditions, they proved that the sequence {xn} converges strongly to PF(T)f(y∗) and {yn} converges strongly to PF(S)f(x∗), respectively, where x∗ ∈ F(T), y∗ ∈ F(S), and PF(T) and PF(S) are the metric projection of H onto F(T) and F(S), respectively. After that, many authors have developed and used this algorithm to solve the fixed-point problems of many nonlinear operators in real Hilbert spaces (see for example [21–27]). Question: can we prove the strong convergence theorem of two sequences of split monotone variational inclusion problems and fixed-point problems of nonlinear mappings in real Hilbert spaces?

The purpose of this paper is to modify an intermixed algorithm to answer the question above and prove a strong convergence theorem of two sequences for finding a common element of the set of solutions of (SMVI) (4) and (5) and the set of solutions of a finite family of variational inequality problems in real Hilbert spaces. Furthermore, by applying our main result, we obtain some additional results involving split convex minimization problems (SCMPs) and split feasibility problems (SFPs). Finally, we give some numerical examples for supporting our main theorem.

2. Preliminaries

Let H be a real Hilbert space and C be a nonempty closed convex subset of H. We denote the strong convergence of {xn} to x and the weak convergence of {xn} to x by notations “xn⟶x as n⟶∞” and “xn⇀x as n⟶∞,” respectively. For each x, y, z ∈ H and α, β, γ ∈ [0,1] with α + β + γ = 1, we have
(8)

Definition 1. Let H be a real Hilbert space and C be a closed convex subset of H. Let S : C⟶C be a mapping. Then, S is said to be

  • (1)

    Monotone, if 〈Sx − Sy, x − y〉 ≥ 0, ∀x, y ∈ H

  • (2)

    Firmly nonexpansive, if 〈Sx − Sy, x − y〉 ≥ ‖Sx  − Sy‖2, ∀x, y ∈ H

  • (3)

    Lipschitz continuous, if there exists a constant L > 0 such that ‖Sx − Sy‖ ≤ L‖x − y‖, ∀x, y ∈ H

  • (4)

    Nonexpansive, if =  ‖Sx − Sy‖ ≤ ‖x − y‖, ∀x, y ∈ H

It is well known that if S is α-inverse strongly monotone, then it is 1/α-Lipschitz continuous and every nonexpansive mapping S is 1-Lipschitz continuous. We note that if S : H⟶H is a nonexpansive mapping, then it satisfies the following inequality (see Theorem 3 in [28] and Theorem 1 in [29]):
(9)
Particularly, for every x ∈ H and y ∈ F(S), we have
(10)
For every x ∈ H, there is a unique nearest point PCx in C such that
(11)

Such an operator PC is called the metric projection of H onto C.

Lemma 1. (see [30]). For a given z ∈ H and u ∈ C,

(12)

Furthermore, PC is a firmly nonexpansive mapping of H onto C and satisfies

(13)

Moreover, we also have the following lemma.

Lemma 2. (see [31]). Let H be a real Hilbert space, let C be a nonempty closed convex subset of H, and let A be a mapping of C into H. Let u ∈ C. Then, for λ > 0,

(14)
where PC is the metric projection of H onto C.

Lemma 3. Let C be a nonempty closed and convex subset of a real Hilbert space H. For every i = 1,2, …, N, let Ai : C⟶H be the αi-inverse strongly monotone with . If , then

(15)
where 0 < ai < 1 for all i = 1,2, …, N and . Moreover, is a nonexpansive mapping for all .

Proof. By Lemma 4.3 of [32], we have that . Let and let x, y ∈ C. As the same argument as in the proof of Lemma 8 in [16], we have as nonexpansive.

Lemma 4. (see [33]). Let H be a real Hilbert space, A : H⟶H be a single-valued nonlinear mapping, and M : H⟶2H be a set-valued mapping. Then, a point u ∈ H is a solution of variational inclusion problem if and only if , i.e.,

(16)

Furthermore, if A is α-inverse strongly monotone and λ ∈ (0,2α], then VI(H, A, M) is a closed convex subset of H.

Lemma 5. (see [33]). The resolvent operator associated with M is single-valued, nonexpansive, and 1-inverse strongly monotone for all λ > 0.

The following two lemmas are the particular case of Lemmas 7 and 8 in [16].

Lemma 6. (see [16]). For every i = 1,2, let Hi be real Hilbert spaces, let be a multivalued maximal monotone mapping, and let Ai : Hi⟶Hi be an αi-inverse strongly monotone mapping. Let T : H1⟶H2 be a bounded linear operator with adjoint T∗ of T, and let be a mapping defined by , for all x ∈ H1. Then, , for all x, y ∈ H1, where L is the spectral radius of the operator T∗T, λ1 ∈ (0,2α1), λ2 ∈ (0,2α2), and γ > 0. Furthermore, if 0 < γ < 1/L, then is a nonexpansive mapping.

Lemma 7. (see [16]). Let H1 and H2 be Hilbert spaces. For i = 1,2, let be a multivalued maximal monotone mapping and let Ai : Hi⟶Hi be an αi-inverse strongly monotone mapping. Let T : H1⟶H2 be a bounded linear operator with adjoint T∗. Assume that Ω ≠ ϕ. Then, x∗ ∈ Ω if and only if , where is a mapping defined by

(17)
for all x ∈ H1, λ1 ∈ (0,2α1), λ2 ∈ (0,2α2), and 0 < γ < 1/L,  where L is the spectral radius of the operator T∗T.

Next, we give an example to support Lemma 7.

Example 1. Let ℝ be a set of real number and H1 = H2 = ℝ2, and let 〈·, ·〉 : ℝ2 × ℝ2⟶ℝ be inner product defined by 〈x, y〉 = x·y = x1y1 + x2y2, for all x = (x1, x2) ∈ ℝ2 and y = (y1, y2) ∈ ℝ2 and the usual norm ‖·‖ : ℝ2⟶ℝ given by , for all x = (x1, x2) ∈ ℝ2. Let T : H1⟶H2 be defined by Tx = (2x1, 2x2) for all x = (x1, x2) ∈ ℝ2 and T∗ : ℝ2⟶ℝ2 be defined by T∗z = (2z1, 2z2) for all z = (z1, z2) ∈ ℝ2. Let be defined by M1x = {(3x1 − 5,3x2  − 5)} and M2x = {(x1/3 − 2, x2/3 − 2)}, respectively, for all x = (x1, x2) ∈ ℝ2. Let the mapping A1, A2 : ℝ2⟶ℝ2 be defined by A1x = ((x1 − 4)/2, (x2 − 4)/2) and A2x = ((x1 − 2)/3, (x2 − 2)/3), respectively, for all x = (x1, x2) ∈ ℝ2. Then, (2,2) is a fixed point of . That is, .

Proof. It is obvious to see that Ω = {(2,2)}, A1 is 2-inverse strongly monotone, and A2 is 3-inverse strongly monotone. Choose λ1 = 1/3. Since M1x = {(3x1 − 5,3x2 − 5)} and the resolvent of for all x = (x1, x2) ∈ ℝ2, we obtain that

(18)

Choose λ2 = 1. Since M2x = {(x1/3 − 2, x2/3 − 2)} and the resolvent of for all x = (x1, x2) ∈ ℝ2, we obtain that

(19)

Since the spectral radius of the operator T∗T is 4, we choose γ = 0.1. Then, from (18) and (19), we get that

(20)
for all x = (x1, x2) ∈ ℝ2. Then, by Lemma 7, we have that .

Lemma 8. (see [34]). Let {sn} be a sequence of nonnegative real numbers satisfying sn+1 ≤ (1 − αn)sn + δn, ∀n ≥ 0 where {αn} is a sequence in (0,1) and {δn} is a sequence in ℝ such that

  • (1)

    .

  • (2)

    lim supn⟶∞αn/δn ≤ 0 or . Then limn⟶∞sn = 0.

3. Main Results

In this section, we introduce an iterative algorithm of two sequences which depend on each other by using the intermixed method. Then, we prove a strong convergence theorem for solving two split monotone variational inclusion problems and a finite family of variational inequality problems.

Theorem 2. Let H1 and H2 be Hilbert spaces, and let C be a nonempty closed convex subset of H1. Let T : H1⟶H2 be a bounded linear operator, and let f, g : H1⟶H1 be ρf, ρg-contraction mappings with ρ = max{ρf, ρg}. For i = 1,2, let be multivalued maximal monotone mappings and let be inverse strongly monotone mappings, respectively. For i = 1,2, …, N, let be inverse strongly monotone mappings, respectively, , and . Let be defined by , and , respectively, where , and 0 < γx, γy < 1/L with L being a spectral radius of T∗T. Assume that and . Let {xn} and {yn} be sequences generated by x1, y1 ∈ H1 and

(21)
for all n ≥ 1 where {δn}, {σn}, {ηn}, {αn}⊆[0,1] with δn + σn + ηn = 1, , and . Assume the following condition holds:
  • (1)

    , and for some a, b ∈ ℝ.

  • (2)

    .

  • (3)

    .

  • (4)

    , for all n ∈ ℕ, for some .

  • (5)

    . Then, {xn} converges strongly to and {yn} converges strongly to .

Proof. We divided the proof into five steps.

Step 1. We will show that {xn} and {yn} are bounded. Let x∗ ∈ ℱx and y∗ ∈ ℱy. Then, from Lemma 7 and Lemma 6, we get

(22)

From (21), Lemma 3, and (22), we have

(23)

Similarly, from definition of yn, we have

(24)

Hence, from (23) and (24), we obtain

(25)

By induction, we have

(26)
for every n ∈ ℕ. Thus, {xn} and {yn} are bounded.

Step 2. We will show that limn⟶∞‖xn+1 − xn‖ = limn⟶∞‖yn+1 − yn‖ = 0. Put , , , and , for all n ≥ 1. From Lemma 6, we have

(27)

By applying Lemma 3, we get that

(28)

From the definition of {xn}, (27), and (28), we have

(29)

By the same argument as in (27) and (29), we also have

(30)
(31)

From (29) and (31), we obtain that

(32)

From (32), conditions (1), (2), and (5), and Lemma 8, we obtain that

(33)
(34)

Step 3. We show that . From (21), we have that

(35)
(36)

Then, we have

(37)

Observe that

(38)

From (33) and (37), we have

(39)

By the same argument as above, we also have that

(40)

Note that

(41)

By (37) and (39), we get that

(42)

By the same argument as (41), we also obtain

(43)

Consider

(44)

By (33) and (39), we get that

(45)

However,

(46)

It follows from (33) and (45) that

(47)

Consider

(48)

From (39) and (47), we obtain

(49)

Applying the same method as (48), we also have

(50)

Step 4. We will show that and , where and . First, we take a subsequence of {zn} such that

(51)

Since {xn} is bounded, there exists a subsequence of {xn} such that as k⟶∞. From (39), we get that . Next, we need to show that . Assume that q1 ∉ Ωx. By Lemma 7, we get that . Applying Opial’s condition and (49), we get that

(52)

This is a contradiction. Thus, q1 ∈ Ωx.

Assume that . Then, from Lemma 3 and Lemma 2, we have . From Opial’s condition and (42), we obtain

(53)

This is a contradiction. Thus, , and so,

(54)

However, . From (54) and Lemma 1, we can derive that

(55)

By the same method as (55), we also obtain that

(56)

Step 5. Finally, we show that the sequences {xn} and {yn} converges strongly to and , respectively. From the definition of zn, we have

(57)
which implies that
(58)

From the definition of {xn} and (58), we get

(59)

Applying the same argument as in (58) and (59), we get

(60)

From (58) and (59), we have

(61)

According to condition (2) and (4), (61), and Lemma 8, we can conclude that {xn} and {yn} converge strongly to and , respectively. Furthermore, from (39) and (40), we get that {zn} and {wn} converge strongly to and , respectively. This completes the proof. □

One of the great special cases of the SMVIP is the split variational inclusion problem that has a wide variety of application backgrounds, such as split minimization problems and split feasibility problems.

If we set and in Theorem 2, for all i = 1,2, then we get the strong convergence theorem for the split variational inclusion problem and the finite families of the variational inequality problems as follows:

Corollary 1. Let H1 and H2 be Hilbert spaces, and let C be a nonempty closed convex subset of H1. Let T : H1⟶H2 be a bounded linear operator, and let f, g : H1⟶H1 be ρf, ρg-contraction mappings with ρ = max{ρf, ρg}. For every i = 1,2, let be multivalued maximal monotone mappings. For i = 1,2, …, N, let be inverse strongly monotone with and . Let and . Assume that and . Let {xn} and {yn} be sequences generated by x1, y1 ∈ H1 and

(62)
for all n ≥ 1, where {δn}, {σn}, {ηn}, {αn}⊆[0,1] with δn + σn + ηn = 1, , for all i = 1,2, and 0 < γx, γy < 1/L with L being a spectral radius of T∗T. Assume the following conditions hold:
  • (1)

    , and for some a, b ∈ ℝ.

  • (2)

    .

  • (3)

    .

  • (4)

    , for all n ∈ ℕ, for some .

  • (5)

    . Then, {xn} converges strongly to and {yn} converges strongly to .

4. Applications

In this section, by applying our main result in Theorem 2, we can prove strong convergence theorems for approximating the solution of the split convex minimization problems and split feasibility problems.

4.1. Split Convex Minimization Problems

Let φ : H⟶ℝ be a convex and differentiable function and ψ : H⟶(−∞, ∞] be a proper convex and lower semicontinuous function. It is well known that if ∇φ is 1/α-Lipschitz continuous, then it is α-inverse strongly monotone, where ∇φ is the gradient of φ (see [10]). It is also known that the subdifferential ∂ψ of ψ is maximal monotone (see [35]). Moreover,
(63)
Next, we consider the following the split convex minimization problem (SCMP): find
(64)
and such that y∗ = Tx∗ ∈ H2 solves
(65)
where T : H1⟶H2 is a bounded linear operator with adjoint T∗, φi,  and ψi defined as above, for i = 1,2. We denoted the set of all solutions of (64) and (65) by Θ. That is, Θ = {x∗ which solves(64) : Tx∗ solves (65)}.

If we set , and , for i = 1,2, in Theorem 2, then we get the strong convergence theorem for finding the common solution of the split convex minimization problems and the finite families of the variational inequality problems as follows.

Theorem 3. Let H1 and H2 be Hilbert spaces, and let C be a nonempty closed convex subset of H1. Let T : H1⟶H2 be a bounded linear operator, and let f, g : H1⟶H1 be ρf, ρg-contraction mappings with ρ = max{ρf, ρg}. For i = 1,2, let be proper convex and lower semicontinuous functions, and let be convex and differentiable function such that and be -Lipschitz continuous and -Lipschitz continuous, respectively. For i = 1,2, …, N, let be inverse strongly monotone with and . Let be defined by , and , respectively, where and 0 < γx, γy < 1/L with L is a spectral radius of T∗T. Assume that and . Let {xn} and {yn} be sequences generated by x1, y1 ∈ H1 and

(66)
for all n ≥ 1 where {δn}, {σn}, {ηn}, {αn}⊆[0,1] with δn + σn + ηn = 1, , and . Assume the following condition holds:
  • (1)

    , and for some a, b ∈ ℝ.

  • (2)

    .

  • (3)

    .

  • (4)

    , for all n ∈ ℕ, for some .

  • (5)

    . Then, {xn} converges strongly to and {yn} converges strongly to .

4.2. The Split Feasibility Problem

Let H1 and H2 be two real Hilbert spaces. Let C and Q be the nonempty closed convex subset of H1 and H2, respectively. The split feasibility problem (SFP) is to find
(67)

The set of all solutions (SFP) is denoted by Ψ = {x ∈ C : Ax ∈ Q}. This problem was introduced by Censor and Elfving [8] in 1994. The split feasibility problem was investigated extensively as a widely important tool in many fields such as signal processing, intensity-modulated radiation therapy problems, and computer tomography (see [36–38] and the references therein).

Let H be a real Hilbert space, and let h be a proper lower semicontinuous convex function of H into (−∞, +∞]. The subdifferential ∂h of h is defined by ∂h(x) = {z ∈ H : h(x) + 〈z, u − x〉 ≤ h(u), ∀u ∈ H} for all x ∈ H. Then, ∂h is a maximal monotone operator [39]. Let C be a nonempty closed convex subset of H, and let iC be the indicator function of C, i.e., iC(x) = 0 if x ∈ C and iC(x) = ∞ if x ∉ C. Then, iC is a proper, lower semicontinuous and convex function on H, and so the subdifferential ∂iC of iC is a maximal monotone operator. Then, we can define the resolvent operator of ∂iC for λ > 0, by .

Recall that the normal cone NC(u) of C at a point u in H is defined by NC(u) = {z ∈ H : 〈z, u − v ≤ 0〉, ∀v ∈ C} if u ∈ C and NC(u) = ∅ if u ∉ C. We note that ∂iC = NC, and for λ > 0, we have that if and only if u = PCx (see [31]).

Setting M1 = ∂iC, M2 = ∂iQ, and in (SMVI) (4) and (5), then (SMVI) (4) and (5) are reduced to the split feasibility problem (SFP) (67)

Now, by applying Theorem 2, we get the following strong convergence theorem to approximate a common solution of SFP (67) and a finite family of variational inequality problems.

Theorem 4. Let H1 and H2 be Hilbert spaces, and let C and Q be the nonempty closed convex subset of H1 and H2, respectively. Let T : H1⟶H2 be a bounded linear operator with adjoint T∗, and let f, g : H1⟶H1 be ρf, ρg-contraction mappings with ρ = max{ρf, ρg}. For i = 1,2, …, N, let be inverse strongly monotone with and . Assume that and . Let {xn} and {yn} be sequences generated by x1, y1 ∈ H1 and

(68)
for all n ≥ 1, where {δn}, {σn}, {ηn}, {αn}⊆[0,1] with δn + σn + ηn = 1, , , for all i = 1,2, and 0 < γx, γy < 1/L with L being a spectral radius of T∗T. Assume the following condition holds:
  • (1)

    , and for some a, b ∈ ℝ.

  • (2)

    .

  • (3)

    .

  • (4)

    , for all n ∈ ℕ, for some .

  • (5)

    . Then, {xn} converges strongly to and {yn} converges strongly to .

Proof. Set , , and in Theorem 2. Then, we get the result.

The split feasibility problem is a significant part of the split monotone variational inclusion problem. It is extensively used to solve practical problems in numerous situations. Many excellent results have been obtained. In what follows, an example of a signal recovery problem is introduced.

Example 2. In signal recovery, compressed sensing can be modeled as the following under-determined linear equation system:

(69)
where x ∈ ℝN is a vector with m non-zero components to be recovered, y ∈ ℝM is the observed or measured data with noisy δ, and A : ℝN⟶ℝM(M < N) is a bounded linear observation operator. An essential point of this problem is that the signal x is sparse; that is, the number of nonzero elements in the signal x is much smaller than the dimension of the signal x. To solve this situation, a classical model, convex constraint minimization problem, is used to describe the above problem. It is known that problem (69) can be seen as solving the following LASSO problem [40]:
(70)
where t > 0 is a given constant and ‖·‖1 is ℓ1 norm. In particular, LASSO problem (70) is equivalent to the split feasibility problem (SFP) (67) when C = {x ∈ ℝN : ‖x‖1 ≤ t} and Q = {y}.

5. Numerical Examples

In this section, we give some examples for supporting Theorem 2. In example 3, we give the computer programming to support our main result.

Example 3. Let ℝ be a set of real number and H1 = H2 = ℝ2. Let C = [−20,20] × [−20,20], and let 〈·, ·〉 : ℝ2 × ℝ2⟶ℝ be inner product defined by 〈x, y〉 = x·y = x1y1 + x2y2, for all x = (x1, x2) ∈ ℝ2 and y = (y1, y2) ∈ ℝ2 and the usual norm ‖·‖ : ℝ2⟶ℝ given by , for all x = (x1, x2) ∈ ℝ2. Let T : ℝ2⟶ℝ2 be defined by Tx = (2x1, 2x2) for all x = (x1, x2) ∈ ℝ2 and T∗ : ℝ2⟶ℝ2 be defined by T∗z = (2z1, 2z2) for all z = (z1, z2) ∈ ℝ2. Let be defined by , respectively, for all x = (x1, x2) ∈ ℝ2. Let the mapping be defined by , respectively, for all x = (x1, x2) ∈ ℝ2. For every i = 1,2, …, N, let the mappings be defined by , respectively, for all x = (x1, x2) ∈ ℝ2, and let . Let the mappings f, g : ℝ2⟶ℝ2 be defined by f(x) = (x1/7, x2/7) and g(x) = (x1/9, x2/9), respectively, for all x = (x1, x2) ∈ ℝ2.

Choose γx and γy = 0.1,  . Setting {δn} = {n/(9n + 3)}, {σn} = {(4n + (2/3))/(9n + 3)}, {ηn} = {(4n + (7/3))/(9n + 3)}, {αn} = {1/20n}, , and . Let and , and let the sequences {xn} and {yn} be generated by (21) as follows:

(71)
for all n ≥ 1, where and . By the definition of , for all i = 1,2,  , for all i = 1,2, …, N, and f and g, we have that and . Also, it is easy to see that all parameters satisfy all conditions in Theorem 2. Then, by Theorem 2, we can conclude that the sequence {xn} converges strongly to (1,1) and {yn} converges strongly to (−2, −2).

Table 1 and Figure 1 show the numerical results of {xn} and {yn} where x1 = (−10,10), y1 = (−10,10), and n = N = 50.

Table 1. Values of {xn} and {yn} with initial values x1 = (−10,10), y1 = (−10,10), and n = N = 50.
n
1 (−10.000000, 10.000000) (−10.000000, 10.000000)
2 (−4.093342, 5.126154) (−5.481385, 3.338182)
3 (−1.544910, 3.037093) (−3.639877, 0.575101)
4 (−0.307347, 2.029037) (−2.789106, −0.719370)
⋮ ⋮ ⋮
30 (0.998745, 0.996821) (−1.996611, −1.998243)
⋮ ⋮ ⋮
47 (0.998973, 0.998235) (−1.998394, −1.999022)
48 (0.998986, 0.998280) (−1.998454, −1.999055)
49 (0.999000, 0.998324) (−1.998511, −1.999087)
50 (0.999013, 0.998365) (−1.998566, −1.999118)
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Convergence of {xn} and {yn} with initial values x1 = (−10,10), y1 = (−10,10), and n = N = 50.

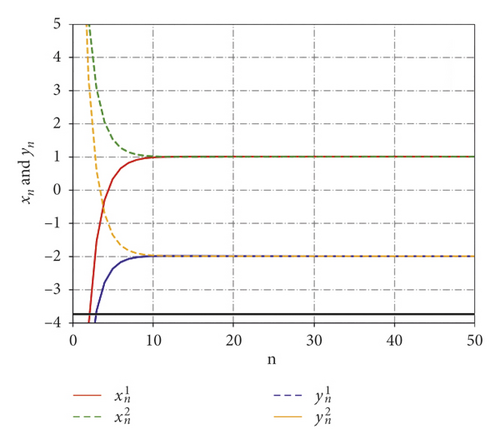
Next, in Example 4, we only show an example in infinite-dimensional Hilbert space for supporting Theorem 2. We omit the computer programming.

Example 4. Let H1 = H2 = C = ℓ2 be the linear space whose elements consist of all 2-summable sequence (x1, x2, …, xj, …) of scalars, i.e.,

(72)
with an inner product 〈·, ·〉 : ℓ2 × ℓ2⟶ℝ defined by , where , and a norm ‖·‖ : ℓ2⟶ℝ defined by where . Let T : ℓ2⟶ℓ2 be defined by Tx = (x1/2, x2/2, …, xj/2, …) for all . And, T∗ : ℓ2⟶ℓ2 be defined by Tx = (z1/2, z2/2, …, zj/2, …) for all . Let be defined by and , respectively, for all . Let the mapping be defined by respectively, for all . For every i = 1,2, …, N, let the mappings be defined by and , respectively, for all , and let . Let the mappings f, g : ℓ2⟶ℓ2 be defined by f(x) = (x1/5, x2/5, …, xj/5, …), g(x) = (x1/4, x2/4, …, xj/4, …), respectively, for all .

Let . Since L = 1/4, we choose γx and γy = 0.5. Let and , and let {xn} and {yn} be the sequences generated by (2) as follows:

(73)
for all n ≥ 1, where and . It is easy to see that , , T, f, g, and all parameters satisfy Theorem 2. Furthermore, we have that and . Then, by Theorem 2, we can conclude that the sequence {xn} converges strongly to 0 and {yn} converges strongly to 1.

6. Conclusion

  • (1).

    Table 1 and Figure 1 in Example 3 show that the sequence {xn} converges to and {yn} converges to

  • (2)

    Example 4 is an example in infinite-dimensional Hilbert space for supporting Theorem 2

  • (3)

    Theorem 2 guarantees the convergence of {xn} and {yn} in Example 3 and Example 4

Conflicts of Interest

The authors declare no conflicts of interest.

Acknowledgments

The authors would like to thank the Faculty of Science and Technology, Rajamangala University of Technology Thanyaburi (RMUTT), Thailand, for the financial support.

    Data Availability

    No data were used to support this study.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.