Connectivity Indices of Intuitionistic Fuzzy Graphs and Their Applications in Internet Routing and Transport Network Flow
Abstract
Connectivity index has a vital role in real-world problems especially in Internet routing and transport network flow. Intuitionistic fuzzy graphs (IFGs) allow to describe two aspects of information using membership and nonmembership degrees under uncertainties. Keeping in view the importance of in real life problems and comprehension of IFGs, we aim to develop some in the environment of IFGs. We introduce two types of , namely, and average , in the frame of IFGs. In spite of that, certain kinds of nodes called IF connectivity enhancing node (IFCEN), IF connectivity reducing node (IFCRN), and IF neutral node are introduced for IFGs. We have introduced strongest strong cycles, θ-evaluation of vertices, cycle connectivity, and of strong cycle. Applications of the in two different types of networks are done, Internet routing and transport network flow, followed by examples to show the applicability of the proposed work.
1. Introduction
Zadeh [1] presented the idea of fuzzy set (FS) by giving membership grades to the objects of a set ranging from zero to one. Many concepts of crisp set theory like inclusion, union, intersection, complement, etc., were established for FSs. FS theory opened the way to fuzzy logic and fuzzy control systems. In the beginning, probability theory was the only tool to handle problems of uncertainty, facing science, technology, and real life problems. FS theory has many applications in different areas such as inventory control model [2], decision-making problems [3], and intelligence science [4]. More applications can be found in [5, 6]. A recent research to treat COVID-19 disease with FS approach is given in [7].
In 1975, Rosenfeld [8] studied fuzzy graphs (FGs). After that, Yeh and Bang [9] presented the same concept independently during the same period. Rosenfeld defined some basic properties of fuzzy relations including fuzzy bridges and trees with their properties, while Yeh and Bang gave the concept of connectedness of FGs along with applications. Mordeson [10] proposed the work for fuzzy line graphs. Massa’deh [11, 12] introduced complete FGs, regular FGs, complement of FGs, and some other properties. Mathew and Sunitha introduced types of arcs such as α-strong, β-strong, and δ-arcs in FGs [13]. The authors gave various concepts like strong arcs in [14], fuzzy end nodes in [15], and geodesic in [16]. Recently, Akram presented concepts like bipolar FGs in [17] and energy of bipolar FGs in [18]. Jan et al. studied the concept of cubic bipolar FGs with an application in a social network [19]. FGs are useful in representing relationships under uncertainty. FGs are used in various areas like human trafficking, disaster management system, decision-making method, etc.
The extension of FS is intuitionistic fuzzy set (IFS) presented by Atanassov [20] in 1986. He added a new component in the definition of FS, which is known as the degree of nonmembership or falsity degree. IFS is the generalization of FS with the requirement that the sum of both degrees cannot exceed 1. Many researchers have applied IFSs in decision-making problems. Chen [21] proposed to measure the degree of similarity between vague sets. Similarity measures for discrete, as well as for continuous, sets are given in [22] and applied in pattern recognition problems. More work on IFSs can be found in [23–25]. Fields of applications of IFSs are Computer Science, Engineering, Medicine, Chemistry, Economics, etc.
The generalization of FG is intuitionistic fuzzy graph (IFGs) explained elaborately by Parvathi and Karunambigai [26]. They also gave the concepts of path, bridge, and cut vertices in IFGs. Dhavudh and Srinivasan [27] defined IFG of second kind, and IFG of nth type was developed by Davvaz et al. [28]. Karunambigai and Buvaneswari [29] introduced arcs in IFGs like strong arcs, weakest arcs, strong path, α-strong, β-strong, and δ-weak arcs. Karunambigai and kalaivani [30] presented IFGs as the matrix representation. Mishra and Pal [31, 32] discussed the product of two interval valued IFGs, their properties, and regular interval valued IFGs in 2013 and 2017. Fallatah et al. [33] and Alanser et al. [34] introduced new concepts as IF soft graphs and bipolar IFGs. Akram and Alshehri [35] introduced IF cycles and trees. Some misconceptions in the definitions of several generalizations of IFGs are corrected by Jan et al. [36]. IFGs are applied in different areas such as cellular network and decision support systems [37, 38].
Connectivity is the most fundamental and normal parameter related to a network. The stability of a network depends on its connectivity. Binu et al. introduced two measures on connectivity, namely, cyclic and average cyclic of FGs [39]. Poulik and Ghorai brought the concept of , average , and types of connectivity nodes under bipolar fuzzy graph environment with applications [40]. Mathew and Mordeson [41] introduced and , studied their properties, and investigated their applications. Binu et al. discussed the concept of Wiener index and relationship between Wiener index and connectivity index with an application to illegal immigration networks [42]. FGs describe only one type of opinion, that is, membership degree, while IFGs describe two types of opinions with the help of membership and nonmembership degrees.
In our paper, we have considered IFG and discussed certain concepts related to IFG. In Section 2, preliminary requirements are given for the work of this paper. In Section 3, we have extended concepts of and bounds of for IFG. Section 4 provides of vertex and edge deleted IF subgraphs. Section 5 presents concepts of the strongest strong cycles, θ-evaluation of vertices, cycle connectivity (CC), and of strong cycle for IFG. Section 6 deals with along with its properties. Applications of are discussed in Section 7. Finally Section 8 concludes this study.
2. Preliminaries
Throughout this section, definitions and examples are presented to recall concepts related to IFG, arcs in IFG, and IF-cycles relevant to the present work. Most of the definitions in preliminaries are taken from [29, 35, 43].
The notion of IFG was proposed by Akram and Davvaz [43] and given as follows:
Definition 1 (see [43].)An IFG is a pair G = (N, M) such that
- (1)
V = {u1, u2, u3, …, un} with TN : V⟶[0,1] and FN : V⟶[0,1] representing the truth-membership degree and falsity-membership degree of the vertex ui ∈ V and 0 ≤ TN(ui) + FN(ui) ≤ 1 for each ui ∈ V(0 ≤ i ≤ n).
- (2)
E⊆V × V with TM : E⟶[0,1] and FM : E⟶[0,1] being as follows:
(1)and 0 ≤ TM(ui, uj) + FM(ui, uj) ≤ 1 for every edge (ui, uj) ∈ E.
The next definition is related to complete IFG given by Parvathi et al. [29].
Definition 2 (see [29].)An IFGG is complete if TM(ui, uj) = min{TN(ui), TN(uj)} and FM(ui, uj) = max{FN(ui), FN(uj)} for each (ui, uj) ∈ E.
The role of path is extremely famous and important in IFGs. The following definition gives us the concept of path in IFGs.
Definition 3. [29] A sequence u1, u2, u3, …, un of distinct vertices is a path P in an IFG, provided it has one of the conditions given below for some i and j.
- (1)
TM(ui, uj) > 0 and FM(ui, uj) = 0
- (2)
TM(ui, uj) = 0 and FM(ui, uj) > 0
- (3)
TM(ui, uj) > 0 and FM(ui, uj) > 0
The strength of paths plays a significant role in IFG settings. The following definition gives us component-wise and whole strength of paths in IFGs.
Definition 4 (see [29].)Let P = u1, u2, u3, …, un be a path in an IFG. Then,
- (1)
The T-strength of P is denoted and defined by ST = min{TM(ui, uj)}∀i, j
- (2)
The F-strength of P is denoted and defined by SF = max{FM(ui, uj)}∀i, j
- (3)
SP = (ST, SF) is called the strength P if both ST and SF exist for the same edge
The highly connected nodes have significant role to a network. The next definition is about the strength of connectedness between the nodes.
Definition 5 (see [29].)The T-strength of connectedness between two vertices ui and uj is defined by CONNT(G)(ui, uj) = max{ST} and F-strength of connectedness between ui and uj is defined by CONNF(G)(ui, uj) = min{SF} for all possible paths between ui and uj,
where , denote the T-strength of connectedness and F-strength of connectedness between ui and uj attained by removing the edge (ui, uj) from G, respectively.
The following definition gives us the idea of a bridge whose deletion from an IFG increase its number of connected components.
Definition 6 (see [29].)An edge (vi, vj) is called a bridge in G if either
In other words, deletion of (ui, uj) reduces the strength of connectedness between any pair of vertices.
The concept of strong and weakest edges is of much importance in IFGs as well as in our study. The next definition is related to the notions of strong and weakest edges.
Definition 7 (see [29].)An edge (ui, uj) in an IFG is
- (1)
Strong if TM(ui, uj) ≥ CONNT(G)(ui, uj) and FM(ui, uj) ≤ CONNF(G)(ui, uj) for each ui, uj ∈ V
- (2)
Weakest if TM(ui, uj) < CONNT(G)(ui, uj) and FM(ui, uj) > CONNF(G)(ui, uj) for each ui, uj ∈ V
The coming definition gives us the strongest paths between two vertices. This definition is relevant to our work.
Definition 8 (see [29].)A strongest path between two vertices in an IFGG is a path P having its strength equal to CONNT(G)(ui, uj) and CONNF(G)(ui, uj) lying in the same edge.
The following definition tells us the concept of strong path.
Definition 9 (see [29].)Let G = (N, M) be an IFG. A path P : ui − uj in G is called strong path if P consists of only strong edges.
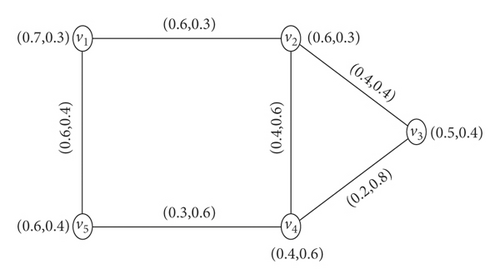
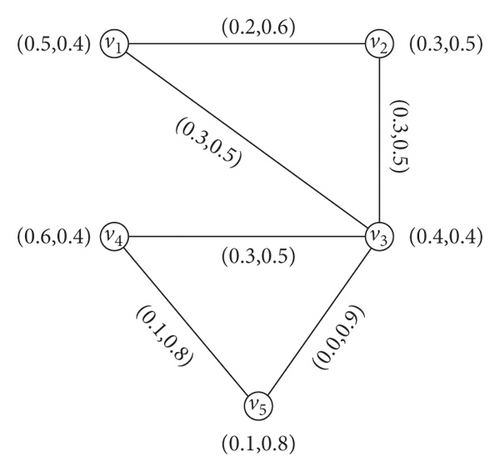
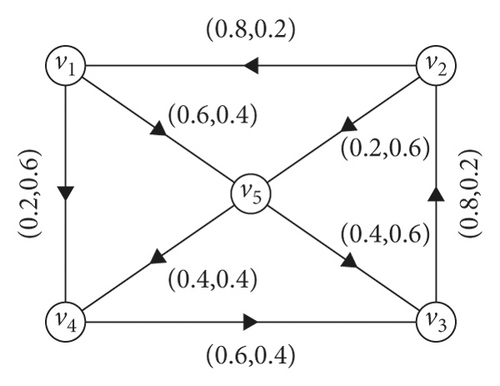
Example 1. In Figure 1, TM(v1, v2) = 0.6 = CONNT(G)(v1, v2) and FM(v1, v2) = 0.6 = CONNF(G)(v1, v2), which implies that (v1, v2) is a strong arc. Similarly, (v2, v3), (v1, v5), (v2, v4) are strong arcs and (v3, v4), (v4, v5) are weakest arcs. Here, P = v1v2v3 is a strong path. In fact, it is the strongest path.
The next definition provides us types of strong arcs in IFG.
Definition 10 (see [29].)An arc (ui, uj) in an IFGG = (N, M) is
- (1)
Called α -strong if and
- (2)
Called β -strong if and
- (3)
Called δ -weak if and
Example 2. In Figure 2, the arcs (v1, v4), (v2, v3), (v4, v5), (v1, v3) are α-strong, (v3, v4) is β-strong, and (v1, v2), (v3, v5) are δ-weak.
The following definition gives us different types of strong paths in IFGs.

Definition 11 (see [29].)A path in an IFG containing only α-strong arcs is called α-strong and a path having only β-strong arcs is called β-strong.
The concept of a cycle has a vital role in IFGs. The following definition gives us the concept of a cycle in IFGs environment.
Definition 12 (see [35].)
- (1)
G = (N, M) is called a cycle if G∗ = (N∗, M∗) is cycle
- (2)
G is called an IF cycle if G∗ = (N∗, M∗) is cycle and ∄ unique (x, y) ∈ M∗ such that
(3)
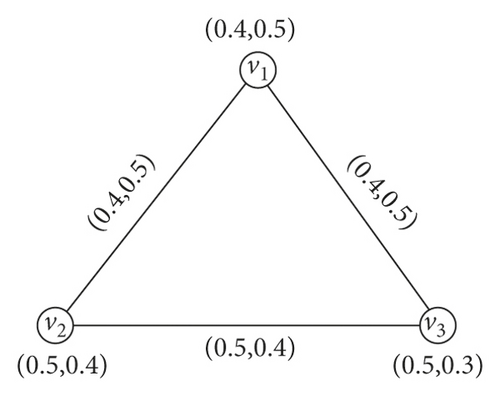
Example 3. In this example, we take (TN(u), FN(u)) = (0.3, 0.2) for all u ∈ N∗. Here, min{TM(u, v)} = 0.2 and max{FM(u, v)} = 0.3. Clearly, G = (N, M) is an IF cycle. The graph is shown in Figure 3.
The main goal of our study is to bring more accuracy and precision to the study of topological indices, especially in the context of connectivity indices. FGs have less information in comparison with IFGs. In particular situations like vagueness and uncertainty, FGs are described by only membership grades, but IFGs are characterized by the two grades known by membership and nonmembership. Due to the description of opinions using two membership grades, IFGs have less information loss as compared to FGs. So, that is why we aim to propose the concepts of several for IFGs and study their applications.
3. Connectivity Index for Intuitionistic Fuzzy Graphs
When we talk about the network like Internet or transport network, naturally, we think about the connectivity of this network. The connectivity means how stable and dynamic this network is! So, we can say that this measure of connectivity is the most fundamental and natural. The measure of connectivity is already available in FGs. But IFG is the generalization of FG, and it gives better results in situations where FGs are not preferable. So, because of this reason, we have proposed this concept of connectivity from FGs to IFGs. We have made some results of connectivity of FGs to IFGs. We define formally as follows.
Definition 13. The of an IFGG = (N, M) is defined as
Example 4. Refer to Figure 1,
So, .
It may be observed that TCI(G) > FCI(G), which shows that the level of FCI(G) is lower than the level of TCI(G) in this problem. This comparison is interesting and useful in applications of connectivity index.
Theorem 1. Let G = (N, M) be a complete IFG with N∗ = {v1, v2, v3, …, vn} such that t1 ≤ t2 ≤ ⋯≤tn and s1 ≥ s2 ≥ s3 ≥ ⋯≥sn, where ti = TN(vi) and si = FN(vi). Then,
Proof. Let v1 be the vertex having least truth-membership value t1. For a complete IFG, CONNT(G)(u, v) = TM(u, v) for each u, v ∈ N∗. So, TM(v1, vi) = t1 ; 2 ≤ i ≤ n and hence, ; 2 ≤ i ≤ n. Taking summation over i, we have
Similarly, for vertex v2, we obtain
By adding all the above equations, we get
Now, let v1 be the vertex with the largest falsity-membership value s1. For a complete IFG, CONNF(G)(u, v) = FM(u, v) for each u, v ∈ N∗. Thus, FM(v1, vi) = s1 ; 2 ≤ i ≤ n and hence, ; 2 ≤ i ≤ n. Summing over i, we have
Similarly, for vertex v2, we have
By adding all the above equations, we get
Hence, by the definition of connectivity, we see
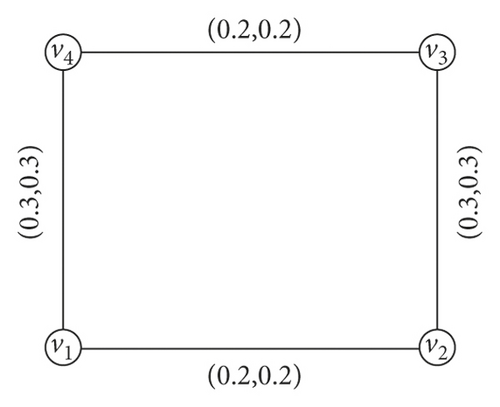
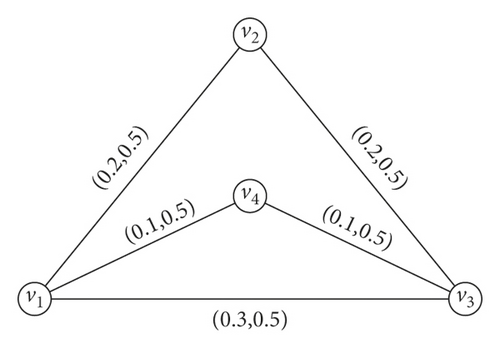
Example 5. In Figure 4, it can be easily seen that k3 is a complete IFG. So,
Therefore, .
Now, we use above theorem
Adding these two summations, we get
Hence, it is verified that
4. Edge Deleted and Vertex Deleted IFGs with Connectivity Index
The is affected or not by deleting a vertex or an edge. It is based on the nature of vertex and edge to be removed.
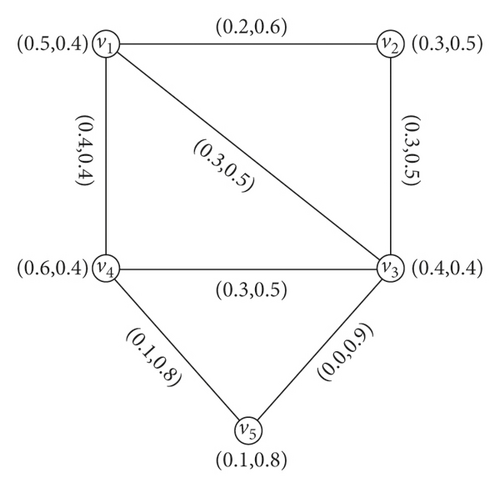
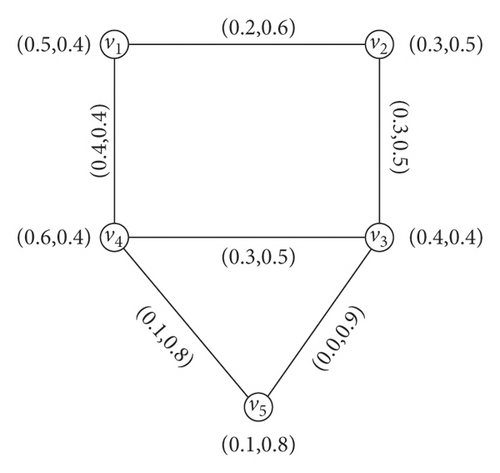
Example 6. Taking the G = (N, M) shown in Figure 5. Here, (v1, v4), (v2, v3), (v4, v5) are α-strong arcs, (v1, v3), (v3, v4) are β-strong arcs, and (v1, v2), (v3, v5) are δ-arcs. Then,
So, we have .
So, we have . Thus, , which means that of G has been reduced by deleting α -strong edge (v1, v4). The IFG, G − (v1, v2) is shown in Figure 6(a). If we delete the β -strong edge (v1, v3), then the strength of connectedness between every pair of vertices is invariant, i.e., and , so . The graph of G − (v1, v3) is shown in Figure 6(b). Similarly, when we delete the δ -arc (v1, v2), then the strength of connectedness between every pair of vertices does not change, and so is the . The graph of G − (v1, v2) is shown in Figure 6(c).
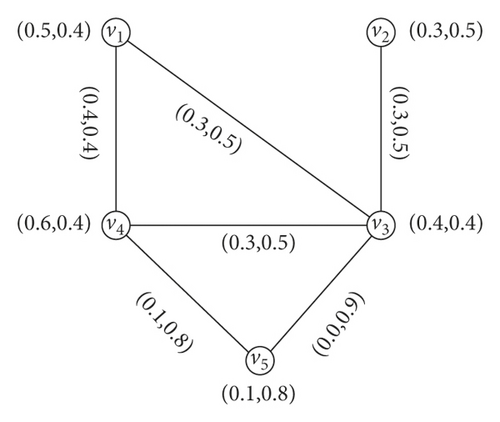
Theorem 2. Let H be the IF subgraph of an IFG G = (N, M) formed by removing an edge uv ∈ MG from G. Then, or iff uv is a bridge.
Proof. Take uv as a bridge. According to the definition, there exit u and v such that their strength of connectedness will be decreased. So, we conclude that or .
Conversely, suppose that or and consider the possibilities given below.
-
Case 1: suppose that uv is a δ-arc. Then, CONNT(G)−uv(u, v) = CONNT(G)(u, v) and CONNF(G)−uv(u, v) = CONNF(G)(u, v). So, we have and and therefore, .
-
Case 2: take uv as β-strong edge. Then, TM(u, v) = CONNT(G)−uv(u, v) , FM(u, v) = CONNF(G)−uv(u, v). This implies that there is another u − v path different from uv edge. Therefore, the removal of the arc uv will have no effect on the strength of connectedness between u and v. So, .
-
Case 3: now, take uv as α-strong edge. Then, TM(u, v) > CONNT(G)−uv(u, v), FM(u, v) < CONNF(G)−uv(u, v). So, the only strongest path is uv edge having strength equal to (TM(u, v), FM(u, v)). Then, clearly , or or since α-strong edges are IF bridges. This implies that uv is a bridge.
Corollary 1. Let H be the IF subgraph of an IFG G = (N, M) formed by removing an edge uv ∈ MG from G. Then, iff uv is either δ edge or β-strong.
Corollary 2. Suppose that uv an edge of a complete IFG G = (N, M). Then, iff uv is a unique IF bridge of G.
Proof. Let G = (N, M) be a complete IFG. Suppose that . Then, uv is the only IF bridge of G.
Conversely, let uv be a unique IF bridge of G. Hence, by Theorem 2, it follows that .
Theorem 3. Let G1 = (N1, M1) and G2 = (N1, M2) be the two isomorphic IFGs. Then, .
Proof. Suppose that G1 = (N1, M1) and G2 = (N2, M2) are isomorphic IFGs. Then, ∃ is a mapping h : N1⟶N2 such that h is bijective and and for all ui ∈ N∗ as well as and for (ui, uj) ∈ M∗. As G1 and G2 are isomorphic, then the strength of any strongest path between ui and uj is equal to that between h(ui) and h(uj) in G2. Thus, for u, v ∈ N∗
So, we have
Thus, . This implies that .
5. Strongest Strong Cycles, θ-Evaluation of Vertices, Cycle Connectivity, and CI of Strong Cycle
This section contains some concepts about IF cycles. IF strongest strong cycles, θ-evaluation of IF vertices, IF cycle connectivity, and of IF strong cycles are defined in the current section. Also, some properties related to these concepts are studied.
Definition 14. The truth and falsity values of the weakest edge in a cycle C are defined to be the strength of C in an IFGG.
Definition 15. Let C denote a cycle in an IFGG. Then, C is called IF strongest strong cycle (IFSSC) if it is the union of two strongest strong u − v paths for each of u and v in C with the exception when uv in C is an IF bridge of G.
Remark 1. We observe that when uv is an IF bridge of G and it lies in C, the condition for C to be the union of two strongest strong u to v paths can be omitted for u and v. Also, CONNT(G)(a, b) = CONNT(C)(a, b) and CONNF(G)(a, b) = CONNF(C)(a, b)∀a, b ∈ G.
Definition 16. If C is a cycle in an IFGG, then C is said to be strong, provided each of its edges is strong.
Example 7. In Figure 7, we take (TN(u), FN(u)) = (0.6, 0.3) for all u ∈ N∗. The edges (v1, v2), (v3, v5) are bridges in G. C1 = v1v2v3v5v1 and C2 = v5v3v4v5 are strongest strong cycles as C3 = v1v2v3v4v5v1 is not the union of two strongest strong v3 − v5 paths. So, it is not a strong cycle. Also, CONNT(G)(v3, v5) = 0.6 and CONNF(G)(v3, v5) = 0.3. But C3 has no strongest v3 − v5 path. Moreover, we see that (v3, v5) is a fuzzy bridge of G that is outside of C3.
Definition 17. Let G be an IFG. Then, Tθ -evaluation of two vertices ui and uj in G is the set θT(ui, uj) defined by
Note 1. If cycles through u and v do not exist, then θT(ui, uj) = ϕ and θF(ui, vj) = ϕ. With this θ-evaluation, we define another connectivity measure in IFGs called cyclic connectivity (CC).
Definition 18. Let G be an IFG. Then, cycle T-connectivity between ui and uj in G is denoted and defined by
Similarly, cycle F-connectivity between ui and uj in G is denoted and defined by
Note 2. If θT(ui, uj) = ϕ and θF(ui, uj) = ϕ for any two vertices ui and uj, then we define cycle T-connectivity and cycle F-connectivity to be zero, i.e., and .
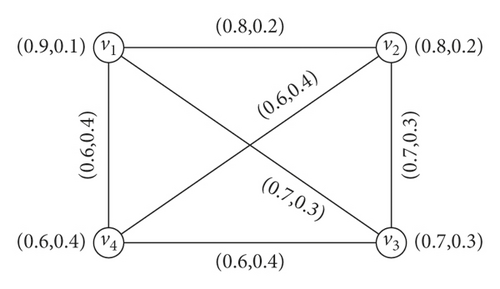
Example 8. From Figure 8, we have θT(v1, v3) = {0.7, 0.6} and hence, . Similarly, θF(v1, v3) = {0.3, 0.4} and therefore, .
Theorem 4. Let G be an IFG and for any ui, uj ∈ N∗, both ui and uj lie on a common SC. Then,
Proof. Suppose that ui, uj ∈ N∗ such that both of them lie on a common IFSSC. Then, , where θT(ui, uj) = {α ∈ (0,1] : α is T − strength of a strong cycle through u and v}. Therefore, and hence,
Similarly, , where θF(ui, uj) = {β ∈ (0,1] : β is F − strength of a strong cycle through u and v}. Thus, we obtain and hence,
So, we obtain
6. Average Connectivity Index of an IFG
The concept of average connectivity index is present in the literature of FGs. So, we introduced this concept for IFGs. The stability of a network is guaranteed by its average flow.
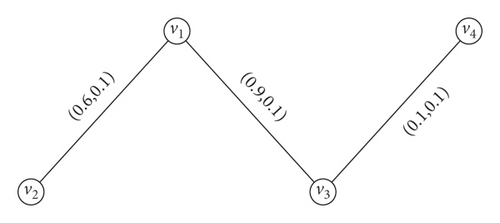
Example 9. Let G = (N, M) be the IFG in Figure 9, with (TN(v), FN(v)) = (0.9, 0.1) for all v ∈ N∗. Then, by routine calculations, we have and .
From Example 10, and the number of pairs in G is . By averaging the and , we get , and . Now, consider G − V4, and we have and . On averaging them, we have and . The overall connectivity of G is increased by deleting vertex v4 from G. The following definitions and results are led by this example.
Definition 19. Let G = (N, M) be an IFG. Then, the average T-connectivity index of G is denoted and defined as
Definition 20. Let G = (N, M) be an IFG. The average connectivity index of G is defined to be the sum of average T- connectivity index and average F- connectivity index of G, i.e.,
Note 3. Obviously, will not be enhanced by the removal of an edge, and therefore, also. For an IFG, .
Definition 21. Let G = (N, M) be an IFG and u ∈ N∗. Then, u is said to be an IF connectivity reducing node (IFCRN) of G if . u is said to be an IF connectivity enhancing node (IFCEN) of G if . u is said to be an IF neutral node of G if .
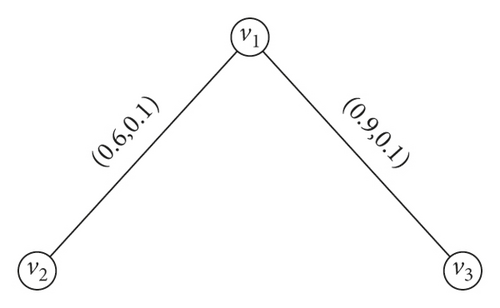
Example 10. Consider the IFGG as shown in Figure 10. We have taken here (TN(u), FN(u)) = (0.5, 0.5) for all u ∈ N∗. , and .Thus v1, v3 are IFCRN s, v2 is an IF neutral node, and v4 is a IFCEN. We characterize these nodes using in the following theorem.
Theorem 5. Let G = (N, M) be an IFG and u ∈ N∗ with |N∗| ≥ 3. Let . u is a IFCEN iff r < n/(n − 2). u is a IFCRN iff r > n/(n − 2). u is an IF neutral node iff r = n/(n − 2).
Proof. Suppose that u is an IF neutral node. Then, by definition, . By definition of average connectivity index, we obtain
From here, we get
The converse part can be proved by reversing the arguments. Similarly, we can prove other cases.
Note 4. An isolated vertex w in an IFG, and G = (N, M) is an IFCEN. Further, if denote complement of IFGG = (N, M), then and therefore,
Theorem 6. Let G = (N, M) be an IFG with |N∗| ≥ 3. If w ∈ N∗ is an end vertex of G, let . Then,
- (1)
w is an IFCEN if
- (2)
w is an IFCRN if
- (3)
w is an IF neutral node if
Proof. Let w be an IF neutral node. Then, by definition, . We see that
The converse part can be proved by reversing these steps. Similarly, we can prove other parts.
At this stage, we can classify an IFG depending on the nature of vertices in it.
Definition 22. An IFGG containing at least one IFCEN is called an IF connectivity enhancing graph. If there is no IFCEN node in G and at least one IFCRN, then G is said to be an IF connectivity reducing graph. If G has all vertices as IF neutral nodes, then it is said to be an IF neutral graph.
7. Applications
In this section, two applications are given. One is on Internet routing, and the other is on transport network flow.
7.1. Internet Routing
The strength of connectedness between points in a network has much importance in various areas, for example, shortest path problem, routing problem, network flow problem, and maximum band width problem. Consider a network G that connects routers in a part of a network. For convenience in calculations, we have taken (TN(v), FN(v)) = (0.9, 0.1) for all v. Here, the edge values represent maximum bandwidth between the corresponding routers. Membership value of the edge represents correct information and nonmembership value for incorrect information. Also, if P is a path connecting two routers in the network, then ST(P) denotes the truth bandwidth of P and similarly, SF(P) is for falsity bandwidth of P. Hence, CONNT(G)(u, v) and CONNF(G)(u, v) denote the maximum possible truth bandwidth and the minimum possible falsity bandwidth between u and v. Consider the fuzzified network as shown in Figure 11.
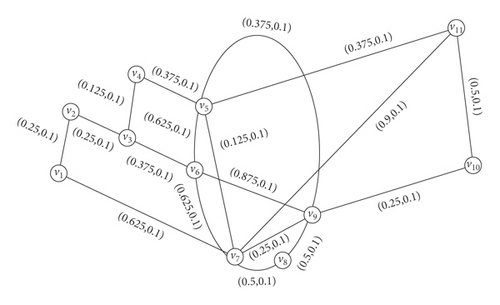
After computations, we have , . By removal routers v11 and v2, we obtain , , . Hence, , . We see that and . This implies that v2 is IFCEN, and v11 is a IFCRN.
This problem has less incorrect information because . Also, the average bandwidth of the network is increased by the removal of router v2 and removal of v11 causes reduction in average bandwidth.
7.2. Transport Network Flow
By adding all the entries of , we obtain . Thus, .
By calculations, we have and . Thus, . As , which implies that v5 is IFCRN.
We have after calculations, and . Thus, . As , which implies that v1 is also IFCRN.
From the above matrices, we obtain and . Thus, . As , which implies that v4 is IFCEN. So, the removal of junction v4 increases the average connectivity amongst the other junctions. Table 1 shows that there is a small difference between and . So, the removal of v4 has no too much effect on the network.
| G − vi | ||
|---|---|---|
| G − v1 | 0.508 | 0.1872 |
| G − v2 | 0.576 | 0.1192 |
| G − v3 | 0.3229 | 0.3723 |
| G − v4 | 0.74 | 0.0448 |
We also see that the difference between and is highest than other differences, so the removal of v3 has maximum negative effects on the connectivity.
8. Conclusion
- (i)
We introduced the notion of for IFGs and developed results on . Examples are also given to support results of .
- (ii)
of edge and vertex deleted IFGs with an example is also given.
- (iii)
We developed SSC, θ-evaluation of vertices, CC, and of SC and related results.
- (iv)
of IFG is defined.
- (v)
Types of connectivity nodes, namely, CEN, CRN, and neutral node, and results on them are introduced.
- (vi)
Applications in two types of networks, namely, Internet routing and transport flow network.
In the future, we aim to extend our work to the environment of picture fuzzy graphs [44] and T-spherical fuzzy graphs [45]. We also aim to introduce some other connectivity indices in IFGs and investigate their applications.
9. Advantages
- (i)
The main feature of our study is to develop the concept of under IFGs environment due to the fact that IFGs handle uncertain information with two membership grades.
- (ii)
IFGs are described by two types of components that is membership and nonmembership, while FGs are characterized by only one component.
- (iii)
Our findings are the generalization of the results of in FGs. For example, if we neglect the second component, then our results are converted into the results of FGs. Thus, the results of in FGs become the special case of our results in IFGs.
- (iv)
Comparatively, our study proves that IFGs would have less loss of information as compared to FGs.
Conflicts of Interest
The authors declare no conflicts of interest about the publication of the research article.
Acknowledgments
The authors are grateful to the Deanship of Scientific Research, King Saud University for supporting through Vice Deanship of Scientific Research Chairs.
Open Research
Data Availability
No data were used to support this study.




