Numerical Simulation of Nanosilica Sol Grouting for Deep Tunnels Based on the Multifield Coupling Mechanism
Abstract
Grouting is an effective technical way for the construction of deep tunnels in unfavorable geological conditions. The fluid-solid-chemical coupling mechanism of grouting process is analyzed from the following three aspects: influence of physical properties of silica sol on permeability coefficient, dynamic changes of porosity and permeability of geotechnical media with seepage pressure, and governing equations for flow and mass transfer characteristics. A dynamically changing model for nanosilica sol grouting in deep tunnels is established, considering the changing physical properties of grout and surrounding rock. Based on the Xianglushan Tunnel of Yunnan Water Diversion Project, the temporal and spatial evolution of silica sol grout is studied. The effect characteristics of grouting pressure and initial permeability are clarified. The rationality of this model is verified by classical Newtonian fluid grouting theory. The main conclusions: with the molar concentration as the index, the grout range can be divided into the raw grout region and the transition region; with the decrease of the grouting pressure, the growth rate of the normal grouting radius and the axial grouting radius will gradually decrease; due to the mechanical dispersion and molecular diffusion, the range of the transition region will gradually increase with time. The ratio of the transition region to grouting radius fluctuates slightly with time under the initial permeability of 5 D. The fluctuation increases with the decrease of initial permeability, and the average ratio increases with the decrease of grouting pressure. This study can provide theoretical guidance for grouting design of deep tunnel engineering.
1. Introduction
Due to the influence of crustal movement, human excavation engineering, and weathering erosion, the rock mass contains not only macroscopic defects such as joints and cracks but also microscopic defects such as microcracks and micropores [1–4]. Grouting is an effective technical way for the construction of deep tunnels in unfavorable geological conditions [5–7]. Due to nanoparticle size, low viscosity, high injectability, and friendly to ecological environment, silica sol grouting has been widely used in petroleum engineering, groundwater protection engineering, tunnel construction, nuclear waste storage, liquefiable soil improvement, and other geotechnical fields [8–11].
Wang et al. [10, 12] investigated the rheological properties of nanosilica sol grout and derived an equation of real-time viscosity and permeability length. Fujita and Kobayashi [13] studied the transport mechanism of colloidal silica in unsaturated sand and the effect of charging properties of sand and silica particles by sand column experiment. In order to study the penetration law of silica sol in microcracks with a width of 40-50 microns, fluorescent whitening agent-ultraviolet observation method, microscopic observation method, and hydraulic experiment method were used to jointly predict and verify the penetration length and sealing effect of silica sol [14]. The influence of gel effect on the migration ability of silica sol in liquefied soil was studied by using soil column experiments and a pilot-scale facility [15–17]. The migration process of silica sol along the whole length of soil column, the gel capacity of silica sol when it reached the target area, the injection amount of silica sol, and the migration amount of silica sol with the concentration of chloride ion as the indexes were monitored during the soil column experiment. The flow laws of silica sol, epoxy resin, polyurethane, and cement-based grout in one-dimensional and two-dimensional fractured rock mass with different grouting modes (constant flow grouting, constant pressure grouting, and constant energy grouting) were studied by theoretical analysis [18]. An analytical model of colloidal silica gelling in groundwaters with varying pH and background electrolyte concentrations was developed and validated [19]; the model was then applied to a hypothetical case study to demonstrate its use in grout design, based on published in situ groundwater data from the Olkiluoto area of Finland. The pulsating grouting technology of silica sol was tested in a 500-meter-deep tunnel at Mizunami Underground Research Laboratory in Japan [20]. Pan et al. [21, 22] studied the influence characteristics and mechanism of fragmental size of broken coal mass on the injection regularity of silica sol grouting. Injection regularity of silica sol grouting in broken coal mass generally presented a three-stage regularity. The fragmental size had a great impact on the 2nd and 3rd stages.
In summary, previous experts have achieved fruitful research results about the injection law of silica sol grouting through numerical simulations, column tests, and field experiments. However, there are still some deficiencies in the study of the synergy effect of grouting material-surrounding rock physical properties on silica sol grouting in deep tunnels, and the study of multifield mechanism for silica sol grouting in deep tunnels is still insufficient.
In this paper, in order to explore the theoretical mechanism of nanosilica sol grouting technology for deep tunnels in unfavorable geological conditions, a dynamically changing model for silica sol grouting in deep tunnels is established, taking into account the changing physical properties of grout and surrounding rock. Based on the project background of Xianglushan Tunnel of Central Yunnan Water Diversion Project, the temporal and spatial evolution of Darcy velocity, viscosity, molar concentration, and fluid pressure of silica sol grouting are analyzed. The effects of grouting pressure and initial permeability of surrounding rock on permeability grouting characteristics of silica sol are explored. The rationality of this model is verified by combining the column theory and sphere theory.
2. Engineering Background and Grouting Material
Xianglushan Tunnel was located on the head of the Dali I Section, which was the first section of the main channel of the Central Yunnan Water Diversion Project (Figure 1). At the feasibility study stage, the total length of the section was 63.426 km [23]. For Xianglushan Tunnel, the burial depth in the area to the north of the trough valley of the Runan River was 600~1000 m. According to the stress assessment results of tunnel surrounding rock in the geological survey stage, the average weight of rock mass can be calculated as 26.5 kN/m3. The vertical stress of the surrounding rock at a buried depth of 1000 m was 26.50 MPa, which was a high level of ground stress. The statistics of conventional water pressure tests results showed that the overall permeability of the rock formations in the study area was weak water permeability (1 ≤ q (permeability rate) < 10 Lu, 10−5 ≤ K (permeability coefficient) < 10−4 cm/s), and some were medium permeable. The permeability of karst strata was stronger than that of nonkarst strata. Part of the medium permeability is mainly concentrated limestone, dolomitic limestone, argillaceous limestone, and sandstone of Songgui formation.
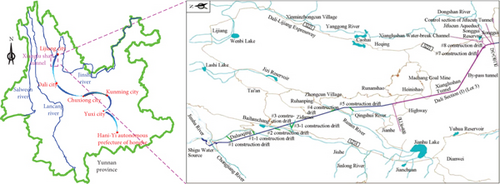
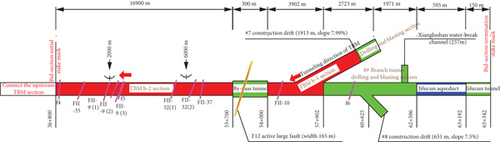
The drilling and blasting method and TBM method were used to construct the Xianglushan Tunnel, in which the TBM section was 35.37 km long. According to the information of exploration and design, the tunnel diameter of downstream TBM section was 9.8 m, in which Class IV and V surrounding rocks accounted for 53.14% (Table 1), and large deformation surrounding rocks accounted for 16.62%. Under the condition of naked tunnel, the length of the main tunnel section of Xianglushan Tunnel was 33.085 km with a specific yield greater than 3 m3/m·d in dry season.
| Rock mass quality [24] | Uniaxial compression strength (MPa) | Intactness index of rock mass | Unit weight (kN/m3) | Shear strength (MPa) | Deformation modulus (GPa) | Poisson’s ratio | |
|---|---|---|---|---|---|---|---|
| Major classification | Minor classification | ||||||
| IV | IVa | 30-40 | 0.45 | 23.5 | 0.6-0.7 | 3-5 | 0.27-0.28 |
| IVb | 15-25 | 0.6 | 23.5 | 0.4-0.6 | 2-3 | 0.28-0.29 | |
| IVc | 5-10 | 0.55 | 22 | 0.3-0.4 | 1.5-2 | 0.29-0.30 | |
| V | Va | 10-20 | 0.4 | 22 | 0.2-0.3 | 0.7-1.5 | 0.30-0.31 |
| Vb | 5-10 | 0.3 | 22 | 0.1-0.2 | 0.2-0.7 | 0.31-0.32 | |
| Vc | 1-3 | 0.24 | 22 | 0.05-0.1 | 0.1-0.2 | 0.32-0.34 | |
Considering environmental protection, ecology, and flow control in the tunnel, in order to avoid more leakages in the tunnel, reduce the impact of pumping and drainage on groundwater environment and tunnel construction, groundwater should be plugged and drained in a way that followed the principle of “first plugging, and limited drainage.” When the local hydraulic head of groundwater was less than 60 m, it was better to adopt the full plugging method; when the hydraulic head of groundwater was more than 60 m, drainage and guide mode should be adopted.
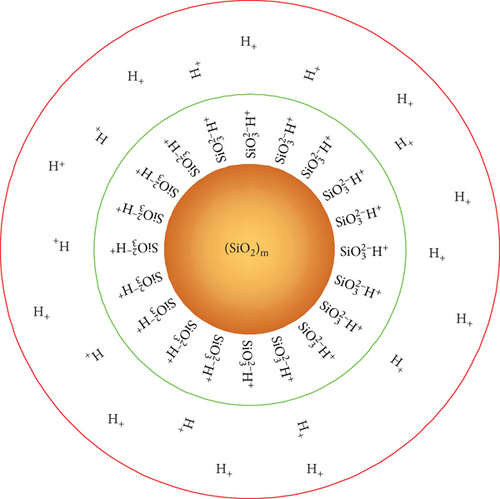
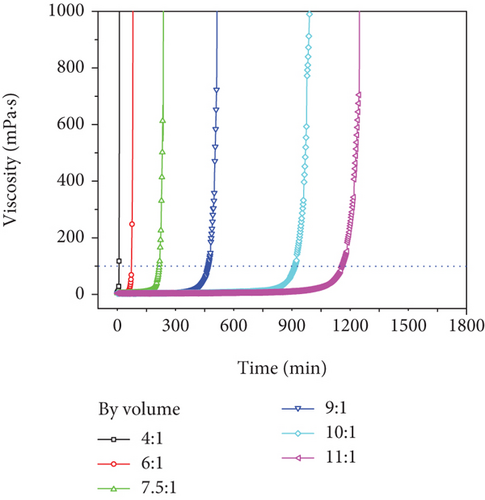
Silica sol was selected as sealing grouting material. It was a one-component nanogrouting material, which belonged to colloidal solution, odorless and nontoxic. Silica sol had a typical double-electron layer structure. The dominant size of the silica particles in silica sol was 8–12 nm. When strong electrolyte solution (i.e., catalyst) was added, the double-electron layer of colloidal particles was compressed and thinned, and the gel reaction began to take place. The viscosity of colloidal particles increased gradually [25, 26]. The catalyst chosen in the experiment was NaCl solution (Table 2). The gel time of silica sol can be adjusted according to the amount of catalyst. The gel reaction products had a good transmittance and compact microstructure (Figure 2).
| Properties | Silica sol | Catalyst |
|---|---|---|
| Viscosity | ~10 mPa·s | ~1 mPa·s |
| Density | 1.1 kg/L | 1.07 kg/L |
| pH | 10 | 7 |
| Concentration (% by weight) | SiO2 15% | NaCl 10% |



3. A Dynamically Changing Model for Silica Sol Grouting in Deep Tunnels Based on the Multifield Coupling Mechanism
The injection process in a tunnel is a complex and changeable system problem: (a) geotechnical medium is multiscale, and different stress states of surrounding rocks at different positions in a tunnel lead to uneven development of fracture and pore; (b) geotechnical environment is multi-interface, such as grout-rock, grout-gas, and grout-water interfaces; the permeability grouting presents nonlinear characteristics because of the different states, structures, and physical and chemical properties of the interfaces; (c) in the grouting process, there are many reactions, such as convection, molecular diffusion, mechanical dispersion, adsorption and retention, and gel reaction between silica sol and catalyst. These reactions will change the migration characteristics of fluids [27]. In this paper, the injection process of silica sol in deep tunnels is regarded as a multireaction coupled flow in porous media. The fluid-solid-chemical coupling mechanism of grouting process is analyzed from the following three aspects.
3.1. Influence of Physical Properties of Silica Sol on Permeability Coefficient
Assuming that the rock mass does not undergo hydration or expansion, the permeability coefficient of grout is mainly restricted by two aspects: (a) the redistribution of surrounding rock stress field caused by engineering disturbances such as excavation and grouting; (b) the change of viscosity and density of grout caused by self-gel and dilution in groundwater. Self-gel is embodied in the dependence of viscosity on time; adsorption retention and dilution in groundwater are embodied in the dependence of viscosity on concentration and density on concentration.
3.1.1. Three-Dimensional Surface Equation for Viscosity-Time-Concentration of Grout

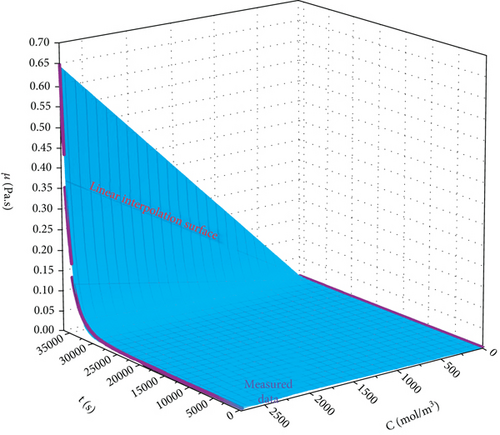
3.1.2. Relationship between Density and Molar Concentration of Grout
3.2. Dynamic Changes of Porosity and Permeability of Geotechnical Media with Seepage Pressure
3.3. Governing Equations for Flow and Mass Transfer Characteristics
3.3.1. Governing Equations for Grout Flow
3.3.2. Governing Equation for Mass Transfer
Because the gel reaction of silica sol is the gradual connection of colloidal particles into a network structure, the gel reaction can be regarded as not affecting the molar concentration of silica.
4. Numerical Model and Boundary Conditions
4.1. Parameter Values
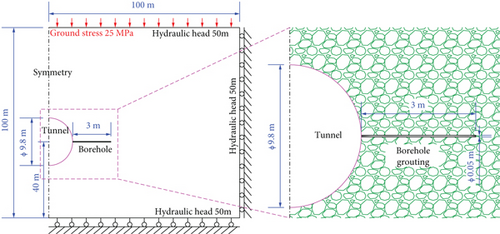
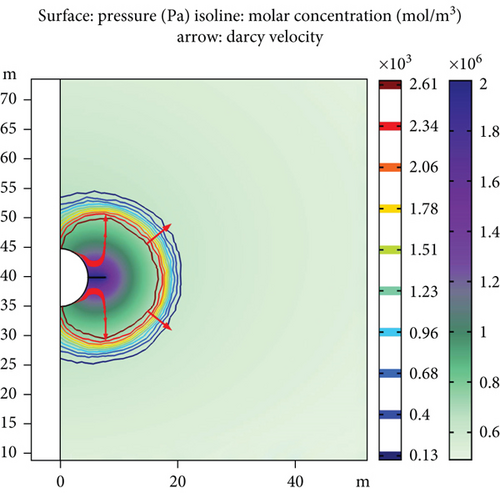
COMSOL software is used for numerical calculation. As shown in Figure 4, the model size is 100 × 100 m, the diameter of tunnel is 9.8 m, the diameter of grouting borehole is 5 cm, and the length of borehole is 3 m. The numerical simulation process can be divided into three steps: in situ stress initialization, tunnel excavation, and borehole grouting. The values of parameters in the numerical model are shown in Table 1.
4.2. Boundary Conditions
4.2.1. Boundary Conditions for Solid Mechanics
The upper boundary condition is given stress of 25 MPa, the lower boundary condition is fixed constraint, the left boundary condition is symmetrical boundary condition, and the right boundary condition is roller support. The boundary condition of the tunnel is simplified to free. After boring, the grouting pipe is put in, and the boundary condition is simplified to zero radial displacement.
4.2.2. Boundary Conditions for Darcy’s Law
The upper, lower, and right boundary conditions of the model are given hydraulic head of 50 m, and the left boundary condition is symmetrical. After tunnel excavation, timely grouting behind shield closes the cracks in surrounding rock, and the boundary condition for surrounding rock of tunnel is nonflowing. The boundary condition of borehole is given pressure of 2 MPa to simulate grouting pressure.
4.2.3. Boundary Conditions for Transport of Diluted Species in Porous Media
The upper, lower, and right boundary conditions of the model are given pressure of 0 mol/m3, and the left boundary condition is symmetrical. The boundary condition of borehole is 2750 mol/m3, which simulates the grout concentration at the injection end.
5. Results and Discussion
5.1. Injection Characteristics of Model with a Grouting Pressure of 2 MPa and an Initial Permeability of 5 D
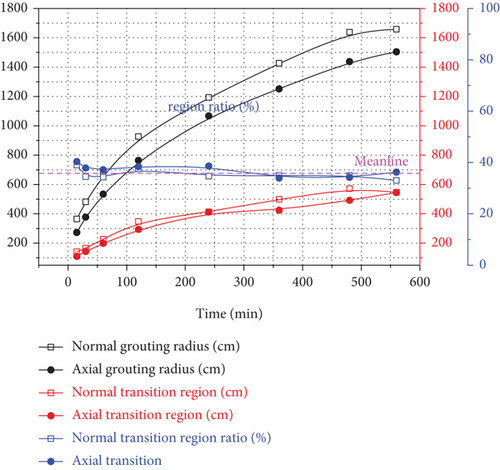
Taking a calculation model with a grouting pressure of 2 MPa and an initial permeability of 5 D as an example, a monitoring line of 80 m in length is laid vertically in the grouting hole, and the permeability law of silica sol grouting in tunnel is analyzed. As shown in Figures 5(a)–5(e), there is a certain transition zone between groundwater and grout. Because Darcy velocity, viscosity, and permeability coefficient are dependent variables of molar concentration, 10% of initial molar concentration of grout (27.50 mol/m3) is used as the index of grout penetration radius. Define the 10%~95% (27.50~2612.50 mol/m3) of initial molar concentration for the transition region and 95%~100% of initial concentration for the raw grout region. The grouting radius and transition region in different directions at different times are calculated, as shown in Figure 5(f).
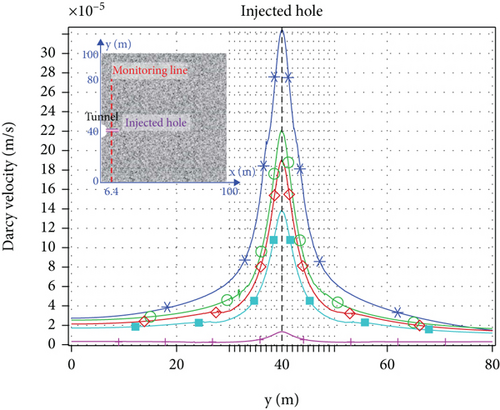
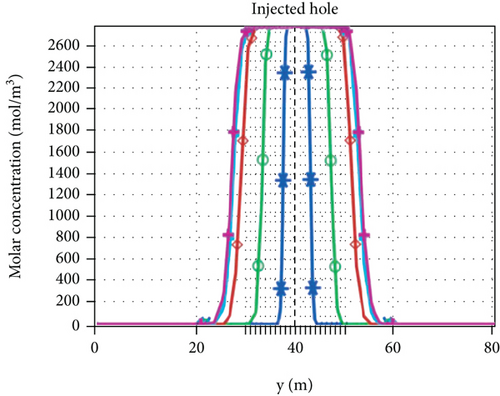
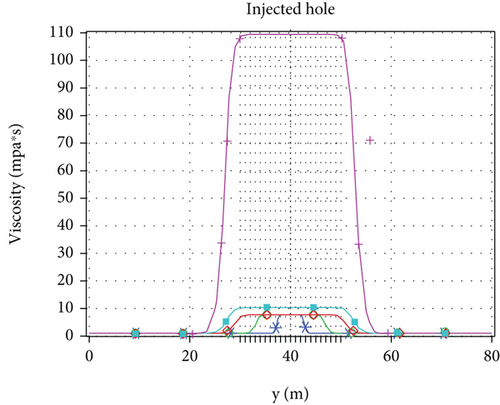
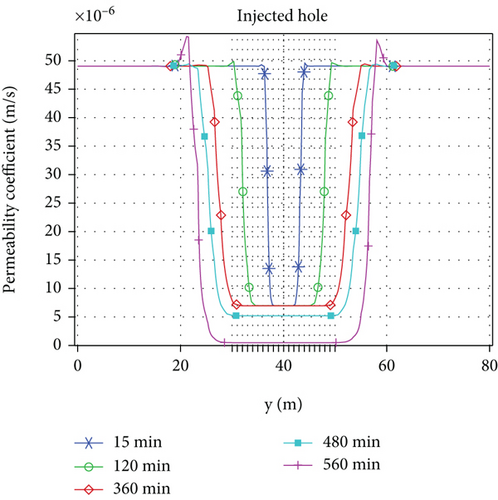
The viscosity, molar concentration, and permeability coefficient in the raw grout region remain basically unchanged at the same time. The viscosity and molar concentration in the transition region decrease with the distance from the grouting hole, while the permeability coefficient increases with the distance from the grouting hole. Moreover, when the gel time is not exceeded, the viscosity increases slowly and remains at a low level for a long time, which basically coincides with the indoor test.
The Darcy velocity at the same location decreases with the increase of time. The maximum Darcy velocity at the 15th minute is 3.21 × 10−4 m/s, the maximum Darcy velocity at the 480th minute is 1.37 × 10−4 m/s, and the maximum Darcy velocity at the 560th minute drops sharply to 1.32 × 10−5 m/s. This is closely related to the late sharp increase in viscosity.
The normal grouting radius is higher than the axial grouting radius; the normal grouting radius, the axial grouting radius, and the transition region all increase with time, but the ratio of the transition region to the grouting radius remains at 36.22%.
5.2. Effect of Grouting Pressure on the Injection Characteristics
| Number | Medium | Parameters | Unit | Value or expression |
|---|---|---|---|---|
| 1 | Geotechnical medium | Deformation modulus | [Pa] | 1.1 × 109 |
| 2 | Poisson’s ration | [1] | 0.3 | |
| 3 | Density | [kg/m3] | 2200 | |
| 4 | Cohesion | [Pa] | 0.25 × 106 | |
| 5 | Angle of internal friction | [degree] | 30 | |
| 6 | Initial porosity | [1] | 14% | |
| 7 | Initial permeability | [m2] | 5 × 10−12 | |
| 8 | Dynamic porosity | [1] | Equation (4) | |
| 9 | Dynamic permeability | [m2] | Equation (5) | |
| 10 | Grout | Viscosity | [Pa·s] | Equation (2) |
| 11 | Density | [kg/m3] | Equation (3) | |
| 12 | Molecular diffusion ∗ | [m2/s] | 1.2 × 10−11 | |
| 13 | Mechanical dispersion | [m2/h] | 8.4 × 10−4 [17] |
- Note: ∗Stocks-Einstein equation can be used to calculate molecular diffusion [31].
Under the same initial permeability of 5 D, the numerical models with a grouting pressure of 2 MPa, 1.5 MPa, and 1 MPa are calculated, respectively. As shown in Figure 6, the numerical simulation and theoretical calculation of grout frontier under different grouting pressures are presented. The normal grouting radius is slightly higher than the axial grouting radius, the axial grouting radius is significantly higher than the column theoretical value, and the column theoretical value is higher than the sphere theoretical value. With the decrease of grouting pressure, the growth rates of normal grouting radius and axial grouting radius gradually decrease. When the grouting pressure is 2 MPa and 1.5 MPa, respectively, the numerical simulation value is larger than the calculation value of column theory, and the excess value is equal to the range of the transition region. The coincidence between the axial raw grout region and the column theoretical value is high, which indicates that column theory can explain the injection characteristics of raw grout region. The range of the transition region increases with time, which is attributed to the increasing effect of mechanical dispersion and molecular diffusion. The ratio of transition region to grouting radius fluctuates slightly with time under the same grouting pressure, and the average ratio increases slightly with the decrease of grouting pressure. The grouting design of the tunnel engineering should take into account not only the scope of the raw grout region but also the affluence factor of the transition region.
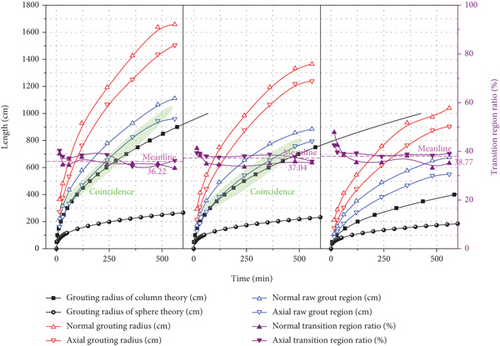
5.3. Effect of Initial Permeability on the Injection Characteristics
Under the same grouting pressure of 2 MPa, the numerical models with an initial permeability of 5 D, 0.5 D, and 0.05 D are calculated, respectively. As shown in Figure 7, the numerical simulation and theoretical calculation of grout frontier under different grouting pressures are presented.
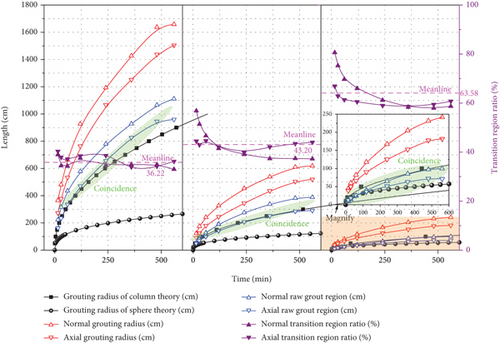
The normal grouting radius is slightly higher than the axial grouting radius, and the axial grouting radius is significantly higher than the value of column theory. With the decrease of initial permeability, the growth rates of normal and axial grouting radius decrease gradually. Under all initial permeability conditions, the axial raw grout region has a high degree of coincidence with the column theory, which indicates that the column theory can explain the injection characteristics of the axial raw grout region. And under the initial permeability of 0.05 D, the range of the raw grout region is basically equal to the calculated values of column theory and sphere theory, which indicates that in the geotechnical medium media with low permeability, the multifield coupling mechanism of permeability grouting can explain the column theory and sphere theory well. The range of the transition region increases with time. Under the initial permeability of 5 D, the fluctuation of the ratio of the transition region to grouting radius is small, and the fluctuation increases with the decrease of the initial permeability, and the average ratio increases gradually with the decrease of the grouting pressure. The results show that for the grouting of low-permeability rock and soil medium, although the grouting radius is small, the range of the concentration gradient increases. Therefore, it is necessary to make full use of this phenomenon to develop a grouting material which is easy to diffuse and disperse. In addition, the maximum grouting radius is more than 16 m, so the “super grouting” technology can be developed without affecting the construction period. The fully enclosed grouting in full section of tunnel can be completed by using only two symmetrical grouting boreholes.
6. Conclusions
- (1)
The grout range can be divided into the raw grout region and the transition region with the molar concentration of silica as the index. Viscosity, molar concentration, and permeability coefficient in the raw grout region remain basically unchanged at the same time; in the transition region, viscosity and molar concentration decrease with the distance from the grouting hole, while the permeability coefficient increases with the distance from the grouting hole
- (2)
With the decrease of grouting pressure, the growth rates of normal grouting radius and axial grouting radius will gradually decrease; due to mechanical dispersion and molecular diffusion, the range of the transition region will gradually increase with time
- (3)
The ratio of the transition region to grouting radius fluctuates slightly with time under the initial permeability of 5 D, and the fluctuation increases with the decrease of initial permeability, and the average ratio increases with the decrease of grouting pressure
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Nos. 51978668, 42002281, and 51674244), the China Postdoctoral Science Foundation (No. 2020M683155), the Natural Science Foundation of Henan Province of China (Nos. 202300410001 and 202300410002), the Research and Development Program of China Railway Group Limited (No. 2020-zhongdazhuanxiang-04), and the Science and Technology Innovation Program of China Railway Tunnel Group Co., Ltd. (No. Suiyanhe 2020-12).
Open Research
Data Availability
The data used to support the findings of this study are available from the corresponding author upon request.




