[Retracted] On the Edge Metric Dimension of Certain Polyphenyl Chains
Abstract
The most productive application of graph theory in chemistry is the representation of molecules by the graphs, where vertices and edges of graphs are the atoms and valence bonds between a pair of atoms, respectively. For a vertex w and an edge f = c1c2 of a connected graph G, the minimum number from distances of w with c1 and c2 is called the distance between w and f. If for every two distinct edges f1, f2 ∈ E(G), there always exists w1 ∈ WE⊆V(G) such that d(f1, w1) ≠ d(f2, w1), then WE is named as an edge metric generator. The minimum number of vertices in WE is known as the edge metric dimension of G. In this paper, we calculate the edge metric dimension of ortho-polyphenyl chain graph On, meta-polyphenyl chain graph Mn, and the linear [n]-tetracene graph T[n] and also find the edge metric dimension of para-polyphenyl chain graph Ln. It has been proved that the edge metric dimension of On, Mn, and T[n] is bounded, while Ln is unbounded.
1. Introduction and Preliminaries
In chemical graph theory, we use the concepts of graphs to describe the chemical structures. We can present the atomic structure of chemical compounds with the help of graphs. Atoms of molecules are expressed by the vertices of the graph and bonds of atoms are denoted by the edges. Johnson represented the new technique for graphs to show the structural changes in different chemical compounds (see [1]). The idea of metric dimension in graphs was initiated by Slater to find the location of an intruder in a network (see [2]). Harary and Melter further extended the same idea in [3]. Chartrand et al. worked on the resolvability in graphs and studied the application of drug discovery in [4]. Chartrand et al. have studied the application of chemistry by representing the distinct representations of different chemical compounds on labeled graphs (see [5]). Imran et al. discussed the application of plane graphs and calculated the metric dimension of some convex polytopes in [6]. Khuller et al. studied the application of robot navigation by using fix number of landmarks as a basis (see [7]). Caceres et al. discussed the application of games like mastermind and coin weighing and further computed the Cartesian product of graphs in [8]. Melter and Tomescu studied the application of metric dimension in digitizing an image and problems of pattern recognition (see [9]). Hallaway et al. calculated the metric dimension of graph permutations in [10]. Nadeem et al. computed the metric dimension of the ortho-polyphenyl chain, meta-polyphenyl chain, and para-polyphenyl chain graphs in [11]. Soleimani et al. computed the topological indices and polynomials for a family of linear [n]-tetracene graphs in [12]. Moreover, the resolvability of graphs was calculated by Chartrand and Zhang in [13].
Let G = (V(G), E(G)) be a simple, connected graph. The total number of edges adjacent to vertex v1 ∈ V(G) is s ∈ Z+, and then s is called degree of v1. Δ(G) and δ(G) denote the maximum and minimum degree of G, respectively. Let x1 and x2 be two distinct vertices of G, then d(x1, x2) represents the distance between them and it is defined as the number of edges in the shortest path between x1 and x2. If d(x1, v1) ≠ d(x2, v1), then we say that vertex v1 ∈ V(G) distinguishes x1, x2 ∈ V(G). If any two vertices of G can be distinguished by some vertex in W⊆V(G), then W is called metric generator of G. The cardinality of minimum W is known as the metric dimension for G, denoted by dim(G).
If for every two distinct edges e1, e2 ∈ E(G), there always exists x ∈ WE⊆V(G) such that d(e1, x) ≠ d(e2, x), then WE is named as an edge metric generator. Minimum WE is known as the edge basis for graph G and the minimum number of vertices in WE is known as the edge metric dimension denoted by edim(G). Here we represent the edge metric dimension by edim.
Zubrilina showed that the ratio of edim to usual metric is not bounded above (see [15]). Zhang and Gao computed the edim of some complex convex polytopes in [16]. Peterin and Yero calculated the edim of corona product and lexicographic of graphs in [17]. Kratica et al. worked on the edim of generalized Petersen graphs in [18]. Ahsan et al. studied the edim of circulant graphs Cn(1, k) for k = 1 and 2 (see [19]). Yang et al. calculated the edim of some families of wheel-related graphs in [20]. Wei et al. studied the edim of some complex convex polytopes in [21]. Deng et al. computed the edim of triangular, square, and hexagonal Mobius ladder networks in [22]. Ahmad et al. calculated the edim of the benzenoid tripod structure in [23]. Furthermore, Ahsan et al. computed the edim of flower graph and prism-related graphs in [24].
The following propositions are helpful throughout this article.
Proposition 1 (see [14].)For a simple, connected graph G,
- (1)
edim(G) ≥ 1 + ⌈log2 δ(G)⌉
- (2)
edim(G) ≥ ⌈log2 Δ(G)⌉
Ortho-polyphenyl chain graph On, meta-polyphenyl chain graph Mn, and para-polyphenyl chain graph Ln under topological indices have been discussed in [25]. In the present paper, we shall discuss these polyphenyl chains under the edge metric invariant.
The rest of the paper is explicit as follows. The edim of ortho-polyphenyl chain graph On, meta-polyphenyl chain graph Mn, the linear [n]-tetracene graph T[n], and the para-polyphenyl chain graph Ln are calculated in Sections 2, 3, 4, and 5, respectively. In the last section, the conclusion of the article is stated.
2. Edge Metric Dimension of Ortho-Polyphenyl Chain On
In this section, we will find the edim(On). The graph On has V(On) = {wi, vi, ui : 1 ≤ i ≤ 2n} and E(On) = {v2i+1w2i+1, w2i+1w2i+2, w2i+2v2i+2, v2i+2u2i+2, u2i+1u2i+2, v2i+1u2i+1, u2ju2j+1 : 0 ≤ i ≤ n − 1,1 ≤ j ≤ n − 1}. The graph On for n = 4 is shown in Figure 1.
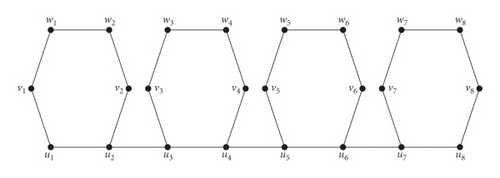
Now, we will find the edge dimension of ortho-polyphenyl chain On.
Theorem 2. For n ≥ 2, edim(On) is 2.
Proof. Let WE = {v1, u2n} ⊂ V(On), we will prove that WE is an edge basis of On. For this, each edge of On is represented in the following:
-
-
-
-
-
r(u2i+1u2i+2|WE) = (2i + 1,2n − 2i − 2) for n − 1 ≥ i ≥ 0
-
r(v2i+2u2i+2|WE) = (2i + 2,2n − 2i − 2) for n − 1 ≥ i ≥ 0
-
r(u2iu2i+1|WE) = (2i, −1 + 2n − 2i) for n − 1 ≥ i ≥ 0
We see that no two tuples have the same representations. This proves that edim(On) ≤ 2. Since by Proposition 1, edim(On) ≥ 2. Hence, edim(On) = 2.
3. Edge Metric Dimension of Meta-Polyphenyl Chain Mn
In this section, we will find the edim(Mn). The graph Mn has V(Mn) = {wi, vi, ui : 1 ≤ i ≤ 2n} and E(Mn) = {u2i+2w2i+2, u2i+1w2i+2, v2i+1u2i+1, v2i+1w2i+1, w2i+1v2i+2, v2i+2u2i+2, u2j+2u2j+3 : 0 ≤ i ≤ n − 1,0 ≤ j ≤ n − 2}. The graph Mn for n = 5 is shown in Figure 2.
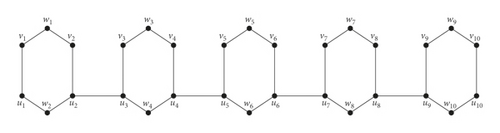
Now, we will find the edge dimension of meta-polyphenyl chain Mn.
Theorem 3. For n ≥ 2, edim(Mn) is 2.
Proof. Let WE = {w2, u2n} ⊂ V(Mn), we will prove that WE is an edge basis of Mn. For this, each edge of Mn is represented in the following:
-
-
-
-
-
-
-
r(u2i+2u2i+3|WE) = (3i + 1,3n − 3i − 5) for 0 ≤ i ≤ n − 2
We see that no two tuples have the same representations. This proves that edim(Mn) ≤ 2. Since by Proposition 1, edim(Mn) ≥ 2. Hence, edim(Mn) = 2.
4. Edge Metric Dimension of the Linear [n]-Tetracene
In this section, we will find the edim(T[n]). The graph T[n] has V(T[n]) = {vi, ui, wj : 1 ≤ i ≤ 5n, 1 ≤ j ≤ 8n} and . The graph T[n] for n = 3 is shown in Figure 3.
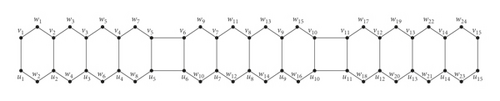
We will find the edge dimension of linear [n]-tetracene T[n].
Theorem 4. For n ≥ 2, edim(T[n]) is 2.
Proof. Let WE = {v1, v5n} ⊂ V(T[n]), we have to prove that WE is an edge basis of T[n]. For this, each edge of T[n] is represented in the following:
-
r(v5i+1w8i+1|WE) = (9i, 9n − 9i − 2) for 0 ≤ i ≤ n − 1
-
r(v5i+2w8i+3|WE) = (9i + 2,9n − 9i − 4) for 0 ≤ i ≤ n − 1
-
r(v5i+3w8i+5|WE) = (9i + 4,9n − 9i − 6) for 0 ≤ i ≤ n − 1
-
r(v5i+4w8i+7|WE) = (9i + 6,9n − 9i − 8) for 0 ≤ i ≤ n − 1
-
r(w8i+1v5i+2|WE) = (9i + 1,9n − 9i − 3) for 0 ≤ i ≤ n − 1
-
r(w8i+3v5i+3|WE) = (9i + 3,9n − 9i − 5) for 0 ≤ i ≤ n − 1
-
r(w8i+5v5i+4|WE) = (9i + 5,9n − 9i − 7) for 0 ≤ i ≤ n − 1
-
r(w8i+7v5i+5|WE) = (9i + 7,9n − 9i − 9) for 0 ≤ i ≤ n − 1
-
r(v5i+2u5i+2|WE) = (9i + 2,9n − 9i − 3) for 0 ≤ i ≤ n − 1
-
r(v5i+3u5i+3|WE) = (9i + 4,9n − 9i − 5) for 0 ≤ i ≤ n − 1
-
r(v5i+4u5i+4|WE) = (9i + 6,9n − 9i − 7) for 0 ≤ i ≤ n − 1
-
r(v5i+5u5i+5|WE) = (9i + 8,9n − 9i − 9) for 0 ≤ i ≤ n − 1
-
r(u5i+2w8i+2|WE) = (9i + 2,9n − 9i − 2) for 0 ≤ i ≤ n − 1
-
r(u5i+3w8i+4|WE) = (9i + 4,9n − 9i − 4) for 0 ≤ i ≤ n − 1
-
r(u5i+4w8i+6|WE) = (9i + 6,9n − 9i − 6) for 0 ≤ i ≤ n − 1
-
r(u5i+5w8i+8|WE) = (9i + 8,9n − 9i − 8) for 0 ≤ i ≤ n − 1
-
r(u5i+1w8i+2|WE) = (9i + 1,9n − 9i − 1) for 0 ≤ i ≤ n − 1
-
r(u5i+2w8i+4|WE) = (9i + 3,9n − 9i − 3) for 0 ≤ i ≤ n − 1
-
r(u5i+3w8i+6|WE) = (9i + 5,9n − 9i − 5) for 0 ≤ i ≤ n − 1
-
r(u5i+4w8i+8|WE) = (9i + 7,9n − 9i − 7) for 0 ≤ i ≤ n − 1
-
r(v5i+1u5i+1|WE) = (9i, 9n − 9i − 1) for 0 ≤ i ≤ n − 1
-
r(v5iv5i+1|WE) = (9i − 1,9n − 9i − 1) for 1 ≤ i ≤ n − 1;r(u5iu5i+1|WE) = (9i, 9n − 9i) for 1 ≤ i ≤ n − 1
Since every two tuples have different representations. This proves that edim(T[n]) ≤ 2. Since by Proposition 1, edim(T[n]) ≥ 2. Hence, edim(T[n]) = 2.
5. Edge Metric Dimension of Para-Polyphenyl Chain Ln
In this section, we will find the edim(Ln). The graph Ln has V(Ln) = {vi, wi, ui : 1 ≤ i ≤ 2n} and E(Ln) = {w2i+1v2i+1, v2i+1v2i+2, v2i+2w2i+2, w2i+2u2i+2, u2i+1u2i+2, u2i+1w2i+1, w2jw2j+1 : 0 ≤ i ≤ n − 1,1 ≤ j ≤ n − 1}. The graph Ln for n = 6 is shown in Figure 4.
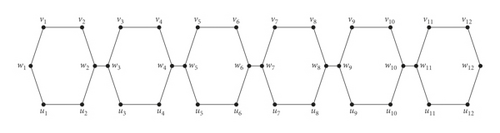
Now, we will find the edge dimension of para-polyphenyl chain Ln.
Lemma 5. Let Y = {v1, v2, v3, …, v2n}⊆V(Ln). Then any edge metric generator WE of Ln has at least n vertices of Y.
Proof. Suppose on contrarily that WE has at most n − 1 vertices of Y. Without loss of generality for 1 ≤ k ≤ n, we assume that v2k−1, v2k ∉ WE, and then we have (v2k−1v2k|WE) = (u2k−1u2k|WE), (v2k−1w2k−1|WE) = (u2k−1w2k−1|WE), and (v2kw2k|WE) = (u2kw2k|WE), so we get a contradiction.
Remark 5. Let WE is an edge basis of Ln. For all n, WE contains all vertices of Y having vertex indices odd.
Theorem 5. For n ≥ 2, we have
Proof. Let WE = {v1, v3, v5, …, v2n−1}. We will prove that WE is an edge basis of Ln.
For 3 ≤ k ≤ n, let W1 = {v1, v3, v2k−1}. Now, each edge representation of Ln with respect to W1 is given in the following:
From above representation we see that (v2i−1v2i|W1) = (u2i−1u2i|W1), (v2i−1w2i−1|W1) = (u2i−1w2i−1|W1) and (v2iw2i|W1) = (u2iw2i|W1) when 1 ≤ i ≤ n and i ≠ 1,2, k and no other edges have same representation. If we take 1 ≤ i ≤ n and i ≠ 1,2, k such that , (v2i−1w2i−1|W1 ∪ {v2i−1}) ≠ (u2i−1w2i−1|W1 ∪ {v2i−1}) and (v2iw2i|W1 ∪ {v2i−1}) ≠ (u2iw2i|W1 ∪ {v2i−1}). It follows that (v2i−1v2i|WE) ≠ (u2i−1u2i|WE), (v2i−1w2i−1|WE) ≠ (u2i−1w2i−1|WE), and (v2iw2i|WE) ≠ (u2iw2i|WE) for 1 ≤ i ≤ n. So from Lemma 5 and Remark 5, WE is an edge basis for Ln and edim(Ln) = n.
6. Conclusion
In this paper, we have calculated the edim of ortho-polyphenyl chain graph On, meta-polyphenyl chain graph Mn, linear [n]-tetracene graph T[n], and the para-polyphenyl chain graph Ln. It has been proved that the edim of these polyphenyl chain graphs is constant while the para-polyphenyl chain graph Ln has unbounded.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Open Research
Data Availability
The data used to support the findings of this study are available from the corresponding author upon request.