The Application of Tree-Based Algorithms on Classifying Shunting Yard Departure Status
Abstract
Shunting yards are one of the main areas impacting the reliability of rail freight networks, and delayed departures from shunting yards can further also affect the punctuality of mixed-traffic networks. Methods for automatic detection of departures, which are likely to be delayed, can therefore contribute towards increasing the reliability and punctuality of both freight and passenger services. In this paper, we compare the performance of tree-based methods (decision trees and random forests), which have been highly successful in a wide range of generic applications, in classifying the status of (delayed, early, and on-time) departing trains from shunting yards, focusing on the delayed departures as the minority class. We use a total number of 6,243 train connections (representing over 21,000 individual wagon connections) for a one-month period from the Hallsberg yard in Sweden, which is the largest shunting yard in Scandinavia. Considering our dataset, our results show a slight difference between the application of decision trees and random forests in detecting delayed departures as the minority class. To remedy this, enhanced sampling for minority classes is applied by the synthetic minority oversampling technique (SMOTE) to improve detecting and assigning delayed departures. Applying SMOTE improved the sensitivity, precision, and F-measure of delayed departures by 20% for decision trees and by 30% for random forests. Overall, random forests show a relative better performance in detecting all three departure classes before and after applying SMOTE. Although the preliminary results presented in this paper are encouraging, future studies are needed to investigate the computational performance of tree-based algorithms using larger datasets and considering additional predictors.
1. Introduction
The “single wagonload” railway traffic has the potential to increase the modal share of rail freight transportation in Europe. The single wagonload traffic refers to wagonload shipments transported through a series of trains and shunting yards, instead of just on one train, from origin to destination [1]. In Europe, almost two-thirds of the single wagonload traffic is international; thus, promoting the single wagonload traffic can contribute to the economic growth of Europe by increasing international trades [2]. However, a recent study of 13 key countries of Europe showed that the single wagonload traffic shares only 27% of the total rail freight volume [2]. In fact, the single wagonload traffic loses a great part of its market to its road counterpart, particularly for small/medium shipments, due to low service reliability.
The low service reliability stems from the nature of single wagonload operations; wagons are detached from one train and attached to another train to continue their trip in typically large shunting yards. In European railways, shunting yard operations are high-priced from cost and time perspectives; in terms of costs, shunting and marshalling operations comprise 22% of the transport chain costs [2], and in terms of transit time, around 10–50% of the total transit time of freight trains is spent at shunting yards [3].
Increasing the predictability of shunting yard operations can improve the service reliability of single wagonload railway. The main outcome of shunting yard operations is punctual train departures, and the predictability of train departures can be beneficial for both shunting yard operators and infrastructure managers. The former can use departure predictions to enhance shipment delivery times, whereas the latter can use it for improved planning of the interactions between the shunting yard departures and the punctuality of other trains on the line. Previously, shunting yards were considered as single entities to operate effectively without considering any interaction with the rest of the railway network. In recent years, however, the importance of analyzing the interaction between shunting yards and the railway network has increased [4, 5]. In fact, shunting yards are in constant interaction with the rest of the railway network; the lack of punctuality in receiving trains from the railway network can hinder train formations in shunting yards. On the contrary, the lack of punctuality in dispatching trains to the railway network may impact the punctuality of other trains in the railway network. In American railways, it was shown that the arrival time flexibility to shunting yards increases the average wagon dwell time and leads to wagons missing their departing train connections [5]. In European railways, a series of large-scale collaborative projects have been launched to model shunting yard-network interactions [4].
Predicting delayed departures from shunting yards, which is the focus of this paper, is clearly an important problem. In conjunction with the recent studies above, we therefore propose the application of tree-based machine learning algorithms to classify the status of departures from shunting yards. The approach presented in this paper is a preliminary step towards implementing an elaborate machine learning approach for departure delay prediction from shunting yards.
2. Related Work
The availability of large datasets in railways has led to the application of data-driven approaches for comprehensive railway operation analysis [6]. One of the methods to evaluate the quality of railway operations is combining the punctuality and delay measures [7], which has been studied extensively in three main areas: the prediction of train events, the prediction of train delays, and the propagation of train delays. In the prediction of train events, the main focus is on estimating running and dwelling times from predicting departure and arrival events [8, 9]. Delay prediction models aim at predicting primary delays of train arrivals and/or departures [10, 11]. Train delay propagation models express the development of secondary delays throughout a train journey by analyzing the impact of events, such as meetings and overtakings [12–14].
Since the scope of this paper is related to departure delay prediction models, a brief overview of the most relevant works is presented below. Previous research in this area has mainly focused on the arrival time estimation of passenger trains using data-driven approaches.
Wang and Work [15] proposed a historical regression model to predict passenger train delays before the beginning of the train trips in the US; the model was extended also to predict real-time delays using information from the previous stations and other trains on a corridor. Using data from Iranian railways, Yaghini et al. [16] showed that neural networks perform better than decision trees and multinomial logistic regression models in terms of training time and prediction accuracy. Marković et al. [10] were the first to apply the support vector regression for predicting passenger train arrival delays. Using data from Serbian railways, they concluded that results obtained from the support vector regression performed better than artificial neural networks. Oneto et al. [17–20] provided an extensive study of big data analytics implemented in a train delay prediction system for large-scale railway networks with data from Italian railways. In their papers, they proposed the application of shallow and deep extreme learning machines for trains’ delays. Nair et al. [21] developed a large-scale ensemble passenger train delay model in German railways. By combining a statistical random forest-based model, a kernel regression model, and a mesoscopic simulation model, they demonstrated a 25% improvement potential in the prediction accuracy and 50% reduction in root mean squared errors compared to the published schedule.
Although the number of studies using data-driven approaches for passenger train delays is substantial, the application of these approaches for the freight train delay prediction is quite recent. The main reason is that passenger and freight trains differ inherently in stopping patterns, dispatching priority, and train characteristics. In general, implementing delay prediction models for freight trains in mixed railway networks is more complex due to the prioritized running of passenger trains [22]. This prioritization sometimes imposes initial departure delays and/or long meeting and overtaking times during freight train runs, which may lead to delayed arrivals as well, all of which are complicated to mathematically grasp in a delay prediction model for freight trains. Apart from this, freight train operators may not be willing to share the operational data, as it may contain commercially sensitive information.
In a freight train delay context, Gorman [23] applied econometric methods for predicting congestion delays using data from the US. Barbour et al. [24] implemented a support vector regression model for estimating train arrival (ETAs) of individual freight trains. They achieved an improvement of 21% over a baseline prediction method at some locations and average 14% across the study area. Later, Barbour et al. [11] compared the predictive performance of linear and nonlinear support vector regression, random forest regression, and deep neural network models using data from the US. They showed that the maximum ETA error reduction of support vector machines and deep neural networks was 26% better than a statistical baseline predictor. They achieved the best performance in the random forest models, which achieved an error reduction of 60% compared to the baseline predictor at some points, and an average error reduction of 42%.
So far, studies on freight train delays have been dedicated to arrival delays, whereas the nature of departure and arrival delays differ for freight trains [25]. Arrival delays are the result of the accumulation of delays along the train journey, whereas departure delays are the result of shunting yard improper functioning. In Sweden, delayed departures from shunting yards were one of the five main causes of delays due to operator error [26].
3. Method
In this section, the data, the specifics of the shunting yard departure status prediction problem, the application of supervised machine learning, and the two applied machine learning methods (decision trees and random forests) are presented.
3.1. Data
In this paper, we combine two different datasets from the Hallsberg yard in Sweden, the largest shunting yard in Scandinavia, provided by the main yard operator in Sweden. Hallsberg has the conventional European shunting yard characteristics [27] and layout, which comprises of three subyards for arrivals, classification, and departures, respectively (see Figure 1). Trains are received in the arrival yard, where their wagons are then decoupled. Then, via a hump (a small hill), the wagons are rolled to the classification yard, where the arrangement of wagons is changed to form new trains for new destinations. When departing trains are ready, they are sent to the departing yard, where the locomotive is attached and the train is prepared to be dispatched to the network.

The first dataset used in this paper is a wagon connection dataset, which gives the information about connections between arriving and departing trains, in particular, information on which wagon arrived in which train and departed by which train. The total number of connections between an arriving train and a departing train were 6,243 (representing 21,381 wagon connections) in a one-month period, October 2015. The second dataset contains train punctuality data giving the actual arrival and departure times of trains in minutes.
As the obtained datasets did not cover a large number of parameters, the predictors that could be extracted from these two datasets for modelling were limited, but chosen to represent the performance of the three subyards to a reasonable extent. Table 1 shows the selected predictors for each subyard.
| Subyard | Predictors |
|---|---|
| Arrival | Scheduled arrival time |
| Scheduled arrival date | |
| Actual arrival time | |
| Actual arrival date | |
| Arriving train number | |
| Train arrival time deviation | |
| Classification | Wagon standing time |
| Departure | Scheduled departure time |
| Scheduled departure date | |
| Actual departure time | |
| Actual departure date | |
| Departing train number | |
In Swedish practice, freight train departures are typically classified as early, on-time, or delayed. In particular, any train departing before their scheduled departure time is classified as early, and shunting yard operators are allowed to dispatch trains early provided that there is free capacity slot on the line. This is a common practice in Swedish railways to compensate for further disturbances that might occur during a freight train run. Trains that depart with a delay of at most five minutes from their scheduled departure time are furthermore classified as on-time. Any deviation over five minutes from the scheduled departure time indicates a delayed departure.
3.2. Problem Definition
- (i)
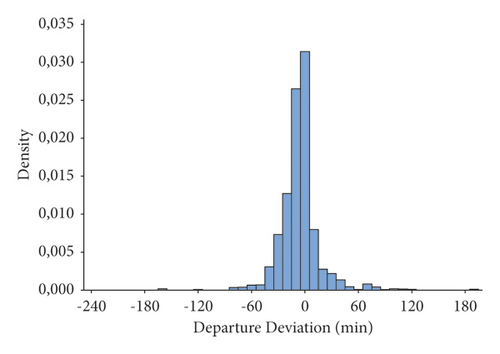
Departure deviations typically have long tails, and depicting the histogram of departure deviations shows the long tails in both positive and negative values (see Figure 2). It is already difficult to fit a probability distribution to such deviations, and they are notoriously difficult to model in machine learning. Because of this, performance generally suffers when the data exhibit this characteristic.
- (ii)
The departure status classes show great disparity. For example, as shown in Figure 3, the majority of departures in the considered dataset are early (65%), whereas the share of on-time (19%) and delayed departures is almost similar (15%). This disparity makes the dataset imbalanced and makes predictions biased towards the majority class. This is discussed further in Section 3.5.
- (iii)
Shunting yard operations are highly human-dependent, and almost all disturbances in shunting yard operations are handled by the shunting personnel. However, most of these human interventions are not discernible in the dataset. This makes the modelling process difficult since we cannot allocate proper model parameters to these human interventions. Furthermore, in later stages of the modelling, this potential source of error makes a proper interpretation of any predictions much harder to do.

In the big picture, shunting yard departure prediction can be decomposed into different levels with different priorities from the shunting yard operator and infrastructure manager perspectives. The first level is to classify the departure status; delayed departures comprise a small part of the dataset, but are critical for both the shunting yard operator and the infrastructure manager. In addition, delayed departures have a different distribution from early departures [25, 28], which may result in distinct models for delayed departures. Once delayed departures are classified, the actual delay can be predicted in the second level [21]. In the third level, delayed departures can be mitigated by re-booking delayed wagons to different trains in order to minimize the departure delays. This paper considers only modelling and evaluation of the first level, i.e., classification of departure status.
3.3. Supervised Machine Learning for Shunting Yard Departure Status Prediction
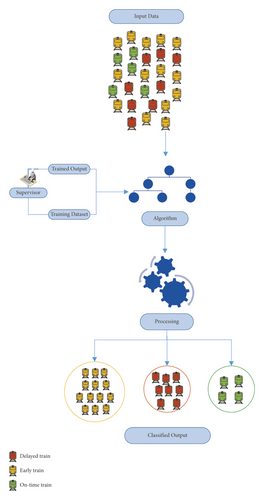
We applied the concept of supervised learning to predict shunting yard departure status using the KNIME analytics platform [29]. For our specific problem, the supervised learning can be described as follows. We implement a machine learning model by taking a set of training data on departing trains’ parameters with known departure status. Then, we minimize a prediction error for predicting the output which classifies the departure status into delayed, early, or on-time classes using another part of the data called test data; this process is depicted schematically in Figure 4.
3.3.1. Decision Tree
Decision trees are based on a hierarchy of if/else questions resulting in a decision. A tree is made up of nodes and branches; each node represents either a question about an input feature or an end node (a leaf which is associated to a class). At each node, the data is branched on an input feature generating two or more branches. As the tree develops, more branches partition the original data; this procedure is continued until no further branches are possible. The final goal of a decision tree algorithm is to partition the training dataset into subsets until each partition is either “pure” (containing only samples of one class) in terms of the target class or sufficiently small.
3.3.2. Random Forest
Random forest is an ensemble version of decision trees; ensemble methods compound different machine learning models to overcome the low performance of each model and create a robust model. Therefore, a random forest is a collection of decision trees, where each decision tree is trained on a subset of the original dataset. Each tree might perform well on a subset of the dataset, but it might overfit on a part of the subset. Therefore, combining various trees which perform well but overfit in different parts of the data can decrease the overfitting by averaging the results, while maintaining the predictive ability of each tree.
3.4. Resampling Procedure and Splitting Criteria
Resampling techniques are used to estimate model performance; by resampling, the model is trained by a subset of data and the rest of data is used to evaluate the model efficiency. The method in which the subsets are resampled is important to overcome bias and variance of the model generalization. We applied a common 10-fold cross-validation for the resampling procedure [31]. After sampling, we specify how to partition the data to reach the purest subset, where a pure group contains a larger proportion of one class in each node. Purity can be achieved by maximizing accuracy or minimizing misclassification error. However, in maximizing accuracy, the focus is on partitioning the data with minimal misclassification, whereas in maximizing purity, we mainly aim at partitioning the data by placing the samples in one particular class. The Gini index [32] is a measure that focuses on purity and is often used for this purpose. Basically, at each partitioning step, the split point value that minimizes the impurity is selected. In this paper, we use the formulation in [31] for calculating the Gini index.
3.5. Decision Tree and Random Forest Improved by SMOTE
In many classification problems, some classes are typically more important for the modeller than others, but the number of instances of those classes in the dataset is in minority. Examples from the railway domain include classification of maintenance needs for vehicles or track and signaling equipment. When using machine learning, this situation may lead to imbalanced learning, when a majority of the instances are erroneously predicted to belong to the majority class. Imbalanced learning can be combated through three different approaches: problem redefinition, data-level approaches, or algorithm-level approaches [33]. In our dataset, the majority of the instances are early trains. To examine the model performance considering the imbalanced dataset, we applied the data-level sampling technique called synthetic minority oversampling technique (SMOTE) for training the model. SMOTE oversamples the data from the minority classes by averaging on a number of the nearest neighbours [33]. In this paper, we used 15 nearest neighbors and oversampled the delayed and on-time minority classes.
3.6. The Evaluation Criteria
There are various criteria for evaluating the performance of a machine learning model. The selection of these criteria depends on the purpose of the model and the modeller’s choice. In our model, the primary interest is to have an acceptable performance on the delayed class, and the secondary interest is to evaluate how good the model performance is on classifying all three classes. Therefore, we used the confusion matrix to compare the results of each model. The confusion matrix summarizes whether the observed instances are correctly or incorrectly classified. In general, the table cells indicate the number of the true positives (TP: correctly classified in the positive class), false positives (FP: incorrectly classified in the positive class), true negatives (TN: correctly classified in the negative class), and false negatives (FN: incorrectly classified in the negative class). Table 2 shows a schematic view of the confusion matrix to classify the delayed class. Here, the delayed class is the positive class and the two other classes are the negative ones. The same procedure is conducted for the two other classes.
| Observed | Classified | ||
|---|---|---|---|
| Delayed | Early | On-time | |
| Delayed | TP | FN | FN |
| Early | FP | TN | TN |
| On-time | FP | TN | TN |
To evaluate how the model performs on a single-class level, we calculated precision, sensitivity, specificity, and F-measure. To evaluate the overall performance on a multiclass level, we calculated overall accuracy and Cohen’s Kappa [31].
Overall accuracy is calculated by dividing the total number of correctly classified instances to the total number of instances. Overall accuracy does not make any distinction between classes and evaluates overall results.
The model predictions and actual class values are assumed to be independent, and Pe sums Pe of all classes in equation (6), where Pei,actual is the proportion of actual class values (TP + FN) from the total number of instances and Pei,predicted is the proportion of predicted class values (TP + FP) from the total number of instances [34]. In equation (5), Po − Pe shows the difference between the observed overall accuracy of the model and the overall accuracy that can be obtained by chance, and 1 − Pe stands for the maximum value for this difference. Cohen’s Kappa lies between 0 and 1. When the observed difference and the maximum difference are close to each other, Cohen’s Kappa is close to 1 representing a good model, whereas in a random model, the overall accuracy depends on the random chance, so the difference Po − Pe is zero, and Cohen’s Kappa is 0.
Overall, when Cohen’s Kappa is closer to 0, the agreement between the actual classes and predicted classes is lower, whereas the closer it is to 1, the agreement between the actual classes and predicted classes is higher. In general, Cohen’s Kappa can be interpreted, as shown in Table 3 [35].
| κ | Interpretation |
|---|---|
| 0 | Agreement equivalent to chance |
| 0.10 − 0.20 | Slight agreement |
| 0.21 − 0.40 | Fair agreement |
| 0.41 − 0.60 | Moderate agreement |
| 0.61 − 0.80 | Substantial agreement |
| 0.81 − 0.99 | Near-perfect agreement |
| 1 | Perfect agreement |
4. Results and Discussion
We implemented the models in the KNIME analytics platform [29]. Table 4 compares results from all four models. First, we discuss the results for the delayed class since it is the primary interest of this paper. Then, we discuss the generality of the model in classifying all three classes.
| Model | Class | True positives | False positives | True negatives | False negatives | Sensitivity (%) | Precision (%) | Specificity (%) | F-measure (%) | Cohen’s Kappa | Overall accuracy (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Decision tree | Delayed | 308 | 486 | 4778 | 633 | 33 | 39 | 91 | 35 | 0.28 | 64 |
| Early | 3195 | 1097 | 1051 | 862 | 79 | 74 | 49 | 76 | |||
| OnTime | 499 | 620 | 4378 | 708 | 41 | 45 | 88 | 43 | |||
| Decision tree (SMOTE) | Delayed | 2084 | 1450 | 6664 | 1973 | 51 | 59 | 82 | 55 | 0.42 | 61 |
| Early | 3090 | 1516 | 6598 | 967 | 76 | 67 | 81 | 71 | |||
| OnTime | 2297 | 1734 | 6380 | 1760 | 57 | 57 | 78 | 56 | |||
| Random forest | Delayed | 262 | 267 | 4997 | 679 | 28 | 49 | 95 | 36 | 0.39 | 72 |
| Early | 3644 | 1162 | 986 | 413 | 90 | 76 | 46 | 82 | |||
| OnTime | 592 | 278 | 4720 | 615 | 49 | 68 | 94 | 57 | |||
| Random forest (SMOTE) | Delayed | 2323 | 1158 | 6956 | 1734 | 57 | 67 | 86 | 62 | 0.53 | 68 |
| Early | 3419 | 1425 | 6689 | 638 | 84 | 71 | 82 | 77 | |||
| OnTime | 2580 | 1266 | 6848 | 1477 | 64 | 67 | 84 | 65 | |||
Delayed departures comprise a small portion of the departures, which makes their predictability difficult; comparing the decision tree and random forest models before using SMOTE shows this difficulty in terms of sensitivity and precision parameters. The models detect approximately one third of the delayed departures (33% for the decision tree model and 28% for the random forest model). The models are further not precise enough to assign the delayed departures to the delayed class; precision of the two models are slightly better than the sensitivity: 39% and 49% for decision tree and random forest, respectively.
In our model evaluation, both sensitivity and precision are important parameters to evaluate the model in detecting and assigning the positive instances. However, F-measure, the combination of these two parameters, shows similar low performance of the two models: decision tree (35%) and random forest (36%). In problems with imbalanced data, F-measure is an appropriate measure to compare the models. However, when we examine F-measure to compare the decision tree and random forest, in terms of the generalization for all three classes, we see the disparity between the F-measures for the three classes. The imbalanced dataset makes it difficult to select between the two models; the F-measure is high for the majority class 76% in decision tree and 82% in random forest and very low for minority classes.
The imbalanced proportion of the class instances reflects the low performance of the decision tree and random forest, especially in the delayed class. Therefore, the results are also compared after having imbalanced data modified by SMOTE. For the delayed class, in the decision tree model, an improvement of 18% in sensitivity and 20% in precision is observed. The improvement for random forest in these two parameters is 29% and 28%, respectively. The F-measure is also improved with almost the same proportion, 20% for decision trees with SMOTE and 26% for the random forest with SMOTE. Using SMOTE mainly balanced the F-measure in the three classes in both models, which shows that models are improved in terms of overall classification of the three classes after having applied SMOTE. The major improvement that SMOTE made to both models was balancing the specificity in all three classes which means that the models assign the same proportion of false positives to the three classes. However, it is observed that specificity and sensitivity for all three classes are inversely related, which is often the case in classification problems with imbalanced classes. In general, selecting the optimal balance between sensitivity and specificity in a classification model is dependent on the goal of the classification purpose. In this paper, the main interest was on the minority class of delayed departures.
Considering the small initial dataset of one month and the specific purpose of this paper, we concluded two main conjectures: first, using tree-based algorithms to classify departures without treating the imbalanced data may not give a satisfactory level of sensitivity and precision, especially for the minority class. In addition, random forest as an ensemble method showed better results than a single decision tree model. The results from an ensemble model are preferred as they reduce the bias and variance. This is also reflected in the measure of Cohen’s Kappa for the random forest model with SMOTE at 0.53, which shows moderate agreement between the predicted classes and the actual classes. It is worthy to note that overall accuracy does not show much improvement after applying SMOTE in models since overall accuracy does not reflect the imbalanced classes. Thus, it may not be an adequate criteria in our model assessment.
The final point of reflection is the predictors used for classification. We used a small set of predictors that were present in our dataset. These predictors may not represent departures entirely. There are other predictors that may have more impact on the departures, such as weather condition parameters, train characteristics, and the experience level of shunting yard operator staff. One of the limitations in studying shunting yards is the complexity of obtaining these data; shunting yards have security importance for infrastructure managers; in addition, shunting yard operators may not be willing to share most of their data due to business-related issues.
5. Conclusion
n this paper, we discussed the problem of classifying departure status from shunting yards as a first step to implement an elaborate departure prediction model for shunting yards in the future. Departure status from shunting yards impact the punctuality of other trains on the network. A delayed departure from the shunting yard may delay consequent freight train departures or interfere with passenger trains running on the line connected to the shunting yard. Additionally, delayed departures from shunting yards can mostly lead to delayed arrivals to the next shunting yard causing delayed shipment delivery and customer loss for rail freight operators. One of the main advantages of shunting yard departure prediction models is assisting infrastructure managers in improved allocation of capacity on the lines connected to the shunting yards. Particularly, in a railway context such as Swedish railways, where the infrastructure manager and yard operator are two different stakeholders, the infrastructure manager requires more transparency from the yard operation side to control its impact on the punctuality of the network. On the contrary, these models help shunting yard operators to become more agile in better utilization of train capacity when re-planning of wagons is required due to missed connections. However, there is a lack of practical models for shunting yard departure prediction in the previous literature; to the best of our knowledge, no previous research has been conducted to predict the status of departures from shunting yards.
We aimed at comparing the performance of tree-based (decision tree and random forest) algorithms which have shown an overall adequate performance in comparison with other machine learning algorithms on delay prediction in the previous research. Typically, the departure status from shunting yards are imbalanced; delayed departures are in minority, whereas they are arguably much more important to predict. Our results showed that decision trees and random forests both require oversampling to improve the sensitivity and precision in classifying delayed departures. Applying the synthetic minority oversampling technique (SMOTE) in both models improved the sensitivity, precision, and F-measure of delayed departures. The improvement was approximately 20% for decision tree and 30% for random forest. We achieved the overall best results using the random forest algorithm improved by SMOTE. By applying SMOTE to our small case study, we showed how promising tree-based algorithms can be for departure status prediction when larger datasets are available.
Hence, we propose future directions that can contribute to improved insight into shunting yard departure status prediction. First, it would be beneficial to examine the computational performance of decision tree and random forest algorithms using larger datasets. Second, there are other predictors that affect shunting yard departures; adding operational parameters, train characteristics parameters, weather condition parameters, and parameters representing shunting yard staff performance may enhance the accuracy of the models. Third, future attempts can use shunting yard departure status models to develop models for predicting the actual departure time deviations. Such models can then be combined with network simulation models to analyze the overall shunting yard-network interactions.
Disclosure
Some of the results presented in this paper have previously been presented in the final deliverable of the European FR8HUB project [30].
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
The authors would like to thank Magnus Wahlborg and Fredrik Lundström from the Swedish Transport Administration (Trafikverket) for their continuous support during the time of conducting this research and Jonatan Gjerdrum from Green Cargo for providing the data and sharing his expertise to improve our analysis. This research was supported by Trafikverket (the Swedish Transport Administration) (Grant no. TRV2017/68055) and FR8HUB Project within the European H2020-Shift2Rail IP5 (Grant agreement no. 777402—FR8HUB—H2020-S2RJU-2017/H2020–S2RJU-CFM-2017).
Open Research
Data Availability
The data used to support the findings of the study are available from the corresponding author upon request.




