Volume 2021, Issue 1 3143024

Research Article

Open Access

Quantitative Identification of the Water Resistance Capacity of Composite Strata in Mining Coal Seam Floors

Xinyi Wang

orcid.org/0000-0002-1730-1753

Institute of Resources & Environment, Henan Polytechnic University, Jiaozuo 454000, China hpu.edu.cn

Collaborative Innovation Center of Coalbed Methane and Shale Gas for Central Plains Economic Region, Jiaozuo 454100, China

Collaborative Innovation Center of Coal Work Safety and Clean High Efficiency Utilization, Jiaozuo 454100, China

Search for more papers by this author

Fang Li,

Fang Li

orcid.org/0000-0002-4291-8114

Institute of Resources & Environment, Henan Polytechnic University, Jiaozuo 454000, China hpu.edu.cn

Search for more papers by this author

Qi Wang,

Corresponding Author

Qi Wang

[email protected]

orcid.org/0000-0001-9908-3392

College of Geosciences and Engineering, North China University of Water Resources and Electric Power, Zhengzhou 450045, China ncwu.edu.cn

Search for more papers by this author

Bo Chen,

Bo Chen

Institute of Resources & Environment, Henan Polytechnic University, Jiaozuo 454000, China hpu.edu.cn

Search for more papers by this author

Yu Zou,

Yu Zou

Jiangmen Branch Bureau of Hydrology, Guangdong Provincial Bureau of Hydrology, Jiangmen 529000, China

Search for more papers by this author

Bo Zhang,

Bo Zhang

Institute of Energy and Chemical Industry, China Pingmei Shenma Group, Pingdingshan 467000, China

Search for more papers by this author

Xinyi Wang,

Xinyi Wang

orcid.org/0000-0002-1730-1753

Institute of Resources & Environment, Henan Polytechnic University, Jiaozuo 454000, China hpu.edu.cn

Collaborative Innovation Center of Coalbed Methane and Shale Gas for Central Plains Economic Region, Jiaozuo 454100, China

Collaborative Innovation Center of Coal Work Safety and Clean High Efficiency Utilization, Jiaozuo 454100, China

Search for more papers by this author

Fang Li,

Fang Li

orcid.org/0000-0002-4291-8114

Institute of Resources & Environment, Henan Polytechnic University, Jiaozuo 454000, China hpu.edu.cn

Search for more papers by this author

Qi Wang,

Corresponding Author

Qi Wang

[email protected]

orcid.org/0000-0001-9908-3392

College of Geosciences and Engineering, North China University of Water Resources and Electric Power, Zhengzhou 450045, China ncwu.edu.cn

Search for more papers by this author

Bo Chen,

Bo Chen

Institute of Resources & Environment, Henan Polytechnic University, Jiaozuo 454000, China hpu.edu.cn

Search for more papers by this author

Yu Zou,

Yu Zou

Jiangmen Branch Bureau of Hydrology, Guangdong Provincial Bureau of Hydrology, Jiangmen 529000, China

Search for more papers by this author

Bo Zhang,

Bo Zhang

Institute of Energy and Chemical Industry, China Pingmei Shenma Group, Pingdingshan 467000, China

Search for more papers by this author

First published: 20 October 2021

https://doi.org/10.1155/2021/3143024

Citations: 3

Academic Editor: Chuangzhou Wu

Share a link

Email
Wechat
Bluesky

Abstract

In coal seam mining, the water resistance of the floor composite strata is the key to determining whether water disaster occurs or not and to formulating water control countermeasures. Taking the Pingdingshan Coalfield No. 8 mine and Shoushan mine as the research objects, the thickness ratio of plastic brittle rock, core recovery rate, thickness of effective aquiclude, fault complexity, composite compressive strength, and equivalent water resistance coefficient were selected as the index factors. The comprehensive weight of each index factor was determined by using the entropy weight theory. The water resistance of the J_16-17 coal seam floor composite rock in the study area was quantitatively evaluated using the fuzzy variable set mathematical model and was divided into five grades: extremely weak, weak, medium, strong, and very strong. The results show that the J_16-17 coal floor composite rock layers with strong and very strong water resistance areas account for 23.64% of the total area, the medium areas account for 58.26%, and the weak and extremely weak areas account for 18.1%. These results provide support for the accurate assessment of water inrush hazards of a coal floor.

1. Introduction

In the process of mining Permian Carboniferous coal seams in North China coalfields, water inrush from an Ordovician or Cambrian thick limestone aquifer is always a threat. These bottom plates usually experience high water pressure and are rich in water [1, 2]. The composite rock layer is composed of sandstone, mudstone, thin limestone, and a thin coal seam. Between the coal seam and thick limestone is the barrier for resisting high water pressure and preventing groundwater from rising. Therefore, it is of great theoretical and practical significance to quantitatively evaluate the water resistance capacity of the composite rock strata, which can scientifically formulate water prevention and control countermeasures to reduce the degree of harm from water inrush in an area.

At present, many experts and scholars have carried out research work on the water resistance of rock formations. Yang [3] believed that the essence of mining under pressure is the existence of combined water, which makes the rock strata have the ability of water resistance and decompression, and proposed the concept of water resistance coefficient. Qian et al. [4] and Miao and Qian [5] put forward the “key layer” theory for judging water inrush from coal floors. Xu et al. [6] based on the investigation of the floor lithology, strata combination relationship, and karst development conditions of a certain wellfield proposed that at least 25 m upper Cambrian limestone could be used as an aquiclude, which significantly improved the mining conditions of the coal seam. Zhang et al. [7] studied the relationship between water resistance capacity of rock strata and its structural composition and combination form through laboratory tests and proposed that the combination with better water resistance ability should start with soft rock strata and alternate soft and hard rock strata. Yin and Hu [8] took structure, in situ stress, and rock permeability as the influencing factors of the water resistance capacity of rock strata and concluded that the water resistance capacity of mudstone, siltstone, medium sandstone, and limestone ranges from large to small. Feng et al. [9] used experiments and numerical simulations to study the effects of different lithological characteristics of the aquiclude on its water resistance capacity. Li et al. [10] faced the problem of the stability of the water resistance rock mass of the karst tunnel, only considered the safe thickness of the water resistance rock mass, and did not consider the joints and permeability of the rock mass, which has certain limitations. Sun et al. [11] studied the influence of thickness, layer, length, cohesion, and internal friction angle on the water resistance capacity of the key composite aquiclude and concluded that the water pressure that can withstand is in a quadratic parabola relationship with its thickness. The greater the thickness, the better the water resistance capacity. Xu et al. [12] analyzed the lithology, void structure, and permeability characteristics of Fengfeng Formation from a micro-macro scale and made a quantitative study on its water resistance capacity. Lyu and Xie [13] and Zhang et al. [14] used statistical analysis and laboratory experiments to study the lithologic combination characteristics, rock mechanical strength, water properties, and permeability of coal seam overburden rock and evaluated the comprehensive water resistance capacity. Wang [15] studied the water resistance capacity of overlying rock from the strength, anisotropy, rheology, and expansibility of rock.

As shown above, the research on the water resistance capacity of rock layers has developed from the initial consideration of a single factor such as rock thickness or lithologic difference [16–20] to a comprehensive analysis of multiple factors such as lithology combination, rock mass strength, and permeability, making the evaluation system more and more perfect. However, due to insufficient field data and difficulty in quantifying index factors, the existing evaluation index system often ignores the influence of geological structure, mining failure, and equivalent water resistance of different lithology and rock formations. In addition, in the existing research results, the analytic hierarchy process or grey correlation method is commonly used to calculate the weight of index factors, so that the calculation results are greatly influenced by the subjective shortcomings. In this paper, the thickness ratio of plastic brittle rock, core recovery rate, thickness of effective aquiclude, fault complexity, composite compressive strength, and equivalent water resistance coefficient were selected as index factors, covering many factors affecting the water resistance capacity of composite strata on coal floor. The comprehensive weight determined by entropy weight theory overcomes the subjective and objective randomness of the traditional method. The fuzzy variable set theory can describe the characteristics of things under the combined action of multiple index factors and has realized the quantitative identification of water resistance capacity of composite rock strata. The research results are expected to provide technical support for an accurate evaluation of water inrush risk from coal floors.

2. Determination of Index Factors

2.1. Strata Structure of Coal Seam Floors

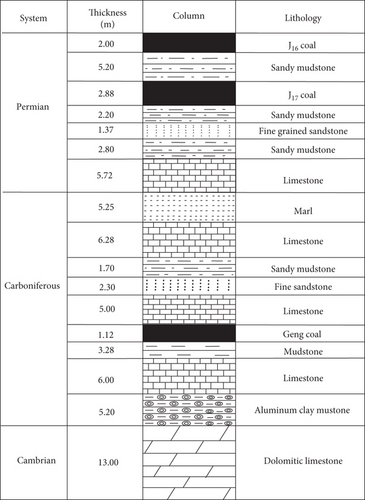
The area of the No. 8 mine and Shoushan mine, located in the eastern Pingdingshan Coalfield, is 68.35 km². At present, mainly the J_16-17 coal is mined. The thickness of the coal seam has a range of 2-3.8 m, with an average thickness of 2.44 m. The main threatening aquifer of the baseplate is a Cambrian limestone aquifer with a thickness greater than 200 m. The coal seam and Cambrian limestone are composed of sandy mudstone, medium-fine sandstone, thin coal seam, thin limestone, and bauxite mudstone. The floor rock structure of the J_16-17 coal is shown in Figure 1. The thickness is 68-77 m, and the mean value is 71.3 m.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Column diagram of coal floor of the J_16-17 Formation.

2.2. Index Factor Selection

During coal mining, the main factors controlling the water resistance of the floor composite rock layer are the lithological structure, integrity, thickness of effective aquiclude, fault development, compressive strength, and permeability.

The floor of the Ji Formation coal seam is an interbed of brittle sand (limestone) and plastic mudstone. The more sand (limestone) layers and the thicker the single layer, the more easily the floor is damaged by excavation; while the mudstone layers depend on elastic deformation to decompose stress under load, the more numerous and thicker the mudstone layers, the better the water resistance of the rock layers. Lithological structure is usually characterized by the ratio of brittle rock thickness to plastic rock thickness revealed by drilling holes (thickness ratio of plastic brittle rock).

The integrity of the rock mass represents the degree of development of cracks in the rock mass. It reflects the permeability and water-bearing capacity of the rock mass. Therefore, it is an important index for evaluating the water resistance of the rock formation. Integrity is often indicated by the ratio of the core length to the thickness of the formation (core recovery rate) during drilling. The lower the recovery is, the more fractured the rock is, the better the permeability is, and the stronger the water-bearing capacity is.

The thickness of the aquiclude is the distance between the mining coal seam and the main threatening aquifer, and the disturbance destroy depth of the floor is the disturbance destroy depth under the mining condition of the coal seam. The thickness of effective aquiclude is the difference between the two. Based on the lithological structure and rock mass integrity, the greater the effective aquiclude is, the stronger the ability to resist water pressure damage, and the lower the possibility of water inrush from the floor.

Faults and associated fissures not only destroy the integrity of the rock layers but also are important water diversion channels. The more developed the interruption layers in the coal seam floor, the denser the tensional faults are, the more serious the rock layers are damaged, and the higher the frequency of water inrush occurs. Once water inrush occurs, the greater the water volume is. Fault development is often indicated by fault complexity.

The ability of the rock formation to resist water pressure is closely related to its own compressive strength. Hard limestone and sandstone have high compressive strength, but poor plasticity and weak water-retaining ability, while soft mudstone has the opposite characteristics: low compressive strength, good plasticity, and good water-retaining ability. The compressive strength of the multirock combination of the coal floor is characterized by the composite compressive strength.

The more permeable the composite rock layer in the coal seam floor is, the higher the rise height of groundwater under the same water pressure and the greater the possibility of water inrush. In order to facilitate the uniform comparison and analysis of permeability for the different lithological rocks, the equivalent water resistance coefficient is often used to indicate the permeability of rocks. When the lithological thickness and equivalent water-proofing coefficient of each rock layer are known, the equivalent water resistance coefficient of the composite rock layer can be obtained as the basis for determining the water-resistance capacity of the floor.

Therefore, we selected six factors, including the thickness ratio of plastic brittle rock, the core recovery rate, the thickness of effective aquiclude, fault complexity, composite compressive strength, and equivalent water resistance as the index factors to evaluate the water resistance of the coal seam floor rock.

3. Index Factor Quantization

3.1. Thickness of Effective Aquiclude

The thickness of effective aquiclude in the coal seam floor can play the role of water blockage [21]. The calculation formula is [22]

(1)

(2)

where t is the effective thickness of the aquiclude, m; M is the total thickness of the aquiclude, m; C_p is the disturbance destroy depth of the floor, m; L is the inclined length of the working face, m; H is the mining depth of the coal layer, m; and α is the inclination angle of the coal layer.

The average destruction depth of the Ji Group coal floor disturbance for the No. 8 mine and Shoushan mine calculated by formula (2) is shown in Table 1.

Table 1. List of disturbance damage depths of the Ji Group coal floor (m).

Mine	α (°)	L (m)	H (m)	C_p (m)
No. 8 mine	17	140	804.76	20.41
Shoushan mine	10.17	160	713	20.65

We take drilling hole No. 1 as an example, located in the No. 8 coal mine. The total thickness of the floor rock of the J_16-17 coal exposed by drilling is 68.14 m. First, the disturbance damage depth of the floor rock is 20.41 m (Table 1). Then, according to Equation (1), the effective thickness of the aquiclude is calculated to be 47.73 m. Analogously, the effective water-resistant thickness of 48 boreholes is calculated, and their contours are drawn (as shown in Figure 2).

3.2. The Complexity of the Fault

Fault complexity is often expressed by fractal dimension and calculated by fractal theory [23]. The smaller the fractal dimension is, the lower the complexity of the fault layer.

(3)

where A is constant and D_S is the fractal dimension value.

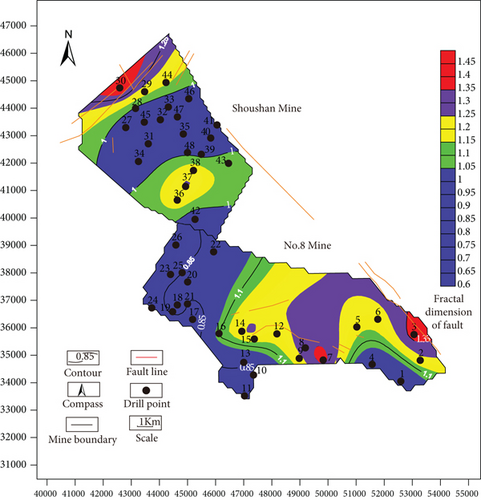
Firstly, the region containing fractal is divided into several square blocks according to certain rules. The blocks containing fractal are numbered one by one, and the similarity ratio r = 1, 1/2, 1/4, and 1/8 are taken, respectively. The blocks are subdivided into 1, 4, 16, and 64 square grids. Count the number of grids N(r) occupied by the fractal body at different scales in a certain segment and establish the lg(r)-lgN(r) double logarithmic coordinate system with formula (3). Then, the slope of the fitted line and the correlation coefficient are obtained by the least square method, and the absolute value of the slope is the value of the fractal dimension.

According to the actual situation, this paper divided the mining area into 600 × 600 mm square blocks. The number of mesh N(r) covering faults when r = 600, 300, 150, and 75 mm is calculated successively, and the obtained results are shown in Table 2. The contour of fault fractal dimension is shown in Figure 3.

Table 2. Quantitative values of the index factors.

Drilling hole	Thickness ratio of plastic brittle rock	Core recovery rate	Thickness of effective aquiclude	Fault factor values	Composite compressive strength	Equivalent water resistance coefficient
1	1.4158	0.7840	47.73	0.8432	4.87	0.9410
2	1.0978	0.8795	54.39	1.2114	5.38	0.9685
3	1.1437	0.7255	60.16	1.4051	5.24	0.9251
4	0.9832	0.7500	61.49	0.8772	5.52	0.9196
5	0.4547	0.7626	82.06	1.1708	6.75	0.8285
6	0.8891	0.6579	68.03	1.1863	5.74	0.9492
7	1.2344	0.6879	51.77	1.3911	5.14	0.9528
8	0.9676	0.8300	59.51	1.3214	5.54	0.9143
9	0.9948	0.8100	62.23	1.2141	5.51	0.9310
10	0.8373	0.7243	50.35	0.8021	5.70	0.9042
11	1.2413	0.5881	55.18	0.7392	5.03	0.8816
12	0.9411	0.5223	56.52	1.1883	5.52	0.8659
13	0.8551	0.7988	72.24	0.8609	5.74	0.8913
14	0.6670	0.7131	66.02	1.2704	6.13	0.8490
15	0.7282	0.7300	54.06	1.1801	5.99	0.8629
16	0.7286	0.6500	55.42	1.1174	5.73	0.8533
17	0.8972	0.5178	80.13	0.6891	5.66	0.9018
18	0.4423	0.5650	87.61	1.0870	6.81	0.8354
19	0.8691	0.5500	81.05	0.8817	5.69	0.8818
20	0.7293	0.6975	69.32	0.9017	6.05	0.9053
21	0.9372	0.4363	89.77	0.8195	5.53	0.8659
22	0.6177	0.9226	75.05	0.8745	6.27	0.8508
23	0.6608	0.7508	59.65	0.7917	6.18	0.8750
24	0.7382	0.5876	74.00	0.6451	5.93	0.8342
25	0.6804	0.9000	65.17	0.8504	6.14	0.8847
26	0.7033	0.8996	66.95	0.7936	6.06	0.8705
27	0.8139	0.9060	61.15	0.8942	5.36	0.9137
28	0.7064	0.8471	74.35	0.9661	5.78	0.8677
29	0.3347	0.7330	58.90	1.1468	6.93	0.8736
30	0.7952	0.7953	54.25	1.3911	5.63	0.8872
31	0.2857	0.8829	60.65	0.8917	7.06	0.8500
32	0.6667	0.9149	62.90	0.8060	5.96	0.9001
33	0.5720	0.9098	56.93	0.8794	6.26	0.9179
34	0.4793	0.8400	60.37	0.8929	6.37	0.8885
35	0.8096	0.8694	68.65	0.8635	5.78	0.9527
36	0.4583	0.8462	55.81	1.1781	6.46	0.8629
37	0.5239	0.8464	55.18	1.2118	6.22	0.8500
38	1.3847	0.8479	55.25	1.1817	4.77	0.9226
39	0.6517	0.8700	77.83	0.9677	5.84	0.8673
40	0.1599	0.7889	79.58	0.8598	7.43	0.7724
41	0.2780	0.6980	75.73	0.8697	6.84	0.7943
42	0.5179	0.8500	78.00	0.8837	6.28	0.8772
43	0.6748	0.8540	77.80	1.0656	5.61	0.8444
44	0.4013	0.9300	81.41	1.1236	6.71	0.8844
45	0.7415	0.9150	86.90	0.7696	5.80	0.9075
46	0.4563	0.8520	77.09	0.9230	6.46	0.8845
47	0.6197	0.9490	79.80	0.8511	6.02	0.9158
48	0.7681	0.8090	80.72	0.9761	5.70	0.9040

3.3. Composite Compressive Strength

In this study, a total of 60 cores were collected from seven boreholes in the J_16-17 coal floor, including 25 mudstone, 25 sandstone, and 10 limestone samples. The test results of the compressive strength are shown in Table 3.

Table 3. Compressive strength of each lithology test in the study area (MPa).

Mine	Mudstone	Sandstone	Limestone
Shoushan mine	41.43	73.72	90.10
No. 8 mine	37.60	84.83	93.12

The order of compressive strength is plastic mudstone < brittle limestone < brittle sandstone. Although brittle rock has a high compressive strength, it easily fractures under load, and its water resistance performance is poor, while plastic mudstone exhibits contrary behaviors. The research results show that when the compressive strength of brittle rock is twice that of plastic rock, the water resistance capacity of the latter is 2.5-3 times that of the former [24]. According to the manual of mine geology [25], the conversion coefficient of the compressive strength for different rocks is shown in Table 4.

Table 4. Conversion coefficient of test compressive strength for each lithology.

Lithology	Conversion factor (MPa/m)
Mudstone, marl, clay, shale	0.05
Sand shale	0.07
Sandstone, no karst limestone, marl	0.10

The compressive strength of the composite rock formation is calculated as follows:

(4)

where

is the composite compressive strength of the rock strata, MPa; P_i is the average compressive strength of each rock layer, MPa; τ_i is the ratio of thickness of each rock layer; and γ_i is the conversion coefficient of the compressive strength of each rock layer, MPa/m.

Taking the No. 1 drilling hole of the No. 8 mine as an example, the thickness ratios of the mudstone, limestone, and sandstone are 58.61%, 31.57%, and 9.83%, respectively. The composite compressive strength calculated by using Equation (4) combined with Tables 3 and 4 is 4.87 MPa. Following the same procedure, the composite compressive strength of the 48 boreholes can be obtained, and the contour lines are drawn (as shown in Figure 4).

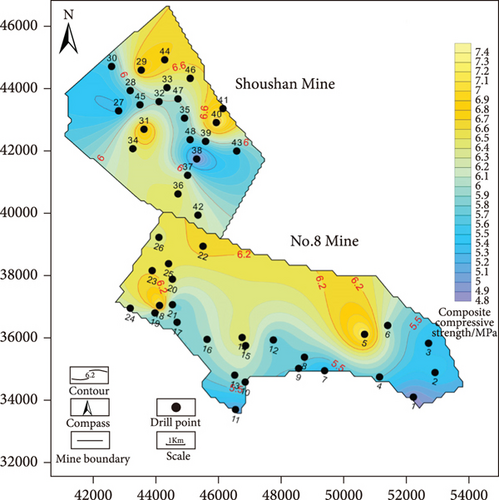
The figure shows that the compressive strength of the J_16-17 coal floor composite rock layer is 4.00-7.43 MPa, and the mean value is 5.71 MPa. At present, the water pressure of the Cambrian limestone in the study area is 0.38-4.94 MPa, and the mean value is 2.63 MPa. The composite rock layer in its natural state can fully resist water pressure. However, under the influence of faults and mining, the water-resistant performance of the coal seam floor rock will be significantly reduced, which shows the necessity of a multifactor evaluation of the water-resistance capability.

3.4. Equivalent Water Resistance Coefficient

Referring to the existing literature [26–28], the equivalent water resistance coefficients of different rock layers are listed in Table 5.

Table 5. Conversion value of the lithology equivalent water resistance coefficient.

Lithology	Conversion value of equivalent water resistance coefficient
Mudstone, marl, clay, shale	1.0
Sandstone	0.4
Sand shale	0.8
Mine	0.7
Gravel, gravel, etc.	0

The equivalent water resistance coefficient of the composite rock formation is calculated as follows [28]:

(5)

where

is the equivalent water resistance coefficient; τ_i is the ratio of thickness of each rock layer; and λ_i is the conversion value of equivalent water resistance coefficient.

Based on the rock layer thickness revealed by drilling and the equivalent water resistance coefficient values listed in Table 5, the equivalent water resistance coefficient of the composite rock layers for the J_16-17 coal floor in 48 drilling holes was obtained. The contours are shown in Figure 5.

3.5. Index Factor Set

The thickness ratio of the plastic brittle rock and core recovery rate can be counted according to the drilling disclosure information. Quantitative values of the six index factors corresponding to the 48 boreholes are shown in Table 2. In order to correspond to the evaluation of the water-resistance of the rock formation, the value of the fault complexity factor is taken as the reciprocal of the fractal dimension.

4. Index Factor Weight

It is very important to choose a scientific mathematical method to determine the weight of the index factors. Referring to the existing research results [29], this paper chooses nine-scale AHP and gray correlation analysis to calculate the subjective and objective weights and then couples them to determine the comprehensive weights.

4.1. Subjective Weight

The AHP establishes a hierarchical structure model, constructs a judgment matrix, and calculates the weight of each factor’s influence on the overall goal [30, 31]. As shown in Table 6, the target layer is the evaluation of the water resistance of the coal seam floors. The criterion layer divides the index factors into 3 categories, and the scheme layer includes 6 index factors.

Table 6. Hierarchical structure performance index of aquiclude.

Target layer	Criteria layer	Scheme layer
Evaluation of water resistance of the coal seam floors (A)	Geological structure and disturbance damage (B1)	The thickness of effective aquiclude (C1)
	Geological structure and disturbance damage (B1)	Fault factor values (C2)
	Compression resistance and permeability (B2)	Composite compressive strength (C3)
	Compression resistance and permeability (B2)	Core recovery rate (C4)
	Lithology combination and water blocking performance (B3)	Equivalent water resistance coefficient (C5)
	Lithology combination and water blocking performance (B3)	Thickness ratio of plastic brittle rock (C6)

Starting from the criterion level, referring to expert opinions to construct secondary indicators, the judgment matrix of geological structure and disturbance damage, compression resistance and permeability, lithology combination and water blocking performance is

(6)

The calculated feature vector ω_B = (0.5242, 0.1973, 0.2785). CR_B = 0.0036 < 0.1; it satisfies the consistency condition.

Similarly, the judgment matrices of the six indicator factors are

(7)

The calculated feature vector ω_C1 = (0.25, 0.75), ω_C2 = (0.2, 0.8), ω_C3 = (0.1667, 0.8333). CR_C1 = CR_C2 = CR_C3 = 0 < 0.1; it satisfies the consistency condition.

The weights of the 6 index factors are

(8)

By calculating CR = 0.0000 < 0.1, it satisfies the consistency condition, indicating that the constructed judgment matrix is reasonable. The subjective weight of the six index factors is shown in Table 7.

Table 7. Subjective weight determined by AHP.

Indicators	Thickness ratio of plastic brittle rock	Core recovery rate	Thickness of effective aquiclude	Fault factor values	Composite compressive strength	Equivalent water resistance coefficient
Subjective weight	0.2321	0.1578	0.1311	0.3932	0.0395	0.0464

4.2. Objective Weight

The objective weight can be calculated by using the grey correlation analysis method. According to the index factor values corresponding to the 48 boreholes (Table 2), the overall reference sequence [32] is obtained as follows:

(9)

After initial value processing of X₀ [33], the correlation degree can be further calculated:

(10)

Then, the weights of the six index factors [34] can be obtained, and their values are shown in Table 8.

Table 8. Objective weight from the grey correlation analysis method.

Indicators	Thickness ratio of plastic brittle rock	Core recovery rate	Thickness of effective aquiclude	Fault factor values	Composite compressive strength	Equivalent water resistance coefficient
Objective weight	0.1366	0.1616	0.1617	0.1529	0.1601	0.2271

4.3. Comprehensive Weights

According to the subjective and objective weights, the following formula can be used to calculate the comprehensive weight [35]:

(11)

where ω_1i and ω_2i are the subjective and objective weights, respectively. Further application of entropy weight theory can calculate the relative entropy value:

(12)

where H(U, V) is the relative entropy of U and V, and n is the number of indicators.

The comprehensive weights of the six index factors determined by formula (11) are shown in Table 9. The relative entropies of the comprehensive weights with the subjective and objective weights can be calculated by formula (12) (as shown in Table 10).

Table 9. Comprehensive weight of index factors.

Indicators	Thickness ratio of plastic brittle rock	Core recovery rate	Thickness of effective aquiclude	Fault factor values	Composite compressive strength	Equivalent water resistance coefficient
Comprehensive weight	0.1955	0.1753	0.1599	0.2692	0.0873	0.1127

Table 10. Relative entropy of weight.

Weight	Comprehensive weight and subjective weight	Comprehensive weight and objective weight
Relative entropy	0.073	0.089

Obviously, the relative entropies are less than 0.1 and tend to 0, which indicates that the consistency between the comprehensive weight and the subjective and objective weight is high [36]. That is, the comprehensive weight can effectively combine the subjective and objective weights, and its weight distribution is more scientific and reasonable.

5. Identification of Water Barrier Ability

5.1. Model Building

5.1.1. Level Matrix Establishment

According to the existing index factor data with reference to the existing research results [37], the water-insulation capacity of the composite strata in the coal seam floor can be divided into five grades, namely, extremely weak (I), weak (II), medium (III), strong (IV), and very strong (V).

Assuming that the mean value of an indicator factor is x and the mean square deviation is s, according to the mean-variance method, a recognition interval composed of five levels can be established. The calculation formulas are as follows:

(13)

The standard interval matrix of the six index factors corresponding to the five levels can be determined:

(14)

The index factor range matrix constructed as

(15)

The index factor matrix is

(16)

5.1.2. Level Eigenvalue Determination

For a borehole, the relative difference matrix and relative subordination matrix can be obtained by comparing the quantified values of the six index factors with the corresponding data of the matrices I_ab, I_cd, and I_M [38, 39]. For borehole 1, the relative difference matrix is

(17)

The relative membership matrix is

(18)

According to the principle of the fuzzy variable set, the relative membership matrix and the corresponding comprehensive weight are combined based on the requirements, and the hierarchical characteristic values under different parameters can be obtained.

(19)

(20)

where i = 1, 2, 3, ^⋯, n; n is the number of indicators; h = 1, 2, 3, ^⋯, m; m is the number of evaluation index grades; w_i is the weight of the evaluation index (as shown in Table 9); μ_A (μ_ih) is the relative membership degree of the ith index under grade h; and α and β are optimization criteria and distance parameters, respectively, usually taking values 1 and 2.

According to formulas (19) and (20), the level eigenvalue of borehole 1 is

(21)

The mean of the level eigenvalue is 3.8091. Similarly, the mean value of the grade characteristics of other boreholes can be calculated as shown in Table 11 (Note: α and β are the parameters of the compound operation of the fuzzy variable sets).

Table 11. Evaluation results of each borehole in the mining area.

Drilling hole	Level eigenvalue					Waterproof ability grade
Drilling hole	α = 1, β = 1	α = 1, β = 2	α = 2, β = 1	α = 2, β = 2	Mean	Waterproof ability grade
1	3.6544	3.5047	4.1654	3.9117	3.8091	IV
2	3.502	3.4306	4.0213	3.9278	3.7204	IV
3	3.6759	3.5109	4.239	3.9485	3.8436	IV
4	3.7136	3.5287	4.2675	3.9754	3.8713	IV
5	2.2395	2.3538	1.9527	2.1855	2.1829	II
6	3.7877	3.6014	4.5335	4.2561	4.0447	IV
7	3.588	3.4534	4.2084	3.9854	3.8088	IV
8	3.7403	3.5429	4.2758	3.9915	3.8876	IV
9	3.6678	3.5091	4.2116	3.9349	3.8308	IV
10	3.2876	3.2574	3.6278	3.5052	3.4195	III
11	3.1764	3.2221	3.2825	3.3479	3.2572	III
12	2.3663	2.2988	2.5043	2.4577	2.4068	II
13	3.3073	3.2887	3.5358	3.5015	3.4083	III
14	2.1647	2.2678	1.9389	2.1243	2.1239	II
15	2.5617	2.606	2.5215	2.6208	2.5775	III
16	2.279	2.3811	2.0797	2.2682	2.252	II
17	3.296	3.2668	3.6164	3.5123	3.4229	III
18	2.2245	2.3447	1.9259	2.1655	2.1652	II
19	3.182	3.2255	3.2919	3.354	3.2634	III
20	3.7163	3.5353	4.1929	3.9606	3.8513	IV
21	2.3663	2.2988	2.5043	2.4577	2.4068	II
22	2.2127	2.3157	1.9924	2.1817	2.1756	II
23	2.9916	3.0838	2.9515	3.1097	3.0342	III
24	2.2272	2.3463	1.9305	2.1691	2.1683	II
25	3.2634	3.2673	3.4148	3.4315	3.3442	III
26	2.8611	2.9716	2.7547	2.9459	2.8833	III
27	3.7387	3.5425	4.2704	3.9899	3.8854	IV
28	2.4441	2.3738	2.5554	2.5058	2.4698	II
29	2.9519	3.0502	2.886	3.0575	2.9864	III
30	3.2971	3.288	3.4872	3.4804	3.3882	III
31	2.1914	2.2944	1.9676	2.1556	2.1522	II
32	3.3017	3.2728	3.608	3.5157	3.4246	III
33	3.7246	3.5343	4.2739	3.9827	3.8789	IV
34	3.3003	3.2884	3.5022	3.4872	3.3945	III
35	3.5887	3.4537	4.2099	3.9861	3.8096	IV
36	2.5617	2.606	2.5215	2.6208	2.5775	III
37	2.1914	2.2944	1.9676	2.1556	2.1522	II
38	4.6934	4.5189	5.2535	4.9613	4.8568	V
39	2.4271	2.3573	2.5431	2.4942	2.4554	II
40	1.8025	1.8694	1.6102	1.7337	1.754	I
41	1.7928	1.8653	1.6009	1.7255	1.7461	I
42	3.0531	3.1345	3.0596	3.1939	3.1103	III
43	2.2044	2.3317	1.8922	2.1376	2.1415	II
44	3.255	3.2636	3.4034	3.4245	3.3366	III
45	4.7221	4.5373	5.2134	4.9691	4.8605	V
46	3.2578	3.2649	3.4072	3.4269	3.3392	III
47	4.7378	4.541	5.2804	4.9908	4.8875	V
48	3.2883	3.2582	3.6268	3.5059	3.4198	III

5.2. Water-Resistant Capacity Zoning

According to the hydrogeological conditions of the study area and the research results of others [38], the eigenvalue thresholds corresponding to the five levels of water insulation capacity are shown in Table 12.

Table 12. Classification standards for water resistance.

Waterproof ability grade	Extremely weak (I)	Weak (II)	Medium (III)	Strong (IV)	Very strong (V)
Level eigenvalue	W < 2.0	2.0 ≤ W < 2.5	2.5 ≤ W < 3.5	3.5 ≤ W < 4.5	W ≥ 4.5

According to the characteristic values of 48 drilling levels of the No. 8 mine and the Shoushan mine listed in Table 11, the water resistance capacity grade can be determined by the classification standard in Table 12. The values are also listed in Table 11. The corresponding partition of the water resistance capacity of the composite strata in the coal floor of the J_16-17 is shown in Figure 6.

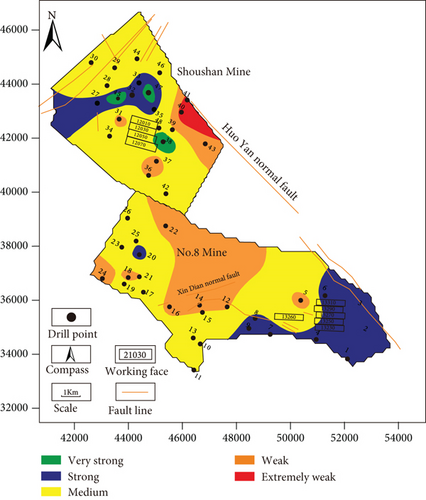
The statistical analyses showed that the strong and very strong water resistance areas occupy 23.64% of the total area. The medium area accounts for 58.26%, and the weak and extremely weak areas account for 18.1%. The medium water insulation capacity is relatively high, and the weak and very weak areas are relatively small.

6. Discussion

It can be seen from the calculation process of AHP that the determination of the weight of indicator factors depends on the expert opinions or scores, and the results are easily affected by the subjective will of experts. Grey correlation method is based on the actual drilling data to determine the weight; it can avoid the impact of evaluator’s subjective will, but the grey correlation analysis method uses the same weight set when calculating the optimal solution, it is difficult to reflect the optimization of the evaluation. Combined with the previous two methods, the comprehensive weight determined by the entropy weight method can not only reduce the interference of human factors but also fully reflect the actual field, and its results are more scientific and reliable.

In the present mine excavation project, the water resistance capacity is usually judged according to the thickness of the aquiclude. It can be seen from Table 2 that the effective water resistance thickness of Nos. 38, 40, and 41 are 55.25 m, 79.58 m, and 75.73 m, respectively. Based on this, it is judged that the water resistance of the rock formation near No. 38 borehole is weaker than 40 and 41 drilling. In fact, the existence of the Huoyan fault near boreholes 40 and 41 not only reduces the distance between the coal seam and the aquifer [39] but also destroys the integrity of the coal seam floor [40–42]. At the same time, it also changed the migration characteristics of groundwater [43], which greatly reduced the water resistance of the rock formation. In this paper, it is determined that the water resistance capacity of the rock strata at borehole No. 38 is class V, and that of the rock strata at boreholes Nos. 40 and 41 is class I (Table 11), that is, the water resistance capacity of borehole No. 38 is greater than that of boreholes Nos. 40 and 41. The results are credible.

It can be seen from Figure 6 that the water resistance level characteristic value of the composite rock layer of the coal seam floor in the west of the Shoushan mine and the southeast of the No. 8 mine is above 2.5, and the water resistance is relatively strong. Therefore, the possibility of water inrush from the floor during coal mining is relatively small. The mining activities of the No. 8 mine and the Shoushan mine are mainly carried out in areas with strong and medium water resistance. The 13230, 13250, 13260, 13270, 13290, and 13310 working faces of No. 8 mine have stopped mining. The 12010, 12030, 12050, and 12070 working faces of Shoushan mine have stopped mining.

There is no floor water inrush accident in these working faces, which shows that the evaluation results are in good agreement with the actual situation.

7. Conclusions

(1)
Based on the comprehensive analysis of multiple influencing factors on the water resistance of the J_16-17 coal seam floor composite rock in the Pingdingshan Coalfield No. 8 mine and the Shoushan mine, we select the thickness ratio of plastic brittle rock, core recovery rate, thickness of effective aquiclude, fault complexity, composite compressive strength, and equivalent water resistance coefficient as the evaluation index factors. It provides a guarantee for identifying the water resistance of the composite rock layer of the coal seam floor
(2)
Based on the analytic hierarchy process and grey relational analysis, the subjective and objective weights of the index factors are defined. The entropy weight theory is used to determine the comprehensive weights. Based on the fuzzy variable set theory, the mathematical model of water resistance evaluation is constructed, and the J_16-17 coal floor is quantitatively identified. The water resistance of the coal seam floor composite rock layer is divided into five grades: extremely weak, weak, medium, strong, and very strong, laying the foundation for the accurate assessment of the water inrush risk from the coal seam floor
(3)
The areas with strong and very strong water resistance capacity of the J_16-17 coal floor composite rock in the No. 8 mine and the Shoushan mine account for 23.64% of the total area, the medium area accounts for 58.26%, and the weak and extremely weak areas account for 18.1%. Areas with medium water-resisting capacity accounting for relatively high, weak, and very weak areas are relatively small. The accurate evaluation and zoning of water-resistance capacity indicate the direction for the mine to take targeted measures to prevent and control floor water hazards
(4)
The comprehensive weight of the index factors determined by the entropy weight theory reduces the interference level of human factors. The fuzzy variable set theory realizes the quantitative evaluation of the water resistance of the composite rock under the action of multiple index factors. The actual excavation results on site have proved the reliability of the evaluation results. It provides a reference method for accurately distinguishing the water resistance of rock formations

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (41802186 and 41972254), Innovative Science and Technology Talents Team Construction Project of Henan Province (CXTD2016053), and Special Funds for Higher Education Basic Scientific Research Funds of Henan Province (NSFRF200103).

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 Dong S. N., Guo X. M., Liu Q. S., Wang H., and Nan S., Model and selection criterion of zonal preact grouting to prevent mine water disasters of coal floor limestone aquifer in North China type coalfield, Coal Geology & Exploration. (2020) 48, no. 4, 1–10.
CAS Google Scholar
2 Wu Q., Progress, problems and prospects of prevention and control technology of mine water and reutilization in China, Journal of China Coal Society. (2014) 39, no. 5, 795–805.
Google Scholar
3 Yang S. A., Water resistance coefficient and its application, Coal Geology & Exploration. (1986) 3, 41–46.
Google Scholar
4 Qian M. G., Miao X. X., and Xu J. L., Study on key strata theory in strata control, Journal of China Coal Society. (1996) 3, 2–7.
Google Scholar
5 Miao X. X. and Qian M. G., Advance in the key strata theory of mining rock mass, Journal of China University of Mining & Technology. (2000) 1, 25–29.
Google Scholar
6 Xu Z. M., Sun Y. J., Sui W. H., Zhang G. W., Li S., and Huang X. L., The water isolating and hydrogeological structure characteristics for upper member of Cambrian limestone in coal floor, Journal of Mining & Safety Engineering. (2010) 27, no. 3, 399–403.
Google Scholar
7 Zhang W. Q., Li B. Y., and Li J. X., Water resistance and its relationship with structure components and configuration of rocks, Coal Geology & Exploration. (1992) 4, 41–44.
Google Scholar
8 Yin S. X. and Hu W. Y., Study of water resist property and its natural intrusion, Coal Geology and Exploration. (2008) 36, no. 1, 34–40.
Google Scholar
9 Feng M. M., Mao X. B., and Zhu Q. H., Effect of lithologic association of the water-resisting strata in coal seam floor on water insulating, Journal of Mining & Safety Engineering. (2010) 27, no. 3, 404–409.
Google Scholar
10 Li T., Zhang L., Jiang Q., Feng C., and Zhao R., Safe thickness and fracture evolution law determined for hydraulic fracturing of water-resistant rock mass with hidden karst based on GDEM, Tunnel Construction. (2021) 41, no. 1, 67–76.
CAS Google Scholar
11 Sun J., Wang L. G., and Hou H. Q., Research on water-isolating capacity of the compound water-resisting key strata in coal seam, Journal of China University of Mining & Technology. (2013) 42, no. 4, 560–566.
Google Scholar
12 Xu F., Jin D. W., Yang J. Z., Huang H., Wang S. D., Ji Y. D., and Shi L., Multi-scale quantitative evaluation of water resistance capacity of Fengfeng formation in Baode Coal Mine, Journal of China Coal Society. (2021) 46, no. 7, 2379–2386.
Google Scholar
13 Lyu D. and Xie Y. X., Study on Paleogene rock structure characteristics and integrated water-resistance performance in Yilan mining area, Safety in Coal Mines. (2020) 41, no. 3, 44–47.
Google Scholar
14 Zhang Y. J., Song Y. J., Chen P. P., and Fan Z. L., Study on comprehensive water insulated performances of deep Jurassic system rock strata, Coal Science and Technology. (2014) 42, no. 8, 98–98.
Google Scholar
15 Wang W. B., Research on lithology characteristic and water-resisting property of overlying strata under sea area, Coal Mining Technology. (2010) 15, no. 3, 10–13.
Google Scholar
16 Hu W. Y. and Yin S. X., Dynamic mechanism of water inrush from floor of mining face, Chinese Journal of Rock Mechanics and Engineering. (2010) 29, no. S1, 3344–3349.
Google Scholar
17 Cybulski K., Malich B., and Wieczorek A., Evaluation of the effectiveness of coal and mine dust wetting, Journal of Sustainable Mining. (2015) 14, no. 2, 83–92, https://doi.org/10.1016/j.jsm.2015.08.012, 2-s2.0-85034799408.
10.1016/j.jsm.2015.08.012
Google Scholar
18 Yi Q., Xie K., Sun P., and Kim Y., Characterization of phosphorus in the sedimentary environments of inundated agricultural soils around the Huainan Coal Mines, Anhui, China, Science of the Total Environment. (2014) 472, 538–549, https://doi.org/10.1016/j.scitotenv.2013.11.060, 2-s2.0-84889674544.
10.1016/j.scitotenv.2013.11.060
CAS PubMed Web of Science® Google Scholar
19 Yang Z. B., Application analysis of Slesarev formula in mine water prevention and control, Safety in Coal Mines. (2016) 47, no. 9, 190–193.
Google Scholar
20 Zhang W., Zhang R. Y., Yan M. H., Wang D. D., Ji F. F., Liu W. W., and Zhang K., Application of GIS technology in the calculation of water inrush coefficient of coal seam floor, Coal and Chemical Industry. (2016) 39, no. 2, 48–51.
CAS Google Scholar
21 Zhang B. and Chang X. F., Prediction method and application of mining failure depth of coal seam floor, Coal Technology. (2018) 37, no. 12, 26–29.
Google Scholar
22 Xu Y. C. and Yang Y., Applicability analysis on statistical formula for failure depth of coal seam floor in deep mine, Coal Science and Technology. (2013) 41, no. 9, 129–132.
Google Scholar
23 Wang D. K., Zeng F. C., Wang J. G., Wei J. P., Jiang Z. G., Zhang P., and Yu C., Dynamic evolution characteristics and fractal law of loaded coal fractures by micro industrial CT, Chinese Journal of Rock Mechanics and Engineering. (2020) 39, no. 6, 1165–1174.
Google Scholar
24 Ping Q., Zhang H., and Su H. P., Study on dynamic compression mechanical properties of limestone with different lengths, Chinese Journal of Rock Mechanics and Engineering. (2018) 37, no. S2, 3891–3897.
Google Scholar
25 Chai D. B., Mine Geological Work Manual, 1986, China Coal Industry Press.
Google Scholar
26 Zhou K. and Wang B. Q., The evaluation of equivalent thickness of water-resisting layer, Coal and Chemical Industry. (2016) 39, no. 2, 45–47.
Google Scholar
27 Han C. H., Wei J. C., Xie D. L., Xu J. G., Zhang W. J., and Zhao Z. C., Evaluation of water abundance of sandstone aquifer based on set pair analysis and variable fuzzy set coupling method: a case study of Jurassic Zhiluo Formation aquifer in Jinjiaqu well field, Ningdong mining area, Journal of China Coal Society. (2020) 45, no. 7, 199–201.
Google Scholar
28 Liu Q. R., Hydrogeological Characteristics and Exploration Evaluation Methods of Solid Deposits in China, 1995, Petroleum Industry Press.
Google Scholar
29 Wang X. Y., Wang T. T., Wang Q., Liu X., Li R., and Liu B. J., Evaluation of floor water inrush based on fractal theory and an improved analytic hierarchy process, Mine Water and the Environment. (2017) 36, no. 1, 87–95, https://doi.org/10.1007/s10230-016-0407-3, 2-s2.0-84976871487.
10.1007/s10230-016-0407-3
CAS Web of Science® Google Scholar
30 Li G. X., Liu N. N., Wu X. M., Liu W. L., and Wang R. M., Application of optimal combination weighting model in water inrush evaluation of floor collapse column, Safety in Coal Mines. (2018) 49, no. 11, 194–198.
Google Scholar
31 Shi L. Q., Zhang R. G., Han J., Cong P. Z., Qin D. X., and Guo Y. C., Water inrush risk assessment with multi-source information type fusion based on EWM-AHP comprehensive weighting, Journal of Henan Polytechnic University. (2020) 39, no. 3, 17–25.
Google Scholar
32 Xu G., Wang L., Wang H. T., Wang K., and Feng Y. Z., Prediction method of coal seam gas content based on grey theory and BP neural network, Coal Technology. (2019) 38, no. 11, 82–85.
Google Scholar
33 Cheng C., Research on Evaluation of Comprehensive Benefits of Isolated Buildings Based on Combined Weight and Grey Relation, 2018, Northeast Forestry University.
Google Scholar
34 Tang H., The application of improved grey correlation analysis method in groundwater evaluation, Northeast Water Resources and Hydropower. (2020) 38, no. 8.
Google Scholar
35 Li K. G., Li M. L., and Qin Q. C., Research on evaluation method of rockburst tendency based on improved comprehensive weighting, Chinese Journal of Rock Mechanics and Engineering. (2020) 39, no. S1, 2751–2762.
Google Scholar
36 Sun G. J., Huo X. Y., and Sun X. J., Evaluation method of four-parameter interval number based on combinator-weighted fuzzy matter-element, Mathematics in Practice and Theory. (2020) 50, no. 19, 288–295.
Google Scholar
37 Chen Y., Wang X., Zhao Y., Shi H., Liu X., and Niu Z., Quantitative evaluation for the threat degree of a thermal reservoir to deep coal mining, Geofluids. (2020) 2020, 15, https://doi.org/10.1155/2020/8885633, 8885633.
10.1155/2020/8885633
Web of Science® Google Scholar
38 Wang X. Y., Yao M. G., Zhang J. G., Zhao W., Huang P. H., Guo J. W., Chen G. S., and Zhang B., Risk assessment of coal seam floor water inrush based on improved AHP method and fuzzy variable set theory, Journal of Mining and Safety Engineering. (2019) 36, no. 3, 558–565.
CAS Google Scholar
39 Song Z. Q., Hao J., Tang J. Q., and Shi Y. K., Study on water inrush from fault’s prevention and control theory, Journal of China Coal Society. (2013) 38, 1511–1515.
Google Scholar
40 Zhang Q. Z., Jang H. S., Bae D. S., Kim G. Y., and Jang B. A., Empirical rock mechanical site-descriptive modeling (RMSDM) for the Korea Atomic Energy Research Institute Underground Research Tunnel (KURT), Environmental Earth Sciences. (2016) 75, no. 10, https://doi.org/10.1007/s12665-016-5596-3, 2-s2.0-84969677224.
10.1007/s12665-016-5596-3
Web of Science® Google Scholar
41 Wu C. Z., Chu J., Wu S. F., and Hong Y., 3D characterization of microbially induced carbonate precipitation in rock fracture and the resulted permeability reduction, Engineering Geology. (2019) 249, 23–30, https://doi.org/10.1016/j.enggeo.2018.12.017, 2-s2.0-85059168135.
10.1016/j.enggeo.2018.12.017
Web of Science® Google Scholar
42 Zhang Q. Z., Wu C. Z., Fei X. C., Jang B. A., and Liu D., Time-dependent behavior of rock joints considering asperity degradation, Journal of Structural Geology. (2019) 121, 1–9, https://doi.org/10.1016/j.jsg.2019.01.004, 2-s2.0-85060888780.
10.1016/j.jsg.2019.01.004
Web of Science® Google Scholar
43 Zhang Y. H., Xiong Z. Q., Li X. F., Peng R. D., and Li Y. C., Study on technology of mine water disaster prevention and control in underground mine under complex hydrogeological conditions, Coal Science and Technology. (2021) 49, no. 3, 167–174.
CAS Google Scholar

Citing Literature

All articles

Quantitative Identification of the Water Resistance Capacity of Composite Strata in Mining Coal Seam Floors

Abstract

1. Introduction

2. Determination of Index Factors