The COVID-19 pandemic has put the world in threat for a long time. It was first identified in Wuhan, China, in December 2019 and has been declared a pandemic by the WHO. This disease is mainly caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). So far, no vaccine or medicine has been developed for the proper treatment of this disease, so people are afraid of getting infected. The pandemic has placed many nations at the door of socioeconomic emergencies. Therefore, it is very important to predict the development trend of this epidemic, and we know mathematical modelling is a basic tool to research the dynamic behaviour of disease and predict the spreading trend of the disease. In this study, we have formulated a mathematical model for the COVID-19 outbreak by introducing a quarantine class with media-induced fear in the disease transmission rate to analyze the dynamic behaviour of this epidemic. We have calculated the basic reproduction number R₀, and we observed that when R₀ < 1, disease-free equilibrium is globally stable whereas if R₀> 1, then the system is permanent and there exists a unique endemic equilibrium point. Global stability of the endemic equilibrium point is developed by using Li and Muldowney’s high-dimensional Bendixson criterion. Finally, some numerical simulations are performed using MATLAB to verify our analytical results.

1. Introduction

Over the past two decades, two known coronavirus outbreaks of SARS [1] and MERS [2] have been detected in humans. COVID-19 is an abbreviated form of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) which has not been identified previously in humans. This disease is mainly transmitted through direct human-to-human contact, but there are pieces of evidence and work which claim that it can also be transmitted indirectly through fomites in the immediate environment around the infected person [3–5]. It is reported that COVID-19 affects different people in different ways. Most infected people develop mild to moderate symptoms such as fever, fatigue, and dry cough, although some patients suffer from headaches, abdominal pain, diarrhoea, and vomiting [6]. On average, symptoms may appear in 5 to 6 days from when someone is infected with the virus, but sometimes it can take up to 14 days [6]. In [7], Jiang et al. estimated that the fatality rate of this virus is nearly about 4.5%, but for the age group of 70–79 years, it has gone up to 8%. This disease is more critical for elder people who have other diseases such as diabetes, asthma, and cardiovascular disease [6]. It is reported that a COVID-19-infected person can make around 2.5 people infected [8]. People are concerned about their health, but the infection rate and death rate of the disease are increasing day by day and they are terrified to see this type of news through the media, so a wave of fear has been developed in the society.

Human behaviour plays an important role in spreading epidemics [9, 10]. They are also affected by a variety of factors, fear being one of them. Modelling studies have shown that fear has a significant effect on reducing the severity of a pandemic [11–13]. Fear has been shown to be directly related to social distance behaviour and caution [14, 15].

Due to fear, people are always scared to come into an open area and they are refraining from their daily activities in free environment. People may be terrified for a variety of reasons such as seeing a person who is suffering from COVID-19, but the fastest way is mass media [16]. The current outbreak has been much more prominent in media coverage than recent epidemics, including Ebola. For example, a Time Magazine study shows that there were 23 times more articles in English-language print news covering the coronavirus outbreak in its first month compared to the same time period for the Ebola epidemic in 2018 [17]. Media influence plays a significant role in spreading useful information’s through various sources such as television, community radio, Internet, and print media (such as newspapers and magazines), resulting in changed behaviour of a community [18]; therefore, it is influencing the progression of a pandemic [19, 20]. So, media-induced fear has a negative effect on the disease reproduction rate. Recently, Mohsen et al. [21] studied the global stability of a COVID-19 model with quarantine strategy and media coverage effects. According to Ahorsu et al. [22], one unique feature of pandemic viral infections is the fear that they can instill across large swathes of the population. Liu et al. [23] showed that mass media exposure had a significant positive impact on social networking service involvement and subjective norms, while preventive behaviour was largely affected by subjective norms; social networking service involvement had a significant positive effect on negative emotions, and excessive preventive intention was mainly influenced by negative emotions. Mathematical modelling is one of the best ways to express the dynamics of an epidemic. There are many infectious disease models, and most of them use differential equation systems for describing population dynamics with different characteristics in relation to infection [24–26]. Sardar et al. [27] study the effects of lockdown on future case counts in some estates and overall India. Sarkar et al. [28] proposed and analyzed a mathematical model to study the transmission dynamics of COVID-19 or SARS-CoV-2, where they performed the model validation with real data from India and some provinces of India. A mathematical model was used by Roy and Roy Bhattacharya [29] to predict the pandemic spread in India by using the data from 1 March 2020 to 23 April 2020 and they showed that the imposition of nationwide lockdown has played a significant role in restricting the spread of the pandemic. Hattaf and Yousfi [30] proposed a within-host model, which describes the interactions between SARS-CoV-2, host pulmonary epithelial cells, and cytotoxic T lymphocyte cells. Feng et al. [31] studied a COVID-19 model with the effects of media and quarantine in the UK. Chang et al. [32] proposed an SIHRS model which incorporated awareness of media coverage, which plays an important role in preventing and controlling infectious diseases. Some other works can be found in [33–36]. Inspired by above all these works, we have formulated a modified SEIR model to discuss the impact of fear on the disease transmission rate through media alertness. Generally, the disease transmission rate is related to the alertness of the disease in healthy people as well as related to the spreading ability of the disease. Thus, media coverage influences disease control in society.

The paper is organized as follows. In Section 2, we have formulated a mathematical model for the epidemic COVID-19, incorporating media coverage. Positivity and boundedness of the solutions of system (2) are performed in Section 3. The basic reproduction number is calculated and the stability of disease-free equilibrium is discussed in Section 4. The local and global stability of the endemic equilibrium point is presented in Section 5. Some numerical simulations are performed in Section 6 to validate our results. A brief discussion is given in Section 7.

2. Model Formulation

In this work, we have presented a modified classic SEIR model to study the effects of fear induced by media on the disease transmission rate of the epidemic COVID-19. In epidemic models, the bilinear incidence rate βSI is frequently used. A recent study [37] indicates that the fear effect will reduce the disease transmission rate, so we modify βSI by multiplying a factor f(α, I) which leads to f(α, I)βSI. Here, the parameter α represents the level of fear. For biological justification of α, I, and f(α, I), it is appropriate to consider the following:

(i)
f(0, I) = 1, i.e., in the absence of fear, there is no reduction in the disease transmission rate
(ii)
f(α, 0) = 1, i.e., when there is no infected population, there is no reduction in the susceptible population due to fear
(iii)
lim_α⟶∞f(α, I) = 0, i.e., when the amount of fear is very large, the disease transmission rate reduces to zero.
(iv)
lim_I⟶∞f(α, I) = 0, i.e., when the infected population is very large, the disease transmission rate reduces to zero due to the large fear factor
(v)
(∂f(α, I)/∂α) < 0, i.e., with the increase of fear, the disease transmission rate reduces
(vi)
(∂f(α, I)/∂I) < 0, i.e., as the infected population increases, the disease transmission rate decreases

For convenience of analysis, we assume the following form for the fear effect:

(1)

Our proposed model is based on splitting the total population N(t), at time t, into the subpopulations of susceptible S(t), exposed E(t) (those who have already been infected but in the incubation period and carry the virus without showing any symptoms), infectious I(t) (with infection capacity and symptomatic), isolated Q(t) (confirmed and infected), and recovered R(t) individuals, so that N(t) = S(t) + E(t) + I(t) + Q(t) + R(t). The model is given by the following system of nonlinear differential equations:

(2)

with initial conditions S(0) > 0, E(0) ≥ 0, I(0) > 0, Q(0) ≥ 0, and R(0) ≥ 0. All the model parameters and their description are given in Table 1.

Table 1. Parameters and their descriptions.

Parameters	Interpretation
r	Recruitment rate of susceptible which includes immigrants and newborns
β	Disease transmission rate
µ	Natural death rate of population
c	Infection rate from exposed class
γ	Rate at which infected people are getting isolated
d	Disease-induced death rate
d₁	The rate at which infected people are recovered
λ	Recovery rate from isolated class
α	The effect of fear through media coverage

3. Positivity and Boundedness of the Solution

For biological validity of system (2), it is necessary to prove that all solutions of system (2) with positive initial values will remain positive for all time t > 0. Thus, in this section, we want to prove the positivity and boundedness of solutions of our considered system.

Lemma 1. All solutions (S(t), E(t), I(t), Q(t), and R(t)) of system (2) with positive initial data will remain positive for all t > 0.

Proof. From the first equation of system (2), we get

(3)

Thus,

(4)

Similarly, it can be shown that E(t) > 0, I(t) > 0, Q(t) > 0, and R(t) > 0 for all t > 0.

Lemma 2. The closed set is positively invariant for system (2).

Proof. Adding all the equations of system (2), we obtained the rate of change of total population, which is given by

(5)

where N = S + E + I + Q + R.

It follows that (dN/dt) ≤ 0 whenN ≥ (r/μ). By using a standard comparison theorem [38], we can show that

(6)

Thus, we have N(t) ≤ (r/μ) as t⟶∞. Hence, Π is positively invariant so that the region Π attracts all solutions in .

4. Reproduction Number and Stability Analysis of Disease-Free Equilibrium

Basic reproduction number is one of the most important threshold parameters which can determine whether the infectious disease will die out or spread through the population as time increases. Here, we calculate the basic reproduction number for the COVID-19 model through the next-generation matrix method [39].

System (2) has a unique disease-free equilibrium point E₁(S⁻, 0,0,0, R⁻), where

and R¯ = 0. Then, using the notation in [39], the reproduction number R₀ of system (2) is calculated from the relation ρ(FV⁻¹), where ρ is the spectral radius of the matrix FV⁻¹ and

(7)

Here, F is a nonnegative matrix and V is a nonsingular M-matrix; therefore, FV⁻¹ is also nonnegative; hence, the spectral radius of FV⁻¹ is

(8)

To study the dynamic behaviour of system (2) around equilibria, we first calculate the Jacobian matrix of system (2) at an arbitrary point E¯(S, E, I, Q, R) which is given by

(9)

Theorem 1. The disease-free equilibrium point E₁ is locally asymptotically stable if R₀ < 1 and unstable if R₀ > 1.

Proof. Local stability of E₁ can be established by evaluating the Jacobian matrix at disease-free equilibrium. The Jacobian matrix at E₁ is given by

(10)

The eigenvalues of the characteristic equation of J(E₁) are −µ, −µ, and −(λ + µ), and the other two eigenvalues are the roots of the equation:

(11)

Clearly, if R₀ < 1, then all roots of equation (11) are negative, and if R₀ > 1, then equation (11) has one positive real root. Hence, if R₀ < 1, then disease-free equilibrium E₁ is locally asymptotically stable; otherwise, it is unstable.

Theorem 2. The disease-free equilibrium E₁ is globally asymptotically stable if R₀ < 1.

Proof. From the first equation of system (2), we obtain (dS/dt) ≤ r − μS. Now S = (r/μ) is the globally asymptotically stable equilibrium of (dS/dt) ≤ r − μS, so for any given ∈>0, we have

(12)

Thus, we get

(13)

System (13) has a unique equilibrium (0, 0, 0) and the corresponding eigenvalues are −(λ + µ) and the roots of the equation:

(14)

For sufficiently small ∈>0, the quantity (c + μ)(γ + d + d₁ + μ) − cβ((r/μ) + ɛ) > 0 if R₀ < 1. Thus, all eigenvalues of equation (14) have negative real parts. Hence, (0, 0, 0) is locally stable. It is easy to prove that equilibrium point (0, 0, 0) is globally asymptotically stable for R₀ < 1. Therefore, by comparison, it follows that lim_t⟶∞E(t) = 0, lim_t⟶∞I(t) = 0 and lim_t⟶∞Q(t) = 0.

Then, for above ɛ> 0, there exists a T > 0 such that if t > T, E(t) < ɛ, I(t) < ∈, and Q(t) < ɛ. From equation (2) of system (2), we get

(15)

For sufficiently small ɛ > 0, we observed that (r/βɛ + μ) is a globally asymptotically stable equilibrium of

(16)

Thus, by comparison, we have

(17)

As, this inequality holds for sufficiently small >0, and thus

(18)

Therefore, from equations (12) and (18), we get

(19)

Hence, disease-free equilibrium E₁ is globally asymptotically stable if R₀ < 1.

5. Existence of Endemic Equilibrium and Stability Analysis

Let us choose m₁ = c + µ, m₂ = d + d₁ + γ + µ, and m₃ = λ + µ.

The system has one interior equilibrium point E₂(S^∗, E^∗, I^∗, Q^∗, R^∗) where

(20)

Therefore, the endemic equilibrium point E₂ will be feasible when R₀ > 1.

Theorem 3. The endemic equilibrium point E₂ is locally asymptotically stable if R₀ > 1.

Proof. The characteristic equation of J(E₂) is given by

(21)

where

(22)

Clearly, equation (21) has two negative real roots t₁ = −µ and t₂ = −(µ + λ) and the other three roots of equation (21) are obtained from the following equation:

(23)

Now if R₀ > 1, then C > 0 and AB−C > 0. So, it follows from Routh–Hurwitz criteria [40] that all roots of equation (23) have negative real parts. Hence, the endemic equilibrium point E₂ is locally asymptotically stable if R₀ > 1.

Remark 1. From the above analysis, we observed that when R₀ < 1, only the disease-free equilibrium E₁ exists and it is locally as well as globally stable. Again when R₀ > 1, the endemic equilibrium point E₂ exists and is asymptotically stable, but in this case the disease-free equilibrium loses its stability and becomes unstable in nature. Therefore, we may conclude that there is a change of feasibility as well as stability at R₀ = 1. Using the articles [41–43], it is concluded that the system undergoes a transcritical bifurcation at R₀ = 1.

Theorem 4. System (2) is uniformly persistent in the region Π if and only if R₀ > 1.

Proof. Consider that η is any point in the positive octant and o(η) is any orbit through the point η where Ω(η) is the bounded omega limit set of the orbit through η. Clearly, Ω(η) is bounded. Suppose the disease-free equilibrium point E₁ is not in Ω(η). If E₁ ∈ Ω(η), then by Butler–McGehee lemma [44], there exists a point x in Ω(η)∩W^s(E₁), where W^s(E₁) is the stable manifold of E₁. Since o(x) lies in Ω(η) and W^s(E₁) is in the S-Q-R plane, it can be concluded that o(x) is unbounded, which is a contradiction. Thus, Ω(η) does not intersect any of the coordinate planes; hence, system (2) is persistent. Again since system (2) is bounded so by the main theorem proposed by Butler et al. [45], the system is uniformly persistent.

Again since system (2) is uniformly persistent, there exists a time T such that (S(t), E(t), I(t), Q(t), R(t)) > for t > T.

To investigate the global stability of the endemic equilibrium point of system (2), we first reduce our system as recovered class does not have any effect on the dynamics of S, E, I, and Q class. So system (2) can be written as

(24)

Here, we apply the high-dimensional Bendixson criterion which is developed by Li and Muldowney [46] to prove the global stability of the endemic equilibrium point E₂. Consider the open set G ⊂ Rⁿ. Let us consider the following differential equation:

(25)

where f: x⟶f(x) ∈ Rⁿ be C¹ for x ∈ G.

Consider B is a general 4 × 4 matrix denoted by B = (a_ij)_4×4, and then, its second additive compound matrix B^² is defined by

(26)

To derive a high-dimensional Bendixson criterion as shown in [38], one has to show that the second compound equation

(27)

with respect to a solution x(t, x₀) ∈ G of system (25) is equiuniformly asymptotically stable, namely, for each x₀ ∈ G, system (27) is uniformly asymptotically stable, and the exponential decay rate is uniform for x₀ in each compact subset of G, where G ⊂ Rⁿ is an open connected set. The equiuniform asymptotic stability of (27) implies that if G is simply connected, then it does not admit any invariant simple closed rectifiable curve, including periodic orbits, homoclinic orbits, and heteroclinic cycles.

Next, we state the following lemma which is used in [47].

Lemma 3 (see [46].)Let G ⊂ Rⁿ be a simply connected region. Assume that the family of linear systems (27) is equiuniformly asymptotically stable. Then

(i)
G contains no simple closed invariant curves, including periodic orbits, homoclinic orbits, and heteroclinic cycles
(ii)
Each semiorbit in G converges to a single equilibrium

In particular, if G is positively invariant and contains a unique equilibrium E¯, then E¯ is globally asymptotically stable in G.

Theorem 5. Assume that N(t) ≤ (r/μ) and R₀ > 1. If there exist ω, θ, ξ, ρ, and ζ. such that max {b₁₁ + (b₁₂ω/θ) + (b₁₄ω/ξ), (b₂₁θ/ω) + b₂₂, (b₃₂/θ) + b₃₃ + (b₃₆/ς), (b₄₂ξ/θ) + b₄₄, b₅₃ρ + (b₅₄ρ/ξ) + b₅₅ + (b₅₆/ζ), (b₆₅ζ/ρ) + b₆₆} < 0, then the endemic equilibrium point E₂ is globally asymptotically stable.

Proof. For model (24), we denote X = (S, E, I, Q)^T and F(x) = (f₁, f₂, f₃, f₄)^T. Then, the second compound matrix of system (24) can be written as

(28)

where

(29)

The second compound system (dZ/dt) = (∂F^[2]/∂X)Z(t) then becomes

(30)

Now, define V(Z) = max{ω|z₁|, θ|z₂|, |z₃|, ξ|z₄|, ρ|z₅|, ζ|z₆|}.

From the direct calculation, we get the following inequalities:

(31)

where (d⁺/dt) denotes the right-hand derivative and

(32)

Therefore, (d⁺/dt)V(Z(t)) ≤ ψVZ(t), with ϕ = max{b₁₁ + (b₁₂ω/θ) + (b₁₄ω/ξ), (b₂₁θ/ω) + b₂₂, (b₃₂/θ) + b₃₃ + (b₃₆/ς), (b₄₂ξ/θ) + b₄₄, b₅₃ρ + (b₅₄ρ/ξ) + b₅₅ + (b₅₆/ζ), (b₆₅ζ/ρ) + b₆₆} < 0.

Thus, from the assumption of the theorem, we find a positive constant η such that φ ≤ −η < 0, and hence, V(Z(t)) ≤ V(Z(s))exp(−η(t − s)), t ≥ s > 0.

This confirmed the equiuniform asymptotic stability of the second compound system. Therefore, system (2) or (24) has no nontrivial periodic solutions; hence, the endemic equilibrium point E₂ of system (2) is globally asymptotically stable.

6. Case Study: World

Here, we performed some numerical simulations with some real data taken from [48,49] and some hypothetical data to observe the dynamics of our proposed COVID-19 model. For this simulation purpose, we used the following set of parameters, values of which are given in Table 2. The parameters are calculated per 1000/day and we assumed that the total population of the world is 7.6 billion. In terms of scaled variables, we assumed the initial population size is (S(0), E(0), I(0), Q(0), R(0)) = (1, 0.05, 0.002, 0.002, 0.003).

Table 2. Parameter estimation for the world.

Parameter	Value	References
r	5.812 × 10⁻⁴	[48]
β	0.5	Estimated
α	0	—
µ	0.001	[48]
c	0.1818	[49,50]
d₁	0.027	[48]
γ	0.0802	[48]
d	9.7 × 10⁻³	[50]
λ	4.87 × 10⁻⁴	[50]

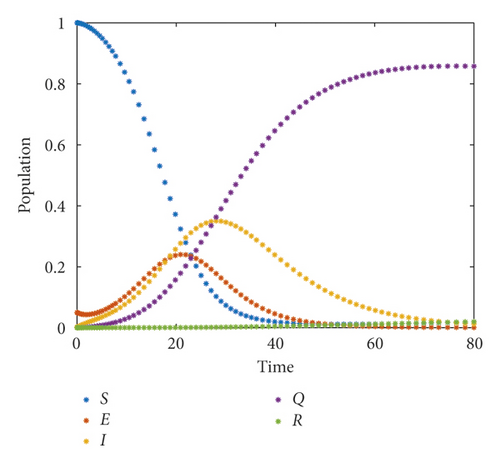
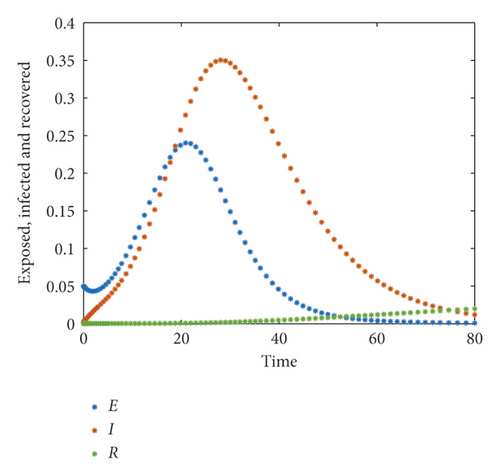
For this set of parameters, we calculate R₀ = 3.1794 > 1. Hence, Theorems 3 and 4 are satisfied which means the system is persistent and it ensures the existence of the endemic equilibrium point E₂. From Figure 1(a), we observed that, in the absence of media coverage, susceptible population is decreasing, but the exposed population and infected population are increasing over time which means more people are being exposed, and within a short time period, a large number of people are infected. From Figure 1(b), we also have seen that the recovered population is not growing as much as the infected population and exposed population. So, as a result, there is an outbreak within a short time span.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Dynamics of (a) all population over time and (b) exposed, infected, and recovered classes over time, when the system has no fear effect.

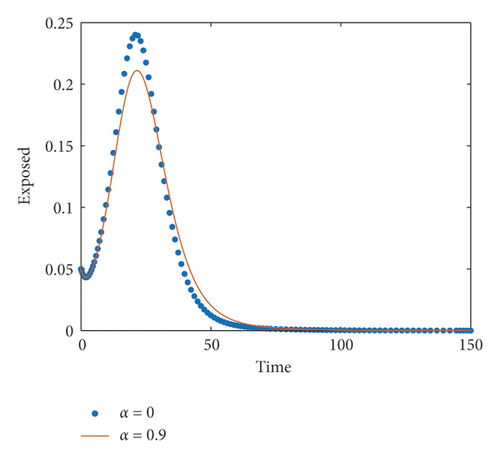
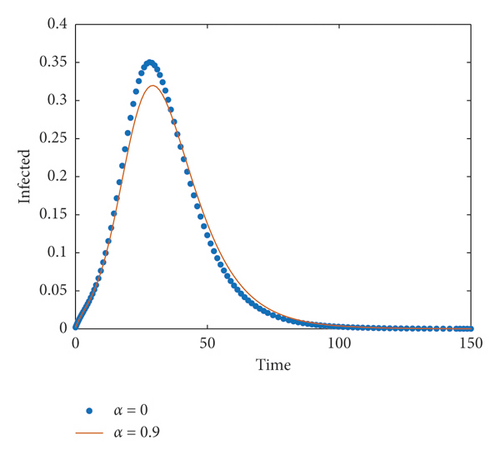
Now we introducing fear effect (α) into the model system (2), and here, our main focus is whether media-induced fear can affect the disease transmission rate or not. From Figure 2, we observed that when the value of α is increasing, the population rate of exposed as well as infected class is decreasing from their original position where remaining all other parameters are as above. So we conclude that fear has an important role in the dynamics of our proposed model.

Sensitivity analysis is one of the most important parts to get an overview of the most influential parameters in modelling an infectious disease. As system stability totally depends on reproduction number (R₀), so we want to verify how the sensitive parameters are related to R₀, and therefore, we compute the sensitivity analysis of R₀ with respect to the model parameters. Here, we are using the model parameters from Table 2. The definition of the normalized sensitivity index of R₀ with respect to β is given by

(33)

The sensitivity indices of R₀ with respect to other parameters are as follows:

(34)

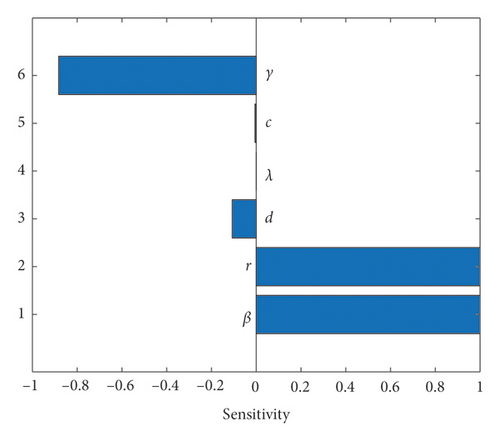
From this analysis, we observed that J_β^R0 = 1, which implies if the disease transmission rate increases by 1%, then it will increase the value of R₀ by 1% and vice versa. Again, we see that that means when increasing the value of γ by 1%, the value of R₀ will be reduced by 0.88%. Thus, it can be concluded that reproduction number is positively correlated with the disease transmission rate but negatively correlated with γ. Therefore, to prevent disease transmission, it is necessary to obey social distancing or lockdown and isolate more infected people. A sensitivity analysis figure is plotted in Figure 3.

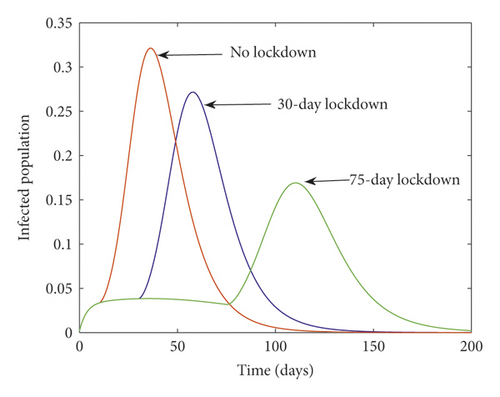
The effectiveness of 30-day lockdown or more is described in Figure 4. From this figure, we observed that 30-day lockdown is not sufficient to control the disease, but if we applied a lockdown for 75 days or more, then it shows that the lowest number of people infected and the epidemic may be under control.

7. Discussion

Media coverage plays an important role in the transmission process of infectious disease. People will be more aware of COVID-19 infection if they learn more about the transmission of the disease through media; as a result, they will change their behaviour and take correct precautions such as frequent handwashing, wearing masks, maintaining social distance, reducing party to take risk aversion, and even isolating themselves at home to avoid contacting with others. Modelling studies have shown that fear has a significant effect on reducing the severity of a pandemic and it has been shown that fear is directly correlated with the increase in social distancing behaviour as well as taking more precautions. Thus, in this paper, we have formulated a mathematical model with media-induced fear to analyze the epidemic of COVID-19. Analytically, we proved that system stability mainly depends on the basic reproduction number R₀. We have seen that if R₀ > 1, then the endemic equilibrium point exists and is globally asymptotically stable which means the disease persists in the system. So, to avoid such circumstances, we must focus on the disease transmission rate. From sensitivity analysis, we also observed that reproduction number is positively correlated with the disease transmission rate. If the disease transmission rate is very low, then people are less exposed and we can control the epidemic. Numerically, from Figure 2, we conclude that if the rate of fear increases through media, then it can reduce the infection rate, and increasing the amount of fear can stabilize the system.

Conflicts of Interest

The author declares that there are no conflicts of interest.

Open Research

Data Availability

All supportable data are given in the main text.

References

1 Donnely C. A., GhaniG A. C., Leung M. et al., Epidemiological determinants of spread of causal agent of severe acute respiratory syndrome in Hong Kong, Lancet. (2003) 361, 1761–1766.
10.1016/S0140-6736(03)13410-1
PubMed Web of Science® Google Scholar
2 Cauchemez S., Fraser C., Van Kerkhove M. D. et al., Middle East respiratory syndrome coronavirus: quantification of the extent of the epidemic, surveillance biases, and transmissibility, The Lancet Infectious Diseases. (2014) 14, 50–56, https://doi.org/10.1016/s1473-3099(13)70304-9, 2-s2.0-84890433761.
10.1016/S1473-3099(13)70304-9
PubMed Web of Science® Google Scholar
3 Cai J., Sun W., Huang J., Gamber M., Wu J., and He G., Indirect virus transmission incluster of COVID-19 cases, Wenzhou, China, 2020, Emerging Infectious Diseases. (2020) 26, https://doi.org/10.3201/eid2606.200412.
10.3201/eid2606.200412
Web of Science® Google Scholar
4 Zhang Y., Chen C., Zhu S. et al., Isolation of 2019-nCoV from a stool specimen ofa laboratory-confirmed case of the coronavirus disease 2019 (COVID-19), China CDC Weekly. (2020) 2, no. 8, 123–124, in Chinesehttps://doi.org/10.46234/ccdcw2020.033.
10.46234/ccdcw2020.033
PubMed Google Scholar
5 Chandan M., Modes of transmission of COVID-19 outbreak- a mathematical study, International Journal of Nonlinear Science. (2020) 30, no. 2-3, 153–162, https://doi.org/10.1101/2020.05.16.20104315.
10.1101/2020.05.16.20104315
Google Scholar
6 https://www.who.int/emergencies/diseases/novel-coronavirus-2019.
Google Scholar
7 Jiang F., Deng L., Zhang L., Cai Y., Cheung C. W., and Xia Z., Review of the clinical characteristics of coronavirus disease 2019 (COVID-19), Journal of General Internal Medicine. (2020) 35, no. 5, 1545–1549.
10.1007/s11606-020-05762-w
PubMed Web of Science® Google Scholar
8 https://www.gavi.org/vaccineswork.
Google Scholar
9 Funk S., The spread of awareness and its impact on epidemic outbreaks, in Proceedings of the National Academy of Sciences. (2009) 106, no. 16, 6872–6877, https://doi.org/10.1073/pnas.0810762106, 2-s2.0-66149153486.
10.1073/pnas.0810762106
CAS PubMed Web of Science® Google Scholar
10 Del Valle S., Effects of behavioral changes in a smallpox attack model, Mathematical Biosciences. (2005) 195, no. 2, 228–251, https://doi.org/10.1016/j.mbs.2005.03.006, 2-s2.0-19544378879.
10.1016/j.mbs.2005.03.006
CAS PubMed Web of Science® Google Scholar
11 Poletti P., The effect of risk perception on the 2009 h1n1 pandemic influenza dynamics, PloS one. (2011) 6, no. 2.
10.1371/journal.pone.0016460
Google Scholar
12 Perra N., Towards a characterization of behavior-disease models, PloS One. (2011) 6, no. 8, https://doi.org/10.1371/journal.pone.0023084, 2-s2.0-79961051637.
10.1371/journal.pone.0023084
Web of Science® Google Scholar
13 Epstein J. M., Coupled contagion dynamics of fear and disease: mathematical and computational explorations, PLoS One. (2008) 3, no. 12, https://doi.org/10.1371/journal.pone.0003955, 2-s2.0-58049191447.
10.1371/journal.pone.0003955
PubMed Web of Science® Google Scholar
14 Kimetal Y., Public risk perceptions and preventive behaviors during the 2009 h1n1 influenza pandemic, Disaster Medicine and Public Health Preparedness. (2015) 9, no. 2, 145–154, https://doi.org/10.1017/dmp.2014.87, 2-s2.0-84928540853.
10.1017/dmp.2014.87
PubMed Web of Science® Google Scholar
15 Cowling B. J., Community psychological and behavioural responses through the first wave of the 2009 influenza a (h1n1) pandemic in Hong Kong, The Journal of Infectious Diseases. (2010) 202, no. 6, 867–876, https://doi.org/10.1086/655811, 2-s2.0-77955956691.
10.1086/655811
PubMed Web of Science® Google Scholar
16 Towers S., Mass media and the contagion of fear: the case of Ebola in America, PloS One. (2015) 10, no. 6, https://doi.org/10.1371/journal.pone.0129179, 2-s2.0-84936088628.
10.1371/journal.pone.0129179
Web of Science® Google Scholar
17 https://theconversation.com/coronavirus-how-media-coverage-of-epidemics-oftenstokes-fear-and-panic-131844.
Google Scholar
18 Wakefield M. A., Use of mass media campaigns to change health behaviour, The Lancet. (2010) 376, no. 9748, 1261–1271, https://doi.org/10.1016/s0140-6736(10)60809-4, 2-s2.0-77958019843.
10.1016/s0140-6736(10)60809-4
PubMed Web of Science® Google Scholar
19 Collinson S. and Heffernan J. M., Modelling the effects of media during an influenza epidemic, BMC Public Health. (2014) 14, no. 1, https://doi.org/10.1186/1471-2458-14-376, 2-s2.0-84899970431.
10.1186/1471-2458-14-376
PubMed Web of Science® Google Scholar
20 Collinson S., The effects of media reports on disease spread and important public health measurements, PloS One. (2015) 10, no. 11, https://doi.org/10.1371/journal.pone.0141423, 2-s2.0-84951129957.
10.1371/journal.pone.0141423
Web of Science® Google Scholar
21 Mohsen A. A., Al-Husseiny H. F., Zhou X., and Hattaf K., Global stability of COVID-19 model involving the quarantine strategy and media coverage effects, AIMS Public Health. (2020) 7, no. 3, 587–605.
10.3934/publichealth.2020047
PubMed Google Scholar
22 Ahorsu D. K., Lin C. Y., Imani V. et al., The fear of COVID-19 scale: development and initial validation, International Journal of Mental Health and Addiction. (2020) 1–9, https://doi.org/10.1007/s11469-020-00270-8.
10.1007/s11469-020-00270-8
Web of Science® Google Scholar
23 Liu L., Xie J., Li K., and Ji S., Exploring how media influence preventive behavior and excessive preventive intention during the COVID-19 pandemic in China, International Journal of Environmental Research and Public Health. (2020) 17, no. 21, 7990, https://doi.org/10.3390/ijerph17217990.
10.3390/ijerph17217990
Web of Science® Google Scholar
24 Singh B. P. and SIngh G., Modeling tempo of COVID-19 pandemic in India and significance of lockdown, Journal of Public Affairs. (2020) 4, e2257.
Google Scholar
25 Hattaf K., Lashari A. A., Louartassi Y., and Yousfi N., A delayed SIR epidemic model with general incidence rate, Electronic Journal of Qualitative Theory of Differential Equations. (2013) 3, 9, https://doi.org/10.14232/ejqtde.2013.1.3.
10.14232/ejqtde.2013.1.3
Google Scholar
26 Maji C., Modes of transmission of COVID-19 outbreak-a mathematical study, International Journal of Nonlinear Science. (2020) 30, no. 1, 76–84.
Google Scholar
27 Sardar T., Nadim S. S., Rana S., and Chattopadhyay J., Assessment of lockdown effect in some states and overall India: a predictive mathematical study on COVID-19 outbreak, Chaos, Solitons and Fractals. (2020) 139, 110078, https://doi.org/10.1016/j.chaos.2020.110078.
10.1016/j.chaos.2020.110078
PubMed Web of Science® Google Scholar
28 Sarkar K., Khajanchi S., and Nieto J. J., Modeling and forecasting of the COVID-19 pandemic in India, Chaos, Solitons and Fractals. (2020) 139, 110049, https://doi.org/10.1016/j.chaos.2020.110049.
10.1016/j.chaos.2020.110049
PubMed Web of Science® Google Scholar
29 Roy S. and Roy Bhattacharya K., Spread of COVID-19 in India: a mathematical model, Journal of Science and Technology. (2000) 5, no. 3, 41–47, https://doi.org/10.46243/jst.2020.v5.i3.pp41-47.
10.46243/jst.2020.v5.i3.pp41-47
Google Scholar
30 Hattaf K. and Yousfi N., Dynamics of SARS-CoV-2 infection model with two modes of transmission and immune response, Mathematical Biosciences and Engineering. (2020) 17, no. 5, 5326–5340, https://doi.org/10.3934/mbe.2020288.
10.3934/mbe.2020288
PubMed Web of Science® Google Scholar
31 Feng L. X., Jing S. L., Hu S. K., Wang D. F., and Huo H. F., Modelling the effects of media coverage and quarantine on the COVID-19 infections in the UK, Math Biosci Eng. (2020) 17, no. 4, 3618–3636, https://doi.org/10.3934/mbe.2020204.
10.3934/mbe.2020204
PubMed Web of Science® Google Scholar
32 Chang X. H., Liu X., Jin Z., and Wang J. R., Studying on the impact of media coverage on the spread of COVID-19 in Hubei Province, China, Math Biosci Eng. (2020) 17, no. 4, 3147–3159, https://doi.org/10.3934/mbe.2020178.
10.3934/mbe.2020178
PubMed Web of Science® Google Scholar
33 Yan Q., Tang Y., Yan D. et al., Impact of media reports on the early spread of COVID-19 epidemic, Journal of Theoretical Biology. (2020) 502, 110385, https://doi.org/10.1016/j.jtbi.2020.110385.
10.1016/j.jtbi.2020.110385
CAS PubMed Web of Science® Google Scholar
34 Zhou W. K., Wang A. L., Xia F. et al., Effects of media reporting on mitigating spread of COVID-19 in the early phase of the outbreak, Mathematical Biosciences and Engineering. (2020) 17, no. 3, 2693–2707, https://doi.org/10.3934/mbe.2020147.
10.3934/mbe.2020147
PubMed Web of Science® Google Scholar
35 Huang F., Ding H., Liu Z. et al., How fear and collectivism influence public’s preventive intention towards COVID-19 infection: a study based on big data from the social media, BMC Public Health. (2020) 20, no. 1, https://doi.org/10.1186/s12889-020-09674-6.
10.1186/s12889-020-09674-6
Web of Science® Google Scholar
36 Kumar S., Sharma B., and Singh V., Modelling the role of media induced fear conditioning in mitigating post-lockdown covid-19 pandemic: perspectives on india, 2004, https://arxiv.org/pdf/2004.13777.
Google Scholar
37 Lin C. Y., Social reaction toward the 2019 novel coronavirus (COVID-19), Social Health and Behavior. (2020) 3, 2, https://doi.org/10.4103/shb.shb_11_20.
10.4103/SHB.SHB_11_20
Google Scholar
38 Smith H. L. and Waltman P., The Theory of the Chemostat, 1995, Cambridge University Press, Cambridge, UK.
10.1017/CBO9780511530043
Google Scholar
39 van den Driessche P. and Watmough J., Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission, Mathematical Biosciences. (2002) 180, 29–48.
10.1016/S0025-5564(02)00108-6
CAS PubMed Web of Science® Google Scholar
40 Murray J. D., Mathematical Biology, 1988, Springer-Verlag, Berlin, Germany.
Google Scholar
41 Guckenheimer G. and Holmes P., Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, 1983, Springer-Verlag, New York, NY, USA.
10.1007/978-1-4612-1140-2
Google Scholar
42 Jana S., Haldar P., and Kar T. K., Mathematical analysis of an epidemic model with isolation and optimal controls, International Journal of Computer Mathematics. (2016) 94, no. 2017, 13181336, https://doi.org/10.1080/00207160.2016.1190009, 2-s2.0-84975527357.
10.1080/00207160.2016.1190009
Web of Science® Google Scholar
43 Kar T. K. and Jana S., A theoretical study on mathematical modeling of an infectious disease with application of optimal control, Bio-Systems. (2013) 111, no. 1, 37–50, https://doi.org/10.1016/j.biosystems.2012.10.003, 2-s2.0-84872389705.
10.1016/j.biosystems.2012.10.003
CAS PubMed Web of Science® Google Scholar
44 Freedman H. I. and Waltman P., Persistence in models of three interacting predator prey populations, Mathematical Biosciences. (1984) 68, 213–231, https://doi.org/10.1016/0025-5564(84)90032-4, 2-s2.0-48749138514.
10.1016/0025-5564(84)90032-4
Web of Science® Google Scholar
45 Butler G. J., Freedman H. I., and Waltman P., Uniformly persistent systems, in Proceedings of the American Mathematical Society. (1986) 96, 425–430, https://doi.org/10.1090/s0002-9939-1986-0822433-4, 2-s2.0-84968505772.
10.1090/S0002-9939-1986-0822433-4
Web of Science® Google Scholar
46 Li M. Y. and Muldowney J., On Bendixson’s criterion, Journal of Differential Equations. (1993) 106, 27–39, https://doi.org/10.1006/jdeq.1993.1097, 2-s2.0-0002153279.
10.1006/jdeq.1993.1097
Web of Science® Google Scholar
47 Sun C. and Loreau M., Dynamics of a three-species food chain model with adaptive traits, Chaos, Solitons and Fractals. (2009) 41, 2812–2819, https://doi.org/10.1016/j.chaos.2008.10.015, 2-s2.0-67649547633.
10.1016/j.chaos.2008.10.015
Web of Science® Google Scholar
48 https://worldpopulationreview.com.
Google Scholar
49 Ivorra B. and Ramos A. M., Application of the Be-CoDiS Mathematical Model to Forecast the International Spread of the 2019–20 Wuhan Coronavirus Outbreak, 2020, Complutense University of Madrid, Madrid, Spain.
Google Scholar
50 https://www.worldometers.info.
Google Scholar

Citing Literature

All articles

Impact of Media-Induced Fear on the Control of COVID-19 Outbreak: A Mathematical Study

Abstract

1. Introduction

2. Model Formulation

3. Positivity and Boundedness of the Solution

4. Reproduction Number and Stability Analysis of Disease-Free Equilibrium

5. Existence of Endemic Equilibrium and Stability Analysis

6. Case Study: World

7. Discussion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Impact of Media-Induced Fear on the Control of COVID-19 Outbreak: A Mathematical Study

Abstract

1. Introduction

2. Model Formulation

3. Positivity and Boundedness of the Solution

4. Reproduction Number and Stability Analysis of Disease-Free Equilibrium

5. Existence of Endemic Equilibrium and Stability Analysis

6. Case Study: World

7. Discussion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information