Based on the nonlocal theory and the theory of saturated porous media, the mathematical and physical model and governing equations of the steady-state response of the incompressible nonlocal saturated poroelastic beam under vertical harmonic loading are established with assumption of the movement of the liquid-phase fluid only in the axial direction of the beam and considering the nonlocal effects such as particle size, pore size, and pore dynamic stress. The dynamic response of a saturated poroelastic cantilever beam with permeability at both ends under a vertical harmonic concentrated force at the free end is studied. In the frequency domain, the analytical expressions of deflection amplification factor and equivalent couple amplification factor of liquid fluid pressure are given. The effects of nonlocal coefficient τ, mechanical parameter α, and geometric parameter β on the deflection amplification factor and equivalent couple amplification factor at the midpoint of the nonlocal saturated poroelastic cantilever beam are studied. The results show that the steady-state vibration of the incompressible nonlocal saturated poroelastic cantilever beam has resonance. When the nonlocal effect is considered, the deflection amplification factor and the equivalent couple amplification factor are larger, so the influence of the nonlocal effect on the steady-state response of the beam should not be ignored. The geometric parameter β has significant effect on the peak positions of the curves of the deflection amplification factor and the equivalent couple amplification factor varying with frequency.

1. Introduction

Saturated porous structures are widely used in civil engineering, aviation, transportation, and other engineering fields because of their good sound absorption and energy consumption. The research on the mechanical behavior of saturated porous structures has significant engineering application value and academic value. Therefore, since Biot put forward the theory of saturated porous media [1, 2], the research on vibration and wave propagation in saturated porous media has attracted the attention of many scholars [3–9]. Since Biot theory assumes that the wave length of saturated porous media is larger than the pore size, the influence of pore size effect on wave propagation is not considered and the influence of pore size is very significant at high frequency [10]. As a method of engineering description, Biot theory has some defects in the model [11] and it is difficult to determine the elastic constant and inertial coupling coefficient in the Biot dynamic equation. The porous media theory based on the mixture axiom and the concept of volume fraction is more rigorous and reasonable. The concept of volume fraction in porous media theory can avoid the incompatibility of the model and can also consider the effects of dynamic, material, and geometric nonlinearity. Aiming at the static and dynamic problems of saturated porous structures, Busse et al. [12] established the dynamic mathematical model of the saturated poroelastic Mindlin plate based on Biot theory and gave the virtual work principle with rotation angle, deflection, and pore stress as basic unknowns. Iesan and Nappa [13] studied the thermal stress of poroelastic cylinders and circular tubes. Li et al. [14] studied the transverse vibration of fluid saturated poroelastic beams and obtained the solutions of free vibration and forced vibration. Cederbaum et al. [15] studied the mechanical behavior of saturated poroelastic beams and rods and pointed out that Mandel–Cryer phenomenon also exists in the deformation response of poroelastic beams and rods. Xiao and Chen [16] established the nonlinear governing equation of large deflection of the incompressible saturated poroelastic beam under the constraint that the pore fluid only diffuses along the axial direction of the beam and studied the nonlinear bending problem of the saturated poroelastic cantilever beam with fixed impermeability at one end and free permeability at another end under a sudden constant transverse concentrated load at the free end. However, in the analysis of mechanical behavior of saturated porous structures, the scale effects such as solid skeleton particle size, pore size, and pore stress are not considered. As the engineering structure is developing towards miniaturization and intelligence, it is more and more important to consider the influence of structural scale effect on mechanical properties. The nonlocal theory in [17, 18] believes that the stress at a point in the continuum is related not only to the strain at that point but also to the strain and deformation history of all points in the area near the point. The nonlocal theory considering the scale effect is mainly used to study the mechanical problems of nanostructures. In recent years, scholars began to combine the nonlocal theory with the Biot saturated soil theory [19, 20] and apply it to the field of geotechnical engineering. In this paper, the dynamic control equation of the incompressible nonlocal saturated poroelastic beam under a vertical simple harmonic load is established by combining the porous medium theory and nonlocal theory and the steady-state response of the saturated poroelastic cantilever beam with permeable ends under simple harmonic concentrated force at the free end is studied.

2. Mathematical Model and Basic Equation

The incompressible two-phase saturated poroelastic cantilever beam under the action of vertical simple harmonic force shown in Figure 1 is studied, where i is an imaginary unit, ω is the frequency of the simple harmonic force, Q₀ is the amplitude, and the surface of the cantilever beam is impermeable. If the mechanical properties of saturated poroelastic beams are described by using the porous medium theory without considering the influence of volume force, the governing equation is

(1)

(2)

(3)

Here, σ^SE is the effective stress of the solid skeleton, p is the pressure of the liquid phase, ρ^S is the macroscopic density of the solid phase, ρ^F is the macroscopic density of the liquid phase, κ is the solid-liquid phase coupling coefficient, u^S is the displacement tensor of the solid phase, v^FS represents the velocity of the liquid phase relative to the solid phase, and n^F is the volume fraction of the liquid phase, from which the volume fraction of the solid phase is n^S = 1 − n^F.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Incompressible nonlocal saturated poroelastic beam under vertical harmonic loading.

The nonlocal theory proposed by Eringen holds that the stress at a point depends not only on the strain at that point but also on the weighted average of all point strains in the whole region. Here, considering the influence of nonlocal effects such as particle size, pore size, and pore dynamic stress of the solid skeleton of the saturated poroelastic beam, it is assumed that the solid skeleton of the saturated poroelastic beam is linear elastic, uniform, and isotropic material. Without the influence of physical force, the basic equation of Eringen’s nonlocal theory is [17]

(4)

(5)

where σ_ij is the nonlocal stress tensor, ε_ij and u_i are the nonlocal strain and displacement tensor, respectively, C_ijkl is the fourth-order elastic tensor, and ∫_Vχ(|r − r^′|, τ) is the nonlocal modulus, which determines the weight coefficient of the corresponding point strain, where τ is the nonlocal kernel function. The influence of the pore dynamic stress, pore size, and particle size of the saturated poroelastic beam is reflected by the nonlocal kernel function; |r − r^′| is the Euclidean distance. At the same time, Eringen also gave the differential formula of Equation (4), that is,

(6)

where

and

represent the nonlocal stress tensor and classical stress tensor, respectively. e₀ represents the nonlocal material constants, a is the internal characteristic length which is related to solid skeleton particle size and pore size, and ∇² is the Laplace operators.

The constitutive equation of solid skeleton under small deformation is

(7)

where σ^LSE is the classical effective stress of the solid skeleton, ε^S is the strain tensor of phase skeleton, I is the identity matrix, and λ^S, μ^S are the Lame constants.

3. Dynamic Control Equation of the Incompressible Nonlocal Saturated Poroelastic Beam

The dynamic problem of the incompressible nonlocal saturated poroelastic beam under a vertical simple harmonic load is one-dimensional, and the displacement of the saturated poroelastic beam is

(8)

where w^S(x, t) is the vertical displacement of the solid phase of the saturated poroelastic beam. Assuming that the liquid phase moves only along the axial direction, the velocities in x, y, and z directions satisfy

(9)

Assuming a small amount of stress

, it can be obtained from equations (6) and (7) that

(10)

(11)

(12)

where

is the volume strain of the solid skeleton,

and

are the normal stress and shear stress on the cross section of the saturated poroelastic beam, respectively, and E^S and G are the elastic modulus and shear modulus of the solid phase of the saturated poroelastic beam, respectively. λ^S and μ^S are the lame constants and satisfy

(13)

Let

(14)

Here,

and

are the solid bending moment and shear force on the cross section of saturated poroelastic beam, respectively, and M_p is the equivalent couple of the pore fluid pressure.

Ignoring the rotational inertia of the pore liquid to the solid skeleton, multiplying the equation in the ox direction of equation (1) by z and integrating it on the cross-sectional area A of the beam, one obtains

(15)

If the equation in the oz direction of equation (1) is integrated on the cross-sectional area A of the beam, we have

(16)

Here,

. For the rotational inertia of the solid skeleton, multiplying the equation in the ox direction of equation (2) by z and integrating it on the cross-sectional area A of the beam, we obtain

(17)

It can be obtained from equations (3) and (10) that

(18)

Both ends of equation (18) are multiplied by z and integrated on the cross-sectional area A of the beam, and we have

(19)

It can be obtained from equations (17) and (19) that

(20)

Multiplying both ends of equation (11) by z and integrating it on area A, we have

(21)

where I = ∬_Az² dy dz is the moment of inertia of the cross section. Integrating both ends of equation (12) on area A, we can obtain

(22)

Calculating

on both ends of equations (15) and (16), respectively, and considering equations (21) and (22), we obtain

(23)

(24)

It can be obtained from equations (20) and (21) that

(25)

Sorting out equations (24)–(26), one obtains

(26)

Equations (25) and (26) are the vertical dynamic control equations of the incompressible nonlocal saturated poroelastic beams.

4. Steady-State Response of the Incompressible Nonlocal Saturated Poroelastic Cantilever Beam under a Vertical Simple Harmonic Load

Here, taking the steady-state response of the incompressible nonlocal saturated poroelastic cantilever beam shown in Figure 2 as an example, the same method can be used to analyze the steady-state response of the incompressible nonlocal saturated poroelastic cantilever beam with other boundaries. A simple harmonic concentrated force Q(t) = q₀e^iωt is acting on the free end of an incompressible nonlocal saturated poroelastic cantilever beam. The corresponding boundary conditions are

(27)

(28)

(29)

(30)

(31)

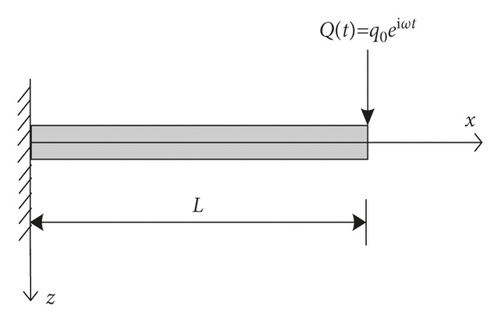
Under the action of the simple harmonic load, the incompressible nonlocal saturated poroelastic cantilever beam vibrates in a steady state. Considering the harmony of the problem, the parameters meet , , and , where , , and are the amplitudes of w^S, M_p, and , respectively. The following equations can be obtained by substituting w^S, M_p, and into vertical dynamic control equations (25) and (26) of the incompressible nonlocal saturated poroelastic beam:

We introduce the dimensionless variables and parameters as follows:

, τ = e₀a/L, T = v/L,

, q = L²Q/E^SI,

, and β = (ρ^S + ρ^F)AL⁴T²/E^SI = (ρ^S + ρ^F)AL²/ρ^SI. The parameter α mainly reflects the influence of mechanical parameters such as liquid-solid coupling coefficient and elastic modulus on the steady-state response of the beam, the parameter β mainly reflects the influence of geometric parameters such as the size of the saturated porous cantilever beam. Substituting the above dimensionless quantity into dimensionless equations (30)–(32), we obtain the following initial value problem:

(32)

(33)

(34)

(35)

where

and

. By solving equations (32) and (33), the general solutions are

(36)

where

, and A₁, A₂, A₃, A₄, A₅, and A₆ are undetermined coefficients. The undetermined coefficients can be determined by boundary condition equations (34) and (35). The deflection amplification factor g, w and the equivalent couple amplification factor of liquid pore pressure are introduced as follows:

(37)

5. Numerical Examples

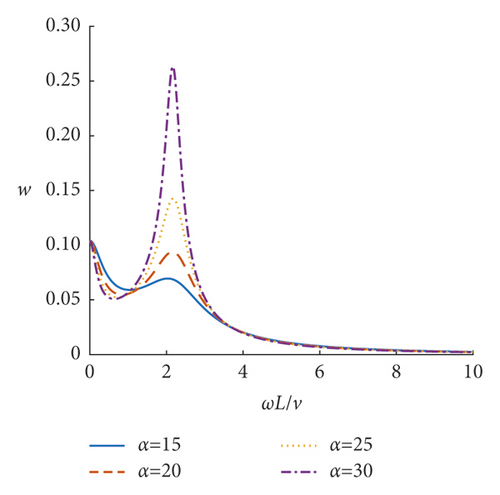
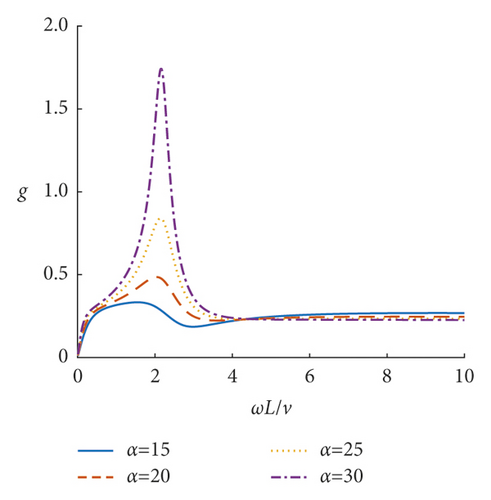
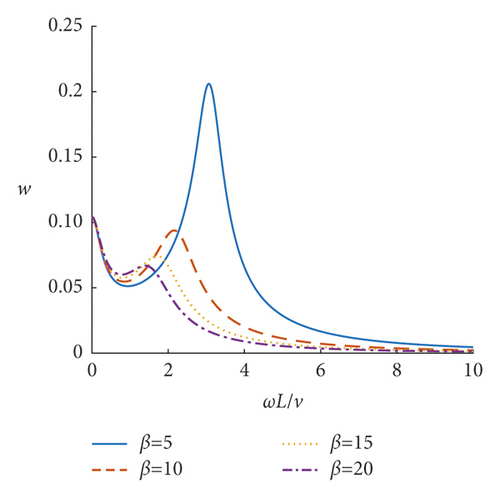
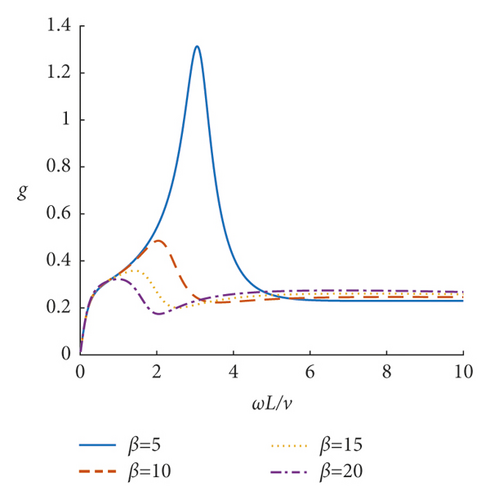
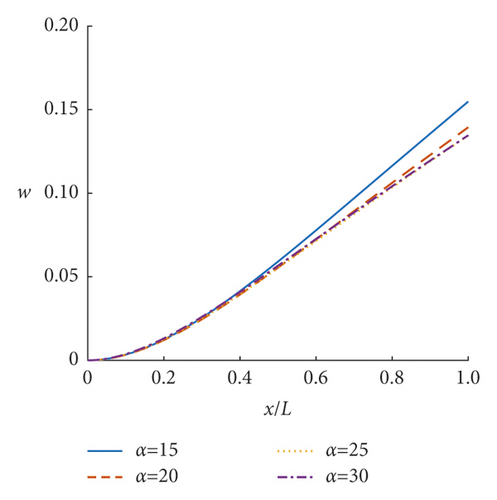
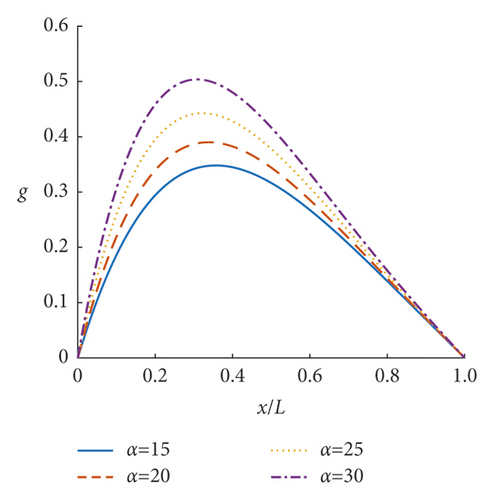
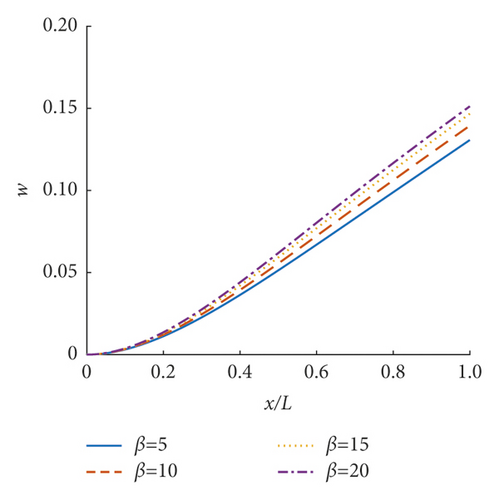
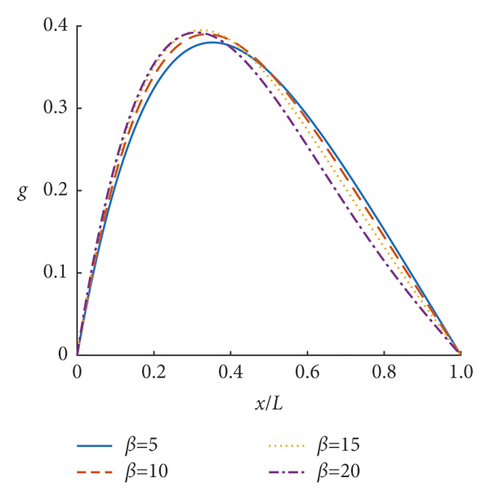
Based on the obtained deflection amplification factor w and equivalent couple amplification factor g of the incompressible nonlocal saturated poroelastic cantilever beam under vertical simple harmonic concentrated force, the steady-state dynamic response characteristics of the incompressible nonlocal saturated poroelastic cantilever beam are analyzed through numerical examples. If there is no special description, the dimensionless quantities are τ = 0.05, α = 20, and β = 10. Figures 3–8 show the curves of mid-span deflection amplification factor w and equivalent couple amplification factor g of the incompressible nonlocal saturated poroelastic cantilever beam varying with dimensionless frequency ωL/ v for different values of nonlocal coefficient τ, mechanical parameter α, and geometric parameter β. Evidently, there are obvious peaks and troughs in the curves, which shows that there is resonance in the vertical vibration of the incompressible nonlocal saturated poroelastic cantilever beam under a simple harmonic load. When the frequency is large, because the structure has no time to reflect, the deflection amplification factor of the cantilever beam gradually approaches zero, while the equivalent couple amplification factor tends to a stable value. Figures 9–14 show the variation curves of the deflection amplification factor and equivalent couple amplification factor at different positions of the beam varying with x/L when the dimensionless frequency ωL/v = 1.0 for different values of nonlocal coefficient τ, mechanical parameter α, and geometric parameter β. Since the external concentrated force acts at x/L = 1, the deflection amplification factor increases gradually with the increase in x/L and the equivalent couple amplification factor in the middle of the span is the largest, which has a certain relationship with its boundary conditions.

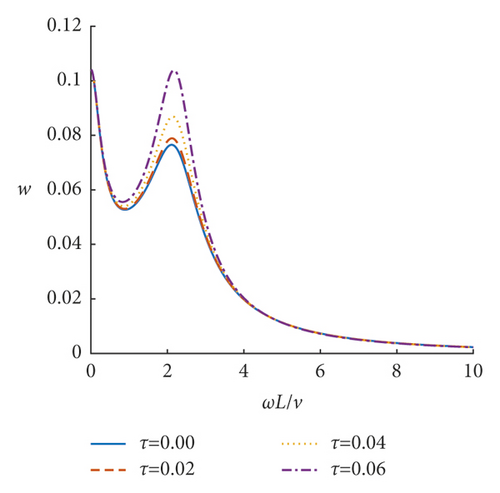
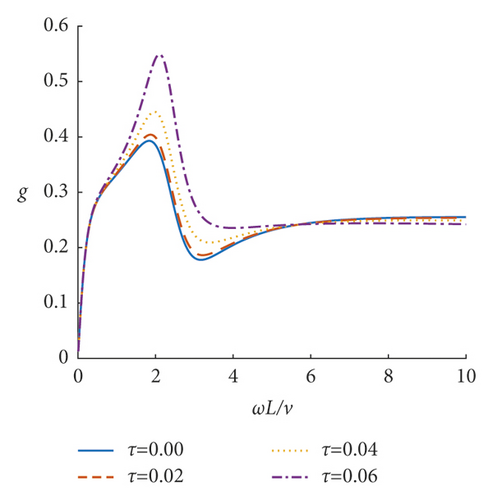
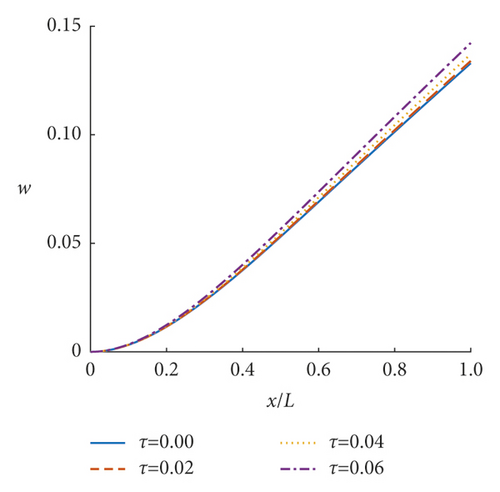
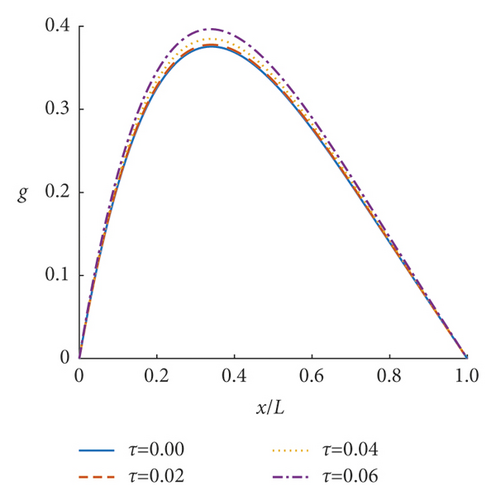
The influence of nonlocal coefficient τ on the deflection amplification factor and equivalent couple amplification factor is shown in Figures 3, 4, 9, and 10; τ = 0 is the result of ignoring the influence of nonlocal effects such as solid particle size and pore size. The deflection amplification factor and equivalent couple amplification factor are larger when nonlocal effects are considered than when they are not considered. Therefore, the influence of nonlocal effects on the steady-state response of the beam should not be ignored, and the deflection amplification factor and equivalent couple amplification factor increase with the increase of nonlocal factors. In addition, when τ is small, because the left end of the beam is a fixed end, the influence of the nonlocal coefficient τ on the deflection amplification factor and the equivalent couple amplification factor is relatively small.

The influence of the mechanical parameter α on the deflection amplification factor and equivalent couple amplification factor is shown in Figures 5, 6, 11, and 12. When the dimensionless frequency is small (ωL/v ＜ 1.0), the larger the parameter α is, the smaller the deflection amplification factor and the larger the valley value will be. When the dimensionless frequency is large (ωL/v ＜ 1.0), the larger the parameter α is, the larger the deflection amplification factor and the greater the peak value will be. The equivalent couple amplification factor increases with the increase in parameter α. But parameter α has little effect on the peak position of the curve of the deflection amplification factor and equivalent couple amplification factor varying with frequency.

The influence of the geometric parameter β on the deflection amplification factor and equivalent couple amplification factor is shown in Figures 7, 8, 13 and 14. The larger the parameter β is, the larger the deflection amplification factor and the smaller the valley value will be, when the dimensionless frequency is small. The larger the parameter β is, the smaller the deflection amplification factor and the smaller the peak value will be, when the dimensionless frequency is large. When the dimensionless frequency is small, the equivalent couple amplification factor increases with the parameter β; when the frequency is large, it shows the opposite, but the difference is relatively small. Different from the parameter α, the parameter β has a significant influence on the peak position of the curve of the deflection amplification factor and equivalent couple amplification factor varying with frequency. With the increase in the parameter β, the frequency corresponding to the peak value of the curve of the deflection amplification factor and equivalent couple amplification factor will increase.

6. Conclusions

Combining the nonlocal elastic theory with the porous medium theory and considering the nonlocal effects such as solid skeleton particle size, pore size, and pore dynamic stress, the dynamic control equation of the incompressible nonlocal saturated poroelastic cantilever beam is established. Taking the saturated porous cantilever beam as an example, the response of the beam under the vertical harmonic concentrated force at the free end is studied. The main conclusions are as follows: (1) there is resonance in the vertical vibration of the incompressible nonlocal saturated poroelastic cantilever beam under a simple harmonic load; (2) the deflection amplification factor and equivalent couple amplification factor with nonlocal effect are larger than those without nonlocal effect, so the influence of the nonlocal effect on the steady-state response of the beam should not be ignored; (3) the mechanical parameter α and geometric parameter β have a significant influence on the deflection amplification factor and the equivalent couple amplification factor, and the influence law has a certain relationship with the frequency; (4) the parameter β has a significant influence on the peak position of the curve of the deflection amplification factor and equivalent couple amplification factor varying with frequency, and α has little effect on the peak position.

Conflicts of Interest

The author declares no conflicts of interest.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (No. U1504505).

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 . M. A., Theory of propagation of elastic waves in a fluid-saturated porous solid.I. low-frequency range, Journal of the Acoustical Society of America. (1956) 28, no. 2, 168–178.
10.1121/1.1908239
Web of Science® Google Scholar
2 . M. A., Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher-frequency range, The Journal of the Acoustical Society of America. (1956) 28, no. 2, 179–191, https://doi.org/10.1121/1.1908241, 2-s2.0-84918383033.
10.1121/1.1908241
Web of Science® Google Scholar
3 Lee V. W. and Trifunac M. D., Response of tunnels to incident SH-waves, Journal of the Engineering Mechanics Division. (1979) 105, no. 4, 643–659, https://doi.org/10.1061/jmcea3.0002511.
10.1061/JMCEA3.0002511
Web of Science® Google Scholar
4 Lee V. W. and Karl J., On deformation near a circular underground cavity subjected to incident plane P waves, European Earthquake Engineering. (1993) 7, no. 1, 29–41.
Google Scholar
5 Karinski Y. S., Shershnev V. V., and Yankelevsky D. Z., Analytical solution of the harmonic waves diffraction by a cylindrical lined cavity in poroelastic saturated medium, International Journal for Numerical and Analytical Methods in Geomechanics. (2007) 31, no. 5, 667–689, https://doi.org/10.1002/nag.554, 2-s2.0-34247162358.
10.1002/nag.554
Web of Science® Google Scholar
6 Yuan Z., Cai Y., and Cao Z., An analytical model for vibration prediction of a tunnel embedded in a saturated full-space to a harmonic point load, Soil Dynamics and Earthquake Engineering. (2016) 86, no. 7, 25–40, https://doi.org/10.1016/j.soildyn.2016.04.004, 2-s2.0-84964414262.
10.1016/j.soildyn.2016.04.004
Web of Science® Google Scholar
7 Tong L. H., Liu Y. S., Geng D. X., and Lai S. K., Nonlinear wave propagation in porous materials based on the Biot theory, Journal of the Acoustical Society of America. (2017) 142, no. 2, 756–770, https://doi.org/10.1121/1.4996439, 2-s2.0-85027280063.
10.1121/1.4996439
CAS PubMed Web of Science® Google Scholar
8 Ciarletta M., Straughan B., and Tibullo V., Acceleration waves in a nonlinear Biot theory of porous media, International Journal of Non-linear Mechanics. (2018) 103, no. 7, 23–26, https://doi.org/10.1016/j.ijnonlinmec.2018.04.005, 2-s2.0-85046091218.
10.1016/j.ijnonlinmec.2018.04.005
Web of Science® Google Scholar
9 Yuan Z., Boström A., Cai Y., and Cao Z., Closed-form analytical solution for vibrations from a tunnel embedded in a saturated poroelastic half-space, Journal of Engineering Mechanics. (2017) 143, no. 9, 04017079, https://doi.org/10.1061/(asce)em.1943-7889.0001302, 2-s2.0-85019995978.
10.1061/(ASCE)EM.1943-7889.0001302
Web of Science® Google Scholar
10 Lee K. I., Humphrey V. F., Kim B. N., and Yoon S. W., Frequency dependencies of phase velocity and attenuation coefficient in a water-saturated sandy sediment from 0.3 to 1.0 MHz, Journal of the Acoustical Society of America. (2007) 121, no. 1, 2553–2560, https://doi.org/10.1121/1.2713690, 2-s2.0-34247866521.
10.1121/1.2713690
PubMed Web of Science® Google Scholar
11 Edelman I. and Wilmanski K., Asymptotic analysis of surface waves at vacuum/porous medium and liquid/porous medium interfaces, Continuum Mechanics and Thermodynamics. (2002) 14, no. 1, 25–44, https://doi.org/10.1007/s001610100069, 2-s2.0-23044532075.
10.1007/s001610100069
CAS Web of Science® Google Scholar
12 Busse A., Schanz M., and Antes H., A poroelastic mindlin-plate, Pammatone. (2003) 3, no. 1, 260–261, https://doi.org/10.1002/pamm.200310402.
10.1002/pamm.200310402
Google Scholar
13 Iesan D. and Nappa L., Thermal stresses in plane strain of poroelastic solid, Meccanica. (2004) 39, no. 2, 125–138.
10.1023/B:MECC.0000005118.15612.01
Web of Science® Google Scholar
14 Li L. P., Cederbaum G., and Schulgasser K., Vibration of poroelastic beams with axial diffusion, Euro J Mech. (1996) 15, no. 6, 1077–1094.
Google Scholar
15 Cederbaum G., Schulgasser K., and Li L. P., Interesting behavior patterns of poroelastic beams and columns, International Journal of Solids and Structures. (1998) 35, no. 34-35, 4931–4943, https://doi.org/10.1016/s0020-7683(98)00102-4, 2-s2.0-0032327431.
10.1016/S0020-7683(98)00102-4
Web of Science® Google Scholar
16 Xiao Y. and Chen W., A nonlinear mathematical model for large deflection of incompressible saturated poroelastic beams, Applied Mathematics and Mechanics. (2007) 28, no. 11, 1587–1595.
10.1007/s10483-007-1205-3
Google Scholar
17 Eringen A. C., On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves, Journal of Applied Physics. (1983) 54, no. 9, 4703–4710, https://doi.org/10.1063/1.332803, 2-s2.0-0020821706.
10.1063/1.332803
Web of Science® Google Scholar
18 Eringen A. C. and Edelen D. G. B., On nonlocal elasticity on nonlocal elasticity, International Journal of Engineering Science. (1972) 10, no. 3, 233–248, https://doi.org/10.1016/0020-7225(72)90039-0, 2-s2.0-0015316502.
10.1016/0020-7225(72)90039-0
Web of Science® Google Scholar
19 Tong L., Yu Y., Hu W., Shi Y., and Xu C., On wave propagation characteristics in fluid saturated porous materials by a nonlocal Biot theory, Journal of Sound and Vibration. (2016) 379, 106–118, https://doi.org/10.1016/j.jsv.2016.05.042, 2-s2.0-84973483885.
10.1016/j.jsv.2016.05.042
Web of Science® Google Scholar
20 Dinga H. B., Tong L. H., Xua C. J., Zhao X. S., and Nie Q. X., Dynamic responses of shallow buried composite cylindrical lining embedded in saturated soil under incident P wave based on nonlocal-Biot theory, Soil Dynamics and Earthquake Engineering. (2019) 121, no. 6, 25–40, https://doi.org/10.1016/j.soildyn.2019.02.018, 2-s2.0-85062504495.
10.1016/j.soildyn.2019.02.018
Web of Science® Google Scholar

Citing Literature

All articles

Steady-State Response Analysis of the Incompressible Nonlocal Saturated Poroelastic Beam under a Vertical Harmonic Load

Abstract

1. Introduction

2. Mathematical Model and Basic Equation

3. Dynamic Control Equation of the Incompressible Nonlocal Saturated Poroelastic Beam

4. Steady-State Response of the Incompressible Nonlocal Saturated Poroelastic Cantilever Beam under a Vertical Simple Harmonic Load

5. Numerical Examples

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Steady-State Response Analysis of the Incompressible Nonlocal Saturated Poroelastic Beam under a Vertical Harmonic Load

Abstract

1. Introduction

2. Mathematical Model and Basic Equation

3. Dynamic Control Equation of the Incompressible Nonlocal Saturated Poroelastic Beam

4. Steady-State Response of the Incompressible Nonlocal Saturated Poroelastic Cantilever Beam under a Vertical Simple Harmonic Load

5. Numerical Examples

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information