A Comparison Study of Numerical Techniques for Solving Ordinary Differential Equations Defined on a Semi-Infinite Domain Using Rational Chebyshev Functions
Abstract
A rational Chebyshev (RC) spectral collocation technique is considered in this paper to solve high-order linear ordinary differential equations (ODEs) defined on a semi-infinite domain. Two definitions of the derivative of the RC functions are introduced as operational matrices. Also, a theoretical study carried on the RC functions shows that the RC approximation has an exponential convergence. Due to the two definitions, two schemes are presented for solving the proposed linear ODEs on the semi-infinite interval with the collocation approach. According to the convergence of the RC functions at the infinity, the proposed technique deals with the boundary value problem which is defined on semi-infinite domains easily. The main goal of this paper is to present a comparison study for differential equations defined on semi-infinite intervals using the proposed two schemes. To demonstrate the validity of the comparisons, three numerical examples are provided. The obtained numerical results are compared with the exact solutions of the proposed problems.
1. Introduction
In the spectral methods, the most common basis functions are Chebyshev polynomials (CPs), which play an important role in the interpolation problems. Many researchers considered CPs to solve differential equations in the finite domain [−1, 1] (see [1–8] and [9]), but they often fail in the larger domain, also if the exact solution of the problem was in a rational form. For this reason, the rational Chebyshev (RC) functions are applied in the large domain [0, l] where l⟶∞, which provide a major success in dealing with differential equations (DEs) defined in the open domain [0, l]. Many researchers studied RC functions for treating man different problems of differential, integrodifferential equations (IDEs), partial, and some other physical-engineering problems as in [10, 11] and [12]. Abbasbandy et al. [13] applied the RC collocation method to get numerical solution of the magnetohydrodynamic flow (MHF) of an incompressible viscous fluid (VF) over a stretching sheet problem. Ramadan et al. in [14, 15] and [16], Yalçınbas et al. in [17], and Parand and Razzaghi in [18] are scrupulous in the use of RC functions to express the approximate solution of high-order ordinary differential equations (ODEs) by different spectral approaches. In [19], Parand and Razzaghi introduced RC functions for solving a population growth of a species within a closed system, named as a Volterra model, where the authors converted the Volterra population model first to an equivalent nonlinear ODE; the solution is approximated by the RC functions with the unknown coefficients. The authors of [20, 21] introduced the RC function approximation with the collocation technique for solving the natural convection of the Darcian fluid (DF) about a vertical full cone embedded in porous media (PM) with a prescribed wall temperature. Ramadan et al. [22, 23] obtained an approximate solution of the applied collocation method based on RC functions to treat high-order linear IDEs with variable coefficients. In [24], the authors applied the RC collocation approach for approximating nonlinear biomathematical problems, namely, the systematic logistic growth, the Lotka-Volterra system (prey-predator model), the simple two-species Lotka-Volterra model, and the prey-predator model with limit cycle (periodic behavior).
All the aforementioned work either relied on the RC functions as a basis defined of an open interval or used it to treat a specific application or used truncated matrices. The truncation in matrices was handled for the first time by us in [15], and it was also an application on open period equations. In this work, a comparison study for solving linear ODEs defined on semi-infinite domains using a spectral collocation method is presented. The equation under investigation is a high-order nonhomogeneous linear variable coefficient ordinary differential equation defined on semi-infinite domain [0, ∞). Two algorithms are considered by the collocation method with the RC functions as basis functions. The matrices of derivative for RC functions introduced with regular definition with truncation and improved one, which lead us to two different schemes. The collocation points that are used here are suggested by us, and they are defined on the interval [0, ∞), which deal with the boundary value problems defend on [0, ∞) or if one of the mixed conditions tends to infinity. So, we suggested new collocation points that are valid for dealing with a problem of this type.
2. Preliminaries
In this section, the definition and some properties of the RC functions are listed; also, the convergence for RC functions will be discussed.
For more details about Tn(x), see Ref. [8].
2.1. The RC Functions
2.2. Function Spaces
Let N be a positive integer such that N < ∞, and .
Theorem 1. For any r ≥ 0, and c is a generic positive constant independent of any variable, and , then
The order of convergence for the RC function approximation will be obtained using several orthonormal projections. From (16), it is clear that fN is the orthogonal projection of f onto with respect to the inner product (10). For all of the above, especially Theorem 1, the following theorem is presented and contains the order of convergence of RC functions.
2.3. Operational Matrix
In addition to k = (−1)i+j+1, c1 = 1 and cj = 2 for j ≥ 2.
And we note here that R(0)(x) = R(x), , for i > N. Definitions (18) and (23) were introduced for the first time in [18, 19], and many works have used them; see, for example, Refs. [20–22], [23, 24], and [17].
3. The Improved Differentiation of the RC Functions
In the present section, an improved definition of differentiation for the RC functions is introduced. There was a need to find an improvement to definition (23), because in the higher derivatives, when using this definition, a week approximation is obtained. The truncated definition (18) and the kth-order derivative (23) give us a regular truncated differentiation of the RC functions (RRC). Generally, the derivative of the rational or fractional functions increases the order of the denominator (in contrast to polynomials that reduce the order at differentiation), so the truncation increases as the order of the derivative increases (more than one column in Equation (18)). For example, the fourth-order derivative of the vector R(x) at N = 3, the truncated terms in the row vector R(x) are (the last four terms) R4, R5, R6, R7. This will lead to unsatisfied approximating in high-order DEs using the presented RRC definition (18). Therefore, an improved definition of the derivative of RC functions will be proposed next.
First, a vector will be inserted into (18) to treat the truncated terms, which will improve the regular definition. This manner will be called an improved derivative of the RC functions and will be indicated by IRC.
Theorem 3. The kth derivative of the matrix vector R(x), in terms of itself, is defined as
Proof. Using the assumption (24) as the first derivative, and differentiating (24), then we get
As a special case, if Z(x) = 0, it leads us to the regular RC definition in relations (18) and (23). The introduced definition (24) and the kth-order derivative (26) give us an improved differentiation of the RC functions.
4. Problem Statement
5. Fundamental Relation-Based Matrix Forms
In the beginning, we provide the fundamental matrix relation of the solution of (30) by two schemes using the RC collocation approach.
Assuming that the solutionf(x)of (30) can be expressed as relation (32), which is a truncated RC series, thenf(x)and itskthderivativef(k)(x)are written in the matrix forms (32) and (33) such thatk = 0, 1, ⋯, m, andm ≤ N, wheref(0)(x) ≡ f(x),a0, a1, ⋯, aNare the RC coefficients to be determined later.
Permanently, the RC functions are convergent at both end points 0 and ∞; in addition, the presence of infinity in the collocation points (x0⟶∞) does not cause a failure in the substitution.
5.1. The RRC Scheme
5.2. The IRC Scheme
We studied the improved and regular differentiating RC functions in the preceding section. Now, we deduce the fundamental matrix relation by the IRC scheme.
6. Method of Solution
Due to the collocation method, the regular (42) and the improved (46) fundamental matrix equations for the proposed problem (30) correspond to a system of algebraic equations with (N + 1) equations for the (N + 1) unknown RC coefficients a0, a1, ⋯, aN..
Therefore, the RC coefficients an, n = 0, 1, ⋯, N are uniquely determined.
7. Test Examples
In the present section, three numerical test examples are given to explain the applicability of the proposed two techniques. Using own codes written in MATHEMATICA 10.0. package, the numerical results and figures are presented, as shown in the illustrative comparison tables.
for the h step size along the interval x ∈ [0, b]. All numeric calculations are carried out on a regular machine Intel(R) Core(TM) i7 CPU, 3.2 GHz.
Example 1. Let us assume the following fourth-order boundary value problem
We have
Substituting by the RC coefficients of the RRC scheme in Equation (32), we get an approximate solution of this problem, while, if we use the RC coefficients of the IRC scheme in Equation (32), we get the exact solution 2x(x − 3)/(x + 1)2. We note that the RRC scheme gives the exact solution at N = 6 while the IRC scheme gives the exact solution at N = 4, which shows that the IRC scheme obtains better accuracy than the RRC due to the truncation found in RRC (18). In addition, the CPU time used for the RRC and IRC schemes at different Nis listed in Table 1. Table 1 shows that the time used for calculating the solution by RRC is less than the time for IRC, because of the added truncated terms in coding. Therefore, the time for getting the exact solution by IRC (better accuracy at N = 4) is close to that given by RRC (at N = 6). The following examples show the comparison of the two schemes strongly with numeric table’s results.
Example 2. Consider Laguerre-eigen problem [26]
Example 3. Consider Whittaker’s equation eigen problem [26] of the form
where λ is the eigen value; it represents a special case of Whittaker’s equation. The exact given solution of (68) is where λ = n, n ≥ 0, is an integer and is the well-known associated Laguerre polynomials of kth order and degree n. If λ = −1, (68) gives a special case or linear Whittaker’s equation as
| N | CPU time used by RRC scheme | CPU time used by IRC scheme |
|---|---|---|
| 4 | 0.094 | 0.155 |
| 5 | 0.11 | 0.19 |
| 6 | 0.156 | 0.241 |
| x | RRC scheme | IRC scheme | ||
|---|---|---|---|---|
| e20 | e30 | e20 | e30 | |
| 0 | 1 | 1 | 1 | 1 |
| 0.5 | 2.23497 × 10−7 | 1.59521 × 10−9 | 4.61847 × 10−8 | 3.66704 × 10−9 |
| 1 | 4.90784 × 10−7 | 5.74586 × 10−10 | 5.93028 × 10−7 | 6.13636 × 10−9 |
| 1.5 | 4.68739 × 10−9 | 2.52918 × 10−9 | 2.2526 × 10−8 | 1.4928 × 10−9 |
| 2 | 1.78495 × 10−7 | 1.33078 × 10−8 | 1.8386 × 10−6 | 9.67304 × 10−9 |
| 2.5 | 1.43122 × 10−6 | 1.99709 × 10−8 | 1.11684 × 10−7 | 9.44468 × 10−9 |
| 3 | 1.35397 × 10−6 | 7.57517 × 10−9 | 2.11749 × 10−6 | 2.75718 × 10−9 |
| 3.5 | 2.16835 × 10−6 | 3.82668 × 10−8 | 1.29148 × 10−6 | 1.00546 × 10−8 |
| 5 | 3.534 × 10−6 | 2.72901 × 10−8 | 1.27908 × 10−6 | 2.26605 × 10−8 |
| 7.5 | 5.73755 × 10−6 | 1.88112 × 10−7 | 2.23981 × 10−7 | 6.70631 × 10−8 |
| 10 | 7.31028 × 10−6 | 2.76595 × 10−7 | 4.59453 × 10−6 | 3.03553 × 10−9 |
| x | RRC scheme | IRC scheme | ||
|---|---|---|---|---|
| e20 | e30 | e20 | e30 | |
| 0 | 1 | 1 | 1 | 1 |
| 0.5 | 3.31737 × 10−6 | 3.91279 × 10−8 | 4.85215 × 10−6 | 2.86433 × 10−7 |
| 1 | 1.21648 × 10−5 | 2.30618 × 10−7 | 6.13597 × 10−6 | 9.11931 × 10−8 |
| 1.5 | 1.68999 × 10−5 | 3.20837 × 10−7 | 2.99644 × 10−5 | 6.97906 × 10−8 |
| 2 | 2.57922 × 10−5 | 3.48555 × 10−7 | 2.71531 × 10−5 | 8.9908 × 10−7 |
| 2.5 | 2.07512 × 10−5 | 4.35107 × 10−7 | 8.88987 × 10−6 | 1.01733 × 10−7 |
| 3 | 3.12895 × 10−5 | 6.64248 × 10−7 | 4.44485 × 10−5 | 3.8419 × 10−7 |
| 3.5 | 1.99079 × 10−5 | 2.69503 × 10−7 | 1.5211 × 10−5 | 1.08309 × 10−6 |
| 5 | 1.14161 × 10−6 | 1.06864 × 10−6 | 2.31729 × 10−5 | 6.46631 × 10−7 |
| 7.5 | 5.4514 × 10−5 | 1.43524 × 10−6 | 2.57514 × 10−5 | 1.97968 × 10−7 |
| 10 | 2.13571 × 10−4 | 2.89479 × 10−6 | 4.48328 × 10−5 | 2.05962 × 10−6 |
| N | RRC scheme | IRC scheme | ||
|---|---|---|---|---|
| 20 | 1.70683 × 10−9 | 7.31028 × 10−6 | 6.74223 × 10−10 | 4.59453 × 10−6 |
| 30 | 2.44349 × 10−12 | 2.76595 × 10−7 | 1.06979 × 10−15 | 9.79285 × 10−8 |
| N | RRC scheme | IRC scheme | ||
|---|---|---|---|---|
| 20 | 1.45682 × 10−6 | 2.13571 × 10−4 | 6.41968 × 10−8 | 5.10902 × 10−5 |
| 30 | 2.67643 × 10−10 | 2.89479 × 10−6 | 1.35486 × 10−11 | 2.05962 × 10−6 |
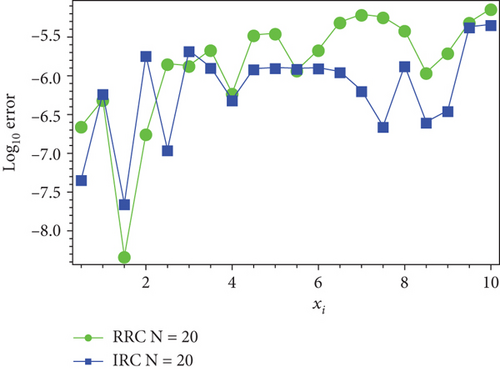
| N | RRC scheme | IRC scheme | ||
|---|---|---|---|---|
| λ = 1 | λ = 2 | λ = 1 | λ = 2 | |
| 20 | 1.173 | 1.172 | 1.938 | 1.985 |
| 30 | 3.89 | 3.858 | 4.591 | 4.61 |
By the same procedure, the RC collocation method using the proposed two schemes is applied to solve (69) with the subjected boundary conditions. In Table 7, the numerical result for N = 20 and 30 using the proposed schemes is compared with the exact values of f(x) = e−0.5x. The computation of L2 and L∞ on interval x ∈ [0, 10] is given in Table 8. In Table 9, the CPU time used for RRC and IRC schemes at different N shows that IRC needs time more than RRC.
| X | RRC scheme | IRC scheme | ||
|---|---|---|---|---|
| e20 | e30 | e20 | e30 | |
| 0 | 1 | 1 | 1 | |
| 0.1 | 2.20484 × 10−8 | 4.0709 × 10−9 | 5.80324 × 10−9 | 7.13895 × 10−10 |
| 0.7 | 8.86658 × 10−9 | 6.84228 × 10−8 | 1.84652 × 10−8 | 6.01463 × 10−8 |
| 2.4 | 5.81316 × 10−7 | 2.90517 × 10−7 | 2.83721 × 10−6 | 1.27556 × 10−7 |
| 3.8 | 3.56672 × 10−6 | 5.43355 × 10−7 | 2.68921 × 10−6 | 2.70375 × 10−8 |
| 5 | 4.19425 × 10−6 | 6.64317 × 10−7 | 1.59222 × 10−6 | 2.63469 × 10−8 |
| 6.7 | 4.01577 × 10−5 | 8.70798 × 10−7 | 4.96175 × 10−6 | 5.53538 × 10−8 |
| 13.8 | 1.06869 × 10−4 | 9.22562 × 10−7 | 1.33586 × 10−5 | 7.21039 × 10−7 |
| 14.4 | 8.5269 × 10−4 | 8.87894 × 10−7 | 2.31729 × 10−5 | 5.63274 × 10−8 |
| 18.6 | 1.26741 × 10−4 | 1.59984 × 10−6 | 1.20205 × 10−5 | 1.12601 × 10−6 |
| 20 | 1.87513 × 10−4 | 1.10906 × 10−6 | 1.20881 × 10−4 | 9.73054 × 10−7 |
| N | RRC scheme | IRC scheme | ||
|---|---|---|---|---|
| 20 | 1.12301 × 10−6 | 8.5269 × 10−4 | 4.667 × 10−7 | 1.20881 × 10−4 |
| 30 | 3.28475 × 10−11 | 8.16818 × 10−6 | 8.92851 × 10−12 | 2.83766 × 10−6 |
| N | CPU time used by RRC scheme | CPU time used by IRC scheme |
|---|---|---|
| 20 | 0.844 | 0.971 |
| 30 | 2.345 | 2.657 |
8. Conclusion
A rational Chebyshev (RC) spectral collocation technique is considered in this paper to solve high-order ordinary differential equations (ODEs) defined on a semi-infinite domain using the proposed two schemes. Two definitions of the derivative of the RC functions are introduced, namely, the regular and improved definitions. Due to the two definitions, two schemes are presented for solving the proposed ODEs with variable coefficients in the semi-infinite interval. According to the convergence of the RC functions at the infinity, the proposed technique deals with the boundary value problem which is defined on semi-infinite domains easily. Furthermore, an intriguing advantage of this approach is the ability to find the analytical exact solutions if the equation has a solution in a rational function form. To demonstrate the applicability of the proposed approach, three illustrative examples are given. The calculated numerical values and comparisons proved that the improved scheme is better with more calculation than the regular scheme which is based on the truncation in the definition. The method may extend to the case of nonlinear DEs with variable coefficients, which the authors are investigating.
Conflicts of Interest
The authors declare that they have no competing interests.
Authors’ Contributions
All authors carried out the proofs and conceived of the study. All authors read and approved of the final form of the manuscript.
Acknowledgments
The researchers would like to thank the Deanship of Scientific Research, Qassim University, for funding the publication of this project.
Open Research
Data Availability
The authors declare that there is no data associated with this research.




