The distance Laplacian matrix of a connected graph G is defined as ℒ(G) = Tr(G) − D(G), where D(G) is the distance matrix of G and Tr(G) is the diagonal matrix of vertex transmissions of G. The largest eigenvalue of ℒ(G) is called the distance Laplacian spectral radius of G. In this paper, we determine the graphs with maximum and minimum distance Laplacian spectral radius among all clique trees with n vertices and k cliques. Moreover, we obtainn vertices and k cliques.

1. Introduction

In this paper, we consider simple connected graphs [1]. A graph G is represented by G = (V(G), E(G)), in which the set V(G) = {v₁, v₂, …, v_n} represents its vertex set and E(G) is the edge set connecting pairs of distinct vertices. The number n = |V(G)| is referred to as the order of G. The distance matrix of G is the n × n matrix , where d_G(u, v) denotes the distance between vertices u and v in G, i.e., the length of a shortest path from u to v in G. For u ∈ V(G), the transmission of u in G, denoted by Tr_G(u), is defined as the sum of distances from u to all other vertices of G. Let Tr(G) be the diagonal matrix of vertex transmissions of G. In 2013, Aouchiche and Hansen [2] first gave the definition of distance Laplacian matrix: for a connected graph G, ℒ(G) = Tr(G) − D(G), where ℒ(G) denotes the distance Laplacian matrix. Obviously, ℒ(G) is a positive semidefinite, symmetric, and singular matrix. The distance Laplacian eigenvalues of G, denoted by λ₁(G) ≥ λ₂(G) ≥ ⋅⋅⋅≥λ_n(G) = 0, are the eigenvalues of ℒ(G). Especially, the largest eigenvalue λ₁(G) is the distance Laplacian spectral radius of G. The positive unit eigenvector, i.e., all components of the eigenvector are positive, corresponding to λ₁(G) is called the Perron eigenvector of ℒ(G).

For a graph G, two vertices are called adjacent if they are connected by an edge and two edges are called incident if they share a common vertex. The set of vertices that are adjacent to a vertex v ∈ V(G) is called the neighborhood of v and is presented by N_G(v). As usual, let K_n, K_1,n−1, and P_n denote the complete graph, the star, and the path with order n, respectively. G is a connected graph, X ∈ V(G), G − X is not connected, and then X is a cut-vertex set. If X has only vertex v, then v is a cut-vertex. A block of G is a maximal connected subgraph of G that has no cut-vertex. A block is a clique if the block is a complete graph. A graph G is a clique tree if each block of G is a clique. We call a clique path if we replace each edge of P_k+1 by a clique such that for i = 1,2, …, k − 2 and for j ≠ i − 1, i + 1 and 2 ≤ i ≤ k − 1. We call a clique star if we replace each edge of the star K_1,k with a clique such that for i ≠ j and i, j = 1,2, …, k (see Figure 1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A clique star and a clique path.

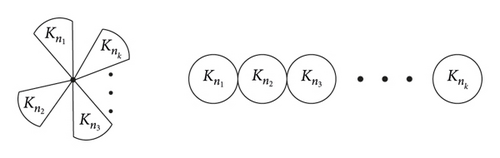
Recently, Xing and Zhou [3] characterized the unique graph with minimum distance Laplacian spectral radius among all the bicyclic graphs with fixed number of vertices; Aouchiche and Hansen [4] showed that the star K_1,n is the unique tree with the minimum distance Laplacian spectral radius among all trees; Lin et al. [5, 6] determined the unique graph with minimum distance Laplacian spectral radius among all the trees with fixed bipartition, nonstar-like trees, noncaterpillar trees, nonstar-like noncaterpillar trees, and the graph with fixed edge connectivity at most half of the order, respectively; Niu et al. [7] determined the unique graph with minimum distance Laplacian spectral radius among all the bipartite graphs with fixed matching number and fixed vertex connectivity, respectively; Fan et al. [8] determined the graph with minimum distance Laplacian spectral radius among all the unicyclic and bicyclic graphs with fixed numbers of vertices, respectively; Lin and Zhou [9] determined the unique graph with maximum distance Laplacian spectral radius among all the unicyclic graphs with fixed numbers of vertices.

In 2019, Cui et al. [10] investigated a convex combination of Tr(G) and D(G) in the form of D_α(G) = αTr(G) + (1 − α)D(G), 0 ≤ α ≤ 1, which is called the generalized distance matrix. Alhevaz et al. [11] gave some new upper and lower bounds for the generalized distance energy of graphs which are established based on parameters including the Wiener index and the transmission degrees and found that the complete graph has the minimum generalized distance energy among all connected graphs; Lin and Drury et al. [12] established some bounds for the generalized distance Gaussian Estrada index of a connected graph, involving the different graph parameters, including the order, the Wiener index, the transmission degrees, and the parameter α ∈ [0,1], and characterized the extremal graphs attaining these bounds; Alhevaz et al. [13] obtained some bounds for the generalized distance spectral radius of graphs using graph parameters like the diameter, the order, the minimum degree, the second minimum degree, the transmission degree, and the second transmission degree and characterized the extremal graphs; Alhevaz et al. [14] studied the generalized distance spectrum of join of two regular graphs and join of a regular graph with the union of two different regular graphs; Shang [15] established better lower and upper bounds to the distance Estrada index for almost all graphs.

The distance Laplacian energy is defined as , where t(G) is the average transmission of G and is defined by . Although there has been extensive work done on the distance Laplacian spectral radius of graphs, relatively little is known in regard to distance Laplacian energy. The distance Laplacian energy was first introduced in [16], where several lower and upper bounds were obtained; Das et al. [17] gave some lower bounds on distance Laplacian energy in terms of n for graphs and trees and characterized the extremal graphs and trees. In this paper, first, we not only get the distance Laplacian eigenvalues of all clique stars but also get their distance Laplacian energies; second, we prove all clique stars are the graphs with minimum distance Laplacian spectral radius among all clique trees with n vertices and k cliques. Then, we show that the clique path for m ≥ 3 is the graph with maximum distance Laplacian spectral radius among all clique trees with n vertices and k cliques.

2. Preliminaries

Let G = (V, E) be a connected graph with V(G) = {v₁, v₂, …, v_n}. A column vector

can be considered as a function defined on V(G) which maps vertex v_i to

, i.e.,

for i = 1,2, …, n. Then,

(1)

and λ is a distance Laplacian eigenvalue with corresponding eigenvector x if and only if x ≠ 0, for each u ∈ V(G),

(2)

or equivalently

(3)

The above equation is called the eigenequation of G at u.

Note that is an eigenvector of ℒ(G) corresponding to λ_n(G) = 0. For n ≥ 2, if x is an eigenvector of ℒ(G) corresponding to λ₁(G), we have x^T1_n = 0.

For a unit column vector x ∈ ℝⁿ, by Rayleigh’s principle, we have λ(G) ≥ x^Tℒ(G)x with equality if and only if x is an eigenvector of ℒ(G) corresponding to λ(G).

The following is the well-known Cauchy interlacing theorem.

Lemma 1 (Cauchy interlace theorem) (see [1].)Let A be a Hermitian matrix with eigenvalues λ₁ ≥ ⋯≥λ_n and B be one of its principal submatrices. Let B have eigenvalues μ₁ ≥ ⋯≥μ_m. Then, the inequalities λ_n−m+i ≤ μ_i ≤ λ_i(i = 1, …, m) hold.

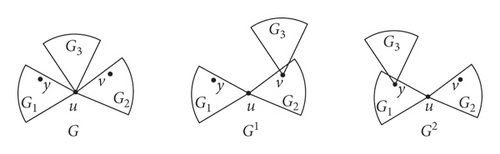
Lemma 2 (see [6].)Let G be a connected graph with three induced subgraphs G₁, G₂, and G₃ such that |V(G_i)| ≥ 2 for i = 1,2,3 and V(G_i)∩V(G_j) = {u} for 1 ≤ i < j ≤ 3 and (see Figure 2). For v ∈ V(G₂)\{u} and y ∈ V(G₁)\{u}, let and . If , then λ₁(G) < λ₁(G¹) or λ₁(G) < λ₁(G²).

3. Minimum Distance Laplacian Spectral Radius of Clique Trees

The diameter of a graph is the maximum distance between any pair of vertices.

Lemma 3. Let S be a clique tree with n vertices and k cliques. If diam(S) ≥ 3, then λ₁(S) > 2n − 1.

Proof. For convenience, let diam(S) = d and be a clique path of S. Denote the cliques of by , . Let for i = 1,2, …, d − 1. Let and . Then, v₀v₁ … v_d is a diameter path of S. We can easily get

(4)

Then, we have

(5)

Let M be the principal submatrix of ℒ(S) indexed by v₀ and v_d. Then,

(6)

and thus

(7)

By Lemma 2, we have λ₁(S) ≥ λ₁(M) > 2n − 1.

Theorem 1. Let be an arbitrary clique star with n vertices and k cliques. Then, .

Proof. Obviously, we have n₁ + n₂ + n₃ + ⋅⋅⋅+n_k = n + k − 1. Let x be a Perron eigenvector of corresponding to . By symmetry, we may assume x_v = x_i for any , i = 1,2, …, k. Let x₀ = x_u, then we have

(8)

Thus, λ₁ is the largest root of the equation , where and

(9)

Therefore, we have n and 0 are also distance Laplacian eigenvalues of .

Combining Lemma 3 and Theorem 1, we have the following result.

Theorem 2. Among all clique trees with n vertices and k cliques, the graphs attaining the minimum distance Laplacian spectral radius are clique stars .

Let I be the identity matrix of order n. The characteristic polynomial of ℒ(G) can be written as ψ(G : λ) = det(λI − ℒ(G)). Let us label the vertices of such that u is the first vertices, and the first n₁ vertices are from , the following n₂ − 1 vertices are from , …, and the last n_k − 1 are from . Let . Combining Theorem 1, by direct calculations, we get the following result.

Corollary 1. The distance Laplacian eigenvalues of are 2n − 1 of multiplicities k − 1, 2n − n_i of multiplicities n_i − 2(1 ≤ i ≤ k), n, and 0.

Theorem 3. Let be an arbitrary clique star with n vertices and k cliques. Then, we have .

Proof. Obviously, we have n₁ + n₂ + n₃ + ⋅⋅⋅+n_k = n + k − 1. For convenience, let . For any , we have Tr_G(v) = Tr_G(w). Let , 1 ≤ i ≤ k. Then, we have Tr_G(v_i) = 2n − n_i − 1 and . By Cauchy–Schwarz inequality, we have . So, we get t(G) < 2n − 1 + ((k − 1 − n²)/n) = n − 1 + (k − 1/n) < n. By Corollary 1, we know λ_i > n > t(G) for i = 1,2, …, n − 1, and λ_n = 0. since is equal to the trail of ℒ(G), i.e., . So, we get .

4. Maximum Distance Laplacian Spectral Radius of Clique Trees

Lemma 4. Let H be a connected graph and S be a clique tree with diam(S) = d. Suppose is a clique path of S with cliques , , and for i = 1,2, …, d − 1. Let H_t be the graph obtained by identifying a vertex v of H and a vertex u of , where 2 ≤ t ≤ d − 1. Then, λ₁(H_d) > λ₁(H_t) or λ₁(H₁) > λ₁(H_t).

Proof. By Lemma 2, we may assume u ≠ v_t−1 or u ≠ v_t for 2 ≤ t ≤ d − 1. Denote the component of S − v_t−1 which contains vertex v_t−2 by and the component of S − v_t which contains vertex v_t+1 by . Let , , and . Suppose x is a Perron eigenvector of ℒ(H_t) corresponding to λ₁(H_t). In the following, we will first prove λ₁(H_t+1) > λ₁(H_t) or λ₁(H_t−1) > λ₁(H_t).

Case 1: . From H_t to H_t+1, we have
(10)

Thus, λ₁(H_t+1) ≥ λ₁(H_t).
In the following, we will prove λ₁(H_t+1) > λ₁(H_t). If λ₁(H_t+1) = λ₁(H_t), then , which implies x_ω = x_h for any ω ∈ S₃\{v_t}, h ∈ V(H)\{v}, and x is also a Perron eigenvector of ℒ(H_t+1) corresponding to λ₁(H_t+1). For arbitrary ω₁ ∈ S₁, from the eigenequations of H_t+1 and H_t at ω₁, we have

(11)

So, we have . Similarly, for arbitrary ω₂ ∈ S₂ and ω₃ ∈ S₃\{v_t}, we have and . Then, we have x_ω = x_w for any ω, w ∈ V(H_t)\{v_t}. Since , we have , which implies and .
From the eigenequation of H_t at v₁ and v₂, we have , which is a contradiction.
Up to now, we have proved λ₁(H_t+1) > λ₁(H_t).
Case 2: .

From H_t to H_t−1, we have

(12)

Then, we have

(13)

Thus, λ₁(H_t−1) > λ₁(H_t).

In the following, we will prove λ₁(H_d) > λ₁(H_t) or λ₁(H₁) > λ₁(H_t).

If λ₁(H_t+1) > λ₁(H_t), we may denote the component of S − v_t which contains vertex v_t−1 by and the component of S − v_t+1 which contains vertex v_t+2 by . Let , , and . Let x^′ be a Perron eigenvector of ℒ(H_t+1) corresponding to λ₁(H_t+1). If , then , and we can get λ₁(H_t) > λ₁(H_t+1), which is a contradiction. So, we have . Then, we have , similar to case 1, and we can get the equal sign in the above inequality does not hold. So, we have λ₁(H_t+2) > λ₁(H_t+1). Repeating the above procedure, we can get λ₁(H_d) > ⋯>λ₁(H_t+2) > λ₁(H_t+1) > λ₁(H_t).

Similarly, if λ₁(H_t−1) > λ₁(H_t), we can prove λ₁(H₁) > ⋯>λ₁(H_t−2) > λ₁(H_t−1) > λ₁(H_t).

Theorem 4. Among all clique trees with n vertices and k cliques, the graph attaining the maximum distance Laplacian spectral radius is for some m ≥ 3.

Proof. Let G be the graph with maximum distance Laplacian spectral radius among all clique trees with n vertices and k cliques. By Lemma 4, we get . Let for i = 1,2, …, k − 1. If k ≤ 2, the result holds. Next, we may assume k ≥ 3. Suppose there exists some 2 ≤ t ≤ k such that n_t ≥ 3. Denote the component of G − v_t−1 which contains vertex v_t−2 by G₁ and the component of G − v_t which contains vertex v_t+1 by G₂. Let S₁ = V(G₁), S₂ = V(G₂), and S₃ = V(G)\(V(G₁) ∪ V(G₂)), i.e., . Let

(14)

i.e.,

and

. Suppose x is a Perron eigenvector of ℒ(G) corresponding to λ₁(G). In the following, we will first prove λ₁(G^t−1) > λ₁(G) or λ₁(G^t+1) > λ₁(G).

Case 1: .
From G to G^t−1, we have
(15)

which implies λ₁(G^t−1) ≥ λ₁(G). Similar to Case 1 of Lemma 4, we can get the equal sign in the above inequality does not hold. So, we have λ₁(G^t−1) ≥ λ₁(G).
Case 2: .
Then, we have
(16)

Thus, we have λ₁(G^t+1) > λ₁(G).

Doing the above graph transformations until n₂ = n₃ = ⋯ = n_k−1 = 2, we get G as for some m ≥ 3.

5. Conclusion

This paper mainly determines the extremal graphs with maximum and minimum distance Laplacian spectral radius among all clique trees with n vertices and k cliques. Moreover, we get the distance Laplacian energies of all the clique stars with n vertices and k cliques. Based on our results, we conjecture that the line graphs of and are the unique graphs with minimum and maximum distance Laplacian spectral radius among all the line graphs of unicyclic graphs, respectively, where is the graph obtained by adding an edge to the star K_1,n−1 of order n and is the graph obtained by adding an edge between a vertex of a triangle and a terminal vertex of a path on n − 3 vertices. Moreover, we can study the distance Laplacian spectral radius of diclique trees in the future.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the NSFC (grant nos. 11501491, 11671347, and 61771019).

Open Research

Data Availability

No data were used to support this study.

References

1 Brouwer A. E. and Haemers W. H., Spectra of Graphs, 2012, Springer, New York, NY, USA.
10.1007/978-1-4614-1939-6
Web of Science® Google Scholar
2 Aouchiche M. and Hansen P., Two Laplacians for the distance matrix of a graph, Linear Algebra and Its Applications. (2013) 439, no. 1, 21–33, https://doi.org/10.1016/j.laa.2013.02.030, 2-s2.0-84876677430.
10.1016/j.laa.2013.02.030
Web of Science® Google Scholar
3 Xing R. and Zhou B., On the distance and distance signless Laplacian spectral radii of bicyclic graphs, Linear Algebra and Its Applications. (2013) 439, no. 12, 3955–3963, https://doi.org/10.1016/j.laa.2013.10.005, 2-s2.0-84889095416.
10.1016/j.laa.2013.10.005
Web of Science® Google Scholar
4 Aouchiche M. and Hansen P., Some properties of the distance Laplacian eigenvalues of a graph, Les Czechoslovak Mathem Atical Journal. (2014) 64, no. 139, 751–761, https://doi.org/10.1007/s10587-014-0129-2, 2-s2.0-84919768674.
10.1007/s10587-014-0129-2
Web of Science® Google Scholar
5 Lin H. and Zhou B., On the distance Laplacian spectral radius of graphs, Linear Algebra and Its Applications. (2015) 475, 265–275, https://doi.org/10.1016/j.laa.2015.02.033, 2-s2.0-84924769377.
10.1016/j.laa.2015.02.033
Web of Science® Google Scholar
6 Lin H. and Zhou B., The changes in distance Laplacian spectral radius of graphs resulting from graft transformations, Discrete Applied Mathematics. (2017) 219, 147–157, https://doi.org/10.1016/j.dam.2016.11.011, 2-s2.0-85008204047.
10.1016/j.dam.2016.11.011
Web of Science® Google Scholar
7 Niu A., Fan D., and Wang G., On the distance Laplacian spectral radius of bipartite graphs, Discrete Applied Mathematics. (2015) 186, 207–213, https://doi.org/10.1016/j.dam.2015.01.023, 2-s2.0-84933279232.
10.1016/j.dam.2015.01.023
Web of Science® Google Scholar
8 Fan D. D., Niu A. H., and Wang G. P., The bicyclic graph with the minimum distance Laplacian spectral radius, Journal of Engineering Mathematics. (2020) 37, 121–130.
Google Scholar
9 Lin H. Y. and Zhou B., The distance Laplacian spectral radius of unicyclic graphs, Mathematics Combinatorics. (2017) 45, 35–46.
Google Scholar
10 Cui S.-Y., He J.-X., and Tian G.-X., The generalized distance matrix, Linear Algebra and Its Applications. (2019) 563, https://doi.org/10.1016/j.laa.2018.10.014, 2-s2.0-85055254983.
10.1016/j.laa.2018.10.014
Web of Science® Google Scholar
11 Alhevaz A., Baghipur M., Ganie H. A., and Shang Y. L., On the generalized distance energy of graphs, Mathematics. (2019) 8, no. 17, https://doi.org/10.3390/math8010017.
10.3390/math8010017
Web of Science® Google Scholar
12 Lin H. Q. and Drury S., The distance spectrum of complements of trees, Linear Algebra and Its Applications. (2017) 530, 185–201, https://doi.org/10.1016/j.laa.2017.05.016, 2-s2.0-85019546247.
10.1016/j.laa.2017.05.016
Web of Science® Google Scholar
13 Alhevaz A., Baghipur M., Ganie H. A., and Shang Y., Bounds for the generalized distance eigenvalues of a graph, Symmetry. (2019) 11, no. 12, https://doi.org/10.3390/sym11121529.
10.3390/sym11121529
Web of Science® Google Scholar
14 Alhevaz A., Baghipur M., Ganie H. A., and Shang Y. L., The generalized distance spectrum of the join of graphs, Symmetry. (2020) 12, no. 169, https://doi.org/10.3390/sym12010169.
10.3390/sym12010169
Web of Science® Google Scholar
15 Shang Y., Distance estrada index of random graphs, Linear and Multilinear Algebra. (2015) 63, no. 3, 466–471, https://doi.org/10.1080/03081087.2013.872640, 2-s2.0-84910155366.
10.1080/03081087.2013.872640
Web of Science® Google Scholar
16 Yang J. S. and Gutman L. H. Y.I., Bounds on the distance Laplacian energy of graphs, Kragujevac Journal of Mathematics. (2013) 37, no. 2, 245–255.
Google Scholar
17 Das K. C., Aouchiche M., and Hansen P., On (distance) Laplacian energy and (distance) signless Laplacian energy of graphs, Discrete Applied Mathematics. (2018) 243, 172–185, https://doi.org/10.1016/j.dam.2018.01.004, 2-s2.0-85044499110.
10.1016/j.dam.2018.01.004
Web of Science® Google Scholar

Citing Literature

All articles

The Distance Laplacian Spectral Radius of Clique Trees

Abstract

1. Introduction

2. Preliminaries

3. Minimum Distance Laplacian Spectral Radius of Clique Trees

4. Maximum Distance Laplacian Spectral Radius of Clique Trees

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Distance Laplacian Spectral Radius of Clique Trees

Abstract

1. Introduction

2. Preliminaries

3. Minimum Distance Laplacian Spectral Radius of Clique Trees

4. Maximum Distance Laplacian Spectral Radius of Clique Trees

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information