Analytical Solution of UCM Viscoelastic Liquid with Slip Condition and Heat Flux over Stretching Sheet: The Galerkin Approach
Abstract
This paper provides a substantial amount of study related to coupled fluid flow and heat conduction of an upper-convected-Maxwell viscoelastic liquid over a stretching plane with slip velocity. A new model, presented by Christov, for thermal convection is employed. The partial differential equations are converted to ordinary differential equations by using appropriate transformation variables. The transformed equations are solved analytically by using the Galerkin method. For the sake of soundness, a comparison is done with a numerical method, and good agreement is found. The impacts of various parameters like slip coefficient, elasticity number, the thermal relaxation time of heat flow, and the Prandtl number over the temperature and velocity fields are studied. Furthermore, the Cattaneo–Christov heat flux model is compared with Fourier’s law. Additionally, the present results are also verified by associating with the published work as a limiting case.
1. Introduction
Heat is a form of energy which is related to temperature. Heat transfer occurs when there is a temperature difference between a system and its surrounding. Many theories and laws were presented to study the heat transfer behavior. Fourier presented the law for heat conduction in [1] and derived an empirical formula which was considered the basis to investigate the thermal phenomenon. An amended form of the Fourier heat conduction law is presented by Cattaneo [2]. He introduced a relaxation time parameter to reduce the “heat conduction paradox,” which is any original disruption and immediately felt throughout the medium under certain conditions [3, 4]. Christov [3] studied the frame invariant generalization of the Maxwell–Cattaneo law by considering upper-convected Oldroyd’s time derivative [5]. Chistov presented a new formulation which gives a single governing expression for temperature. It is shown by Tibullo and Zampoli [4] and Ciarletta and Straughan [6] that the solution of the temperature governing equations along with the Catteneo–Christov model for both extreme value problems is unique. Straughan [7] and Haddad [8] achieved algebraic results for the heat convection of Newtonian incompressible liquid with the Cattaneo–Christov model for heat flow by considering the D2 Chebyshev tau technique.
A significant class of viscoelastic fluid models is the Maxwell fluid. Large number of research outputs on the maxwellian fluid has been published over the past few decades. In these studies, both initial and final value problems of Upper-Covected-Maxwell (UCM) fluid got the attention of the researcher. Choi et al. [9] explored two-dimensional ideal fluid movement of upper-covected-Maxwell fluid in a permeable medium. Sadeghy et al. [10] presented three different methods to evaluate the governing equations, and it is predicted that the wall skin friction coefficient reduces when the Deborah number increases for Sakiadis flow of a Maxwellian fluid. The magnetohydrodynamic (MHD) flows in multidimension over a permeable medium are studied in [11–14]. The stagnation point movement of Maxwellian liquid is explored in [15–20]. Hayat et al. [21] studied the mass transfer of an upper-covected-Maxwell fluid from a uniform two-dimensional MHD boundary layer flux over a permeable contracting plane. The heat transfer of UCM fluid on a floating surface and convective boundary values have been discussed in [22]. Aliakbar et al. [23] discussed the effects of thermal radiation over a stretch surface on the MHD flow of Maxwellian fluids. Rasheed et al. [24, 25] investigated heat transfer analysis in two-dimensional viscoelastic incompressible fluid with nonuniform heat generation over a permeable stretching sheet in the presence of uniform magnetic field. To solve the higher-order differential equation, the Liao’s homotopy analysis method [26, 27] is very useful. A detail analysis of MHD flow and heat transfer procedure of viscoelastic fluid through a porous medium in the wire coating analysis has been studied by Khan et al. [28–31].
Evaluating the physical problems, the analytical solution has effective impacts. According to the recent studies of the researchers, not according to current knowledge of the authors, no work has been conducted which provided the analytical method for temperature-governing equalities with the Cattaneo–Christov heat convective model. In this paper, an analytical solution is obtained through the Galerkin method.
The core theme of this article is to investigate the coupled flow and thermal convection of a boundary surface with the upper-convected-Maxwell model and Cattaneo–Christov heat flux model. The propriate transformations are used to transform the PDs to ODs and then solved analytically by utilizing the Galerkin analysis technique to achieve analytical solutions. The numerical method is also used for comparison purpose. For the validation of the present results, a comparison is also performed with the published work. The impacts of the involved constrains over the temperature and velocity fields are explored.
2. The Basic Equations
3. Solution Procedure of the Galerkin Method
The application and procedure to examine solutions of the considered problem given in equations (9) and (10) by means of a prominent analytical tool known as the Galerkin method are explained for the considered problem here in this section. The general solution process of the Galerkin method is explained well in [33–36]. We present the procedure of the Galerkin method for solving equations (9) and (10). The Galerkin method contains the following steps:
Step 2. The Galerkin method approves the following trial solutions to explore the estimated solutions of equations (12)-(13), which incorporates a linear combination of basic functions as
Step 3. The assumed trial solution by the Galerkin method must satisfy the boundary conditions associated with problem equations (9) and (10). We get the following reduced trial solutions after employing the boundary conditions in equation (11):
Step 4. The residual vectors for f(η) and θ(η) in the Galerkin method are produced as indicated below by plugging the reduced trial solutions (14)-(15) into the problem stated in step 1.
Equality holds when f(η) and θ(η) are the exact solutions of the problem given in equations (9) and (10).
Step 5. To notice the constants, residual must be zero in the discoursed domain as indicated below:
4. Validity of the Proposed Method
For the conformation of the analytical solution, we make the following comparison with the numerical method and published the work which proves the thoroughness of the proposed method. Our comparison is shown in Tables 1 and 2 and Figures 1 and 2. An outstanding contract is observed between our current results and with an already published work reported by Han et al. [36].
| f(η) | Galerkin method | Numerical solution | Han et al. [36] |
|---|---|---|---|
| 0 | 0.00000000000 | 0.00000000000 | 0.00000000000 |
| 1 | 0.3903823668 | 0.3903823574 | 0.3903823643 |
| 2 | 0.5575532542 | 0.5575532342 | 0.5575532472 |
| 3 | 0.6238619488 | 0.6238619576 | 0.6238619357 |
| 4 | 0.6490119937 | 0.6490119786 | 0.6490119658 |
| 5 | 0.6583722240 | 0.6583722341 | 0.6583722547 |
| 6 | 0.6618305727 | 0.6618305653 | 0.6618305658 |
| 7 | 0.6631048609 | 0.6631048754 | 0.6631048935 |
| θ(η) | Galerkin method | Numerical solution | Han et al. [36] |
|---|---|---|---|
| 0 | 1.00000000000 | 1.00000000000 | 1.00000000000 |
| 1 | 0.5241982620 | 0.5241982523 | 0.5241982852 |
| 2 | 0.2230345229 | 0.2230345342 | 0.2230345692 |
| 3 | 0.0864815344 | 0.0864815621 | 0.0864815963 |
| 4 | 0.0324258527 | 0.0324258481 | 0.0324258573 |
| 5 | 0.0120119374 | 0.0120119540 | 0.0120119843 |
| 6 | 0.0044302146 | 0.0044302216 | 0.0044302621 |
| 7 | 0.0016313110 | 0.0016313200 | 0.0016313320 |

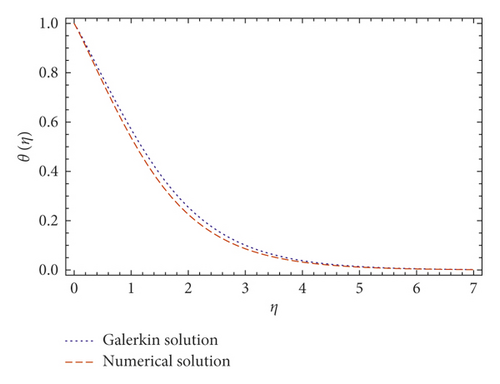
5. Results and Discussion
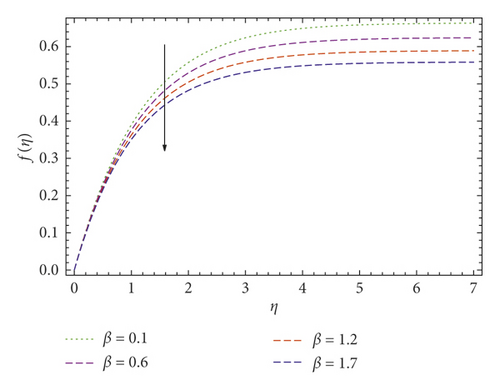
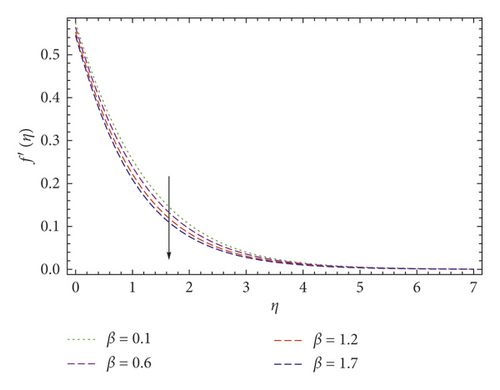
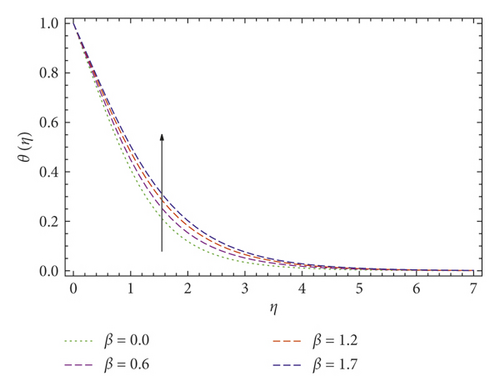
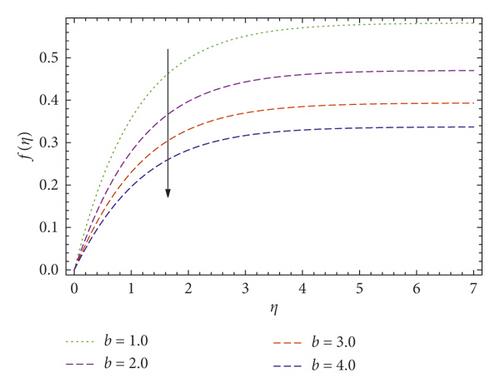
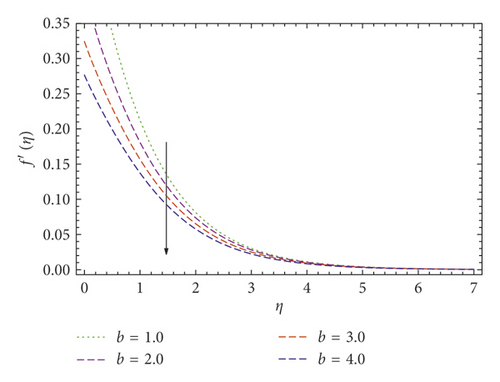
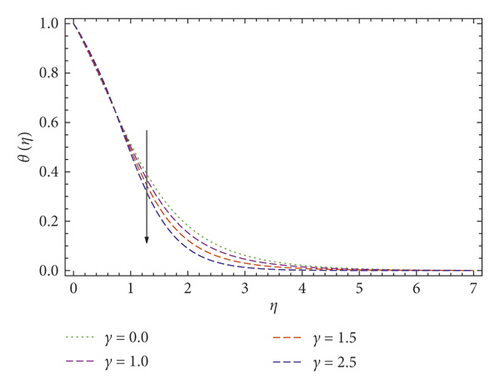
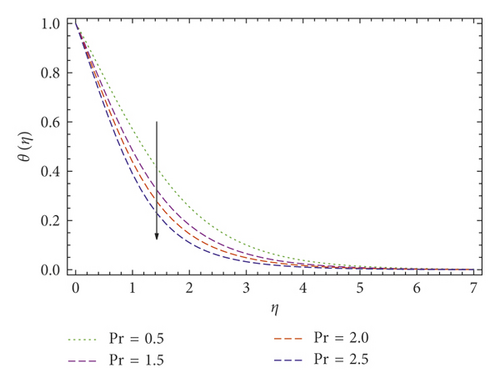
In this publication, we use the UCM and Cattaneo–Christov thermal convective models to study the thermal conduction and boundary layer movement for a viscoelastic liquid over a stretching surface with a velocity slip layer. By using the similarity transformation to the temperature and velocity expressions, a pair of coupled equations is derived. Approximate, well analyzed results of both equations (9) and (10) along with boundary value problems (11) are derived using the Galerkin method. As compared with the Newtonian fluid model, the UCM fluid has a single elastic term which indicates that restoring force has an impact on the flow and heat conduction of viscoelastic fluid. Figures 3, 4–5 provide the behavior of elasticity number β over the temperature and velocity profiles. The elastic pull vanishes when β = 0, and the fluid is converted into a Newtonian fluid, and it observed that the elastic force escalates by rising the elasticity number β. In Figures 3 and 4, the values of f(η) and f′(η) decrease by increasing the elasticity number β, which also points out that the velocity boundary layer gradually decreases by increasing the elasticity number β. The fluid temperature θ(η) rises as βincreases, as displayed in Figure 5. It is also noticed that the elastic pulse increases the heat transfer of the fluid. Figures 6 and 7 investigate the slip effects over velocity profile f′(η) and f(η), respectively. These velocity profiles decrease when the slip parameter b increases. The heat flux model of Cattaneo–Christov is a frame-invariant model in which the fluid velocity is presented with fluid temperature and heat transfer. It points out that heat flow is related to temperature gradient and velocity of the fluid. Figure 8 represents the γ influence over temperature profile θ(η), at γ = 0, the heat flux model obeys Fourier’s law. It is also observed that the thickness of the temperature boundary layer decreases with increasing γ. The impacts of the Prandtl number Pr over energy distribution have been discussed in Figure 9, which indicates that the temperature boundary layer becomes thinner as the Prandtl number Pr increases.
6. Conclusions
- (1)
The elastic pull vanishes when β = 0 and the fluid converted into Newtonian fluid, and it observed that the elastic force escalates by rising the elasticity number β, while the values of f(η) and f′(η) decreases.
- (2)
The velocity boundary layer is gradually decreased by increasing the elasticity number β. The fluid temperature θ(η) rises as βincreases. It also shows that the elastic pulse increases the heat transfer of the fluid.
- (3)
The velocity profile f(η) and f′(η), respectively decrease when the slip parameter b increases. The heat flux model of Cattaneo–Christov is a frame-invariant model in which the fluid velocity is presented with fluid temperature and heat transfer.
- (4)
It is also noticed that the thickness of the temperature boundary layer decreases by increasing γ.
- (5)
It is also investigated that the temperature boundary layer becomes thinner as the Prandtl number Pr increases.
Conflicts of Interest
The authors declare that they have no conflicts of interest about this manuscript.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at Majmaah University for funding this work under Project Number (RGP-2019-3). This work was supported by the Soonchunhyang University Research Fund.
Open Research
Data Availability
The data used to support the findings of this study are available from the corresponding author upon request.




