This paper deals with numerical treatment of singularly perturbed differential difference equations involving mixed small shifts on the reaction terms. The highest-order derivative term in the equation is multiplied by a small perturbation parameter ε taking arbitrary values in the interval (0,1]. For small values of ε, the solution of the problem exhibits exponential boundary layer on the left or right side of the domain and the derivatives of the solution behave boundlessly large. The terms having the shifts are treated using Taylor’s series approximation. The resulting singularly perturbed boundary value problem is solved using exponentially fitted operator FDM. Uniform stability of the scheme is investigated and analysed using comparison principle and solution bound. The formulated scheme converges uniformly with linear order before Richardson extrapolation and quadratic order after Richardson extrapolation. The theoretical analysis of the scheme is validated using numerical test examples for different values of ε and mesh number N.

1. Introduction

Differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology. Currently different authors are working on analytical and numerical solutions of differential equations using different techniques [1, 2]. Differential difference equations (DDEs) are differential equations where the evolution of the system not only depends on the present state of the system but also depends on the past history. Singularly perturbed differential difference equations are differential equations in which the highest-order derivative term is multiplied by a small perturbation parameter ε and involves at least one term with delay. In general, when the perturbation parameter tends to zero, the smoothness of the solution of the singularly perturbed differential difference equations (SPDDEs) deteriorates and it forms boundary layer [3]. Such type of equations has applications in the study of variational problems in control theory [4] and in modelling of neuronal variability [5].

The presence of singular perturbation parameter ε in the equation leads to oscillation in the computed solution, while using standard numerical methods like FDM, FEM, and spline method [6]. To avoid this oscillation, an unacceptably large number of mesh points are required when ε is very small. This is not practical and leads to round-off error. So, to overcome the drawbacks associated with standard numerical methods, different authors have developed schemes that converge uniformly.

Numerical treatments of a class of SPDDEs have received a great deal of attention recently because of their wide applications. It is of theoretical and practical interest to consider numerical methods for such problems. Owing to this, here we present some prior studies on numerical solution of the considered problem. Lange and Miura in [7–10] studied a class of second-order DDEs in which the second derivative term is multiplied by a small parameter. The authors extend the method of matched asymptotic expansions initially developed for solving boundary value problems to obtain approximate solution for SPDDEs. In a series of papers [11–14], Kadalbajoo and Sharma developed uniformly convergent numerical methods using fitted mesh FDMs techniques. Swamy et al. [15–17] considered the problem and developed a numerical scheme using fitted operator finite difference techniques. Melesse et al. [18] applied initial value technique for treating the considered SPDDEs. Ranjan and Prasad [19] used modified fitted operator FDM for solving the problem. Sirisha et al. [20] developed fitted operator finite difference scheme using the procedure of domain decomposition. A number of authors have developed numerical scheme using exponentially fitted method for solving SPDDEs. To the authors’ knowledge, none of them show the uniform convergence of their schemes. This motivates to treat the considered SPDDEs and formulate the uniform convergence analysis of the scheme. Our contribution in this paper is to develop higher-order uniformly convergent numerical scheme using exponentially fitted FDM and to analyse the uniform convergence of the proposed scheme.

Notation 1. The symbol C is used to denote positive constant independent of ε and N. The norm ‖.‖ denotes the maximum norm.

2. Statement of the Problem

A class of second-order singularly perturbed differential difference equations having mixed shift on reaction terms is given by

(1)

with the interval conditions

(2)

where ε ∈ ( 0,1 ] is singular perturbation parameter and δ and η are delay and advance parameters satisfying δ, η < ε. The functions a(x), α(x), ω(x), β(x), f(x), ϕ(x), and ψ(x) are assumed to be sufficiently smooth, bounded, and independent of ε for guaranteeing the existence of unique solution. The coefficient functions α(x), ω(x), and β(x) are assumed to satisfy

(3)

for some constant q^∗.

For the case where δ, η < ε, using Taylor’s series approximation for the terms with shift is appropriate [21]. So, we approximate u(x − δ) and u(x + η) as

(4)

Using the approximation in (4) into (1)-(2) gives

(5)

with the boundary conditions

(6)

where c_ε = ε² − (δ²/2)α − (η²/2)β, p(x) = a(x) − δα(x) + ηβ(x), and q(x) = α(x) + β(x) + ω(x) for α and β are lower bounds of α(x) and β(x), respectively. For small values of δ, η, equations (1)-(2) and (5)-(6) are asymptotically equivalent, since the truncated term in (5)-(6) is order of O(δ³, η³).

Let us denote differential operator L for the differential equation in (5) as

(7)

The solution of the problem in (5)-(6) exhibits regular boundary layer of thickness O(c_ε) and the position of the boundary layer depends on the sign of p(x). If p(x) < 0, left boundary layer exists and, for p(x) > 0, right boundary layer exists. If p(x), x ∈ [0,1] changes sign interior layer will occur [22].

Setting c_ε = 0 in equations (5)-(6) gives the reduced problem. For the case where p(x) > 0, it is given by

(8)

and, for the case where p(x) < 0, it is given by

(9)

It is a first-order initial value problem; for small values of c_ε, the solution of (5)-(6) is very close to the solution of (8) or (9).

2.1. Properties of the Analytical Solution

Lemma 1 (The maximum principle). Let z be a sufficiently smooth function defined on Ω, which satisfies z(0) ≥ 0 and z(1) ≥ 0. Then Lz(x) > 0, ∀ x ∈ Ω, implies that .

Proof. Let be such that and suppose that z(x^∗) < 0. It is clear that x^∗ ∉ {0,1}. Since form extrema values in calculus we have z^′(x^∗) = 0 and z^″(x^∗) ≥ 0 giving that Lz(x^∗) < 0, which is contradiction to the assumption made above: Lz(x^∗) > 0, ∀ x ∈ Ω. Therefore, z(x) ≥ 0, ∀ x ∈ Ω.

Lemma 2 (Stability estimate). Let u be the solution of (5)-(6); then, it satisfies the bound

(10)

where q^∗ is lower bound of q(x).

Proof. Let us define barrier functions ϑ_±(x) as ϑ_±(x) = (‖f‖/q^∗) + max{ϕ(0), ψ(1)} ± u(x) and apply the maximum principle to obtain the required bound.

On the boundary points, we have

(11)

On the differential operator,

(12)

which implies that Lϑ_±(x) ≥ 0. Hence, using the maximum principle in Lemma 1, we obtain

Lemma 3. The derivatives of the solutions of (5)-(6) satisfy the bound

(13)

for left boundary layer problems and

(14)

for right boundary layer problems.

Proof. See [23].

3. Numerical Scheme

First, let us discretize the domain

into N equal number of subintervals with mesh length h = (1/N) as

. Let u(x) be smooth function on the domain

; then, using Taylor series approximation, we have

(15)

Taking the difference in (15), we obtain

(16)

Differentiating (16) two times gives

(17)

Now, multiplying (17) by −(h²/12) and adding with (16) to eliminate the term with

gives

(18)

where τ = O(h⁶). Evaluating (5) at x_i−1, x_i, and x_i+1, respectively, we obtain

(19)

Next, approximate the first derivative terms

, and

in (19), using the right shifted, central, and left shifted finite difference approximations as

(20)

Substituting (20) into (19) and then (19) into (18) gives

(21)

where p_i−1, p_i, and p_i+1 are denoted for p(x_i−1), p(x_i), and p(x_i+1), respectively. We denote U_i for the approximate solution of u(x_i) in the above discretization.

To get small truncation error in boundary layer region, we apply exponentially fitted operator finite difference method (FOFDM). For developing the FOFDM, we use the theory developed in asymptotic method for treating singularly perturbed BVPs. Let us consider and treat the left and the right boundary layer cases separately.

3.1. Left Boundary Layer Problems

In this case, the boundary layer occurs near x = 0. From the theory of singular perturbation given in [24], the zeroth-order asymptotic solution of (5)-(6) is given by

(22)

where u₀ is the solution of the reduced problem. Using Taylor’s series approximation for u₀(x), p(x), and q(x) centred at x_i = ih up to first order and considering c_ε⟶0, the discretized form of (22) becomes

(23)

where ρ = h/c_ε, h = 1/N. Similarly, we write

(24)

To handle the effect of the perturbation parameter, exponential fitting factor σ₁(ρ) is multiplied on the term containing the perturbation parameter as

(25)

Multiplying both sides of (25) by h and substituting ρ for h/c_ε and taking the limit as h⟶0 give

(26)

From (23) and (24), we obtain

(27)

Substituting (27) into (26) and simplifying give

(28)

The exponential fitting factor is obtained as

(29)

Hence, the required finite difference scheme becomes

(30)

where

(31)

with the boundary values U₀ = ϕ(0) and U_N = ψ(1).

3.2. Right Boundary Layer Problems

In this case, the boundary layer occurs near x = 1. From [24], the zeroth-order asymptotic solution of (5)-(6) is given by

(32)

where u₀ is the solution of the reduced problem.

Using Taylor’s series approximation for u₀(x), p(x), and q(x) centred at x_i = ih up to first order and considering c_ε⟶0, the discretized form of (24) becomes

(33)

Using similar procedures as the left boundary layer case, the exponential fitting factor is obtained as

(34)

Hence, the required finite difference scheme becomes

(35)

where

(36)

3.3. Convergence Analysis

In this section, we show the stability and convergence analysis for the right boundary layer problems. In similar manner, it is proved for the left boundary layer case. First, we need to prove the discrete comparison principle for the scheme in (35) for guaranteeing existence of unique discrete solution.

Lemma 4 (Discrete comparison principle). Assume that, for mesh function U_i there exists a comparison function V_i such that and if U₀ ≤ V₀ and U_N ≤ V_N, then U_i ≤ V_i, ∀ i, i = 0,1,2, …, N.

Proof. The matrix associated with operator is of size (N + 1) × (N + 1) and satisfies the property of M-matrix. See the detailed proof in [23].

This lemma gives guarantee for the existence of unique discrete solution. In the next lemma, we discuss the uniform stability of the discrete solution.

Lemma 5 (Discrete stability estimate). The solution U_i of the discrete scheme in (35) satisfies the following bound:

(37)

Proof. Let and define barrier functions by .

On the boundary points, we obtain

(38)

On the discretized spatial domain x_i, 1 < i < N − 1, we obtain

(39)

By the discrete comparison principle in Lemma 4, we obtain . Hence, the required bound is satisfied.

Now, let us denote the right shifted, centred, and left shifted finite differences, respectively, as

(40)

Using Taylor’s series approximation, we obtain the bound

(41)

where

. Similarly, we have

(42)

Now, for ρ > 0, C₁ and C₂ are constants, and we have |ρ coth(ρ) − 1| ≤ C₁ρ², for ρ ≤ 1. For ρ⟶∞, since lim_ρ⟶∞coth(ρ) = 1, |ρ coth(ρ) − 1| ≤ C₁ρ is given. In general, for all ρ > 0, we write

(43)

implying that

(44)

The following theorem gives truncation error bound of the proposed scheme.

Theorem 1. Let u(x_i) and U_i be solutions of (5)-(6) and (35), respectively. Then the following error estimate holds:

(45)

Proof. Consider the truncation error that is given by

(46)

Using the bounds in (44), (41), and (42) gives

(47)

Substituting the bounds for the derivatives of the solution in Lemma 3, we obtain

(48)

Since , we obtain

(49)

Lemma 6. For c_ε⟶0, and for given fixed N, we obtain

(50)

where x_j = jh, h = 1/N, ∀j = 1,2, …, N − 1.

Proof. See [25–27].

Theorem 2. Under the hypothesis of boundedness of discrete solution, the solution of the discrete schemes in (30) satisfies the following uniform error bound:

(51)

Proof. Substituting the results in Lemma 6 into Theorem 1, applying Lemma 5 gives the required bound.

3.4. Richardson Extrapolation

We apply the Richardson extrapolation technique to accelerate the rate of convergence of the proposed scheme. Richardson extrapolation is a convergence acceleration technique that involves combination of two computed approximations of solution. Interested reader can see the details of Richardson extrapolation in [28]. From (34) and Lemma 6, we obtain

(52)

where u(x_i) and U_i are the exact and approximate solutions of (5)-(6), respectively. Applying Lemma 5 in (52) gives

(53)

Let us denote

for an approximate solution on 2N number of mesh points by including the mid-points. Applying the same procedure as in (52) and (53) on 2N number of mesh points, we obtain

(54)

Combining (53) and (54) for removing the term CN⁻¹ results in

(55)

giving

(56)

as the extrapolated solution. The error bound for the extrapolated solution in (56) becomes

(57)

4. Examples and Numerical Results

In this section, we consider numerical examples to illustrate the theoretical findings of the developed schemes.

Example 1. Consider the problem

(58)

with interval conditions u(x) = 1, − δ ≤ x ≤ 0, u(x) = −1, 1 ≤ x ≤ 1 + η.

Example 2. Consider the problem

(59)

with interval conditions u(x) = 1, − δ ≤ x ≤ 0, u(x) = −1, 1 ≤ x ≤ 1 + η.

Example 3. Consider the problem

(60)

with interval conditions u(x) = 1, − δ ≤ x ≤ 0, u(x) = 0, 1 ≤ x ≤ 1 + η.

Example 4. Consider the problem

(61)

with interval conditions u(x) = 1, − δ ≤ x ≤ 0, u(x) = 1, 1 ≤ x ≤ 1 + η.

The exact solution of the constant coefficient interval value problem

(62)

on Ω = (0,1), with the interval conditions u(x) = ϕ(x), x ∈ [−δ, 0], u(x) = ψ(x), x ∈ [1,1 + η], is given by

(63)

where c = α + ω + β,

, and

The exact solutions of the variable coefficient problems are not known. So, we use the procedure of the double mesh technique to calculate maximum absolute error. The maximum absolute error is defined as

(64)

where

denotes the solution of the problem on N number of mesh points and

denotes the numerical solution on 2N number of mesh points by including the mid-points x_{(i + 1)/2} into the mesh numbers. The uniform error estimate is defined as

(65)

The rate of convergence of the scheme is given by

(66)

and the uniform rate of convergence is given as

(67)

In Tables 1–8, the maximum absolute error of Examples 1–4 using the proposed scheme is given. In Tables 1, 3, 5, and 7, the maximum absolute error before the Richardson extrapolation is given, and in Tables 2, 4, 6, and 8, the maximum absolute error after the Richardson extrapolation is given. As one observes in the tables, for each number of mesh interval N as ε⟶0, the maximum absolute error becomes stable and uniform. This indicates that the proposed scheme convergence is independent of the perturbation parameter ε. In the last two rows of each table, we observe the ε-uniform error and the ε-uniform rate of convergence of the scheme. The scheme before the extrapolation gives first-order uniform convergence and the extrapolated scheme gives second-order uniform convergence. In Tables 9 and 10, we compare the maximum absolute error of the proposed scheme with recently published papers in [14, 15, 19]. As one observes, the proposed scheme gives more accurate result.

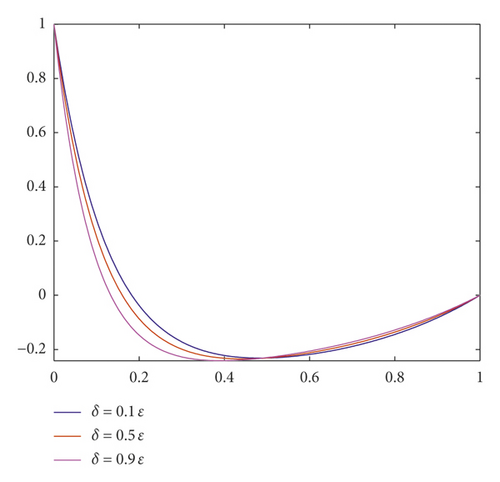
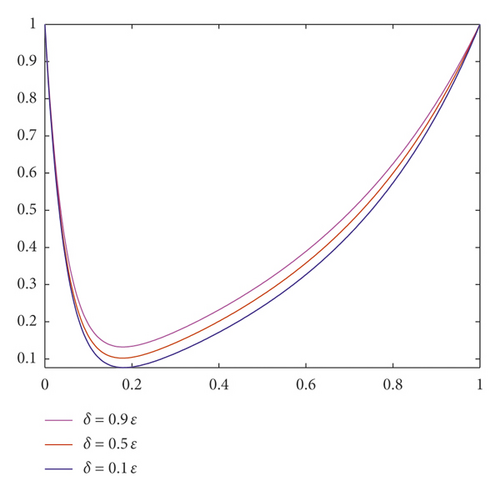
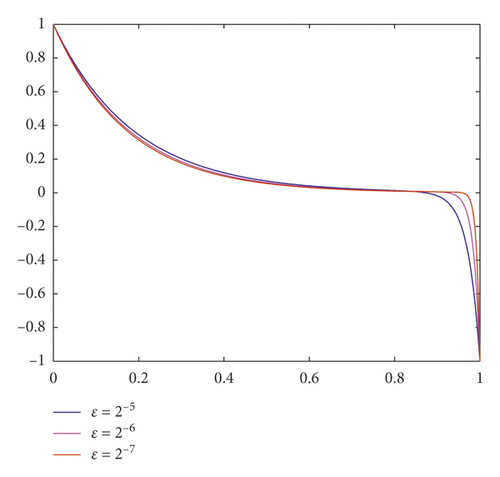
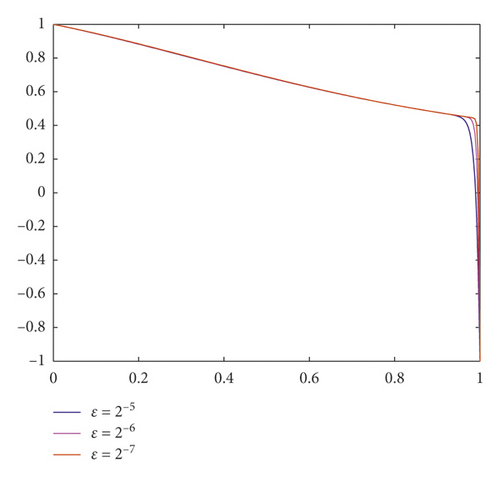
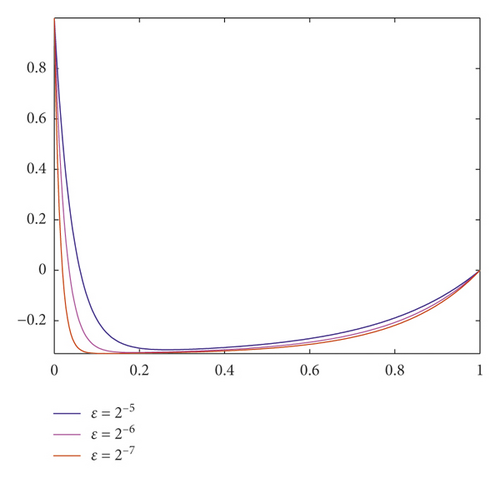
In Figure 1, the influence of the delay parameter on the behaviour of the solution of Examples 3 and 4 is shown for ε = 2⁻³ and δ = 0.1ε, 0.5ε, and 0.9ε. From Figure 2, we observe the numerical solution of Examples 1–4 for different values of the perturbation parameter ε = 2⁻⁵, 2⁻⁶, and 2⁻⁷. As observed in the figures, for ε going small, strong boundary layer is created.

Table 1. Maximum absolute error of Example 1 before Richardson extrapolation for δ = 0.6ε and η = 0.5ε.

ε↓	N⟶8	16	32	64	128	256
2⁰	1.3808e − 03	3.4045e − 04	8.4818e − 05	2.1193e − 05	5.2970e − 06	1.3242e − 06
2⁻⁴	1.7200e − 02	5.0151e − 03	1.4739e − 03	3.5993e − 04	9.0018e − 05	2.2464e − 05
2⁻⁸	4.1828e − 02	2.6301e − 02	1.4357e − 02	6.0620e − 03	1.8873e − 03	5.0407e − 04
2⁻¹²	4.1711e − 02	2.6194e − 02	1.4838e − 02	7.9779e − 03	4.1434e − 03	2.1118e − 03
2⁻¹⁶	4.1704e − 02	2.6186e − 02	1.4834e − 02	7.9750e − 03	4.1418e − 03	2.1124e − 03
2⁻²⁰	4.1703e − 02	2.6186e − 02	1.4833e − 02	7.9748e − 03	4.1417e − 03	2.1123e − 03
2⁻²⁴	4.1703e − 02	2.6186e − 02	1.4833e − 02	7.9748e − 03	4.1417e − 03	2.1123e − 03
2⁻²⁸	4.1703e − 02	2.6186e − 02	1.4833e − 02	7.9748e − 03	4.1417e − 03	2.1123e − 03
2⁻³²	4.1703e − 02	2.6186e − 02	1.4833e − 02	7.9748e − 03	4.1417e − 03	2.1123e − 03
2⁻³⁶	4.1703e − 02	2.6186e − 02	1.4833e − 02	7.9748e − 03	4.1417e − 03	2.1123e − 03
2⁻⁴⁰	4.1703e − 02	2.6186e − 02	1.4833e − 02	7.9748e − 03	4.1417e − 03	2.1123e − 03
E^N	4.1703e − 02	2.6186e − 02	1.4833e − 02	7.9748e − 03	4.1417e − 03	2.1123e − 03
R^N	0.6714	0.8200	0.8953	0.9452	0.9714	–

Table 2. Maximum absolute error of Example 1 after Richardson extrapolation for δ = 0.6ε η = 0.5ε.

ε↓	N⟶8	16	32	64	128	256
2⁰	3.4045e − 04	2.1193e − 05	1.3242e − 06	8.2744e − 08	5.3296e − 09	1.3016e − 09
2⁻⁴	5.0151e − 03	3.5993e − 04	2.2464e − 05	1.4036e − 06	8.7720e − 08	2.2310e − 08
2⁻⁸	2.6301e − 02	6.0620e − 03	5.0407e − 04	3.3479e − 05	2.0797e − 06	4.2147e − 07
2⁻¹²	2.6194e − 02	7.9779e − 03	2.1118e − 03	4.0826e − 04	3.2897e − 05	5.2346e − 06
2⁻¹⁶	2.6186e − 02	7.9750e − 03	2.1124e − 03	5.3615e − 04	1.3446e − 04	3.2541e − 05
2⁻²⁰	2.6186e − 02	7.9748e − 03	2.1123e − 03	5.3614e − 04	1.3446e − 04	3.2541e − 05
2⁻²⁴	2.6186e − 02	7.9748e − 03	2.1123e − 03	5.3614e − 04	1.3446e − 04	3.2541e − 05
2⁻²⁸	2.6186e − 02	7.9748e − 03	2.1123e − 03	5.3614e − 04	1.3446e − 04	3.2541e − 05
2⁻³²	2.6186e − 02	7.9748e − 03	2.1123e − 03	5.3614e − 04	1.3446e − 04	3.2541e − 05
2⁻³⁶	2.6186e − 02	7.9748e − 03	2.1123e − 03	5.3614e − 04	1.3446e − 04	3.2541e − 05
2⁻⁴⁰	2.6186e − 02	7.9748e − 03	2.1123e − 03	5.3614e − 04	1.3446e − 04	3.2541e − 05
E^N	2.6186e − 02	7.9748e − 03	2.1123e − 03	5.3614e − 04	1.3446e − 04	3.2541e − 05
R^N	1.7153	1.9166	1.9781	1.9954	2.0468	–

Table 3. Maximum absolute error of Example 2 before Richardson extrapolation for δ = 0.6ε and η = 0.5ε.

ε↓	N⟶8	16	32	64	128	256
2⁰	3.4492e − 03	1.6925e − 03	8.3747e − 04	4.1601e − 04	2.0724e − 04	1.0343e − 04
2⁻⁴	2.2763e − 02	7.6376e − 03	1.4739e − 03	1.5941e − 03	7.8163e − 04	3.8784e − 04
2⁻⁸	2.3670e − 02	1.1054e − 02	5.2737e − 03	2.5716e − 03	1.2314e − 03	4.9403e − 04
2⁻¹²	2.3670e − 02	1.1054e − 02	5.2735e − 03	2.5654e − 03	1.2638e − 03	6.2704e − 04
2⁻¹⁶	2.3670e − 02	1.1054e − 02	5.2735e − 03	2.5654e − 03	1.2638e − 03	6.2704e − 04
2⁻²⁰	2.3670e − 02	1.1054e − 02	5.2735e − 03	2.5654e − 03	1.2638e − 03	6.2704e − 04
2⁻²⁴	2.3670e − 02	1.1054e − 02	5.2735e − 03	2.5654e − 03	1.2638e − 03	6.2704e − 04
2⁻²⁸	2.3670e − 02	1.1054e − 02	5.2735e − 03	2.5654e − 03	1.2638e − 03	6.2704e − 04
2⁻³²	2.3670e − 02	1.1054e − 02	5.2735e − 03	2.5654e − 03	1.2638e − 03	6.2704e − 04
2⁻³⁶	2.3670e − 02	1.1054e − 02	5.2735e − 03	2.5654e − 03	1.2638e − 03	6.2704e − 04
2⁻⁴⁰	2.3670e − 02	1.1054e − 02	5.2735e − 03	2.5654e − 03	1.2638e − 03	6.2704e − 04
E^N	2.3670e − 02	1.1054e − 02	5.2735e − 03	2.5654e − 03	1.2638e − 03	6.2704e − 04
R^N	1.0985	1.0677	1.0396	1.0214	1.0111	–

Table 4. Maximum absolute error of Example 2 after Richardson extrapolation for δ = 0.6ε and η = 0.5ε.

ε↓	N⟶8	16	32	64	128	256
2⁰	1.6925e − 03	4.1601e − 04	1.0343e − 04	2.5819e − 05	6.4524e − 06	1.1321e − 06
2⁻⁴	7.6376e − 03	1.5941e − 03	3.8784e − 04	9.6460e − 05	2.4085e − 05	7.6001e − 06
2⁻⁸	1.1054e − 02	2.5716e − 03	4.9403e − 04	1.0586e − 04	2.6498e − 05	8.0231e − 06
2⁻¹²	1.1054e − 02	2.5654e − 03	6.2704e − 04	1.5625e − 04	3.0982e − 05	8.2543e − 06
2⁻¹⁶	1.1054e − 02	2.5654e − 03	6.2704e − 04	1.5584e − 04	3.8901e − 05	9.2541e − 06
2⁻²⁰	1.1054e − 02	2.5654e − 03	6.2704e − 04	1.5584e − 04	3.8901e − 05	9.2541e − 06
2⁻²⁴	1.1054e − 02	2.5654e − 03	6.2704e − 04	1.5584e − 04	3.8901e − 05	9.2541e − 06
2⁻²⁸	1.1054e − 02	2.5654e − 03	6.2704e − 04	1.5584e − 04	3.8901e − 05	9.2541e − 06
2⁻³²	1.1054e − 02	2.5654e − 03	6.2704e − 04	1.5584e − 04	3.8901e − 05	9.2541e − 06
2⁻³⁶	1.1054e − 02	2.5654e − 03	6.2704e − 04	1.5584e − 04	3.8901e − 05	9.2541e − 06
2⁻⁴⁰	1.1054e − 02	2.5654e − 03	6.2704e − 04	1.5584e − 04	3.8901e − 05	9.2541e − 06
E^N	1.1054e − 02	2.5654e − 03	6.2704e − 04	1.5584e − 04	3.8901e − 05	9.2541e − 06
R^N	2.1073	2.0326	2.0085	2.0022	2.0716	–

Table 5. Maximum absolute error of Example 3 before Richardson extrapolation for δ = 0.6ε and η = 0.5ε.

ε↓	N⟶8	16	32	64	128	256
2⁰	1.1318e − 03	2.7968e − 04	6.9551e − 05	1.7366e − 05	4.3405e − 06	1.0850e − 06
2⁻⁴	1.4786e − 02	3.6872e − 03	8.5968e − 04	2.1118e − 04	5.2578e − 05	1.3152e − 05
2⁻⁸	4.7613e − 02	2.9531e − 02	1.4879e − 02	5.5516e − 03	1.4704e − 03	3.3684e − 04
2⁻¹²	4.8375e − 02	3.0553e − 02	1.7528e − 02	9.4597e − 03	4.9243e − 03	2.4698e − 03
2⁻¹⁶	4.8423e − 02	3.0586e − 02	1.7549e − 02	9.4718e − 03	4.9323e − 03	2.5185e − 03
2⁻²⁰	4.8426e − 02	3.0589e − 02	1.7550e − 02	9.4725e − 03	4.9327e − 03	2.5187e − 03
2⁻²⁴	4.8426e − 02	3.0589e − 02	1.7550e − 02	9.4725e − 03	4.9328e − 03	2.5187e − 03
2⁻²⁸	4.8426e − 02	3.0589e − 02	1.7550e − 02	9.4725e − 03	4.9328e − 03	2.5187e − 03
2⁻³²	4.8426e − 02	3.0589e − 02	1.7550e − 02	9.4725e − 03	4.9328e − 03	2.5187e − 03
2⁻³⁶	4.8426e − 02	3.0589e − 02	1.7550e − 02	9.4725e − 03	4.9328e − 03	2.5187e − 03
2⁻⁴⁰	4.8426e − 02	3.0589e − 02	1.7550e − 02	9.4725e − 03	4.9328e − 03	2.5187e − 03
E^N	4.8426e − 02	3.0589e − 02	1.7550e − 02	9.4725e − 03	4.9328e − 03	2.5187e − 03
R^N	0.6628	0.8015	0.8897	0.9413	0.9697	–

Table 6. Maximum absolute error of Example 3 after Richardson extrapolation for δ = 0.6ε and η = 0.5ε.

ε↓	N⟶8	16	32	64	128	256
2⁰	2.7968e − 04	1.7366e − 05	1.0850e − 06	6.7812e − 08	4.2386e − 09	1.0101e − 09
2⁻⁴	3.6872e − 03	2.1118e − 04	1.3152e − 05	8.2173e − 07	5.0203e − 08	1.2341e − 08
2⁻⁸	2.9531e − 02	5.5516e − 03	3.3684e − 04	2.0489e − 05	1.2809e − 06	3.7125e − 07
2⁻¹²	3.0553e − 02	9.4597e − 03	2.4698e − 03	3.8494e − 04	2.2756e − 05	4.8133e − 06
2⁻¹⁶	3.0586e − 02	9.4718e − 03	2.5185e − 03	6.3984e − 04	1.5770e − 04	3.8042e − 05
2⁻²⁰	3.0589e − 02	9.4725e − 03	2.5187e − 03	6.3989e − 04	1.6062e − 04	3.9001e − 05
2⁻²⁴	3.0589e − 02	9.4725e − 03	2.5187e − 03	6.3989e − 04	1.6062e − 04	3.9001e − 05
2⁻²⁸	3.0589e − 02	9.4725e − 03	2.5187e − 03	6.3989e − 04	1.6062e − 04	3.9001e − 05
2⁻³²	3.0589e − 02	9.4725e − 03	2.5187e − 03	6.3989e − 04	1.6062e − 04	3.9001e − 05
2⁻³⁶	3.0589e − 02	9.4725e − 03	2.5187e − 03	6.3989e − 04	1.6062e − 04	3.9001e − 05
2⁻⁴⁰	3.0589e − 02	9.4725e − 03	2.5187e − 03	6.3989e − 04	1.6062e − 04	3.9001e − 05
E^N	3.0589e − 02	9.4725e − 03	2.5187e − 03	6.3989e − 04	1.6062e − 04	3.9001e − 05
R^N	1.6912	1.9111	1.9768	1.9942	2.0421	–

Table 7. Maximum absolute error of Example 4 before Richardson extrapolation for δ = 0.6ε and η = 0.5ε.

ε↓	N⟶8	16	32	64	128	256
2⁰	9.0320e − 03	4.5788e − 03	2.2918e − 03	1.1469e − 03	5.7338e − 04	2.8666e − 04
2⁻⁴	3.7979e − 02	1.6150e − 02	6.1639e − 03	2.4525e − 03	1.0562e − 03	4.8456e − 04
2⁻⁸	4.3631e − 02	2.4943e − 02	1.3421e − 02	6.9160e − 03	3.1649e − 03	1.2055e − 03
2⁻¹²	4.3723e − 02	2.4996e − 02	1.3451e − 02	7.0011e − 03	3.5749e − 03	1.8068e − 03
2⁻¹⁶	4.3728e − 02	2.4999e − 02	1.3452e − 02	7.0020e − 03	3.5755e − 03	1.8071e − 03
2⁻²⁰	4.3729e − 02	2.4999e − 02	1.3452e − 02	7.0021e − 03	3.5755e − 03	1.8071e − 03
2⁻²⁴	4.3729e − 02	2.4999e − 02	1.3452e − 02	7.0021e − 03	3.5755e − 03	1.8071e − 03
2⁻²⁸	4.3729e − 02	2.4999e − 02	1.3452e − 02	7.0021e − 03	3.5755e − 03	1.8071e − 03
2⁻³²	4.3729e − 02	2.4999e − 02	1.3452e − 02	7.0021e − 03	3.5755e − 03	1.8071e − 03
2⁻³⁶	4.3729e − 02	2.4999e − 02	1.3452e − 02	7.0021e − 03	3.5755e − 03	1.8071e − 03
2⁻⁴⁰	4.3729e − 02	2.4999e − 02	1.3452e − 02	7.0021e − 03	3.5755e − 03	1.8071e − 03
E^N	4.3729e − 02	2.4999e − 02	1.3452e − 02	7.0021e − 03	3.5755e − 03	1.8071e − 03
R^N	0.8067	0.8940	0.9420	0.9696	0.9845	–

Table 8. Maximum absolute error of Example 4 after Richardson extrapolation for δ = 0.6ε and η = 0.5ε.

ε↓	N⟶8	16	32	64	128	256
2⁰	4.5788e − 03	1.1469e − 03	2.8666e − 04	7.1658e − 05	1.7914e − 05	4.4784e − 06
2⁻⁴	1.6150e − 02	2.4525e − 03	4.8456e − 04	1.1290e − 04	2.7710e − 05	6.5434e − 06
2⁻⁸	2.4943e − 02	6.9160e − 03	1.2055e − 03	1.6886e − 04	3.2527e − 05	8.9632e − 06
2⁻¹²	2.4996e − 02	7.0011e − 03	1.8068e − 03	4.5088e − 04	7.6356e − 05	1.2456e − 05
2⁻¹⁶	2.4999e − 02	7.0020e − 03	1.8071e − 03	4.5547e − 04	1.1410e − 04	2.8541e − 05
2⁻²⁰	2.4999e − 02	7.0021e − 03	1.8071e − 03	4.5548e − 04	1.1410e − 04	2.8541e − 05
2⁻²⁴	2.4999e − 02	7.0021e − 03	1.8071e − 03	4.5548e − 04	1.1410e − 04	2.8541e − 05
2⁻²⁸	2.4999e − 02	7.0021e − 03	1.8071e − 03	4.5548e − 04	1.1410e − 04	2.8541e − 05
2⁻³²	2.4999e − 02	7.0021e − 03	1.8071e − 03	4.5548e − 04	1.1410e − 04	2.8541e − 05
2⁻³⁶	2.4999e − 02	7.0021e − 03	1.8071e − 03	4.5548e − 04	1.1410e − 04	2.8541e − 05
2⁻⁴⁰	2.4999e − 02	7.0021e − 03	1.8071e − 03	4.5548e − 04	1.1410e − 04	2.8541e − 05
E^N	2.4999e − 02	7.0021e − 03	1.8071e − 03	4.5548e − 04	1.1410e − 04	2.8541e − 05
R^N	1.8360	1.9541	1.9882	1.9971	1.9992	–

Table 9. Example 3: comparison of maximum absolute error of proposed scheme and result in [15] for δ = 0.6ε and η = 0.5ε.

ε↓	N⟶8	16	32	64	128	256
Proposed scheme
10⁻⁴	3.0589e − 02	9.4725e − 03	2.5187e − 03	6.3989e − 04	1.6062e − 04	3.9001e − 05
10⁻⁵	3.0589e − 02	9.4725e − 03	2.5187e − 03	6.3989e − 04	1.6062e − 04	3.9001e − 05
10⁻⁶	3.0589e − 02	9.4725e − 03	2.5187e − 03	6.3989e − 04	1.6062e − 04	3.9001e − 05

Result in [15]
10⁻⁴	0.10207612	0.06281638	0.03556178	0.01906740	0.00989895	0.00504914
10⁻⁵	0.10210236	0.06283382	0.03557070	0.01907016	0.00989794	0.00504604
10⁻⁶	0.10210499	0.06283557	0.03557159	0.01907044	0.00989798	0.00504673

Table 10. Example 4: comparison of maximum absolute error of proposed scheme and results in [14, 19] for δ = 0.6ε and η = 0.5ε.

ε↓	N⟶10	100	10	100	10	100
ε↓	Result in [19]		Result in [14]		Proposed scheme
10⁻¹	1.5339e − 02	1.9170e − 04	0.01596700	0.00017254	9.2052e − 03	5.8912e − 04
10⁻²	2.8175e − 02	1.8656e − 03	0.08016582	0.00199505	2.0378e − 02	1.0991e − 03
10⁻³	2.8534e − 02	3.3897e − 03	0.10168369	0.00999987	2.0543e − 02	2.2978e − 03
10⁻⁴	2.8570e − 02	3.3954e − 03	0.10406804	0.01230494	2.0554e − 02	2.3059e − 03

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Effect of delay on the solution behaviour for ε = 2⁻³. (a) Example 3. (b) Example 4.

5. Conclusion

In this paper, singularly perturbed differential difference equations having mixed small shifts on reaction terms of the equation are considered. The considered problem exhibits boundary layer for small values of the perturbation parameter. The bounds and the behaviour of the continuous solution are discussed. Numerical scheme is developed using the technique of exponentially fitted finite difference method. Stability of the scheme is investigated using comparison principle and solution bound. The proposed scheme converges uniformly with rate of convergence of one before Richardson extrapolation and of two after Richardson extrapolation is applied. Test examples exhibiting boundary layers are considered to validate the theoretical finding. The finding in the computation agrees well with the theoretical findings. The proposed scheme gives more accurate results than existing research findings in the literature. In future works, we extend the proposed scheme for singularly perturbed parabolic differential difference equations and singularly perturbed problems with degenerate coefficients.

Conflicts of Interest

The authors declare no conflicts of interest.

Open Research

Data Availability

No data were used to support the study.

References

1 Benia Y., Ruggieri M., and Scapellato A., Exact solutions for a modified Schrödinger equation, Mathematics. (2019) 7, no. 10, https://doi.org/10.3390/math7100908, 2-s2.0-85073772769.
10.3390/math7100908
Web of Science® Google Scholar
2 Benia Y. and Scapellato A., Existence of solution to Korteweg-de Vries equation in a non-parabolic domain, Nonlinear Analysis. (2020) 195, https://doi.org/10.1016/j.na.2020.111758.
10.1016/j.na.2020.111758
Web of Science® Google Scholar
3 Ramesh V. P. and Kadalbajoo M. K., Upwind and midpoint upwind difference methods for time-dependent differential difference equations with layer behavior, Applied Mathematics and Computation. (2008) 202, no. 2, 453–471, https://doi.org/10.1016/j.amc.2007.11.033, 2-s2.0-48049121948.
10.1016/j.amc.2007.11.033
Web of Science® Google Scholar
4 Glizer V. Y., Asymptotic analysis and solution of a finite-horizon H^∞ control problem for singularly-perturbed linear systems with small state delay, Journal of Optimization Theory and Applications. (2003) 117, no. 2, 295–325, https://doi.org/10.1023/a:1023631706975, 2-s2.0-0038403617.
10.1023/A:1023631706975
Web of Science® Google Scholar
5 Stein R. B., Some models of neuronal variability, Biophysical Journal. (1967) 7, no. 1, 37–68, https://doi.org/10.1016/s0006-3495(67)86574-3, 2-s2.0-84954086574.
10.1016/S0006-3495(67)86574-3
CAS PubMed Web of Science® Google Scholar
6 Duressa G. F. and Reddy Y. N., Domain decomposition method for singularly perturbed differential difference equations with layer behavior, International Journal Of Engineering & Applied Sciences. (2015) 7, no. 1, https://doi.org/10.24107/ijeas.251236.
10.24107/ijeas.251236
Google Scholar
7 Lange C. G. and Miura R. M., Singular perturbation analysis of boundary value problems for differential-difference equations III. Turning point problems, SIAM Journal on Applied Mathematics. (1985) 45, no. 5, 708–734, https://doi.org/10.1137/0145042, 2-s2.0-0022145846.
10.1137/0145042
Web of Science® Google Scholar
8 Lange C. G. and Miura R. M., Singular perturbation analysis of boundary value problems for differential-difference equations, SIAM Journal on Applied Mathematics. (1982) 42, no. 3, 502–531, https://doi.org/10.1137/0142036, 2-s2.0-0020148076.
10.1137/0142036
Web of Science® Google Scholar
9 Lange C. G. and Miura R. M., Singular perturbation analysis of boundary value problems for differential-difference equations. V. Small shifts with layer behavior, SIAM Journal on Applied Mathematics. (1994) 54, no. 1, 249–272, https://doi.org/10.1137/s0036139992228120, 2-s2.0-0028369618.
10.1137/S0036139992228120
Web of Science® Google Scholar
10 Lange C. G. and Miura R. M., Singular perturbation analysis of boundary-value problems for differential-difference equations. VI. Small shifts with rapid oscillations, SIAM Journal on Applied Mathematics. (1994) 54, no. 1, 273–283, https://doi.org/10.1137/s0036139992228119, 2-s2.0-0028370364.
10.1137/S0036139992228119
Web of Science® Google Scholar
11 Kadalbajoo M. K., Patidar K. C., and Sharma K. K., ε-Uniformly convergent fitted methods for the numerical solution of the problems arising from singularly perturbed general DDEs, Applied Mathematics and Computation. (2006) 182, no. 1, 119–139, https://doi.org/10.1016/j.amc.2006.03.043, 2-s2.0-33750837751.
10.1016/j.amc.2006.03.043
Web of Science® Google Scholar
12 Kadalbajoo M. K. and Sharma K. K., Numerical analysis of boundary-value problems for singularly-perturbed differential-difference equations with small shifts of mixed type, Journal of Optimization Theory and Applications. (2002) 115, no. 1, 145–163, https://doi.org/10.1023/a:1019681130824, 2-s2.0-0036341039.
10.1023/A:1019681130824
Web of Science® Google Scholar
13 Kadalbajoo M. K. and Sharma K. K., Numerical treatment of a mathematical model arising from a model of neuronal variability, Journal of Mathematical Analysis and Applications. (2005) 307, no. 2, 606–627, https://doi.org/10.1016/j.jmaa.2005.02.014, 2-s2.0-18944375881.
10.1016/j.jmaa.2005.02.014
Web of Science® Google Scholar
14 Kadalbajoo M. K. and Sharma K. K., An ε-uniform convergent method for a general boundary-value problem for singularly perturbed differential-difference equations: small shifts of mixed type with layer behavior, Journal of Computational Methods in Sciences and Engineering. (2006) 6, no. 1–4, 39–55, https://doi.org/10.3233/jcm-2006-61-405.
10.3233/JCM-2006-61-405
Google Scholar
15 Swamy D. K., Phaneendra K., and Reddy Y. N., Solution of singularly perturbed differential difference equations with mixed shifts using Galerkin method with exponential fitting, Chinese Journal of Mathematics. (2016) 2016, 10, 1935853, https://doi.org/10.1155/2016/1935853.
10.1155/2016/1935853
Google Scholar
16 Swamy D. K., Phaneendra K., and Reddy Y. N., Accurate numerical method for singularly perturbed differential difference equations with mixed shifts, Khayyam Journal of Mathematics. (2018) 4, no. 2, 110–122, https://doi.org/10.22034/KJM.2018.57949, 2-s2.0-85056577297.
10.22034/KJM.2018.57949
Google Scholar
17 Swamy D. K., Phaneendra K., and Reddy Y. N., A fitted non standard finite difference method for singularly perturbed differential difference equations with mixed shifts, Journal de Afrikana. (2016) 3, no. 4.
Google Scholar
18 Melesse W. G., Tiruneh A. A., and Derese G. A., Solving linear second-order singularly perturbed differential difference equations via initial value method, International Journal of Differential Equations. (2019) 2019, 5259130, https://doi.org/10.1155/2019/5259130.
10.1155/2019/5259130
Web of Science® Google Scholar
19 Ranjan R. and Prasad H. S., A novel approach for the numerical approximation to the solution of singularly perturbed differential-difference equations with small shifts, Journal of Applied Mathematics and Computing. (2020) In presshttps://doi.org/10.1007/s12190-020-01397-6.
10.1007/s12190-020-01397-6
Web of Science® Google Scholar
20 Sirisha L., Phaneendra K., and Reddy Y. N., Mixed finite difference method for singularly perturbed differential difference equations with mixed shifts via domain decomposition, Ain Shams Engineering Journal. (2018) 9, no. 4, 647–654, https://doi.org/10.1016/j.asej.2016.03.009, 2-s2.0-85048737058.
10.1016/j.asej.2016.03.009
Web of Science® Google Scholar
21 Tian H., The exponential asymptotic stability of singularly perturbed delay differential equations with a bounded lag, Journal of Mathematical Analysis and Applications. (2002) 270, no. 1, 143–149, https://doi.org/10.1016/s0022-247x(02)00056-2, 2-s2.0-0036600954.
10.1016/S0022-247X(02)00056-2
Web of Science® Google Scholar
22 Miller J. H., O’Riordan E., and Shishkin G. I., Fitted Numerical Methods for Singular Perturbation Problems: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions, 2012, World Scientific, Singapore.
10.1142/8410
Google Scholar
23 Kellogg R. B. and Tsan A., Analysis of some difference approximations for a singular perturbation problem without turning points, Mathematics of Computation. (1978) 32, no. 144, https://doi.org/10.1090/s0025-5718-1978-0483484-9, 2-s2.0-84966216257.
10.1090/S0025-5718-1978-0483484-9
Web of Science® Google Scholar
24 O’Malley R. E., Singular Perturbation Methods for Ordinary Differential Equations, 1991, Springer, Berlin, Germany.
10.1007/978-1-4612-0977-5
Google Scholar
25 Woldaregay MM. and Duressa G. F., Parameter uniform numerical method for singularly perturbed differential difference equations, Journal of the Nigerian Mathematical Society. (2019) 38, 223–245.
Google Scholar
26 Turuna D. A., Woldaregay M. M., and Duressa G. F., Uniformly convergent numerical method for singularly perturbed convection-diffusion problems, Kyungpook Mathematical Journal. (2020) 60, no. 3.
Web of Science® Google Scholar
27 Woldaregay M. M. and Duressa G. F., Fitted numerical scheme for singularly perturbed differential equations having two small delays, Caspian Journal of Mathematical Sciences (CJMS). (2020) In press.
Google Scholar
28 Kumar K., Pramod Chakravarthy P., Ramos H., and Vigo-Aguiar J., A stable finite difference scheme and error estimates for parabolic singularly perturbed PDEs with shift parameters, Journal of Computational and Applied Mathematics. (2020) In presshttps://doi.org/10.1016/j.cam.2020.113050.
10.1016/j.cam.2020.113050
Web of Science® Google Scholar

Citing Literature

All articles

Higher-Order Uniformly Convergent Numerical Scheme for Singularly Perturbed Differential Difference Equations with Mixed Small Shifts

Abstract

1. Introduction

2. Statement of the Problem

2.1. Properties of the Analytical Solution