Volume 2020, Issue 1 6301018

Research Article

Open Access

Deflection Calculation Based on SDOF Method for Axially Loaded Concrete-Filled Steel Tubular Members Subjected to Lateral Impact

Luming Wang,

Luming Wang

orcid.org/0000-0002-2102-6301

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Yanhui Liu,

Corresponding Author

Yanhui Liu

[email protected]

orcid.org/0000-0001-6758-2672

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Jiahuan Song,

Jiahuan Song

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Shichun Zhao,

Shichun Zhao

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Zhe Wang,

Zhe Wang

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Yue Zeng,

Yue Zeng

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Xingyu Feng,

Xingyu Feng

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Luming Wang,

Luming Wang

orcid.org/0000-0002-2102-6301

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Yanhui Liu,

Corresponding Author

Yanhui Liu

[email protected]

orcid.org/0000-0001-6758-2672

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Jiahuan Song,

Jiahuan Song

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Shichun Zhao,

Shichun Zhao

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Zhe Wang,

Zhe Wang

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Yue Zeng,

Yue Zeng

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

Xingyu Feng,

Xingyu Feng

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China swjtu.edu.cn

Search for more papers by this author

First published: 2020

https://doi.org/10.1155/2020/6301018

Citations: 2

Academic Editor: Zhixiong Li

Share a link

Email
Wechat
Bluesky

Abstract

Axial force has a great influence on the dynamic behavior and the impact resistance of concrete-filled steel tubular (CFST) members. Based on numerical simulation and theoretical analysis, the impact response and deflection calculation method for axially loaded CFST members subjected to lateral impact are investigated in this paper. The nonlinear numerical model of an axially loaded CFST member considering the strain rate effects has been established, and the simulation accuracy has been validated by comparing with existing test results. The contrastive investigation is carried out to illustrate the influence of axial load on the variation pattern of impact force for CFST members under various structural and impact parameters, and its result indicates that the impact force-time histories for CFST members with different axial loads are mainly characterized by rectangular pulse and triangular pulse. Moreover, a simplified calculation method considering the effect of axial force is proposed based on the equivalent single degree of freedom (SDOF) method, devoted to predicting the deflection of axially loaded CFST members subjected to lateral impact. The comparisons with the numerical simulation prove that the deflection calculation method has a reasonable accuracy; thus, the proposed method can be utilized in the damage assessment and anti-impact design for CFST members subjected to lateral impact and axial load.

1. Introduction

Concrete-filled steel tubular (CFST) members exhibit mechanical benefits of high strength and favorable ductility; hence, they have been widely applied to high-rise and long-span engineering structures [1–3]. During the whole service life cycle, CFST members may inevitably suffer from various impact accidents caused by vehicles, vessels, and trains [4]. Meanwhile, CFST members will always bear the axial load induced by superstructure during the whole impact process. Therefore, in order to well reflect the actual impact situations, it is of realistic significance to further investigate the impact response and deflection calculation method for axially loaded CFST members subjected to lateral impact.

Some researchers have carried out impact tests and simulation analysis on the dynamic response of CFST members under lateral impact [5–9], including a small number of investigations considering the effect of axial force on the mechanical behavior for CFST members. Wang et al. [10] conducted a series of drop weight tests on CFST members with the fixed-sliding boundary conditions. The results showed that the impact force and residual deflection of CFST members varied greatly with the axial load. Due to the increase of the axial load, the duration of impact force would decrease gradually and the impact force would show a more obvious unloading trend. The residual deflection of CFST members changed considerably with the application of axial load, while there was no clear regularity in its variation. In addition, it can be obtained from the tests of Yousuf et al. [11] that the axial force had a weakening effect on the impact strength of CFST members. Aghdamy et al. [12] carried out a parametric sensitivity analysis of CFST members subjected to lateral impact through numerical simulation. It was found that the eigenvalues of impact force, such as initial peak force, residual impact force, and impact duration, decreased slightly with the increase of the axial load. Correspondingly, the deflection of CFST members only increased by a small amplitude. Yang et al. [13] conducted the drop weight impact tests on recycled aggregate CFST members, including the investigation related to the influence of axial load on the dynamic response for CFST members. From the test results, it can be seen that the local buckling appeared at the midspan and the supports of CFST members. With the increase of the axial load ratio, the local buckling phenomenon became more and more serious and the residual deflection of CFST members increased substantially. Aghdamy et al. [14–16] performed a series of impact tests and numerical simulations on concrete-filled double-skin tube (CFDST) members. It was indicated that the increase of axial load was more likely to cause global buckling for CFDST members, which resulted in a greater increase in the maximum and residual deflection of CFDST members. From the above investigations, it can be concluded that there is still no clear conclusion about the influence of axial load on the deflection and impact force for CFST members under lateral impact.

Some investigations have studied the simplification of impact force for different structural members. For the structural members with high impact resistance, the impact energy was absorbed mainly by the global deformation during the impact process. Accordingly, the impact force, which experienced a stable platform stage and maintained for a long period of time after the short peak period, could be reasonably simplified into rectangular pulse [17, 18]. If the impact resistance of structural members was too poor to fully withstand impact energy, the structural members would be damaged locally in a relatively short period of time, and the impact force would be unloaded directly after the peak stage. Consequently, some investigations simplified the impact force into pulse loads such as isosceles and right triangular pulses according to its characteristics [19–23]. However, there is still a lack of research on the variation pattern and equivalence principle of impact force for CFST members considering the effect of axial force, which needs to be further investigated.

The equivalent single degree of freedom (SDOF) method idealizes the actual impact system as a mass-spring model with an equivalent lumped mass, equivalent stiffness, and equivalent impact load. The deflection of actual members is obtained by solving the dynamic differential equation of the equivalent SDOF model [24]. The classical equivalent SDOF method mainly reflects the bending performance of structural members, while without considering the effect of axial force on the calculation method [25, 26]. In order to obtain a more accurate calculation model, some researchers have improved the classical equivalent SDOF method [27–30]. Zhang et al. [31] established an equivalent SDOF model considering the interaction of axial load-bending moment for CFST columns subjected to blast load. This method considered the combined action of axial force and blast load in the process of calculating the ultimate bending strength. Nassr et al. [32] investigated the effect of axial load on the strength and stability of steel columns under blast load based on the equivalent SDOF method. The additional lateral force caused by the second-order effect of the axial load was added to the equivalent impact load in the SDOF differential equation. For axially loaded CFST members subjected to lateral impact, it is recognized that the axial force will generate the geometric stiffness, which will change the joint stiffness of the equivalent SDOF model and affect the calculation results of deflection. Therefore, a more reasonable and feasible way is to modify the differential equation and resistance function of the equivalent SDOF model to reflect the effect of axial force on CFST members subjected to lateral impact.

To address these issues described above, the impact response and deflection calculation method for axially loaded CFST members subjected to lateral impact are investigated in this paper. The finite element analysis model of an axially loaded CFST member considering the strain rate effects and dynamic relaxation is established, and the accuracy of numerical simulation is validated by comparing with existing test results. The contrastive investigation of impact response for axially loaded CFST members with various structural and impact parameters is conducted based on numerical simulation, dedicated to illustrating the effect of axial load on the variation pattern of impact force. On this basis, the impact loads are simplified into pulse loads according to the types of impact force-time histories for CFST members. Moreover, a deflection calculation method of CFST members under lateral impact is established based on the equivalent SDOF method, and it reflects the effect of axial force by modifying the differential equation and the resistance function of the equivalent SDOF model. The general calculation flow of the proposed method is summarized for obtaining the deflection of axially loaded CFST members subjected to lateral impact, and the simulation results are utilized to validate and analyze the accuracy of the deflection calculation method.

2. Development of FEA Model and Experimental Validation

2.1. Finite Element Analysis Model

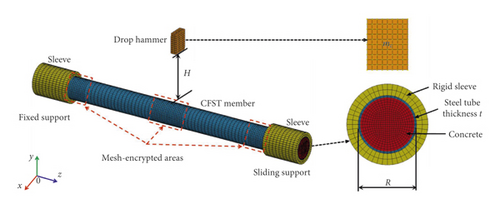
Figure 1 shows the finite element analysis model of CFST member subjected to lateral impact. The steel tube, core concrete, and drop hammer are simulated employing eight-node solid elements with reduced integration. In order to improve the accuracy and efficiency of the simulation, the mesh is encrypted at the impact position and the support areas [33]. The drop hammer is modeled as a rigid cuboid, and its initial velocity is given by the keyword INITIAL_VELOCITY_GENERATION. By limiting the displacement and rotation in other directions, the drop hammer moves only in the vertical direction. The supports are simplified into two hollow cylindrical sleeves. In order to achieve the experimental boundary conditions (fixed-sliding), the one sleeve fixes all the degrees of freedom, and the other sleeve fixes all the degrees of freedom except z direction (axial direction). Slip between the steel and concrete was not observed in the drop weight tests, and hence, the contact surfaces of the steel and concrete share common nodes. The keyword CONTACT_AUTOMATIC_SURFACE_TO_SURFACE is set to simulate the contact between the drop hammer, rigid sleeves, and the CFST member. The commercial finite element program LS-DYNA [34] is used to simulate the impact response of CFST members. The dynamic relaxation function of the implicit solver is utilized to initialize the stress caused by axial load, and then, the dynamic process of CFST members under lateral impact is simulated by explicit solver while the axial load is constant.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Finite element analysis model of the CFST member.

It is well known that the steel and concrete are the strain rate sensitive material, and the strain rate effects have a considerable influence on the impact dynamic behavior of the structure [35]. The apparent strength of the steel and concrete may increase significantly at high strain rates when the CFST members are subjected to lateral impact. The material model MAT_PLASTIC_KINEMATIC [36] of LS-DYNA is adopted for steel simulation. This is because it is an elastic-perfectly plastic model with strain rate effects, and the model can well reflect the isotropic and kinematic hardening plasticity of the material. The Cowper–Symonds [37] model is used to reflect the strain rate effects of steel material, and the yield strength of steel can be directly amplified by the following equation:

\begin{matrix} \frac{σ_{y}}{σ_{0}} = [1 + {(\frac{\dot{ε}}{C})}^{1 / p}], \end{matrix}

(1)

where σ_y is the dynamic yield strength of steel at the strain rate

\dot{ε}

, σ₀ is the static yield strength of steel, and C = 6844 s⁻¹ and p = 3.91 are the strain rate coefficients of steel [2, 10, 38].

The concrete material is modeled with MAT_CONCRETE_DAMAGE_REL3 of LS-DYNA in this paper. The reliability and accuracy of this concrete model have been demonstrated in previous investigations [12, 39–42]. The strain rate effects of concrete material are typically reflected by the dynamic increase factor (DIF). The DIF for the compressive strength of concrete recommended by the CEB-FIP model code [43] is available to estimate the strain rate effects on concrete material properties, and the CDIF is expressed in the following equation:

\begin{matrix} CDIF = \frac{f_{cd}}{f_{cs}} = \{\begin{cases} {(\frac{\dot{ε}}{{\dot{ε}}_{s}})}^{1.026 α}, & \dot{ε} \leq 30 s^{- 1}, \\ γ {(\frac{\dot{ε}}{{\dot{ε}}_{s}})}^{13 /}, & \dot{ε} > 30 s^{- 1}, \end{cases} \end{matrix}

(2)

where f_cd is the dynamic compressive strength at the strain rate

\dot{ε}

, f_cs is the static compressive strength at the strain rate

{\dot{ε}}_{s} = 30 \times 10^{- 6} s^{- 1}

, and γ = 10^6.156α−2, in which

α = {(59 + f_{c} / f_{co})}^{- 1}

and f_co = 10 MPa. The DIF for the tensile strength of concrete is modified by Malvar and Ross [44], and the TDIF equation is given as follows:

\begin{matrix} TDIF = \frac{f_{td}}{f_{ts}} = \{\begin{cases} {(\frac{\dot{ε}}{{\dot{ε}}_{s}})}^{δ}, & \dot{ε} \leq 1 s^{- 1}, \\ β {(\frac{\dot{ε}}{{\dot{ε}}_{s}})}^{13 /}, & \dot{ε} > 1 s^{- 1}, \end{cases} \end{matrix}

(3)

where f_td is the dynamic tensile strength at the strain rate

\dot{ε}

, f_ts is the static tensile strength at the strain rate

{\dot{ε}}_{s} = 10^{- 6} s^{- 1}

, and β = 10^6δ−2, in which

δ = {(18 + f_{c} / f_{co})}^{- 1}

and f_co = 10 MPa. Based on the erosion algorithm, the keyword MAT_ADD_EROSION is set to simulate the failure of concrete. When the maximum principal tensile strain of concrete element exceeds the limit value, LS-DYNA will automatically delete the concrete element to simulate failure.

2.2. Introduction to Experimental Tests

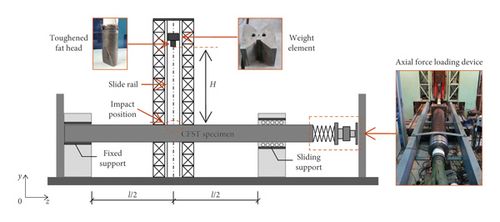
In [10], the authors carried out a series of drop weight tests on CFST members through a DHR9401 drop hammer test machine, as shown in Figure 2. The support restraint device provided the boundary constraints for the CFST member, and the loading device of the axial force applied the axial pressure for the CFST member. The weight of the drop hammer m_c was 229.8 kg, and the different impact energy was obtained by changing the impact height (H). During the tests, the CFST member was first placed on the drop hammer test machine and the boundary condition was set as the fixed sliding, and then the axial load was applied at the sliding end of the CFST member. When the drop hammer was released from the design height, it would fall freely along the slipway and impact the CFST member in the midspan area. Six typical CFST members were selected from Ref. [10] to validate the accuracy of numerical simulation. Table 1 shows the detailed information of each CFST member, where l is the length of CFST member, R is the outer sectional diameter, t is the thickness of steel tube, f_y is the average yield strength of steel, E_s is the elastic modulus of steel, f_cu is the average cube strength of concrete, μ = N/N_sc is the axial load ratio (where N and N_sc represent the axial load and axial bearing capacity of the CFST member, respectively), and v₀ is the initial impact velocity.

Table 1. Test information of CFST members [10].

Number	l (mm)	R (mm)	t (mm)	f_y (MPa)	E_s (MPa)	f_cu (MPa)	μ	v₀ (m/s)
DBF14	1200	114	1.7	232.0	1.92 × 10⁵	48.7	0	3.9
DBF13	1200	114	1.7	232.0	1.92 × 10⁵	48.7	0	4.8
DBF19	1200	114	1.7	232.0	1.92 × 10⁵	48.7	0.3	4.8
DZF22	1200	114	3.5	298.0	2.01 × 10⁵	48.7	0	7.6
DZF26	1200	114	3.5	298.0	2.01 × 10⁵	48.7	0	11.7
DZF31	1200	114	3.5	298.0	2.01 × 10⁵	48.7	0.3	11.7

2.3. Comparison of Simulation and Test Results

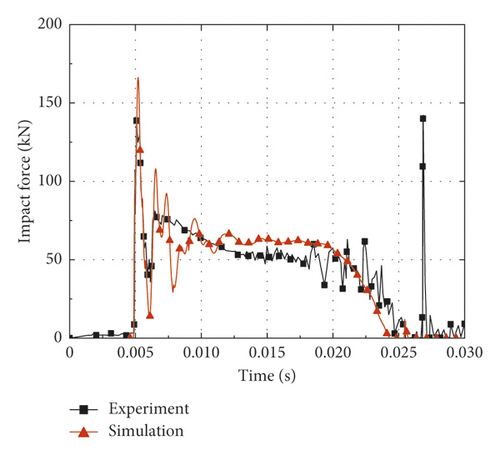
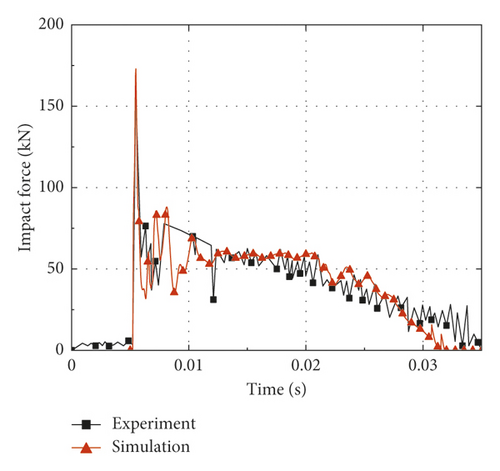
In order to validate the accuracy of numerical simulation, six typical CFST members described in Section 2.2 are calculated based on the finite element analysis method established in Section 2.1, and the comparisons are made between the simulation and test results. Figure 3 shows the predicted and measured impact force-time histories. It is noticed that the impact force reaches the maximum value (peak value) in a short time after the impact process begins. Then, the impact force maintains at the stability stage (platform value) for a long time after several short oscillations; meanwhile, the CFST member enters the global response stage. Finally, the impact force is gradually unloaded to zero. The comparisons between the simulation and test results are summarized in Table 2, where F_stab is the platform value of impact force, t_d is the duration of impact force, and δ_r is the residual deflection. It can be concluded from Table 2 that the average ratios of the simulation results to the test results for F_stab, t_d, and δ_r are 1.02, 0.91, and 0.97, respectively. By comparison, the platform value of impact force obtained by simulation is slightly higher than that of the test result, while the duration of impact force shows the opposite situation. Several factors may account for such discrepancies as follows: the support condition as well as the impactor of the actual impact test is not rigid enough, the energy dissipation caused by heat generation is ignored in numerical simulation, and the limitations for the material model of steel and concrete in numerical simulation. For all that, the predicted and measured residual deflections at the midspan of CFST members are roughly equal, which is mainly due to the fact that the total impulses of the simulations and tests are almost equal in the whole impact process.

Table 2. Comparisons between the simulation and test results.

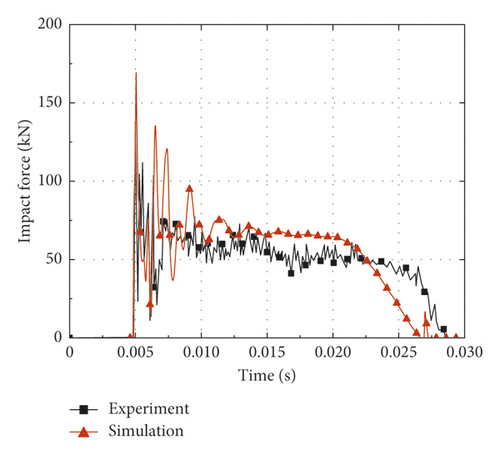
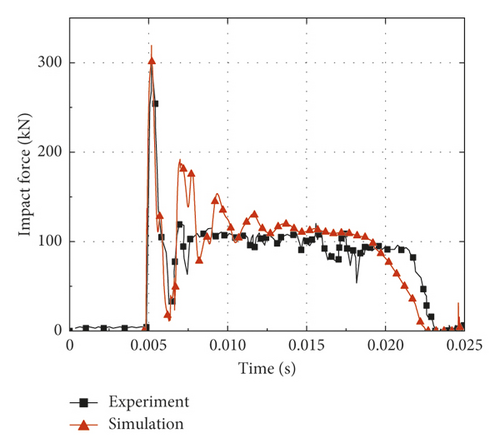
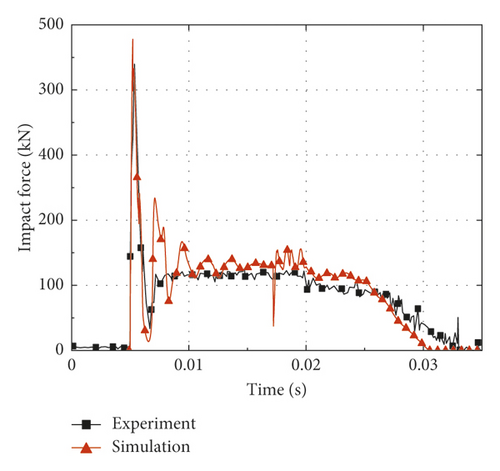
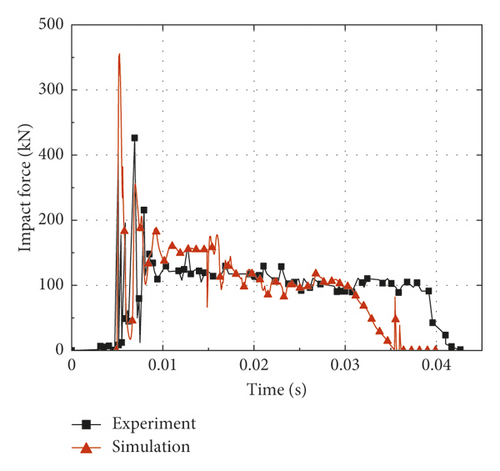
Number	F_{stab, tested} (kN)	F_stab, FEA (kN)	t_d, tested (ms)	t_d, FEA (ms)	δ_r, tested (mm)	δ_r, FEA (mm)
DBF14	59.5	61.2	19.3	19.0	19.44	18.90
DBF13	60.8	62.1	30.0	26.7	41.88	39.20
DBF19	62.7	65.9	24.8	21.9	25.30	24.80
DZF22	112.8	113.6	18.2	17.8	39.42	38.50
DZF26	123.2	125.3	27.0	25.5	87.20	83.70
DZF31	125.7	121.1	38.2	30.7	101.70	98.70

Generally, it can be concluded that the results of the numerical simulation are in good agreement with the test results, regardless of the impact force-time histories or deformation modes. Obviously, the accuracy and reliability of the numerical simulation mentioned above can be validated. In addition, it is found that the axial force has a great influence on the impact response of CFST members during the simulation process. Hence, the following sections of this paper will investigate the effect of axial force on impact response through numerical simulation, and then, a deflection calculation method for axially loaded CFST members subjected to lateral impact is established by combining theoretical analysis and numerical simulation.

3. Influence of Axial Force on Impact Response for CFST Members

3.1. Variation Pattern of Impact Force

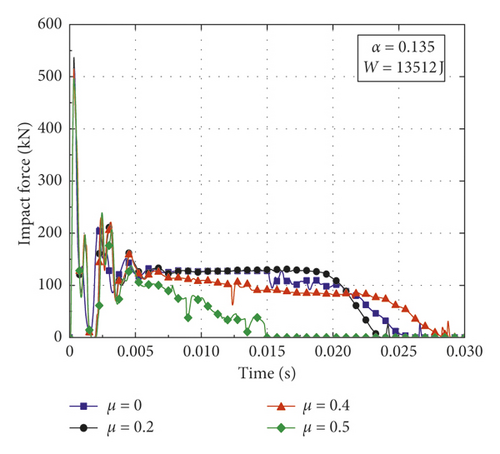
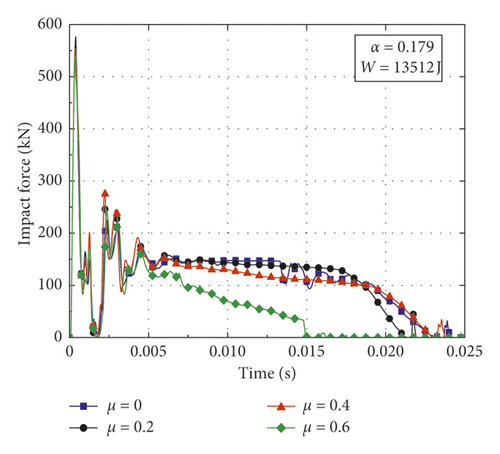
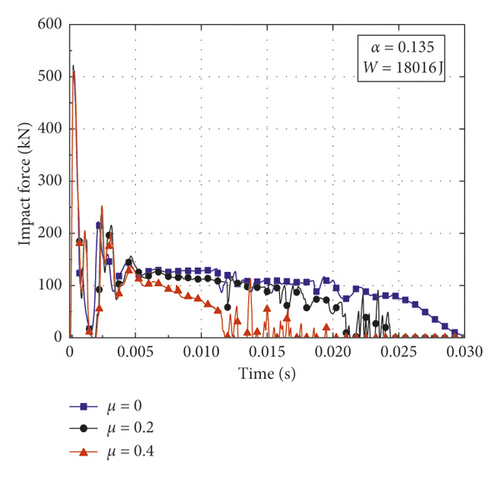
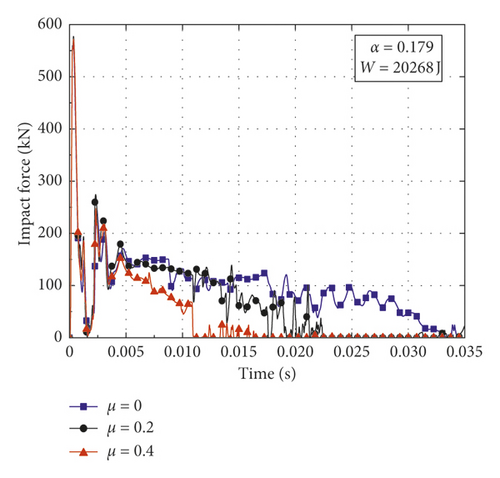
In order to investigate the influence of axial force on the variation pattern of impact force for CFST members with various structural and impact parameters, a contrastive investigation is conducted utilizing the numerical simulation. In this paper, the parameters varied in the numerical simulation including axial load ratio μ, impact energy $W = (m_{c} v_{0}^{2}) / 2$ , and steel ratio α = A_s/A_c (where A_s and A_c are the cross-sectional areas of steel tube and core concrete, respectively). The weight of the drop hammer, the boundary conditions, the outer sectional diameter, and the lengths of the CFST members are determined according to Section 2.2. The thicknesses of steel tubes are set as 3.5 mm and 4.5 mm, and the corresponding steel ratios are 0.135 and 0.179, respectively. The compressive strength of concrete is set as 33.4 MPa, and the yield strength and the elastic modulus of steel are taken as 232 MPa and 206 GPa, respectively. Impact conditions and simulation results of CFST members are summarized in Table 3, where F_max is the peak value of impact force and δ_max is the maximum deflection. Figure 4 presents the impact force-time histories of CFST members with different axial load ratios, impact energy, and steel ratios. From the damage patterns obtained by numerical simulation, it can be observed that the CFST members of A2-3, B3-1, and B3-2 cracks in the midspan, the CFST members of A1-4, A2-4, A3-3, B1-4, B2-4, and B3-3 fractures both in the midspan and the support areas, and the rest of the CFST members undergo different degrees of bending deformation.

Table 3. Impact conditions and simulation results of CFST members.

Number	t (mm)	α	v₀ (m/s)	W (J)	μ	F_max (kN)	t_d (ms)	δ_max (mm)	Damage pattern
A1-1	3.5	0.135	7.67	6756	0	321	19.0	49.9	Bending deformation
A1-2	3.5	0.135	7.67	6756	0.2	356	18.0	46.3	Bending deformation
A1-3	3.5	0.135	7.67	6756	0.4	361	18.0	47.7	Bending deformation
A1-4	3.5	0.135	7.67	6756	0.7	354	22.0	—	Fracture failure
A2-1	3.5	0.135	10.84	13512	0	523	26.0	98.5	Bending deformation
A2-2	3.5	0.135	10.84	13512	0.2	551	24.0	96.4	Bending deformation
A2-3	3.5	0.135	10.84	13512	0.4	523	29.0	108.0	Cracking
A2-4	3.5	0.135	10.84	13512	0.5	500	15.0	—	Fracture failure
A3-1	3.5	0.135	12.52	18016	0	533	30.0	127.0	Bending deformation
A3-2	3.5	0.135	12.52	18016	0.2	535	25.0	125.5	Bending deformation
A3-3	3.5	0.135	12.52	18016	0.4	520	15.0	—	Fracture failure
B1-1	4.5	0.179	7.67	6756	0	377	17.0	45.7	Bending deformation
B1-2	4.5	0.179	7.67	6756	0.2	395	16.0	42.8	Bending deformation
B1-3	4.5	0.179	7.67	6756	0.4	393	16.0	43.5	Bending deformation
B1-4	4.5	0.179	7.67	6756	0.8	372	14.0	—	Fracture failure
B2-1	4.5	0.179	10.84	13512	0	551	23.0	87.1	Bending deformation
B2-2	4.5	0.179	10.84	13512	0.2	588	22.0	84.5	Bending deformation
B2-3	4.5	0.179	10.84	13512	0.4	558	24.0	89.5	Bending deformation
B2-4	4.5	0.179	10.84	13512	0.6	541	15.0	—	Fracture failure
B3-1	4.5	0.179	13.28	20268	0	567	35.0	144.0	Cracking
B3-2	4.5	0.179	13.28	20268	0.2	579	23.0	133.0	Cracking
B3-3	4.5	0.179	13.28	20268	0.4	572	15.0	—	Fracture failure

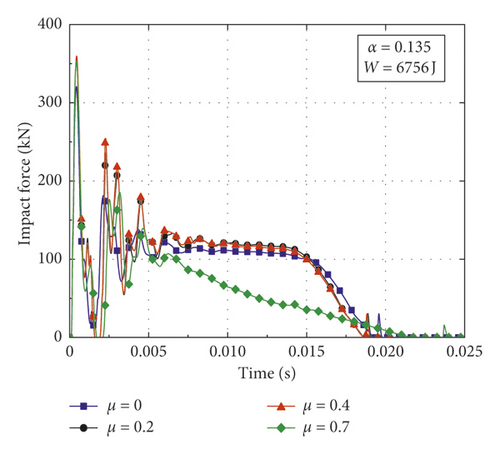
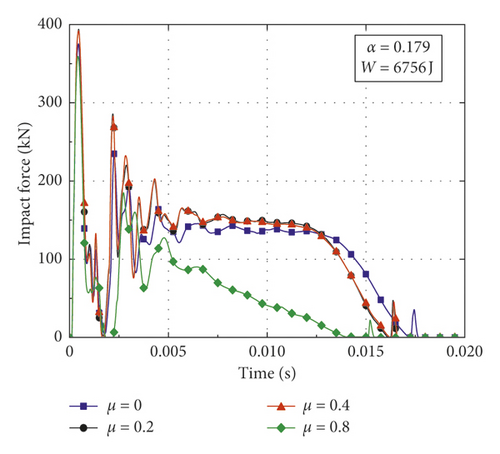
Figures 4(a) and 4(b) show the comparison of impact force-time histories with different axial load ratios when W = 6756 J. It is noticed that the variation patterns of impact force are similar among the two groups of CFST members (A1 series and B1 series). When the axial load ratio increases from 0 to 0.2, both the peak value and the platform value of impact force increase to a certain extent, while the duration of impact force and the midspan deflection vary in an opposite way. Compared with the case in which the axial load ratio is 0.2, the impact force of CFST members has only a slight change when the axial load ratio increases to 0.4. If the axial load ratio continues to increase (A1 series reaches 0.7 and B1 series reaches 0.8), the loading process of impact force will change obviously and the impact force will unload rapidly after reaching its peak value without going through the stable platform stage. At the same time, the CFST members are prone to have the instability damage due to the second-order effect with high axial load ratios.

Figures 4(c) and 4(d) give the impact force-time histories of CFST members when the impact energy increases to 13512 J. In the range of axial load ratio less than 0.2, it is observed that the variation patterns of impact force for A2 series and B2 series are consistent with A1 series and B1 series, respectively. With the increase of axial load ratio (from 0.2 to 0.4), the platform value of impact force gradually decreases and the impact force begins to unload slowly for the CFST members of A2 series and B2 series. When the impact energy is doubled, the critical axial load ratios of A2 series and B2 series for instability damage due to the second-order effect are reduced to 0.5 and 0.6, respectively.

Figures 4(e) and 4(f) present the impact force-time histories of CFST members for A3 series and B3 series. For the CFST members of A3 series, the impact force begins to unload slowly with the axial load ratio of 0.2, and the CFST members will show the instability damage directly when the axial load ratio increases to 0.4. For the CFST members of B3 series, the impact force begins to unload slowly under the excessive impact energy even without applying the axial force. In the process of increasing the axial load ratio (from 0 to 0.4), the duration of impact force will continue decreasing and the CFST members will be destroyed due to excessive impact energy as well as high axial load ratio.

It can be concluded from the above results as follows: (1) The effects of axial force on variation pattern of impact force for CFST members are diverse. The impact force presents different shapes and characteristics under the various axial load ratios, so the corresponding impact response of CFST members is also different. (2) The steel ratio can improve the impact resistance of CFST members and increase the critical axial load ratio of CFST members for instability failure. (3) When the impact energy is within a small range, the appropriate application of axial force can improve the impact resistance of CFST members when the axial load ratio is at a low level, while the CFST members may suffer from instability damage due to the second-order effect when the axial load ratio exceeds the small range. (4) When the impact energy is high, the effect of axial force will significantly weaken the impact resistance of CFST members even in the small range of axial load ratio.

3.2. Equivalence Principle of Impact Force

Since the duration of impact force is very short, generally measured in a millisecond, the impact force-time histories can be taken as pure pulses in previous studies [17–23], such as right triangular pulse, isosceles triangular pulse, and rectangular pulse. There are two different variation patterns of impact force-time histories: (1) within the small range of impact energy and axial load ratio, the impact force gradually stabilizes after several short oscillations and then enters the plateau stage and maintains a long period of time; (2) if the impact energy is high, even within the small range of axial load ratio, the impact force will unload without experiencing a stable platform period. According to the characteristics of the two kinds of curves, the impact force-time histories are simplified into the equivalent rectangular pulse load or the equivalent right triangular pulse load, as shown in Figures 5(a) and 5(b), respectively. Based on the principle of equal impulse (i.e., the equivalent impulse I_e is equal to the actual impulse

I_{a} = \int_{0}^{t_{d}} F (t) d t

), under the condition that the duration of impact force is constant, the equivalent rectangular pulse load can be obtained as follows:

\begin{matrix} F_{E} = \frac{I_{a}}{t_{d}} = \int_{0}^{t_{d}} \frac{F (t) d t}{t_{d}} . \end{matrix}

(4)

Similarly, the equivalent right triangular pulse load can be obtained as follows:

\begin{matrix} F_{E} = \frac{2 I_{a}}{t_{d}} = 2 \int_{0}^{t_{d}} \frac{F (t) d t}{t_{d}} . \end{matrix}

(5)

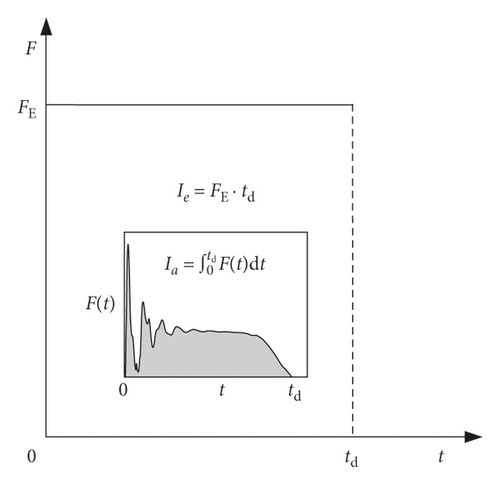
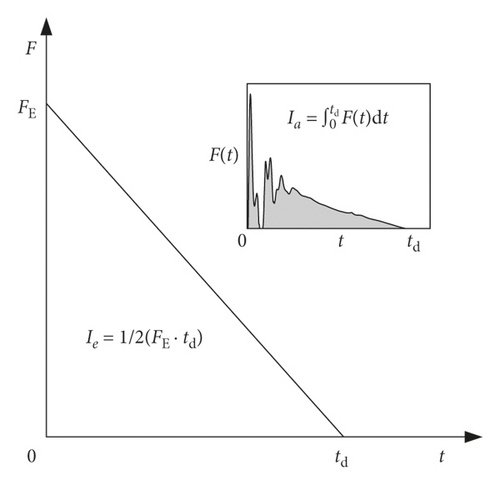
4. Development of SDOF Method considering Axial Force

The classical equivalent SDOF method neglects the effect of axial force when calculating the deflection, which cannot reflect the actual stress of structural members under lateral impact. Some researchers have improved the classical equivalent SDOF method utilized in blast field considering the interaction of axial load-bending moment [31] or considering the additional lateral force caused by the second order effect [32]. In order to establish the deflection calculation method of axially loaded CFST members subjected to lateral impact in this paper, the conversion factors and resistance function are deduced on the basis of the equivalent SDOF method. Then, the differential equation of the equivalent SDOF model considering axial force and lateral impact load is established, and the deflection can be obtained by solving the differential equation. It is necessary to define appropriate basic assumptions as follows: (1) ignoring the damping of the whole impact system; (2) ignoring the initial defect and local deformation of CFST members; (3) the CFST members do not suffer from instability damage; (4) the bending deformation of CFST members is considered and the influence of shear deformation is neglected.

4.1. Equivalent SDOF Model considering Axial Force

In order to adopt the equivalent SDOF method to analyze impact response of CFST members with distributed mass and distributed stiffness, it is necessary to simplify the actual system of CFST members into an equivalent SDOF system with an equivalent lumped mass, equivalent stiffness, and equivalent impact load. The experimental and numerical models of the CFST member involved in Section 2 are simplified into the equivalent SDOF mass-spring system as shown in Figure 6.

The boundary conditions of the equivalent SDOF model are set as fixed sliding, which are consistent with the CFST members of drop weight tests. The axial force is applied at the sliding end, and the impact load is applied at the midspan of the CFST member. It is assumed that the deflected shape function of the CFST member under the concentrated load is φ(x) and the time dependent displacement at the midpoint of CFST members is z(t). Therefore, the displacement function at any point in the system can be expressed as follows:

\begin{matrix} u (x, t) = φ (x) z (t) . \end{matrix}

(6)

According to the principle of virtual work, the differential equation of the equivalent SDOF model is established as follows [45]:

\begin{matrix} m^{*} z^{″} (t) + k_{W}^{*} z (t) - k_{G}^{*} z (t) = F^{*} (t), \end{matrix}

(7)

where m^∗, F^∗(t),

k_{W}^{*}

, and

k_{G}^{*}

represent the generalized mass, generalized equivalent load, generalized bending stiffness, and generalized geometric stiffness, respectively. The mass and bending stiffness per unit length of the CFST member are defined as m(x) and EI(x), respectively. Therefore, the four parameters mentioned above can be derived from the following equations [45]:

\begin{matrix} \{\begin{cases} m^{*} = \int_{0}^{L} m (x) φ {(x)}^{2} d x, \\ F^{*} (t) = F (t), \\ k_{W}^{*} = \int_{0}^{L} E I (x) φ^{″} {(x)}^{2} d x, \\ k_{G}^{*} = N \int_{0}^{L} φ^{'} {(x)}^{2} d x . \end{cases} \end{matrix}

(8)

It is possible to define a generalized joint stiffness as

\begin{matrix} k^{*} = k_{W}^{*} - k_{G}^{*} . \end{matrix}

(9)

Therefore, the differential equation of the SDOF model under the generalized system can be expressed as follows:

\begin{matrix} m^{*} z^{″} (t) + k^{*} z (t) = F^{*} (t) . \end{matrix}

(10)

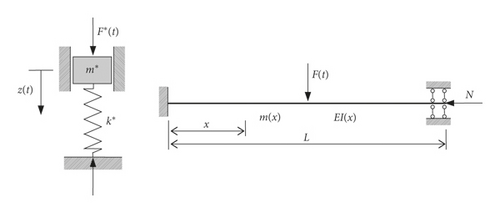
The generalized system should be transformed into the actual system through the conversion factors, and then, the deflection of CFST members can be calculated by solving the differential equation.

4.2. Derivation of Conversion Factors

The conversion factors between the equivalent SDOF system and the actual CFST members include the mass factor K_M = m^∗/M, load factor K_F = F^∗(t)/F(t), and resistance factor K_R = k^∗/k, where M, F(t), and k represent the actual mass, actual load, and actual joint stiffness of real CFST members, respectively. For the CFST members under the axial force, the midspan deflection between the equivalent SDOF system and the actual system is always equal. Assuming that the midspan deflection of CFST members is z, therefore the generalized load of equivalent SDOF system is F^∗(t) = k^∗z and the actual load of CFST members is F(t) = kz. Then, the relationship between the load factor and the resistance factor can be expressed as K_F = F^∗(t)/F(t) = (k^∗z)/(kz) = k^∗/k = K_R [46]. The actual joint stiffness of CFST members is defined as k = k_W − k_G, where k_W and k_G represent the actual bending stiffness and actual geometric stiffness, respectively. In addition, the mass-load factor is defined as K_FM = K_M/K_F. Then, (10) is transformed into

\begin{matrix} K_{FM} \cdot M \cdot z^{″} (t) + k \cdot z (t) = F (t) . \end{matrix}

(11)

When the concentrated force is in the initial stage of loading, the deformation of CFST members is still in the elastic range. In this case, the normalized shape function can be given as follows:

\begin{matrix} φ (x) = \frac{4}{L^{3}} (34 L x^{2} - x^{3}), 0 \leq x \leq \frac{L}{2} . \end{matrix}

(12)

With the increase of impact load, the system enters a plastic yielding stage, and plastic hinges are finally formed at the end and midspan of CFST members. Similarly, the normalized shape function can be given as follows:

\begin{matrix} φ (x) = \frac{2 x}{L}, 0 \leq x \leq \frac{L}{2} . \end{matrix}

(13)

According to the shape functions given above, the conversion factors, generalized bending stiffness, and generalized geometric stiffness of the equivalent SDOF system can be calculated. The results are summarized in Table 4.

Table 4. Equivalent characteristic parameters.

Deformation stage	$k_{W}^{*}$	$k_{G}^{*}$	K_M	K_F	K_FM
Elastic stage	192EI/L³	4.8N/L	0.37	1.0	0.37
Plastic stage	0	4.0N/L	0.33	1.0	0.33

4.3. Derivation of Resistance Function

Structural resistance refers to the ability of the entire structure to withstand the effects of action (internal force, deformation, and crack, etc.), and the resistance function varies with the structural system. Since the destruction of the CFST members has a certain ductility, this paper employs the bilinear resistance function as shown in Figure 7 to carry out the analysis and calculation, which is consistent with Refs. [26, 29] and can well reflect the experimental and actual situations [47].

The resistance

\bar{R} (z)

in the elastic stage of the system is linearly related to the displacement z, and the resistance function at this stage is given by the following equation:

\begin{matrix} \bar{R} (z) = k \cdot z (t) = \frac{1}{K_{F}} (k_{W}^{*} - k_{G}^{*}) z = \frac{k_{W}^{*}}{K_{F}} z - \frac{4.8 N}{L K_{F}} z, 0 \leq z \leq z_{e}, \end{matrix}

(14)

where

R_{W} = (k_{W}^{*} \cdot z) / K_{F}

represents the bending resistance and z_e represents the yield displacement. At the end of the elastic deformation stage (z = z_e), the bending resistance will reach the maximum value

R_{m} = (k_{W}^{*} \cdot z_{e}) / K_{F}

. Therefore, the maximum resistance of the system in the elastic stage can be expressed as

\begin{matrix} {\bar{R}}_{m} = R_{m} - \frac{4.8 N}{L K_{F}} z_{e} . \end{matrix}

(15)

When the plastic hinge appears, the system enters the plastic deformation stage, and then the bending resistance remains constant until structural ductility reaches its limit and failure occurs. In the plastic deformation stage, the resistance function of the system is given by the following equation:

\begin{matrix} \bar{R} (z) = R_{m} - \frac{4 N}{L K_{F}} z, z_{e} < z \leq {\bar{z}}_{m}, \end{matrix}

(16)

where

{\bar{z}}_{m}

represents the ultimate displacement and the system resistance in the initial plastic stage (z = z_e) can be expressed as follows:

\begin{matrix} \bar{R} (z_{e}) = R_{m} - \frac{4 N}{L K_{F}} z_{e} . \end{matrix}

(17)

According to the (14) and (16), the resistance function model under axial force is shown in Figure 8. By comparing (15) and (17), it is found that the resistance value of the system has a sudden change when the displacement is z_e. In addition, it can be observed from Figure 8 that the plastic stiffness of resistance function in the plastic stage is negative, which is consistent with the test results [48]. For the convenience of calculation, it is assumed that the system resistance after entering the plastic deformation stage will remain the maximum resistance value

{\bar{R}}_{m}

of the elastic stage, as shown by the line o-a-d in Figure 8, where z_m represents the equivalent ultimate displacement. Under this assumption, it is necessary to ensure that the area between the o-a-d line and the horizontal axis is equal to the area enclosed by the o-a-b-c line and the horizontal axis, which can keep the energy absorbed by the resistance constant. Then the formula for calculating the ultimate displacement

{\bar{z}}_{m}

is expressed as follows:

\begin{matrix} {\bar{R}}_{m} (z_{m} - z_{e}) = [R_{m} - \frac{2 N (z_{e} + {\bar{z}}_{m})}{L K_{F}}] ({\bar{z}}_{m} - z_{e}) . \end{matrix}

(18)

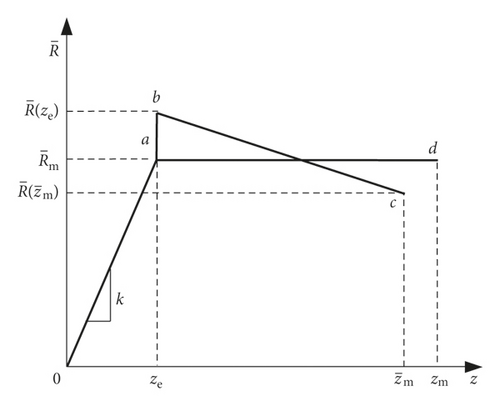
4.4. Dynamic Differential Equation of the Equivalent SDOF Model

When the plastic hinges are formed at the midspan and both ends of CFST members, the bending resistance of the system is the largest and the value is R_m = 8M_u/L [49], where M_u represents the plastic ultimate bending moment. Substituting the conversion factors and resistance functions obtained above into the equivalent SDOF model, the dynamic differential equations of CFST members considering axial force are established, shown as follows:

Elastic deformation stage is

\begin{matrix} 0.370 M z^{″} (t) + (\frac{192 E I}{L^{3}} - \frac{4.8 N}{L}) z (t) = F (t), \leq z \leq z_{e} . \end{matrix}

(19)

Plastic deformation stage is

\begin{matrix} 0.33 M z^{″} (t) + (\frac{8 M_{u}}{L} - \frac{4.8 N}{L} z_{e}) = F (t), z_{e} < z \leq z_{m} . \end{matrix}

(20)

5. Assessment of SDOF Method considering Axial Force

5.1. Result Comparisons between the Proposed Calculation Method and Numerical Simulation

The steps for calculating the deflection of CFST members are summarized as the calculation flowchart shown in Figure 9. Firstly, according to the variation patterns of impact force-time histories, the equivalent impact loads F_E (i.e. rectangular pulse load or right triangular pulse load) can be calculated through the equation (4) or (5); Secondly, the equivalent SDOF model of axially loaded CFST members subjected to lateral impact is established based on the appropriate basic assumptions discussed above, and then, the conversion factors and modified resistance functions can be derived. Finally, the deflection of CFST members can be obtained by solving dynamic differential equations (19) and (20) of the equivalent SDOF model.

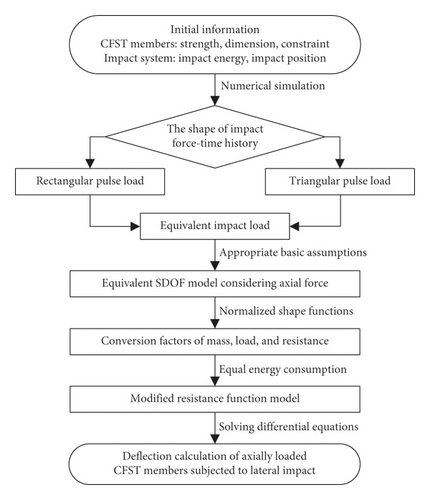
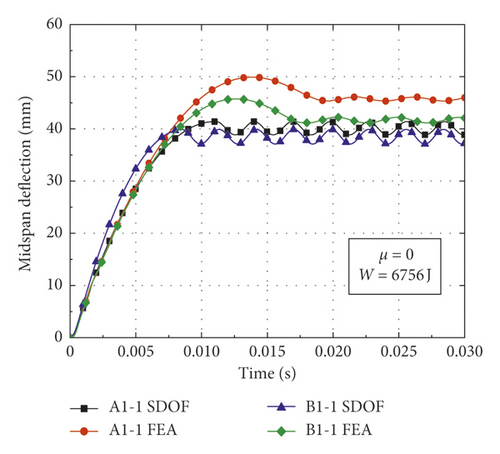
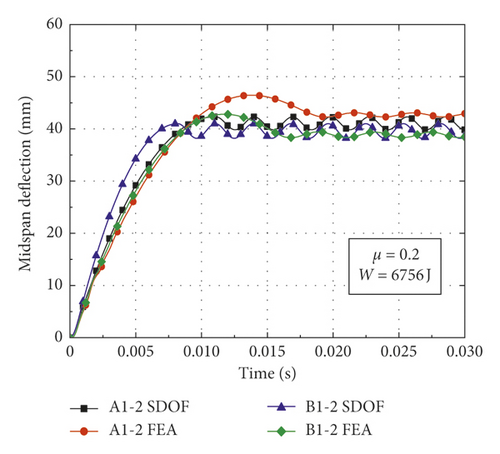
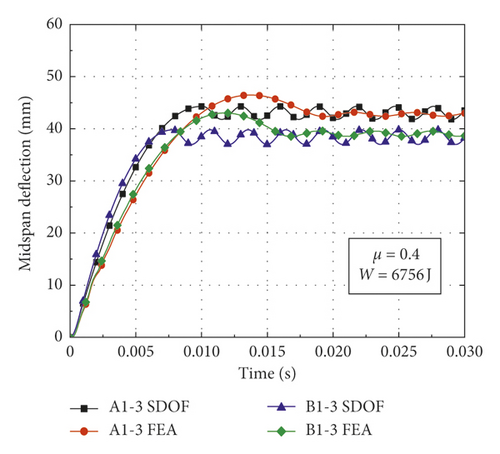
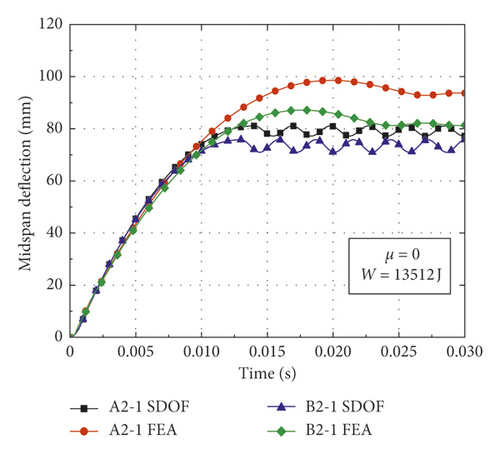
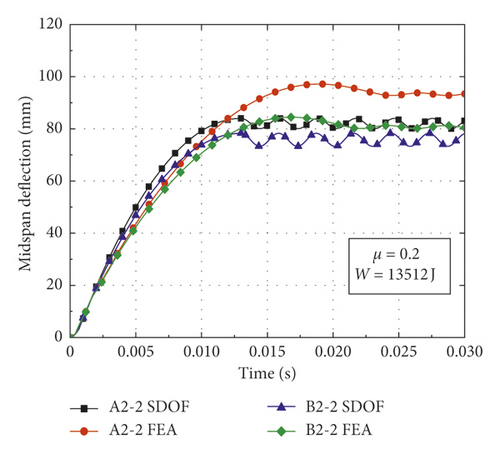
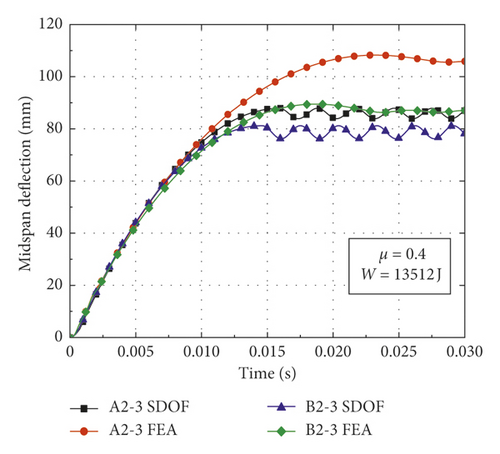
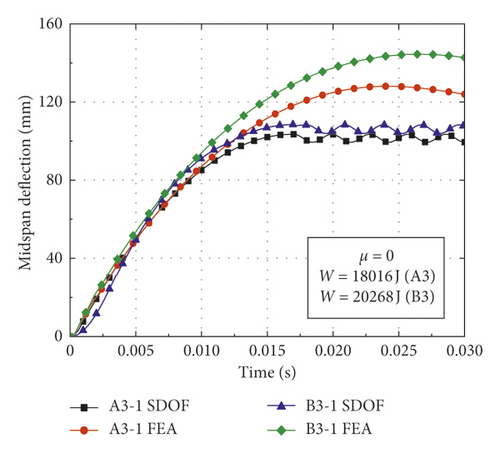
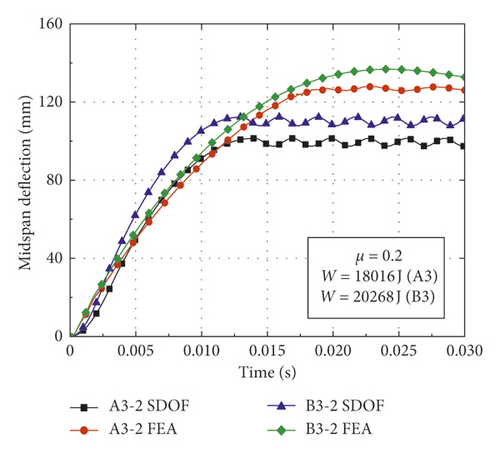
In order to validate the proposed calculation method for obtaining the deflection of CFST members, comparisons could be made between the theoretical calculation results and numerical simulation results. The CFST members with the damage pattern of fracture failure are removed from the simulation conditions, as shown in Table 3. Based on the model modification, appropriate basic assumptions, and theoretical derivation, the deflection of CFST members is calculated according to the flowchart as shown in Figure 9. The result comparisons between the proposed calculation method and numerical simulation are shown in Table 5 and Figure 10, where y_FEA and y_SDOF are the midspan residual deflections obtained by numerical simulation and the proposed calculation method considering axial force, respectively.

Table 5. Result comparisons between the theoretical calculation and numerical simulation.

Number	α	W (J)	μ	F_E (kN)	y_FEA (mm)	y_SDOF (mm)	Impact load
A1-1	0.135	6756	0	96.56	45.72	40.09	Rectangular pulse
A1-2	0.135	6756	0.2	105.10	42.65	41.08	Rectangular pulse
A1-3	0.135	6756	0.4	109.89	42.82	43.03	Rectangular pulse
A2-1	0.135	13512	0	107.45	93.37	79.15	Rectangular pulse
A2-2	0.135	13512	0.2	110.60	93.19	82.01	Rectangular pulse
A2-3	0.135	13512	0.4	92.58	105.75	85.83	Rectangular pulse
A3-1	0.135	18016	0	118.81	124.21	101.59	Rectangular pulse
A3-2	0.135	18016	0.2	189.47	126.80	99.39	Triangular pulse
B1-1	0.179	6756	0	115.36	41.70	38.49	Rectangular pulse
B1-2	0.179	6756	0.2	123.47	38.86	39.60	Rectangular pulse
B1-3	0.179	6756	0.4	127.42	39.02	38.40	Rectangular pulse
B2-1	0.179	13512	0	128.65	81.65	73.39	Rectangular pulse
B2-2	0.179	13512	0.2	133.34	80.78	75.78	Rectangular pulse
B2-3	0.179	13512	0.4	131.19	86.68	78.72	Rectangular pulse
B3-1	0.179	20268	0	192.13	142.74	106.17	Triangular pulse
B3-2	0.179	20268	0.2	221.12	132.94	110.12	Triangular pulse

5.2. Accuracy Analysis of the Proposed Calculation Method

In order to intuitively analyze the accuracy of the proposed calculation method, the results obtained by numerical simulation and equivalent SDOF method considering axial force are plotted in Figure 11. The best-fit line for the midspan deflections of CFST members is y = 0.8368x and the correlation factor is R² = 0.9636, which means the proposed calculation method can be well applied to obtain the midspan deflections for axially loaded CFST members subjected to lateral impact.

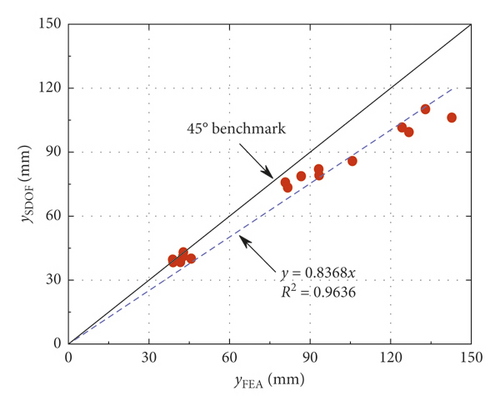
From Table 5 and Figures 10 and 11, the following observations can be made: (1) The midspan residual deflections obtained by the proposed calculation method are less than numerical simulation results. It is primarily attributable to the fact that the equivalent impact loads employed in the SDOF model are slightly lower than the actual impact loads of numerical simulation (i.e., the equivalent rectangular load is slightly lower than the platform value of impact force and the equivalent triangular load is less than the peak value of impact force), which results in the reduction of deflection obtained by the proposed calculation method. (2) The deflections calculated by equivalent rectangular pulse loads are more consistent with the simulation results than those of equivalent triangular pulse loads, which indicates that the equivalent rectangular pulse loads are more suitable for the deflection calculation of CFST members under bending deformation. (3) The changes in the initial parameters such as impact energy, steel ratio, and axial load ratio have a significant effect on the accuracy of proposed calculation method. The CFST members tend to suffer from shear failure when the impact energy exceeds a certain range, which results in an accuracy reduction of the proposed calculation method. In addition, the theoretical calculation results agree well with the simulation results when the axial load ratio is within the small range, while CFST members may occur the instability damage when the axial load ratio is beyond this range, which also reduces the accuracy of proposed calculation method. (4) The deflection time history curves of CFST members obtained by the proposed calculation method are roughly simple harmonic oscillation after entering the stability stage, which is mainly due to the fact that the effect of damping is omitted in the equivalent SDOF model.

6. Conclusions

For the CFST members with various structural and impact parameters, the effect of axial load on the variation pattern of impact force was investigated utilizing the validated finite element analysis model. On this basis, a simplified calculation method was proposed to calculate the deflection of axially loaded CFST members subjected to lateral impact. From the results, the major conclusions can be summarized as follows:

(1)
For the impact conditions with small input energy, the impact force shows a long platform stage and the appropriate application of axial force can improve the impact resistance of CFST members within the certain range of axial load ratio. When the CFST members encounter high impact energy, even within the small range of axial load ratio, the impact force will unload without experiencing a stable platform stage and the axial force will significantly weaken the impact resistance of CFST members.
(2)
According to the variation patterns of impact force-time histories, the impact loads of CFST members can be equivalent to the rectangular pulse loads or right triangular pulse loads through the equivalence principle. Moreover, the results of comparison with numerical simulation indicate that the equivalent rectangular pulse loads are more suitable for the deflection calculation of CFST members under the bending deformation.
(3)
A simplified calculation method has been proposed based on the equivalent SDOF method and appropriate basic assumptions, and it can be utilized to calculate the deflection of axially loaded CFST members subjected to lateral impact. In addition, the differential equation and resistance function of the equivalent SDOF model considering the effect of axial force have been modified and incorporated into the proposed calculation method, which can better reflect the actual stress of axially loaded CFST members subjected to lateral impact.
(4)
The calculation accuracy has been validated by comparing with the numerical simulation, which means the proposed calculation method can be effectively applied to the deflection calculation for CFST members under impact load and axial force. The results of this investigation can provide the theoretical foundation for damage assessment and anti-impact design of axially loaded CFST members subjected to lateral impact.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This research was supported by the National Natural Science Foundation of China (Grant no. 51378427) and the National Key Research and Development Program of China (Grant no. 2016YFC0802205). The authors are grateful for the financial support.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Han L.-H., Li W., and Bjorhovde R., Developments and advanced applications of concrete-filled steel tubular (CFST) structures: members, Journal of Constructional Steel Research. (2014) 100, 211–228, https://doi.org/10.1016/j.jcsr.2014.04.016, 2-s2.0-84900516469.
10.1016/j.jcsr.2014.04.016
Web of Science® Google Scholar
2 Han L.-H., Hou C.-C., Zhao X.-L., and Rasmussen K. J. R., Behaviour of high-strength concrete filled steel tubes under transverse impact loading, Journal of Constructional Steel Research. (2014) 92, 25–39, https://doi.org/10.1016/j.jcsr.2013.09.003, 2-s2.0-84887116958.
10.1016/j.jcsr.2013.09.003
Web of Science® Google Scholar
3 Hou C.-C. and Han L.-H., Life-cycle performance of deteriorated concrete-filled steel tubular (CFST) structures subject to lateral impact, Thin-Walled Structures. (2018) 132, 362–374, https://doi.org/10.1016/j.tws.2018.08.025, 2-s2.0-85052887480.
10.1016/j.tws.2018.08.025
Web of Science® Google Scholar
4 Zhu A.-Z., Xu W., Gao K., Ge H.-B., and Zhu J.-H., Lateral impact response of rectangular hollow and partially concrete-filled steel tubular columns, Thin-Walled Structures. (2018) 130, 114–131, https://doi.org/10.1016/j.tws.2018.05.009, 2-s2.0-85047778468.
10.1016/j.tws.2018.05.009
Web of Science® Google Scholar
5 Remennikov A. M., Kong S. Y., and Uy B., Response of foam-and concrete-filled square steel tubes under low-velocity impact loading, Journal of Performance of Constructed Facilities. (2011) 25, no. 5, 373–381, https://doi.org/10.1061/(asce)cf.1943-5509.0000175, 2-s2.0-81855193708.
10.1061/(ASCE)CF.1943-5509.0000175
Web of Science® Google Scholar
6 Yousuf M., Uy B., Tao Z., Remennikov A., and Liew J. Y. R., Transverse impact resistance of hollow and concrete filled stainless steel columns, Journal of Constructional Steel Research. (2013) 82, 177–189, https://doi.org/10.1016/j.jcsr.2013.01.005, 2-s2.0-84873667160.
10.1016/j.jcsr.2013.01.005
Web of Science® Google Scholar
7 Yousuf M., Uy B., Tao Z., Remennikov A., and Liew R., Behaviour and resistance of hollow and concrete-filled mild steel columns due to transverse impact loading, Australian Journal of Structural Engineering. (2012) 13, no. 1, 65–80, https://doi.org/10.7158/s12-002.2012.13.1, 2-s2.0-84927127491.
10.7158/S12-002.2012.13.1
Google Scholar
8 Shakir A. S., Guan Z. W., and Jones S. W., Lateral impact response of the concrete filled steel tube columns with and without CFRP strengthening, Engineering Structures. (2016) 116, 148–162, https://doi.org/10.1016/j.engstruct.2016.02.047, 2-s2.0-84962527451.
10.1016/j.engstruct.2016.02.047
Web of Science® Google Scholar
9 Bambach M. R., Jama H., Zhao X. L., and Grzebieta R. H., Hollow and concrete filled steel hollow sections under transverse impact loads, Engineering Structures. (2008) 30, no. 10, 2859–2870, https://doi.org/10.1016/j.engstruct.2008.04.003, 2-s2.0-52749086849.
10.1016/j.engstruct.2008.04.003
Web of Science® Google Scholar
10 Wang R., Han L.-H., and Hou C.-C., Behavior of concrete filled steel tubular (CFST) members under lateral impact: experiment and FEA model, Journal of Constructional Steel Research. (2013) 80, 188–201, https://doi.org/10.1016/j.jcsr.2012.09.003, 2-s2.0-84867894747.
10.1016/j.jcsr.2012.09.003
Web of Science® Google Scholar
11 Yousuf M., Uy B., Tao Z., Remennikov A., and Liew J. Y. R., Impact behaviour of pre-compressed hollow and concrete filled mild and stainless steel columns, Journal of Constructional Steel Research. (2014) 96, 54–68, https://doi.org/10.1016/j.jcsr.2013.12.009, 2-s2.0-84893784122.
10.1016/j.jcsr.2013.12.009
Web of Science® Google Scholar
12 Aghdamy S., Thambiratnam D. P., Dhanasekar M., and Saiedi S., Computer analysis of impact behavior of concrete filled steel tube columns, Advances in Engineering Software. (2015) 89, 52–63, https://doi.org/10.1016/j.advengsoft.2015.06.015, 2-s2.0-84940593024.
10.1016/j.advengsoft.2015.06.015
Web of Science® Google Scholar
13 Yang Y.-F., Zhang Z.-C., and Fu F., Experimental and numerical study on square RACFST members under lateral impact loading, Journal of Constructional Steel Research. (2015) 111, 43–56, https://doi.org/10.1016/j.jcsr.2015.04.004, 2-s2.0-84928982497.
10.1016/j.jcsr.2015.04.004
Web of Science® Google Scholar
14 Aghdamy S., Thambiratnam D. P., and Dhanasekar M., Experimental investigation on lateral impact response of concrete-filled double-skin tube columns using horizontal-impact-testing system, Experimental Mechanics. (2016) 56, no. 7, 1133–1153, https://doi.org/10.1007/s11340-016-0156-z, 2-s2.0-84963780897.
10.1007/s11340-016-0156-z
CAS Web of Science® Google Scholar
15 Aghdamy S., Thambiratnam D. P., Dhanasekar M., and Saiedi S., Effects of structure-related parameters on the response of concrete-filled double-skin steel tube columns to lateral impact, Thin-walled Structures. (2016) 108, 351–368, https://doi.org/10.1016/j.tws.2016.08.009, 2-s2.0-84986881474.
10.1016/j.tws.2016.08.009
Web of Science® Google Scholar
16 Aghdamy S., Thambiratnam D. P., Dhanasekar M., and Saiedi S., Effects of load-related parameters on the response of concrete-filled double-skin steel tube columns subjected to lateral impact, Journal of Constructional Steel Research. (2017) 138, 642–662, https://doi.org/10.1016/j.jcsr.2017.08.015, 2-s2.0-85029573778.
10.1016/j.jcsr.2017.08.015
Web of Science® Google Scholar
17 European Committee For Standardization, BS EN 1991-1-7: 2006: Eurocode 1: Actions on Structures-Part 1–7: General Actions-Accidental Actions, 2010, European Committee For Standardization, London, UK.
Google Scholar
18 Ma H., Cao Z., Shi X., and Zhou J., Dynamic amplification factor of shear force on bridge columns under impact load, Shock and Vibration. (2019) 2019, 14, 9483246, https://doi.org/10.1155/2019/9483246, 2-s2.0-85063590073.
10.1155/2019/9483246
Web of Science® Google Scholar
19 Sha Y. and Hao H., Laboratory tests and numerical simulations of barge impact on circular reinforced concrete piers, Engineering Structures. (2013) 46, 593–605, https://doi.org/10.1016/j.engstruct.2012.09.002, 2-s2.0-84866649365.
10.1016/j.engstruct.2012.09.002
Web of Science® Google Scholar
20 Thilakarathna H. M. I., Thambiratnam D. P., Dhanasekar M., and Perera N., Numerical simulation of axially loaded concrete columns under transverse impact and vulnerability assessment, International Journal of Impact Engineering. (2010) 37, no. 11, 1100–1112, https://doi.org/10.1016/j.ijimpeng.2010.06.003, 2-s2.0-77955560788.
10.1016/j.ijimpeng.2010.06.003
Web of Science® Google Scholar
21 Thilakarathna I., Thambiratnam D., Dhanasekar M., and Perera N., Shear-critical impact response of biaxially loaded reinforced concrete circular columns, ACI Structural Journal. (2013) 110, no. 4, 565–574, https://doi.org/10.14359/51685742.
10.14359/51685742
Web of Science® Google Scholar
22 Thilakarathna H. M. I., Vulnerability assessment of reinforced concrete columns subjected to vehicular impacts, 2010, Queensland University of Technology, Brisbane, Australia, Ph.D. thesis.
Google Scholar
23 Zhao W., Qian J., and Jia P., Peak response prediction for RC beams under impact loading, Shock and Vibration. (2019) 2019, 12, 6813693, https://doi.org/10.1155/2019/6813693, 2-s2.0-85061323650.
10.1155/2019/6813693
Web of Science® Google Scholar
24 Biggs J. M., Introduction to Structural Dynamics, 1964, McGraw-Hill, New York, NY, USA.
Google Scholar
25 Qasrawi Y., Heffernan P. J., and Fam A., Dynamic behaviour of concrete filled FRP tubes subjected to impact loading, Engineering Structures. (2015) 100, 212–225, https://doi.org/10.1016/j.engstruct.2015.06.012, 2-s2.0-84934982090.
10.1016/j.engstruct.2015.06.012
Web of Science® Google Scholar
26 Sha Y., Analysis, assessment and mitigation of barge impact load on bridge piers, 2013, The University of Western Australia, Perth, Australia, Ph.D. thesis.
Google Scholar
27 Astarlioglu S., Krauthammer T., Morency D., and Tran T. P., Behavior of reinforced concrete columns under combined effects of axial and blast-induced transverse loads, Engineering Structures. (2013) 55, 26–34, https://doi.org/10.1016/j.engstruct.2012.12.040, 2-s2.0-84886435945.
10.1016/j.engstruct.2012.12.040
Web of Science® Google Scholar
28 Al-Thairy H., A modified single degree of freedom method for the analysis of building steel columns subjected to explosion induced blast load, International Journal of Impact Engineering. (2016) 94, 120–133, https://doi.org/10.1016/j.ijimpeng.2016.04.007, 2-s2.0-84971595029.
10.1016/j.ijimpeng.2016.04.007
Web of Science® Google Scholar
29 Shope R. L., Response of wide flange steel columns subjected to constant axial load and lateral blast load, 2006, Virginia Tech, Blacksburg, VA, USA, Ph.D. thesis.
Google Scholar
30 Heng P., Hjiaj M., Battini J.-M., and Limam A., An enhanced SDOF model to predict the behaviour of a steel column impacted by a rigid body, Engineering Structures. (2017) 152, 771–789, https://doi.org/10.1016/j.engstruct.2017.08.061, 2-s2.0-85042169401.
10.1016/j.engstruct.2017.08.061
Web of Science® Google Scholar
31 Zhang J.-h., Chen B., and Jiang S.-y., A simplified model to predict blast response of CFST columns, Journal of Central South University. (2017) 24, no. 3, 683–691, https://doi.org/10.1007/s11771-017-3469-x, 2-s2.0-85017442669.
10.1007/s11771-017-3469-x
CAS Web of Science® Google Scholar
32 Nassr A. A., Razaqpur A. G., Tait M. J., Campidelli M., and Foo S., Strength and stability of steel beam columns under blast load, International Journal of Impact Engineering. (2013) 55, 34–48, https://doi.org/10.1016/j.ijimpeng.2012.11.010, 2-s2.0-84872285298.
10.1016/j.ijimpeng.2012.11.010
Web of Science® Google Scholar
33 Feng S. Z. and Han X., A novel multi-grid based reanalysis approach for efficient prediction of fatigue crack propagation, Computer Methods in Applied Mechanics and Engineering. (2019) 353, 107–122, https://doi.org/10.1016/j.cma.2019.05.001, 2-s2.0-85066072519.
10.1016/j.cma.2019.05.001
Web of Science® Google Scholar
34 Hallquist J. O., LS-DYNA Keyword User Manual-Nonlinear Dynamic Analysis of Structures, 2006, Livermore Software Technology Corporation, Livermore, CA, USA.
Google Scholar
35 Wang H., Yang B., Zhou X.-H., and Kang S.-B., Numerical analyses on steel beams with fin-plate connections subjected to impact loads, Journal of Constructional Steel Research. (2016) 124, 101–112, https://doi.org/10.1016/j.jcsr.2016.05.016, 2-s2.0-84971530405.
10.1016/j.jcsr.2016.05.016
Web of Science® Google Scholar
36 LS-DYNA, Keyword User’s Manual, 2014, Livermore Software Technology Corporation-LSTC), Livermore, CA, USA.
Google Scholar
37 Cowper G. R. and Symonds P. S., Strain-hardening and Strain-Rate Effects in the Impact Loading of Cantilever Beams, 1957, Brown University, Providence, RI, USA, https://doi.org/10.21236/ad0144762.
10.21236/AD0144762
Google Scholar
38 Abramowicz W. and Jones N., Dynamic axial crushing of square tubes, International Journal of Impact Engineering. (1984) 2, no. 2, 179–208, https://doi.org/10.1016/0734-743x(84)90005-8, 2-s2.0-0021291788.
10.1016/0734-743X(84)90005-8
Google Scholar
39 Qu H., Li G., Chen S., Sun J., and Sozen M. A., Analysis of circular concrete-filled steel tube specimen under lateral impact, Advances in Structural Engineering. (2011) 14, no. 5, 941–951, https://doi.org/10.1260/1369-4332.14.5.941, 2-s2.0-80053489780.
10.1260/1369-4332.14.5.941
Web of Science® Google Scholar
40 Wang Y., Qian X., Liew J. Y. R., and Zhang M.-H., Experimental behavior of cement filled pipe-in-pipe composite structures under transverse impact, International Journal of Impact Engineering. (2014) 72, 1–16, https://doi.org/10.1016/j.ijimpeng.2014.05.004, 2-s2.0-84902178697.
10.1016/j.ijimpeng.2014.05.004
CAS Web of Science® Google Scholar
41 Wang Y., Qian X., Liew J. Y. R., and Zhang M.-H., Impact of cement composite filled steel tubes: an experimental, numerical and theoretical treatise, Thin-walled Structures. (2015) 87, 76–88, https://doi.org/10.1016/j.tws.2014.11.007, 2-s2.0-84912565421.
10.1016/j.tws.2014.11.007
Web of Science® Google Scholar
42 Deng Y. and Tuan C. Y., Design of concrete-filled circular steel tubes under lateral impact, ACI Structural Journal. (2013) 110, no. 4, 691–701, https://doi.org/10.14359/51685754.
10.14359/51685754
Web of Science® Google Scholar
43 Comite Euro-International du Beton, CEB-FIP Model Code 1990, 1993, Redwood Books, Trowbridge, UK.
10.1680/ceb-fipmc1990.35430
Google Scholar
44 Malvar L. J. and Ross C. A., Review of strain rate effects for concrete in tension, ACI Material Journal. (1998) 95, no. 6, 735–739.
CAS Web of Science® Google Scholar
45 Clough R. W. and Penzien J., Dynamics of Structures, 1993, McGraw-Hill, New York, NY, USA.
Google Scholar
46 Smith P. D. and Hetherington J. G., Blast and Ballistic Loading of Structures, 1994, Butterowrth-Heinemenn, Oxford, UK.
Google Scholar
47 Zhang F., Wu C., Wang H., and Zhou Y., Numerical simulation of concrete filled steel tube columns against BLAST loads, Thin-Walled Structures. (2015) 92, 82–92, https://doi.org/10.1016/j.tws.2015.02.020, 2-s2.0-84925018452.
10.1016/j.tws.2015.02.020
Web of Science® Google Scholar
48 Han L. H. and Yang Y. F., The Technology of Modern Concrete Filled Steel Tube structures, 2004, China Building Industry Press, Beijing, China, in Chinese.
Google Scholar
49 Zhong S. T., Unified Theory of Concrete Filled Steel Tube: Research and application, 2006, Tsinghua University Press, Beijing, China, in Chinese.
Google Scholar

Citing Literature

All articles

Deflection Calculation Based on SDOF Method for Axially Loaded Concrete-Filled Steel Tubular Members Subjected to Lateral Impact

Abstract

1. Introduction

2. Development of FEA Model and Experimental Validation

2.1. Finite Element Analysis Model

2.2. Introduction to Experimental Tests

2.3. Comparison of Simulation and Test Results

3. Influence of Axial Force on Impact Response for CFST Members

3.1. Variation Pattern of Impact Force

3.2. Equivalence Principle of Impact Force

4. Development of SDOF Method considering Axial Force

4.1. Equivalent SDOF Model considering Axial Force

4.2. Derivation of Conversion Factors

4.3. Derivation of Resistance Function

4.4. Dynamic Differential Equation of the Equivalent SDOF Model

5. Assessment of SDOF Method considering Axial Force

5.1. Result Comparisons between the Proposed Calculation Method and Numerical Simulation

5.2. Accuracy Analysis of the Proposed Calculation Method

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Deflection Calculation Based on SDOF Method for Axially Loaded Concrete-Filled Steel Tubular Members Subjected to Lateral Impact

Abstract

1. Introduction

2. Development of FEA Model and Experimental Validation

2.1. Finite Element Analysis Model

2.2. Introduction to Experimental Tests

2.3. Comparison of Simulation and Test Results

3. Influence of Axial Force on Impact Response for CFST Members

3.1. Variation Pattern of Impact Force

3.2. Equivalence Principle of Impact Force

4. Development of SDOF Method considering Axial Force

4.1. Equivalent SDOF Model considering Axial Force

4.2. Derivation of Conversion Factors

4.3. Derivation of Resistance Function

4.4. Dynamic Differential Equation of the Equivalent SDOF Model

5. Assessment of SDOF Method considering Axial Force

5.1. Result Comparisons between the Proposed Calculation Method and Numerical Simulation

5.2. Accuracy Analysis of the Proposed Calculation Method

6. Conclusions

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information