1. Introduction

As one of the aircraft’s important components, the brake system mainly makes full use of the friction between the tire and the ground to make the aircraft stop on the runway quickly and safely. The brake system can be used in the taking off, landing, moving, and stopping on the ground stages of the aircraft, which is an important guarantee for aircraft’s safe operation [1]. The brake hydraulic system of aircraft is mainly composed of pressure servo valves, pressure sensitive elements, electromagnetic lock, oil cleaning elements, check valves, solenoid valves, and other parts, in which the performance of various electrohydraulic pressure servo valves determine the performance of the whole brake system.

The electrohydraulic pressure servo valve is essentially a relief valve, after receiving the input electric control signal, which outputs corresponding modulated pressure. The pressure servo valve was first used in the aircraft brake system in 1950; the two-stage pressure servo valve designed and developed in the world mainly includes nozzle flapper pressure valve, jet pipe pressure valve, deflector jet pressure valve, rotary direct drive pressure valve, etc. But at present, the pressure valve widely used in the brake hydraulic system of civil and military aircraft mainly includes nozzle flapper pressure valve and jet pipe pressure valve [2]. The outstanding advantages of the nozzle flapper pressure servo valve (NFPSV) contain three aspects: the inertia of flapper is small, the offset distance is small, there is no effect of the frictional pairs, so its dynamic response speed is fast, its control sensitivity is high, its linearity is good, and its zero drift is small. But the outstanding deficiency of NFPSV is the poor contamination resistant capability.

As we all know, the hydraulic components are sensitive to oil contamination. The data show 70%–80% of failures are caused by oil contamination, that is, oil contamination is always the fatal injury of the hydraulic control system. The distance between nozzle and receiver of jet pipe pressure valve’s pilot stage is 0.2 mm–0.4 mm, while the distance between nozzle and flapper of nozzle flapper pressure valve’s pilot stage is only 0.03–0.05 mm, which determines that the contamination resistant capability of the latter is far lower than that of the jet pipe pressure valve, and the oil cleanliness is required to be no lower than that of NAS6 [3–5]. In actual service, the flapper deflection and erosion wear will cause the dynamic change of erosion distance between nozzle and flapper. Oil deterioration will lead to the dynamic aggravation of erosive wear course, which determines that the erosion wear of nozzle flapper pressure valve’s pilot stage is a dynamic process and finally induces the performance degradation or even failure of the whole brake pressure valve. Therefore, it is of great significance to construct the model of nozzle flapper pressure valve and to study the dynamic erosion wear characteristics for predicting the performance degradation of the brake system and preventing the occurrence of major safety accidents.

The research on the nozzle flapper pressure valve has a long history, but the related published literature mainly focuses on the nozzle flapper flow valve, and the research contents mainly focus on the flow characteristics of its nozzle and secondary valve port, the dynamic characteristics of the flapper and torque motor, the hydrodynamic characteristics of the secondary valve core, the overall mathematical model construction and optimal design of the nozzle flapper valve, and the influence of structural parameters and process parameters on flow field and performance of nozzle flapper valve [6]. The research on the nozzle flapper pressure valve mainly focuses on the electromechanical converter and the application of new materials. However, scholars have carried out research studies on the influence of oil contamination on the same type of hydraulic products by means of experiments, theoretical modeling, and finite element simulation: Wang et al. [7] designed the contamination wear test system with the double nozzle flapper electrohydraulic flow valve as the research object. Through the pretest of the servo valve, it was determined that the sensitive stress was the oil contamination level, and the performance degradation parameters of the test were pressure gain and internal leakage. Finally, the test method that accelerated degradation of step stress in contamination wear is given. Aiming at the outstanding problem that the brake system of military aircraft has a high failure rate due to oil contamination, Wang et al. [8] elaborated the main failure mode of the nozzle flapper servo valve after oil contamination and provided the specific countermeasures to improve the reliability of the aircraft brake system. Du et al. [9] analyzed the common failure mechanism of the double nozzle flapper flow valve due to its low contamination resistant capability. By disassembling and analyzing a large number of fault servo valves, the main reason for the stuck failure of the nozzle flapper servo valve was obtained. Li et al. [10] analyzed the dominant progressive failure mode of the LEHA. The piecewise linearization method is applied to update the concentration of contaminated particles within the LEHA; the main contribution of the proposed model is the application of the dynamic concentration of contamination particles in erosion analysis of electrohydraulic servo valves (EHSVs), throttle valves, spool valves, and needle valves. Liu et al. [11] investigated the erosive behavior and influence of solid particles in hydraulic spool valve without notches. The CFD simulation of solid-liquid two-phase flow was carried out by discrete phase model (DPM) to analyze the erosion failure. The exact calculation method of the orifice area under erosion was discussed and put forward. For the erosion of jet pipe servo valve’s pilot stage, the trajectory of the oil and particles in the multiphase flow was analyzed by Yin et al. [12], and then the influence law of parameters such as the velocity and impact angle of particles to the erosion wear was carried out. Based on the Fluent software, Chu et al. [13] established a visual simulation model of nozzle to receiver in the pilot stage and then carried out simulation of erosion rate and calculation of the servo valve’s theoretical life. Based on the above, the main deficiencies about current research studies of the nozzle flapper pressure valve under oil contamination conditions are as follows: (1) most analyses about the influence of oil contamination to pilot stage are only qualitative analyses; (2) the real-time distance between nozzle and flapper is not considered; (3) the influence of oil contamination level’s change is not considered; and (4) the quantitative analysis of the service life of entire pressure valve under dynamic erosion wear conditions is not performed.

To solve these issues, this paper is focused on the dynamic erosion wear characteristics analysis and service life prediction of a NFPSV. Firstly, the structural feature and working principle of the nozzle flapper pressure valve are analyzed using the brake cavity as the load blind cavity; this is the basis of all research work. Secondly, the dynamics simulation model and the experiment system of the pressure valve are separately constructed; the purpose of the established NFPSV mathematical model validated by the experiment is to simulate and determine the threshold value of deterioration parameter that will induce the failure of pressure valve. Finally, the degradation process models induced by the dynamic erosion wear are established, and then the dynamic erosion wear characteristics under dynamic structural distance and contamination conditions are analyzed, which are combined with the failure threshold value determined by the dynamics simulation to finish the service life prediction of the nozzle flapper pressure valve.

2. Structural Feature and Working Principle of the NFPSV

The nozzle flapper pressure valve is composed of torque motor, nozzle flapper assembly, slide valve, return spring, and pressure feedback path. The structure of nozzle flapper pressure valve is shown in Figure 1, where R, P, J, and S represent the oil return port, slide valve pressure inlet, pilot stage pressure inlet, and brake port of the servo valve, respectively, P and J provide 21 MPa oil pressure for the servo valve, and when the brake port J is connected with the aircraft brake system, the brake cavity is a special blind cavity structure [14].

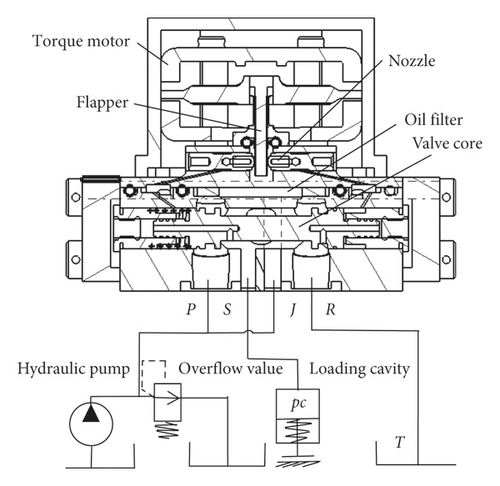
When the control signal is input to the coil of the servo valve, a control torque is generated in the armature assembly, which makes the armature assembly deflect anticlockwise, the flapper deviates to the right, and the clearances between the flapper and the two nozzles are different, so a control pressure difference is generated on the annular surface at both ends of the valve core, which makes the valve core move to the left; the oil return control edge is gradually closed, the oil inlet control edge is gradually opened, and the brake pressure is increased. When the control force acting on the valve core is balanced with the feedback force, the valve core is stable at a certain position (the oil inlet port, the brake port, and the oil return port are not mutually connected) and the servo valve outputs a brake pressure proportional to the input current to realize the pressure control with positive gain.

3. Mathematical Model of the NFPSV

3.1. Model Construction of the NFPSV

3.1.1. Balance Equation of the Torque Motor

The function of torque motor in servo valve is to convert electrical signal into mechanical motion, after receiving input current signal i_c, and output the final driving torque T_m:

$$ (1)

where K_t = (2aN_cϕ_g/L) is the middle position electromagnetic torque coefficient of torque motor; $$ is the electromagnetic spring stiffness of torque motor; a is the radius from armature shaft to center of guide magnet. L is the length of armature; N_c represents the coil turns; φ_g is the fixed flux; R_g is the reluctance; and θ is the deflection angle of the armature.

The stable process of armature assembly is the balance process of various moments acting on it, and the motion equation of armature assembly is as follows:

$$ (2)

where J_a is the moment inertia of armature assembly; B_a is the viscous damping coefficient of armature assembly; K_a is the stiffness of spring pipe; and T_L is the moment of flow force on the flapper, which is calculated as

$$ (3)

where P_p is the pressure difference of nozzle front cavities, which is also the pressure difference of valve core’s control cavities; A_p is the area of nozzle hole; C_p is the flow coefficient of variable orifice between the nozzle and flapper; x_d0 is the clearance between the nozzle and flapper; and P_s is the oil pressure of the pilot stage.

3.1.2. Displacement Equation of the Flapper

The flapper deflects under the action of torque motor, the deflecting angle is θ, and the displacement of flapper is x_d; their relation is expressed as follows:

$$ (4)

where r is the distance from the end of flapper to its rotating center.

3.1.3. Equation between the Flapper and Slide Valve

The nozzle flapper amplifier is a throttling hydraulic amplifier, the comprehensive characteristic equation of which is shown as

$$ (5)

where Q_p is the output flow; k_qp is the flow gain; and k_cp is the flow-pressure gain.

The nozzle flapper amplifier provides the power to drive the valve core. Ignoring the oil leak, the flow for valve core’s moving is deduced as

$$ (6)

where V_p is the single cavity volume of slide valve when the valve core is at the zero position and E_y is the bulk modulus of elasticity of oil.

The valve core is driven by combined action of the pressure difference of control cavity, the pressure difference of feedback cavity, and the return spring. When the valve core moves in the valve sleeve, the force it receives also includes inertia force, damping force, friction force, etc. Therefore, the dynamic equation of the nozzle flapper pressure valve’s valve core can be expressed as

$$ (7)

where x_v is the displacement of valve core; m_v is the quality of valve core; B_v is the viscous damping of valve core and load; A_v is the sectional area of control cavity; A_f is the sectional area of feedback cavity; K_h is the stiffness of return spring; P_s is the brake pressure; P_r is the return oil pressure; K_s is the stiffness of flow force; and F_f is the friction induced by contamination stagnation.

Based on equations (5)–(7), the relation between flapper and slide valve can be obtained and its Laplace transformation result is shown as

$$ (8)

3.1.4. Output Equation of the Slide Valve

When the flapper deflects in the positive direction, the pressure difference between the control cavities causes the valve core to move in the positive direction. The input high-pressure oil enters the brake cavity to increase the brake pressure. Simultaneously, the brake cavity is connected with the feedback cavity on one side of the valve core, and the return oil is connected with the feedback cavity on the other side to generate the pressure difference of the feedback cavity. Thus, the flow equation of slide valve can be obtained as

$$ (9)

where C_v is the flow coefficient; W is the area gradient of valve core opening; x_v is the displacement of spool core; x₀ is the overlap between spool core and spool sleeve; P_h is the supply oil pressure; and P_s is the brake pressure.

Furthermore, the relation between load flow Q_L and the brake cavity pressure P_s is shown as

$$ (10)

3.1.5. Mathematical Model of the Entire Valve

Based on equations (1)–(10), Laplace transformation is conducted; thus, the dynamic characteristics block diagram of the nozzle flapper pressure valve can be obtained as Figure 2.

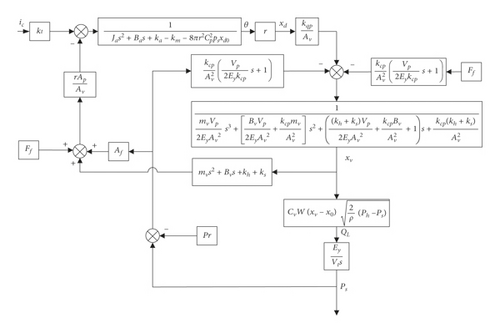
3.2. Model Validation of the NFPSV

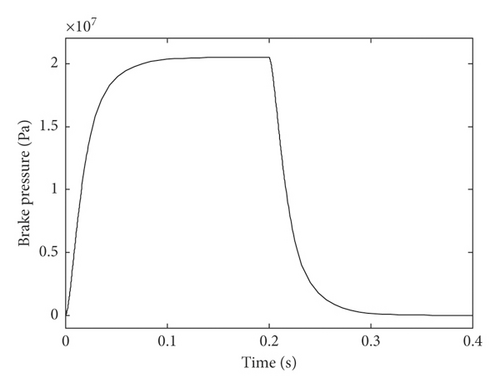
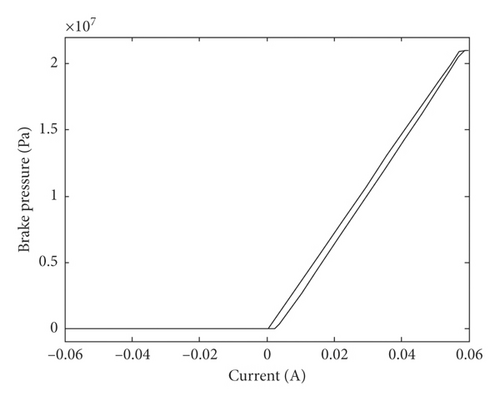
We build a MATLAB/SIMULINK simulation program and set the simulation parameters as Table 1. The pressure response of the nozzle flapper servo valve when the square wave signal is input is shown in Figure 3. It can be seen under the initial structural parameters that the system pressure quickly stabilizes at 21 MPa after receiving the 60 mA input signal. However, the output pressure will gradually deteriorate because of the extension of service time and the increase of the oil contamination level. Figure 4 shows the control brake pressure curve of nozzle flapper pressure valve; the brake pressure is not symmetrical to current because the slide valve structure is dissymmetric.

Table 1. The value of simulation parameters.

Parameter	Value
kt (Nm/A)	1.06
Ja (kg·m2)	1.2e − 7
Ba (Nm/rad·s)	7e − 5
ka (Nm/rad)	20.85
km (Nm/rad))	11.4
r (m)	0.017
Cp	0.7
ρ (kg/m3)	1070
xd0 (m)	5e − 5
kqp (m3/s/m)	9.2e − 2
Ey (Pa)	7e9
Av (m2)	2.87e − 5
Ap (m2)	2.83e − 7
Vp (m3)	4.28e − 8
mv (kg)	0.004
Vt (mL)	400
Bv (N/m/s)	50
kh (N/m)	20.6
ks (N/m)	2.58
Ff (N)	0
Pr (MPa)	0.5
Af (m2)	3.74e − 6
Ph (MPa)	21
W (m)	3.5e − 3

For providing an accurate threshold value of deterioration parameter inducing the failure of NFPSV, the experiment shown as Figure 5 is established to validate the dynamic simulation model shown in Figure 2. Figure 5(a) shows the hydraulic system principle diagram of the NFPSV’s test bench, in which the NFPSV selected by dotted line is shown in Figure 5(b), where P, S, and R are, respectively, the oil inlet port, brake port, and the oil return port. And the NFPSV, the pressure sensor, the check solenoid valve, and so on are connected with computer for measurement and control. During the experiment, the pressure of oil inlet port P and oil return port R are set as 21 MPa and 0.5 MPa, and then a square wave signal with amplitude of 60 mA and width of 0.2 s is sent to the NFPSV; also, the pressure response of brake port P is measured and analyzed.

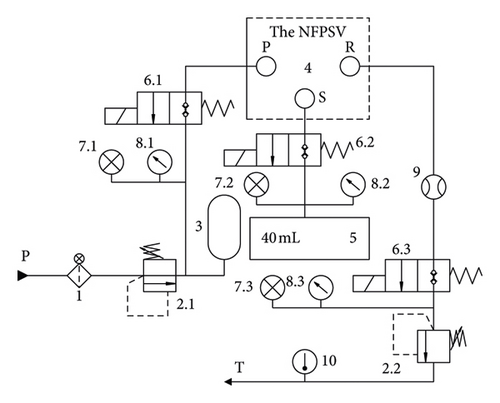
The comparison between simulation and experiment results is shown in Table 2; it can be seen that the maximum error between simulation and experiment results is 10%; also, the simulation value and experiment value of all performance indexes meet the engineering design requirements; therefore, we can conclude that the construction model is relatively reasonable and can be used in the service life prediction of NFPSV.

Table 2. The comparison between simulation and experiment.

Performance index	Simulation value	Experiment valve	Error (%)
Rise time (ms)	44	43	2.27
Fall time (ms)	45	47	4.44
Overshoot	0	0	0.00
Steady-state error	0	0	0.00
Linearity	2.8%	3%	7.14
Hysteresis	2%	1.80%	10.0
Dead zone (mA)	3.2	3.5	9.38

4. Dynamic Erosion Wear Characteristics of the NFPSV

4.1. The Dynamic Erosion Wear Characteristics of the NFPSV

4.1.1. Mathematical Model of the Degradation Process

(1) Basic Fluid Flow. Neglecting the heat conduction and compressibility of the flow, the numerical simulation of oil flow in the pilot stage of the nozzle flapper pressure valve can be performed through the mass conservation equation, the momentum conservation equation, and the standard k-ε transport equation. The mass conservation equation and momentum conservation equation are shown as follows:

$$ (11)

$$ (12)

where ρ is the fluid density; v is the fluid velocity; p is the pressure on fluid microelement; τ is the stress tensor; and ρg and F are gravitational body force and force body force.

(2) Discrete Phase Model. The volume fraction of solid particles in the hydraulic oil of servo valve is far less than 10%; thus, the discrete phase model (DPM) in Fluent can be used to simulate the movement of solid particles.

•  

  Particle force equation: analyzing the force of particles, the particle motion equation is established as equation (13), solving the differential equation in Lagrangian coordinate system to obtain the motion orbit of particles.

$$ (13)

•  

  where u_p and u are the velocity of particle and liquid; ρ_p and ρ are the densities of particle and liquid; F_d(u − u_p) is the drag force on particles; (g_x(ρ_p − ρ)/ρ_p) is the gravity of particles; and F_x is the additional force.

•  

  Wall collision model: the particles move with hydraulic oil and will be back to the flow field when bounced against the wall. The rebound coefficient proposed by Grant and Tabakoff [15] is used to describe the change of normal and tangential directions’ momentum of particles before and after collision with the wall.

$$ (14)

$$ (15)

•  

  Particle distribution model: different diameter particles are distributed in the contaminated oil, which can be expressed by the Rosin-Rammler equation:

$$ (16)

•  

  where d and $$ are the diameter and the mean diameter of particles (the value of $$ is obtained by noting the value of d at which y_d = e⁻¹ ≈ 0.368); y_d is the mass fraction with diameter greater than d; and n is the spread parameter, whose value is given as

$$ (17)

•  

  Erosion wear model: the model was proposed by Edwards et al. [16] through erosion experiments of sand to surface of carbon steel, which is used for the erosion rate calculation of servo valve:

$$ (18)

•  

  where R_e is the erosion rate; p is the particle number; m_p is the mass flow rate of particle; d_p is the diameter of particle; C(d_p) is the function of particle diameter; α is the impact angle between particle trajectory and wall; f(α) is the function of impact angle (the value of f(α) is shown in Table 3 [17]); b(v) is the function of particle’s relative velocity; and A_f is the area of particle impact wall.

Table 3. The relationship between f(α) and α.

Number	Angle α (°)	f(α) valve
1	0	0
2	20	0.8
3	30	1
4	45	0.5
5	90	0.4

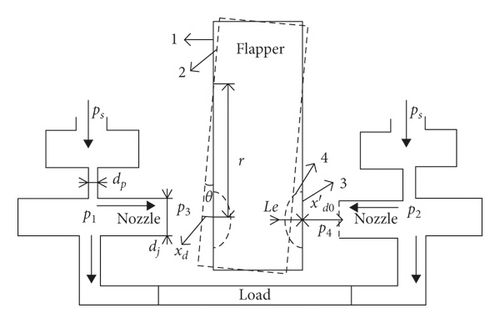
(3) Performance Degradation Mechanism Model. The nozzle flapper amplifier shown in Figure 6 is the core of nozzle flapper pressure valve, in which the oil enters the nozzle flapper amplifier with pressure p_s from the top and then ejects from the fixed orifice with p₁ and p₂ after accelerating and reducing pressure. When the flapper deflects x_d, the two settable orifices between the flapper and nozzles are no longer aligned, which results in the left back pressure p₁ and control pressure p₃ not being equal to the right p₂ and p₄.

On the other hand, the contaminated oil is ejected from the nozzle at a high speed and impact angle, and erosion will occur on the flapper, which causes material removal at the two sides of the flapper as shown in Figure 6. Therefore, the dynamic erosion wear characteristics of the NFPSV mainly need to consider the influence of oil contamination level and the real-time distance L_d between the nozzle and flapper. The former is conducted in the simulation by changing the contaminated particle’s mass flow rate, and the latter is calculated as follows:

$$ (19)

$$ (20)

where $$ is the initial clearance between the nozzle and flapper in the zero position; x_d0 is the clearance after erosion in the zero position; and L_e is the erosion distance.

With the increase of erosion distance, the performance of nozzle flapper pressure valve degrades gradually because the flow gain k_qp0 and flow-pressure coefficient k_cp0 of the nozzle flapper amplifier are changed, which are simulated as follows [18]:

$$ (21)

$$ (22)

where a is the liquid conductivity ratio between the settable orifice and the fixed orifice, which is determined by the following equation:

$$ (23)

4.1.2. The Simulation of Dynamic Erosion Wear Characteristics

The flow field from nozzle to flapper is relatively complicated, and the erosion rate is the largest; thus, the grid is encrypted in these places, and numerical simulation of erosion rate is performed using Fluent. Set 21 MPa pressure as the inlet boundary condition, 0.5 MPa pressure as the outlet boundary condition, 1070 kg/m³ as the oil density, and 0.0123 Pa·s as the oil dynamic viscosity. For improving the precision of calculation, the second-order upwind is selected and all the residuals are ensured less than 10⁻⁵ in the simulation. On the basis of continuous phase’s convergence, the discrete phase model is set up to simulate the movement of particles and calculate the erosion rate. The concentration and distribution of particles in the oil are determined according to the GJB420B standard. The particles distribution obey the Rosin-Rammler distribution, the average diameter of particles is set as 44 μm, the spread parameter is set as 1.52, and the discrete random walk model is used to deal with the interaction between the particles and the discrete vortex of the fluid; based on the above setting, the actual different operating conditions are numerically simulated as shown in Figure 7.

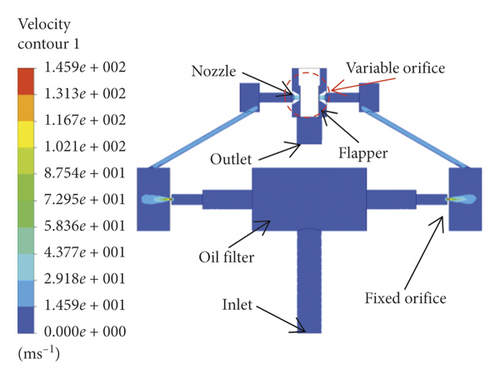
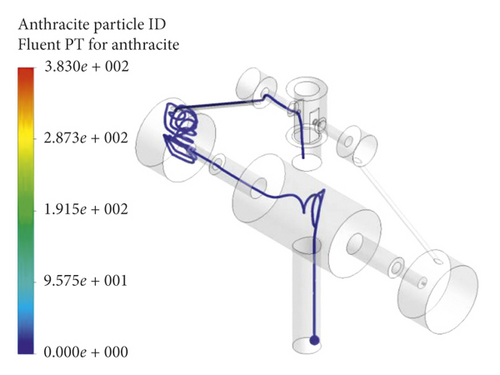
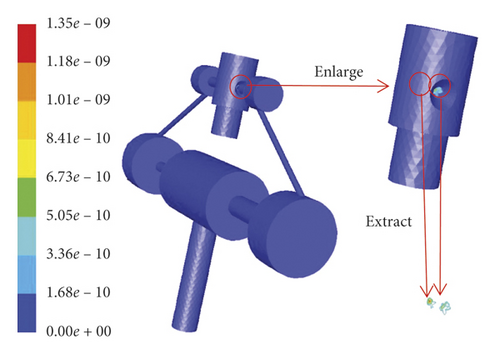
(1) Simulation When the Flapper Is in Zero Position. When the flapper is in zero position, the flow velocity distribution of the pilot stage is shown in Figure 8. The oil enters the oil filter from the inlet, decreases pressure and increases speed at the fixed orifice, flows through the nozzle and collides with the flapper, and finally goes back to the outlet. The trajectory of the single contaminated particle moving along is shown in Figure 9. It can be found the place where the most intense collision of particle is the projection area of the two nozzles on the flapper, and according to the model of erosion rate shown as equation (18) about the impact angle and velocity parameters, it can be inferred the erosion rate distribution is shown in in Figure 10, its maximum value is 1.35e − 9 (kg/m²s).

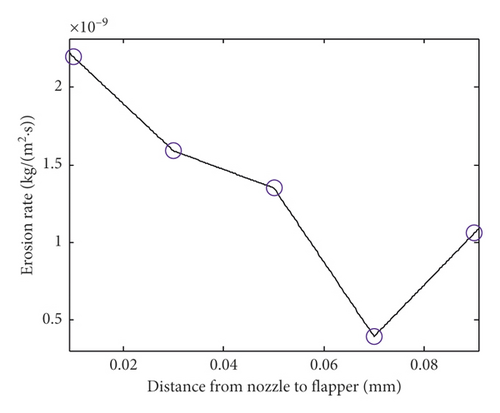
(2) The Relation between Erosion Rate and Distance from Nozzle to Flapper. According to the actual situation, several groups of erosion rate are calculated after changing the distance between nozzle and flapper; the relation curve shown in Figure 11 is fitted using MATLAB. It is easy to find that the erosion rate decreases on the whole with the increase of distance from 0.01 mm to 0.09 mm, but it reaches the minimum value 3.9e − 10 (kg·m²·s⁻¹) at 0.07 mm.

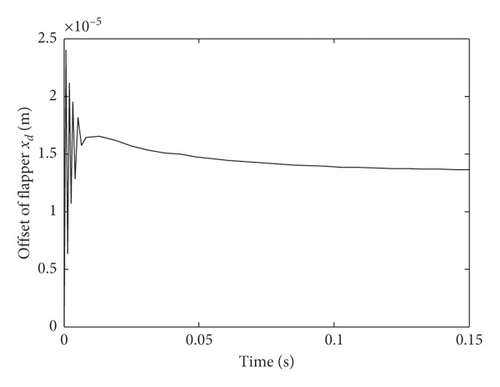
The initial clearance between nozzle and flapper $$ is 0.05 mm, and the distance between nozzle and flapper L_d also includes the offset of flapper x_d and the erosion distance L_e. Figure 12 shows the response of flapper under the step input of nozzle flapper pressure servo valve. In the starting time 0.01 s, the offset of flapper rises rapidly to 24 μm and fluctuates up and down and then stabilizes at 14 μm. Furthermore, the dynamic erosion rate under dynamic distance from nozzle to flapper can be obtained as Figure 13 by combining the relation between erosion rate and distance from nozzle to flapper and the response of flapper.

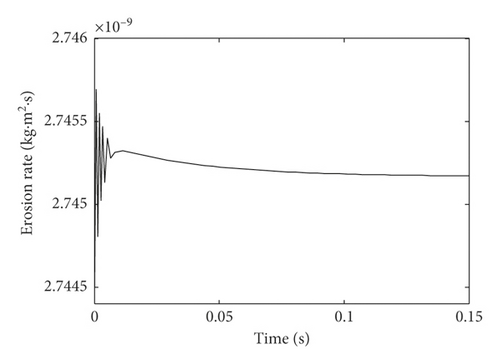
From Figure 13, we know the dynamic erosion rate response has the general same regulation as the offset of flapper. For the service life prediction of nozzle flapper pressure valve, the average erosion rate can be determined by integrating the dynamic erosion rate with respect to time and taking the average value about time. Assuming the erosion time is 120 seconds, the dynamic erosion rate is used to simulate the erosion length L_e (1.514e − 10 m), which is added into the clearance between nozzle and flapper to simulate again; it is found that the change of the average erosion rate is small, so it is ignored in the real-time distance between nozzle and flapper.

(3) The Relation between the Erosion Rate and Oil Contamination Level. The diameter of particles is set as 1 μm, 3 μm, 5 μm, 7 μm, 10 μm, 20 μm, 50 μm, 80 μm, and 100 μm, respectively, and other parameters are completely consistent. The simulation and fitting results shown in Figure 14 are the relation curves between erosion rate and particle diameter. It is not difficult to know that the erosion rate decreases with the increase of particle diameter and then increases to the maximum value when the particle diameter is 5 μm; after that, the erosion rate decreases and fluctuates under a small value. The reason is the erosion rate is mainly influenced by the number of particles in the oil and the impact energy of particles under the same condition of other parameters. Under the same mass flow rate, the number of small diameter particles is more than that of the bigger ones. Furthermore, the action of traction and other additional forces on the particles make the velocity of big diameter particles lower than the smaller ones, that is, the impact energy of big diameter particles is lower than that of the small diameter particles when their masses are equal. Based on above factors, the erosion rate decreases with the increase of the particle diameter on the whole and reaches the maximum value when the particle diameter is 5 μm.

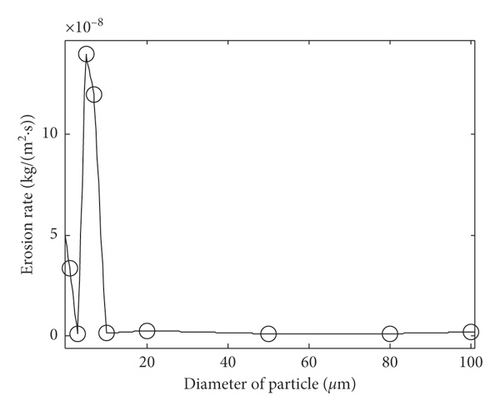
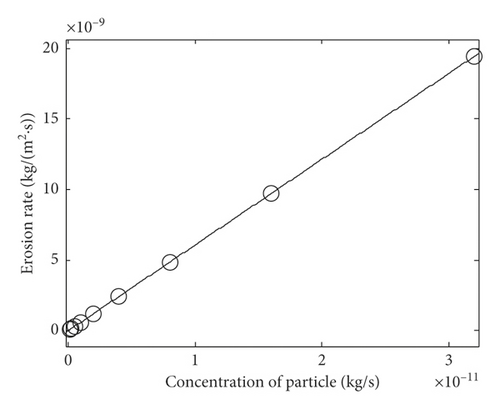
Figure 15 shows the relation curve between the erosion rate and concentration of particles, in which the particle diameter is fixed at 20 μm, the concentration of particles is set, respectively, as 1.25e − 13 kg/s, 2.5e − 13 kg/s, 5e − 13 kg/s, 1e − 12 kg/s, 2e − 12 kg/s, 4e − 12 kg/s, 8e − 12 kg/s, 16e − 12 kg/s, and 32e − 12 kg/s, and other parameters are completely consistent. The relationship between the increase of erosion rate and the increase of particle concentration is almost linear because in the effective range of particle concentration, the removal amount of the receiver as the target is directly proportional to the amount of contamination particles.

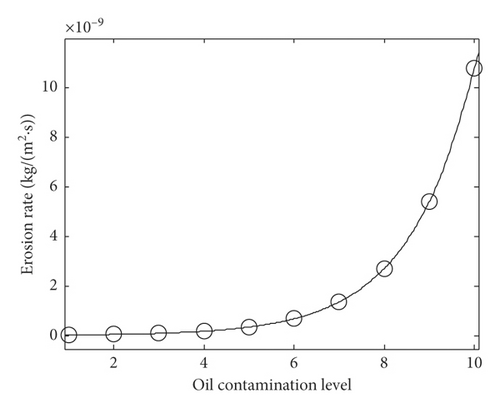
According to GJB420B, different oil contamination levels contain the same particle diameter distribution, but the particle concentration is different. The oil contamination level is set as 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10, respectively, the particle distribution obeys the Rosin-Rammler distribution, and other parameters are completely consistent. The simulation and fitting result shown in Figure 16 is the relation curve between oil erosion rate and oil contamination level. The erosion rate increases exponentially with the increase of oil contamination level. The reason for this result is that although the particle diameter distribution of different oil contamination levels is completely consistent, but the particle concentration between adjacent oil contamination level meets the relationship of twice according to GJB420B.

4.2. The Service Life Prediction of the NFPSV

Under the condition of oil contamination, the service life of the whole nozzle flapper pressure valve is determined by the dynamic erosion wear of the pilot stage consisting of nozzles and flapper. From the analysis and calculation, the dynamic erosion rate of pilot stage varies with the change of distance between the nozzles and flapper and the oil contamination level. Based on the dynamic erosion rate, the more practical service life of nozzle flapper pressure valve can be obtained by combining the failure threshold value of the key deterioration parameter x_d0.

4.2.1. The Determination of Failure Threshold Value

According to the regulation time, overshoot, and steady-state error of pressure valve’s dynamic response, the failure threshold value of its service life is determined. There are many kinds of actual systems and there is no unified system index requirement. In this paper, α_s is set as the multiple of required initial regulation time t_s, that is, with the decline of system performance, when the regulation time exceeds α_st_s, the system is considered failed to work. β_σ is the required overshoot index, γ_E is the ratio of required steady-state error E_Δ to the desired output of the system, and the failure threshold value of the system is determined according to equation (24). Select α_s = 2, β_σ = 25%, and γ_E = 20% to determine the threshold value of the parameters when the pressure valve fails.

$$ (24)

where p_a is the threshold value of valve failure parameter; p_αs is the threshold value determined by regulating time of valve failure parameter; p_βσ is the threshold value determined by overshoot of valve failure parameter; and p_γE is the threshold value determined by the steady-state error of valve failure parameter.

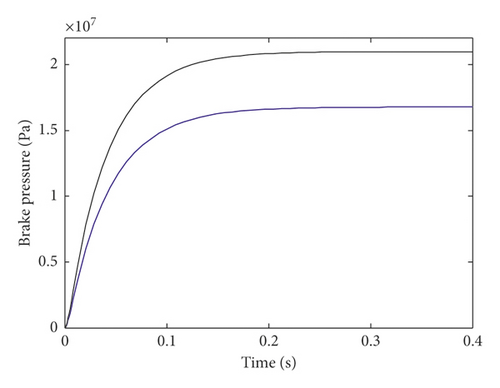
Figure 17 shows the step response of nozzle flapper pressure value; the black curve is under the initial clearance 50 μm and the blue curve is under the threshold clearance 61 μm between nozzle and flapper. From which, we conclude the change of clearance between nozzle and flapper can induce the dynamic performance degradation until the failure of NFPSV when the threshold value is determined by the 20% steady state error according to equation (24).

4.2.2. The Service Life Prediction Model

Figure 18 shows the mission profile of an aircraft’s brake system. In one flight cycle, the servo valve receives the electric control signal from the flight control system except the flight phase, in which the servo valve does not work. Therefore, in one flight cycle, the time of pilot stage’s erosion wear is 20 min, and then the service life of pilot stage’s erosion is carried out according to the following equations:

$$ (25)

$$ (26)

$$ (27)

where N_e is the erosion service life in flight takeoff landing; L_i is the erosion distance generated under the oil contamination level of i; E_i is the erosion rate under the oil contamination level of i; T₀ is the erosion time of single flight takeoff landing; ρ is the density of receivers; n_i is the maintenance number of oil contamination level from i to i + 1 (it can be determined according to the actual maintenance); and M is the number of flight takeoff and landing experienced in single maintenance.

4.2.3. The Service Life Prediction of Nozzle Flapper Pressure Valve under the Dynamic Erosion Wear

Actually, the service life prediction is relatively complex because the erosion wear progress of pilot stage is dynamic which is affected by the distance between nozzle and flapper and the oil contamination level. It is necessary to comprehensively consider the two factors. The dynamic erosion rate considering real-time distance and oil contamination is, respectively, calculated, then the erosion length that can be eroded is determined by the judgment rule, based on equations (25)–(27), the life under different oil contamination levels is determined, and finally the service life of nozzle flapper pressure valve is determined as shown in Table 4.

Table 4. The service life under erosion wear.

Item	Value
Oil contamination level	6	7	8	9
Dynamic erosion rate Ed (kg/(m2s))	2.7452 (×10−9)	5.490 (×10−9)	1.0981 (×10−8)	2.1962 (×10−8)
Erosion length (mm)	0.011
Number of flight takeoff landing M	500
Maintenance number ni	10
Life under single oil level (flight takeoff)	35729	17866	8932	4466
Erosion distance (μm)	1.5394	3.0787	6.1575	0.2244
Service life (flight takeoff landing)	15091

5. Conclusion

Conflicts of Interest

The authors declare that they have no conflicts of interest.